A New Decentralized PQ Control for Parallel Inverters in Grid-Tied Microgrids Propelled by SMC-Based Buck–Boost Converters
Abstract
:1. Introduction
- The proposed control-technique-based parallel DGs are completely decentralized. It is necessary that each DG be aware of its own power-sharing basis, which enables the proposed method to function as a plug-and-play solution due to its plug-and-play capacity.
- This paper proposes a robust discrete-time PQ control structure by designing digital PR controllers for the power and current control loops of each DG to improve the accuracy and load-sharing capability of the parallel inverters operating in an MG framework.
- Parallel decentralized mode SMC-based BB converters have been adopted to avoid voltage error and provide stable DC voltages for the related parallel inverters. SMC enables the controlled converters to operate flawlessly in high-signal operating conditions, allowing them to maintain efficient regulation and dynamic performance even when there are significant changes in the line, load, and system parameters.
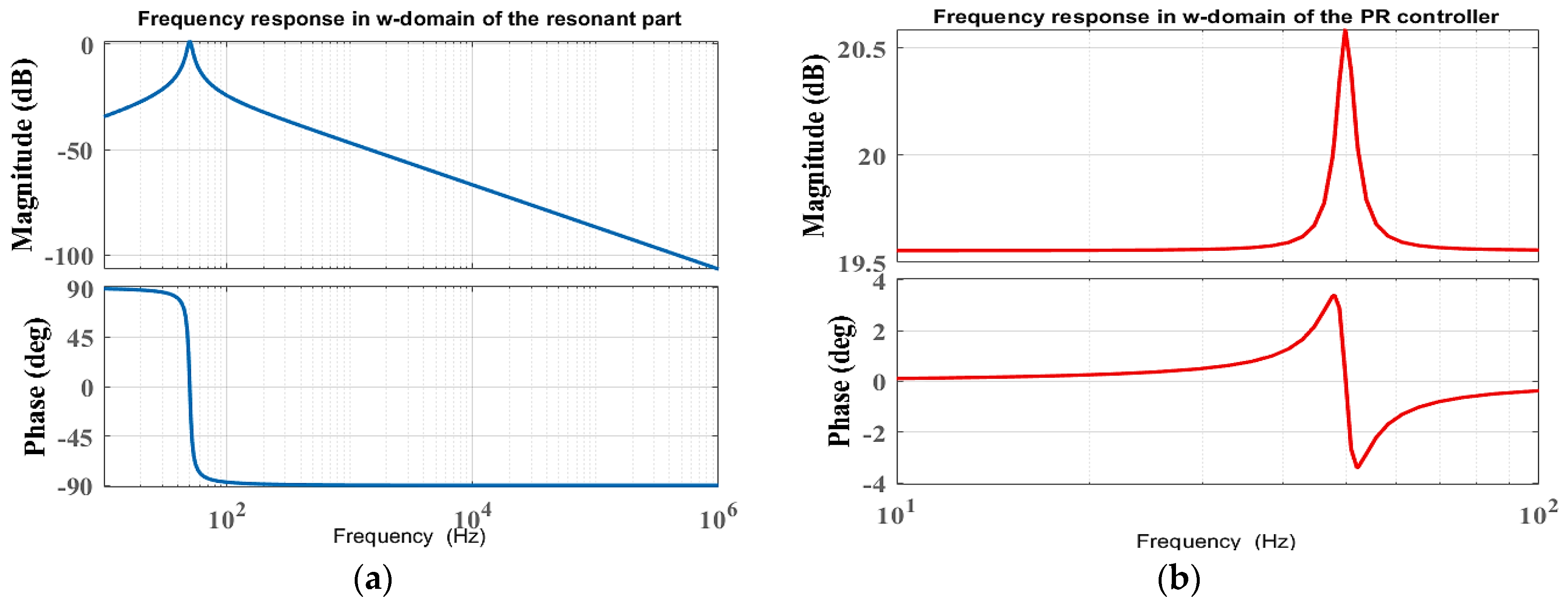
- The design process for digital power and current PR controller-based inverters is discussed in this paper. The procedure explains how to calculate resonant and proportional gains, as well as the resonant path coefficients, step by step. Its main contribution is to make researchers’ jobs easier by facilitating and assisting them in developing inverters that incorporate existing control strategies in a digital environment. A frequency-domain analysis of a digital PR controller will also be presented in the paper. A fictitious w-domain was used in this study. The inverter’s efficacy was demonstrated in the case study when it was used in conjunction with digital PR power and current controllers designed using the proposed procedure.
- The proposed technique is compared to MPC and droop control techniques. The proposed technique outperforms the other techniques in terms of overall power flow control performance.
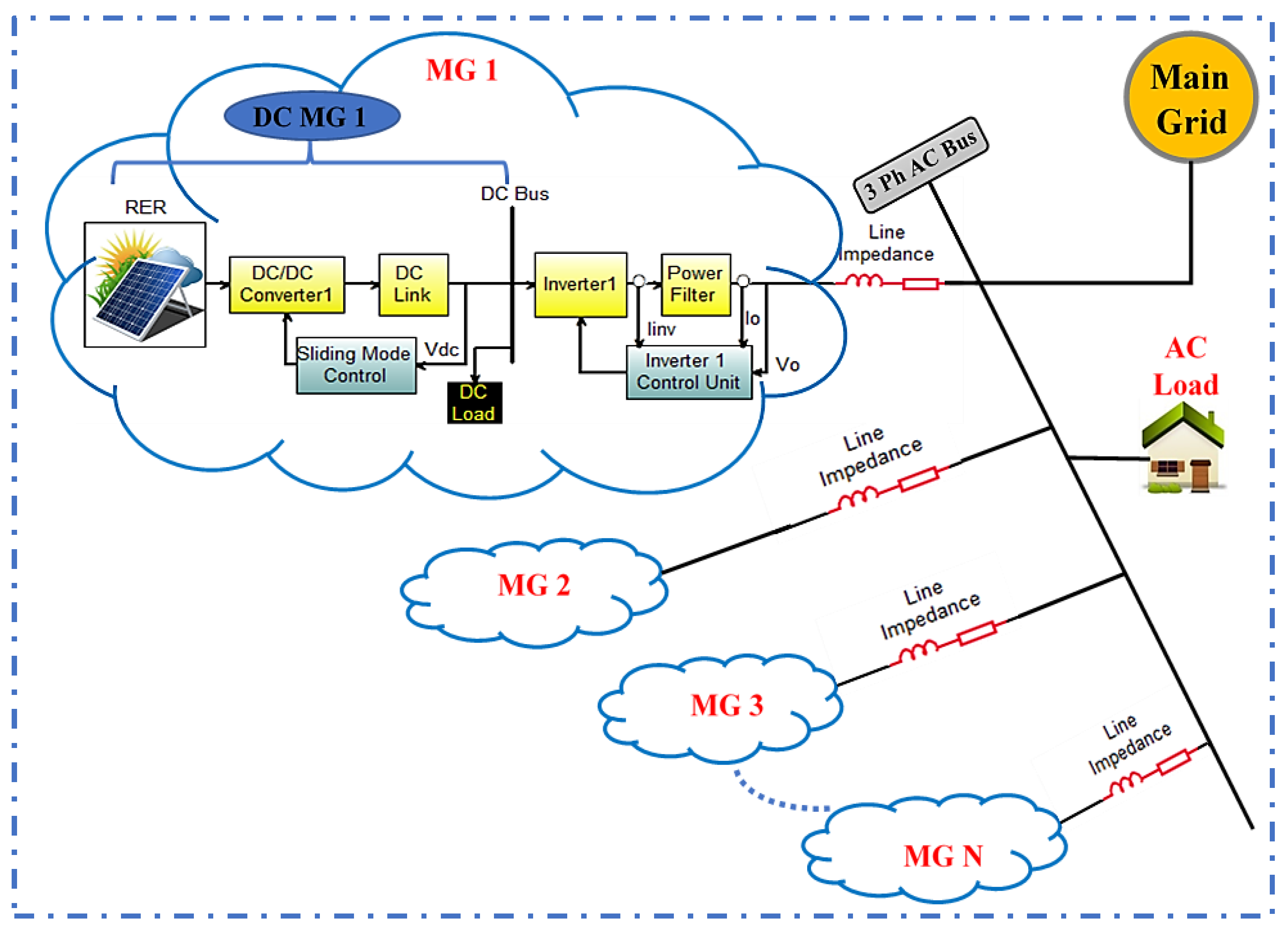
2. Grid-Tied Parallel DG System
3. Load-Sharing Power Flow Control
4. Proposed Control Technique
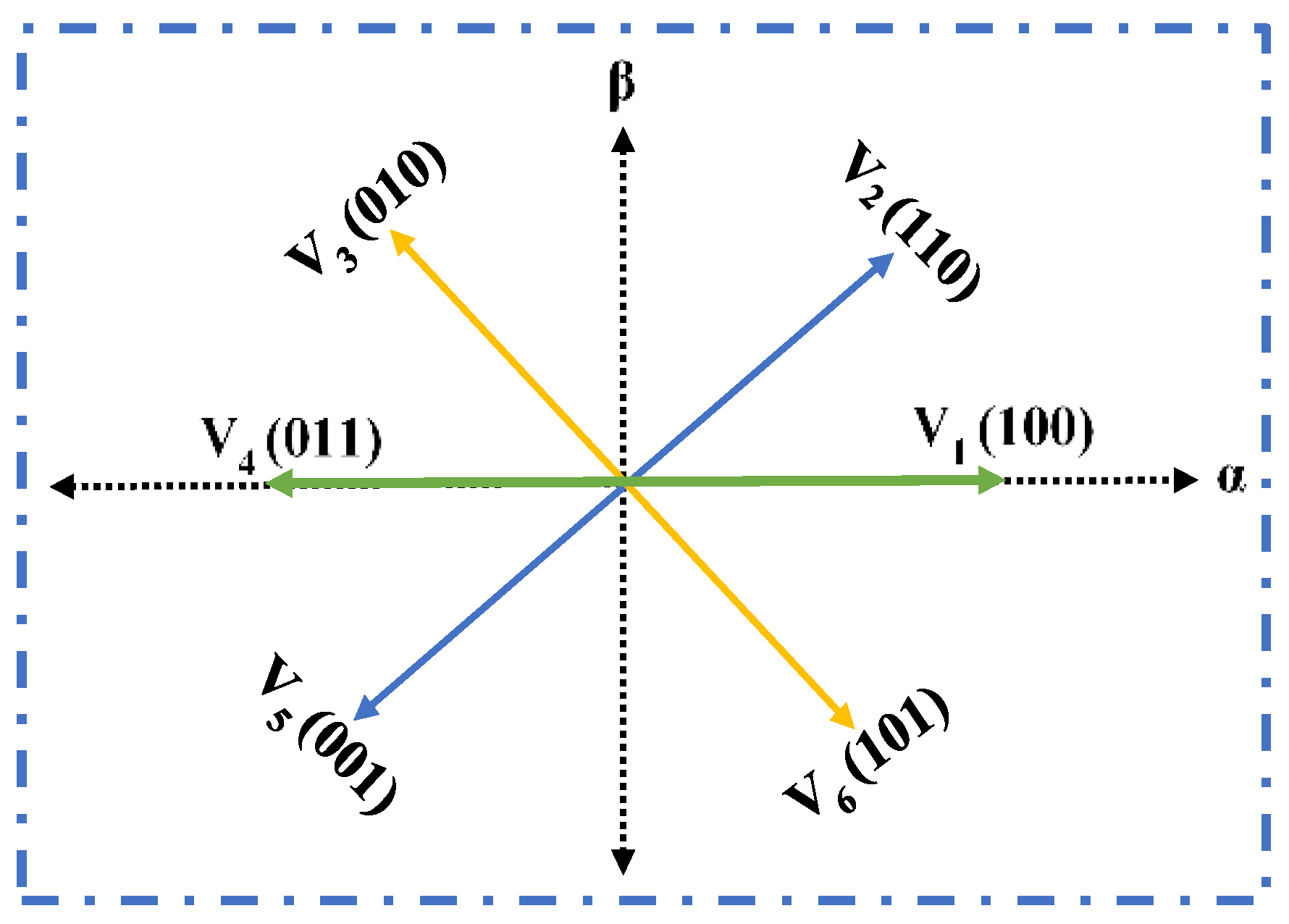
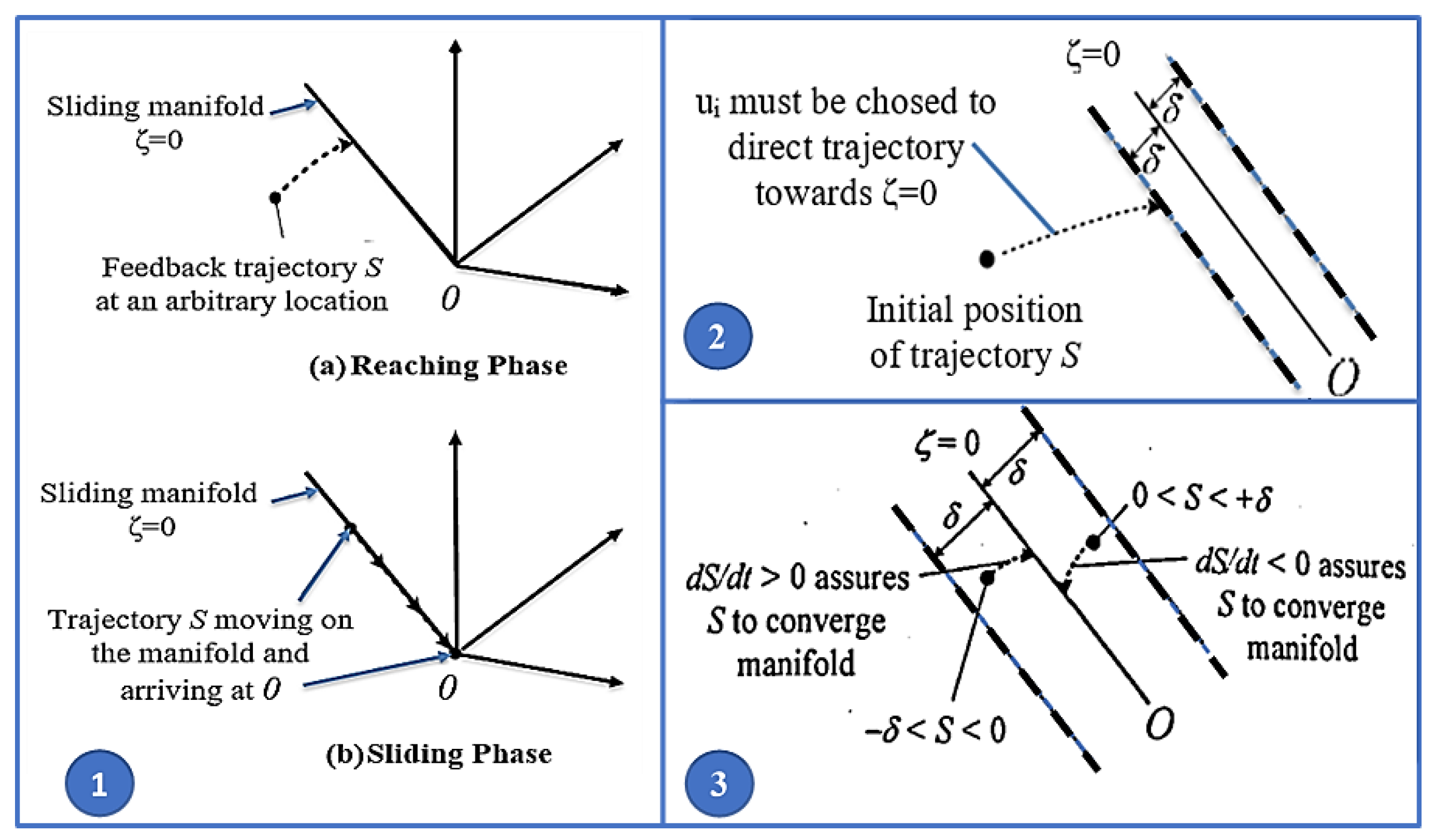
4.1. SMC for BB-Converter-Based DC MG Control
4.1.1. Control Gain Parameters of SMC
- (a)
- When MOSFET (switch SW) is ON, u = 1 and then
- (b)
- When switch SW is OFF, u = 0 and then
4.1.2. Sliding Coefficient Ratios
4.2. Decentralized PQ Control Based on Digital PR Controllers
5. Power Flow Control Based on MPC
5.1. System Modeling
5.2. Cost Function
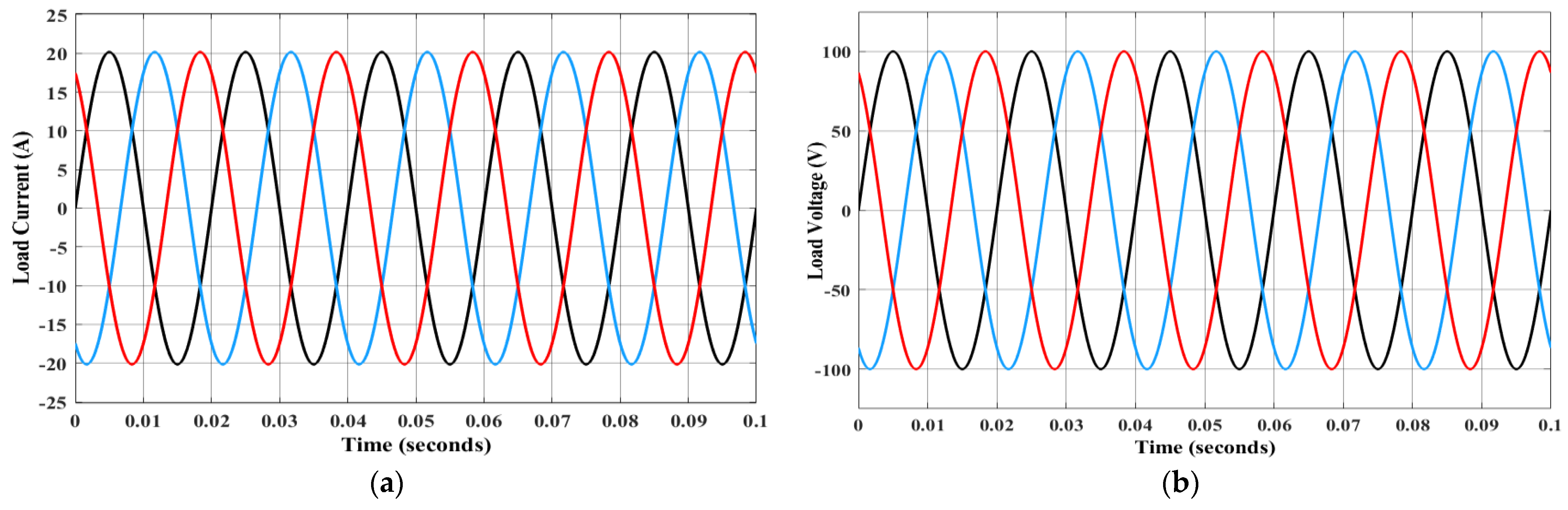
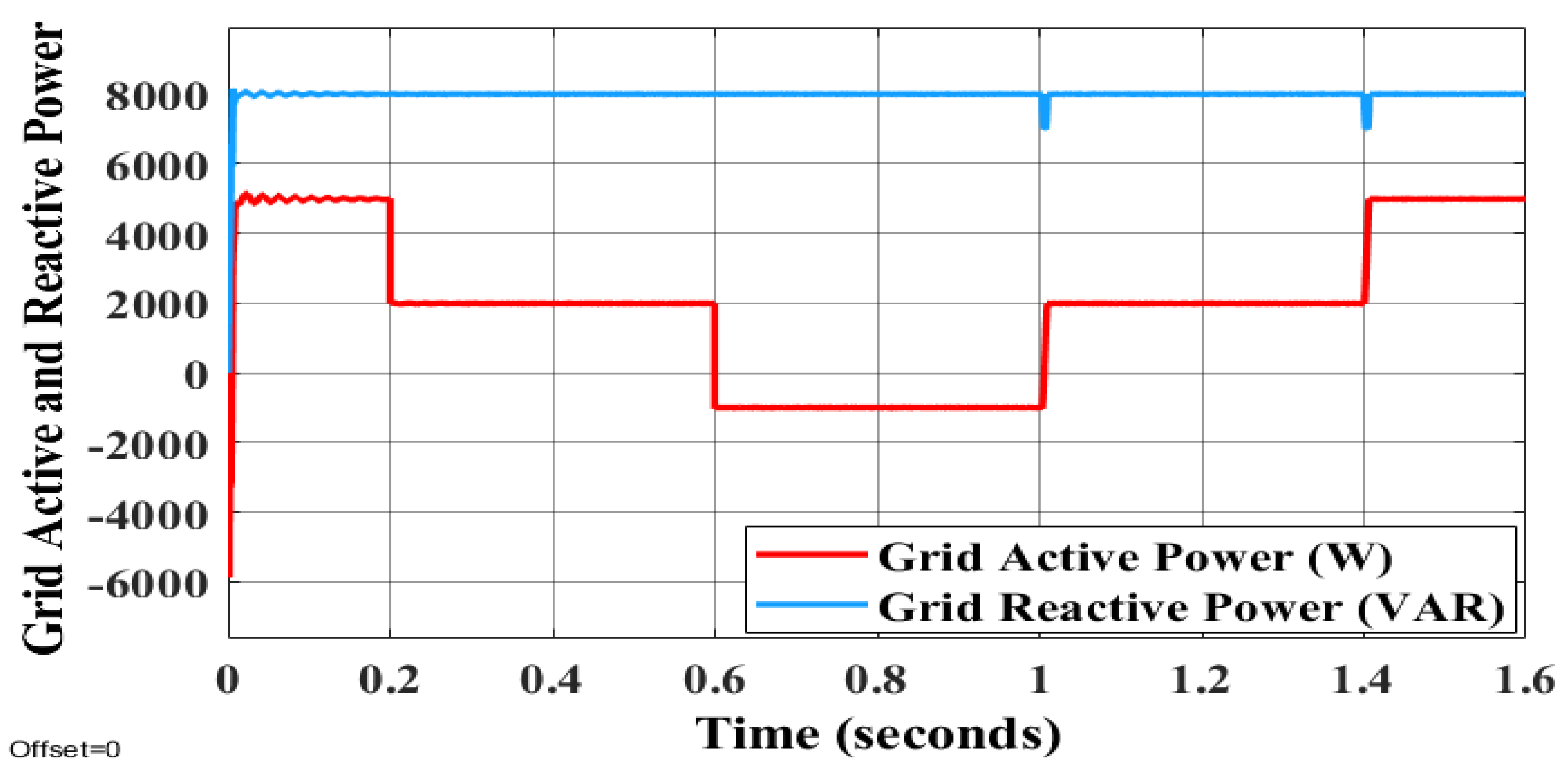
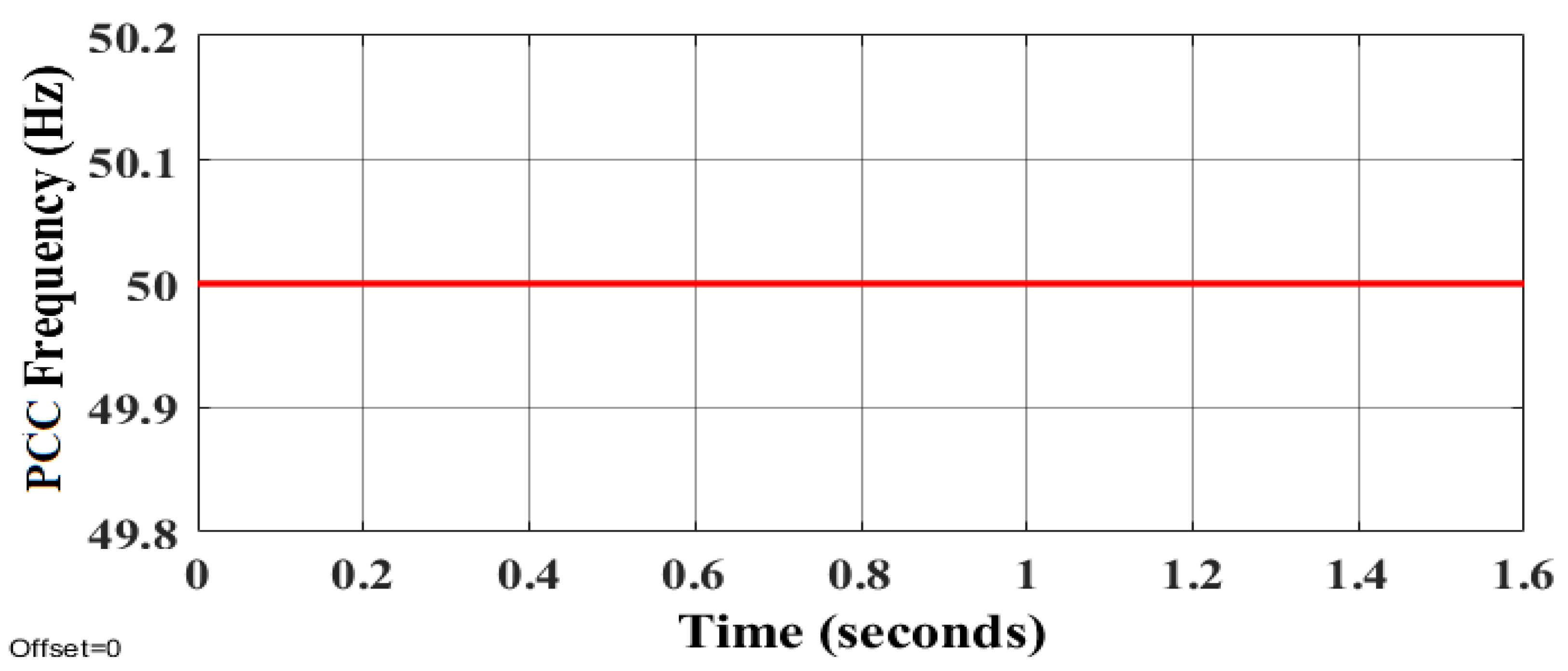
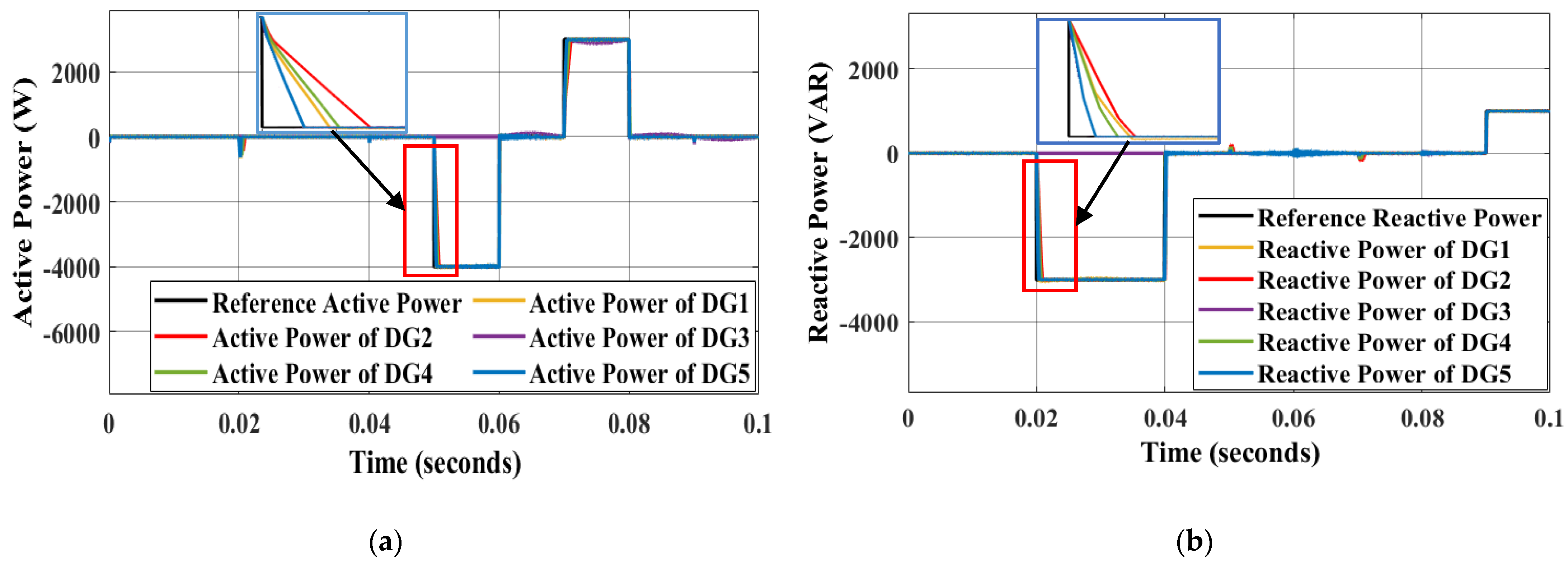
6. Simulation Results and Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jasim, A.M.; Jasim, B.H.; Bureš, V. A novel grid-connected microgrid energy management system with optimal sizing using hybrid grey wolf and cuckoo search optimization algorithm. Front. Energy Res. 2022, 10, 960141. [Google Scholar] [CrossRef]
- Jasim, A.M.; Jasim, B.H.; Kraiem, H.; Flah, A. A Multi-Objective Demand/Generation Scheduling Model-Based Microgrid Energy Management System. Sustainability 2022, 14, 10158. [Google Scholar] [CrossRef]
- Alhasnawi, B.N.; Jasim, B.H.; Issa, W.; Anvari-Moghaddam, A.; Blaabjerg, F. A New Robust Control Strategy for Parallel Operated Inverters in Green Energy Applications. Energies 2020, 13, 3480. [Google Scholar] [CrossRef]
- González, I.; Sánchez-Squella, A.; Langarica-Cordoba, D.; Yanine-Misleh, F.; Ramirez, V. A PI + Sliding-Mode Controller Based on the Discontinuous Conduction Mode for an Unidirectional Buck–Boost Converter with Electric Vehicle Applications. Energies 2021, 14, 6785. [Google Scholar] [CrossRef]
- Sahoo, S.K.; Sinha, A.K.; Kishore, N.K. Control techniques in AC, DC, and hybrid AC–DC microgrid: A Review. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 6, 738–759. [Google Scholar] [CrossRef]
- Xin, H.; Zhang, L.; Wang, Z.; Gan, D.; Wong, K.P. Control of island AC microgrids Using a fully distributed approach. IEEE Trans. Smart Grid 2014, 6, 943–945. [Google Scholar] [CrossRef]
- Jiang, Q.; Xue, M.; Geng, M. Energy management of microgrid in grid-connected and stand-alone modes. IEEE Trans. Power Syst. 2013, 28, 3380–3389. [Google Scholar] [CrossRef]
- Colet-Subirachs, A.; Ruiz-Alvarez, A.; Gomis-Bellmunt, O.; Alvarez-Cuevas-Figuerola, F.; Sudria-Andreu, A. Centralized and distributed active and reactive power control of a utility connected microgrid using IEC61850. IEEE Syst. J. 2011, 6, 58–67. [Google Scholar] [CrossRef]
- Jasim, A.M.; Jasim, B.H.; Mohseni, S.; Brent, A.C. Consensus-Based Dispatch Optimization of a Microgrid Considering Meta-Heuristic-Based Demand Response Scheduling and Network Packet Loss Characterization. Energy AI 2022, 11, 100212. [Google Scholar] [CrossRef]
- Alhasnawi, B.; Jasim, B. Adaptive Energy Management System for Smart Hybrid Microgrids. The 3rd Scientific Conference of Electrical and Electronic Engineering Researches (SCEEER). Iraqi J. Electr. Electron. Eng. 2020, 73–85. [Google Scholar] [CrossRef]
- Arafat, M.N.; Elrayyah, A.; Sozer, Y. An Effective Smooth Transition Control Strategy Using Droop-Based Synchronization for Parallel Inverters. IEEE Trans. Ind. Appl. 2015, 51, 2443–2454. [Google Scholar] [CrossRef]
- He, J.; Li, Y.; Harris, B. Investigation and active damping of multiple resonances in a parallel-inverter-based microgrid. IEEE Trans. Power Electron. 2013, 28, 234–246. [Google Scholar] [CrossRef]
- Choi, W.; Lee, W.; Sarlioglu, B. Effect of grid inductance on grid current quality of parallel grid-connected inverter system with output LCL filter and closed-loop control. In Proceedings of the 2016 IEEE Applied Power Electronics Conference and Exposition (APEC), Long Beach, CA, USA, 20–24 March 2016. [Google Scholar]
- Hu, J.; Zhu, J.; Guerrero, J.M. Model predictive control of smart microgrids. In Proceedings of the 2014 17th International Conference on Electrical Machines and Systems (ICEMS), Hangzhou, China, 22–25 October 2014; pp. 2815–2820. [Google Scholar]
- Quevedo, D.; Geyer, T. Performance of multistep finite control set model predictive control for power electronics. IEEE Trans. Power Electron. 2015, 30, 1633–1644. [Google Scholar]
- Aghdam, M.M.; Li, L.; Zhu, J.; Palizban, O. Finite Control Set Model Predictive Control-A Powerful Control Algorithm for Grid-Connected Power Converters. In Proceedings of the 2016 11th IEEE Conference on Industrial Electronics and Applications (ICIEA), Hefei, China, 5–7 June 2016. [Google Scholar]
- Shuai, Z.; Sun, Y.; Shen, Z.J.; Tian, W.; Tu, C.; Li, Y.; Yin, X. Microgrid stability: Classification and a review. Renew. Sustain. Energy Rev. 2016, 58, 167–179. [Google Scholar] [CrossRef]
- Jena, S.; Babu, C.; Mishra, G.; Naik, A. Reactive power compensation in inverter-interfaced distributed generation. In Proceedings of the 2011 International Conference on Energy, Automation, and Signal (ICEAS), Bhubaneswar, India, 28–30 December 2011; pp. 1–6. [Google Scholar]
- Hornik, T.; Zhong, Q. A Current-control strategy for voltage-source inverters in microgrids based on H∞ and repetitive control. IEEE Trans. Power Electron. 2011, 26, 943–952. [Google Scholar] [CrossRef]
- Zhang, N.; Tang, H.; Yao, C. A systematic method for designing a PR controller and active damping of the LCL filter for single-phase grid-connected PV inverters. Energies 2014, 7, 3934–3954. [Google Scholar] [CrossRef] [Green Version]
- Jeong, H.; Kim, G.; Lee, K. Second-order harmonic reduction technique for photovoltaic power conditioning systems using a proportional-resonant controller. Energies 2013, 6, 79–96. [Google Scholar] [CrossRef] [Green Version]
- Schonardie, M.; Coelho, R.; Schweitzer, R.; Martins, D. Control of the active and reactive power using dq0 transformation in a three-phase grid-connected PV system. In Proceedings of the 2012 IEEE International Symposium Industrial Electronic, Hangzhou, China, 23–26 September 2012; pp. 264–269. [Google Scholar]
- Bayo-Salas, A.; Beerten, J.; Rimez, J.; Van Hertem, D. Analysis of control interactions in multi-infeed VSC HVDC connections. IET Gener. Transm. Distrib. 2016, 10, 1336–1344. [Google Scholar] [CrossRef]
- Li, G.-J.; Ruan, S.-Y.; Ooi, B.-T.; Sun, Y.-Z.; Choi, S.S. Autonomous AC grid based on multi-infeed voltage source converter stations. Electr. Power Compon. Syst. 2010, 38, 558–574. [Google Scholar] [CrossRef]
- Kammer, C.; D’Arco, S.; Endegnanew, A.G.; Karimi, A. Convex optimization-based control design for parallel grid-connected inverters. IEEE Trans. Power Electron. 2019, 34, 6048–6061. [Google Scholar] [CrossRef] [Green Version]
- Mahdieh, S.; Qobad, S. Decentralized Multivariable Vector Current Control of Grid-connected Voltage Source Inverters. IFAC-PapersOnLine 2020, 53, 12410–12415. [Google Scholar]
- Jang, M.; Mihai, C.; Agelidis, V.G. A single-phase grid-connected fuel cell system based on a boost-inverter. IEEE Trans. Power Electron. 2013, 28, 279–288. [Google Scholar] [CrossRef]
- Adhikari, S.; Li, F.X. Coordinated V-f and P-Q control of solar photovoltaic generators with MPPT and battery storage in microgrids. IEEE Trans. Smart Grid 2014, 5, 1270–1281. [Google Scholar] [CrossRef]
- Lia, S.; Jaithwaa, I.; Suftaha, R.; Fua, X. Direct-current vector control of three-phase grid-connected converter with L, LC, and LCL filters. Electr. Power Compon. Syst. 2015, 43, 1644–1655. [Google Scholar] [CrossRef]
- Mahlagha, M.; Li, L.; Jianguo, Z. A Model Predictive Control of Parallel Inverters for Distributed Generations in Microgrids. In Proceedings of the IEEE International Conference on Power System Technology (POWERCON), Wollongong, Australia, 28 September–1 October 2016. [Google Scholar]
- Zhu, Y.; Zhuo, F.; Shi, H. Accurate Power Sharing Strategy for Complex Microgrid based on Droop Control Method. In Proceedings of the 5th IEEE ECCE Asia Downunder, Melbourne, Australia, 3–6 June 2013. [Google Scholar]
- He, J.; Li, Y.W.; Blaabjerg, F. An enhanced islanding microgrid reactive power, imbalance power, and harmonic power sharing scheme. IEEE Trans. Power Electron. 2015, 30, 3389–3401. [Google Scholar] [CrossRef]
- Zhong, Q.C.; Wang, Y.; Ren, B. UDE-based robust droop control of inverters in parallel operation. IEEE Trans. Ind. Electron. 2017, 64, 7552–7562. [Google Scholar] [CrossRef]
- Jasim, M.A.; Jasim, H.B. Grid-Forming and Grid-Following Based Microgrid Inverters Control. Iraqi J. Electr. Electron. Eng. 2022, 18, 111–131. [Google Scholar] [CrossRef]
- Siew-Chong, T.; Yuk-Ming, L.; Chi Kong, T. Sliding Mode Control of Switching Power Converters Techniques and Implementation; CRC Press Taylor & Francis Group: Boca Raton, FL, USA, 2011; ISBN 978-1-4398-3025-3. [Google Scholar]
- Tan, S.C.; Lai, Y.M.; Tse, C.K.; Cheung, M.K. A Fixed-Frequency Pulsewidth Modulation Based Quasi-Sliding-Mode Controller for Buck Converters. IEEE Trans. Power Electron. 2005, 20, 1379–1392. [Google Scholar] [CrossRef] [Green Version]
- Hanifi, G. Study of Sliding Mode Control of DC-DC Buck Converter. Energy Power Eng. 2011, 3, 401–406. [Google Scholar]
- Vadim, U.; Jurgen, G.; Jingxin, S. Sliding Mode Control in Electro-Mechanical Systems, 2nd ed.; CRC Press Taylor & Francis Group: Boca Raton, FL, USA, 2009; ISBN 978-1-4200-6560-2. [Google Scholar]
- Zaghba, L.; Borni, A.; Bouchakour, A.; Terki, N. Buck-Boost Converter System Modelling and Incremental Inductance Algorithm for Photovoltaic System via Matlab/Simulink. In Proceedings of the 2nd International Seminar on New and Renewable Energies, Paris, France, 7–8 May 2014; pp. 63–70. [Google Scholar]
- Salazar, P.; Ayala, P.; Jiménez, S.G.; Correa, A.F. Design of a Sliding Mode Control for a DC-to-DC Buck-Boost Converter. In Proceedings of the 25th Chinese Control and Decision Conference (CCDC), Guiyang, China, 25–27 May 2013; pp. 4661–4666. [Google Scholar]
- Tan, S.C.; Lai, Y.M.; Tse, C.K.; Martinez-Salamero, L. Special family of PWM-based sliding-mode voltage controllers for basic DC–DC converters in discontinuous conduction mode. IET Electr. Power Appl. 2007, 1, 64–74. [Google Scholar] [CrossRef] [Green Version]
- Lai, Y.M.; Tan, S.C.; Wu, C.K. Design of a PWM Based Sliding Mode Controlled Buck-Boost Converter in Continuous Conduction Mode. ECTI Trans. Electr. Eng. Electron. Commun. 2007, 5, 129–133. [Google Scholar]
- Khaild, A.; Hairik, H.A. Static and Dynamic Performances of PWM Based SMCBB Converter: Experimental Investigation. IOSR J. Electr. Electron. Eng. 2016, 11, 9–18. [Google Scholar]
- Khaild, A.; Hairik, H.A. Checking the Robustness of a PWM Sliding Mode Controlled DC/DC Buck-Boost Converter Using its Matlab/Simulink Model. In Proceedings of the 2016 Al-Sadeq International Conference on Multidisciplinary in IT and Communication Science and Applications (AIC-MITCSA), Baghdad, Iraq, 9–10 May 2016. [Google Scholar]
- Bilal, N.; Basil, H. A New Coordinated Control of Hybrid Microgrids with Renewable Energy Resources Under Variable Loads and Generation Conditions. Iraqi J. Electr. Electron. Eng. 2020, 16, 1–20. [Google Scholar] [CrossRef]
- Cha, H.; Vu, T.K.; Kim, J.E. Design and Control of Proportional-Resonant Controller Based Photovoltaic Power Conditioning System. In Proceedings of the 2009 IEEE Energy Conversion Congress and Exposition, San Jose, CA, USA, 20–24 September 2009. [Google Scholar]
- Shabib, G.; Abd-Elhameed, E.H.; Magdy, G. A New Approach to the Digital Implementation of Analog Controllers for a Power System Control. Int. J. Sci. Eng. Res. 2014, 5, 419–427. [Google Scholar]
- Busarello, T.D.C.; Pomilio, J.A.; Simoes, M.G. Design Procedure for a Digital Proportional-Resonant Current Controller in a Grid Connected Inverter. In Proceedings of the 2018 IEEE 4th Southern Power Electronics Conference (SPEC), Singapore, 10–13 December 2018. [Google Scholar]
- Jasim, M.A.; Jawad, M.R.; Ramzy, A.S. Design and Implementation of a Musical Water Fountain Based on Sound Harmonics Using IIR Filters. Int. J. Comput. Digit. Syst. 2020, 9, 319–333. [Google Scholar]
- Alhasnawi, B.N.N.; Jasim, B.H.; Issa, W.; Esteban, M.D. A Novel Cooperative Controller for Inverters of Smart Hybrid AC/DC Microgrids. Appl. Sci. 2020, 10, 6120. [Google Scholar] [CrossRef]
- Stefan, L. Internal Model–Based Control Strategies for Voltage Source Converters. Master’s Thesis, Graz University of Technology in Cooperation with Washington State University, Pullman, WA, USA, 2016. [Google Scholar]




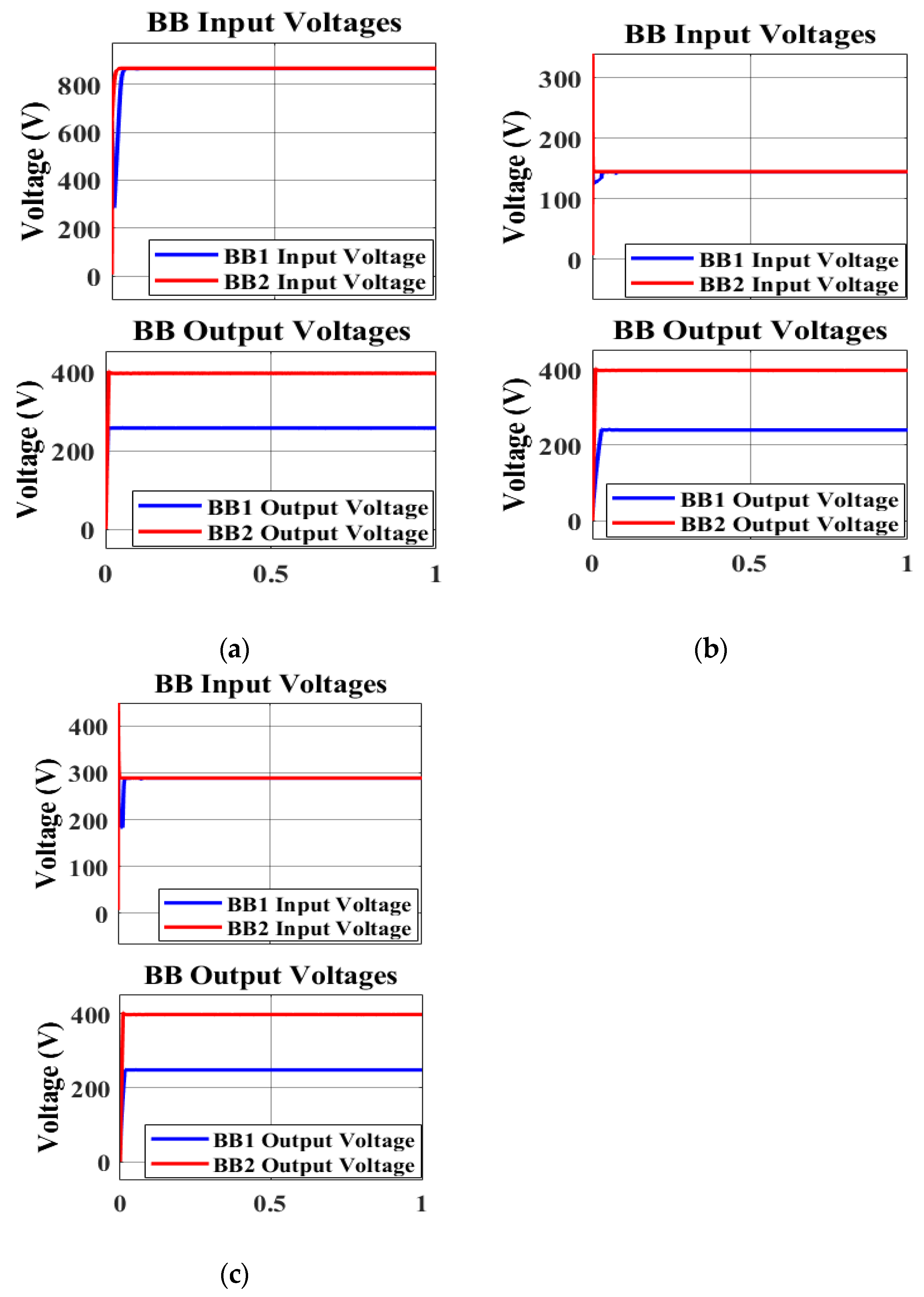

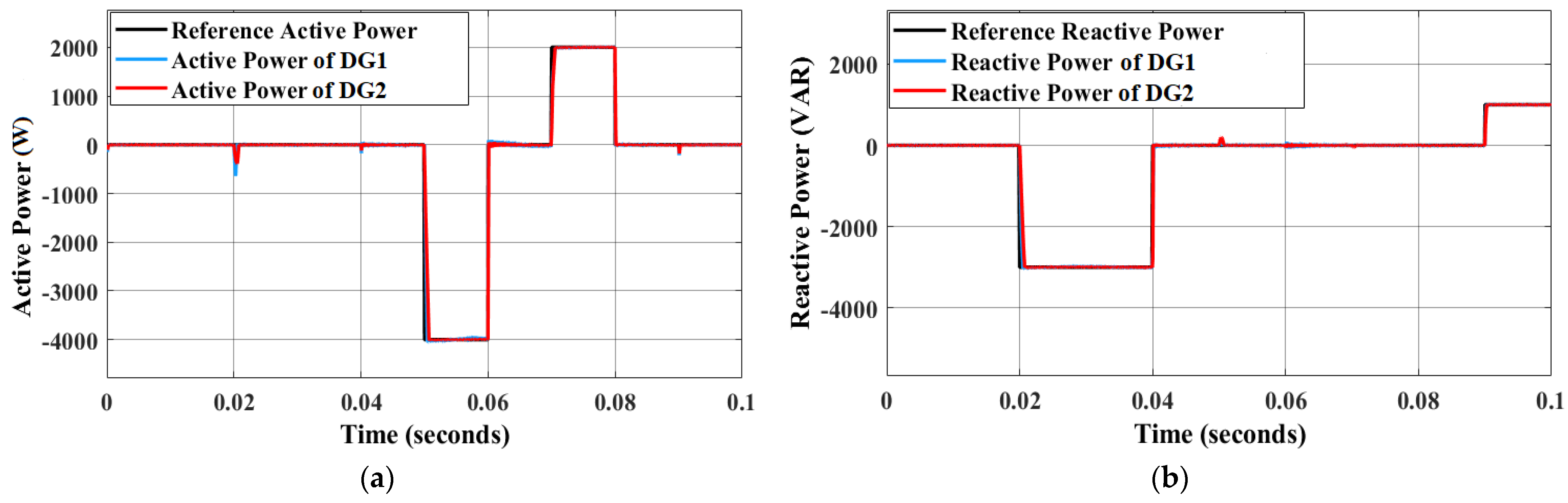
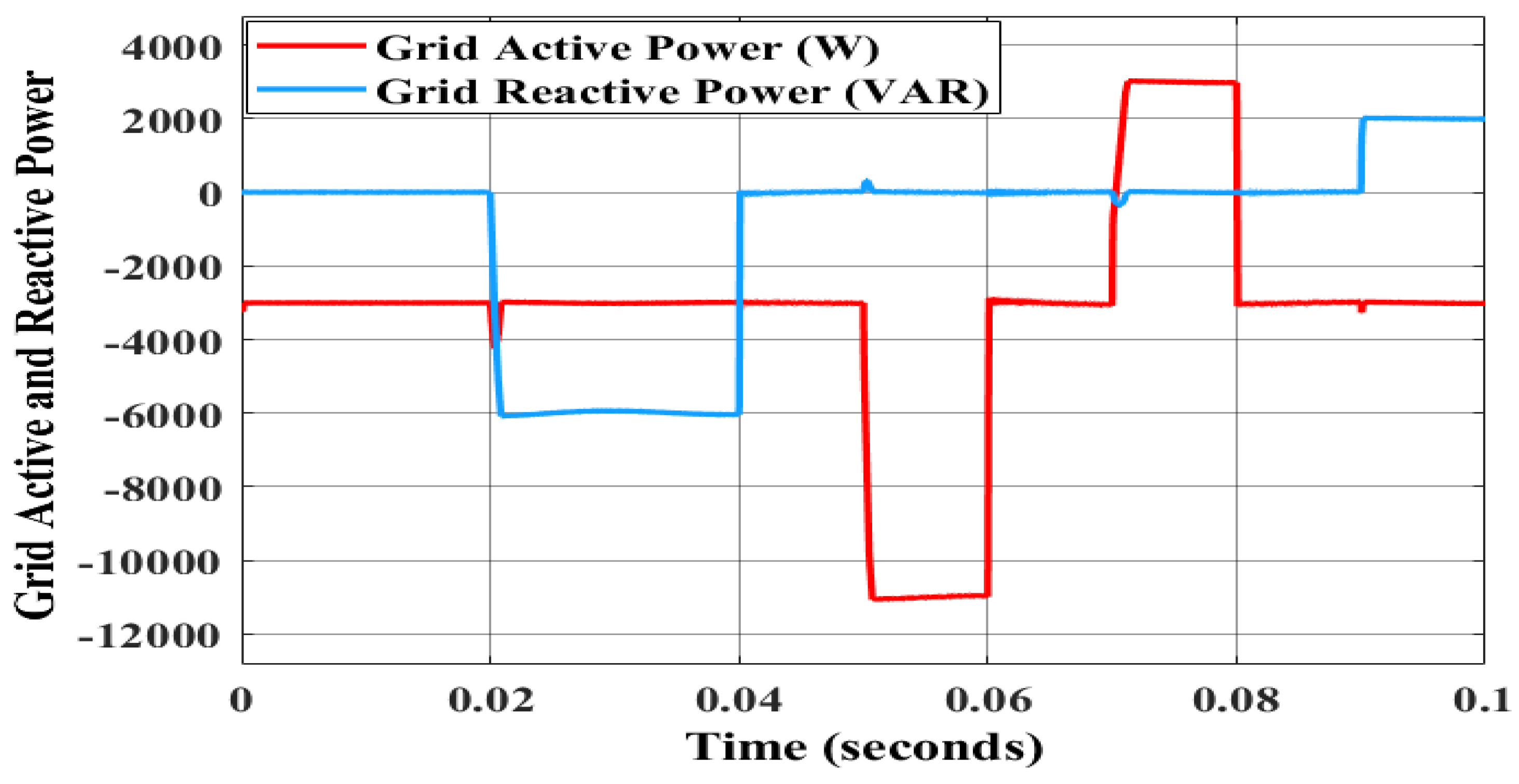
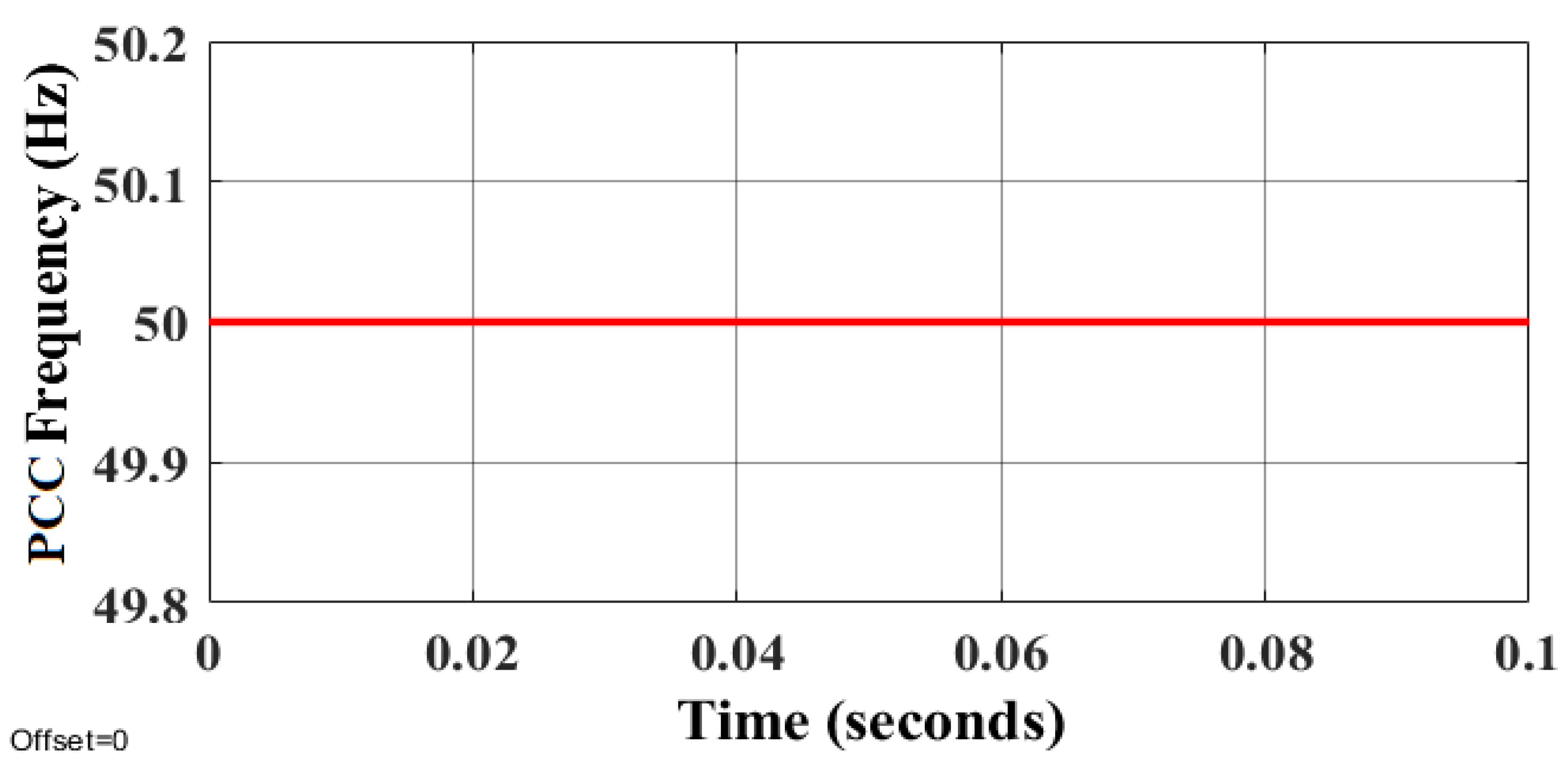




| Description | Symbol | Nominal Value | Unit |
|---|---|---|---|
| Input voltage | 850 | V | |
| Output voltages | 250 (DG1) and 400 (DG2) | V | |
| Main capacitor | 1000 | μF | |
| Main capacitor-resistance | 36 | mΩ | |
| Main inductor | 200 | μH | |
| Main inductor-resistance | 0.12 | Ω | |
| Switching frequency [43,44] | 200 | kHz | |
| Load resistance Input capacitor | 140 500 | Ω μF |
| Description | Symbol | Nominal Value |
|---|---|---|
| Settling time of SMC | TS | 1.5 msec |
| SM damping coefficient | 1.34 | |
| Ratios of the SM coefficients | and | 19,939 and 102,846,495 |
| Beta of SM | 850/250 and 850/400 | |
| SM control gains | and | 1 and 4.53 |
| Parameter Name | Acronym | Value |
|---|---|---|
| Bandwidth revolves around AC frequency | ||
| AC nominal frequency | ||
| Proportional gain PR voltage compensator | 22 | |
| Integral gain PR voltage compensator | 22 | |
| Damping coefficient PR current and power compensators | 0.95 | |
| Proportional gain PR current compensator | 0.027 | |
| Integral gain PR current compensator | 4.38 | |
| Measured signal gain for DG1 and DG 2 | 1 |
| Parameter Name | Acronym |
|---|---|
| 1.146039290275440 × 104 | |
| 0 | |
| −1.146039290275440 × 104 | |
| 1 | |
| −1.999976025486589 | |
| 0.999976124181453 |
| Description | Symbol | Nominal Value |
|---|---|---|
| Grid voltage | 100 V | |
| Active power of the load | 3 kW | |
| Power frequency | 50 Hz | |
| Sampling time | 50 μs | |
| DG1 | ||
| Line resistance | 0.51 Ω | |
| Line inductance | 4.8 mH | |
| DC input of BB converter | 850 V | |
| DC output of BB converter | 250 V | |
| DG2 | ||
| Line resistance | 1 Ω | |
| Line inductance | 10 mH | |
| DC input of BB converter | 850 V | |
| DC output of BB converter | 400 V | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jasim, A.M.; Jasim, B.H.; Neagu, B.-C. A New Decentralized PQ Control for Parallel Inverters in Grid-Tied Microgrids Propelled by SMC-Based Buck–Boost Converters. Electronics 2022, 11, 3917. https://doi.org/10.3390/electronics11233917
Jasim AM, Jasim BH, Neagu B-C. A New Decentralized PQ Control for Parallel Inverters in Grid-Tied Microgrids Propelled by SMC-Based Buck–Boost Converters. Electronics. 2022; 11(23):3917. https://doi.org/10.3390/electronics11233917
Chicago/Turabian StyleJasim, Ali M., Basil H. Jasim, and Bogdan-Constantin Neagu. 2022. "A New Decentralized PQ Control for Parallel Inverters in Grid-Tied Microgrids Propelled by SMC-Based Buck–Boost Converters" Electronics 11, no. 23: 3917. https://doi.org/10.3390/electronics11233917
APA StyleJasim, A. M., Jasim, B. H., & Neagu, B.-C. (2022). A New Decentralized PQ Control for Parallel Inverters in Grid-Tied Microgrids Propelled by SMC-Based Buck–Boost Converters. Electronics, 11(23), 3917. https://doi.org/10.3390/electronics11233917







