Multi-Model Inference Accelerator for Binary Convolutional Neural Networks

Abstract

Binary convolutional neural networks (BCNN) have shown good accuracy for small to medium neural network models. Their extreme quantization of weights and activations reduces off-chip data transfer and greatly reduces the computational complexity of convolutions. Further reduction in the complexity of a BCNN model for fast execution can be achieved with model size reduction at the cost of network accuracy. In this paper, a multi-model inference technique is proposed to reduce the execution time of the binarized inference process without accuracy reduction. The technique considers a cascade of neural network models with different computation/accuracy ratios. A parameterizable binarized neural network with different trade-offs between complexity and accuracy is used to obtain multiple network models. We also propose a hardware accelerator to run multi-model inference throughput in embedded systems. The multi-model inference accelerator is demonstrated on low-density Zynq-7010 and Zynq-7020 FPGA devices, classifying images from the CIFAR-10 dataset. The proposed accelerator improves the frame rate per number of LUTs by 7.2× those of previous solutions on a ZYNQ7020 FPGA with similar accuracy. This shows the effectiveness of the multi-model inference technique and the efficiency of the proposed hardware accelerator.

1. Introduction

Deep neural networks, in particular convolutional neural networks (CNN), are evolving continuously in complexity and their ability to perform a wide range of tasks such as speech recognition [1], autonomous driving [2], image classification [3], and object detection [4].

The widespread use of convolutional neural networks on low-cost embedded systems is constrained by the high amount of memory and computational power required to run the network. Fully binarized convolutional neural networks (BCNN) address this problem by quantizing all internal values, such as weights and activations, to only one bit. As such, memory consumption and computational complexity are significantly reduced, as multiplication can be replaced by a XNOR logical operation. BCNN inference achieves an accuracy close to that achieved by a non-binarized model with small to medium-sized datasets [5] such as CIFAR-10 [6].

Previous works on the design of binary convolutional neural networks have focused on improved training methods and efficient accelerators (see [7,8] for an extensive review of binarized neural networks). Courbariaux et al. [5] showed that BCNNs can be implemented with much fewer resources, because multiplications are replaced by XNORs and accumulations by popcounts. Umuroglu et al. [9,10] proposed a framework to automatically map BCNNs with reconfigurable logic. The work considered small networks mapped on embedded reconfigurable computing devices. The framework supports dense layers, pooling layers, and non-padded convolutional layers. The work was extended by Fraser et al. [11] with architectural modifications to improve scalability and implement padded convolutional layers, which improves the accuracy of the models. To reduce the number of parameters of a BCNN, Nakahara et al. [12] replaced the hidden fully connected layers with an average pooling layer to reduce the number of weights in the classification layers by $3\times$ while maintaining the same accuracy. Zhao et al. [13] used high-level synthesis to design a three-module accelerator for BCNNs. The binary convolutions use a variable-width line buffer to support different sizes of feature maps. To avoid using a different module for the first layer of the BCNN, whose inputs are not binarized, Guo et al. [14] proposed a uniform implementation of all convolutional layers. The first layer is converted to a full binary convolutional layer at the cost of extra processing. Fu et al. [15] explored input and kernel similarity to reduce computation redundancy and accelerate BCNN inference. However, the level of optimization of the method depends on the model and application. Recently, Kim et al. [16] proposed a method to reduce the computational complexity by skipping redundant operations. They skip multiplications of padded zeros and redundant operations associated with input elements of a pooling window which do not affect the pooling. The results are for a single dot product calculation. The technique is less effective when multiple feature maps are calculated in parallel, as the parallelism must be synchronized.

All these works accelerate the inference of a BCNN assuming a unique model. However, some images are easier to classify than others and a less complex BCNN can be used in these cases. Therefore, a sequence of CNNs can be used to sequentially extract important features at a particular level which are sent to the next CNN. Cascading CNNs for improved accuracy of computer vision algorithms is a method explored by several authors in different areas. For example, Angelova et al. [17] applied deep network cascades for real-time pedestrian detection, Diba et al. [18] designed a cascade of CNNs for object detection, and [19] proposed a cascade CNN for traffic sign recognition. In these two works, using a CNN cascade to replace a single, more complex CNN achieved better accuracy.

Another line of research using multiple CNNs to solve a problem considers a sequence of models with different accuracy levels. The underlying principle of this is based on the fact that a small subset of features is enough to correctly classify some images, while other images need more feature information. So, the full capacity of a CNN is required only for a subset of complex images. The idea of using successively more complex classifiers in a cascade was proposed in [20] for real-time face detection. In this case, classifiers with different complexity are cascaded, focusing only on promising regions. A confidence of the prediction of a classifier is used to determine if it stops or should proceed to the next classifier.

Kouris et al. [21] proposed an automated toolflow to generate a two-stage cascade CNN for image classification. The work generates a second lower precision model from a higher precision CNN without retraining. All images are inferred using the lower precision model. Only images not classified with high confidence by this model are sent to be classified by the second model, which has a higher accuracy. This work was limited to a single CNN model with different quantizations and a two-stage cascade was considered.

Following the idea of cascade classifiers, we propose a multi-model inference technique that uses two or more BCNNs with different accuracy/complexity ratios. In this technique, we start with a small network model to classify the image. After classification, a confidence predictor is used to decide if the image should be considered well classified or not. If it is considered to be well classified, the process stops. Otherwise, the image is forwarded to a more accurate model. The process can be repeated with multiple levels of models. The method allows us to perform inference with an accuracy close to that of the most accurate model, but with a lower runtime than the single most accurate model.

In this work, we implement and test the multi-model inference technique and a hardware accelerator to speed up its execution in FPGA. The multi-model is developed with a parameterizable BCNN model with a single dense layer for classification. The number of filters in the convolutional layers is parameterizable, which determines the accuracy of the model and the runtime. The accelerator has dedicated modules for the first and last layers and a configurable module to run the hidden convolutional layers.

The system was implemented in two small Zynq-7 SoC-FPGAs (ZYNQ7010 and ZYNQ7020) and evaluated using the CIFAR-10 dataset, achieving an overall speedup of $15.5\times$ over the best state-of-the-art accelerator with the same accuracy and the same ZYNQ7020 FPGA device.

As far as we know, this is the first work that explores multi-model inference in the context of binary neural networks and accelerates the inference of the model with a scalable dedicated hardware architecture targeting low-density FPGAs.

2. Convolutional Neural Network

CNN image classifiers take an image as an input and classify that image into a certain class. They output a classification score vector where the highest value corresponds to the class predicted by the CNN.

The main layer within a CNN is the convolutional layer. Convolutional layers hold a set of 3D tensors of weights, called filters, of size ($n_{out},i{n}_z,k_{xy},k_{xy}$) and a bias vector of size $(1,n_{out})$, where $n_{out}$ is the number of different filters, $i{n}_z$ is the depth of each filter (equal to the depth of the input image), and $k_{xy}$ is the size of the 2D window of a filter.

Each 3D convolution between one filter and the input map (followed by an activation function) generates a two-dimensional output map. After repeating the process for all filters, the result is a 3D image of size ($n_{out},n_{y_{in}}-k_{xy}+1,n_{x_{in}}-k_{xy}+1$). This output is a feature map that has higher values if certain features were detected on the input image.

CNNs can be equally applied to 1D signals. In this case, 1D CNNs using both 1D convolutions that consist of inner products between activations and weights are used.

The behavior of each layer can be modified with two parameters: the stride and the padding. Stride determines how the filter runs over the input map, that is, the number of shifts that each kernel slides over the map. A stride of one means that the kernel runs over the whole map. A stride above one reduces the size of the output map. Padding helps preserve the output map size. When a non-unitary filter is applied to an input map, the spatial dimension of the output map reduces. Padding the input map with, for example, zeros allows preserving the dimension of the maps.

The kernel may be expanded to cover a broader area of the input map without increasing the number of parameters with a technique known as dilated convolution. This technique inserts holes inside the kernel between consecutive elements. The dilation factor determines the kernel expansion. A normal convolution has a dilation factor of one.

Fully connected or dense layers have a matrix of weights w of size ($n_{in}$, $n_{out}$) and a bias vector b with size (1, $n_{out}$). Their output function is $A(x.w+b)$, where $A(·)$ is an activation function.

Equation (1) illustrates the multiply and accumulate operation required to calculate the $n_{out}$ outputs.

$$ou{t}_j=\sum _{i=1}^{n_{in}}{x}_i·w_{ij}+b_j,out\in {\mathbf{R}}^{n_{out}}$$

(1)

Batch normalization [22] is a method used for accelerating and improving the training of neural networks. It normalizes the layer inputs to a mean of 0 and variance of 1, and then scales and shifts the normalized inputs with learnable variables, $\gamma$ and $\beta$.

In the training step, the image set is divided into batches of size M. Batch normalization then uses each batch to estimate a vector of means, $\mu \in {\mathbf{R}}^N$, and a vector of variances, ${\sigma }^2\in {\mathbf{R}}^N$, for each channel of the input image. The input shape will be $(M,C,Y,X)$, where M is the batch size and C is the number of $X\times Y$ planes.

The mean and variance are used to normalize, scale, and shift the inputs according to Equation (2), where $\gamma$ and $\beta$ are learnable variables obtained during the training process and $ϵ$ is a small constant value, commonly ${10}^{-5}$, used for numerical stability [22].

$$\begin{array}{cc}\hfill \widehat{I}& =\frac{I-\mu }{\sqrt{{\sigma }^2+ϵ}}\hfill \\ \hfill I_{BN}& =\gamma ·\widehat{I}+\beta \hfill \end{array}$$

(2)

The pooling layer downsamples the input channels, reducing the size of the next input channels. A window of elements of an input channel is replaced by the maximum (max pooling) or the mean (average pooling) of all elements of the window.

Binary Neural Network

Quantization is a CNN optimization to reduce the computational complexity and memory storage required to run a CNN model. During training, weights, outputs, and gradients are typically represented in a 32-bit floating-point format, but using lower precision during inference does not critically affect the prediction performance [23].

Binarization is an extreme form of quantization where values are quantized to one bit using Equation (3). Negative values are represented with a ‘0’ and positive values with a ‘1’.

$$X_B=\left\{\begin{array}{cc}+1\hfill & x\ge 0\hfill \\ -1\hfill & x<0\hfill \end{array}\right.$$

(3)

Binary neural networks can be placed in two main categories, binary weight networks, where only the weights are binarized or fully binarized networks, where both the weights and the layer outputs are binarized.

Binary weight networks remove the need for multiplications, and fully binarized networks can replace the multiply–accumulate (MAC) operations used in the dot products in fully connected and convolutional layers with XNOR and popcount operations. The authors in [24] designated this merged operation xNorDotProduct (see Equation (4)).

$$\begin{array}{cc}\hfill & x_b\in {\{0,1\}}^n,w_b\in {\{0,1\}}^n\hfill \\ \hfill & x·w=xnorDotProduct(x_b,w_b)\hfill \end{array}$$

(4)

It works by applying a XNOR operation between the binary representations of the inputs and weights and then counting the number of set bits and subtracting that number with the number of unset bits. This is equivalent to $2\times$ the number of set bits minus the total number of bits (see Equation (5)).

$$\begin{array}{cc}xnorDotProduct\left(x\right)& =\left(\mathrm{number}\mathrm{of}\mathrm{bits}\mathrm{set}\mathrm{to}\mathrm{one}\mathrm{in}x\right)\times 2\hfill \\ & -\left(\mathrm{total}\mathrm{number}\mathrm{of}\mathrm{bits}\mathrm{in}x\right)\hfill \end{array}$$

(5)

3. Multi-Model Binarized Neural Network

This section describes the proposed parameterizable binarized convolutional neural network and the multi-model inference technique based on the configurable binarized neural network. However, the proposed multi-model inference technique and the hardware accelerator are independent of the architecture of the BCNN.

3.1. Configurable Binarized Neural Network

The network architecture considered in this work has six convolutional layers and a single final dense layer for classification.

The network design step started with a neural network model similar to those in [13,14] and explored different combinations of the number of convolutional, dense, and pooling layers. It was concluded that a single dense layer achieves results very close to those obtained with three dense layers used, for example, in [14]. It was also concluded that pooling can be applied multiple times without a reduction in accuracy and a reduction in operations and weights. From this model design exploration, the configuration that achieved a slightly better accuracy than previous works was chosen, allowing a margin for further optimization with the multi-model inference technique.

Three convolutional layers are followed by pooling, and batch normalization is applied to the output of all convolutional layers. The number of filters in each convolutional layer is configurable using a multiplicative factor, N. This permits model space exploration and generates models with different trade-offs between accuracy and complexity (see the architecture of the configurable BCNN in

Table 1. Network architecture.

i	${\mathit{Layer}}^{\mathit{i}}$	No Filters	Input	Output
0	Conv ($3\times 3$)	$N\times 32$	(32, 32, 3)	(32, 32, $N\times 32$)
1	Conv ($3\times 3$)	$N\times 32$	(32, 32, $N\times 32$)	(32, 32, $N\times 32$)
	Pooling		(32, 32, $N\times 32$)	(16, 16, $N\times 32$)
2	Conv ($3\times 3$)	$N\times 64$	(16, 16, $N\times 32$)	(16, 16, $N\times 64$)
3	Conv ($3\times 3$)	$N\times 64$	(16, 16, $N\times 64$)	(16, 16, $N\times 64$)
	Pooling		(16, 16, $N\times 64$)	(8, 8, $N\times 64$)
4	Conv ($3\times 3$)	$N\times 128$	(8, 8, $N\times 64$)	(8, 8, $N\times 128$)
5	Conv ($3\times 3$)	128	(8, 8, $N\times 128$)	(8, 8, 128)
	Pooling		(8, 8, 128)	(4, 4, 128)
6	Dense	$N_c$	(4, 4, 128)	(1, $N_c$)

).

As can be seen in Table 1, all convolutional layers have a number of filters that is a multiple of N, except the last convolutional layer that has a fixed number of filers, 128. The fully connected layer has $N_c$ filters, equal to the number of classes.

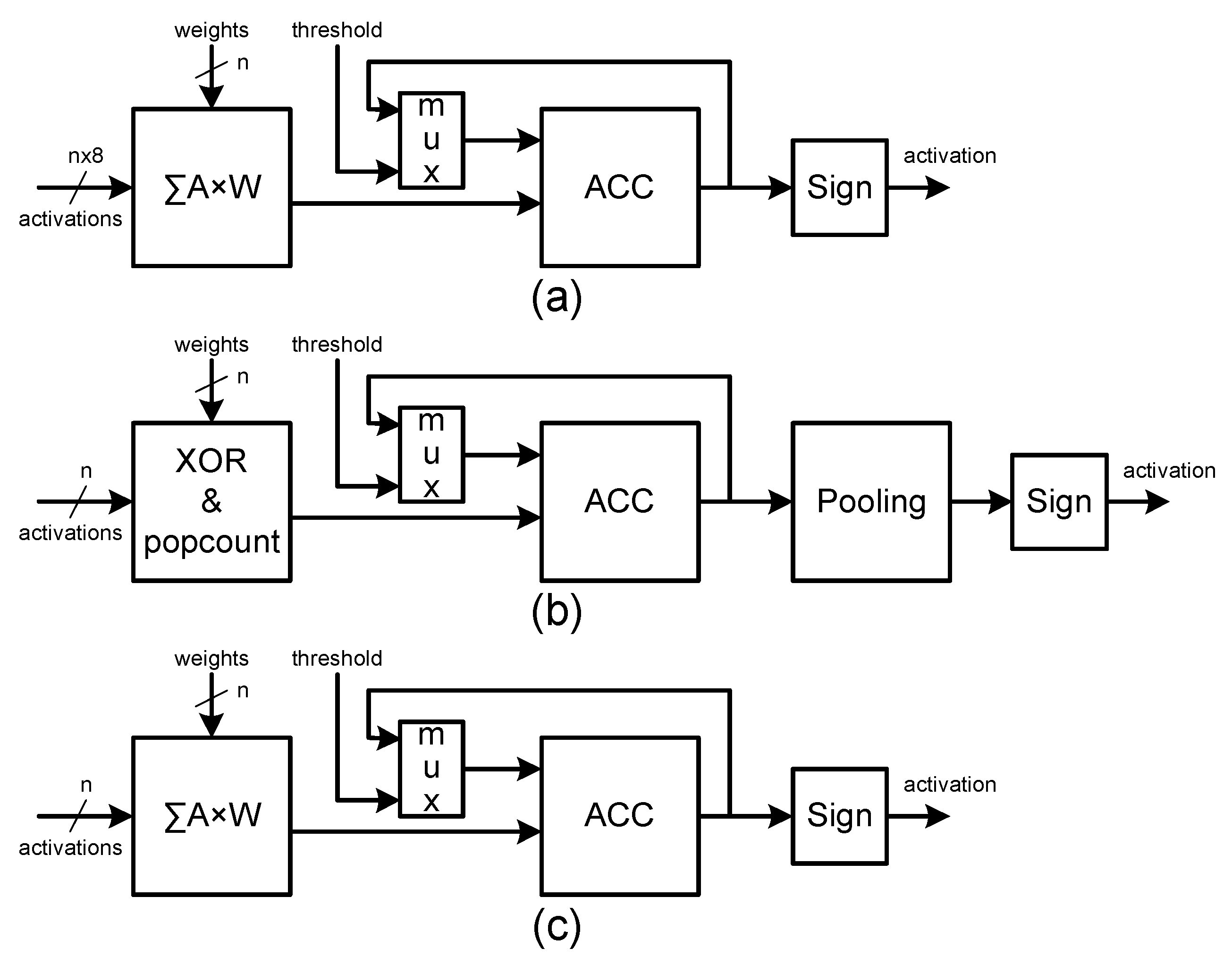
The binarized neural network has both weights and activations represented with a single bit, as explained in the previous section. The only inputs that are not binarized are the inputs to the first layer. In this case, weights are binary but the inputs are 8 bit.

Batch normalization is placed between layers and the real-valued weights are kept for the parameter update when performing forward and backward propagation during training. The main difference in this work is that the layer outputs are also binarized. Bias is removed from fully connected and convolutional layers.

The binarization function, Equation (3), is non-differentiable, making it difficult to use with stochastic gradient descendant (SGD). To solve this issue, Equation (6) was chosen by [24] as a good gradient approximation.

$$\frac{dsign\left(x\right)}{dx}=\left\{\begin{array}{cc}1\hfill & \left|x\right|<1\hfill \\ 0\hfill & otherwise\hfill \end{array}\right.$$

(6)

This approach has shown very good accuracy for image classification with the MNIST, CIFAR10, and SVHN datasets [5].

A standard implementation of batch normalization follows Equation (7) applied directly to the outputs. However, because the normalized values are going to be binarized, it is possible to achieve the same binarized result without the arithmetic operations. When the training is complete, the four parameters become fixed, and so batch normalization becomes a linear transformation.

As [9] demonstrates, because the results of the batch normalization are to be binarized, then it is possible to pre-calculate a value $\tau$ that functions as a binarization threshold. The value of $\tau$ is obtained by solving $batchnorm(\tau ,\Theta )=0$, where $\Theta =(\mu ,\sigma ,\gamma ,\beta )$, and $batchnorm$ represents the batch normalization Equation (7). The solution for the value of $\tau$ can then be seen in Equation (8).

$$batchnorm(x,\Theta )=\frac{x-\mu }{\sqrt{{\sigma }^2+ϵ}}·\gamma +\beta$$

(7)

$$\tau =\mu -\frac{\sqrt{{\sigma }^2+ϵ}}{\gamma }\beta$$

(8)

With the value of $\tau$, the binarization of the results from the batch normalization can be calculated without having to perform arithmetic operations using Equation (9).

$$x_b=binarize\left(batchnorm(x,\Theta )\right)=\left\{\begin{array}{cc}+1\hfill & x\ge \tau \hfill \\ -1\hfill & x<\tau \hfill \end{array}\right.$$

(9)

To reduce the number of operations of inference, batch normalization is merged with Equation (5), where the output of the xNorDotProduct(x) is batch normalized by subtracting $\tau$ (see Equation (10)).

$$\begin{array}{cc}{x}_b& =sign\left[\right(\mathrm{number}\mathrm{of}\mathrm{bits}\mathrm{set}\mathrm{to}\mathrm{one}\mathrm{in}x)\times 2\hfill \\ & -\left(\mathrm{total}\mathrm{number}\mathrm{of}\mathrm{bits}\mathrm{in}x\right)-\tau ]\hfill \end{array}$$

(10)

The total number of bits in x is constant for each convolutional layer and $\tau$ is constant for each filter. Therefore, the accumulator of the number of ‘1’ bits is initialized with $[-(\mathrm{total}\mathrm{number}\mathrm{of}\mathrm{bits}\mathrm{in}x)-\tau ]$ and the binarization is the inverse of the sign of the final value of the accumulator.

Max pooling is implemented with a simple logical OR between all elements of the pooling window. This is possible because max pooling can be implemented after batch normalization [9].

3.2. Multi-Model Inference with the Configurable Binarized Neural Network

In a dataset of images, some samples are easier to classify than others because the number of features necessary to classify them is smaller. Therefore, a simpler model could be used in these cases. A more feature-rich neural network model is required only for a subset of the images that is not well classified with a simpler model. An implementation that uses a single high-accuracy model for all images is inefficient when performing inference of “easier” inputs.

The utilization of a cascade of classifiers with increased accuracy and complexity was proposed in [20,25] for real-time face detection. Classifiers with increasing complexity are cascaded, focusing only on promising regions. Sub-windows not rejected by a classifier are processed by a sequence of more complex classifiers. The algorithm uses a confidence predictor to determine if the classification should stop or proceed to the next better classifier.

The work proposed in this paper applies the concept of cascaded classifiers with our configurable binarized neural network. The network has a variable number of filters given by the parameter N. The accuracy of the model increases with the number of filters and also the complexity. Initially, the inference is executed with a low number of filters. Then, a confidence predictor is used to determine if the image was well classified or needs to proceed to a model with more filters. The sequence of models to be considered depends on the accuracy of each model and its complexity, and it is determined a priori before inference.

The confidence predictor determines if the image was well classified or should proceed to a better classifier. A few works have considered the difference between the highest probability and the accumulation of one or more of the remaining probabilities to assess the confidence of the model outcome [21]. However, this metric is relatively weak for determining the robustness of the model. Some authors have considered entropy to be a more robust metric [26]. Both methods were tested and the entropy metric provided better results. Therefore, we adopted entropy.

In this work, we consider a top-one confidence predictor (a top-five confidence predictor should be used for a top-five classification). The top-one confidence value, $con{f}_{top1}$, is determined as the absolute value of the entropy of the probability output array of the final dense layer as follows:

$$Con{f}_{top1}=|-\sum _i{p}_i\times log\left(p_i\right)|$$

(11)

where $p_i$ are the probabilities associated with each class. One classification is considered confident if $Con{f}_{top1}\le t{h}_{entropy}$, where $t{h}_{entropy}$ is the entropy threshold of the confidence measurement determined after training.

The thresholds establish the trade-off between accuracy and average inference runtime. The lower the threshold, the higher the accuracy, because more images are reanalyzed with the next more confident model. However, the average runtime of inference reduces because the more accurate model requires more time to execute. Multi-model cascading introduces an accuracy error associated with false positives (images erroneously classified by the lowest accuracy model with high confidence). False negatives (images correctly classified by the lowest accuracy model, but with low confidence and therefore also sent to the more accurate model) increase the average inference time because images that were already well classified are still sent to the more complex models for reclassification.

Let us consider a case with two models, M0 and M1 (the most accurate, but more computationally complex), with accuracy values A0 = 0.7 and A1 = 0.9 and computational complexities C0 and C1, respectively. The relative computational complexity, $C1/C0$, is assumed as 4. The inference with the most accurate model has a complexity $C1=4\times C0$ and an accuracy of 90%. A cascade of the two models would generate an inference with computational complexity of $CC1$, given by Equation (12).

$$\begin{array}{c}\hfill CC1=C0+C1\times (1-A0-f{p}_e+f{n}_e)\\ \hfill =C0\times (1+4\times (1-A0-f{p}_e+f{n}_e))\end{array}$$

(12)

where $f{p}_e$ and $f{n}_e$ are the errors of the confidence predictor given by the false positives and false negatives. Assuming, for example, $f{p}_e=f{n}_e=1\%$, the computational complexity of the dual model is $2.2\times C0$. So, the dual model is about $4/2.2=1.8\times$ faster.

In this example, an estimation of the accuracy of the dual model is given by $A1-f{p}_e$, where $f{p}_e$ is the error associated with false positives. For example, with $f{p}_e=1\%$, the accuracy of the dual model of the example is equal $0.9-0.01=0.89\%$.

Multiple models can be considered in the cascade of classifiers by changing the number of filters. However, in this work, we only consider cascades of two and three models. The number of false positives after applying each successive model introduces a cumulative error that reduces the efficacy of multi-model inference with more than three models.

A design flow was developed to find solutions with different accuracy levels and inference runtimes by testing combinations of models. This allowed the designer to find a multi-model combination to replace a single model with an accuracy within an error threshold $Eth$ and a lower inference runtime. In all cases, it obtained a multi-model solution with an accuracy close to that of the single model but with a faster inference runtime.

The application receives a set of trained models with different accuracy levels, an error threshold, $Eth$, and a target accuracy (equal to one of the single models). It then finds the fastest multi-model configuration with an accuracy within the error threshold relative to the target accuracy. It exhaustively explores the multi-model inference with all sets with two and three models. For each set of models, it runs the design flow illustrated in Figure 1.

The design flow consists of the following steps:

• Model training—Train the models to be considered in the multi-model. These can be trained or obtained from a zoo of trained models;
• Setting the entropy threshold—Set the initial entropy threshold and entropy increment. The entropy threshold determines the inputs that are considered to be correct, that is, an input sample with an entropy lower than the entropy threshold is considered to be correct. The lower the entropy, the higher the probability of a correct positive, but more input samples are sent to the next model. Both parameters were set to 0.1;
• Multi-model inference—The multi-model inference is run, starting with the lowest entropy threshold;
• Accuracy—Determination of the accuracy and comparison with the accuracy of the more accurate model. If the difference is lower than the error threshold, it increases the entropy threshold and repeats the process. Otherwise, it stops the iterative process. The best accuracy was achieved with values of the threshold close to 1.0;
• Runtime—Estimate the speedup as follows:

  $$\frac{M{3}_{OPS}}{M{1}_{OPS}+M{2}_{OPS}\times S2+M{3}_{OPS}\times S3}$$

  where $M{X}_{OPS}$ is the number of operations of the model, and $S_X$ is the percentage of inputs executed by model X.

The data flow was developed in python and integrated in the Pytorch platform. It receives two or three models as inputs, an error threshold, an initial and a final entropy threshold, and the output file. The output includes the best results for all entropy thresholds and the best configuration, that is, the configuration that accomplishes the error requirement and has the best accuracy.

The application was utilized to generate different classifications solutions with a variable trade-off between accuracy and runtime. Basically, a lower entropy threshold improves the accuracy but increases the execution time.

4. Architecture of the Hardware Accelerator for Multi-Model Binarized Neural Network Inference

The architecture of the hardware accelerator for binarized neural networks consists of three main modules, one for the first layer, one for the last dense layer, and a third one for the hidden convolutional layers. This subdivision allows us to optimize each module to the particular features of the first, the last, and the hidden layers.

4.1. Organization of the Architecture

All three modules have a similar structure with an input and an output buffer, distributed weight buffer, and an array of processing cores (see Figure 2).

The output buffer of the module for the first layer is shared with the input buffer of the module for the hidden layers. Furthermore, the input buffer of the module for the last layer is shared with the output buffer of the module for hidden layers (see Figure 3).

The inner module processes several hidden layers. Therefore, the input buffer is also used to store intermediate feature maps. Weights, image, and classification results are transferred from and to the external memory using a direct memory access (DMA) module. The weight memory stores one $(w_z,w_x,w_y)$ filter while having enough room to receive the next filter. Input and output memory buffers are configured as dual port memories, which allows simultaneous reading and writing in a ping-pong configuration.

The hardware accelerator explores different forms of parallelism available in convolutional neural networks and binarized neural networks, in particular:

• Intra-convolution parallelism—multiple multiplications and additions for a convolution are performed in parallel. This is greatly explored in the proposed architecture. The number of parallel multiplications is configurable as 64, 128, or 256;
• Inter-feature map parallelism—Each resulting channel of an output feature map is independent of the other channels. So, several output channels are computed in parallel. This is implemented with multiple cores, where each operates with a single filter, producing an independent output channel. The number of cores is also configurable as 16, 32, or 64;
• Inter-layer parallelism—Layers are executed in a pipeline. The three main modules operate in a pipelined data flow using ping-pong buffers to allow continuous processing of images;
• Batch parallelism—Multiple images from a batch are processed in parallel, providing a significant acceleration when implementing batch processing. The batch size is also configurable as 1, 2, 3, or 4.

Batch parallelism is optimized using shared weights among all batches (see Figure 4).

Several images are processed in parallel. Therefore, weights are shared among the modules. This reduces the required weight memories and reduces external memory accesses, as the same weights are used for a batch of images.

4.2. Implementation of Convolutions

Most works implement 3D convolutions by adding the results from 2D convolutions from each channel. As such, input feature maps and weights are usually ordered as $(x\times y\times z)$. This approach complicates the calculation of parallel 2D convolutions because it requires buffers and reading multiples of nine weights from memory. Furthermore, to run models with multiple kernel sizes, it requires some extra buffering and logic to adapt the 2D convolution to different kernel sizes.

Instead, we consider inputs and weights ordered as $(z\times x\times y)$ and directly execute 3D convolutions. With this ordering, a convolution is performed by streaming the input and weight values into the core starting with the z coordinate, then the x coordinate, then jumping to the next y when a line has finished streaming.

This allows a core to receive a full block of pixels instead of a plane and process the 3D convolution as several dot products. It also allows a core to receive z pixels $x\times y$ times, making the approach independent of the window size of the kernel. To guarantee the flow of layer executions without further data manipulation in the intermediate feature maps, the output feature map from a 3D convolution is stored in the same $(z\times x\times y)$ order.

The correct sequence of readings and writings of feature maps is guaranteed by configurable address generators associated with the weight and map memories.

Initial calculations, shown in Equations (13) and (14), are performed at the start of each convolution to determine the output dimensions. $({I_X}_{size},{I_Y}_{size})$ are the input image dimensions, $({W_X}_{size},{W_Y}_{size})$ are the filters dimension, $pad$ is either 0 or 1, and $pool$ is either 1 or 2.

$${O_X}_{size}={\displaystyle \frac{{I_X}_{size}-{W_X}_{size}+2\ast pad+1}{pool}}$$

(13)

$${O_Y}_{size}={\displaystyle \frac{{I_Y}_{size}-{W_Y}_{size}+2\ast pad+1}{pool}}$$

(14)

The following counters are used by the address generators to calculate all addresses, input, weight and output, where ${O_X}_{size}$ and ${O_Y}_{size}$ are calculated with Equations (13) and (14), respectively:

• $I_Z$ counter $\in [0,{\displaystyle \frac{Z_{size}}{N_i}}-1]$
• $W_X$ counter $\in [0,{W_X}_{size}-1]$
• $W_Y$ counter $\in [0,{W_Y}_{size}-1]$
• $X_{pool}$ counter $\in [0,pool-1]$
• $Y_{pool}$ counter $\in [0,pool-1]$
• $O_X$ counter $\in [0,{O_X}_{size}-1]$
• $O_Y$ counter $\in [0,{O_Y}_{size}-1]$
• $W_N$ counter $\in [0,{W_N}_{size}-1]$

Using the counters together with the image and weight dimensions, the addresses are calculated using the following equations.

$$\begin{array}{cc}\hfill & I_Z+(O_X\ast pool+X_{pool}+W_X-padding)\ast {\displaystyle \frac{{I_Z}_{size}}{N_i}}+\hfill \\ \hfill & (O_Y\ast pool+Y_{pool}+W_Y-padding)\ast {\displaystyle \frac{{I_Z}_{size}}{N_i}}\ast {I_X}_{size}\hfill \end{array}$$

(15)

$$I_Z+W_X\ast {\displaystyle \frac{{I_Z}_{size}}{N_i}}+W_Y\ast {\displaystyle \frac{{I_Z}_{size}}{N_i}}\ast {W_X}_{size}$$

(16)

$$W_N+{\displaystyle \frac{O_X\ast {W_N}_{size}+O_Y\ast {W_N}_{size}\ast {O_X}_{size}}{N_o}}$$

(17)

Equation (15) is used for the input image address, Equation (16) is used for the weight address, and Equation (17) is used for the output image address.

These equations are simplified in the first and last layers. The first layer does not have pooling and the last layer does not have pooling or padding.

Compared to the traditional 2D convolution method, the method considered in this work also offers a better way to explore parallelism, not constrained by the kernel window size.

4.3. Architecture of Cores

Each module has cores optimized for the execution of the associated layers (see Figure 5).

In the first layer, the cores implement the inner product between 1 bit weights and 8-bit pixels. The intra-convolution parallelism, $N_i$, is configurable. The result of the inner product is then accumulated.

The core of the module for hidden layers implements the inner product between 1 and bit weights and 1-bit activations using XNOR for multiplication and popcount for addition. Similar to the first layer module, the intra-convolution parallelism, $N_i$, is also configurable. Additionally, this module supports pooling. Max pooling is implemented with a simple boolean OR between all elements of the pooling window, as explained in Section 3.1. Once it receives the last pool signal, the register is reinitialized, and the last registered output is validated to the final stage for binarization.

The core of the last layer module is similar to the one used in the hidden layers, except that pooling is not used in dense layers.

The accumulators of the modules are initialized with $[-(\mathrm{total}\mathrm{number}\mathrm{of}\mathrm{bits}\mathrm{in}x)-\tau ]$, ($\tau$ is the binarization threshold, as explained in Section 3.1) so that the signal of the final accumulation determines the binarization.

4.4. Execution Data Flow of the Binarized Neural Network

The runtime execution of the architecture is configured and controlled by a host processor in a pipelined data flow.

The first- and last-layer modules are configured according to the sizes of these layers. These configurations stay fixed for the whole execution of the model. The module for hidden layers is configured for each different hidden layer. The configuration step includes the configuration of the address generators and the optional execution of pooling.

The first module loads the input image and filters and then starts the execution of convolutions. After finishing the convolution and writing the output result in the buffer of the next module, it is ready for the next image. As long as the output buffer is free to receive a new map, the module restarts the execution.

The module for hidden layers has a similar execution, except that the module is used sequentially for all hidden layers. After executing one layer, the module is reconfigured for the next layer. After the execution of the last hidden layer, the output feature map is sent to the last module.

The last module has a similar execution running the dense layer. The result of the layer is sent back to external memory.

When an output feature map is larger than the size of the output buffers, the image is partitioned in the y direction. In these cases, the last layer is only executed when the full feature map is available.

When the architecture is designed with parallel data paths to explore batch parallelism, the weights are shared by all paths. Therefore, all data paths must run the same model. To run multi-model inference in a batch processing architecture, a model with higher accuracy is only executed when there are enough images to fully utilize all parallel data paths of the architecture.

Running the multi-model inference is straightforward. It first runs the model with the lowest accuracy. Then, it determines the entropy and decides which model to run next. The entropy calculation is performed in software but could also be implemented in hardware. When using the architecture with multiple batches, all models are executed in batches.

4.5. Accelerator Analysis

The proposed architecture is configurable and consists of three modules working independently in a data flow. Therefore, it is important to balance their execution times to reduce the idle times of the modules. We have developed a performance model of the architecture to estimate its execution time. This model is used to optimize the architecture for a specific model configuration.

Each $laye{r}^i$ processes the convolution of the input image by a set of $W_n^i$ filters, ($w_z^i,w_x^i,w_y^i)$. The number of cycles required to process each filter is determined from the number of input pixels that are given to the core, $N_i$. The more cores we have, the more filters can be processed simultaneously, which reduces the total number of cycles required to calculate the final output image by $N_o$. However, each core requires one set of $(w_z^i,w_x^i,w_y^i)$ filters. This introduces a communication bound bottleneck as more cores require more filters to be retrieved from memory.

The number of total cycles required to process each layer can be calculated through Equation (18), where $N_{layer}^i$ is the total number of cycles required for the hardware to process all outputs corresponding to layer i, $N_{fetch}^i$ is the number of cycles required to download $N_o$ filters from the stream, $N_{filter}^i$ is the number of cycles required to process one output feature map, and $O_z^i$ is the number of feature maps of the output image. The $MAX$ operation considers the longer time taken between the communication and computation. Because a new set of filters is downloaded while the current set of filters is being processed, if the download takes more time, the operation will have to wait for the download to finish.

$$N_{layer}^i=MAX(N_{fetch}^i,N_{filter}^i)\ast \frac{O_z^i}{N_o}$$

(18)

The number of cycles required to fetch each set of filters, $N_{fetch}^i$, is shown in Equation (19), where $(w_x,w_y,w_z)$ represent the dimensions of each filter and $N_t$ is the number of bits fetched per cycle plus one cycle for the $\tau$ value for the batch normalization.

$$N_{fetch}^i=N_o\ast (\frac{w_x^i\ast w_y^i\ast w_z^i}{N_t}+1)$$

(19)

The number of cycles needed to process each filter, $N_{filter}^i$, is shown in Equation (20). $(O_x,O_y)$ represent the output image’s dimensions, calculated through Equations (13) and (14), respectively. $pool$ is 1 if no max pooling is used and 2 otherwise, and $(w_x,w_y,w_z)$ represent the dimensions of each filter.

$$N_{filter}^i=O_x^i\ast O_y^i\ast {\left(poo{l}^i\right)}^2\ast \frac{w_x^i\ast w_y^i\ast w_z^i}{N_i}$$

(20)

These two equations present a scaling limit for the overall throughput where $N_{filter}^i$ needs to be higher than $N_{fetch}^i$. Higher values for $N_i$ reduce the number of cycles necessary to process the current filter, Equation (20), and higher values for $N_o$ make the fetching process take more cycles, Equation (19). The only way to increase this limit is to increase the number of bits fetched per cycle, $N_t$.

$N_{fetch}^i$ can be compared with $N_{filter}^i$, resulting in condition (21), which needs to be true; otherwise, the fetching takes longer than the operations.

$$\begin{array}{cc}\hfill N_o\ast (\frac{w_x^i\ast w_y^i\ast w_z^i}{N_t}+1)& <O_x^i\ast O_y^i\ast {\left(poo{l}^i\right)}^2\ast \frac{w_x^i\ast w_y^i\ast w_z^i}{N_i}\simeq \hfill \\ \hfill \simeq N_o& <O_x\ast O_y\ast poo{l}^2\ast \frac{N_t}{N_i}\hfill \end{array}$$

(21)

These equations allow us to determine the number of cores in each module so that they have a similar runtime execution. It also determines the maximum number of cores as a function of the memory bandwidth.

The data size determines the number of BRAM. A single-port BRAM has a maximum port size of 64 bits. Therefore, data sizes of 128 and 256 bits require at least two and four BRAMs, respectively. Each core is associated with a local weight memory. So, the number of cores also establishes the number of required BRAM. The number of batch data flows only determines the number of BRAMs required to implement the input and output buffers, because the weight memories are shared by all batch data flows.

5. Results

This section presents and discusses the accuracy results obtained with the configurable binarized neural network, the execution throughput of the proposed hardware accelerator, and the improvements achieved with the multi-model inference.

5.1. Binarized Neural Network Accuracy

We considered Brevitas [27] for binary quantization of the neural network model. Brevitas is a PyTorch (https://pytorch.org/, accessed on 10 October 2022) library used for quantization-aware training that implements a set of building blocks at different levels of abstraction to model a reduced precision hardware data path at training time. This library provides several quantized versions of the standard PyTorch layers that can be replaced with the original PyTorch model.

The CIFAR-10 (https://www.cs.toronto.edu/~kriz/cifar.html, accessed on 10 October 2022) dataset, used in many previous works, was used to test and compare the proposed BCNN. CIFAR-10 has ten distinct classes, namely airplane, automobile, bird, cat, deer, dog, frog, horse, ship, and truck. This dataset is used as a standard benchmark in many state-of-the-art works and serves as a guide to verify if binary neural networks can achieve similar accuracy levels. The data set consists of 60,000 $3\times 32\times 32$ colored images: 50,000 training images and 10,000 evaluation images.

The configurable binarized neural network described in Section 3.1 was successfully trained using PyTorch/Brevitas. The training program follows the same structure used to train a standard network. The first inputs are 8-bit integers normalized in the range $[-127,127]$. The outputs of each layer are normalized using batch normalization. The last layer has 10 filters equal to the number of classes of the CIFAR-10 dataset.

From the training results, a set of weight values for each layer plus a set of 16-bit signed $\tau$ values used for the binary batch normalization are obtained. The number of bits for $\tau$ was evaluated at the end of the training, and observing that the trained values were lower than $2^{15}-1$, 16 bits was chosen as the smallest possible size to help save hardware resources without sacrificing precision.

The number of filters in the first five convolutional layers was varied with $(32\ast N)$ to study the relation between the number of convolutions, accuracy, and model complexity. The results for CIFAR-10 are shown in Figure 6, where accuracy is measured.

From the figure, it is evident that a higher computational effort is required to achieve the same accuracy increase. For example, N = 3 has an accuracy of 87.59% and N = 5 has an accuracy around 2.4 p.p higher. This accuracy improvement was obtained with a 2.6× increase in model complexity. A close accuracy improvement can be achieved from N = 5 to N = 12. However, this time, the accuracy improvement was obtained with a 5.5× increase in model complexity.

5.2. Hardware/Software Evaluation

The accelerator was integrated in a hardware/software system and implemented in two low-density ZYNQ devices from Xilinx: Zynq7010 and Zynq7020. The Zynq architecture consists of two major parts, the processing system (PS), which contains two ARM A9 cores, and programmable logic (PL), which contains the FPGA subsystem.

The binarized neural network HW/SW architecture was implemented executing the software component in one ARM processor and the accelerator implemented in the programmable logic.

The PL accesses the external memory directly using a direct memory access (DMA) component controlled by the software. The DMA’s access to the external memory is facilitated through a 64-bit high-performance (HP) port. The configuration of the accelerator and the DMA is executed by the processor through a 32-bit general-purpose (GP) port.

The module for the first layer has a fixed configuration with eight cores and the module for the last layer has a single core configured with a data size of 64 bits. Different configurations of the module for the hidden layers were implemented by varying the data size, the number of cores, and the number of channels (see results in

Table 2. Resource utilization for different configurations of the accelerator.

Data Size	Core	Batch	LUT	BRAM (N = 8)
64	64	1	12,329	84
64	64	2	22,155	97
64	64	3	31,981	110
64	64	4	41,807	123
64	32	1	6793	52
64	32	2	11,797	65
64	32	3	16,801	78
64	32	4	21,805	91
64	16	1	3961	36
64	16	2	6479	49
64	16	3	8997	62
64	16	4	11,515	75
128	32	1	11,057	81
128	32	2	20,333	97
128	32	3	29,609	110
128	32	4	38,885	123
128	16	1	6099	52
128	16	2	10,801	65
128	16	3	15,487	78
128	16	4	20,173	91
256	16	1	10,281	84
256	16	2	19,143	97
256	16	3	28,005	110
256	16	4	36,867	123

), limited by the maximum number of resources of the ZYNQ7020. The accelerator is scalable and can be configured with a higher number of cores, limited only by the available resources of the FPGA.

The number of BRAMs depends on the number of cores, the data size, and the number of filters. The number of BRAMs shown in the table are for N = 8.

From the table, it is possible to identify solutions with the same peak performance (data size × core × batch) but different numbers of resources. For example, the configuration $64\times 32\times 4$ uses 21,805 LUTs and 91 BRAMs, while the configuration $128\times 16\times 4$ uses 20,173 LUTs and 91 BRAMs. Another observation is that architectures with higher data sizes are more efficient, that is, considering architectures with the same peak performance, the one with a larger data size consumes a lower number of LUTs.

We have executed the inference of the binarized neural network with different values of N using an accelerator with a data size of 128 bits, 32 cores, and a batch of four on a ZYNQ7020. The circuit consumes 42,859 LUTs and 135 BRAM (see results in Figure 7)

As expected, the average execution time follows the complexity of the network. The average frames per second (FPS) varies from 559 (N = 12) up to 62,066 (for N = 1).

The same test was performed on a ZYNQ7010 to show that the proposed architecture is also scalable to very-small-density FPGAs. In this case, the architecture was configured with a data size of 128, 16 cores, and a batch of 1. The hardware/software architecture consumes 14,775 LUTs and 58 BRAMs (see results in Figure 8). In the ZYNQ7010, an average frame rate from 140 up to 15,625 was achieved.

Because the proposed accelerator is configurable, it can be optimized for a specific target frame rate. As a test case, we configured the accelerator for a frame rate around 550 with different values of N and determined the resources (see Figure 9).

As can be seen from the figure, the proposed accelerator achieves high accuracy levels with very small solutions. For example, an accuracy close to 85% of CIFAR-10 inference is achieved with less than 2000 LUTs and 22 BRAMs.

5.3. Multi-Model Inference Results

The multi-model with two (2M) and three (3M) different BCNN models was applied to the binarized neural network. After training the models for different N, the design flow of the multi-model inference technique was applied to find the best set of models and threshold with an accuracy close (within 0.1%) to the accuracy of the single models (SM). A full design space exploration was considered with all combinations of models to find the combinations with the best speedup for a particular accuracy (see results in

Table 3. Speedup achieved with incremental inference against inference with a single model. The results include the number of frames per second (FPS), total size of weights in KB, and the speedup compared to the solution of a single model.

Acc.	FPS SM	Weights	FPS 2M	Speedup	Weights	3M	Speedup	Weights
84.85%	17,699	106.2	21,858	1.23	143.7	23,529	1.33	352.4
87.59%	8282	208.7	10,782	1.30	314.9	12,739	1.54	488.6
89.13%	4773	344.9	6515	1.36	382.4	8097	1.70	659.8
89.97%	3103	514.9	5579	1.80	723.6	6410	2.07	966.0
90.70%	2214	781.6	4474	2.02	927.3	4884	2.21	1272.3
91.14%	1612	956.1	3623	2.25	1164.8	4154	2.58	1679.7
91.34%	1241	1227.3	3008	2.42	1436.0	3613	2.91	2154.7
91.64%	962	1532.3	2616	2.72	1741.0	3077	3.20	2459.7
91.85%	801	1871.1	2100	2.62	1741.0	2394	2.99	3172.1
92.11%	664	2243.5	1612	2.43	3368.4	1803	2.72	3544.6
92.43%	559	2649.8	1282	2.30	3368.4	1366	2.44	4120.8
92.86%	—	—	859	1.54	4182.1	1071	1.91	4900.7

).

As can be seen from the results in Table 3, the method achieves speedups from 1 to 3.2 times those of a single model with the same accuracy. However, the speedup with the multi-model inference is not constant. The model with N = 2 has an accuracy of 84.85%. This accuracy is achieved with the multi-model incremental inference at around the same execution time (speedup close to 1). The speedup achieved with the two-model case improves with an accuracy up to 2.72× that of the single model (with N = 8). From here, the speedup begins to decrease. The three-model case has a similar behavior.

Comparing both two- and three-model inferences, it can be observed that the three-model case is faster, with a maximum speedup of 3.2 versus 2.7 for the two-model case. The cost of increasing the number of cascade models is the increase in memory to store the weights of all models. This is an important aspect, because it determines the viability and applicability of the method. The increase in memory size when using a dual model instead of a single model is on average around 1.2×. In the three-model case, as expected, the increase is higher, but the speedup also improves. With only 20% more memory, the speedup can go up to 2.7×. Achieving the same speedup would require an increase in hardware resources of at least the same factor. Therefore, the method is viable and applicable as a speedup technique of the inference of deep neural models.

Another interesting achievement of the multi-model inferences is that they not only improve the frame rate but also improve on the highest accuracy obtained with the single model, from 92.43% to 92.86%.

5.4. Comparison with Previous Works

The proposed accelerator with the three-model inference technique was compared with previous works in terms of accuracy, frame throughput, and resource utilization (see

Table 4. Comparison with previous works for BCNN inference of CIFAR-10.

	[9]	[13]	[12]	[14]	[28]	[15]	[16]	Ours	Ours
Device	Z7045	Z7020	Z7020	Z7020	V7-VX690	ZU7EV	Cyclone V	Z7020	Z7010
LUT	46,200	46,900	14,509	29,600	342,100	45,000	2000	38,885	11,057
BRAM	186	94	16	103	1007	126	73	123	58
Peak GMACS	473	208	329	257	7663	411	83	2343	585
Model GMAC	134	1.425	0.78	1.764	1.396	1.425	1.425	0.378	0.378
Acc. (%)	80.1	88.18	81.80	88.61	87.80	88.81	88.88	89.09	89.09
FPS	3534	168	422	521	6017	288	58	8097	2024
FPS/kLUT	76.5	3.6	29.1	17.6	17.6	6.4	29	208	183

).

The proposed accelerator was compared with previous works considering a solution with an accuracy 89.06%, above the accuracy of previous works. As can be seen, the proposed solution achieves the highest frame rate and the highest frame rate per kLUT efficiency.

Compared to the work with the highest frame rate and a close accuracy ([28]), our accelerator still has a higher frame rate ($1.35\times$) and a $10.4\times$ better frame rate efficiency. The work in [9] has less than half of the frame rate efficiency of the proposed work. However, all layers are implemented in a pipeline where all the weight values are stored in internal FPGA memory, removing any communication bottleneck, but requires 50% more BRAM than ours and is not feasible for very-low-density devices, such as the devices considered in this work. Additionally, it achieves a lower accuracy ($80.1\%$). The work from [12] successfully reduced the number of BRAMs by only storing the input and output feature maps. The weight values were kept in external memory and streamed into buffers when used for the convolutions. With high memory bandwidth, this work was capable of having 256 cores with $3\times 3$ inputs. The lack of fully connected layers also helped with the overall execution time but decreased the accuracy significantly to only 81.8%.

The scalability of the proposed architecture for small-density FPGAs is shown with the implementation on the ZYNQ7010. The architecture achieves a frame rate of 2024 FPS with a lower frame rate efficiency compared to the solution on the ZYNQ7020, but still higher than any of the previous works.

The promising results obtained with the ZYNQ7010 show that the proposed model and architecture can be deployed in very-low-density FPGAs. As shown in Table 2, the scalability of the accelerator allows for the design of very small architectures with a proportional reduction in the image processing throughput.

6. Conclusions

This work proposes a configurable binarized neural network model, a configurable hardware accelerator, and a multi-model inference technique. The architecture is scalable and can be implemented in FPGAs of any density. Its scalability permits an increase in the number of cores so that the performance can also be improved when implemented in higher-density FPGAs.

The accelerator was implemented in a ZYNQ7020 FPGA and a ZYNQ7010 FPGA. The accelerator was integrated in a hardware/software system-on-chip solution programmed to run the binarized neural network, and the two- and three-model inference techniques were tested with CIFAR-10 dataset.

The results show improvements of up to 7.2× the frame rate efficiency compared to previous works with the same accuracy. The multi-model inference technique also improves execution time of the single model inference up to 3.2×.

The utilization of multiple models in the inference process has been scarcely explored. There are many ways to achieve CNN cascades, and some of them can only be explored with dedicated accelerators. We have considered multiple configurations of a single model, which has not been considered before, but there are others way to achieve it that deserve deep research. Furthermore, we have considered the method in the context of binarized neural networks, because we were looking for very-low-cost solutions, but it can also be used in non-binarized models.

It considerably improves previous binarized solutions not only by using the multi-model inference but also with a very efficient hardware accelerator with dedicated units for the input layer, the dense layer, and the hidden layers.

The multi-model technique can be applied to any network model, for example, ResNet-based models [29] and to other applications, such as object detection. Other important aspects of this method include sharing model structures and parameters to reduce the number and size of parameters of the multi-model and hardware-friendly design. These aspects are already undergoing research by the authors of this paper.