A Miniaturized Quartz Crystal Microbalance (QCM) Measurement Instrument Based on a Phase-Locked Loop Circuit
Abstract
:1. Introduction
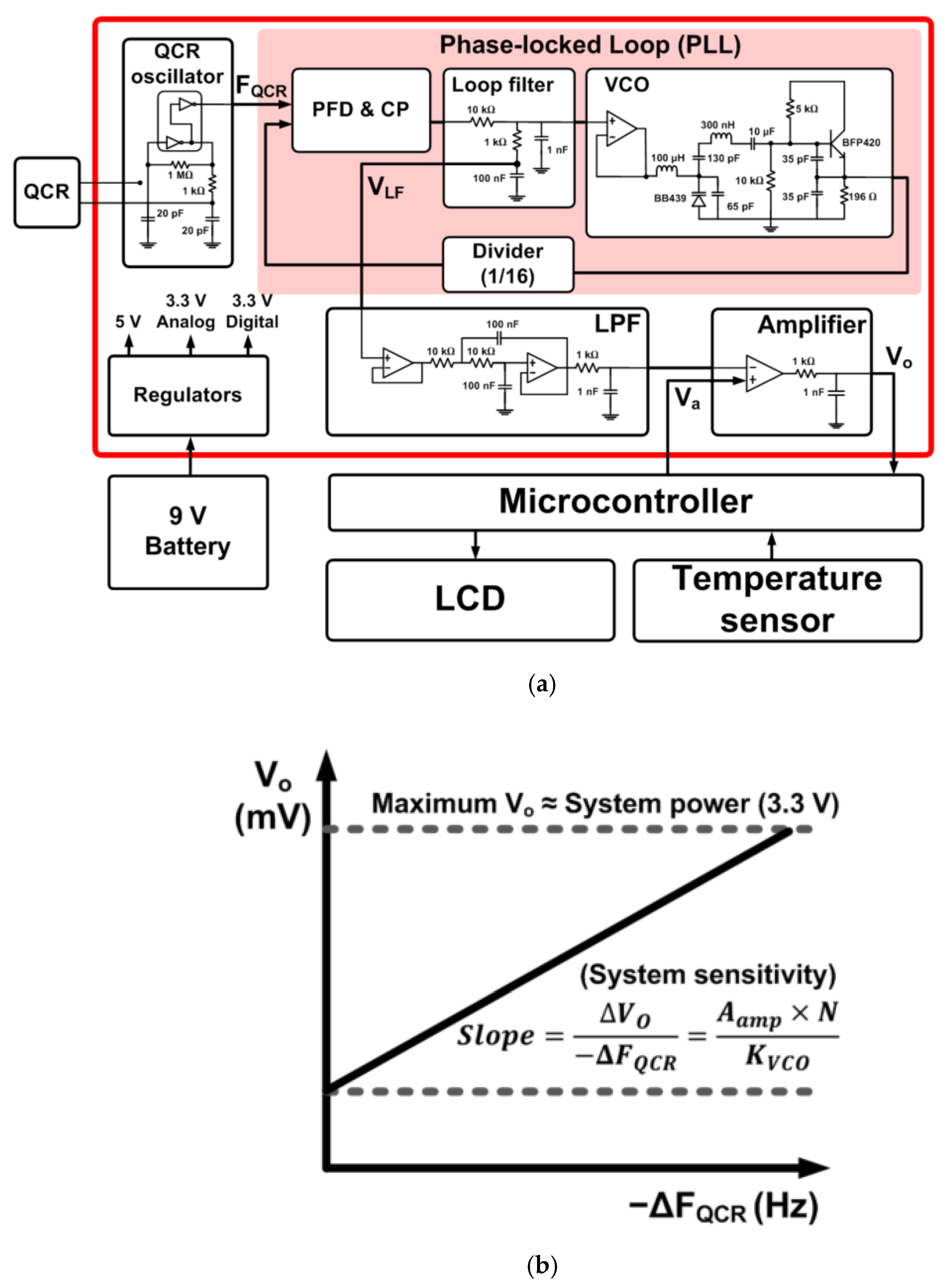
2. Measurement Circuit Design
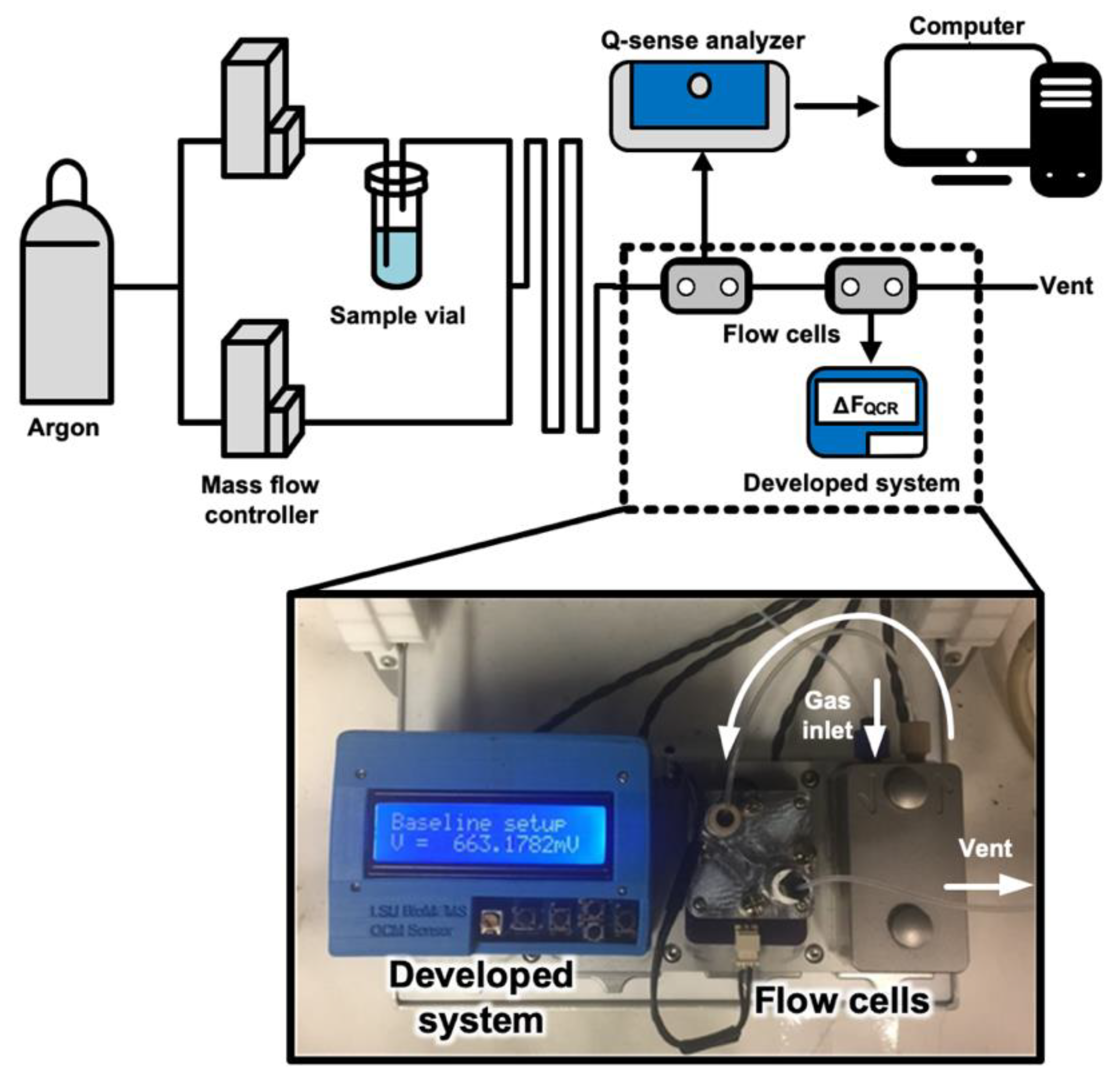
3. Experiments
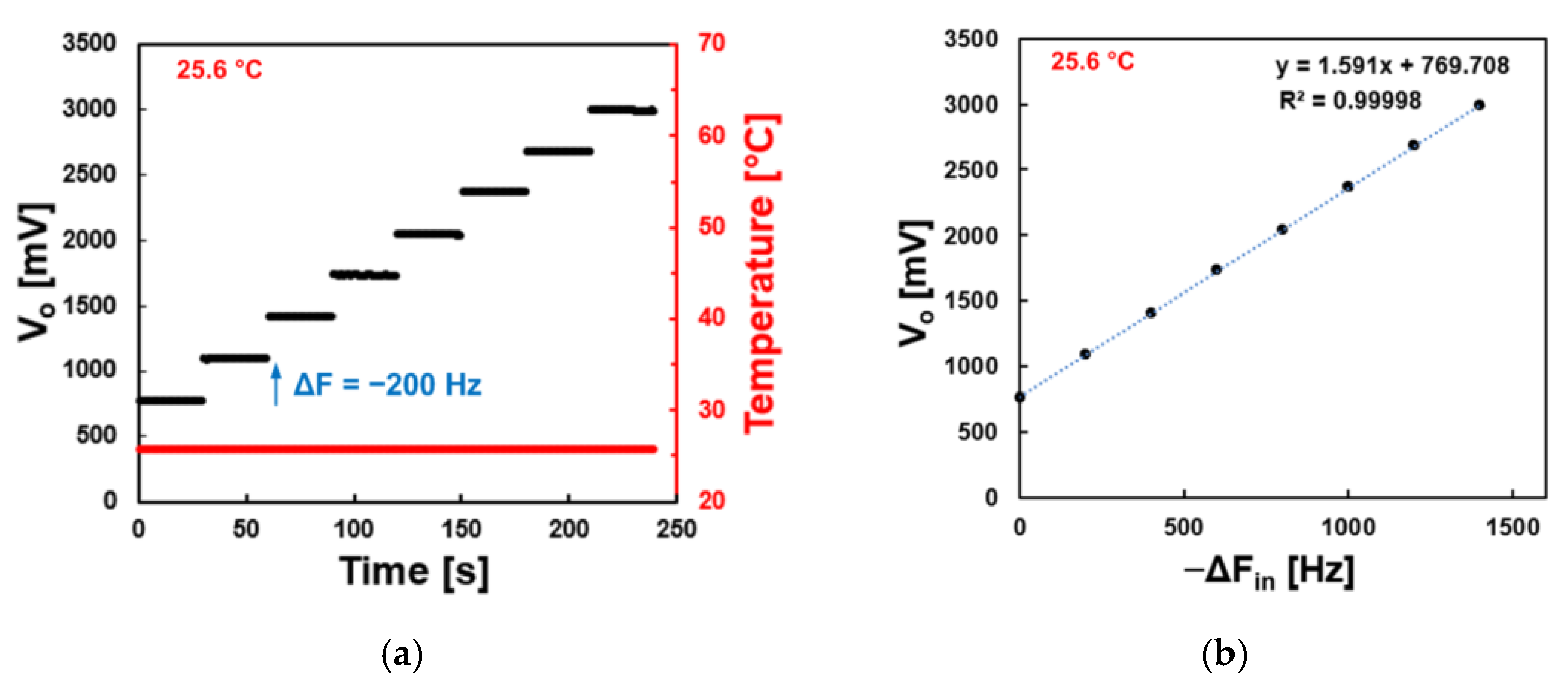
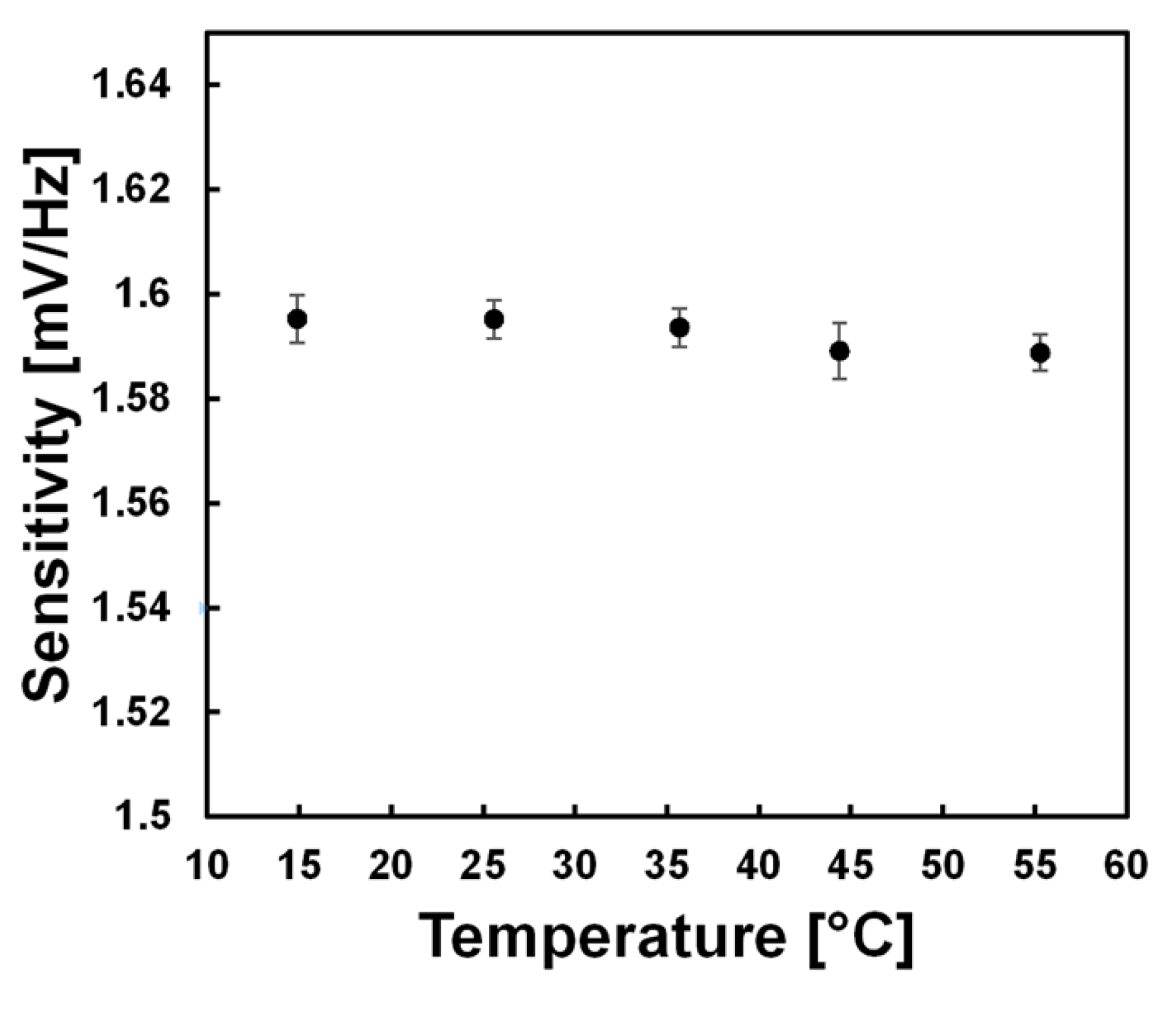
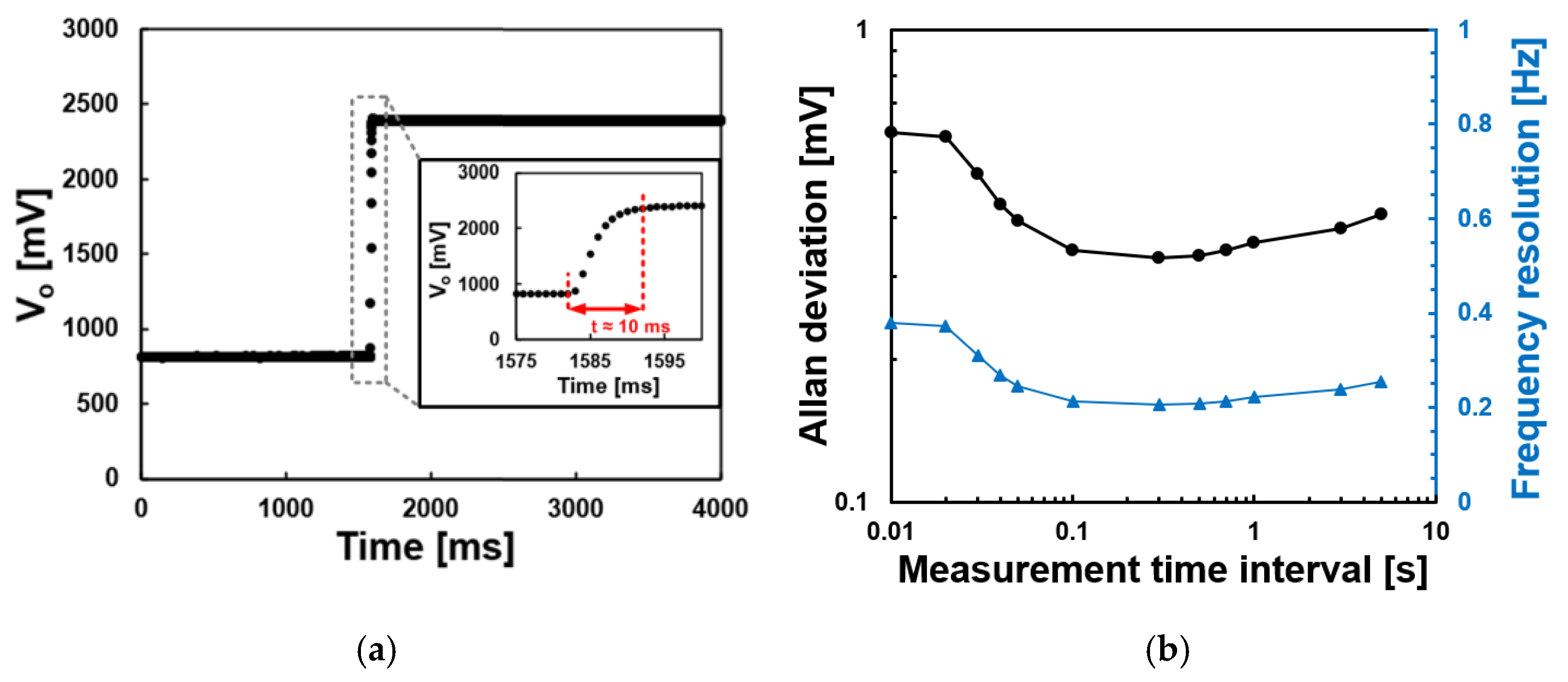
3.1. System Characterization
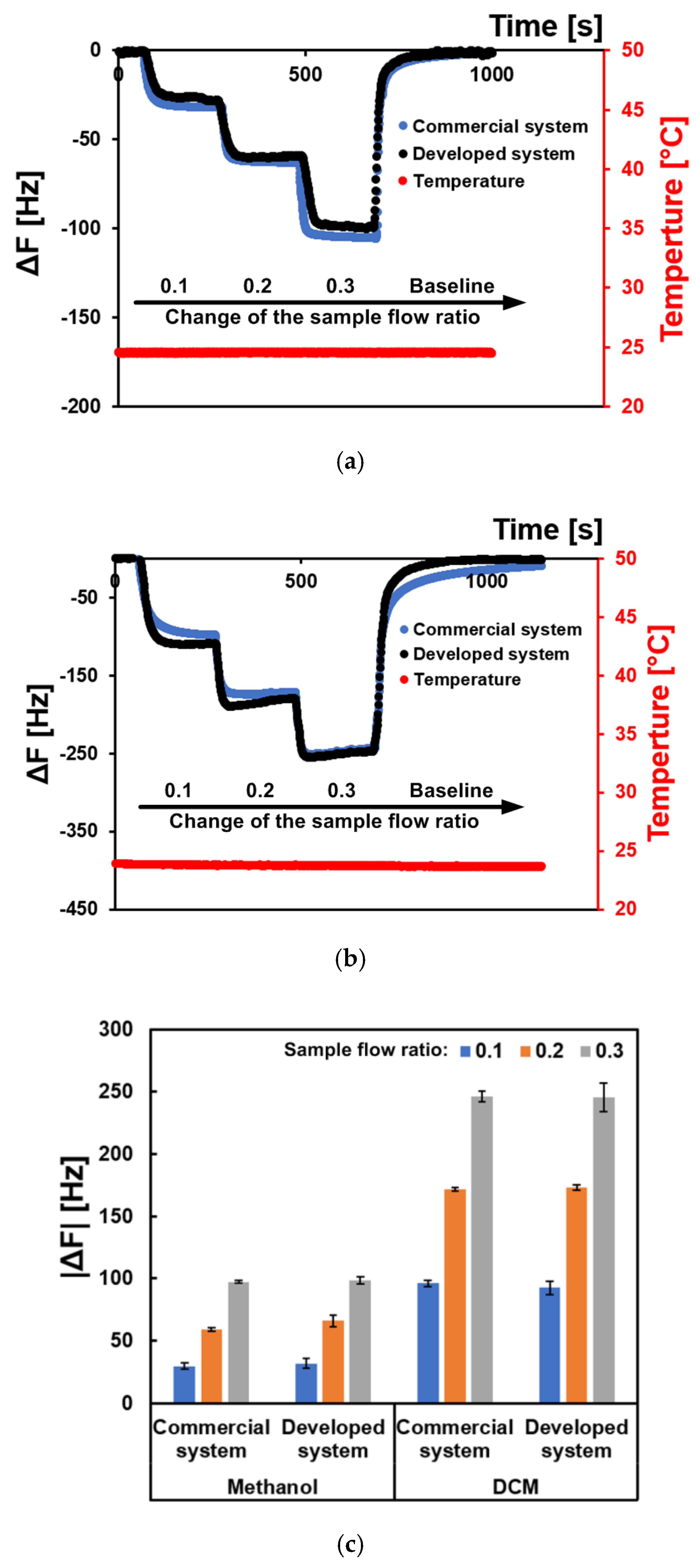
3.2. System Validation
4. Results and Discussions
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Sharma, P.; Ghosh, A.; Tudu, B.; Sabhapondit, S.; Baruah, B.D.; Tamuly, P.; Bhattacharyya, N.; Bandyopadhyay, R. Monitoring the fermentation process of black tea using QCM sensor based electronic nose. Sens. Actuators B Chem. 2015, 219, 146–157. [Google Scholar] [CrossRef]
- Li, Q.; Gu, Y.; Wang, N. Application of random forest classifier by means of a QCM-based e-nose in the identification of Chinese liquor flavors. IEEE Sens. J. 2017, 17, 1788–1794. [Google Scholar] [CrossRef]
- Aydemir, F.; Ebeoglu, M.A. A QCM sensor array-based electronic tongue with the optimized oscillator circuit using FPGA. IEEE Trans. Instrum. Meas. 2018, 67, 431–438. [Google Scholar] [CrossRef]
- Deisingh, A.K.; Stone, D.C.; Thompson, M. Applications of electronic noses and tongues in food analysis. Int. J. Food Sci. Technol. 2004, 39, 587–604. [Google Scholar] [CrossRef]
- Toniolo, R.; Pizzariello, A.; Dossi, N.; Lorenzon, S.; Abollino, O.; Bontempelli, G. Room temperature ionic liquids as useful overlayers for estimating food quality from their odor analysis by quartz crystal microbalance measurements. Anal. Chem. 2013, 85, 7241–7247. [Google Scholar] [CrossRef]
- Sankaran, S.; Panigrahi, S.; Mallik, S. Odorant binding protein based biomimetic sensors for detection of alcohols associated with Salmonella contamination in packaged beef. Biosens. Bioelectron. 2011, 26, 3103–3109. [Google Scholar] [CrossRef]
- Selig, M.J.; Gamaleldin, S.; Celli, G.B.; Marchuk, M.A.; Smilgies, D.-M.; Abbaspourrad, A. The stabilization of food grade copper-chlorophyllin in low pH solutions through association with anionic polysaccharides. Food Hydrocoll. 2020, 98, 105255. [Google Scholar] [CrossRef]
- Bwambok, D.; Siraj, N.; Macchi, S.; Larm, N.; Baker, G.; Pérez, R.; Ayala, C.; Walgama, C.; Pollard, D.; Rodriguez, J.; et al. QCM sensor arrays, electroanalytical techniques and NIR spectroscopy coupled to multivariate analysis for quality assessment of food products, raw materials, ingredients and foodborne pathogen detection: Challenges and breakthroughs. Sensors 2020, 20, 6982. [Google Scholar] [CrossRef]
- Speller, N.C.; Siraj, N.; Vaughan, S.; Speller, L.N.; Warner, I.M. QCM virtual multisensor array for fuel discrimination and detection of gasoline adulteration. Fuel 2017, 199, 38–46. [Google Scholar] [CrossRef]
- Vaughan, S.R.; Speller, N.C.; Chhotaray, P.; Mccarter, K.S.; Siraj, N.; Pérez, R.L.; Li, Y.; Warner, I.M. Class specific discrimination of volatile organic compounds using a quartz crystal microbalance based multisensor array. Talanta 2018, 188, 423–428. [Google Scholar] [CrossRef]
- Yang, M.; He, J. A copper–manganese composite oxide as QCM sensing layers for detection of formaldehyde gas. RSC Adv. 2018, 8, 22–27. [Google Scholar] [CrossRef] [Green Version]
- Bearzotti, A.; Macagnano, A.; Papa, P.; Venditti, I.; Zampetti, E. A study of a QCM sensor based on pentacene for the detection of BTX vapors in air. Sens. Actuators B Chem. 2017, 240, 1160–1164. [Google Scholar] [CrossRef]
- Wilson, A.D. Recent progress in the design and clinical development of electronic-nose technologies. Nanobiosensors Dis. Diagn. 2016, 5, 15–27. [Google Scholar] [CrossRef] [Green Version]
- Park, J.-Y.; Choi, J.-W. Electronic circuit systems for piezoelectric resonance sensors. J. Electrochem. Soc. 2020, 167, 037560. [Google Scholar] [CrossRef]
- Arnau, A. A review of interface electronic systems for AT-cut quartz crystal microbalance applications in liquids. Sensors 2008, 8, 370–411. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mills, C.; Chai, K.; Milgrew, M.; Glidle, A.; Cooper, J.; Cumming, D. A multiplexed impedance analyzer for characterizing polymer-coated QCM sensor arrays. IEEE Sens. J. 2006, 6, 996–1002. [Google Scholar] [CrossRef] [Green Version]
- Wudy, F.; Multerer, M.; Stock, C.; Schmeer, G.; Gores, H. Rapid impedance scanning QCM for electrochemical applications based on miniaturized hardware and high-performance curve fitting. Electrochim. Acta 2008, 53, 6568–6574. [Google Scholar] [CrossRef]
- Tumurbaatar, B.; Kim, M.-J.; Park, C.-H.; Kim, C.S. A portable and computer-simulation analysis for the real-time measurement of the QCMD systems for the biomedical application. Sens. Bio-Sens. Res. 2018, 21, 75–81. [Google Scholar] [CrossRef]
- Johansson, S. New frequency counting principle improves resolution. In Proceedings of the 2005 IEEE International Frequency Control Symposium and Exposition, Vancouver, BC, Canada, 29–31 August 2005; pp. 628–635. [Google Scholar]
- Karapınar, M.; Gürkan, S.; Öner, P.A.; Doğan, S. Design of a multi-channel quartz crystal microbalance data acquisition system. Meas. Sci. Technol. 2018, 29, 075009. [Google Scholar] [CrossRef]
- Syahbana, M.A.; Santjojo, D.J.H.D.; Sakti, S.P. High-resolution multiple channel frequency counter using spartan-3E FPGA. In Proceedings of the 2016 International Seminar on Sensors, Instrumentation, Measurement and Metrology (ISSIMM), Malang, Indonesia, 10–11 August 2016; pp. 111–114. [Google Scholar]
- Molanes, R.F.; Farina, J.; Rodriguez-Andina, J.J. Field-programmable system-on-chip for high-accuracy frequency measurements in QCM sensors. In Proceedings of the 39th Annual Conference of the IEEE Industrial Electronics Society (IECON 2013), Vienna, Austria, 10–13 November 2013; pp. 2267–2272. [Google Scholar]
- Torres, R.; Arnau, A.; Perrot, H. Electronic system for experimentation in AC electrogravimetry II: Implemented design. Revista EIA 2007, 7, 63–73. [Google Scholar]
- Wang, L.; Lin, A.; Kim, E.S. Miniature sensing system with FBAR-based oscillators and frequency shift detector. IEEE Sens. J. 2018, 18, 7633–7637. [Google Scholar] [CrossRef]
- Guha, A.; Sandström, N.; Ostanin, V.P.; Wijngaart, W.V.D.; Klenerman, D.; Ghosh, S.K. Simple and ultrafast resonance frequency and dissipation shift measurements using a fixed frequency drive. Sens. Actuators B Chem. 2019, 281, 960–970. [Google Scholar] [CrossRef]
- Robertson, D.G.E.; Dowling, J.J. Design and responses of butterworth and critically damped digital filters. J. Electromyogr. Kinesiol. 2003, 13, 569–573. [Google Scholar] [CrossRef]
- Land, D.V.; Levick, A.P.; Hand, J.W. The use of the Allan deviation for the measurement of the noise and drift performance of microwave radiometers. Meas. Sci. Technol. 2007, 18, 1917–1928. [Google Scholar] [CrossRef] [Green Version]
- Allan, D.W. Should the classical variance be used as a basic measure in standards metrology? IEEE Trans. Instrum. Meas. 1987, 36, 646–654. [Google Scholar] [CrossRef]
- Hung, K.K.; Ko, P.K.; Hu, C.; Cheng, Y.C. A unified model for the flicker noise in metal-oxide-semiconductor field-effect transistors. IEEE Trans. Electron Devices 1990, 37, 654–665. [Google Scholar] [CrossRef]
- Christensson, S.; Lundström, I.; Svensson, C. Low frequency noise in MOS transistors-I Theory. Solid-State Electron. 1968, 11, 797–812. [Google Scholar] [CrossRef]
- Allan, D.W. Statistics of atomic frequency standards. Proc. IEEE 1966, 54, 221–230. [Google Scholar] [CrossRef] [Green Version]
- Witt, T.J. Using the Allan variance and power spectral density to characterize DC nanovoltmeters. IEEE Trans. Instrum. Meas. 2001, 50, 445–448. [Google Scholar] [CrossRef]
- Witt, T.J.; Reymann, D. Using power spectra and Allan variances to characterise the noise of Zener-diode voltage standards. IEEE Proc.-Sci. Meas. Technol. 2000, 147, 177–182. [Google Scholar] [CrossRef]
- Lee, J.; Shen, W.; Payer, K.; Burg, T.P.; Manalis, S.R. Toward attogram mass measurements in solution with suspended nanochannel resonators. Nano Lett. 2010, 10, 2537–2542. [Google Scholar] [CrossRef] [Green Version]
- Bwambok, D.K.; El-Zahab, B.; Challa, S.K.; Li, M.; Chandler, L.; Baker, G.A.; Warner, I.M. Near-infrared fluorescent nanoGUMBOS for biomedical imaging. ACS Nano 2009, 3, 3854–3860. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Warner, I.M.; El-Zahab, B.; Siraj, N. Perspectives on moving ionic liquid chemistry into the solid phase. Anal. Chem. 2014, 86, 7184–7191. [Google Scholar] [CrossRef]
- Azevedo, A.M.O.; Santos, J.L.M.; Warner, I.M.; Saraiva, M.L.M.F.S. GUMBOS and nanoGUMBOS in chemical and biological analysis: A review. Anal. Chim. Acta 2020, 1133, 180–198. [Google Scholar] [CrossRef] [PubMed]

| Temperature (°C) | Sensitivity (mV/Hz) | Error (%) | |
|---|---|---|---|
| Average | Standard Deviation | ||
| 14.9 | 1.60 | 4.54 × 10−3 | 0.006 |
| 25.6 | 1.60 | 3.74 × 10−3 | NA |
| 35.7 | 1.59 | 3.59 × 10−3 | 0.100 |
| 44.4 | 1.59 | 5.37 × 10−3 | 0.382 |
| 55.3 | 1.59 | 3.39 × 10−3 | 0.401 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, J.-Y.; Pérez, R.L.; Ayala, C.E.; Vaughan, S.R.; Warner, I.M.; Choi, J.-W. A Miniaturized Quartz Crystal Microbalance (QCM) Measurement Instrument Based on a Phase-Locked Loop Circuit. Electronics 2022, 11, 358. https://doi.org/10.3390/electronics11030358
Park J-Y, Pérez RL, Ayala CE, Vaughan SR, Warner IM, Choi J-W. A Miniaturized Quartz Crystal Microbalance (QCM) Measurement Instrument Based on a Phase-Locked Loop Circuit. Electronics. 2022; 11(3):358. https://doi.org/10.3390/electronics11030358
Chicago/Turabian StylePark, Jong-Yoon, Rocío L. Pérez, Caitlan E. Ayala, Stephanie R. Vaughan, Isiah M. Warner, and Jin-Woo Choi. 2022. "A Miniaturized Quartz Crystal Microbalance (QCM) Measurement Instrument Based on a Phase-Locked Loop Circuit" Electronics 11, no. 3: 358. https://doi.org/10.3390/electronics11030358
APA StylePark, J.-Y., Pérez, R. L., Ayala, C. E., Vaughan, S. R., Warner, I. M., & Choi, J.-W. (2022). A Miniaturized Quartz Crystal Microbalance (QCM) Measurement Instrument Based on a Phase-Locked Loop Circuit. Electronics, 11(3), 358. https://doi.org/10.3390/electronics11030358








