A Survey on Capacitor Voltage Control in Neutral-Point-Clamped Multilevel Converters
Abstract
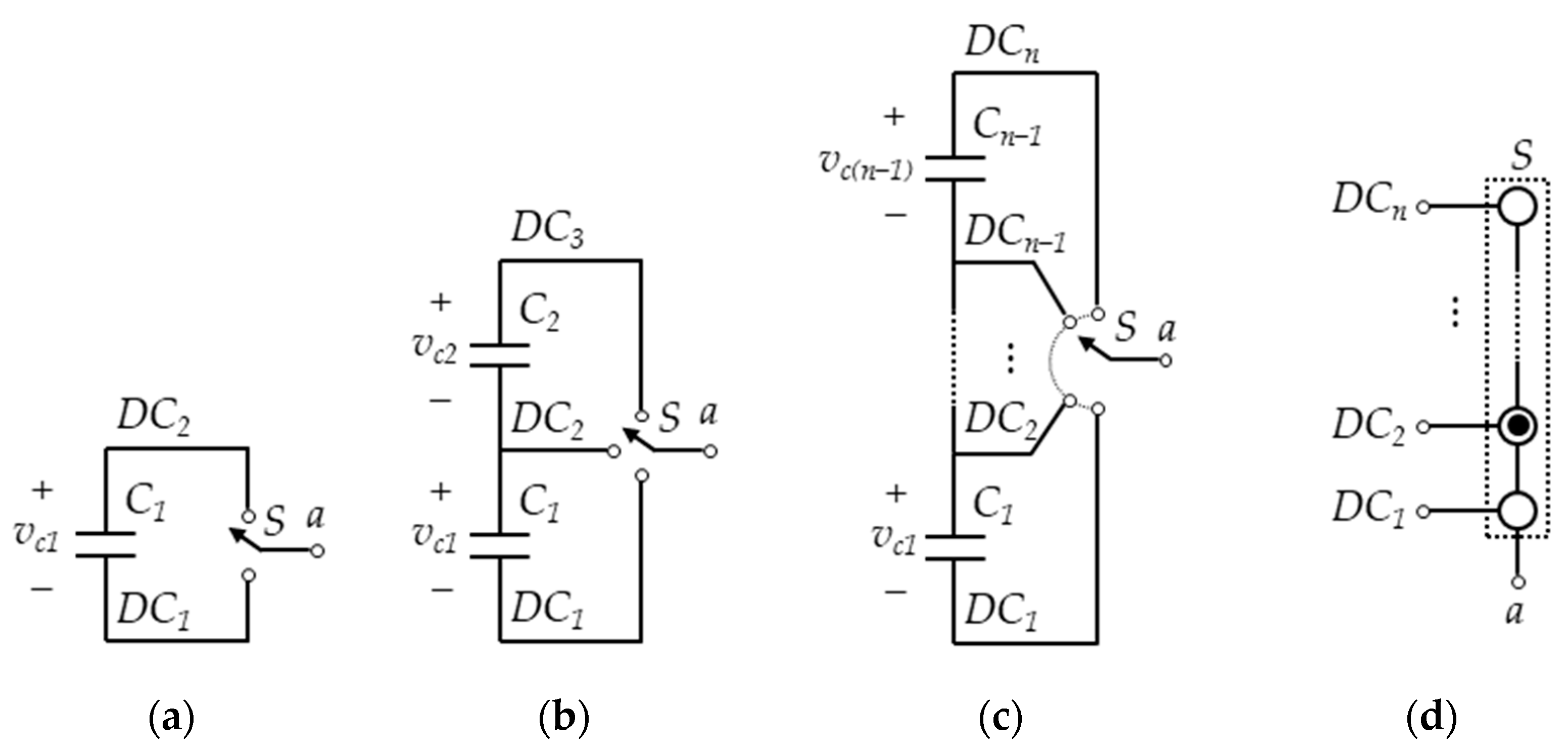
:1. Introduction
2. Fundamentals of NPC Multilevel Converters
2.1. Functional Diagram and Operating Principle
- The passive energy storage components such as capacitors and inductors are placed outside the power semiconductor array, enabling compact converter implementations with higher power density.
- Since the power devices only have to block VDC/(n − 1) voltage, typically, it enables higher converter DC-link voltage and power ratings.
- Better loss sharing among converter devices, improving the temperature performance of the converter and, subsequently, enhancing its reliability [39].
- The number of power semiconductor devices increases significantly with the number of levels.
- Typically, the DC-link capacitor voltages must be kept balanced at all time [16]. Unbalanced DC-link capacitor voltages cause some power devices to block more than one voltage level VDC/(n − 1), which is unacceptable in most cases as it can lead to a device overvoltage failure. Moreover, it typically generates low-frequency output voltage distortion [40,41].
2.2. Topologies
2.3. Modulations
2.3.1. Space Vector Control
2.3.2. Programmed Pulse Width Modulation (PWM)
2.3.3. Carrier-Based PWM
2.3.4. Space Vector Modulation (SVM)
2.3.5. Modulations for DC–DC Conversion
2.4. Control Methods without a Modulator
3. Analysis of the Capacitor Voltage Balance
4. Open-Loop Techniques
5. Closed-Loop Techniques
6. Hardware Methods
7. Balance in DC–DC Conversion
8. Converter Operation beyond Balance
9. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| ANPC | Active neutral-point-clamped converter |
| DAB | Dual active nridge |
| DPC | Direct power control |
| DTC | Direct torque control |
| FPGA | Field programmable gate array |
| MPC | Model predictive control |
| NPC | Neutral-point-clamped converter |
| NTV-SVM | Nearest-three-vectors SVM |
| PI | Proportional-integral controller |
| PID | Proportional-integral-derivative controller |
| PWM | Pulse width modulation |
| SHE | Selective harmonic elimination |
| SVM | Space vector modulation |
| VV-SVM | Virtual-vector SVM |
| 3D-SVM | Three-dimensional SVM |
References
- Nabae, A.; Takahashi, I.; Akagi, H. A New Neutral-Point-Clamped PWM Inverter. IEEE Trans. Ind. Appl. 1981, IA-17, 518–523. [Google Scholar] [CrossRef]
- Bhagwat, P.M.; Stefanovic, V.R. Generalized Structure of a Multilevel PWM Inverter. IEEE Trans. Ind. Appl. 1983, IA-19, 1057–1069. [Google Scholar] [CrossRef]
- Rodriguez, J.; Bernet, S.; Steimer, P.K.; Lizama, I.E. A Survey on Neutral-Point-Clamped Inverters. IEEE Trans. Ind. Electron. 2010, 57, 2219–2230. [Google Scholar] [CrossRef]
- Busquets-Monge, S. Neutral-Point-Clamped DC-AC Power Converters. In Wiley Encyclopedia of Electrical and Electronics Engineering; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2018; pp. 1–20. [Google Scholar]
- Choi, N.S.; Cho, J.G.; Cho, G.H. A General Circuit Topology of Multilevel Inverter. In Proceedings of the IEEE Power Electronics Specialists Conference (PESC), Cambridge, MA, USA, 24–27 June 1991; IEEE: Piscataway, NJ, USA, 1991; pp. 96–103. [Google Scholar]
- Yuan, X.; Barbi, I. Fundamentals of a new diode clamping multilevel inverter. IEEE Trans. Power Electron. 2000, 15, 711–718. [Google Scholar] [CrossRef]
- Abu-Rub, H.; Holtz, J.; Rodriguez, J.; Baoming, G. Medium-Voltage Multilevel Converters—State of the Art, Challenges, and Requirements in Industrial Applications. IEEE Trans. Ind. Electron. 2010, 57, 2581–2596. [Google Scholar] [CrossRef]
- Rodriguez, J.; Bernet, S.; Wu, B.; Pontt, J.O.; Kouro, S. Multilevel Voltage-Source-Converter Topologies for Industrial Medium-Voltage Drives. IEEE Trans. Ind. Electron. 2007, 54, 2930–2945. [Google Scholar] [CrossRef]
- Rodriguez, J.; Franquelo, L.G.; Kouro, S.; Leon, J.I.; Portillo, R.; Prats, M.A.M.; Perez, M.A. Multilevel Converters: An Enabling Technology for High-Power Applications. Proc. IEEE 2009, 97, 1786–1817. [Google Scholar] [CrossRef] [Green Version]
- Leon, J.I.; Vazquez, S.; Franquelo, L.G. Multilevel Converters: Control and Modulation Techniques for Their Operation and Industrial Applications. Proc. IEEE 2017, 105, 2066–2081. [Google Scholar] [CrossRef]
- Franquelo, L.G.; Rodriguez, J.; Leon, J.I.; Kouro, S.; Portillo, R.; Prats, M.A.M. The age of multilevel converters arrives. IEEE Ind. Electron. Mag. 2008, 2, 28–39. [Google Scholar] [CrossRef] [Green Version]
- Akagi, H. Multilevel Converters: Fundamental Circuits and Systems. Proc. IEEE 2017, 105, 2048–2065. [Google Scholar] [CrossRef]
- Rodriguez, J.; Lai, J.-S.; Peng, F.Z. Multilevel inverters: A survey of topologies, controls, and applications. IEEE Trans. Ind. Electron. 2002, 49, 724–738. [Google Scholar] [CrossRef] [Green Version]
- Mittal, N.; Singh, B.; Singh, S.; Dixit, R.; Kumar, D. Multilevel inverters: A literature survey on topologies and control strategies. In Proceedings of the 2012 2nd International Conference on Power, Control and Embedded Systems, Allahabad, India, 17–19 December 2012; pp. 1–11. [Google Scholar] [CrossRef]
- Sato, Y.; Ito, T. Experimental verification of loss reduction in diode-clamped multilevel inverters. In Proceedings of the 2011 IEEE Energy Conversion Congress and Exposition, Phoenix, AZ, USA, 17–22 September 2011; pp. 190–196. [Google Scholar] [CrossRef]
- Lai, J.; Peng, F.Z. Multilevel converters-a new breed of power converters. IEEE Trans. Ind. Appl. 1996, 32, 509–517. [Google Scholar] [CrossRef]
- Peng, F.Z. A generalized multilevel inverter topology with self voltage balancing. IEEE Trans. Ind. Appl. 2001, 37, 611–618. [Google Scholar] [CrossRef]
- Meynard, T.; Foch, H. Dispositif Électroniquede Conversion d’énergie Électrique 1991. pp. 1–57. Available online: https://patents.google.com/patent/WO1993002501A1/fr (accessed on 10 December 2021).
- Debnath, S.; Qin, J.; Bahrani, B.; Saeedifard, M.; Barbosa, P. Operation, Control, and Applications of the Modular Multilevel Converter: A Review. IEEE Trans. Power Electron. 2014, 30, 37–53. [Google Scholar] [CrossRef]
- Gateau, G.; Meynard, T.A.; Foch, H. Stacked Multicell Converter (SMC): Properties and Design. In Proceedings of the IEEE Power Electronics Specialists Conference (PESC), Vancouver, BC, Canada, 17–22 September 2001; Volume 3, pp. 1583–1588. [Google Scholar]
- Busquets-Monge, S.; Nicolas-Apruzzese, J. A Multilevel Active-Clamped Converter Topology—Operating Principle. IEEE Trans. Ind. Electron. 2010, 58, 3868–3878. [Google Scholar] [CrossRef]
- Vemuganti, H.P.; Sreenivasarao, D.; Ganjikunta, S.K.; Suryawanshi, H.M.; Abu-Rub, H. A Survey on Reduced Switch Count Multilevel Inverters. IEEE Open J. Ind. Electron. Soc. 2021, 2, 80–111. [Google Scholar] [CrossRef]
- Menzies, R.W.; Steimer, P.; Steinke, J.K. Five Level GTO Inverters for Large Induction Motor Drives. In Proceedings of the IEEE Industry Applications Conference (IAS), 2–8 October 1993; IEEE: Piscataway, NJ, USA; Volume 1, pp. 595–601. [Google Scholar]
- Kouro, S.; Malinowski, M.; Gopakumar, K.; Pou, J.; Franquelo, L.G.; Wu, B.; Rodriguez, J.; Perez, M.A.; Leon, J.I. Recent Advances and Industrial Applications of Multilevel Converters. IEEE Trans. Ind. Electron. 2010, 57, 2553–2580. [Google Scholar] [CrossRef]
- Welchko, B.A.; de Rossiter Correa, M.B.; Lipo, T.A. A Three-Level MOSFET Inverter for Low-Power Drives. IEEE Trans. Ind. Electron. 2004, 51, 669–674. [Google Scholar] [CrossRef]
- Teichmann, R.; Bernet, S. A Comparison of Three-Level Converters Versus Two-Level Converters for Low-Voltage Drives, Traction, and Utility Applications. IEEE Trans. Ind. Appl. 2005, 41, 855–865. [Google Scholar] [CrossRef]
- Schweizer, M.; Kolar, J.W. Design and Implementation of a Highly Efficient Three-Level T-Type Converter for Low-Voltage Applications. IEEE Trans. Power Electron. 2012, 28, 899–907. [Google Scholar] [CrossRef]
- Daher, S.; Schmid, J.; Antunes, F.L.M. Multilevel Inverter Topologies for Stand-Alone PV Systems. IEEE Trans. Ind. Electron. 2008, 55, 2703–2712. [Google Scholar] [CrossRef]
- Bezerra, P.A.M.; Krismer, F.; Kolar, J.W.; Aljameh, R.K.; Paredes, S.; Heller, R.; Brunschwiler, T.; Francese, P.A.; Morf, T.; Kossel, M.A.; et al. Electrical and Thermal Characterization of an Inductor-Based ANPC-Type Buck Converter in 14 nm CMOS Technology for Microprocessor Applications. IEEE Open J. Power Electron. 2020, 1, 456–468. [Google Scholar] [CrossRef]
- Marchesoni, M.; Tenca, P. Diode-clamped multilevel converters: A practicable way to balance DC-link voltages. IEEE Trans. Ind. Electron. 2002, 49, 752–765. [Google Scholar] [CrossRef]
- Ogasawara, S.; Akagi, H. Analysis of variation of neutral point potential in neutral-point-clamped voltage source PWM inverters. In Proceedings of the Conference Record of the 1993 IEEE Industry Applications Conference Twenty-Eighth IAS Annual Meeting, Toronto, ON, Canada, 2–8 October 1993; IEEE: Piscataway, NJ, USA, 1993; Volume 2, pp. 965–970. [Google Scholar] [CrossRef] [Green Version]
- Busquets-Monge, S.; Rocabert, J.; Rodriguez, P.; Alepuz, S.; Bordonau, J. Multilevel Diode-Clamped Converter for Photovoltaic Generators With Independent Voltage Control of Each Solar Array. IEEE Trans. Ind. Electron. 2008, 55, 2713–2723. [Google Scholar] [CrossRef]
- Busquets-Monge, S.; Filba-Martinez, A.; Alepuz, S.; Nicolas-Apruzzese, J.; Luque, A.; Roca, A.C.; Bordonau, J. Multibattery-Fed Neutral-Point-Clamped DC–AC Converter With SoC Balancing Control to Maximize Capacity Utilization. IEEE Trans. Ind. Electron. 2019, 67, 16–27. [Google Scholar] [CrossRef]
- Nicolas-Apruzzese, J.; Busquets-Monge, S.; Bordonau, J.; Alepuz, S.; Calle-Prado, A.; Filba-Martinez, A. Experimental Effi-ciency Comparison between a Four-Level Active-Clamped and a Two-Level Topology. In Proceedings of the IEEE Industrial Electronics Conference (IECON), Vienna, Austria, 10–14 November 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 6227–6232. [Google Scholar]
- Lim, Z.; Maswood, A.I.; Ooi, G.H.P.; Ooi, H.P.G. Common-Mode Reduction for ANPC With Enhanced Harmonic Profile Using Interleaved Sawtooth Carrier Phase-Disposition PWM. IEEE Trans. Ind. Electron. 2016, 63, 7887–7897. [Google Scholar] [CrossRef]
- Yaramasu, V.; Wu, B.; Rivera, M.; Narimani, M.; Kouro, S.; Rodriguez, J. Generalised approach for predictive control with common-mode voltage mitigation in multilevel diode-clamped converters. IET Power Electron. 2015, 8, 1440–1450. [Google Scholar] [CrossRef]
- Lezana, P.; Pou, J.; Meynard, T.; Rodriguez, J.; Ceballos, S.; Richardeau, F. Survey on Fault Operation on Multilevel Inverters. IEEE Trans. Ind. Electron. 2009, 57, 2207–2218. [Google Scholar] [CrossRef] [Green Version]
- Azer, P.; Ounie, S.; Narimani, M. A New Post-Fault Control Method Based on Sinusoidal Pulse Width Modulation Technique for a Neutral Point Clamped (NPC) Inverter. In Proceedings of the IEEE Applied Power Electronics Conference and Exposition (APEC), Anaheim, CA, USA, 17–21 March 2019; pp. 2499–2504. [Google Scholar] [CrossRef]
- Bruckner, T.; Bernet, S.; Guldner, H. The Active NPC Converter and Its Loss-Balancing Control. IEEE Trans. Ind. Electron. 2005, 52, 855–868. [Google Scholar] [CrossRef]
- Celanovic, N.; Boroyevich, D. A comprehensive study of neutral-point voltage balancing problem in three-level neutral-point-clamped voltage source PWM inverters. IEEE Trans. Power Electron. 2000, 15, 242–249. [Google Scholar] [CrossRef]
- Jiang, W.-D.; Du, S.-W.; Chang, L.-C.; Zhang, Y.; Zhao, Q. Hybrid PWM Strategy of SVPWM and VSVPWM for NPC Three-Level Voltage-Source Inverter. IEEE Trans. Power Electron. 2010, 25, 2607–2619. [Google Scholar] [CrossRef]
- Hatti, N.; Hasegawa, K.; Akagi, H. A 6.6-kV Transformerless Motor Drive Using a Five-Level Diode-Clamped PWM Inverter for Energy Savings of Pumps and Blowers. IEEE Trans. Power Electron. 2009, 24, 796–803. [Google Scholar] [CrossRef]
- Hasegawa, K.; Akagi, H. Low-Modulation-Index Operation of a Five-Level Diode-Clamped PWM Inverter With a DC-Voltage-Balancing Circuit for a Motor Drive. IEEE Trans. Power Electron. 2012, 27, 3495–3504. [Google Scholar] [CrossRef]
- Lee, J.-S.; Lee, K.-B. New Modulation Techniques for a Leakage Current Reduction and a Neutral-Point Voltage Balance in Transformerless Photovoltaic Systems Using a Three-Level Inverter. IEEE Trans. Power Electron. 2013, 29, 1720–1732. [Google Scholar] [CrossRef]
- Naik, T.; Wandhare, R.G.; Agarwal, V. Three-Level NPC Inverter with Novel Voltage Equalization for PV Grid Interface Suitable for Partially Shaded Conditions. In Proceedings of the IEEE Power and Energy Conference at Illinois (PECI), Urbana, IL, USA, 22–23 February 2013; pp. 186–193. [Google Scholar]
- Alepuz, S.; Busquets-Monge, S.; Bordonau, J.; Gago, J.; Gonzalez, D.; Balcells, J. Interfacing Renewable Energy Sources to the Utility Grid Using a Three-Level Inverter. IEEE Trans. Ind. Electron. 2006, 53, 1504–1511. [Google Scholar] [CrossRef]
- Yaramasu, V.; Wu, B.; Rivera, M.; Rodriguez, J. A New Power Conversion System for Megawatt PMSG Wind Turbines Using Four-Level Converters and a Simple Control Scheme Based on Two-Step Model Predictive Strategy—Part I: Modeling and Theoretical Analysis. IEEE J. Emerg. Sel. Top. Power Electron. 2013, 2, 3–13. [Google Scholar] [CrossRef]
- Yaramasu, V.; Wu, B.; Rivera, M.; Rodriguez, J. A New Power Conversion System for Megawatt PMSG Wind Turbines Using Four-Level Converters and a Simple Control Scheme Based on Two-Step Model Predictive Strategy—Part II: Simulation and Experimental Analysis. IEEE J. Emerg. Sel. Top. Power Electron. 2013, 2, 14–25. [Google Scholar] [CrossRef]
- Faulstich, A.; Steinke, J.K.; Wittwer, F. Medium Voltage Converter for Permanent Magnet Wind Power Generators up to 5 MW. In Proceedings of the European Conference on Power Electronics and Applications (EPE), Dresden, Germany, 11–14 September 2005; IEEE: Piscataway, NJ, USA, 2005; pp. 1–9. [Google Scholar]
- Shu, Z.; Ding, N.; Chen, J.; Zhu, H.; He, X. Multilevel SVPWM With DC-Link Capacitor Voltage Balancing Control for Diode-Clamped Multilevel Converter Based STATCOM. IEEE Trans. Ind. Electron. 2012, 60, 1884–1896. [Google Scholar] [CrossRef]
- Friedemann, R.A.; Krismer, F.; Kolar, J.W. Design of a minimum weight dual active bridge converter for an Airborne Wind Turbine system. In Proceedings of the 2012 Twenty-Seventh Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Orlando, FL, USA, 5–9 February 2012; pp. 509–516. [Google Scholar] [CrossRef]
- Yuan, X. Derivation of Voltage Source Multilevel Converter Topologies. IEEE Trans. Ind. Electron. 2016, 64, 966–976. [Google Scholar] [CrossRef] [Green Version]
- Bruckner, T.; Bemet, S. Loss Balancing in Three-Level Voltage Source Inverters Applying Active NPC Switches. In Proceedings of the IEEE Power Electronics Specialists Conference (PESC), Vancouver, BC, Canada, 17–21 June 2001; IEEE: Piscataway, NJ, USA, 2001; Volume 2, pp. 1135–1140. [Google Scholar]
- Brückner, T.; Bernet, S.; Steimer, P.K. Feedforward Loss Control of Three-Level Active NPC Converters. IEEE Trans. Ind. Appl. 2007, 43, 1588–1596. [Google Scholar] [CrossRef]
- Dixon, J.; Moran, L. High-level multistep inverter optimization using a minimum number of power transistors. IEEE Trans. Power Electron. 2006, 21, 330–337. [Google Scholar] [CrossRef]
- Wang, J.; Yuan, X.; Dagan, K.J.; Bloor, A. Optimal Neutral Point Voltage Balancing Algorithm for Three-phase Three-level Converters with Hybrid Zero-sequence Signal Injection and Virtual Zero-level Modulation. IEEE Trans. Ind. Appl. 2020, 56, 1. [Google Scholar] [CrossRef]
- Wang, J.; Yuan, X.; Jin, B.; Laird, I. Closed-Loop DC-Link Voltage Balancing Algorithm for a Four-Level π-Type Converter. In Proceedings of the IEEE Industrial Electronics Conference (IECON), Lisbon, Portugal, 1 October 2019; pp. 3529–3534. [Google Scholar]
- Jin, B.; Yuan, X. Topology, Efficiency Analysis, and Control of a Four-Level $\pi$ -Type Converter. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 7, 1044–1059. [Google Scholar] [CrossRef]
- Rodriguez, J.; Moran, L.; Correa, P.; Silva, C. A vector control technique for medium-voltage multilevel inverters. IEEE Trans. Ind. Electron. 2002, 49, 882–888. [Google Scholar] [CrossRef]
- Dahidah, M.S.A.; Konstantinou, G.; Agelidis, V.G. A Review of Multilevel Selective Harmonic Elimination PWM: Formulations, Solving Algorithms, Implementation and Applications. IEEE Trans. Power Electron. 2014, 30, 4091–4106. [Google Scholar] [CrossRef]
- Leon, J.I.; Kouro, S.; Franquelo, L.G.; Rodriguez, J.; Wu, B. The Essential Role and the Continuous Evolution of Modulation Techniques for Voltage-Source Inverters in the Past, Present, and Future Power Electronics. IEEE Trans. Ind. Electron. 2016, 63, 2688–2701. [Google Scholar] [CrossRef]
- McGrath, B.; Holmes, D. Multicarrier PWM strategies for multilevel inverters. IEEE Trans. Ind. Electron. 2002, 49, 858–867. [Google Scholar] [CrossRef]
- Carrara, G.; Gardella, S.; Marchesoni, M.; Salutari, R.; Sciutto, G. A new multilevel PWM method: A theoretical analysis. IEEE Trans. Power Electron. 1992, 7, 497–505. [Google Scholar] [CrossRef]
- van der Broeck, H.; Skudelny, H.-C.; Stanke, G. Analysis and realization of a pulsewidth modulator based on voltage space vectors. IEEE Trans. Ind. Appl. 1988, 24, 142–150. [Google Scholar] [CrossRef]
- Holmes, D.G.; Lipo, T.A. Pulse Width Modulation for Power Converters-Principles and Practice; IEEE Press-John Wiley & Sons: Piscataway, NJ, USA, 2003. [Google Scholar]
- Celanovic, N.; Boroyevich, D. A fast space-vector modulation algorithm for multilevel three-phase converters. IEEE Trans. Ind. Appl. 2001, 37, 637–641. [Google Scholar] [CrossRef]
- Seo, J.H.; Choi, C.H.; Hyun, D.-S. A new simplified space-vector PWM method for three-level inverters. IEEE Trans. Power Electron. 2001, 16, 545–550. [Google Scholar] [CrossRef]
- Tan, Z.; Li, Y.; Li, M. A Direct Torque Control of Induction Motor Based on Three-Level NPC Inverter. In Proceedings of the IEEE Power Electronics Specialists Conference (PESC), Vancouver, BC, Canada, 17–21 June 2001; Volume 3, pp. 1435–1439. [Google Scholar]
- Busquets-Monge, S.; Bordonau, J.; Boroyevich, D.; Somavilla, S. The nearest three virtual space vector PWM - A modulation for the comprehensive neutral-point balancing in the three-level NPC inverter. IEEE Power Electron. Lett. 2004, 2, 11–15. [Google Scholar] [CrossRef]
- Gui, S.W.; Lin, Z.J.; Huang, S.H. A Varied VSVM Strategy for Balancing the Neutral-Point Voltage of DC-Link Capacitors in Three-Level NPC Converters. Energies 2015, 8, 2032–2047. [Google Scholar] [CrossRef] [Green Version]
- Prats, M.; Franquelo, L.G.; Portillo, R.; Leon, J.I.; Galvan, E.; Carrasco, J. A 3-D space vector modulation generalized algorithm for multilevel converters. IEEE Power Electron. Lett. 2003, 1, 110–114. [Google Scholar] [CrossRef]
- Franquelo, L.; Prats, M.; Portillo, R.; Galvan, J.; Perales, M.; Carrasco, J.; Diez, E.; Jimenez, J. Three-dimensional space-vector modulation algorithm for four-leg multilevel converters using abc coordinates. IEEE Trans. Ind. Electron. 2006, 53, 458–466. [Google Scholar] [CrossRef]
- Holmes, D. The general relationship between regular-sampled pulse-width-modulation and space vector modulation for hard switched converters. In Proceedings of the Conference Record of the 1992 IEEE Industry Applications Society Annual Meeting, Houston, TX, USA, 4–9 October 1992; Volume 1, pp. 1002–1009. [Google Scholar] [CrossRef]
- Bowes, S.; Lai, Y.-S. The relationship between space-vector modulation and regular-sampled PWM. IEEE Trans. Ind. Electron. 1997, 44, 670–679. [Google Scholar] [CrossRef]
- Zhou, K.; Wang, D. Relationship between space-vector modulation and three-phase carrier-based PWM: A comprehensive analysis [three-phase inverters]. IEEE Trans. Ind. Electron. 2002, 49, 186–196. [Google Scholar] [CrossRef]
- Wang, F. Sine-triangle versus space-vector modulation for three-level PWM voltage-source inverters. IEEE Trans. Ind. Appl. 2002, 38, 500–506. [Google Scholar] [CrossRef]
- Chen, J.; He, Y.; Hasan, S.U.; Liu, J. A Comprehensive Study on Equivalent Modulation Waveforms of the SVM Sequence for Three-Level Inverters. IEEE Trans. Power Electron. 2015, 30, 7149–7158. [Google Scholar] [CrossRef]
- Sourkounis, C.; Al-Diab, A. A comprehensive analysis and comparison between Multilevel Space-Vector Modulation and Multilevel Carrier-Based PWM. In Proceedings of the 2008 13th International Power Electronics and Motion Control Conference, Poznan, Poland, 1–3 September 2008; pp. 1710–1715. [Google Scholar] [CrossRef]
- Busquets-Monge, S.; Alepuz, S.; Bordonau, J. A novel bidirectional multilevel boost-buck dc-dc Convert. In Proceedings of the 2009 IEEE Energy Conversion Congress and Exposition, San Jose, CA, USA, 20–24 September 2009; pp. 707–714. [Google Scholar] [CrossRef] [Green Version]
- Liu, P.; Chen, C.; Duan, S.; Zhu, W. Dual Phase-Shifted Modulation Strategy for the Three-Level Dual Active Bridge DC–DC Converter. IEEE Trans. Ind. Electron. 2017, 64, 7819–7830. [Google Scholar] [CrossRef]
- Filba-Martinez, A.; Busquets-Monge, S.; Bordonau, J. Modulation and Capacitor Voltage Balancing Control of Multilevel NPC Dual Active Bridge DC–DC Converters. IEEE Trans. Ind. Electron. 2019, 67, 2499–2510. [Google Scholar] [CrossRef]
- Sapin, A.; Steimer, P.K.; Simond, J.-J. Modeling, Simulation, and Test of a Three-Level Voltage-Source Inverter With Output $LC$ Filter and Direct Torque Control. IEEE Trans. Ind. Appl. 2007, 43, 469–475. [Google Scholar] [CrossRef]
- Rivera, S.; Kouro, S.; Wu, B.; Alepuz, S.; Malinowski, M.; Cortes, P.; Rodriguez, J. Multilevel Direct Power Control—A Generalized Approach for Grid-Tied Multilevel Converter Applications. IEEE Trans. Power Electron. 2013, 29, 5592–5604. [Google Scholar] [CrossRef]
- Vargas, R.; Cortes, P.; Ammann, U.; Rodriguez, J.; Pontt, J. Predictive Control of a Three-Phase Neutral-Point-Clamped Inverter. IEEE Trans. Ind. Electron. 2007, 54, 2697–2705. [Google Scholar] [CrossRef]
- Martins, C.; Roboam, X.; Meynard, T.; Carvalho, A. Switching frequency imposition and ripple reduction in DTC drives by using a multilevel converter. IEEE Trans. Power Electron. 2002, 17, 286–297. [Google Scholar] [CrossRef]
- Cortes, P.; Rodriguez, J.; Quevedo, D.E.; Silva, C. Predictive Current Control Strategy With Imposed Load Current Spectrum. IEEE Trans. Power Electron. 2008, 23, 612–618. [Google Scholar] [CrossRef]
- Verne, S.A.; Gonzalez, S.A.; Valla, M.I. An optimization algorithm for capacitor voltage balance of N-level Diode Clamped Inverters. In Proceedings of the 2008 34th Annual Conference of IEEE Industrial Electronics, Orlando, FL, USA, 10–13 November 2008; pp. 3201–3206. [Google Scholar] [CrossRef]
- Steinke, J. Switching frequency optimal PWM control of a three-level inverter. IEEE Trans. Power Electron. 1992, 7, 487–496. [Google Scholar] [CrossRef]
- Wang, K.; Zheng, Z.; Xu, L.; Li, Y. A Generalized Carrier-Overlapped PWM Method for Neutral-Point-Clamped Multilevel Converters. IEEE Trans. Power Electron. 2020, 35, 9095–9106. [Google Scholar] [CrossRef]
- Busquets-Monge, S.; Bordonau, J.; Rocabert, J. A Virtual-Vector Pulsewidth Modulation for theFour-Level Diode-Clamped DC–AC Converter. IEEE Trans. Power Electron. 2008, 23, 1964–1972. [Google Scholar] [CrossRef]
- Imarazene, K.; Chekireb, H.; Berkouk, E.M. Balancing DC Link Using the Redundant States Method in Selective Harmonics Elimination PWM. In Proceedings of the International Symposium on Advanced Electromechanical Motion Systems and Electric Drives (ELECTROMOTION), Lillie, France, 1–3 July 2009. [Google Scholar]
- Wu, M.; Li, Y.W.; Konstantinou, G. A Comprehensive Review of Capacitor Voltage Balancing Strategies for Multilevel Converters Under Selective Harmonic Elimination PWM. IEEE Trans. Power Electron. 2020, 36, 2748–2767. [Google Scholar] [CrossRef]
- Pan, Z.; Peng, F.Z.; Corzine, K.; Stefanovic, V.; Leuthen, J.; Gataric, S. Voltage Balancing Control of Diode-Clamped Multilevel Rectifier/Inverter Systems. IEEE Trans. Ind. Appl. 2005, 41, 1698–1706. [Google Scholar] [CrossRef]
- Celanovic, N.; Celanovic, I.; Boroyevich, D. The feedforward method of controlling three-level diode clamped converters with small DC-link capacitors. In Proceedings of the 2001 IEEE 32nd Annual Power Electronics Specialists Conference, Vancouver, BC, Canada, 17–21 June 2001; Volume 3, pp. 1357–1362. [Google Scholar] [CrossRef]
- Seo, J.H.; Choi, C.H. Compensation for the Neutral-Point Potential Variation in Three-Level Space Vector PWM. In Proceedings of the IEEE Applied Power Electronics Conference and Exposition (APEC), Anaheim, CA, USA, 4–8 March 2001; Volume 2, pp. 1135–1140. [Google Scholar]
- Mouton, H.D.T. Natural balancing of three-level neutral-point-clamped PWM inverters. IEEE Trans. Ind. Electron. 2002, 49, 1017–1025. [Google Scholar] [CrossRef]
- Stala, R. A Natural DC-Link Voltage Balancing of Diode-Clamped Inverters in Parallel Systems. IEEE Trans. Ind. Electron. 2012, 60, 5008–5018. [Google Scholar] [CrossRef]
- Shen, J.; Schröder, S.; Rösner, R.; Elbarbari, S.F.S. A Comprehensive Study of Neutral-Point Self-Balancing Effect in Neutral-Point-Clamped Three-Level Inverters. IEEE Trans. Power Electron. 2011, 26, 3084–3095. [Google Scholar] [CrossRef]
- Newton, C.; Sumner, M. Neutral Point Control for Multi-Level Inverters: Theory, Design and Operational Limitations. In Proceedings of the IEEE Industry Applications Conference (IAS), New Orleans, LA, USA, 5–9 October 1997; pp. 1336–1343. [Google Scholar]
- Fracchia, M.; Ghiara, T.; Marchesoni, M.; Mazzucchelli, M. Optimized Modulation Techniques for the Generalized N-Level Converter. In Proceedings of the IEEE Power Electronics Specialists Conference (PESC), Toledo, Spain, 29 June–3 July 1992; Institute of Electrical and Electronics Engineers Inc.: Manhattan, NY, USA; pp. 1205–1213. [Google Scholar]
- Marchesoni, M.; Tenca, P. Theoretical and Practical Limits in Multilevel MPC Inverters with Passive Front Ends. In Proceedings of the European Conference on Power Electronics and Applications (EPE), Graz, Austria, 22–24 June 2001; pp. 1–10. [Google Scholar]
- Busquets-Monge, S.; Ortega, J.D.; Bordonau, J.; Beristain, J.A.; Rocabert, J. Closed-Loop Control of a Three-Phase Neutral-Point-Clamped Inverter Using an Optimized Virtual-Vector-Based Pulsewidth Modulation. IEEE Trans. Ind. Electron. 2008, 55, 2061–2071. [Google Scholar] [CrossRef]
- Lee, D.H.; Lee, S.R.; Lee, F.C. An Analysis of Midpoint Balance for the Neutral-Point-Clamped Three-Level VSI. In Proceedings of the IEEE Power Electronics Specialists Conference (PESC), Fukuoka, Japan, 22–22 May 1998; Volume 1, pp. 193–199. [Google Scholar]
- Pou, J.; Pindado, R.; Boroyevich, D.; Rodriguez, P. Evaluation of the Low-Frequency Neutral-Point Voltage Oscillations in the Three-Level Inverter. IEEE Trans. Ind. Electron. 2005, 52, 1582–1588. [Google Scholar] [CrossRef]
- Wang, C.; Li, Y. Analysis and Calculation of Zero-Sequence Voltage Considering Neutral-Point Potential Balancing in Three-Level NPC Converters. IEEE Trans. Ind. Electron. 2009, 57, 2262–2271. [Google Scholar] [CrossRef]
- Busquets-Monge, S.; Alepuz, S.; Rocabert, J.; Bordonau, J. Pulsewidth Modulations for the Comprehensive Capacitor Voltage Balance of $n$-Level Three-Leg Diode-Clamped Converters. IEEE Trans. Power Electron. 2009, 24, 1364–1375. [Google Scholar] [CrossRef] [Green Version]
- Busquets-Monge, S.; Alepuz, S.; Rocabert, J.; Bordonau, J. Pulsewidth Modulations for the Comprehensive Capacitor Voltage Balance of $n$-Level Two-Leg Diode-Clamped Converters. IEEE Trans. Power Electron. 2009, 24, 1951–1959. [Google Scholar] [CrossRef]
- Monge, S.B.; Somavilla, S.; Bordonau, J.; Boroyevich, D. Capacitor Voltage Balance for the Neutral-Point- Clamped Converter using the Virtual Space Vector Concept With Optimized Spectral Performance. IEEE Trans. Power Electron. 2007, 22, 1128–1135. [Google Scholar] [CrossRef]
- Busquets-Monge, S.; Ruderman, A. Carrier-Based PWM Strategies for the Comprehensive Capacitor Voltage Balance of Mul-tilevel Multileg Diode-Clamped Converters. In Proceedings of the IEEE International Symposium on Industrial Electronics (ISIE), Bari, Italy, 4–7 July 2010; pp. 688–693. [Google Scholar]
- Busquets-Monge, S.; Maheshwari, R.; Munk-Nielsen, S. Overmodulation of $n$-Level Three-Leg DC–AC Diode-Clamped Converters With Comprehensive Capacitor Voltage Balance. IEEE Trans. Ind. Electron. 2012, 60, 1872–1883. [Google Scholar] [CrossRef]
- Maheshwari, R.; Munk-Nielsen, S.; Busquets-Monge, S. A carrier-based approach for overmodulation of three-level neutral-point-clamped inverter with zero neutral-point current. In Proceedings of the 2012 IEEE Energy Conversion Congress and Exposition (ECCE), Raleigh, NC, USA, 15–20 September 2012. [Google Scholar] [CrossRef]
- Busquets-Monge, S.; Bordonau, J.; Beristáin, J.A. Comparison of Losses and Thermal Performance of a Three-Level Three-Phase Neutral-Point-Clamped Dc-Ac Converter under a Conventional NTV and the NTV 2 Modulation Strategies. In Proceedings of the IEEE Industrial Electronics Conference (IECON), Paris, France, 6–10 November 2006; pp. 4819–4824. [Google Scholar]
- Wang, K.; Zheng, Z.; Li, Y. A Novel Carrier-Overlapped PWM Method for Four-Level Neutral-Point Clamped Converters. IEEE Trans. Power Electron. 2018, 34, 7–12. [Google Scholar] [CrossRef]
- Wang, K.; Zheng, Z.; Xu, L.; Li, Y. Neutral-Point Voltage Balancing Method for Five-Level NPC Inverters Based on Carrier-Overlapped PWM. IEEE Trans. Power Electron. 2020, 36, 1428–1440. [Google Scholar] [CrossRef]
- Xia, C.; Shao, H.; Zhang, Y.; He, X. Adjustable Proportional Hybrid SVPWM Strategy for Neutral-Point-Clamped Three-Level Inverters. IEEE Trans. Ind. Electron. 2012, 60, 4234–4242. [Google Scholar] [CrossRef]
- Fazio, P.; Maragliano, G.; Marchesoni, M.; Vaccaro, L. A New Capacitor Balancing Technique in Diode-Clamped Multilevel Converters with Active Front End for Extended Operation Range. In Proceedings of the European Conference on Power Electronics and Applications (EPE), Birmingham, UK, 30 August–1 September 2011; pp. 1–10. [Google Scholar]
- Pou, J.; Boroyevich, D.; Pindado, R. New feedforward space-vector PWM method to obtain balanced AC output voltages in a three-level neutral-point-clamped converter. IEEE Trans. Ind. Electron. 2002, 49, 1026–1034. [Google Scholar] [CrossRef]
- Li, Y.; Gao, Y.; Hou, X. A general SVM Algorithm for Multilevel Converters Considering Zero-Sequence Component Control. In Proceedings of the IEEE Industrial Electronics Conference (IECON), Raleigh, NC, USA, 6–10 November 2005; Volume 2005, pp. 508–513. [Google Scholar]
- Wang, J.; Wang, J.; Xiao, B.; Gui, Z.; Jiang, W. Full Range Capacitor Voltage Balance PWM Strategy for Diode-Clamped Multilevel Inverter. Electronics 2020, 9, 1263. [Google Scholar] [CrossRef]
- Pou, J.; Zaragoza, J.; Ceballos, S.; Saeedifard, M.; Boroyevich, D. A Carrier-Based PWM Strategy With Zero-Sequence Voltage Injection for a Three-Level Neutral-Point-Clamped Converter. IEEE Trans. Power Electron. 2010, 27, 642–651. [Google Scholar] [CrossRef]
- Shen, J.; Schroder, S.; Duro, B.; Roesner, R. A Neutral-Point Balancing Controller for a Three-Level Inverter With Full Power-Factor Range and Low Distortion. IEEE Trans. Ind. Appl. 2012, 49, 138–148. [Google Scholar] [CrossRef]
- Kim, J.-S.; Kwon, J.-M. Direct Space Vector Modulation with Novel DC-link Voltage Balancing Algorithm for Easy Software Implementation of Three-Phase Three-Level Converter. Electronics 2020, 9, 1841. [Google Scholar] [CrossRef]
- Qamar, M.A.; Wang, K.; Zheng, Z.; Wang, S.; Li, Y. A Simplified Virtual Vector PWM Algorithm to Balance the Capacitor Voltages of Four-Level Diode-Clamped Converter. IEEE Access 2020, 8, 180896–180908. [Google Scholar] [CrossRef]
- Busquets-Monge, S.; Alepuz, S.; Bordonau, J.; Peracaula, J. Voltage Balancing Control of Diode-Clamped Multilevel Converters With Passive Front-Ends. IEEE Trans. Power Electron. 2008, 23, 1751–1758. [Google Scholar] [CrossRef]
- Xiang, C.-Q.; Shu, C.; Han, D.; Mao, B.-K.; Wu, X.; Yu, T.-J. Improved Virtual Space Vector Modulation for Three-Level Neutral-Point-Clamped Converter With Feedback of Neutral-Point Voltage. IEEE Trans. Power Electron. 2017, 33, 5452–5464. [Google Scholar] [CrossRef]
- Xia, S.; Wu, X.; Zheng, J.; Li, X.; Wang, K. A Virtual Space Vector PWM With Active Neutral Point Voltage Control and Common Mode Voltage Suppression for Three-Level NPC Converters. IEEE Trans. Ind. Electron. 2021, 68, 11761–11771. [Google Scholar] [CrossRef]
- Jiang, W.; Wang, P.; Ma, M.; Wang, J.; Li, J.; Li, L.; Chen, K.; Weidong, J. A Novel Virtual Space Vector Modulation With Reduced Common-Mode Voltage and Eliminated Neutral Point Voltage Oscillation for Neutral Point Clamped Three-Level Inverter. IEEE Trans. Ind. Electron. 2019, 67, 884–894. [Google Scholar] [CrossRef]
- Hu, C.; Yu, X.; Holmes, D.G.; Shen, W.; Wang, Q.; Luo, F.; Liu, N. An Improved Virtual Space Vector Modulation Scheme for Three-Level Active Neutral-Point-Clamped Inverter. IEEE Trans. Power Electron. 2016, 32, 7419–7434. [Google Scholar] [CrossRef]
- Li, C.; Yang, T.; Kulsangcharoen, P.; Calzo, G.L.; Bozhko, S.; Gerada, C.; Wheeler, P.; Gerada, C. A Modified Neutral Point Balancing Space Vector Modulation for Three-Level Neutral Point Clamped Converters in High-Speed Drives. IEEE Trans. Ind. Electron. 2018, 66, 910–921. [Google Scholar] [CrossRef]
- Guo, F.; Yang, T.; Diab, A.M.; Yeoh, S.S.; Bozhko, S.; Wheeler, P. An Enhanced Virtual Space Vector Modulation Scheme of Three-Level NPC Converters for More-Electric-Aircraft Applications. IEEE Trans. Ind. Appl. 2021, 57, 5239–5251. [Google Scholar] [CrossRef]
- Maheshwari, R.; Munk-Nielsen, S.; Busquets-Monge, S. Design of Neutral-Point Voltage Controller of a Three-Level NPC Inverter With Small DC-Link Capacitors. IEEE Trans. Ind. Electron. 2012, 60, 1861–1871. [Google Scholar] [CrossRef]
- Busquets-Monge, S.; Maheshwari, R.; Nicolas-Apruzzese, J.; Lupon, E.J.; Munk-Nielsen, S.; Bordonau, J. Enhanced DC-Link Capacitor Voltage Balancing Control of DC–AC Multilevel Multileg Converters. IEEE Trans. Ind. Electron. 2014, 62, 2663–2672. [Google Scholar] [CrossRef]
- Busquets-Monge, S.; Grino, R.; Nicolas-Apruzzese, J.; Bordonau, J. Decoupled DC-Link Capacitor Voltage Control of DC–AC Multilevel Multileg Converters. IEEE Trans. Ind. Electron. 2015, 63, 1344–1349. [Google Scholar] [CrossRef] [Green Version]
- Nicolas-Apruzzese, J.; Lupon, E.; Busquets-Monge, S.; Conesa, A.; Bordonau, J.; García-Rojas, G. FPGA-Based Controller for a Permanent-Magnet Synchronous Motor Drive Based on a Four-Level Active-Clamped DC-AC Converter. Energies 2018, 11, 2639. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Yuan, X.; Jin, B. Carrier-based Closed-loop DC-link Voltage Balancing Algorithm for Four Level NPC Converters Based on Redundant Level Modulation. IEEE Trans. Ind. Electron. 2020, 68, 11707–11718. [Google Scholar] [CrossRef]
- Giri, S.K.; Mukherjee, S.; Kundu, S.; Banerjee, S.; Chakraborty, C. An Improved PWM Scheme for Three-Level Inverter Extending Operation Into Overmodulation Region With Neutral-Point Voltage Balancing for Full Power-Factor Range. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 6, 1527–1539. [Google Scholar] [CrossRef]
- Imarazene, K.; Chekireb, H.; Berkouk, E.M. Redundant States in Five-Level Inverter Using Selective Harmonics Elimination PWM. In Proceedings of the International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Pisa, Italy, 14–16 June 2010; IEEE Computer Society: Piscataway, NJ, USA, 2010; pp. 198–203. [Google Scholar]
- Pulikanti, S.R.; Dahidah, M.S.A.; Agelidis, V.G. Voltage Balancing Control of Three-Level Active NPC Converter Using SHE-PWM. IEEE Trans. Power Deliv. 2010, 26, 258–267. [Google Scholar] [CrossRef]
- Busquets-Monge, S.; Filba-Martinez, A.; Alepuz, S.; Calle-Prado, A. A Modulation Strategy to Operate Multilevel Multiphase Diode-Clamped and Active-Clamped DC–AC Converters at Low Frequency Modulation Indices With DC-Link Capacitor Voltage Balance. IEEE Trans. Power Electron. 2016, 32, 7521–7533. [Google Scholar] [CrossRef]
- Rojas, R.; Ohnishi, T.; Suzuki, T. Method for Neutral-Point-Clamped Inverters. IEEE Trans. Power Electron. 1995, 10, 666–672. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, W.; Ma, M.; Zhang, Q.; Jiang, W. Discontinuous PWM Strategy for Neutral Point Clamped Three-Level Inverter to Achieve Multiple Control Objectives. IEEE Access 2019, 7, 158533–158544. [Google Scholar] [CrossRef]
- Yaramasu, V.; Wu, B. Predictive Control of a Three-Level Boost Converter and an NPC Inverter for High-Power PMSG-Based Medium Voltage Wind Energy Conversion Systems. IEEE Trans. Power Electron. 2013, 29, 5308–5322. [Google Scholar] [CrossRef]
- Barros, J.; Rocha, L.; Silva, J. Backstepping Predictive Control of Hybrid Microgrids Interconnected by Neutral Point Clamped Converters. Electronics 2021, 10, 1210. [Google Scholar] [CrossRef]
- Calle-Prado, A.; Alepuz, S.; Bordonau, J.; Cortes, P.; Rodriguez, J. Predictive Control of a Back-to-Back NPC Converter-Based Wind Power System. IEEE Trans. Ind. Electron. 2016, 63, 4615–4627. [Google Scholar] [CrossRef] [Green Version]
- Yaramasu, V.; Wu, B.; Chen, J. Model-Predictive Control of Grid-Tied Four-Level Diode-Clamped Inverters for High-Power Wind Energy Conversion Systems. IEEE Trans. Power Electron. 2013, 29, 2861–2873. [Google Scholar] [CrossRef]
- Verne, S.A.; Valla, M.I. Predictive Control of a Back to Back Diode Clamped Multilevel Converter. In Proceedings of the IEEE International Conference on Industrial Technology (ICIT), 14–17 March 2010; IEEE: Piscataway, NJ, USA; pp. 1814–1819. [Google Scholar]
- Salem, A.; Mamdouh, M.; Abido, M.A. Capacitor Balancing and Common-Mode Voltage Reduction of a SiC Based Dual T-Type Drive System Using Model Predictive Control. IEEE Access 2019, 7, 41066–41077. [Google Scholar] [CrossRef]
- Adam, G.P.; Finney, S.J.; Massoud, A.M.; Williams, B.W. Capacitor Balance Issues of the Diode-Clamped Multilevel Inverter Operated in a Quasi Two-State Mode. IEEE Trans. Ind. Electron. 2008, 55, 3088–3099. [Google Scholar] [CrossRef]
- Kang, K.-P.; Cho, Y.; Kim, H.-S.; Baek, J.-W. DC-Link Capacitor Voltage Imbalance Compensation Method Based Injecting Harmonic Voltage for Cascaded Multi-Module Neutral Point Clamped Inverter. Electronics 2019, 8, 155. [Google Scholar] [CrossRef] [Green Version]
- Wang, K.; Zheng, Z.; Li, Y.; Xu, L.; Ma, H. Multi-Objective Optimization PWM Control for a Back-to-Back Five-Level ANPC Converter. In Proceedings of the IEEE Energy Conversion Congress and Exposition (ECCE), Raleigh, NC, USA, 15–20 September 2012; pp. 3514–3519. [Google Scholar]
- Xu, X.; Zheng, Z.; Wang, K.; Yang, B.; Li, Y. A Comprehensive Study of Common Mode Voltage Reduction and Neutral Point Potential Balance for a Back-to-Back Three-Level NPC Converter. IEEE Trans. Power Electron. 2019, 35, 7910–7920. [Google Scholar] [CrossRef]
- Newton, C.; Sumner, M. A Novel Arrangement for Balancing the Capacitor Voltages of a Five Level Diode Clamped Inverter. In Proceedings of the IEE International Conference on Power Electronics and Variable Speed Drives, 21–23 September 1998; IEEE: Piscataway, NJ, USA; pp. 465–470. [Google Scholar]
- Lim, S.K.; Kim, J.H.; Nam, K. DC-Link Voltage Balancing Algorithm for 3-Level Converter Using the Zero Sequence Current. In Proceedings of the IEEE Power Electronics Specialists Conference (PESC), Charleston, SC, USA, 1 July 1999; Volume 2, pp. 1083–1088. [Google Scholar]
- León, J.I.; Franquelo, L.G.; Portillo, R.C.; Prats, M.M. DC-Link Capacitors Voltage Balancing in Multilevel Four-Leg Di-ode-Clamped Converters. In Proceedings of the IEEE Industrial Electronics Conference (IECON), Raleigh, NC, USA, 6–10 November 2005; Volume 2005, pp. 1254–1259. [Google Scholar]
- Ceballos, S.; Pou, J.; Robles, E.; Gabiola, I.; Zaragoza, J.; Villate, J.L.; Boroyevich, D. Three-Level Converter Topologies With Switch Breakdown Fault-Tolerance Capability. IEEE Trans. Ind. Electron. 2008, 55, 982–995. [Google Scholar] [CrossRef]
- Shukla, A.; Ghosh, A.; Joshi, A. Flying-Capacitor-Based Chopper Circuit for DC Capacitor Voltage Balancing in Diode-Clamped Multilevel Inverter. IEEE Trans. Ind. Electron. 2009, 57, 2249–2261. [Google Scholar] [CrossRef] [Green Version]
- Shu, Z.; He, X.; Wang, Z.; Qiu, D.; Jing, Y. Voltage Balancing Approaches for Diode-Clamped Multilevel Converters Using Auxiliary Capacitor-Based Circuits. IEEE Trans. Power Electron. 2012, 28, 2111–2124. [Google Scholar] [CrossRef]
- Corzine, K.A.; Ieee, M. Analysis of a Four-Level DC/DC Buck Converter Department of Electrical Engineering. Electr. Eng. 2001, 1882–1888. [Google Scholar]
- Hasegawa, K.; Akagi, H. A New DC-Voltage-Balancing Circuit Including a Single Coupled Inductor for a Five-Level Diode-Clamped PWM Inverter. IEEE Trans. Ind. Appl. 2010, 47, 841–852. [Google Scholar] [CrossRef]
- Ito, T.; Kamaga, M.; Sato, Y.; Ohashi, H. An investigation of voltage balancing circuit for DC capacitors in diode-clamped multilevel inverters to realize high output power density converters. In Proceedings of the IEEE Energy Conversion Congress and Exposition (ECCE), Atlanta, GA, USA, 12–16 September 2010; pp. 3675–3682. [Google Scholar]
- Boora, A.A.; Nami, A.; Zare, F.; Ghosh, A.; Blaabjerg, F. Voltage-sharing converter to supply single-phase asymmetrical four-level diode-clamped inverter with high power factor loads. IEEE Trans. Power Electron. 2010, 25, 2507–2520. [Google Scholar] [CrossRef]
- Stala, R. Application of Balancing Circuit for DC-Link Voltages Balance in a Single-Phase Diode-Clamped Inverter With Two Three-Level Legs. IEEE Trans. Ind. Electron. 2010, 58, 4185–4195. [Google Scholar] [CrossRef]
- Filba-Martinez, A.; Busquets-Monge, S.; Nicolas-Apruzzese, J.; Bordonau, J. Operating Principle and Performance Optimization of a Three-Level NPC Dual-Active-Bridge DC–DC Converter. IEEE Trans. Ind. Electron. 2015, 63, 678–690. [Google Scholar] [CrossRef] [Green Version]
- Moonem, M.A.; Duman, T.; Krishnaswami, H. Capacitor Voltage Balancing in a Neutral-Point Clamped Multilevel DC-DC Dual Active Bridge Converter. In Proceedings of the IEEE International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Florianopolis, Brazil, 17–20 April 2017; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2017; pp. 1–7. [Google Scholar]
- Awal, M.A.; Bipu, R.H.; Montes, O.A.; Feng, H.; Husain, I.; Yu, W.; Lukic, S. Capacitor Voltage Balancing for Neutral Point Clamped Dual Active Bridge Converters. IEEE Trans. Power Electron. 2020, 35, 11267–11276. [Google Scholar] [CrossRef]
- Filba-Martinez, A.; Busquets-Monge, S.; Bordonau, J. Modulation and Capacitor Voltage Balancing Control of a Four-Level Active-Clamped Dual-Active-Bridge DC-DC Converter. In Proceedings of the European Conference on Power Electronics and Applications (EPE), Karlsruhe, Germany, 5–9 September 2016; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2016; pp. 1–8. [Google Scholar]
- Deng, Z.; Wang, G.; Wang, K.; Hao, Y. Analysis and Control of N-Level Neutral-Point Clamped Dual Active Bridge DC-DC Converter with Capacitor Voltage Balance. In Proceedings of the IEEE International Conference on Power System Technology (POWERCON), Guangzhou, China, 6–8 November 2018; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2018; pp. 2407–2413. [Google Scholar]
- Joebges, P.; Gorodnichev, A.; de Doncker, R.W. Modulation and Active Midpoint Control of a Three-Level Three-Phase Du-al-Active Bridge DC-DC Converter under Non-Symmetrical Load. In Proceedings of the IEEE International Power Electronics Conference (IPEC), Niigata, Japan, 20–24 May 2018; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2018; pp. 375–382. [Google Scholar]
- Lee, J.Y.; Choi, H.J.; Jung, J.H. Three Level NPC Dual Active Bridge Capacitor Voltage Balancing Switching Modulation. In Proceedings of the IEEE International Telecommunications Energy Conference (INTELEC), Broadbeach, QLD, Australia, 22–26 October 2017; Institute of Electrical and Elec-tronics Engineers Inc.: Piscataway, NJ, USA, 2017; Volume 1, pp. 438–443. [Google Scholar]
- Lee, J.-Y.; Cho, Y.-P.; Jung, J.-H. Single-Stage Voltage Balancer With High-Frequency Isolation for Bipolar LVDC Distribution System. IEEE Trans. Ind. Electron. 2019, 67, 3596–3606. [Google Scholar] [CrossRef]
- Ye, Z.; Xu, Y.; Wu, X.; Tan, G.; Deng, X.; Wang, Z. A Simplified PWM Strategy for a Neutral-Point-Clamped (NPC) Three-Level Converter With Unbalanced DC Links. IEEE Trans. Power Electron. 2015, 31, 3227–3238. [Google Scholar] [CrossRef]
- Hyun, S.-W.; Hong, S.-J.; Lee, J.-H.; Lee, C.-B.; Won, C.-Y. A Method to Compensate the Distorted Space Vectors in the Unbalanced Neutral Point Voltage of 3-level NPC PWM Inverters. J. Power Electron. 2016, 16, 455–463. [Google Scholar] [CrossRef] [Green Version]
- Wu, X.; Tan, G.; Ye, Z.; Yao, G.; Liu, Z.; Liu, G. Virtual-Space-Vector PWM for a Three-Level Neutral-Point-Clamped Inverter With Unbalanced DC-Links. IEEE Trans. Power Electron. 2017, 33, 2630–2642. [Google Scholar] [CrossRef]
- Park, Y.; Sul, S.-K.; Lim, C.-H.; Kim, W.-C.; Lee, S.-H. Asymmetric Control of DC-Link Voltages for Separate MPPTs in Three-Level Inverters. IEEE Trans. Power Electron. 2012, 28, 2760–2769. [Google Scholar] [CrossRef]
- Teymour, H.R.; Sutanto, D.; Muttaqi, K.; Ciufo, P. Solar PV and Battery Storage Integration using a New Configuration of a Three-Level NPC Inverter With Advanced Control Strategy. IEEE Trans. Energy Convers. 2014, 29, 354–365. [Google Scholar] [CrossRef]
- Jayasinghe, S.G.; Vilathgamuwa, D.M.; Madawala, U.K. Diode-Clamped Three-Level Inverter-Based Battery/Supercapacitor Direct Integration Scheme for Renewable Energy Systems. IEEE Trans. Power Electron. 2011, 26, 3720–3729. [Google Scholar] [CrossRef]


















| Open-Loop Methods | ||||
| • No variable is fed back. • Typically not enough to keep balance because of non-idealities or perturbations. | ||||
| Conventional PWM/SVM | VV-SVM | Carrier-overlapped PWM | Hybrid modulations | Self-balancing |
| + Lower number of commutations per switching cycle than other alternatives. − Balance in every switching cycle not possible for high values of m; the limit depends on the load power factor. − For more than three levels, in the region where balancing is not possible, capacitor voltages collapse. | + Balance in every switching cycle under all operating conditions. + Lower required capacitance than with alternative modulations. − Higher number of commutations per switching cycle than other alternatives. | + Balance in every line cycle. + Lower number of commutations than VV–SVM. − Higher required capacitance than VV–SVM. − Higher number of commutations than conventional PWM/SVM. | • The applied modulation is selected depending on m. + Takes advantage of the benefits of each modulation in each operating region. − Increased complexity compared to other alternatives. | • It is a “do-nothing” method. − Balance only for the 3-level case with restricted operating conditions and small disturbances. |
| Closed-Loop Methods | ||||
| • DC-link capacitor voltages are fed back (currents are also fed back in a few cases). | ||||
| Modification of modulating signals | Selection of redundant vectors | Modification of switching angles | Predictive Control | |
| • Applicable to carrier-based PWM strategies with one or more modulating signals per phase. The modification typically represents the introduction of a zero-sequence voltage. + Simple. − Effectiveness limited by the inherent limitations of the employed PWM strategy. | • In SVM strategies, the proper redundant vector is selected or the share of redundant vectors is modified to correct the imbalance. This implies the introduction of a zero-sequence voltage. + Computationally intensive. − Effectiveness limited by the inherent limitations of the employed SVM strategy. | • In programmed PWM strategies, the switching angles are modified to correct the imbalance. + Simple. − Introduction of low-frequency distortion in the synthesized AC voltage while modifying the switching angles. | + Balance in all operating regions. − Typically, introduces variable switching frequency and spread harmonic spectrum. − Significant computation burden for high number of levels. | |
| Hardware Methods | ||||
| • Extra hardware added to the NPC converter to guarantee a balanced operation. + Provides robust balance, uncoupled from the NPC converter operation. − Reduces the overall efficiency and introduces significantly higher cost and complexity. | ||||
| Separate DC sources | Auxiliary balancing circuit | Back-to-back | ||
| • Use of independent n−1 DC voltage sources, typically generated through a power converter. | • Additional dedicated circuit connected at the DC side or AC side to aid in the redistribution of the DC-link capacitor bank energy. | • Two DC–AC converters connected back-to-back where each converter counteracts the effect of the other converter on the balance. | ||
| DC-DC Conversion | ||||
| • DC–DC conversion can be implemented with NPC multilevel converters. | ||||
| Back-to-back structure | Dual-active Bridge | |||
| + Bidirectional power flow. + Full balance control. − Limited range of voltage conversion ratios. − No galvanic isolation. | + Bidirectional power flow. + Full balance control. + Galvanic isolation. − Higher hardware complexity than in the back-to-back structure. | |||
| Operation beyond balance | ||||
| • Operation of NPC multilevel converters under DC-link capacitor voltage unbalance is feasible. • This feature can be used to improve the system performance in some applications. | ||||
| Photovoltaic power systems | Battery powered systems | |||
| + Independent control of the voltage of each photovoltaic array. + Maximum power extracted from each photovoltaic array, despite different panel conditions and irradiation levels. + Increased total power extraction. | + Independent control of each battery module current. + Balancing of the state of charge of each battery module, despite different state-of-health and loading. + Extended battery range. | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alepuz, S.; Busquets-Monge, S.; Nicolás-Apruzzese, J.; Filbà-Martínez, À.; Bordonau, J.; Yuan, X.; Kouro, S. A Survey on Capacitor Voltage Control in Neutral-Point-Clamped Multilevel Converters. Electronics 2022, 11, 527. https://doi.org/10.3390/electronics11040527
Alepuz S, Busquets-Monge S, Nicolás-Apruzzese J, Filbà-Martínez À, Bordonau J, Yuan X, Kouro S. A Survey on Capacitor Voltage Control in Neutral-Point-Clamped Multilevel Converters. Electronics. 2022; 11(4):527. https://doi.org/10.3390/electronics11040527
Chicago/Turabian StyleAlepuz, Salvador, Sergio Busquets-Monge, Joan Nicolás-Apruzzese, Àlber Filbà-Martínez, Josep Bordonau, Xibo Yuan, and Samir Kouro. 2022. "A Survey on Capacitor Voltage Control in Neutral-Point-Clamped Multilevel Converters" Electronics 11, no. 4: 527. https://doi.org/10.3390/electronics11040527
APA StyleAlepuz, S., Busquets-Monge, S., Nicolás-Apruzzese, J., Filbà-Martínez, À., Bordonau, J., Yuan, X., & Kouro, S. (2022). A Survey on Capacitor Voltage Control in Neutral-Point-Clamped Multilevel Converters. Electronics, 11(4), 527. https://doi.org/10.3390/electronics11040527










