Index Matrices—Based Software Implementation of Power Electronic Circuit Design
Abstract
:1. Introduction
2. Mathematical Methods and Models
2.1. Basic Definitions on Index Matrices with Real Number Elements
2.2. Classical Matrix Models on First-Order Discrete Dynamical Systems
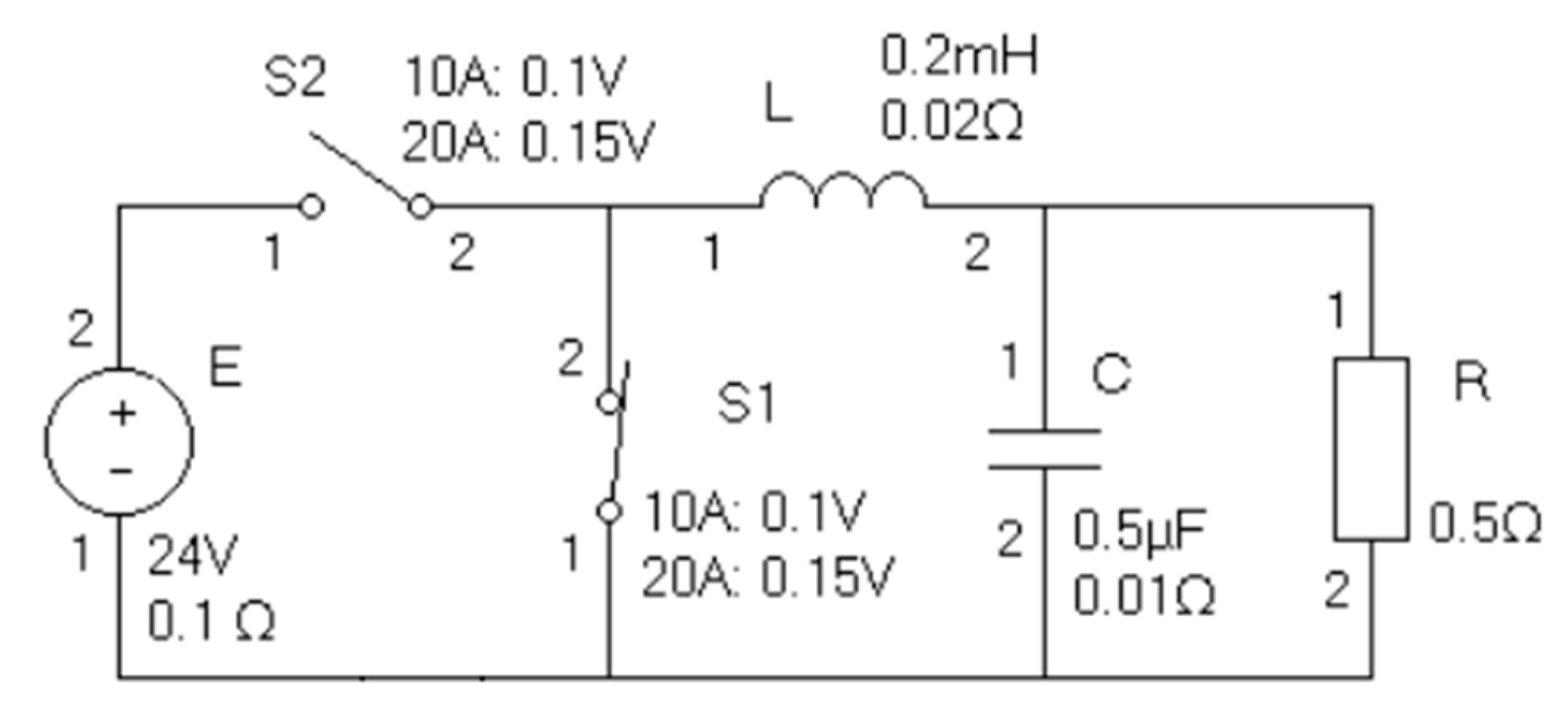
2.3. R-IM Models of Electronic Components, Circuits and Devices
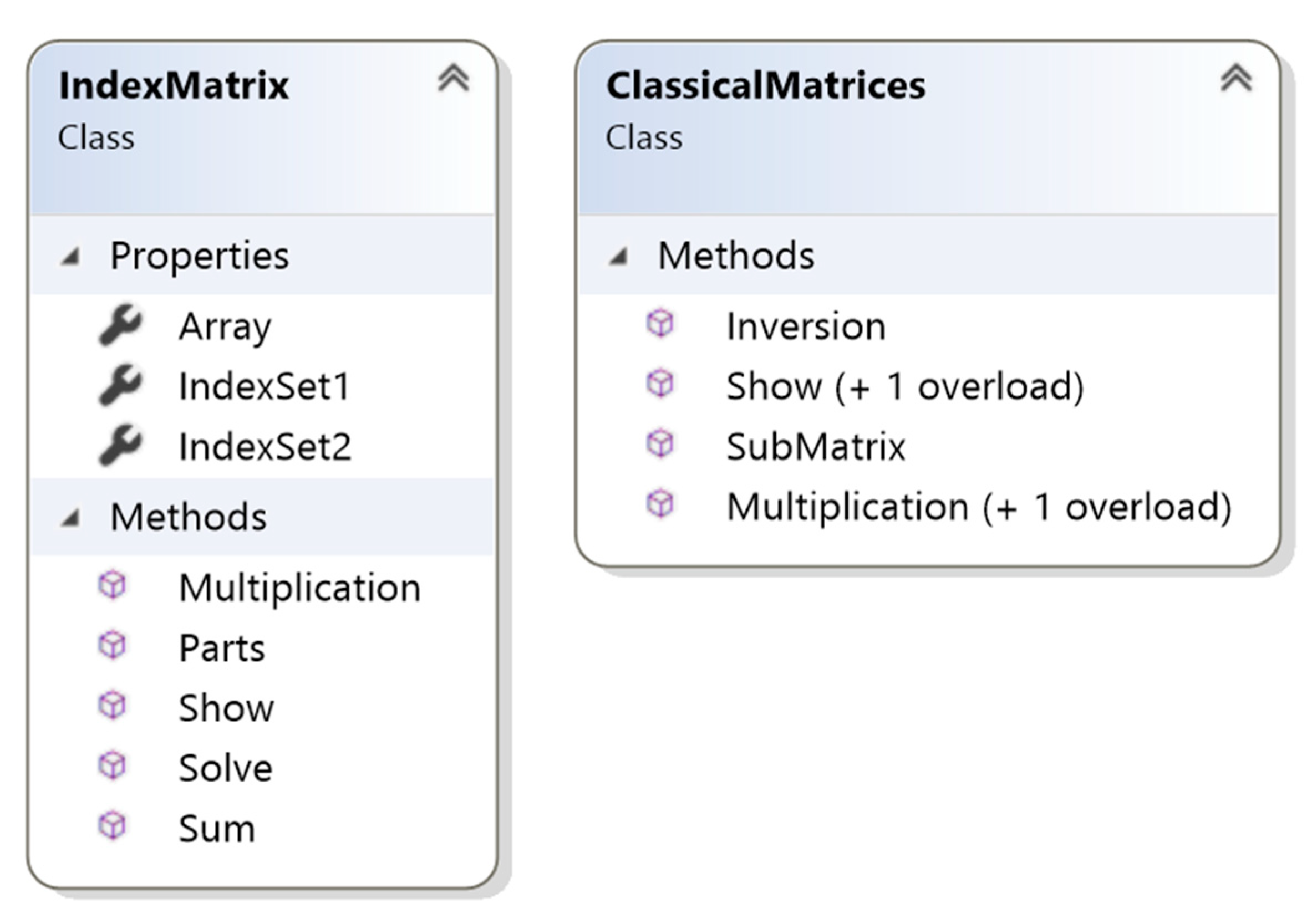
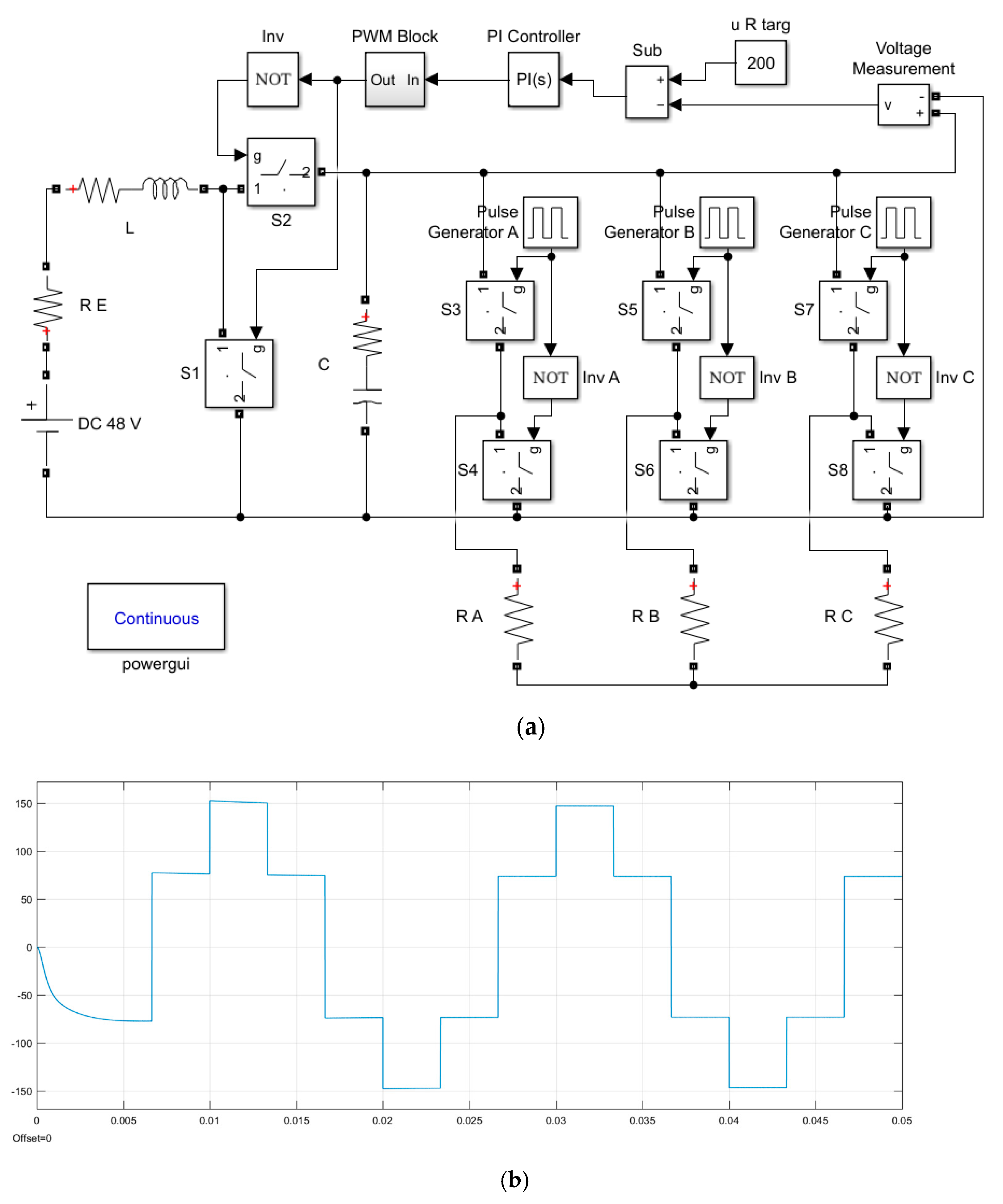
3. Software Implementation Based on R-IMs
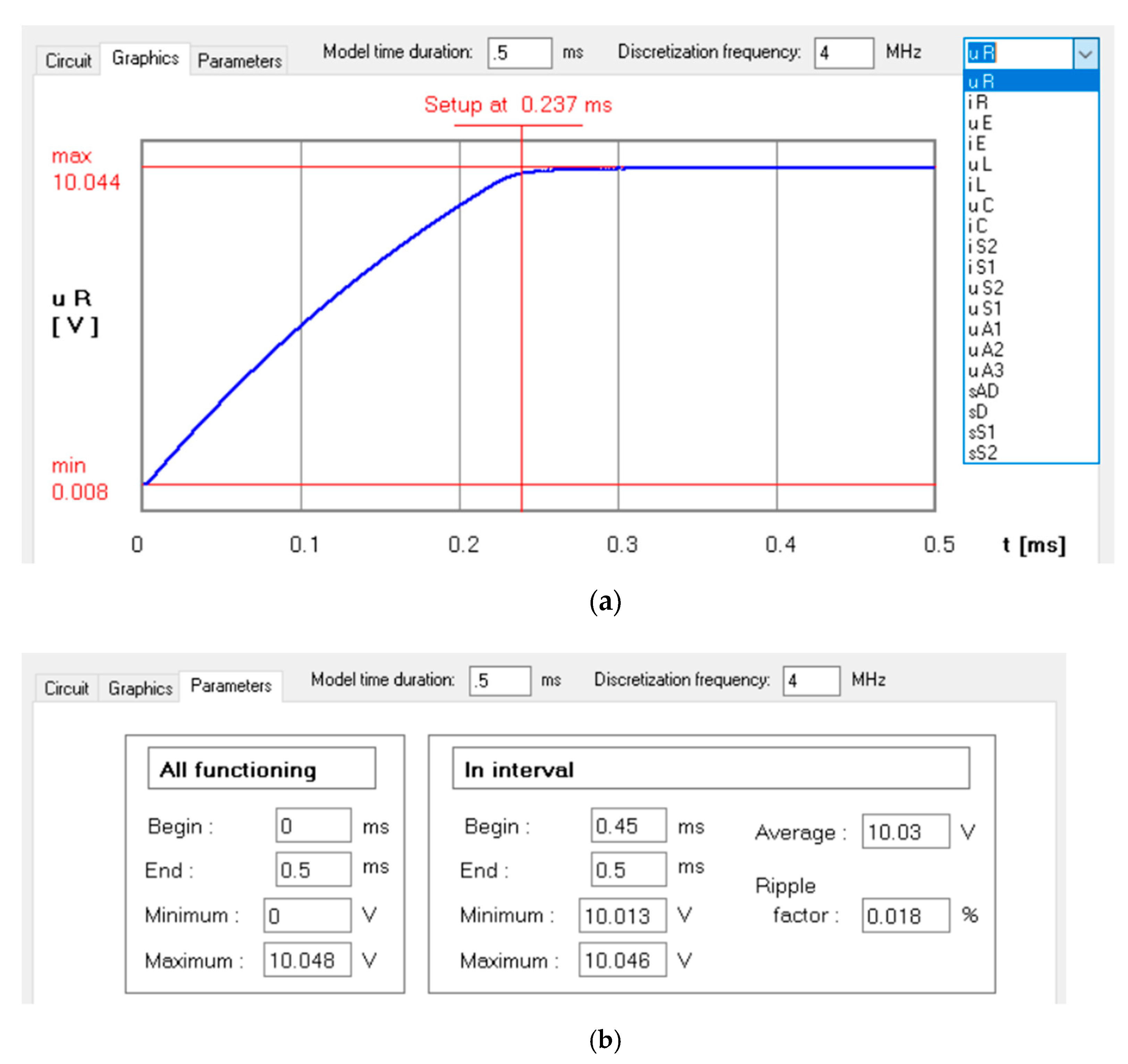
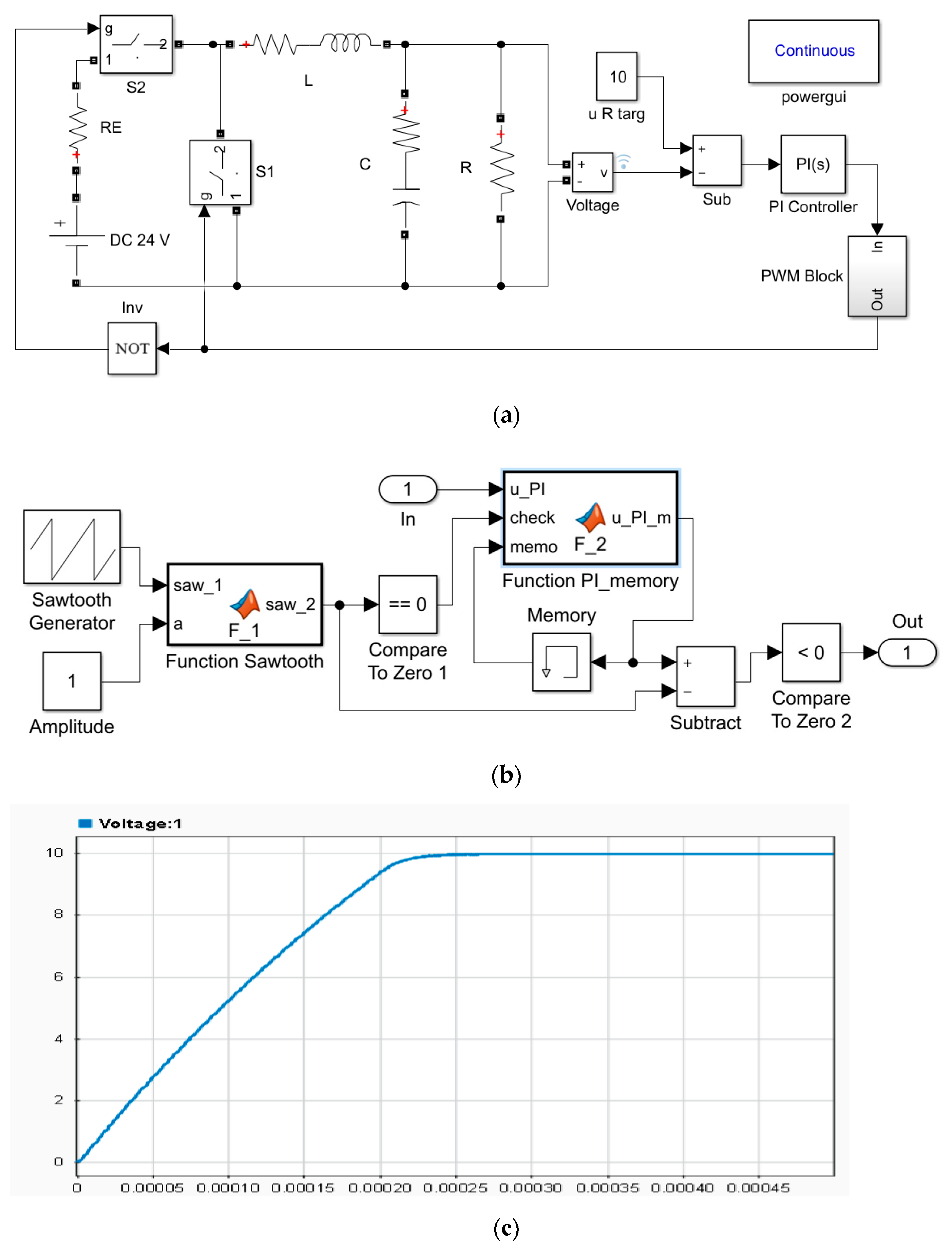
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Karris, S. Introduction to Simulink with Engineering Applications; Orchard Publications: San Antonio, TX, USA, 2006; Available online: neuron.eng.wayne.edu/auth/ece4340/Simulink_Introduction.pdf (accessed on 23 December 2021).
- Araujo, E.; Leite, A.; Freitas, D. Modelling and simulation of power electronic systems using a bond graph formalism. In Proceedings of the 10th Mediterranean Conference on Control and Automation MED2002, Lisbon, Portugal, 9–12 July 2002. [Google Scholar]
- Galor, O. Discrete Dynamical Systems; Springer-Verlag: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Gocheva, P.; Hinov, N.; Gochev, V. Matrix based estimation of current and voltage magnitude in electronic circuits. AIP Conf. Proc. 2018, 2048, 060026. [Google Scholar]
- Gochev, V.; Gocheva, P.; Hinov, N. NET implementation of electronic circuit design. AIP Conf. Proc. 2021, 2333, 070016. [Google Scholar]
- Hinov, N.; Gocheva, P.; Gochev, V. Index Matrices Based Modelling of a DC-DC Buck Converter with PID Controller and GUI on It. In Proceedings of the 34th International Conference on Information Technologies InfoTech 2020—Proceedings, Varna, Bulgaria, 17–18 September 2020. [Google Scholar]
- Cerny, D.; Dobes, J. Adaptive sparse matrix indexing technique for simulation of electronic circuits based on λ-calculus. In Proceedings of the 2015 European Conference on Circuit Theory and Design (ECCTD), Trondheim, Norway, 24–26 August 2015; pp. 1–4. [Google Scholar] [CrossRef]
- Cerny, D.; Dobes, J. Functional Programming Languages in Computer Simulation of Electronics Circuits. In Proceedings of the Computational Science and Computational Intelligence (CSCI) 2014 International Conference, Las Vegas, NV, USA, 10–13 March 2014; Volume 1. [Google Scholar]
- Xia, W.; Liu, J.; Cao, M.; Johansson, K.H.; Başar, T. Generalized Sarymsakov Matrices. IEEE Trans. Autom. Control 2018, 64, 3085–3100. [Google Scholar] [CrossRef] [Green Version]
- Atanassov, K. Index Matrices: Towards an augmented matrix calculus. In Studies in Computational Intelligence; Springer International Publishing: Cham, Switzerland, 2014; Volume 573. [Google Scholar]
- Traneva, V.; Tranev, S. Index Matrices as a Tool for Managerial Decision Making; Publishing House of the Union of Scientists: Sofia, Bulgaria, 2017. (In Bulgarian) [Google Scholar]
- Gochev, V.; Hinov, N.; Gocheva, P. Mathematical Modelling of Basic Electronic Components with Index Matrices. In Proceedings of the 33th International Conference on Information Technologies InfoTech 2019—Proceedings, Varna, Bulgaria, 19–20 September 2019. [Google Scholar]
- Hinov, N.; Gocheva, P.; Gochev, V. Representation with Index Matrices of Single Ended Primary Inductor Converter Functioning. In Proceedings of the International Conference on High Technology for Sustainable Development HiTech 2019, Sofia, Bulgaria, 10–11 October 2019. [Google Scholar]
- Atanassov, K. Conditions in generalized nets. In Proceedings of the XIII Spring Conference of the Union of Bulgarian Mathematical, Sunny Beach, Bulgaria, 6–9 April 1984; pp. 219–226. [Google Scholar]
- Atanassov, K. Generalized Nets; World Scientific: Singapore, 1991. [Google Scholar]
- Atanassov, K. On Generalized Nets Theory. “Prof. Marin Drinov”; Academic Publising House: Sofia, Bulgaria, 2007. [Google Scholar]
- Alexieva, J.; Choy, E.; Koycheva, E. Review and bibliography on generalized nets theory and applications. In A Survey of Generalized Nets, Raffles KvB Monograph; Choy, E., Krawczak, M., Shannon, A., Szmidt, E., Eds.; World Scientific: Singapore, 2007; Volume 10, pp. 207–301. [Google Scholar]
- Vardeva, I.; Staneva, L. Automated Design of Electronic Circuits Modeled with Generalized Networks; Industrial Technologies; University “Prof. Dr. Asen Zlatarov”: Burgas, Bulgaria, 2014; Volume I, pp. 74–77. Available online: www.researchgate.net/publication/306346628_Avtomatizirano_proektirane_na_elektronni_shemi_modelirani_s_obobseni_mrezi (accessed on 23 December 2021). (In Bulgarian)
- Ali, U.; Raza, H.; Ahmed, Y. On Normalized Laplacians, Degree-Kirchhoff Index and Spanning Tree of Generalized Phenylene. Symmetry 2021, 13, 1374. [Google Scholar] [CrossRef]
- Kallioras, N.A.; Nordas, A.N.; Lagaros, N.D. Deep Learning-Based Accuracy Upgrade of Reduced Order Models in Topology Optimization. Appl. Sci. 2021, 11, 12005. [Google Scholar] [CrossRef]
- Benômar, Y.; Croonen, J.; Verrelst, B.; Van Mierlo, J.; Hegazy, O. Model-Based Control System Design of Brushless Doubly Fed Reluctance Machines Using an Unscented Kalman Filter. Energies 2021, 14, 8222. [Google Scholar] [CrossRef]
- Belhaj, F.Z.; El Fadil, H.; Idrissi, Z.E.; Koundi, M.; Gaouzi, K. Modeling, Analysis and Experimental Validation of the Fuel Cell Association with DC-DC Power Converters with Robust and Anti-Windup PID Controller Design. Electronics 2020, 9, 1889. [Google Scholar] [CrossRef]
- El Fadil, H.; Giri, F.; Chaoui, F.; El Magueri, O. Accounting for Input Limitation in the Control of Buck Power Converters. IEEE Trans. Circuits Syst. I Regul. Pap. 2009, 56, 1260–1271. [Google Scholar] [CrossRef]
- Duda, J. Lyapunov matrices approach to the parametric optimization of a time delay system with a PI controller. In Proceedings of the 2016 21st International Conference on Methods and Models in Automation and Robotics (MMAR), Miedzyzdroje, Poland, 29 August–1 September 2016; pp. 1206–1210. [Google Scholar] [CrossRef]
- Akundi, A.; Tseng, T.-L.B.; Almeraz, C.N.; Lopez-Terrazas, R.J.; Luan, H. A Novel Approach to Behavior Design for Model Based Systems Engineering Application Using Design Structure Matrix. In Proceedings of the 2021 IEEE International Systems Conference (SysCon), Vancouver, BC, Canada, 15 April–15 May 2021; pp. 1–7. [Google Scholar] [CrossRef]




| Model time duration [ms] | 0.2 | 0.4 | 0.6 | 0.8 | 1 |
| Simulation duration in Simlink [ms] | 510 | 530 | 547 | 567 | 595 |
| Simulation duration in the authors’ software [ms] | 18.1 | 19.9 | 21.9 | 23.9 | 26.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hinov, N.; Gocheva, P.; Gochev, V. Index Matrices—Based Software Implementation of Power Electronic Circuit Design. Electronics 2022, 11, 675. https://doi.org/10.3390/electronics11050675
Hinov N, Gocheva P, Gochev V. Index Matrices—Based Software Implementation of Power Electronic Circuit Design. Electronics. 2022; 11(5):675. https://doi.org/10.3390/electronics11050675
Chicago/Turabian StyleHinov, Nikolay, Polya Gocheva, and Valeri Gochev. 2022. "Index Matrices—Based Software Implementation of Power Electronic Circuit Design" Electronics 11, no. 5: 675. https://doi.org/10.3390/electronics11050675
APA StyleHinov, N., Gocheva, P., & Gochev, V. (2022). Index Matrices—Based Software Implementation of Power Electronic Circuit Design. Electronics, 11(5), 675. https://doi.org/10.3390/electronics11050675







