Innovative Hyperspectral Image Classification Approach Using Optimized CNN and ELM
Abstract
:1. Introduction
- (1)
- For the slow convergence and low accuracy of the PSO, an enhanced PSO based on fusing multi-strategy (CWLPSO) is proposed by adding new acceleration factor strategy and inertia weight linear decreasing strategy.
- (2)
- For the difficultly determining the parameters of the CNN, an optimized CNN model using CWLPSO is developed to effectively extract the deep features of HRSIs.
- (3)
- The ELM with strong generalization ability, fast learning ability, and the constructed feature vector are combined to realize the accurate classification of HRSIs.
- (4)
- An innovative classification method of HRSIs based on CWLPSO, CNN, and ELM, namely, IPCEHRIC is proposed.
2. Basic Methods
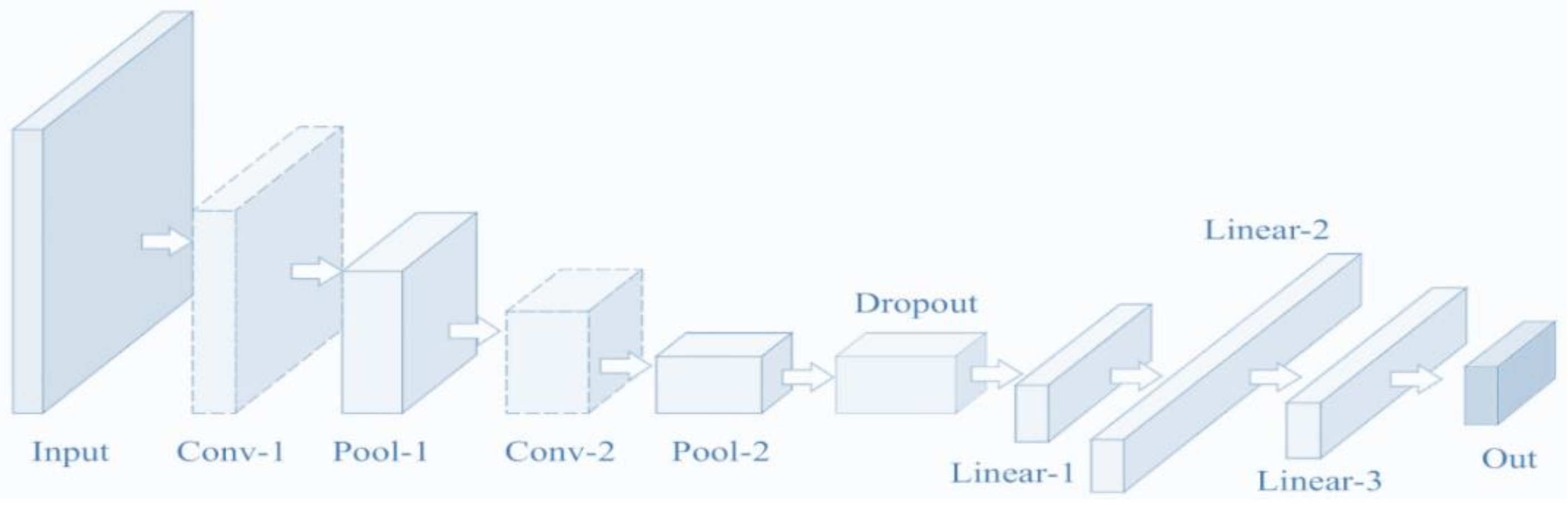
2.1. CNN
2.2. PSO
2.3. ELM
3. Improved Learning Factor and Inertia Weight
3.1. Improve Learning Factors
3.2. Linear Decreasing of Inertia Weight
4. Optimize CNN Using CWLPSO
4.1. Optimized Idea for CNN
4.2. Model of Optimized CNN
5. An Innovative Classification Method of HRSIs Using Optimized CNN and ELM
- (1)
- Preprocess HRSIs
- (2)
- Optimize parameters of CNN
- (3)
- Extract features
- (4)
- Construct feature matrix
- (5)
- Establish ELM classifier
6. Experiment Verification and Result Analysis
6.1. Experimental Environment and Parameter Setting
6.2. Pavia University Data
6.2.1. Data Description
6.2.2. Experimental Results and Analysis
6.3. Actual HRSI after Jiuzhaigou M7.0 Earthquake
6.3.1. Description of HRSI after Jiuzhaigou 7.0 Earthquake
6.3.2. Experimental Results and Analysis
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dumke, I.; Ludvigsen, M.; Ellefmo, S.L. Underwater hyperspectral imaging using a stationary platform in the Trans-Atlantic Geotraverse hydrothermal field. IEEE Trans. Geosci. Remote Sens. 2019, 57, 2947–2962. [Google Scholar] [CrossRef] [Green Version]
- Chen, H.; Miao, F.; Chen, Y.; Xiong, Y.; Chen, T. A hyperspectral image classification method using multifeature vectors and optimized KELM. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2021, 14, 2781–2795. [Google Scholar] [CrossRef]
- Ma, K.Y.; Chang, C.I. Iterative training sampling coupled with active learning for semisupervised spectral–spatial hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2021, 59, 8672–8692. [Google Scholar] [CrossRef]
- Chen, Y.; Xiao, Z.; Chen, G. Detection of oasis soil composition and analysis of environmental parameters based on hyperspectral image and GIS. Arab. J. Geosci. 2021, 14, 1050. [Google Scholar] [CrossRef]
- Shimoni, M.; Haelterman, R.; Perneel, C. Hypersectral imaging for military and security applications: Combining myriad processing and sensing techniques. IEEE Geosci. Remote Sens. Mag. 2019, 7, 101–117. [Google Scholar] [CrossRef]
- Luo, X.; Shen, Z.; Xue, R. Unsupervised band selection method based on importance-assisted column subset selection. IEEE Access 2018, 7, 517–527. [Google Scholar] [CrossRef]
- Chang, C.I.; Kuo, Y.M.; Chen, S. Self-mutual information-based band selection for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2021, 59, 5979–5997. [Google Scholar] [CrossRef]
- Lin, Z.; Yan, L. A support vector machine classifier based on a new kernel function model for hyperspectral data. Mapp. Sci. Remote Sens. 2015, 53, 85–101. [Google Scholar] [CrossRef]
- Kang, X.; Xiang, X.; Li, S. PCA-based edge-preserving features for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 7140–7151. [Google Scholar] [CrossRef]
- Yuan, H.; Tang, Y.Y.; Lu, Y. Spectral-spatial classification of hyperspectral image based on discriminant analysis. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2014, 7, 2035–2043. [Google Scholar] [CrossRef]
- Tran, T.V.; Julian, J.P.; Beurs, K.M. Land cover heterogeneity effects on sub-pixel and per-pixel classifications. ISPRS Int. J. Geo-Inf. 2014, 3, 540–553. [Google Scholar] [CrossRef] [Green Version]
- Khodadadzadeh, M.; Li, J.; Plaza, A.; Ghassemian, H.; Bioucas-Dias, J.M.; Li, X. Spectral-spatial classification of hyperspectral data using local and global probabilities for mixed pixel characterization. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6298–6314. [Google Scholar] [CrossRef]
- Li, S.T.; Lu, T.; Fang, L.Y.; Jia, X.P.; Benediktsson, J.A. Probabilistic fusion of pixel-level and superpixel-level hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2016, 54, 7416–7430. [Google Scholar] [CrossRef]
- Li, W.; Wu, G.D.; Zhang, F.; Du, Q.; Hyperspectral, A. Image classification using deep pixel-pair features. IEEE Trans. Geosci. Remote Sens. 2017, 55, 844–853. [Google Scholar] [CrossRef]
- Mei, J.; Wang, Y.B.; Zhang, L.Q.; Zhang, B.; Liu, S.H.; Zhu, P.P.; Ren, Y.C. PSASL: Pixel-level and superpixel-level aware subspace learning for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 4278–4293. [Google Scholar] [CrossRef]
- Pan, Z.B.; Wu, X.Q.; Li, Z.Y. Central pixel selection strategy based on local gray-value distribution by using gradient information to enhance LBP for texture classification. Expert Syst. Appl. 2019, 120, 319–334. [Google Scholar] [CrossRef]
- Bey, A.; Jetimane, J.; Lisboa, S.N.; Ribeiro, N.; Sitoe, A.; Meyfroidt, P. Mapping smallholder and large-scale cropland dynamics with a flexible classification system and pixel-based composites in an emerging frontier of Mozambique. Remote Sens. Environ. 2020, 239, 111611. [Google Scholar] [CrossRef]
- Yan, L.; Fan, B.; Liu, H.M.; Huo, C.L.; Xiang, S.M.; Pan, C.H. Triplet adversarial domain adaptation for pixel-level classification of VHR remote sensing images. IEEE Trans. Geosci. Remote Sens. 2020, 58, 3558–3573. [Google Scholar] [CrossRef]
- Li, Y.; Lu, T.; Li, S.T. Subpixel-pixel-superpixel-based multiview active learning for hyperspectral images classification. IEEE Trans. Geosci. Remote Sens. 2020, 58, 4976–4988. [Google Scholar] [CrossRef]
- Ma, K.Y.; Chang, C.I. Kernel-based constrained energy minimization for hyperspectral mixed pixel classification. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5510723. [Google Scholar] [CrossRef]
- Chen, Y.; Lin, Z.; Zhao, X. Deep learning-based classification of hyperspectral data. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2014, 7, 2094–2107. [Google Scholar] [CrossRef]
- Liu, L.; Wang, Y.; Peng, J. Latent relationship guided stacked sparse autoencoder for hyperspectral imagery classification. IEEE Trans. Geosci. Remote Sens. 2020, 58, 3711–3725. [Google Scholar] [CrossRef]
- Romero, A.; Gatta, C.; Camps-Valls, G. Unsupervised deep feature extraction for remote sensing image classification. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1349–1362. [Google Scholar] [CrossRef] [Green Version]
- Sharma, A.; Liu, X.W.; Yang, X.J.; Shi, D. A patch-based convolutional neural network for remote sensing image classification. Neural Netw. 2017, 95, 19–28. [Google Scholar] [CrossRef] [PubMed]
- Maggiori, E.; Tarabalka, Y.; Charpiat, G.; Alliez, P. Convolutional neural networks for large-scale remote-sensing image classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 645–657. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.Z.; Zhang, J.B.; Liu, P.; Choo, K.K.; Huang, F. Spectral-spatial multi-feature-based deep learning for hyperspectral remote sensing image classification. Appl. Soft Comput. 2017, 21, 213–221. [Google Scholar] [CrossRef]
- Ji, S.P.; Zhang, C.; Xu, A.J.; Shi, Y.; Duan, Y.L. 3D convolutional neural networks for crop classification with multi-temporal remote sensing images. Remote Sens. 2018, 10, 75. [Google Scholar] [CrossRef] [Green Version]
- Ben, H.A.; Benoit, A.; Lambert, P.; Ben, A.C. 3-D deep learning approach for remote sensing image classification. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4420–4434. [Google Scholar]
- Xu, S.H.; Mu, X.D.; Chai, D.; Zhang, X.M. Remote sensing image scene classification based on generative adversarial networks. Remote Sens. Lett. 2018, 9, 617–626. [Google Scholar] [CrossRef]
- Tao, Y.T.; Xu, M.Z.; Lu, Z.Y.; Zhong, Y.F. DenseNet-based depth-width double reinforced deep learning neural network for high-resolution remote sensing image per-pixel classification. Remote Sens. 2018, 10, 779. [Google Scholar] [CrossRef] [Green Version]
- Liang, P.; Shi, W.Z.; Zhang, X.K. Remote sensing image classification based on stacked denoising autoencoder. Remote Sens. 2018, 10, 16. [Google Scholar] [CrossRef] [Green Version]
- Li, P.; Ren, P.; Zhang, X.Y.; Wang, Q.; Zhu, X.B.; Wang, L. Region-wise deep feature representation for remote sensing images. Remote Sens. 2018, 10, 871. [Google Scholar] [CrossRef] [Green Version]
- Li, G.; Li, L.L.; Zhu, H.; Liu, X.; Jiao, L.C. Adaptive multiscale deep fusion residual network for remote sensing image classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 8506–8521. [Google Scholar] [CrossRef]
- Yuan, Y.; Fang, J.; Lu, X.Q.; Feng, Y.C. Remote sensing image scene classification using rearranged local features. IEEE Trans. Geosci. Remote Sens. 2019, 57, 1779–1792. [Google Scholar] [CrossRef]
- Zhang, C.J.; Li, G.D.; Du, S.H. Multi-scale dense networks for hyperspectral remote sensing image classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 9201–9222. [Google Scholar] [CrossRef]
- Zhang, C.J.; Li, G.D.; Lei, R.M.; Du, S.H.; Zhang, X.Y.; Zheng, H.; Wu, Z.F. Deep feature aggregation network for hyperspectral remote sensing image classification. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2020, 13, 5314–5325. [Google Scholar] [CrossRef]
- Chen, C.; Ma, Y.; Ren, G.B. Hyperspectral classification using deep belief networks based on conjugate gradient update and pixel-centric spectral block features. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2020, 13, 4060–4069. [Google Scholar] [CrossRef]
- Xiong, W.; Xiong, Z.Y.; Cui, Y.Q.; Lv, Y.F. Deep multi-feature fusion network for remote sensing images. Remote Sens. Lett. 2020, 11, 563–571. [Google Scholar] [CrossRef]
- Tong, W.; Chen, W.T.; Han, W.; Li, X.J.; Wang, L.Z. Channel-attention-based densenet network for remote sensing image scene classification. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2020, 13, 4121–4132. [Google Scholar] [CrossRef]
- Zhu, H.; Ma, W.P.; Li, L.L.; Jiao, L.C.; Yang, S.Y.; Hou, B. A dual-branch attention fusion deep network for multiresolution remote-sensing image classification. Inf. Fusion 2020, 58, 116–131. [Google Scholar] [CrossRef]
- Raza, A.; Huo, H.; Sirajuddin, S.; Fang, T. Diverse capsules network combining multiconvolutional layers for remote sensing image scene classification. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2020, 13, 5297–5313. [Google Scholar] [CrossRef]
- Li, J.T.; Shen, Y.L.; Yang, C. An adversarial generative network for crop classification from remote sensing timeseries images. Remote Sens. 2021, 13, 65. [Google Scholar] [CrossRef]
- Gu, S.W.; Zhang, R.; Luo, H.X.; Li, M.Y.; Feng, H.M.; Tang, X.G. Improved SinGAN integrated with an attentional mechanism for remote sensing image classification. Remote Sens. 2021, 13, 1713. [Google Scholar] [CrossRef]
- Guo, D.E.; Xia, Y.; Luo, X.B. Self-supervised GANs with similarity loss for remote sensing image scene classification. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2021, 14, 2508–2521. [Google Scholar] [CrossRef]
- Li, Y.S.; Zhu, Z.H.; Yu, J.G.; Zhang, Y.J. Learning deep cross-modal embedding networks for zero-shot remote sensing image scene classification. IEEE Trans. Geosci. Remote Sens. 2021, 59, 10590–10603. [Google Scholar] [CrossRef]
- Lei, R.M.; Zhang, C.J.; Liu, W.C.; Zhang, L.; Zhang, X.Y.; Yang, Y.C.; Huang, J.W.; Li, Z.X.; Zhou, Z.Y. Hyperspectral remote sensing image classification using deep convolutional capsule network. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2021, 14, 8297–8315. [Google Scholar] [CrossRef]
- Cui, X.P.; Zou, C.; Wang, Z.S. Remote sensing image recognition based on dual-channel deep learning network. Multimed. Tools Appl. 2021, 80, 27683–27699. [Google Scholar] [CrossRef]
- Peng, C.; Li, Y.Y.; Jiao, L.C.; Shang, R.H. Efficient convolutional neural architecture search for remote sensing image scene classification. IEEE Trans. Geosci. Remote Sens. 2021, 59, 6092–6105. [Google Scholar] [CrossRef]
- Guo, D.G.; Xia, Y.; Luo, X.B. GAN-based semisupervised scene classification of remote sensing image. IEEE Geosci. Remote Sens. Lett. 2021, 18, 2067–2071. [Google Scholar] [CrossRef]
- Dong, S.X.; Quan, Y.H.; Feng, W.; Dauphin, G.; Gao, L.R.; Xing, M.D. A pixel cluster CNN and spectral-spatial fusion algorithm for hyperspectral image classification with small-size training samples. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2021, 14, 4101–4114. [Google Scholar] [CrossRef]
- Li, Y.S.; Zhang, Y.J.; Zhu, Z.H. Error-tolerant deep learning for remote sensing image scene classification. IEEE Trans. Cybern. 2021, 51, 1756–1768. [Google Scholar] [CrossRef] [PubMed]
- Li, B.Y.; Guo, Y.L.; Yang, J.G.; Wang, L.G.; Wang, Y.Q.; An, W. Gated recurrent multiattention network for VHR remote sensing image classification. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5606113. [Google Scholar] [CrossRef]
- Dong, R.M.; Zhang, L.X.; Fu, H.H. RRSGAN: Reference-based super-resolution for remote sensing image. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5601117. [Google Scholar] [CrossRef]
- Wu, E.Q.; Zhou, M.; Hu, D.; Zhu, L.; Tang, Z.; Qiu, X.Y.; Deng, P.Y.; Zhu, L.M.; Ren, H. Self-paced dynamic infinite mixture model for fatigue evaluation of pilots’ brains. IEEE Trans. Cybern. 2021. [Google Scholar] [CrossRef] [PubMed]
- Karadal, C.H.; Kaya, M.C.; Tuncer, T.; Dogan, S.; Acharya, U.R. Automated classification of remote sensing images using multileveled MobileNetV2 and DWT techniques. Expert Syst. Appl. 2021, 185, 115659. [Google Scholar] [CrossRef]
- Ma, W.P.; Shen, J.C.; Zhu, H.; Zhang, J.; Zhao, J.L.; Hou, B.; Jiao, L.C. A novel adaptive hybrid fusion network for multiresolution remote sensing images classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5400617. [Google Scholar] [CrossRef]
- Cai, W.W.; Wei, Z.G. Remote sensing image classification based on a cross-attention mechanism and graph convolution. IEEE Geosci. Remote Sens. Lett. 2022, 19, 80002005. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, S.H.; Zhang, Y.; Chen, W.B. RS-DARTS: A convolutional neural architecture search for remote sensing image scene classification. Remote Sens. 2022, 14, 141. [Google Scholar] [CrossRef]
- Hilal, A.M.; Al-Wesabi, F.N.; Alzahrani, K.J.; Al Duhayyim, M.; Hamza, M.A.; Rizwanullah, M.; Diaz, V.G. Deep transfer learning based fusion model for environmental remote sensing image classification model. J. Remote Sens. 2022. [Google Scholar] [CrossRef]
- Li, R.; Zheng, S.Y.; Duan, C.X.; Wang, L.B.; Zhang, C. Land cover classification from remote sensing images based on multi-scale fully convolutional network. GEO Spat. Inf. Sci. 2022. [Google Scholar] [CrossRef]
- Wei, Y.Y.; Zhou, Y.Q.; Luo, Q.F.; Deng, W. Optimal reactive power dispatch using an improved slime mould algorithm. Energy Rep. 2021, 7, 8742–8759. [Google Scholar] [CrossRef]
- Deng, W.; Zhang, X.; Zhou, Y.; Liu, Y.; Zhou, X.; Chen, H.; Zhao, H. An enhanced fast non-dominated solution sorting genetic algorithm for multi-objective problems. Inf. Sci. 2022, 585, 441–453. [Google Scholar] [CrossRef]
- Li, T.; Qian, Z.; Deng, W.; Zhang, D.; Lu, H.; Wang, S. Forecasting crude oil prices based on variational mode decomposition and random sparse Bayesian learning. Appl. Soft Comput. 2021, 113, 108032. [Google Scholar] [CrossRef]
- Deng, W.; Xu, J.; Zhao, H.; Song, Y. A novel gate resource allocation method using improved PSO-based QEA. IEEE Trans. Intell. Transp. Syst. 2020. [Google Scholar] [CrossRef]
- Cui, H.; Guan, Y.; Chen, H. Rolling element fault diagnosis based on VMD and sensitivity MCKD. IEEE Access 2021, 9, 120297–120308. [Google Scholar] [CrossRef]
- Wang, X.; Wang, H.; Du, C.; Fan, X.; Cui, L.; Chen, H.; Deng, F.; Tong, Q.; He, M.; Yang, M.; et al. Custom-molded offloading footwear effectively prevents recurrence and amputation, and lowers mortality rates in high-risk diabetic foot patients: A multicenter, prospective observational study. Diabetes Metab. Syndr. Obes. 2022, 15, 103–109. [Google Scholar]
- Deng, W.; Shang, S.; Cai, X.; Zhao, H.; Zhou, Y.; Chen, H.; Deng, W. Quantum differential evolution with cooperative coevolution framework and hybrid mutation strategy for large scale optimization. Knowl. Based Syst. 2021, 224, 107080. [Google Scholar] [CrossRef]
- Deng, W.; Xu, J.; Gao, X.; Zhao, H. An enhanced MSIQDE algorithm with novel multiple strategies for global optimization problems. IEEE Trans. Syst. Man Cybern. Syst. 2020, 52, 1578–1587. [Google Scholar] [CrossRef]
- Zhang, Z.H.; Min, F.; Chen, G.S.; Shen, S.P.; Wen, Z.C.; Zhou, X.B. Tri-partition state alphabet-based sequential pattern for multivariate time series. Cogn. Comput. 2021. [Google Scholar] [CrossRef]
- Ran, X.; Zhou, X.; Lei, M.; Tepsan, W.; Deng, W. A novel k-means clustering algorithm with a noise algorithm for capturing urban hotspots. Appl. Sci. 2021, 11, 11202. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, Q.; Luo, J. An enhanced Bacterial Foraging Optimization and its application for training kernel extreme learning machine. Appl. Soft Comput. 2020, 86, 105884. [Google Scholar] [CrossRef]
- Cui, H.; Guan, Y.; Chen, H.; Deng, W. A novel advancing signal processing method based on coupled multi-stable stochastic resonance for fault detection. Appl. Sci. 2021, 11, 5385. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. IEEE Int. Conf. Neural Netw. Perth 1995, 4, 1942–1948. [Google Scholar]






| Data | Pavia University |
|---|---|
| Collection location | Northern Italy |
| Acquisition equipment | ROSIS |
| Spectral coverage (μm) | 0.43–0.86 |
| Data size (pixel) | 610 × 340 |
| Spatial resolution (m) | 1.3 |
| Number of bands | 115 |
| Number of bands after denoising | 103 |
| Sample size | 42,776 |
| Number of categories | 9 |
| Types | Class | Training Samples | Test Samples | Samples |
|---|---|---|---|---|
| 1 | Asphalt | 1326 | 5305 | 6631 |
| 2 | Meadows | 3722 | 14,927 | 18,649 |
| 3 | Gravel | 418 | 1681 | 2099 |
| 4 | Trees | 612 | 2452 | 3064 |
| 5 | Painted metal sheets | 268 | 1077 | 1345 |
| 6 | Bare Soil | 1004 | 4025 | 5029 |
| 7 | Bitumen | 266 | 1064 | 1330 |
| 8 | Self-Blocking Bricks | 736 | 2946 | 3682 |
| 9 | Shadows | 188 | 759 | 947 |
| Total | 8540 | 34,236 | 42,776 | |
| Types | Class | CNN | LBP-CNN | CNN-ELM | LBP-CNN-ELM | LBP-PCA-CNN-ELM | IPCEHRIC |
|---|---|---|---|---|---|---|---|
| 1 | Asphalt | 90.00 | 89.64 | 94.72 | 95.72 | 99.92 | 99.96 |
| 2 | Meadows | 89.99 | 89.79 | 93.00 | 95.00 | 99.12 | 99.67 |
| 3 | Gravel | 89.70 | 91.63 | 99.94 | 99.94 | 100.00 | 100.00 |
| 4 | Trees | 88.90 | 87.10 | 89.15 | 94.17 | 96.88 | 99.84 |
| 5 | Painted metal sheets | 86.00 | 89.91 | 92.26 | 96.68 | 99.72 | 100.00 |
| 6 | Bare Soil | 88.15 | 89.90 | 95.00 | 96.27 | 100.00 | 100.00 |
| 7 | Bitumen | 90.45 | 92.00 | 94.15 | 96.15 | 99.15 | 99.82 |
| 8 | Self-Blocking Bricks | 89.83 | 91.86 | 93.25 | 95.01 | 99.66 | 100.00 |
| 9 | Shadows | 87.50 | 93.87 | 90.90 | 97.74 | 97.94 | 99.15 |
| OA (%) | 85.67 | 88.75 | 92.63 | 95.64 | 98.95 | 99.21 | |
| AA (%) | 88.95 | 90.63 | 93.60 | 96.30 | 99.15 | 99.83 | |
| STD | 1.467 | 1.939 | 3.022 | 1.722 | 1.075 | 0.279 | |
| Types | Class | Samples |
|---|---|---|
| 1 | Villages | 12,575 |
| 2 | Water | 14,953 |
| 3 | Grassland | 38,790 |
| 4 | Trees | 39,159 |
| Total | 105,477 | |
| Types | Class | Samples |
|---|---|---|
| 1 | Villages | 1608 |
| 2 | Bareland | 25 |
| 3 | Grassland | 376,651 |
| 4 | Trees | 110,409 |
| 5 | Water | 5558 |
| 6 | Rocks | 2469 |
| Total | 495,087 | |
| Times | CNN | LBP-CNN | CNN-ELM | LBP-CNN-ELM | LBP-PCA-CNN-ELM | IPCEHRIC |
|---|---|---|---|---|---|---|
| 1 | 41.47 | 36.68 | 69.80 | 64.38 | 65.67 | 89.76 |
| 2 | 41.80 | 36.68 | 75.84 | 64.25 | 65.16 | 88.96 |
| 3 | 41.75 | 36.68 | 75.98 | 64.16 | 65.33 | 89.99 |
| 4 | 41.73 | 36.68 | 75.38 | 64.40 | 65.14 | 89.26 |
| 5 | 41.85 | 37.02 | 61.45 | 64.47 | 65.47 | 89.76 |
| 6 | 41.70 | 37.02 | 75.80 | 64.12 | 65.56 | 90.58 |
| 7 | 41.86 | 37.02 | 74.04 | 63.83 | 65.40 | 91.64 |
| 8 | 41.77 | 37.02 | 60.02 | 64.44 | 65.19 | 92.12 |
| 9 | 41.78 | 36.68 | 74.80 | 64.38 | 65.49 | 90.99 |
| 10 | 41.76 | 37.02 | 75.46 | 64.10 | 65.81 | 89.94 |
| AA (%) | 41.75 | 36.85 | 71.86 | 64.25 | 65.42 | 90.30 |
| STD | 0.109 | 0.179 | 6.145 | 0.201 | 0.223 | 1.019 |
| Types | Class | CNN | LBP-CNN | CNN-ELM | LBP-CNN-ELM | LBP-PCA-CNN-ELM | IPCEHRIC |
|---|---|---|---|---|---|---|---|
| 1 | Villages | 50.47 | 46.76 | 79.16 | 74.64 | 75.70 | 92.46 |
| 2 | Water | 41.80 | 35.43 | 78.37 | 70.47 | 73.28 | 90.73 |
| 3 | Grassland | 39.26 | 33.58 | 73.78 | 63.19 | 72.45 | 89.15 |
| 4 | Trees | 40.73 | 36.29 | 76.12 | 69.24 | 75.42 | 91.48 |
| OA (%) | 41.75 | 36.85 | 71.86 | 64.25 | 65.42 | 90.30 | |
| AA (%) | 43.07 | 38.02 | 76.86 | 69.39 | 74.21 | 90.96 | |
| STD | 5.046 | 5.939 | 2.422 | 4.733 | 1.597 | 1.396 | |
| Times | CNN | LBP-CNN | CNN-ELM | LBP-CNN-ELM | LBP-PCA-CNN-ELM | IPCEHRIC |
|---|---|---|---|---|---|---|
| 1 | 79.77 | 79.83 | 99.21 | 85.12 | 85.12 | 99.99 |
| 2 | 79.78 | 79.85 | 99.78 | 84.80 | 84.14 | 100.0 |
| 3 | 79.84 | 79.84 | 99.99 | 84.14 | 84.01 | 99.98 |
| 4 | 79.78 | 79.86 | 99.26 | 84.80 | 84.22 | 99.78 |
| 5 | 79.86 | 79.84 | 99.99 | 85.12 | 85.46 | 100.0 |
| 6 | 79.87 | 79.81 | 99.21 | 84.76 | 86.13 | 99.77 |
| 7 | 79.88 | 79.59 | 99.98 | 85.46 | 84.57 | 100.0 |
| 8 | 79.87 | 79.59 | 99.27 | 86.08 | 85.12 | 99.98 |
| 9 | 79.86 | 79.80 | 99.98 | 85.46 | 86.02 | 100.0 |
| 10 | 79.86 | 79.84 | 99.77 | 86.43 | 84.80 | 99.99 |
| AA (%) | 79.84 | 79.79 | 99.64 | 85.22 | 84.96 | 99.95 |
| STD | 0.043 | 0.104 | 0.360 | 0.672 | 0.753 | 0.092 |
| Types | Class | CNN | LBP-CNN | CNN-ELM | LBP-CNN-ELM | LBP-PCA-CNN-ELM | IPCEHRIC |
|---|---|---|---|---|---|---|---|
| 1 | Villages | 82.34 | 85.46 | 99.46 | 87.45 | 90.35 | 99.98 |
| 2 | Bareland | 86.05 | 86.04 | 99.64 | 89.62 | 93.46 | 100.0 |
| 3 | Grassland | 79.98 | 85.32 | 99.06 | 87.17 | 90.67 | 100.0 |
| 4 | Trees | 78.46 | 84.14 | 99.31 | 86.43 | 89.86 | 99.81 |
| 5 | Water | 83.49 | 87.25 | 99.78 | 87.69 | 90.34 | 100.0 |
| 6 | Rocks | 82.16 | 85.68 | 99.34 | 88.03 | 92.05 | 99.85 |
| OA (%) | 79.84 | 79.79 | 99.64 | 85.22 | 84.96 | 99.95 | |
| AA (%) | 82.08 | 85.65 | 99.43 | 87.73 | 91.12 | 99.94 | |
| STD | 2.658 | 1.013 | 0.256 | 1.072 | 1.367 | 0.086 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, A.; Zhou, X.; Miao, F. Innovative Hyperspectral Image Classification Approach Using Optimized CNN and ELM. Electronics 2022, 11, 775. https://doi.org/10.3390/electronics11050775
Ye A, Zhou X, Miao F. Innovative Hyperspectral Image Classification Approach Using Optimized CNN and ELM. Electronics. 2022; 11(5):775. https://doi.org/10.3390/electronics11050775
Chicago/Turabian StyleYe, Ansheng, Xiangbing Zhou, and Fang Miao. 2022. "Innovative Hyperspectral Image Classification Approach Using Optimized CNN and ELM" Electronics 11, no. 5: 775. https://doi.org/10.3390/electronics11050775
APA StyleYe, A., Zhou, X., & Miao, F. (2022). Innovative Hyperspectral Image Classification Approach Using Optimized CNN and ELM. Electronics, 11(5), 775. https://doi.org/10.3390/electronics11050775






