Resilient Consensus for Multi-Agent Systems in the Presence of Sybil Attacks

Abstract

This paper investigates the problem of resilient consensus control for discrete-time linear multi-agent systems under Sybil attacks. We consider a node to be a Sybil node if it can generate a large number of false identities in the graph as a way of gaining disproportionate influence on the consensus performance of the network. Such attacks can easily invalidate existing resilient consensus algorithms that assume an upper bound on the number of malicious nodes in the network. To this end, we first built a new attack model based on the characteristics of the Sybil nodes. In addition, a quantized-data-based transmission scheme was developed for identifying and resisting Sybil nodes in the network. Then, an attack-resilient consensus algorithm was developed, where each normal node sends the quantitative data information with a specific label, which is generated by truncated normal distribution sampling to their neighbors. We give sufficient graphical conditions for attack models considering limited energy to ensure the consensus of linear multi-agent systems. Finally, numerical simulation examples are provided to validate the effectiveness of the proposed methods.

1. Introduction

In the last decade, cooperative control of multi-agent systems (MASs) has attracted significant attention from researchers and can be found in various fields [1,2,3], for instance, distributed computing, sensor networks, autonomous vehicles, and the Internet of Things. As one of the fundamental problems of MASs, consensus control is the combination of graph theory and control systems, which aims to make these distributed and locally cooperative agents reach an agreement in terms of some interests. However, as MASs are often in an open environment, some agents may become non-cooperative or crash when cyber attacks or network failures occur in the system, which will lead to the failure of consensus. Therefore, resilient consensus, the consensus in the face of some agents in the network subject to faults or attacks, has been investigated by many researchers in recent years.

Recently, many works have been dedicated to resilient consensus for MASs with different network situations or types of cyber-attacks [4,5,6,7]. Roughly speaking, the goal of resilient consensus is to prevent the malicious agents from influencing the system’s consensus process by appropriate consensus strategy and designing sufficient redundancy in the underlying network [8,9,10]. For the case of a time-varying network, the authors in [11] provided sufficient and necessary conditions for the design of resilient consensus protocols. Furthermore, the author in [12] studied the resilient consensus problem for switched MASs. On the other hand, based on the impact of different cyber-attack characteristics on MASs, constructing corresponding control system attack models is also a research hotspot [13,14,15]. In MASs, the most commonly used attack strategy is data falsification (Byzantine) attack, where the attackers, in an adversarial manner, send inconsistent information to their neighboring nodes [16,17,18,19]. In [5], DoS attack models in multi-agent networks are discussed, and a resilient consensus control law is given based on the static output feedback mechanism. Utilizing the information of the neighbors, a distributed event-triggered algorithm for resilient consensus is provided in [20] by considering the impact of deception attacks on the MASs. Moreover, crashed attack models are also one of the research fields that have recently been considered in the resilient consensus problem [21,22,23]. However, nearly all of the existing work designed the consensus protocol on the assumption that there is an upper bound on the number of malicious nodes in the multi-agent network.

A particularly challenging attack on this assumption is the so-called Sybil attack [24], in which a malicious agent can create multiple fake or captured identities to gain a disproportionate influence on the distributed networks. The Sybil attack was first studied by Douceur in the context of peer-to-peer networks [25]. Such an attack has a devastating effect on routing distributed networks such as voting, resource storage, and social networks. To date, there have been some works on MASs under Sybil attacks. Dong and Liu [26] considered the Sybil attack in sensor networks and proposed a robust and secure time-synchronization protocol with a graph-theoretical approach. Jamshidi et al. [27] recently introduced a precise and straightforward algorithm for detecting Sybil attacks in WSNs with the observer monitoring behavior of nodes. Huang et al. [28] introduced a so-called “ScatterID” system which attaches backscatter tags to single-antenna robots to defend against Sybil attacks in multi-robot networks. Wheeler et al. [29] proposed a secure consensus algorithm against Sybil attack by controlling the network communication topology through Wi-Fi signals. A proof-of-concept protocol called ReCon is presented in [30], where the nodes in the network achieve Sybil-resistant consensus by establishing blockchain technology.

It is important to note that the majority of the existing defensive methods against Sybil attack benefit from specific mechanisms, such as central trust authority, and reliable methods to distinguish the physical fingerprints of signals from neighboring nodes [14,31,32,33]. However, in practice, the trust central authority mechanism is not suitable for the large-scale distributed MAS network. In addition, fingerprint recognition and reputation mechanisms mean extra network components and computing expenditure, which may not be ideal for the MASs, because each agent is resource-limited. Thus, the lightweight attack-tolerant consensus algorithm becomes promising to effectively resist such scenarios that are challenging to be handled otherwise. To the best of our knowledge, the integration of an identity authentication mechanism with an agent update and lightweight Sybil defense algorithm is still a gap in the research of MASs.

Inspired by the above facts, the purpose of our paper is to investigate the resilient consensus problem for MASs under Sybil attacks, where the malicious agents attempt to multicast an excessive amount of state information with different fictitious identities to cause the normal agent state value to be unable to reach a consensus. To describe the characteristics induced by the Sybil attacks in the multi-agent networks, a novel attack model focus on the internal relationships of nodes is introduced for the first time in this paper. Based on the attack model, necessary network topology conditions are obtained for the MASs under a directed graph. Inspired by [34,35], we propose a random label generation and verification mechanism that uses the truncated normal distribution. Such a mechanism can help us to identify the Sybil nodes in the distributed MASs. Then, as a natural extension to our previous work [36], and inspired by the work of Dibaji et al. [37], here, we employ a quantized version of the mean sub-sequence reduced (MSR) algorithm called the QW-MSR algorithm to reach a consensus on the state value of all nodes, which can also effectively reduce the calculation and communication burden of the system. Specifically, we set the state value of each agent to be composed of the integer part generated by the quantization process and the fractional part generated by the label sampling mechanism. It is worth noting that the values generated by the sampling mechanism are time-sensitive and independent and will not affect the integer state value. Some numerical examples are given to demonstrate the effectiveness of our methods.

So, focused on the characteristics of the Sybil attack and compared with the existing literature, which utilizes detection and verification mechanisms against the Sybil attack with extra components, our contributions with this paper can be summarized as follows:

• Compared with [4,9,10], we give a novel network attack model to describe the behavioral characteristics of Sybil attack in MASs.
• Compared with [28,29,30], we propose a random label generation and verification mechanism incorporating the node information transmission process to detect and mitigate Sybil attacks in the network.
• Compared with [26,27], we propose a novel quantization mechanism during the computation and update of node state information, which makes the consensus algorithm more lightweight and consumes less energy.

The paper is organized as follows: In Section 2, we present some notions in graph theory and propose the Sybil attack model. The node label sampling and verification mechanism and the consensus algorithm are proposed in Section 3. The main results are given in Section 4. Simulation tests are performed to show the effectiveness of our results in Section 5, and the conclusions are presented in Section 6.

2. Preliminaries

2.1. Graph Theory

We model the MAS with a directed graph which is defined as a triple $\mathcal{G}=\{\mathcal{V},\mathcal{E},\mathcal{A}\}$, where $\mathcal{V}$ donates the node set, $\mathcal{E}=\mathcal{V}\times \mathcal{V}$ represents the directed link set and $\mathcal{A}\in {\mathbb{R}}^{n\times n}$ represents the adjacency matrix. In this paper, the node set is composed of the normal node set ${\mathcal{V}}_n$ and Sybil node set ${\mathcal{V}}_S$, i.e., $\mathcal{V}={\mathcal{V}}_n\cup {\mathcal{V}}_S,{\mathcal{V}}_n\cap {\mathcal{V}}_S=\varnothing$. The directed edge $(j,i)$ is called the incoming edge of i, which means node i can receive information from node j. For node i, the set of its neighbors is denoted by ${\mathcal{N}}_i=\{j:(j,i)\in \mathcal{E}\}$, and the number of neighbors is noted by $|{\mathcal{N}}_i|$. The element $a_{ij}$ in $\mathcal{A}$ is defined by $a_{ij}\in [\mu ,1)$ if $(i,j)\in \mathcal{E}$ where $\mu >0$, otherwise $a_{ij}=0$. Next, several concepts of the so-called robust graph are introduced below. Further details and examples can be found in [4].

Definition 1.

r-reachable set: A nonempty set $\mathcal{S}\subseteq \mathcal{V}$ is said to be r-reachable if there exists at least one node $i\in \mathcal{S}$ that $|{\mathcal{E}}_i|\ge r,r\in {\mathbb{Z}}^{+}$, where ${\mathcal{E}}_i$ donates the set of incoming edges that are outside the set $\mathcal{S}$.

Definition 2.

$(r,s)$-reachable set: A nonempty set $\mathcal{S}\subseteq \mathcal{V}$ is said to be $(r,s)$-reachable if there are at least s nodes in node set S, each of which has at least r neighbors outside of S, where $r,s\in {\mathbb{Z}}^{+}$.

Definition 3.

r-robustness: A directed graph is said to be r-robust if for every pair of nonempty disjoint subsets in $\mathcal{V}$, at least one of the subsets is r-reachable.

Definition 4.

$(r,s)$-robustness: We say graph $\mathcal{G}=(\mathcal{V},\mathcal{E})$ is $(r,s)$-robust if for each pair of nonempty disjoint subsets ${\mathcal{S}}_1,{\mathcal{S}}_2\subset \mathcal{V}$, at least one of the following conditions is met (define ${\mathcal{X}}_{{\mathcal{S}}_k}^r=\{i\in {\mathcal{S}}_k:|{\mathcal{V}}_i\backslash {\mathcal{S}}_k|\ge r\},k\in \{1,2\}$):

1 

$|{\mathcal{X}}_{{\mathcal{S}}_1}^r|=|{\mathcal{S}}_1|$;

2 

$|{\mathcal{X}}_{{\mathcal{S}}_2}^r|=|{\mathcal{S}}_2|$;

3 

$|{\mathcal{X}}_{{\mathcal{S}}_1}^r|+|{\mathcal{X}}_{{\mathcal{S}}_2}^r|\ge s$.

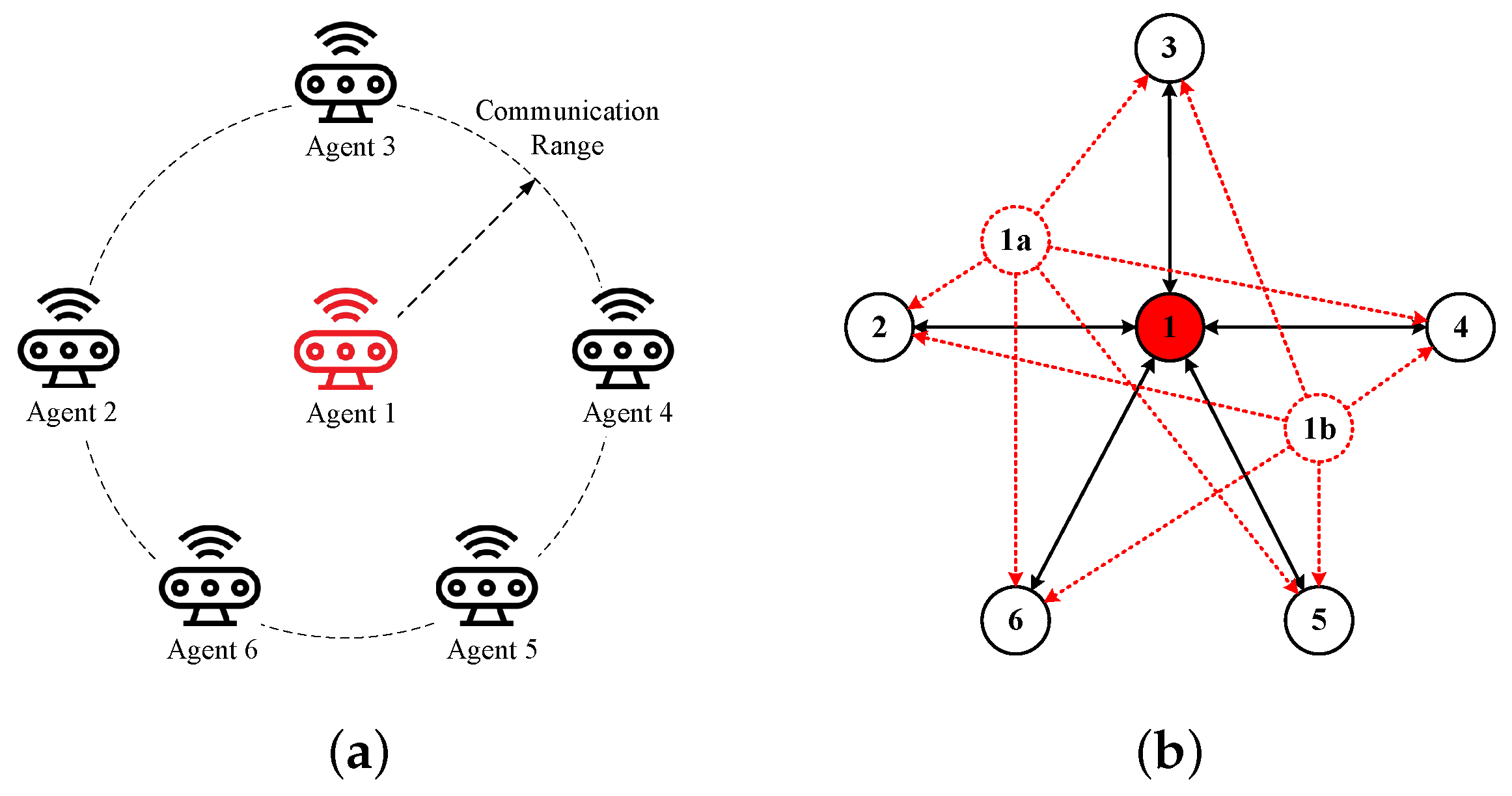
2.2. Sybil Attack Model

As discussed earlier in this paper, we focus on the case of having a small number of Sybil nodes in a MAS network. Each Sybil node can generate multiple fabricated (or fake) identities to gain a disproportionate advantage to control or affect a large number of legitimate nodes in the network. It is worth noting that although the network with Sybil nodes seems to add multiple nodes (fake identities), the number of physical nodes in the network has not increased. Multiple fabricated identities, which are called child nodes, generated by the first Sybil node, which is called parent node, simultaneously send malicious messages to their neighbors.

Next, we define two types of Sybil nodes in the MAS for Sybil attackers.

Definition 5.

(Sybil parent node and Sybil child node) Consider a MAS under Sybil attacks, where each agent is regarded as a node in a directed graph, denoted by $\mathcal{G}=\{\mathcal{V},\mathcal{E}\}$. The first compromised or captured node is called the Sybil parent node, and the fabricated identities generated by the Sybil parent node are called the Sybil child nodes.

We denote by ${\mathcal{V}}_{Sp}$ the set of Sybil parent nodes, and by ${\mathcal{V}}_{Sc}$ the set of Sybil child nodes. The whole Sybil node-set is composed of the Sybil parent nodes and the Sybil child nodes, which we denote by ${\mathcal{V}}_S={\mathcal{V}}_{Sp}\cup {\mathcal{V}}_{Sc}$.

Remark 1.

In the previous research on Sybil attack or spoof attack [13,14,27,32], researchers usually identify these Sybil nodes by their attack behavior and characteristics. For the nature of Sybil attack-forged identities, we believe that the internal relationship and generation order of Sybil nodes can be used for Sybil node detection and exclusion. Thus, we divide Sybil nodes into parent nodes reprogrammed with physical entities and replica-forged identities as child nodes.

In this paper, we assume the Sybil attack dimensions are direct, fabricated, and simultaneous, which means that Sybil nodes as well as fabricated identities can directly connect to their neighboring nodes and send malicious information simultaneously. An example of the type of Sybil nodes discussed in the above definition is shown in Figure 1. Here, we consider a group of six agents with the directed communication topology. The attacker compromised agent 1 and turned it into a Sybil parent node, as shown in Figure 1a. Then, the Sybil parent node generated two Sybil child nodes, i.e., node 1a and node 1b. The entire communication network under Sybil attacks is shown in Figure 1b.

Considering the limited ability and spending, the attackers often cannot compromise all nodes in the network. A standard assumption model in the area of resilient consensus problems is the so-called F-local attack model or F-total attack model. In such a model, the scope of the malicious nodes is usually assumed to be bounded by a constant F in the neighborhood of each node (F-local attack model) or the total area of all nodes (F-total attack model) [4,12,15]. The above assumptions are invalid for Sybil attacks that can arbitrarily generate fabricated nodes. Therefore, it is necessary to redefine the scope model of Sybil attacks according to the different types of Sybil nodes. In this paper, we have the following definitions.

Definition 6.

(F-parent local attack model): A network is considered to be under F-parent local Sybil attack if there are mostly F Sybil parent nodes in the neighborhood of each normal node.

Definition 7.

(F-parent total attack model): A network is considered to be under F-parent total Sybil attack if there are mostly F Sybil parent nodes in the network.

To achieve the purpose of destroying the system consensus process, both Sybil parent node and child node will behave as malicious nodes that will not obey the pre-designed control rules and update their state information arbitrarily. This paper assumes that the information generated and sent by the Sybil child node is the same as that of its own Sybil parent node.

3. Node Verification Mechanism and Consensus Algorithm

Here, we consider a MAS of N agents cooperating over a directed graph $\mathcal{G}=(\mathcal{V},\mathcal{E},\mathcal{A})$. All the agents take the following form:

$$x_i[k+1]=x_i\left[k\right]+u_i\left[k\right],$$

(1)

where $k\in {\mathbb{N}}_0$, $i=1,2,\dots ,N$, $x_i\left[k\right]\in \mathbb{R}$ is the state of node i at time step k, and $u_i\left[k\right]$ is the control input of node i to be designed.

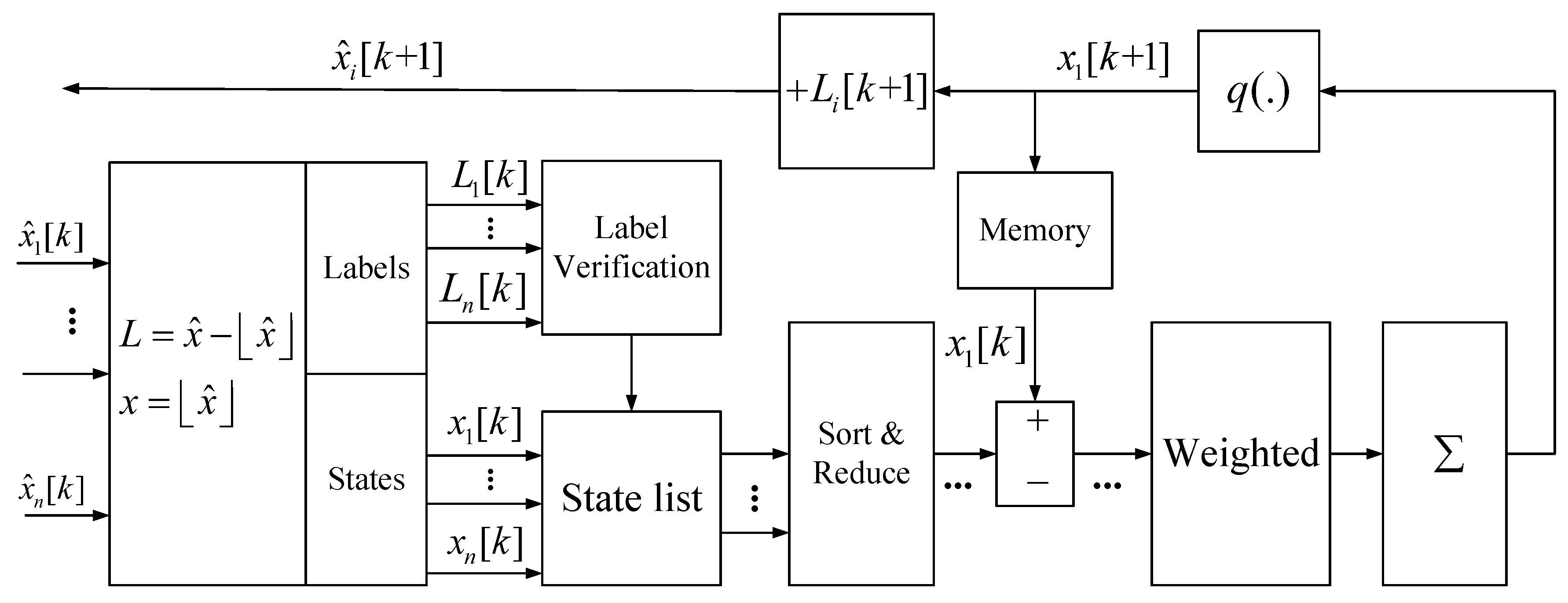
3.1. Information Processing and Verification Framework

The information that the agent communicates in the network consists of two parts, namely, the status value in integer form and the validation value in decimal form. The status value in integer form is achieved by designing an appropriate quantizer, while the validation value in decimal form is realized by designing a reasonable random distribution function.

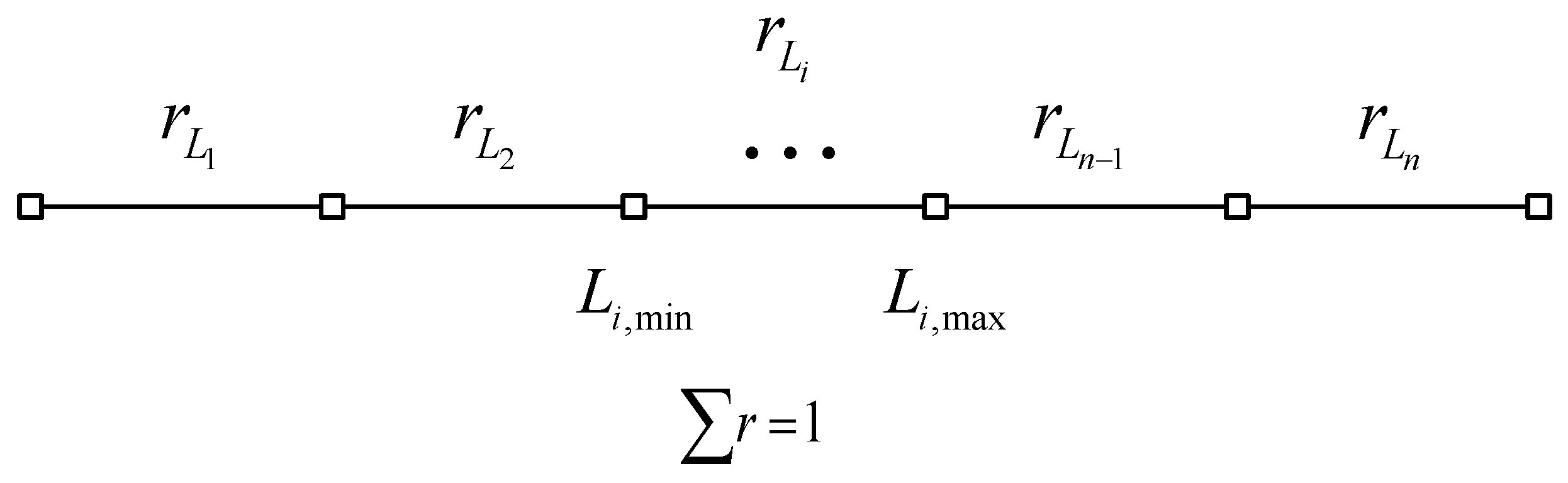
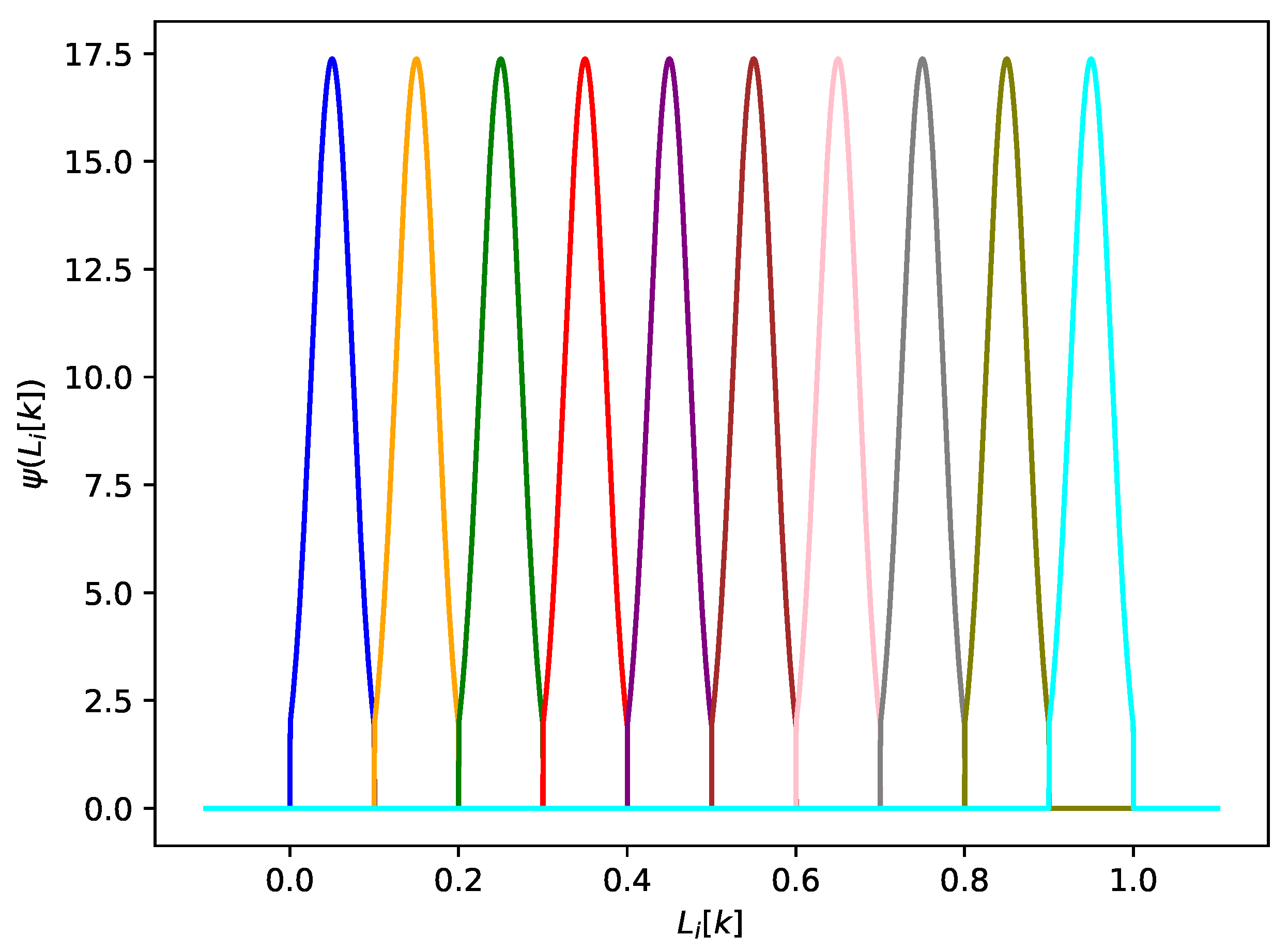
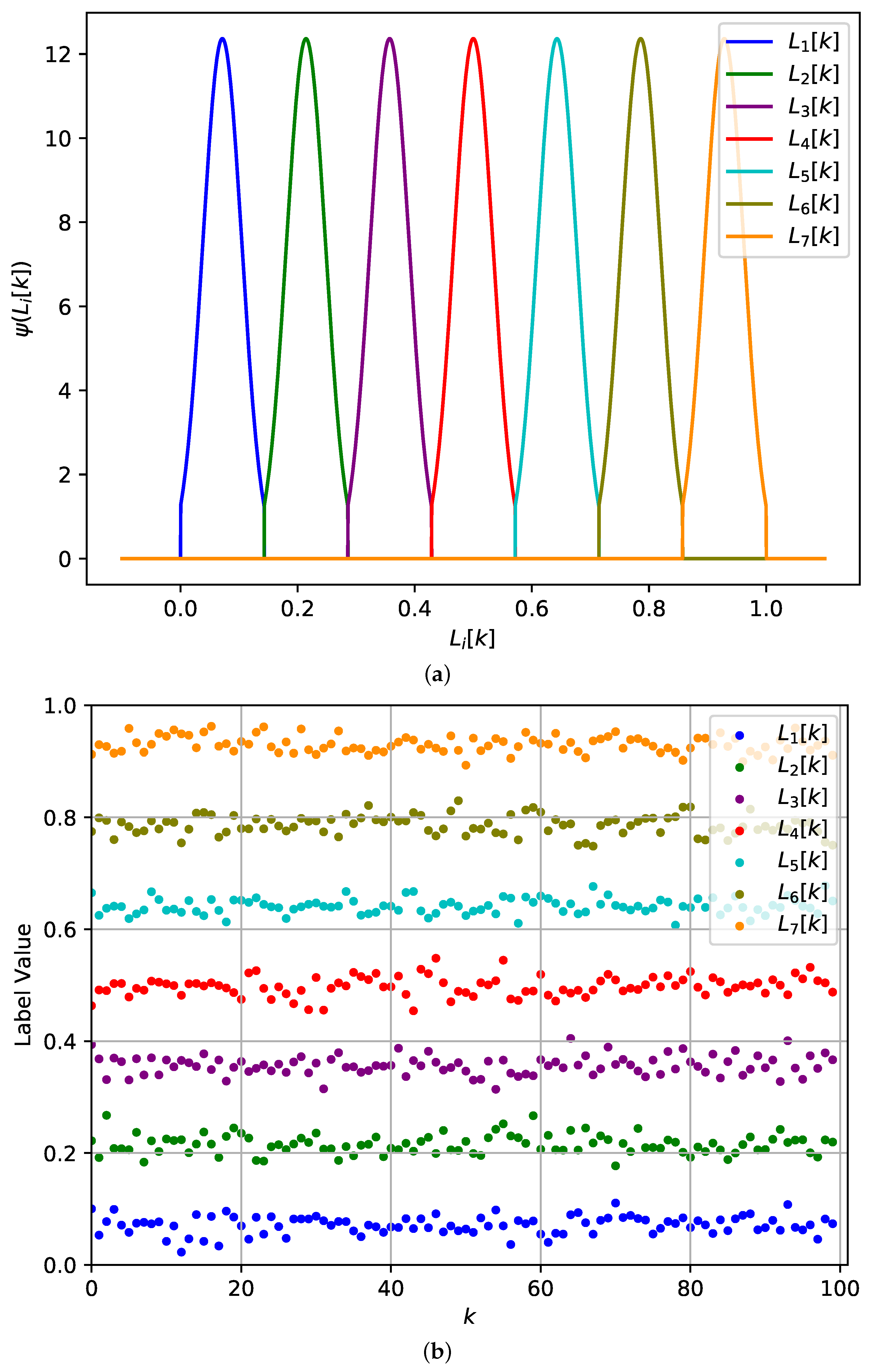
3.1.1. State Value Probabilistic Quantization

Inspired by the consensus problem for MASs with quantized communication, in this section we propose a distributed local quantizer $q(·):\mathbb{R}\to \mathbb{Z}$ aiming to transform each agent’s real-valued state to a quantized integer value.

Each agent adopts a uniform integer quantization function $q(·)$ with quantization step $\mathsf{\Delta }$:

$$q\left(y\right)=s\mathsf{\Delta },(s-\frac{1}{2})\le y\le s+\frac{1}{2}$$

(2)

where $y\in \mathbb{R}$ is the real-valued state input, and s is the quantization level. In this problem, we only set quantization step $\mathsf{\Delta }=1$, as we wanted each agent to have an integer state value.

Consider the deterministic quantization error $e\left(y\right)$, which is defined as:

$$e\left(y\right)=y-q\left(y\right).$$

(3)

According to Equation (2), it is easy to find that $e\left(y\right)$ is variable in the interval $[-1/2,1/2]$. Then, the quantizer for the MAS (1) is presented as follows:

$$q\left(y\right)=\left\{\begin{array}{cc}s\hfill & \mathrm{with}\mathrm{probability}⌈y⌉-y\\ s+1\hfill & \mathrm{with}\mathrm{probability}y-⌊y⌋\end{array}\right.$$

(4)

where the quantizer uses the percentage of the quantization step size occupied by the quantization error as the probability to select the upper and lower bounds of the quantization result. Combining the control input with the quantizer $q(·)$ yields

$$u_i\left[k\right]=q(\sum _{j\in {\mathcal{N}}_i}{a}_{ij}(x_j\left[k\right]-x_i\left[k\right])),$$

(5)

where $a_{ij}\left[k\right]$ is the $(i,j)$ entry of the adjacency matrix $\mathcal{A}$ of the graph at time k. We assume that the probabilistic quantizer in each node is independent but share the same quantization step at each time. Thus, the control law (5) can be implemented in a distributed fashion.

Next, we will present an identity verification mechanism using random labels in the following subsection, aiming to tackle Sybil child nodes’ fabricating identities in the network.

3.1.2. Verification Using Random Labels

Using information labels to verify a node’s identity is one of the typical methods in distributed networks against malicious attacks. It usually requests a specific label verification algorithm and labels information storage space. It should be noted that if a Sybil child node copies the legal label of their parent, the verification mechanism of the fixed label will be invalid. Thus, we develop a random decimal label instead of a fixed one to ensure that the label can be uniquely generated, used, and thrown away, not taking up any extra memory space. With the quantizer transforming the real-valued input into an integer value, the decimal part is used to restore the label information. Thus, the message sent by a normal node i to its neighbors is composed of the latest integer state value and its label value, i.e.,

$${\widehat{x}}_i\left[k\right]=x_i\left[k\right]+L_i\left[k\right],i\in {\mathcal{V}}_n$$

(6)

where ${\widehat{x}}_i\left[k\right]$ represents the message sent by node i, and $L_i\left[k\right]$ represents the decimal label generated by random sampling at time step k. Equation (7) below shows the messages sent by Sybil nodes in the network:

$${\widehat{x}}_i\left[k\right]=\left\{\begin{array}{cc}{x}_i\left[k\right]+L_i\left[k\right]& i\in {\mathcal{V}}_{Sp}\\ x_i\left[k\right]+L_p\left[k\right]& i\in {\mathcal{V}}_{Sc}^p,p\in {\mathcal{V}}_{Sp}\end{array}\right.$$

(7)

where ${\mathcal{V}}_{Sc}^p$ denotes the set of Sybil child nodes generated by the Sybil parent node p. For the Sybil child node, due to the lack of a physical entity, we assume that all the child nodes in ${\mathcal{V}}_{Sc}^p$ use the same label, generated by its Sybil parent node.

Remark 2.

Each normal node will generate a random decimal label before it sends information to its neighbors each time. Then, the generated label is combined with the quantized state value to generate new information for transmission. The advantage of such processing is that no additional computing equipment is required and the computing consumption within the node itself is reduced.

Since sending the messages of agents uses the integer value plus decimal value label, we have $⌊{\widehat{x}}_i\left[k\right]⌋=x_i\left[k\right]$. Combining Equation (6), it is easy to find that the following formula is established.

$$L_i\left[k\right]={\widehat{x}}_i\left[k\right]-⌊{\widehat{x}}_i\left[k\right]⌋.$$

(8)

All Sybil parent nodes have a physical entity that is used for executing the corresponding label generation algorithm, while all Sybil child nodes have no exclusive labels for their spoof identities. This is the break-point that we use to distinguish the Sybil child nodes. We give the relevant label generation requirement of such a quantization network in the face of Sybil attacks below:

• To avoid affecting the status value during the process of quantification, the label value shall be strictly less than one quantization step;
• To avoid different nodes generating the same label, the random label range of one agent shall be an open interval;
• To make labels time-sensitive, one node generates a random label at each time step.

According to the above requirements for labels, we set the sample range of random labels in one quantization step, i.e., $\mathsf{\Delta }=1$. Then, according to the number of agents, we ensure that the random distribution range can not coincide. When all agents generate labels by sampling from one normal distribution, the labels of different agents have a chance to be identical. Therefore, we use the sampling method based on a disjoint truncated normal distribution to generate labels to avoid being identified. Each agent generates a random label by sampling distribution to select one item from the range of legal values, using the probability density function as the probability of selection.

Figure 2 is a schematic diagram of our sampling process. In the figure, the sum of random label sample ranges of n agents is one quantization step $\mathsf{\Delta }=1$ in one time step, and those ranges have the same length on the axis, i.e., $r_{L_i}=\frac{1}{n},\forall i\in \mathcal{V}$, where $n=|{\mathcal{V}}_n\cup {\mathcal{V}}_{Sp}|$. As we know, the Sybil parent node is the first compromised agent. Thus, parameter n is the number of agents in the original system. According to the total number of agents n and the value of quantization step $\mathsf{\Delta }=1$, we have the maximum and minimum of the label of each node at time step k as $L_{i,min}=\frac{i-1}{n}$ and $L_{i,max}=\frac{i}{n}$.

The mean and variance of truncated normal distribution based on $r_{L_i}$ are ${\mu }_i=\frac{L_{i,max}+L_{i,min}}{2}$ and $\sigma =\frac{|r_{L_i}|}{2}$, respectively. To eliminate the probabilities of the same labels, the random label value distribution range of agent i is modified to an open interval $(L_{i,min},L_{i,max})$. Thus, the probability density function of the corresponding label value is given as

$$f^{\prime }\left(L_i\right)=\left\{\begin{array}{cc}{c}_i\frac{1}{\sqrt{2\pi }\sigma }{e}^{-0.5{\left(\frac{L_i-{\mu }_i}{\sigma }\right)}^2},& L_{i,min}<L_i<L_{i,max}\\ 0,& others\end{array}\right.$$

(9)

where ${\mu }_i$ and $\sigma$ represent the mean of i’ label and standard deviation, respectively. Parameter $c_i$ is used to make sure the cumulative probability of $f^{\prime }\left(L_i\right)$ is 1 in the interval $(L_{i,min},L_{i,max})$. For the truncated normal distribution in the $(L_{i,min},L_{i,max})$, $F^{\prime }\left(L_i\right)=c_i\left[F\left(L_i\right)-F\left(L_{i,min}\right)\right]$; thus, we have parameter $c_i^{-1}=F\left(L_{i,min}⩽L_i⩽L_{i,max}\right)$. According to the total number of agents and the quantization length, parameters in Equation (9) can be set as follows:

$$\begin{array}{c}{\mu }_i=\frac{2i-1}{2n},\end{array}$$

(10)

$$\begin{array}{c}\sigma =\frac{1}{2n},\end{array}$$

(11)

$$\begin{array}{c}{L}_{i,min}=\frac{i-1}{n},\end{array}$$

(12)

$$\begin{array}{c}{L}_{i,max}=\frac{i}{n},\end{array}$$

(13)

$$\begin{array}{c}{c}_i^{-1}={\int }_{L_{i,min}}^{L_{imax}}\frac{1}{\sqrt{2\pi }\sigma }exp\left(\frac{1}{2}{\left(\frac{L_i-{\mu }_i}{\sigma }\right)}^2\right)\mathrm{d}{L}_i.\end{array}$$

(14)

The truncated normal distribution function $F^{\prime }$ can be calculated according to the following three situations:

• If $L_i\le L_{i,min}$, then $F^{\prime }\left(L_i\right)={\int }_{-\infty }^{L_i}{f}^{\prime }\left(u\right)\mathrm{d}u=0$.
• If $L_{i,min}<L_i<L_{i,max}$, then
  $$\begin{gathered} F^{\prime }\left(L_i\right)={\int }_{-\infty }^{L_i}{f}^{\prime }\left(u\right)\mathrm{d}u={\int }_{L_{i,min}}^{L_i}{f}^{\prime }\left(u\right)\mathrm{d}u \\ =c_i\left[{\int }_{-\infty }^{L_i}\frac{1}{\sqrt{2\pi }\sigma }{\mathrm{e}}^{-0.5{\left(\frac{u-{\mu }_i}{\sigma }\right)}^2}\mathrm{d}u-\right.\left.{\int }_{-\infty }^{\infty }\frac{1}{\sqrt{2\pi }\sigma }{\mathrm{e}}^{-0.5{\left(\frac{u-{\mu }_i}{\sigma }\right)}^2}\mathrm{d}u\right] \\ =c_i\left[F\left(L_i\right)-F\left(L_{i,min}\right)\right] \end{gathered}$$.
• If $L_i\ge L_{i,max}$, then
  $F^{\prime }\left(L_i\right)={\int }_{L_{i,min}}^{L_i}{f}^{\prime }\left(u\right)\mathrm{d}u={\int }_{L_{i,min}}^{L_{i,max}}{f}^{\prime }\left(u\right)\mathrm{d}u=c_i\left[F\left(L_{i,max}\right)-F\left(L_{i,min}\right)\right]=1$.

With label sampling from such a truncated normal distribution, each agent can generate the corresponding random label. The random label generation model complies with a truncated normal probability density function as

$$L_i\sim \psi (\frac{2i-1}{2n},{\left(\frac{1}{2n}\right)}^2,\frac{i-1}{n},\frac{i}{n};L_i).$$

(15)

In Figure 3, we give an example of the probability distribution function of 10 agents in quantization step $\mathsf{\Delta }=1$, where different colors represent the label probability density curve of 10 different nodes. The random label of each agent is distributed in the corresponding truncated range centered on the half of $r_{L_i}$.

The main idea of the label generation design is that the label value merges with the quantized status value and becomes a quantified part. Since each agent label is sampled from the corresponding truncated normal distribution range $L_i\left[k\right]\in (L_{i,min},L_{i,max})$, one can identify each individual agent in the MAS. At the same time, since the child node and the parent node have the same label value, the redundant fake child nodes that have been generated can be easily distinguished and ignored by the normal nodes. After label verification and the removal of redundant individuals with the same label, the total number of nodes in the network is maintained at n.

In the following subsection, we provide the solution to the resilient consensus problem with Sybil nodes in the network.

3.2. Distributed Consensus Control Law Design

Recall that the malicious nodes in MAS shall be divided into a Sybil parent node and Sybil child node. Thus, ${\mathcal{V}}_S={\mathcal{V}}_{Sp}\cup {\mathcal{V}}_{Sc}$. Combined with the local quantification process, the updated rule for the nodes can be written in the following form:

$$x_i[k+1]=\left\{\begin{array}{cc}q({\displaystyle \sum _{j\in {\mathcal{N}}_i\cup \left\{i\right\}}}{a}_{ij}\left[k\right]x_j\left[k\right])& i\in {\mathcal{V}}_n\\ x_i\left[k\right]+u_i\left[k\right]& i\in {\mathcal{V}}_s\end{array}\right.$$

(16)

The existing typical methods against Sybil attacks are adopting a strict identity distribution mechanism or using physical fingerprints as authentication. Such methods always require extra modules and computing consumption. Before giving our distributed control protocol, we first need to introduce the notion of resilient consensus for the network of probabilistic quantized agents in the face of malicious attacks.

Definition 8.

(Quantized Resilient Consensus) For a quantization consensus system under malicious attacks, if the following conditions are met, then the network is said to reach a quantized resilient consensus:

1 

Safety condition:For each set of quantized values of the normal agents, with the maximum value $M\left(0\right)$ and minimum value $m\left(0\right)$ of the initial state values of normal nodes, there exists a set $\mathcal{S}\subseteq \left[m\right(0),M(0\left)\right]$ such that for all normal agents $i\in {\mathcal{V}}_n$, it holds that $x_i\left[k\right]\in \mathcal{S}$ for $k\ge 0$.

2 

Agreement condition:There exists a finite time $k_c\ge 0$ such that $Prob\{x^{{\mathcal{V}}_n}\left(k_c\right)\in {\mathcal{C}}_{{\mathcal{V}}_n}|x\left(0\right)\}=1$, where the consensus ${\mathcal{C}}_{{\mathcal{V}}_n}$ is defined as

$${\mathcal{C}}_{{\mathcal{V}}_n}=\{x\in {\mathbb{Z}}^{{\mathcal{V}}_n}|x_1=\cdots =x_{{\mathcal{V}}_n}\}$$

(17)

Next, we give our distributed consensus algorithm, which is mainly inspired by the weighted mean subsequence reduced (QW-MSR) algorithm [37], and incorporates the previously designed label generation and verification mechanism, referred to as the QWL-MSR algorithm.

Description of QWL-MSR Algorithm

At each time step k, the normal node i will receive the messages of its neighbors. We assume that there are at most f Sybil parent nodes among the node i’ neighbors, and each Sybil parent node can generate up to n Sybil child nodes. Therefore, node i will receive at most $nf+f$ pieces of malicious messages. The pseudocode of QWL-MSR can be seen in Algorithm 1.

Algorithm 1 QWL-MSR

Input:$i,f,n,{\mathcal{N}}_i,\mathcal{A},x_i\left[k\right],k$ Output:$x_i[k+1]$ 1: $L_i\left[k\right]=rand\left(x\right)$ 2: $x={\psi }^{-1}(\frac{2i-1}{2n},{\left(\frac{1}{2n}\right)}^2,\frac{i-1}{n},\frac{i}{n};L_i)$ 3: ${\widehat{x}}_i\left[k\right]=x_i\left[k\right]+L_i\left[k\right]$ 4: Send ${MSG}_i\left[k\right]=\{k,i,{\widehat{x}}_i\left[k\right]\}$ to neighbor nodes 5: Empty ${LBL}_i,{ST}_i$ 6: Receive ${MSG}_j\left[k\right]$ from neighbors, $j\in {\mathcal{N}}_i$ 7: for$j\in {\mathcal{N}}_i$do 8:    $L_j\left[k\right]={\widehat{x}}_j\left[k\right]-\lfloor {\widehat{x}}_j\left[k\right]\rfloor$ 9:    $x_j\left[k\right]=\lfloor {\widehat{x}}_j\left[k\right]\rfloor$ 10:    ${LBL}_i\leftarrow$ Append $L_j\left[k\right]$ 11: end for 12: ${\mathcal{N}}_S\left[k\right]\leftarrow LabelVerification\left({LBL}_i\right)$ 13: $S{T}_i\leftarrow$ Append $x_j\left[k\right]$ where j not in ${\mathcal{N}}_S\left[k\right]$ 14: ${\mathcal{N}}_S\left[k\right]\leftarrow$ Append $StateFiltration(x_i\left[k\right],S{T}_i,f)$ 15: $x_i[k+1]=q({\displaystyle \sum _{j\in \{{\mathcal{N}}_i\cup \left\{i\right\}\}\backslash {\mathcal{N}}_S\left[k\right]}}{a}_{ij}\left[k\right]x_j\left[k\right])$ 16: return$x_i[k+1]$

In Algorithm 1, node i first generates a truncated normal distribution function based on the input values, and then generates label $L_i\left[k\right]$ by sampling in the generated function. Subsequently, node i merges the state value and the label value and sends it to its neighbor nodes. When node i receives the message value ${MSG}_j\left[k\right]$ from its neighbor node $j\in {\mathcal{N}}_i$, the label value and state value will be separated. The Sybil nodes are excluded into the Sybil node-set ${\mathcal{N}}_S$ though label verification and state filtration. Under this mechanism, node i will update its own state value without interference from Sybil nodes. Specifically, the following five steps can be used to describe the whole process of node information processing.

• Label Generation: At each time step k, each node $i\in \mathcal{V}$ (including Sybil nodes) calculates and generates an exclusive random label $L_i\left[k\right]$;
• Message Exchange: Once node i updates its own state value, it will combine the message value with its newly generated status value and label value, i.e., ${\widehat{x}}_i\left[k\right]=x_i\left[k\right]+L_i\left[k\right]$. Then, it sends this message to its neighbors, and receives the message values from its neighbors $j\in {\mathcal{N}}_i$.
• Label Verification: After step 2, node i executes the label stripping algorithm (8) to the message value of the nodes in the list, then puts the labels into list ${LBL}_i$. If there are any nodes with the same label value in the list, node i groups these nodes into the Sybil neighbor set ${\mathcal{N}}_S\left[k\right]$, but only reserves the first node with that label value. It sorts the remaining state values into a descending order list ${ST}_i$ at the same time.
• State Filtration: If there are less than f nodes for which state values are strictly larger or smaller than $x_i\left[k\right]$ in the list ${ST}_i$, node i groups these nodes into the Sybil neighbor set ${\mathcal{N}}_S\left[k\right]$. Otherwise, it groups the f largest and f smallest values of the nodes in the list into the set ${\mathcal{N}}_S\left[k\right]$.
• State Update: According to the set ${\mathcal{N}}_S\left[k\right]$ obtained by the above operation, node i applies the following update:

  $$x_i[k+1]=q(\sum _{j\in \{{\mathcal{N}}_i\cup \left\{i\right\}\}\backslash {\mathcal{N}}_S\left[k\right]}{a}_{ij}\left[k\right]x_j\left[k\right]).$$

  (18)

Figure 4 shows the data flow model of QWL-MSR for normal agent i. In the figure, the state value $x_i\left[k\right]$ of node i, is subtracted from each of the other states, including its own state in the memory. The resulting relative states are verified and filtered by order. Finally, the remaining elements are weighted, summed, and quantized to the next state.

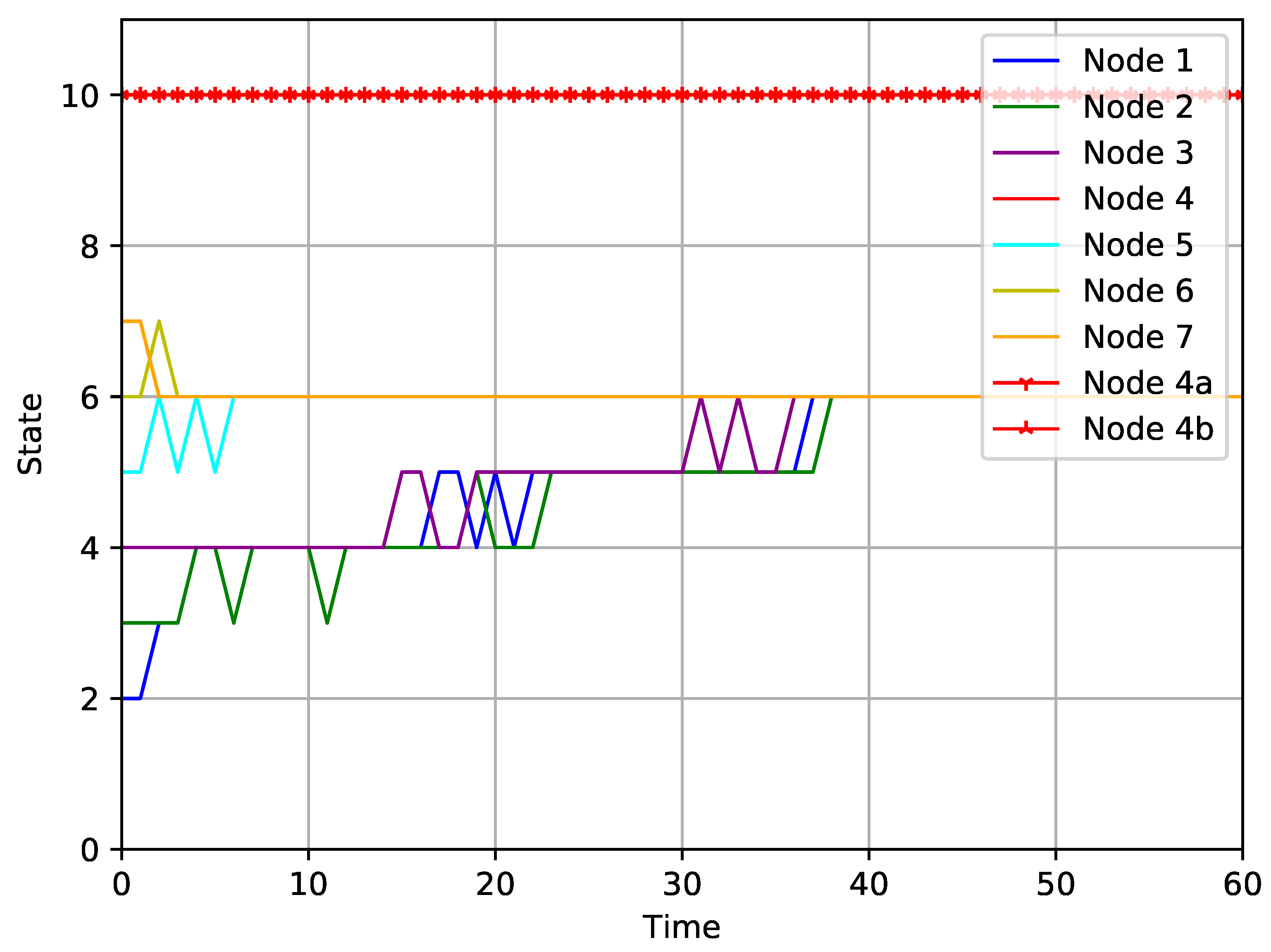
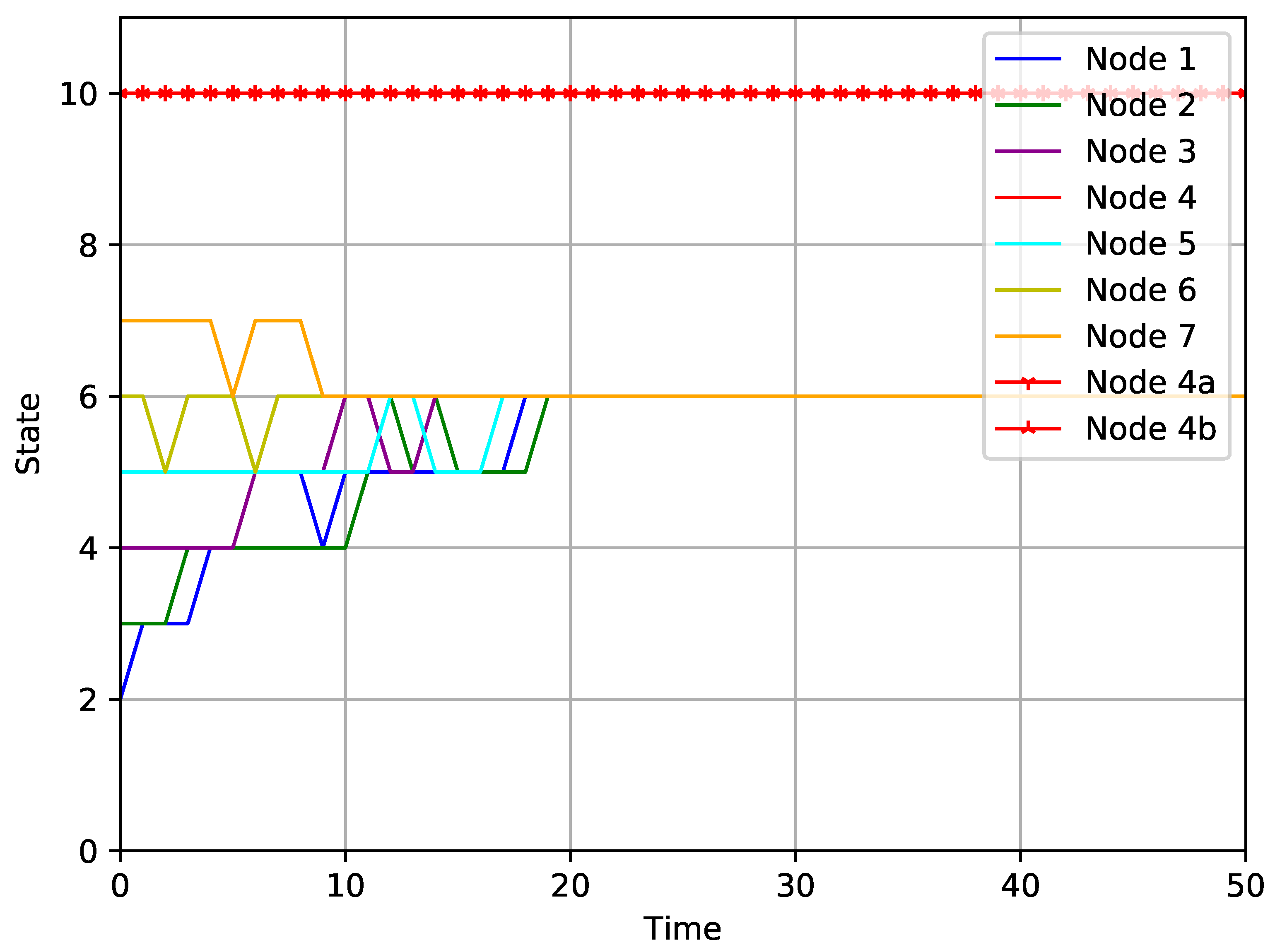
4. Main Results

We now present our main theorems for quantized resilient consensus in the presence of Sybil attacks. The network underlying a robust graph that guarantees sufficient connectivity and information redundancy for agents strengthens the incoming counter attacks. Let us revisit the definition of security interval S by

$$\mathcal{S}=[min{x}^{{\mathcal{V}}_n}\left[0\right],max{x}^{{\mathcal{V}}_n}\left[0\right]],$$

(19)

where $min{x}^{{\mathcal{V}}_n}\left[0\right]$ and $max{x}^{{\mathcal{V}}_n}\left[0\right]$ represent the minimum and maximum initial state values of all nodes in the MAS, respectively. Note that we assume that the initial value of each agent is an integer, i.e., $x_i\left[0\right]\in \mathbb{Z},i\in \mathcal{V}$.

Since we choose to run probability quantization during the node state value update process, the discussions of consensus under probabilistic conditions are inevitable. The following three conditions, which are argued in [37] for the probabilistic quantized consensus problem, are also adopted in our paper.

(1)

C1. There is a finite state set $\mathcal{S}$ for each normal node i, such that, for any $k\ge 0$, $x_i\left[k\right]\in \mathcal{S}$.

(2)

C2. There exists a finite time $k_x$, such that, for state value $x\left[k\right]=x_0\in \mathcal{S}$, $\mathrm{Prob}\{x^{{\mathcal{V}}_n}[k+k_x]\in {\mathcal{C}}_{{\mathcal{V}}_n}|x\left[k\right]=x_0\}>0$.

(3)

C3. If $x\left[k\right]\in {\mathcal{C}}_{{\mathcal{V}}_n}$, then $x\left[k^{\prime }\right]\in {\mathcal{C}}_{{\mathcal{V}}_n},\forall k^{\prime }>k$.

Theorem 1.

Under the f-parent total Sybil attack model, the MAS (1) for which each node updates its state according to the QWL-MSR algorithm with parameter f reaches quantized resilient consensus almost surely if, and only if, the system’s network topology is $(f+1,f+1)$-robust.

Proof of Theorem 1.

(Necessity) Although all Sybil child nodes could be removed after the step of label verification, there are still f values of Sybil parent nodes retained in the network. Then, in the step of state filtration, if the underlying graph $\mathcal{G}$ is not $(f+1,f+1)$-robust, the node-set includes two disjointed and nonempty subsets, ${\mathcal{V}}_1$ and ${\mathcal{V}}_2$, that do not meet any conditions in Definition 4. Thus, the incoming edges of any disjointed and nonempty subset ${\mathcal{V}}_1$ or ${\mathcal{V}}_2$ is less than $f+1$. With the QWL-MSR algorithm, the normal node will ignore all of its neighbors’ values that are different from its state and will not update its state, which will cause the state value consensus process to fail to complete.

(Sufficiency) We first show that the state value of each normal node in the update process satisfies the safety condition. We denote the minimum and maximum values of normal nodes at time step k by

$$\underline{x}\left[k\right]=min{x}^{{\mathcal{V}}_n}\left[k\right],\overline{x}\left[k\right]=max{x}^{{\mathcal{V}}_n}\left[k\right].$$

(20)

Since we consider the f-parent total Sybil attack model, that means there are at most f Sybil parent nodes in the network. Each Sybil parent node will fabricate n Sybil child nodes. Therefore, it is equivalent to the existence of at most $(n+1)f$ malicious nodes in the entire network. At each time k, all the Sybil child nodes’ values will be ignored in the step of label verification of the QWL-MSR algorithm. Then, in the step of state filtration of our algorithm, the normal node i will remove the first f and last f values in the sorted list of its all neighbors. This ensures that the information used in the update of node i is not beyond the interval $[\underline{x}\left[k\right],\overline{x}\left[k\right]]$.

According to the update rule (18) and the remain neighbor set ${\varphi }_i\left[k\right]=\{{\mathcal{N}}_i\cup \left\{i\right\}\}\backslash {\mathcal{N}}_S\left[k\right]\}$, the value of next time step of normal node i will be upper bounded by

$$x_i[k+1]\le q(\sum _{j\in {\varphi }_i\left[k\right]}{a}_{ij}\left[k\right]x_j\left[k\right])\le q(\sum _{j\in {\varphi }_i\left[k\right]}{a}_{ij}\left[k\right]\overline{x}\left[k\right])=q\left(\overline{x}\left[k\right]\right)=\overline{x}\left[k\right].$$

This implies that $x_i[k+1]\le \overline{x}\left[k\right]$ and $\overline{x}\left[k\right]$ is a monotonically non-increasing function of time. Hence, node i’s value at the next time step has a lower bound value function $\underline{x}\left[k\right]$, i.e.,

$$x_i[k+1]\ge q(\sum _{j\in {\varphi }_i\left[k\right]}{a}_{ij}\left[k\right]x_j\left[k\right])\ge q(\sum _{j\in {\varphi }_i\left[k\right]}{a}_{ij}\left[k\right]\overline{x}\left[k\right])=q\left(\underline{x}\left[k\right]\right)=\underline{x}\left[k\right].$$

Consequently, node i’s state value satisfies $x_i\left[k\right]\in [\underline{x}\left[k\right],\overline{x}\left[k\right]]$ for all time steps, which implies that the safety condition of MAS (1) is ensured.

We next show that the state value of each normal node $i\in {\mathcal{V}}_n$ in the update process (18) satisfies the agreement condition. Let the set $\mathcal{S}$ be a set of all normal nodes’ state values at all times. Since $\underline{x}\left[k\right]$ and $\overline{x}\left[k\right]$ are both monotone functions, they will eventually converge to the values ${\underline{x}}^{*}$ and ${\overline{x}}^{*}$ with probability at a finite time $k^{\prime }$, respectively. We will show that ${\underline{x}}^{*}$ and ${\overline{x}}^{*}$ tend to be the same as the time becomes infinite. We prove this by contradiction. Assume that ${\underline{x}}^{*}<{\overline{x}}^{*}$. In this case, the shortest distance between ${\underline{x}}^{*}$ and ${\overline{x}}^{*}$ is one quantization step $\mathsf{\Delta }$, thus $\overline{x}\left[k\right]-\underline{x}\left[k\right]=\mathsf{\Delta }$. As the state values tend to remain unchanged, we denote the set of nodes (including Sybil nodes) for which state values are greater than or equal to ${\overline{x}}^{*}$ and the set of nodes (including Sybil nodes) for which state values are less than or equal to ${\underline{x}}^{*}$ by ${\mathcal{X}}_1\left[k\right]$ and ${\mathcal{X}}_2\left[k\right]$, respectively, i.e.,

$$\begin{array}{c}\hfill {\mathcal{X}}_1\left[k\right]=\{i\in \mathcal{V}:x_i\left[k\right]\ge {\overline{x}}^{*}\},\\ \hfill {\mathcal{X}}_2\left[k\right]=\{i\in \mathcal{V}:x_i\left[k\right]\le {\underline{x}}^{*}\}.\end{array}$$

(21)

Since the network of MAS (1) satisfies a $(f+1,f+1)$-robust graph, we know that for any pair of nonempty disjointed subsets of $\mathcal{V}$, at least one of the three conditions in Definition 4 is satisfied. We let ${\mathcal{X}}_1\left[k\right]$ and ${\mathcal{X}}_2\left[k\right]$ be such a pair of subsets. In this case, there always exists a normal node i, either in ${\mathcal{X}}_1\left[k\right]$ or ${\mathcal{X}}_2\left[k\right]$, with $(f+1)$ incoming edges from $\mathcal{V}\backslash {\mathcal{X}}_1\left[k\right]$ or $\mathcal{V}\backslash {\mathcal{X}}_2\left[k\right]$. We suppose node i in ${\mathcal{X}}_1\left[k\right]$ has this property and its state value is $x_i\left[k\right]={\overline{x}}^{*}$. If there are any Sybil nodes around node i, in the step of label verification, node i will ignore at most $nf$ incoming edges from them. Then, in the step of state filtration, node i will neglect at most f values from $\mathcal{V}\backslash {\mathcal{X}}_1\left[k\right]$ and at most f values larger than ${\overline{x}}^{*}$ which are sent from f Sybil nodes. That means node i will receive at least one node’s value in ${\mathcal{X}}_2\left[k\right]$, which is smaller than ${\overline{x}}^{*}$. Thus, by the update rule (18), we have

$$x_i[k+1]\le q((1-a){\overline{x}}^{*}+a{\underline{x}}^{*})=q((1-a){\overline{x}}^{*}+a({\underline{x}}^{*}-1)=q({\overline{x}}^{*}-a),$$

(22)

where $a<1$ is node i’ self-weight. With random quantizer (4), we have $q({\overline{x}}^{*}-a)={\overline{x}}^{*}-1$ with probability $1-a$. Thus,

$$x_i\left[k\right]\le \overline{x}-1={\underline{x}}^{*}.$$

(23)

This indicates that there is at least one node in ${\mathcal{X}}_1\left[k\right]$ that will update and decrease its state value at time step k.

We now show that there is a positive probability that none of the nodes in $\mathcal{V}\backslash {\mathcal{X}}_1\left[k\right]$ will be placed into set ${\mathcal{X}}_1[k+1]$ at the next time step. According to (18) and (22), the normal node i will choose the value ${\overline{x}}^{*}-1$ with probability a. In another words, node i will not be placed into ${\mathcal{X}}_1[k+1]$ with probability $1-a$. By applying the same argument, nodes in $\mathcal{V}\backslash {\mathcal{X}}_2\left[k\right]$ will not be placed into ${\mathcal{X}}_2[k+1]$ according to their updated state values.

By the above analysis, we conclude that for any $k\ge k^{\prime }+\left|{\mathcal{V}}_n\right|$, one of sets (${\mathcal{X}}_1\left[k\right]$ and ${\mathcal{X}}_2\left[k\right]$) will be empty with a positive probability. Clearly, it arrives at a contradiction with the definition of a $(f+1,f+1)$-robust graph. Hence, we proved ${\underline{x}}^{*}={\overline{x}}^{*}$.

According to the above discussion, one can clearly see that the safety condition of node i in MAS (1) also satisfies the C1 in the quantized consensus problem, while the agreement condition of node i in MAS (1) also satisfies the C2 and C3 in the quantized consensus problem. Thus, the proof is completed. □

Theorem 2.

Under the f-parent local Sybil attack model, the MAS (1) that each normal node updates its state value with according to the QWL-MSR algorithm with parameter f reaches quantized resilient consensus almost surely if, and only if, the network’s topology is $(2f+1)$-robust.

Proof 

(Proof of Theorem 2). (Necessity) We will prove by contradiction. Assume the network topology does not satisfy a $(2f+1)$-robust graph; each node in the nonempty disjoint subsets ${\mathcal{V}}_1$ or ${\mathcal{V}}_2$ will have at most f neighbors from the outside. Although the Sybil child nodes could be removed after the step of label verification, the normal nodes in ${\mathcal{V}}_1$ and ${\mathcal{V}}_2$ will ignore all of the neighbors that have different values. This will cause the normal nodes not to update their state values. This also means that consensus cannot be achieved.

(Sufficiency) The proof is similar to the proof of the sufficiency of Theorem 1 and hence is omitted here. Note that by the steps of label verification and state filtration of QWL-MSR algorithm, the safety condition and agreement condition are guaranteed if the network is $(2f+1)$-robust. □

5. Numerical Simulation

In this section, a numerical simulation is proposed to illustrate the effectiveness of the theoretical results for MAS under f-parent total model and f-parent local Sybil attack model, respectively.

Consider the MAS with $n=7$ agents. The connections among agents are represented in Figure 5a,b. According to Definition 4, one can verify that the graph in Figure 5a is $(2,2)$-robust, and the graph in Figure 5b is 3-robust. Suppose node 4 is infected by a Sybil attack and becomes a malicious Sybil parent node. Then, node 4 generates two Sybil child nodes, 4a and 4b. The figure shows that the Sybil child and Sybil parent nodes share the same adjacency matrix. Hence, the normal nodes connected to the Sybil parent node will also receive malicious information from Sybil child nodes. The initial values of all nodes are $x\left[0\right]={[2,3,4,10,5,6,7]}^T$. Thus, the safety interval is $[2,7]$. Let all Sybil nodes maintain their values $x_4\left[k\right]=x_{4a}\left[k\right]=x_{4b}\left[k\right]=10$ for the entirety of the time step k. In this scenario, the adversary is aimed at driving the system out of the safe set $[2,7]$.

First, we will check the state value trajectories of all nodes applying the existing QW-MSR algorithm in the $(2,2)$-robust graph under 1-parent total Sybil attack. It is observed in Figure 6 that all normal nodes are misguided by the malicious values and reach the consensus value $x^{*}=10$, which is out of the safety interval $[2,7]$. This means that the traditional QW-MSR algorithm is insufficient for such Sybil attacks.

Next, we examine the performance of the case with the same network communication topology, but each node runs our proposed QWL-MSR algorithm. First, each node generates its own label according to a truncated normal distribution in the value range of the corresponding label. With a total number of agents $n=7$, the sampling of each agent’s label conforms to the truncated normal distribution $L_i\left[k\right]\sim \psi (\frac{2i-1}{14},{\left(\frac{1}{14}\right)}^2,\frac{i-1}{7},\frac{i}{7};L_i\left[k\right])$. Figure 7a shows the probability distribution function curve of random label sampling for each agent. The scatter points in Figure 7b more intuitively indicate that the random labels of each agent generated at each time step k are distributed in the corresponding range and will not overlap with each other.

Under the one-parent total Sybil attack, with the QWL-MSR algorithm applied to the MAS of seven agents, the trajectory of each agent state value is shown in Figure 8. From the figure, we can see that all normal agents reach a consensus value $x^{*}=6$ after 38 steps. This simulation result verifies the validity of Theorem 1.

Now, we consider the case when the MAS topology satisfies a 3-robust graph (see Figure 5b). The attack model, in this case, is a one-parent local Sybil attack model. The simulation results are shown in Figure 9. The figure shows that all normal agents acquire a consensus value $x^{*}=6$ after 19 time steps. This simulation result verifies the validity of Theorem 2.

In order to verify the necessity of network robustness for our proposed algorithm, we design a (2,1)-robust graph by deleting links (1,3), (3,1), (5,7) and (7,5) from Figure 5b. The newly designed network communication topology is shown in Figure 5c. Likewise, we newly design a graph (see Figure 5d) that no longer satisfies 3-robust but that is still strongly connected by reducing links. Under the same network attack situation and running the same control algorithm, the state value trajectories of all normal agents are shown in Figure 10 and Figure 11, respectively. It can be seen from the simulation results that the node state value cannot reach consensus, which further verifies the correctness of our theories.

6. Conclusions

In this paper, we considered the distributed resilient consensus problem of MASs under Sybil attacks. A consensus algorithm based on random label values was applied to each agent to determine valid neighbor agents and realize the state value convergence under Sybil attacks. The proposed algorithm is computationally lightweight and suitable for use in distributed MASs. Using graph theory and mathematical analysis, we have proved the effectiveness of the consensus algorithm under consideration. Numerical simulations are also provided to confirm our methods.