The Design Considerations and Challenges in MOS-Based Temperature Sensors: A Review

Abstract

This review paper categorizes the state-of-the-art MOS (metal oxide semiconductor)-based temperature sensors according to their thermal sensing principles, including: type I, the logic, saturation and linear MOS-based temperature sensors; type II, the subthreshold MOS-based temperature sensors; and type III, the gate leakage-based temperature sensors. It also discusses in detail the design considerations and challenges of MOS-based temperature sensors, in terms of area, energy efficiency, supply voltage, inaccuracy, noise, as well as process and power supply variations. Based on the aforementioned discussions, the paper concludes that the future MOS-based temperature sensors will mostly likely be based on subthreshold MOS operation, with better trade-offs between area, energy efficiency and accuracy, and with reduced power supply sensitivity and level, as well as a lower-cost, fewer-point calibration method.

1. Introduction

In industry, common temperature sensors include integrated circuit (IC) temperature sensors, thermistors, the resistor temperature detector (RTD) and thermocouples, among which, in turn, the temperature measurement range and the sensor size increase, in general. For example, the ultrasonic transducers, which were reviewed in [1], are capable of measuring temperatures higher than 150 °C in hazardous environments, belonging to the RTD category. IC temperature sensors are required for applications such as human body temperature monitoring, VLSI thermal monitoring and management, etc. Modern microprocessors, such as Intel i7, rely on the on-chip temperature sensors to trigger an alert when their temperatures reach a predefined threshold. The speed of the fans on the microprocessors are adjusted according to the temperature sensors’ readings. Typical thermal management approaches include dynamic voltage scaling and dynamic frequency scaling, which reduce the voltage or the frequency dynamically for circuitries at the hotspots [2]. For high voltage, high temperature applications (e.g., between −20 and 180 °C), a thermal shutdown circuit is employed and its output voltage drops as its sensed temperature reaches a threshold, e.g.,140 °C [3]. Its sensing core consists of a bipolar junction transistor (BJT) whose current decreases with temperature. As its current crosses the reference level through a current mirror, the output MOS transistor is driven into its triode region and its drain-source (output) voltage drops to nearly ground level, hence turning off the circuits that follow. The state-of-the-art IC temperature sensors can be categorized into three major types: the MOS based [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34], the BJT based [35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75], and the (polysilicon) resistor based [76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106] types. Figure 1a–c compare the above-mentioned three types on their area and resolution figures of merit (RFOM), as well as their supply voltage levels, in the papers published in [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106]. Figure 2 shows the trade-offs between energy efficiency and area for all three types. A few observations can be made from Figure 1 and Figure 2, as follows: (1) The smallest sensor belongs to the MOS-based type, for the last 5 years; (2) Among the temperature sensors that have the smallest RFOM, the majority belong to the resistor-based type. RFOM is calculated as energy/conversion∙resolution² and is a representation of the energy efficiency in reference to its resolution; However, the MOS-based type is better than its BJT counterpart, for RFOM, on average (Figure 1b); (3) The majority of sensors with the lowest supply voltage belong to the MOS-based type (Figure 1c). (4) The MOS and the resistor-based types have better energy efficiency and area trade-offs than their BJT-based counterparts (Figure 2), in general. For VLSI thermal management, multiple temperature sensors are required at hotspots for thermal monitoring and they are preferred to share the digital voltage supply level, which scales with the technology nodes. Therefore, to target for small area and low voltage supply applications, this review focuses on the MOS-based temperature sensors. This review is organized as follows. Section 2 describes the operating principles of different subtypes of MOS-based temperature sensors, which are categorized according to their thermal sensing principles, namely: type I, the logic, saturation and linear MOS-based temperature sensors; type II, the subthreshold MOS-based temperature sensors; and type III, the gate leakage-based temperature sensors. The design considerations and challenges of the MOS-based temperature sensor design, such as area, power and accuracy trade-offs, as well as the process and voltage supply sensitivity are discussed in Section 3. Section 4 concludes this paper.

2. Subtypes of MOS-Based Temperature Sensors

In this paper, the state-of-the-art MOS-based temperature sensors are categorized according to their thermal sensing principle into three categories, from type I to type III, where the MOSFETs (metal–oxide–semiconductor field-effect transistors) are working in their saturation/linear, subthreshold and gate leakage regions, respectively. This method of categorization is in contrast to [107], which categorizes the delay line-based temperature sensors by their ways of quantization.

2.1. The Logic, Saturation and Linear MOS-Based Temperature Sensors (Type I)

It is well known that the propagation delay of a CMOS logic inverter, as shown in Figure 3, increases with temperature. This temperature dependency arises from the thermal coefficient of surface carrier mobility and the threshold voltage, as shown in Figure 4, which is simulated between −55 and 125 °C, for TT corner, using a 55 nm CMOS technology. The discharging propagation delay can be deduced to be [108]

$$t_{dis}=\frac{\left(\frac{L}{W}\right)C_L}{\mu C_{ox}\left(V_{DD-}{V}_{TH}\right)}\left(\frac{2V_{TH}}{V_{DD}-V_{TH}}+\ln \frac{1.5V_{DD}-2V_{TH}}{0.5V_{DD}}\right)$$

(1)

$$\mu \left(T\right)=\mu {\left(\frac{T}{T_C}\right)}^{-k_{\mu }}$$

$$V_{TH}\left(T\right)=V_{TH}\left(T\right)-{\alpha }_v\left(T-T_C\right)$$

(2)

where k_µ and α_v are treated as positive constants. V_TH, µ, W/L, C_L, C_OX are the threshold voltage, carrier mobility, aspect ratio, loading capacitance and MOS oxide capacitance, respectively, and are affected by the doping and lithography variations. V_DD is the supply voltage, which is affected by the workload conditions during operation. Equation (1) is deduced based on the condition that initially, the discharging nMOS works in its saturation region while later, it works in its triode region, as its drain-source voltage decreases.

The total propagation delay of a single inverter is the sum of the above-mentioned discharging delay and the charging delay. However, when the input Vi is only composed of either a rising or a falling edge, the propagation delay is either the discharging or the charging delay, rather than the sum of the two, as illustrated by Figure 3. It can be seen from Equation (1) that the thermal effect from V_TH counteracts that from µ; however, when V_DD is relatively larger, the latter’s effect is much stronger and Equation (1) is dominated by µ, having a negative thermal coefficient. It can also be observed from Equation (1) that a single inverter’s delay is sensitive to the temperature as well as the supply voltage, as shown in Figure 5, indicating that as the supply voltage decreases, the propagation delay’s thermal dependency may change from negative to positive. Figure 5 is for the temperature range between −55 and 125 °C, versus the supply voltage levels between 0.7 V and 1.2 V, for TT corner, in a cadence environment using a 55 nm CMOS technology.

The temperature sensors presented in [4,5,6,7,8] belong to this category where their sensing front-ends are all logic delay lines. In [4], the temperature-dependent delay is quantized by a phase locked loop (PLL) that was implemented on chip; in [6,8], the delay is quantized by a temperature-independent delay line; in [5], the delay line was closed to form a ring oscillator whose frequency increases with temperature, and is quantized by a following counter.

Saturation-region MOS-based temperature sensors [9], despite not being fully logic delay lines, are also classified into this category, as their thermal coefficient and operating principle are very similar to the delay line-based ones. It is well known that an MOS working in its saturation region can be expressed as [10]

$$I_{sat}=\frac{1}{2}\mu C_{OX}\left(\frac{W}{L}\right){\left(V_{gs}-V_{TH}\right)}^2\left(1+\lambda V_{ds}\right)$$

(3)

where V_TH, µ, W/L, C_OX are threshold voltage, carrier mobility, aspect ratio, and MOS oxide capacitance, respectively; V_gs is the gate-source voltage of the MOS. The current shown in Equation (3) can be employed to control a delay line, as shown in Figure 6, where VBIASN equals V_gs in Equation (3). For instance, by reducing the V_gs voltage, I_sat’s thermal coefficient may change from negative to positive, as both µ and V_TH have negative thermal coefficients but V_TH’s sign is negative in Equation (3). As V_gs decreases, the weight of (V_gs$-$V_TH)’s positive thermal coefficient increases, and thus counteracts µ’s negative coefficient and consequently changes the sign of the overall thermal coefficient. In other words, the thermal coefficient for the current-starved cell’s delay changes from positive to negative, as V_gs reduces, since t_dis = C_L∙V_DD/I_dis. This change in the sign of thermal coefficient is similar to that illustrated in Figure 5. For example, it can be deduced from Figure 5 that the delay line’s thermal coefficient may become zero when V_DD is around 0.75 V. The same zero temperature coefficient may apply to the current-starved delay line, e.g., when VBIASN = 0.75 V for Figure 6, and this point is called the zero temperature coefficient (ZTC), which is the basis for the temperature insensitive reference delay line described in [6,8,10].

Temperature sensors that rely on the thermal coefficient of V_TH only and quantized by current-starved oscillators [11,12] are also classified into this category since they have similar power supply and process variation characteristics. In [12], the temperature is estimated from the ratio of the oscillation frequencies between two voltage-controlled ring oscillators with different V_TH. In this way, the temperature sensor’s power supply sensitivity is suppressed, compared to a single oscillator alternative. The temperature sensor described in [13] also belongs to this type, despite its output is a voltage instead of a delay and one of its sensing devices works in the triode region. The temperature-dependent delay may also be quantized by a time-domain delta-sigma analog-to-digital converter (ADC), as presented in [14].

The MOS temperature sensors working in their linear region [15] are also listed here although they are less sensitive to power supply levels. Their drain current, when V_ds is small, can be approximated as

$$I_{lin}\approx \mu C_{OX}\left(\frac{W}{L}\right)\left(V_{gs}-V_{TH}\right) V_{ds}$$

(4)

The thermal coefficient of a linear MOS’s drain current, as expressed in Equation (4), is normally complementary to absolute temperature (CTAT), and dominated by µ when V_gs is large enough. However, it has been demonstrated in [15] that when V_gs is around 0.7 V for the 0.18 µm technology, the nonlinearity of the temperature sensor is at its minimum, when employing the linear metal–oxide–semiconductor field-effect transistor (MOSFET) as its current bias. In [15], the aforementioned CTAT current is discharged through a capacitor, whose propagation delay is proportional to absolute temperature (PTAT), as t_dis = C_L∙V_DD/I_dis. When V_ds in Equation (3) is biased proportional to V_DD from a supply sensor, e.g., which contains a few diode-connected MOSFETs adjoined in series between V_DD and ground in [15], t_dis becomes less supply sensitive.

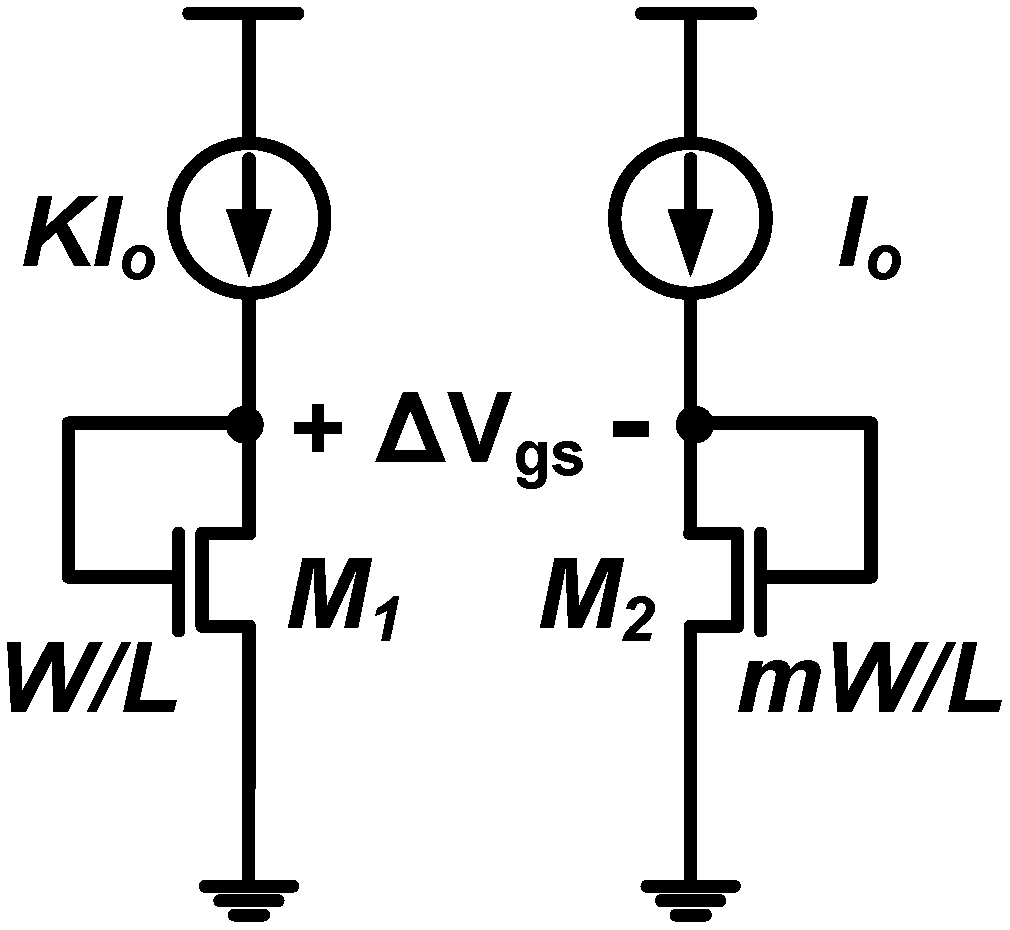
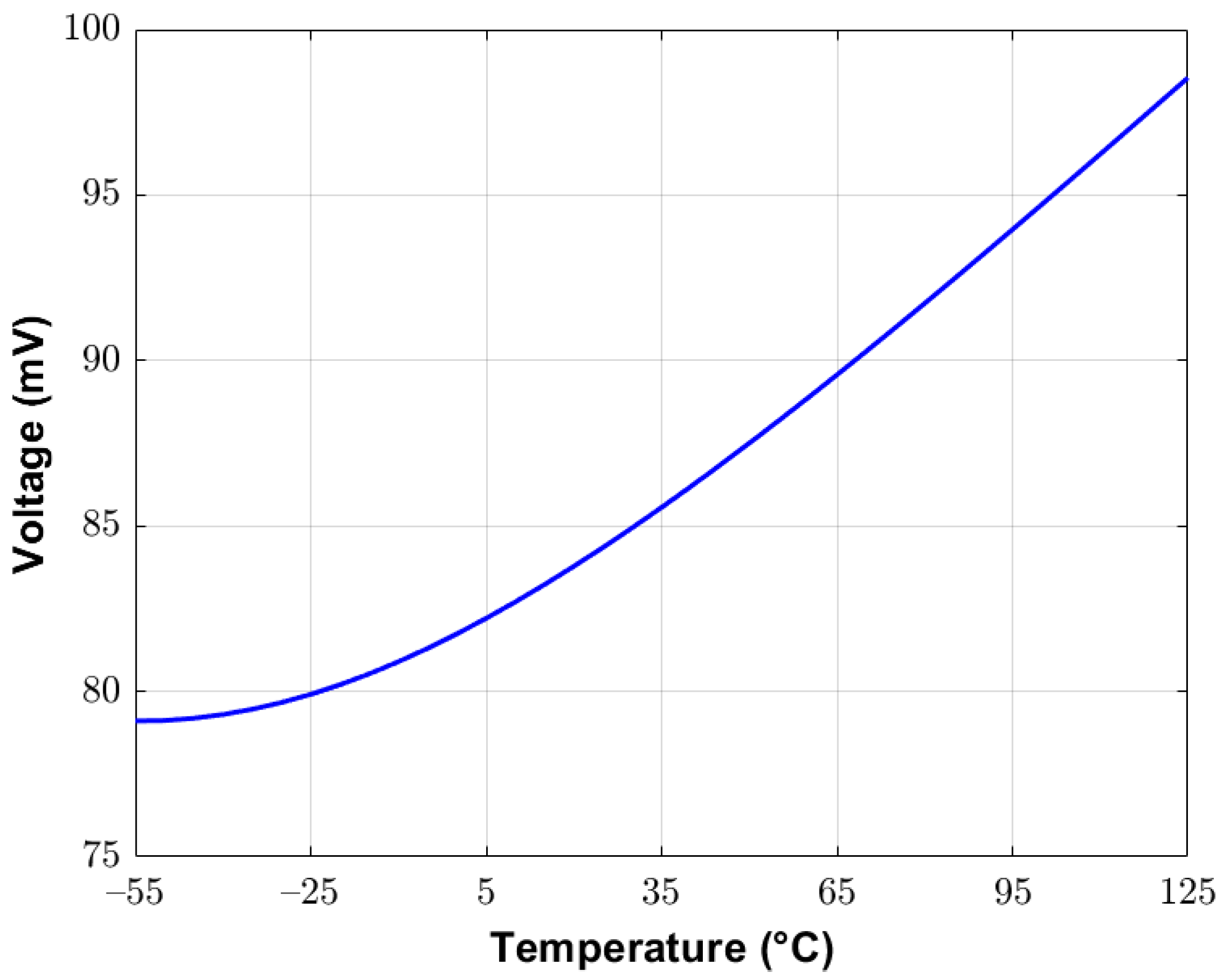
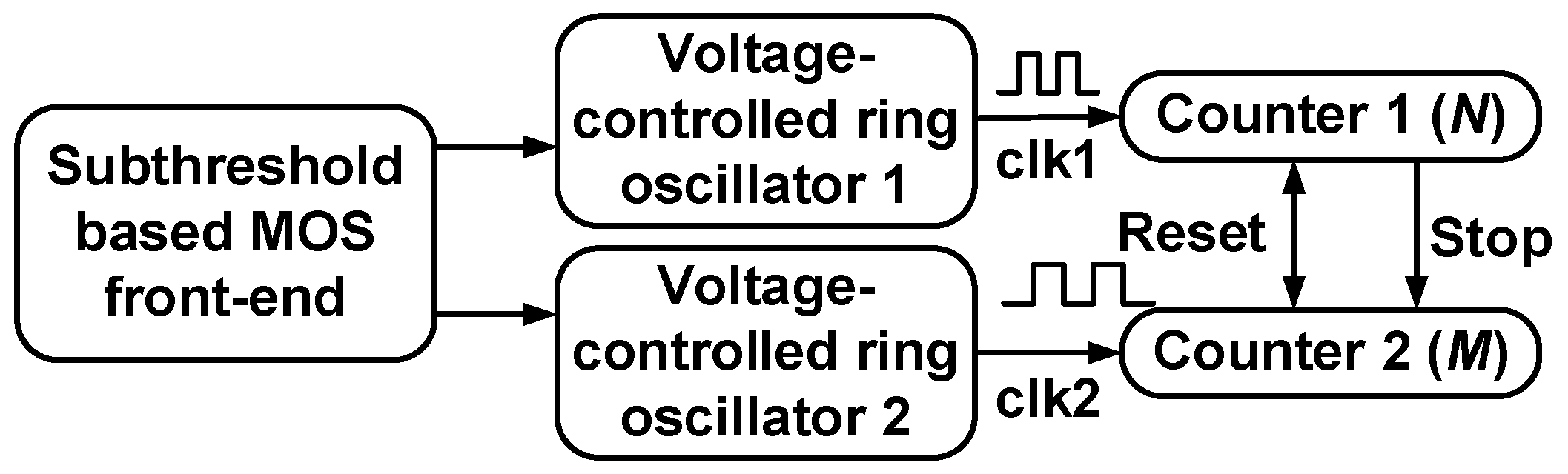
2.2. Subthreshold MOS-Based Temperature Sensor (Type II)

The temperature sensors described in the previous Section 2.1 make use of the MOSFETs working in their saturation and linear regions. In contrast, when a MOSFET is working its subthreshold region (when V_gs < V_TH), its drain current can be expressed by [16,17]

$$I_{sub}=\mu C_{OX}\left(\frac{W}{L}\right)V_T^{2}exp\left(\frac{V_{gs}-V_{TH}}{n{V}_T}\right)\left[1-exp\left(\frac{-V_{ds}}{V_T}\right)\right]$$

(5)

where V_TH, µ, W/L, C_OX are the threshold voltage, carrier mobility, width and length ratio and MOS oxide capacitance. V_T is the thermal voltage kT/q. when V_ds > 3V_T, Equation (5) can be reduced to

$$I_{sub}=\mu C_{OX}\left(\frac{W}{L}\right)V_T^{2}exp\left(\frac{V_{gs}-V_{TH}}{n{V}_T}\right)$$

(6)

Figure 7 illustrates the generation of PTAT voltage: when two MOSFETs M₁ and M₂ are working in their subthreshold regions with proportional current density, their drain current can be expressed as

$$\mu C_{OX}\left(\frac{W}{L}\right)V_T^{2}exp\left(\frac{V_{gs,1}-V_{TH,1}}{n{V}_T}\right)=K·\mu C_{OX}\left(\frac{mW}{L}\right)V_T^{2}exp\left(\frac{V_{gs,2}-V_{TH,2}}{n{V}_T}\right)$$

(7)

Then their gate-source voltage difference ΔV_gs can be deduced to be

$$\Delta V_{gs}=V_{gs,1}-V_{gs,2}=n{V}_T\ln \left(m·K\right)$$

(8)

where m∙K > 1, supposing no mismatches exist between M₁ and M_2′s V_TH. Equation (8) is analogous to a BJT-based PTAT, despite it not being absolutely PTAT due to the influence from V_ds, which was ignored in Equation (6). Another source that deviates Equation (8) from PTAT is n that is sensitive to process variations. Figure 8 shows the simulated ΔV_gs vs. temperature, when m = 4, K = 2, using a 55 nm CMOS technology, indicating its PTAT characteristic is only valid over a limited temperature range. It is simulated for m = 4, K = 2, between −55 and 125 °C, for TT corner, using a 55 nm CMOS technology.

Publications [16,17,18] belong to this category of subthreshold MOS-based temperature sensors where the PTAT voltage similar to that shown in Equation (8) was converted into a PTAT current through a resistor with negligible thermal coefficient. In [16], the PTAT current was further converted into a CTAT delay through a capacitor, as t_dis = C_L∙V_DD/I_dis. In [17], the PTAT current was employed to control the ring oscillator, whose oscillation frequency becomes CTAT, which is in turn quantized by a following counter. Temperature sensors that rely on the subthreshold current-controlled ring oscillator are presented in [19,20,21,22,28]. To get rid of the need for a frequency reference, the ratio of the oscillation frequencies between two current-starved ring oscillators/delay cells working in the subthreshold region is obtained as a digital representation of temperature [24,25,26,27], where the two ring oscillators are either controlled with proportional currents or devices with different V_TH.

In reference [29,30,31], a PTAT voltage similar to that expressed in Equation (8) and shown in Figure 7, is further quantized by the following delta-sigma ADCs, hence achieving better resolution and accuracy [30,31], or a wider temperature range [29]. In [30,31], the body and gate of the nMOS pair (as shown in Figure 7) are connected together, so that they work as a diode and the pair functions analogously to a BJT-based PTAT precision temperature sensor.

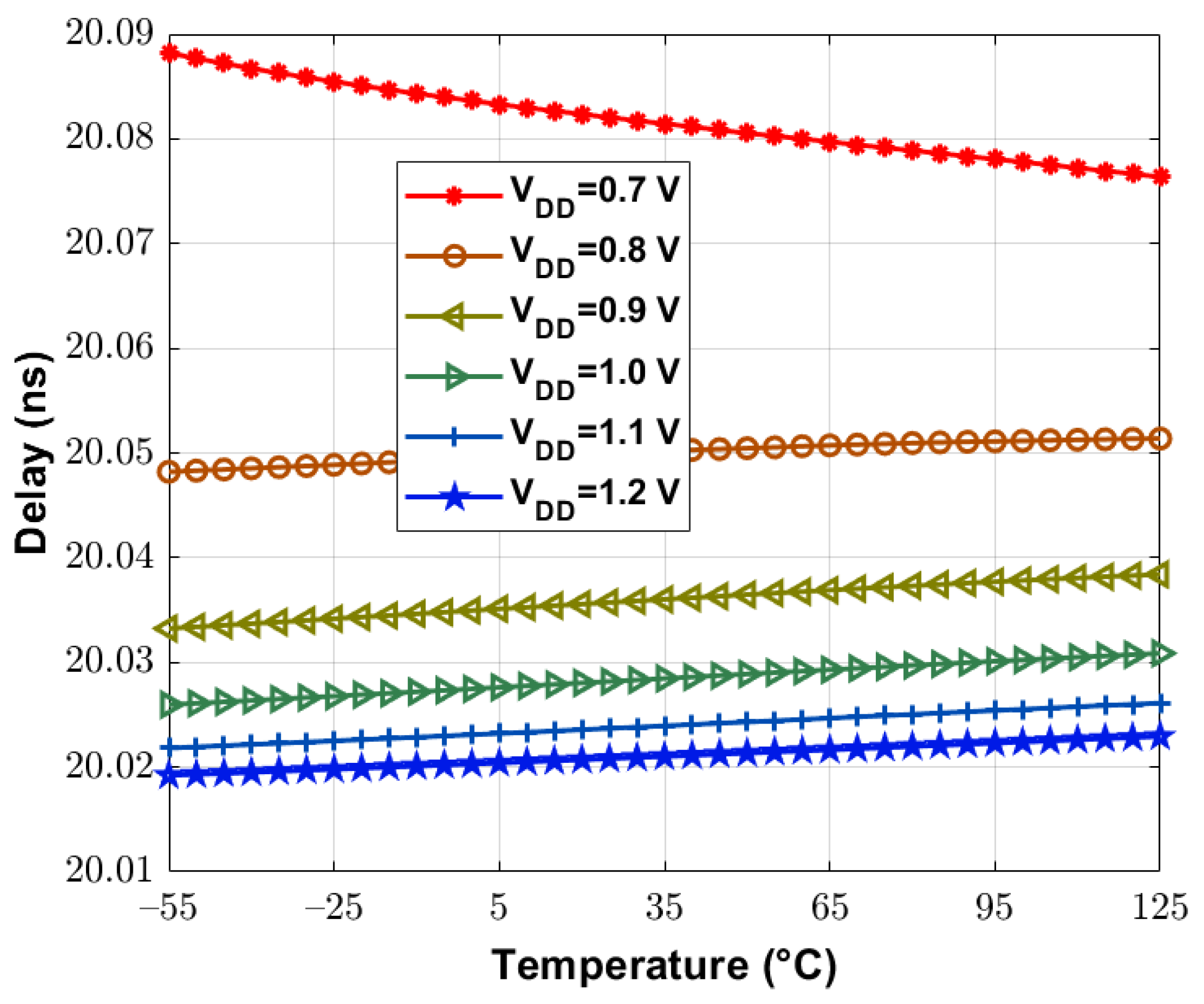
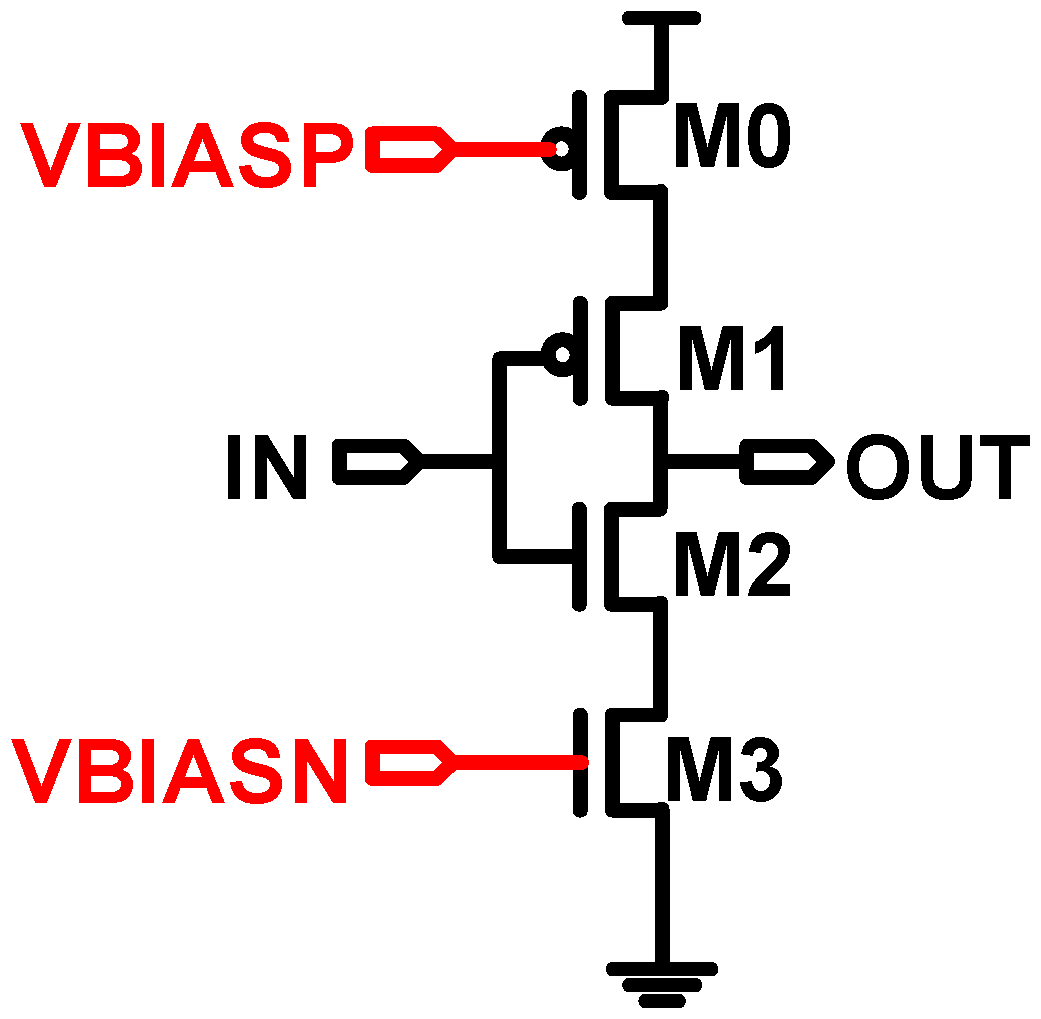
2.3. Gate Leakage-Based Temperature Sensors (Type III)

In 2017, a gate leakage-based temperature sensor was presented at CICC [32]. The temperature sensor stacked a MOSFET between the power supply and the current-starved ring oscillator. The MOSFET’s gate was connected to the power supply. Its drain, source and body were connected together, as node S, which was connected to the ring oscillator’s supply node. In this way, the MOSFET’s gate leakage current controlled the oscillation frequency of the ring oscillator. One obvious advantage of the gate leakage-based temperature sensor proposed in [32] was its energy efficiency, which was seven times better than the state-of-the-art works at its time of publication, as its sensing front-end was based on the gate leakage current, and consumed only 640 pW. Reference [33] relies on both thermal dependent gate-leakage current and subthreshold MOSFETs but is classified into this category due to its power efficiency.

3. Design Considerations and Challenges for the MOS-Based Temperature Sensors

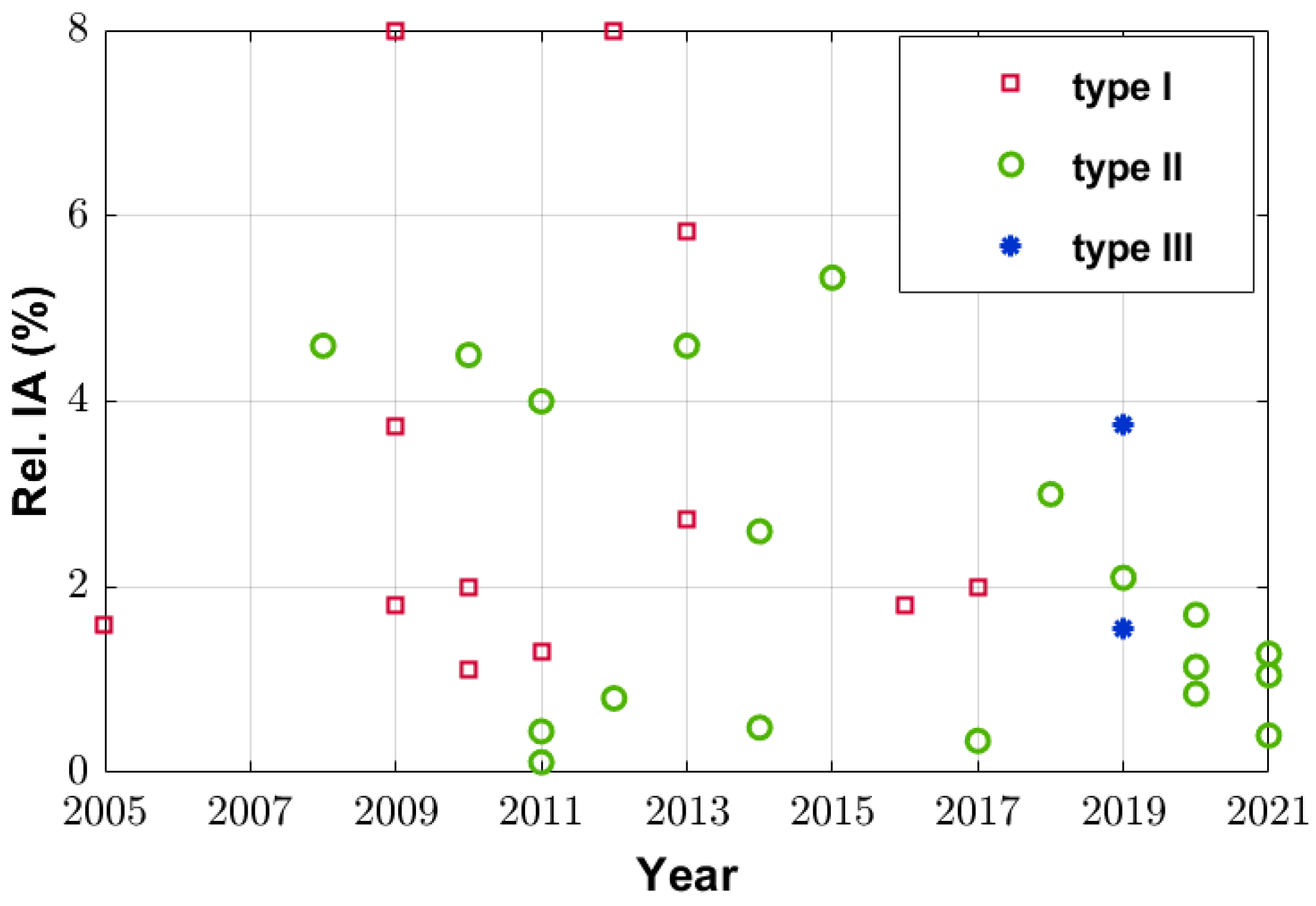
3.1. The Type of Choice Versus Year of Publication

Figure 9 shows the aforementioned three types’ areas versus the year of publication. From the figure, one can observe that type II, the subthreshold MOS-based temperature sensors, have gained popularity over the last 5 years. The reasons for this trend will be explained in the next subsection.

3.2. Area

The areas for the three types of temperature sensors are plotted in Figure 9. It can be seen from Figure 9 that the smallest three sensors belong to type II, the subthreshold types. One of the possible reasons is that for type I, logic or saturation MOS-based temperature sensors, a larger portion of the delay is unused for thermal sensing. A case in point is when comparing Figure 5 and Figure 8, only approximately 0.6% of the propagation delay of the logic inverter (type I) shown in Figure 5, is thermal dependent, while the rest is thermal independent. In contrast, in Figure 8, for the subthreshold-based type II, around 22% of the delay depends on temperature. In other words, for a similar resolution, the total delay lines for type I have to be longer than those for type II. Another reason, which also explains why the second type becomes more popular, is as the power supply level decreases with the technology node, the thermal coefficient for type I’s delay becomes smaller, as simulated in Figure 5. Another observation that can be made from Figure 9 is that the gate leakage-based type III is less area efficient, compared with the other two alternatives. 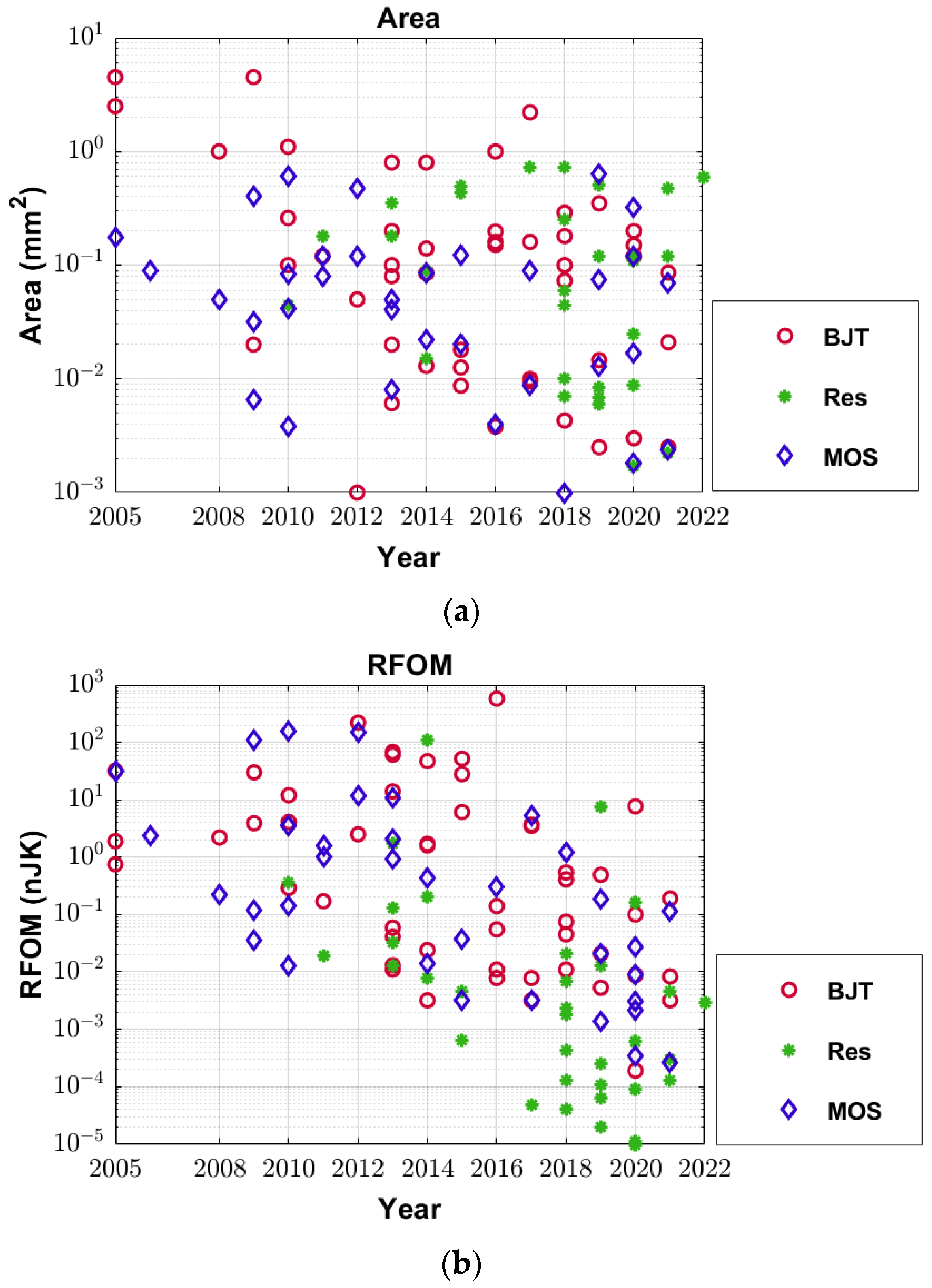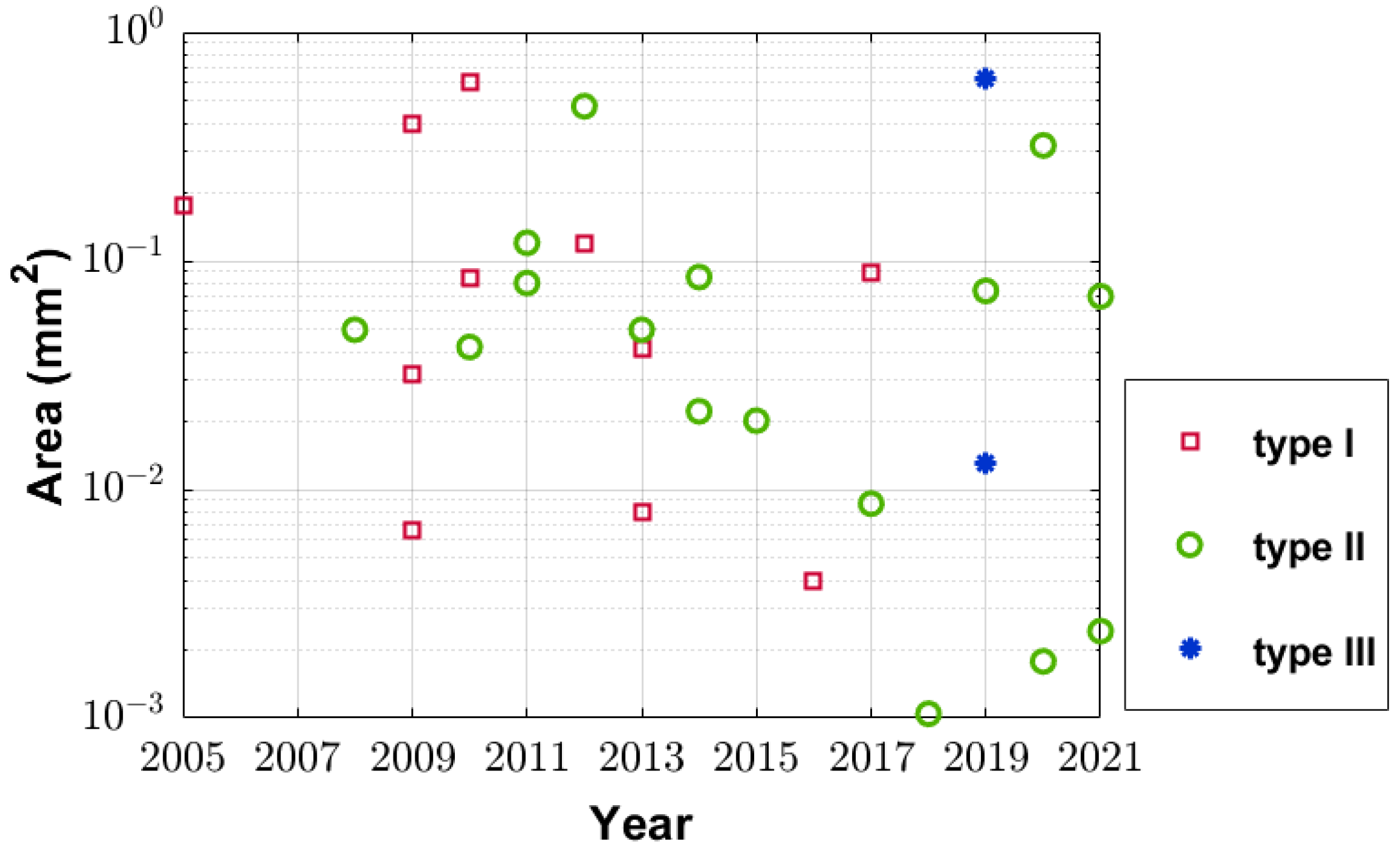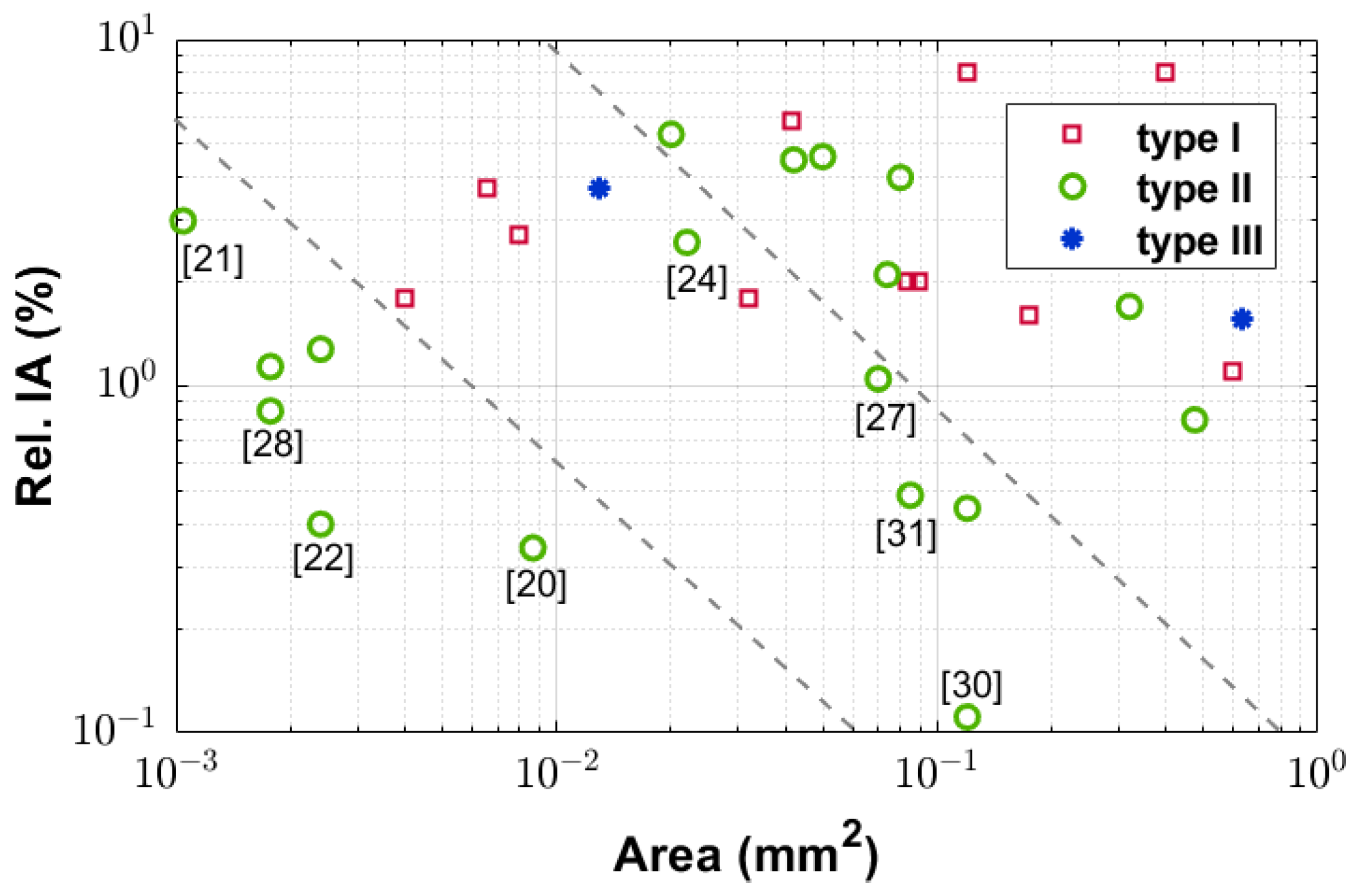The reason is the gate leakage current is normally smaller, and therefore requires either a larger sensing device or a more carefully designed quantizer, which, in turn, requires area.

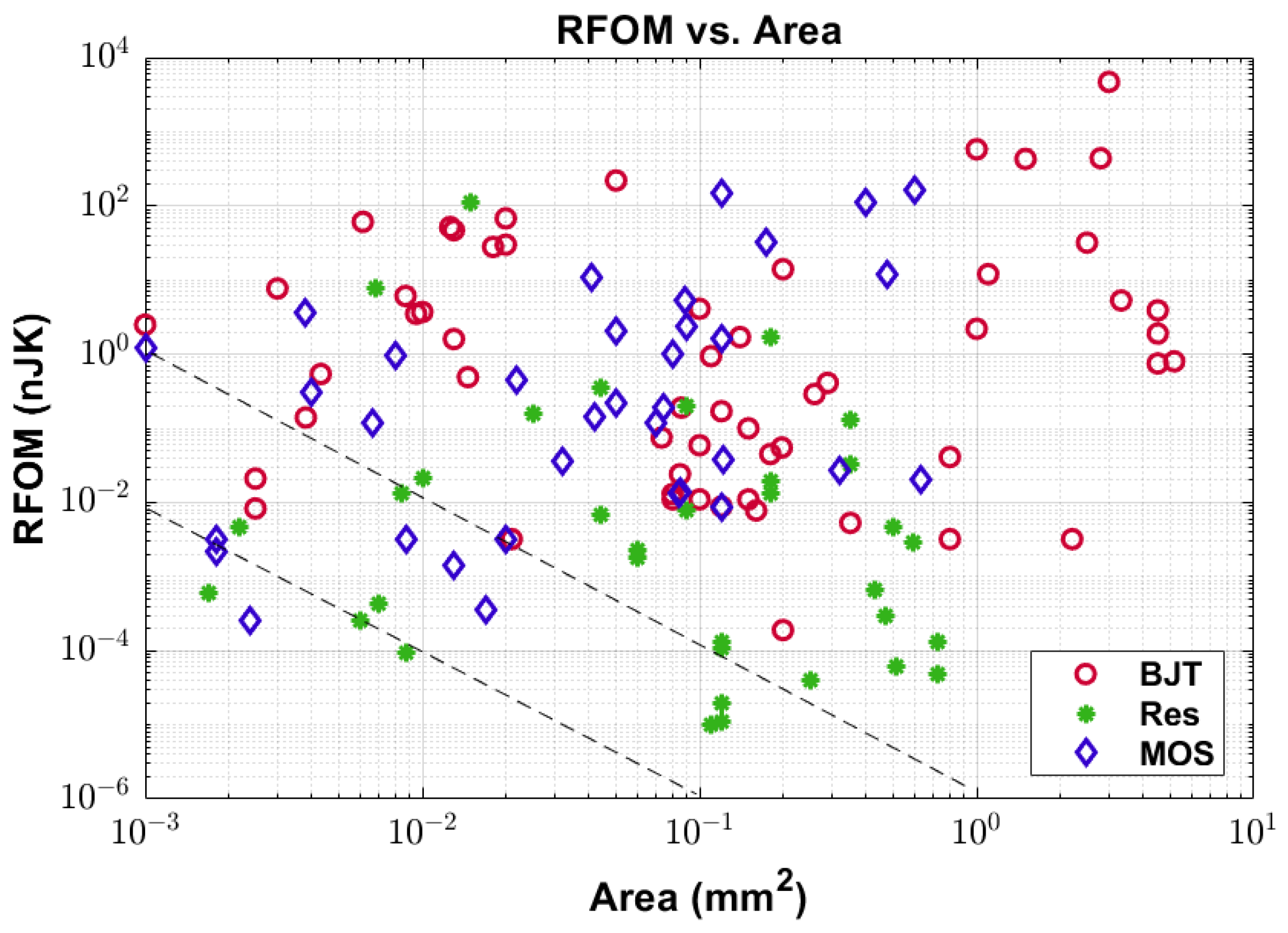
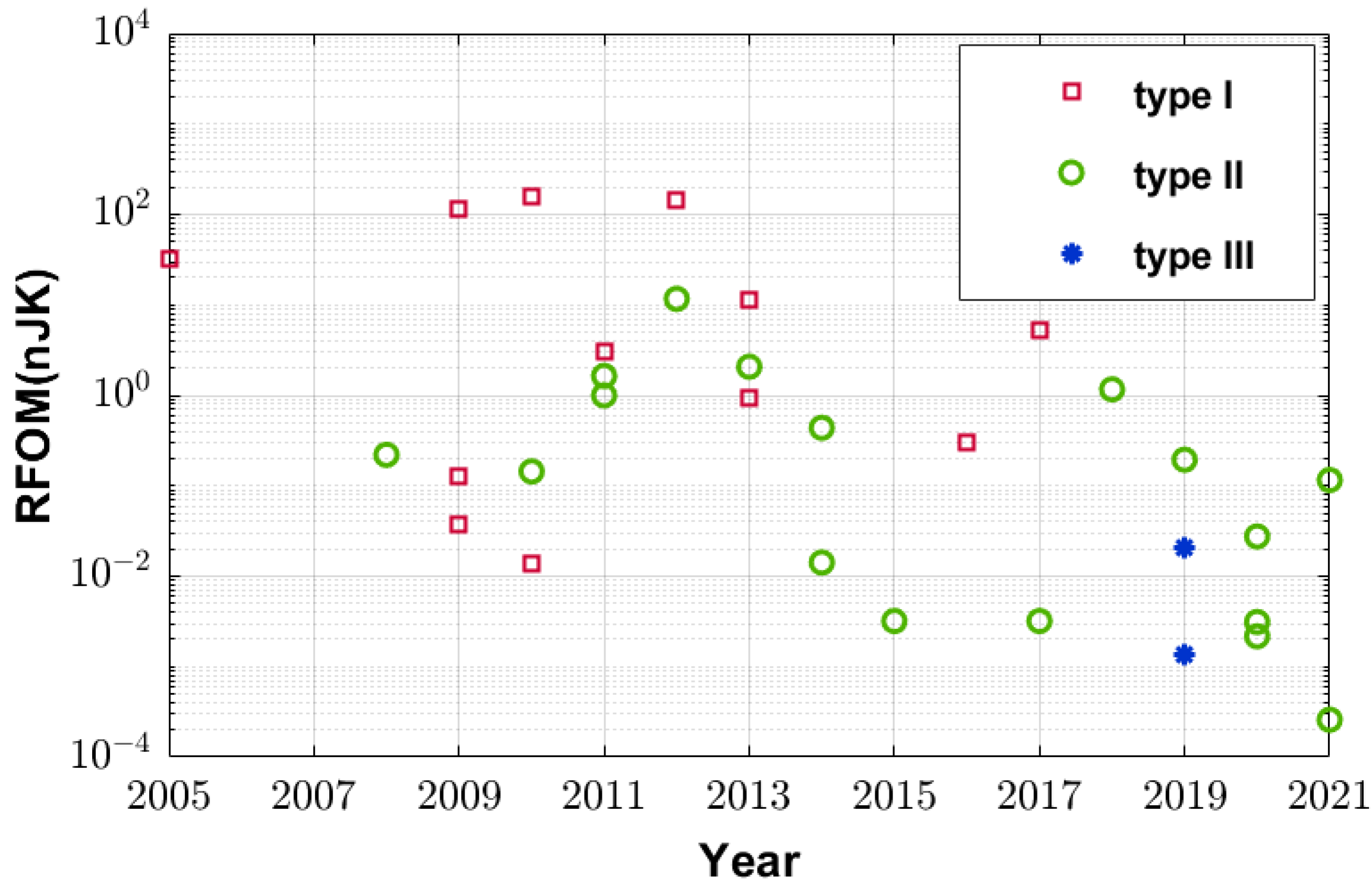
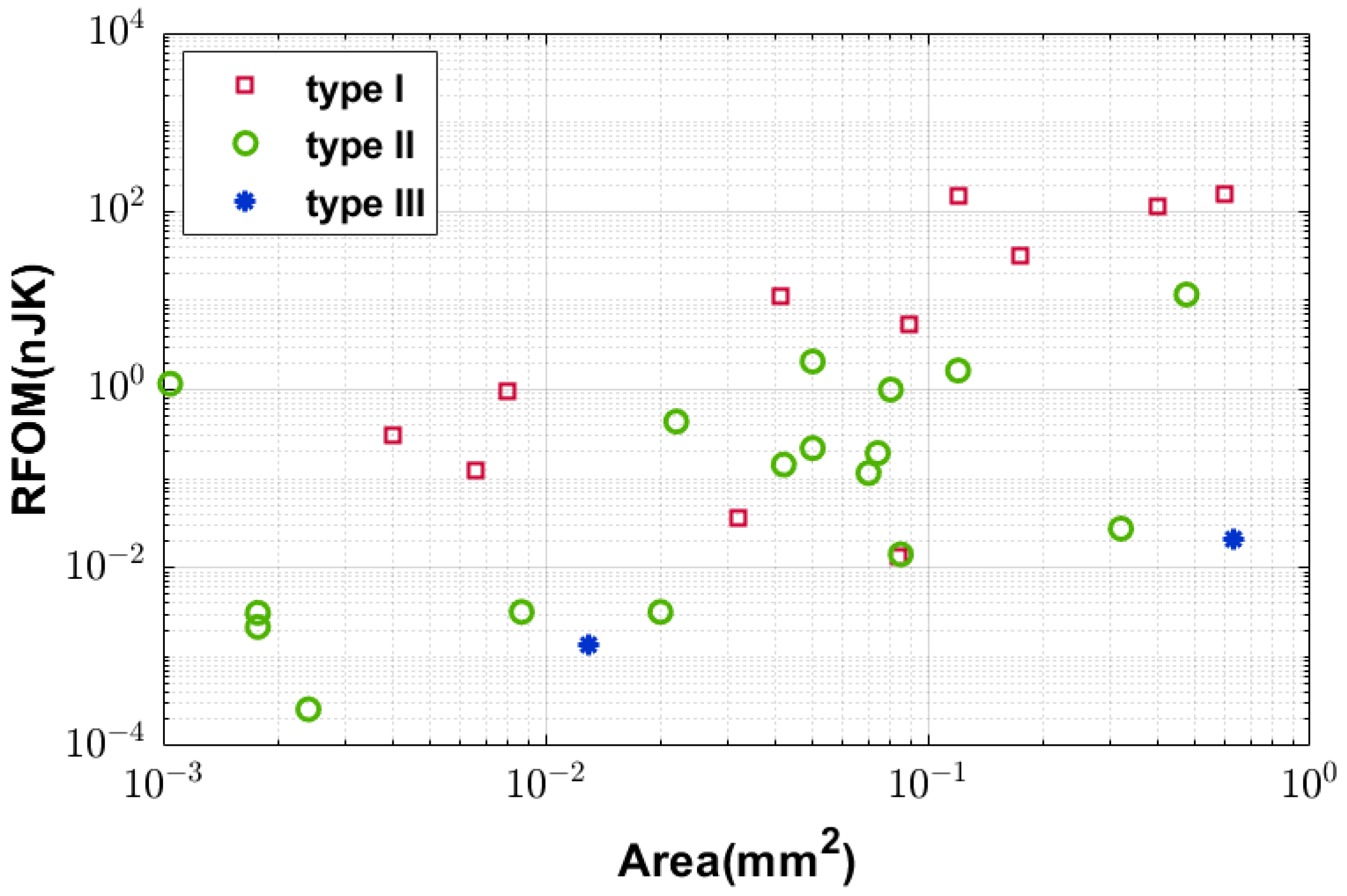
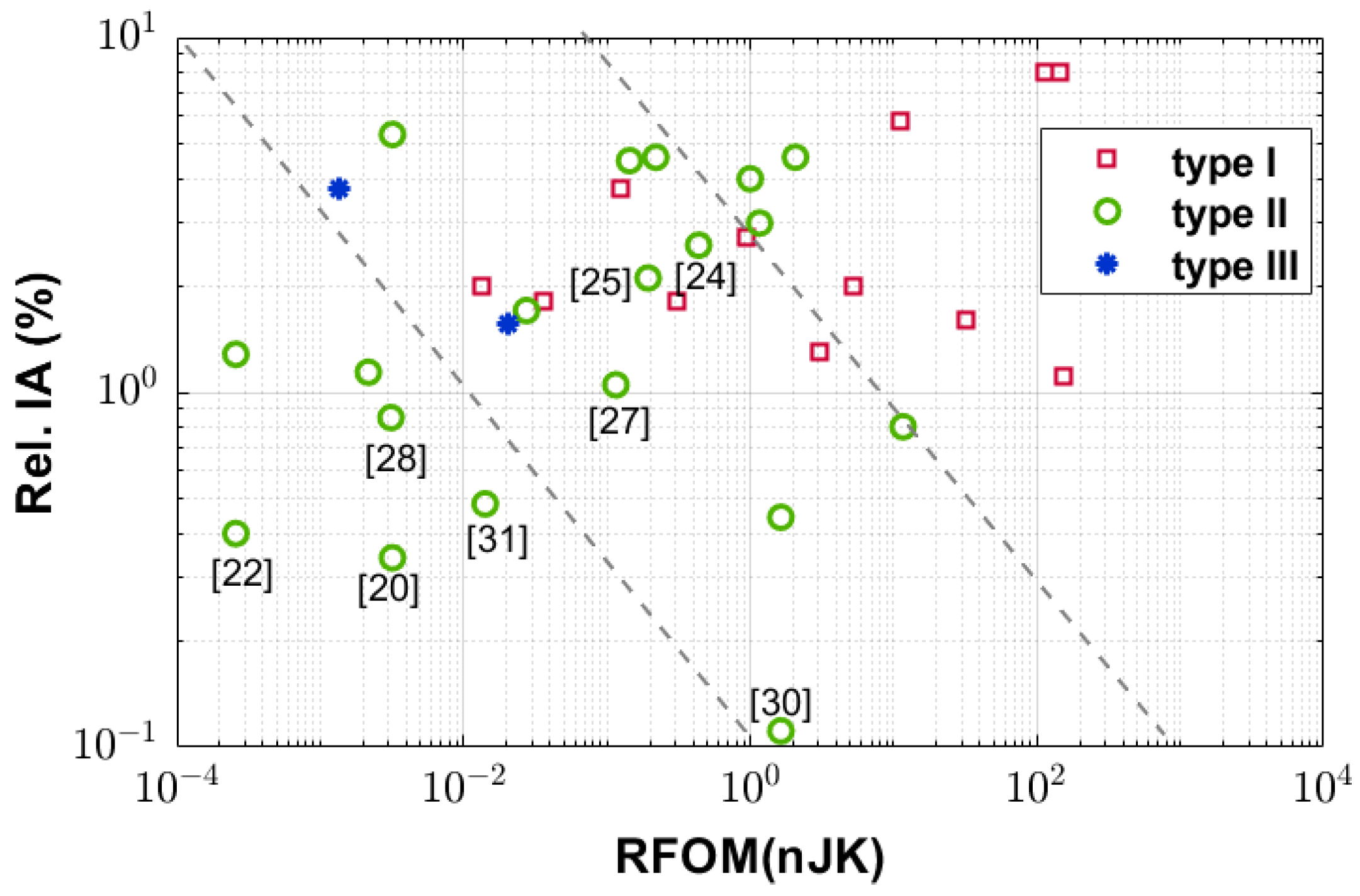
3.3. The Resolution Figure of Merit (RFOM) Versus Area

The resolution figure of merit (RFOM) is calculated as the energy/conversion∙resolution² and is a measure of energy efficiency in reference to its resolution. The RFOM versus the year of publication and the area are plotted in Figure 10 and Figure 11, respectively, for all three types. From Figure 10, one can observe that the RFOM is declining over the years and the type II sensors are among those with the smallest RFOM. A few observations can also be made from Figure 11, as follows: (1) The general trend is the RFOM increases with area, for all three types; (2) For most cases, for the same design area, type I has the larger RFOM than type II and type III, which indicates that type I has a worse energy efficiency, in general.

When a designer targets a lower RFOM or better energy efficiency, one should consider using a smaller number of devices or smaller sized circuit components, given it meets other design requirements. To some degree, this is understandable, as J = CV², therefore, the smaller the C (the total loading capacitance), the lower the energy consumption.

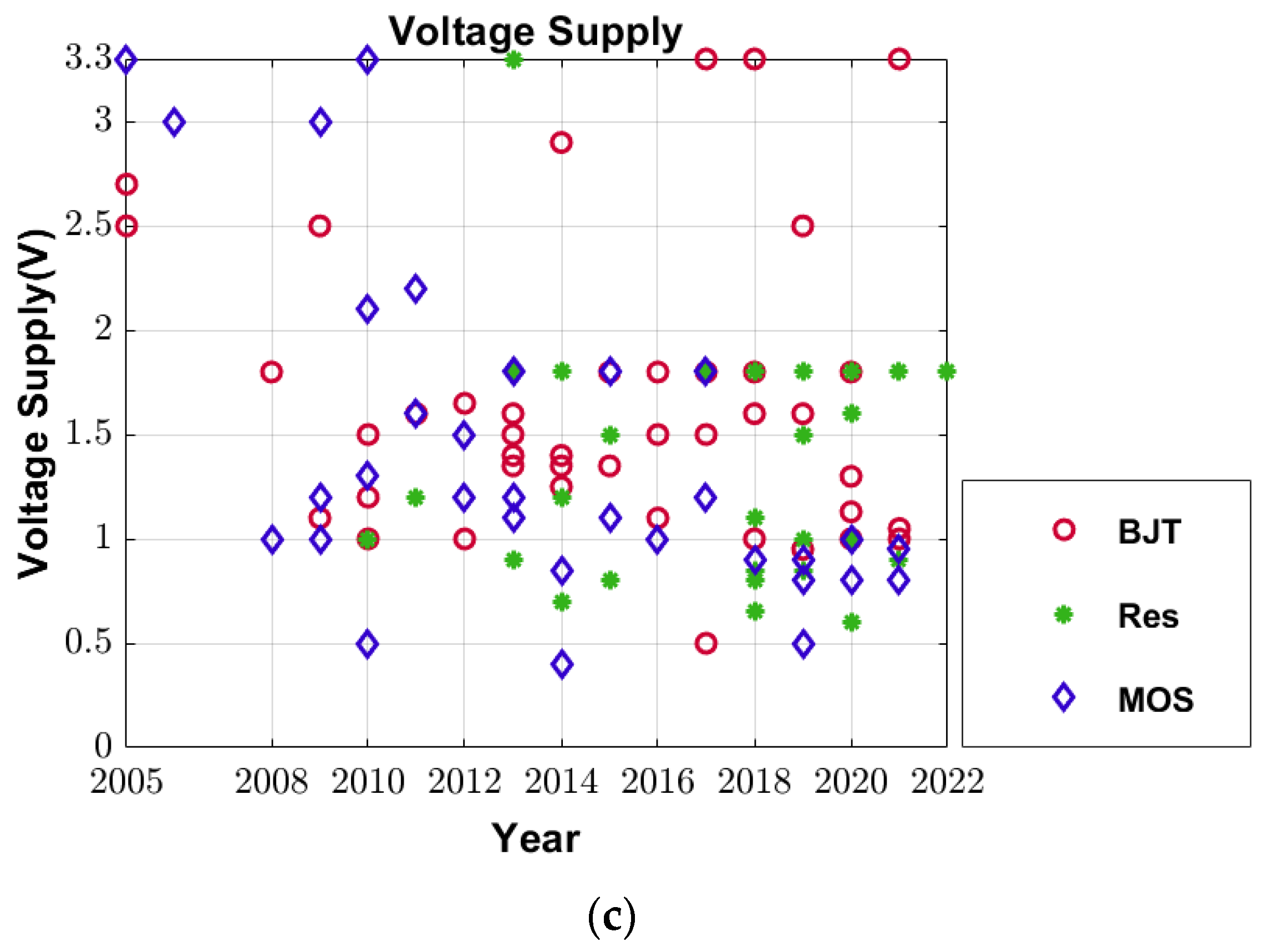
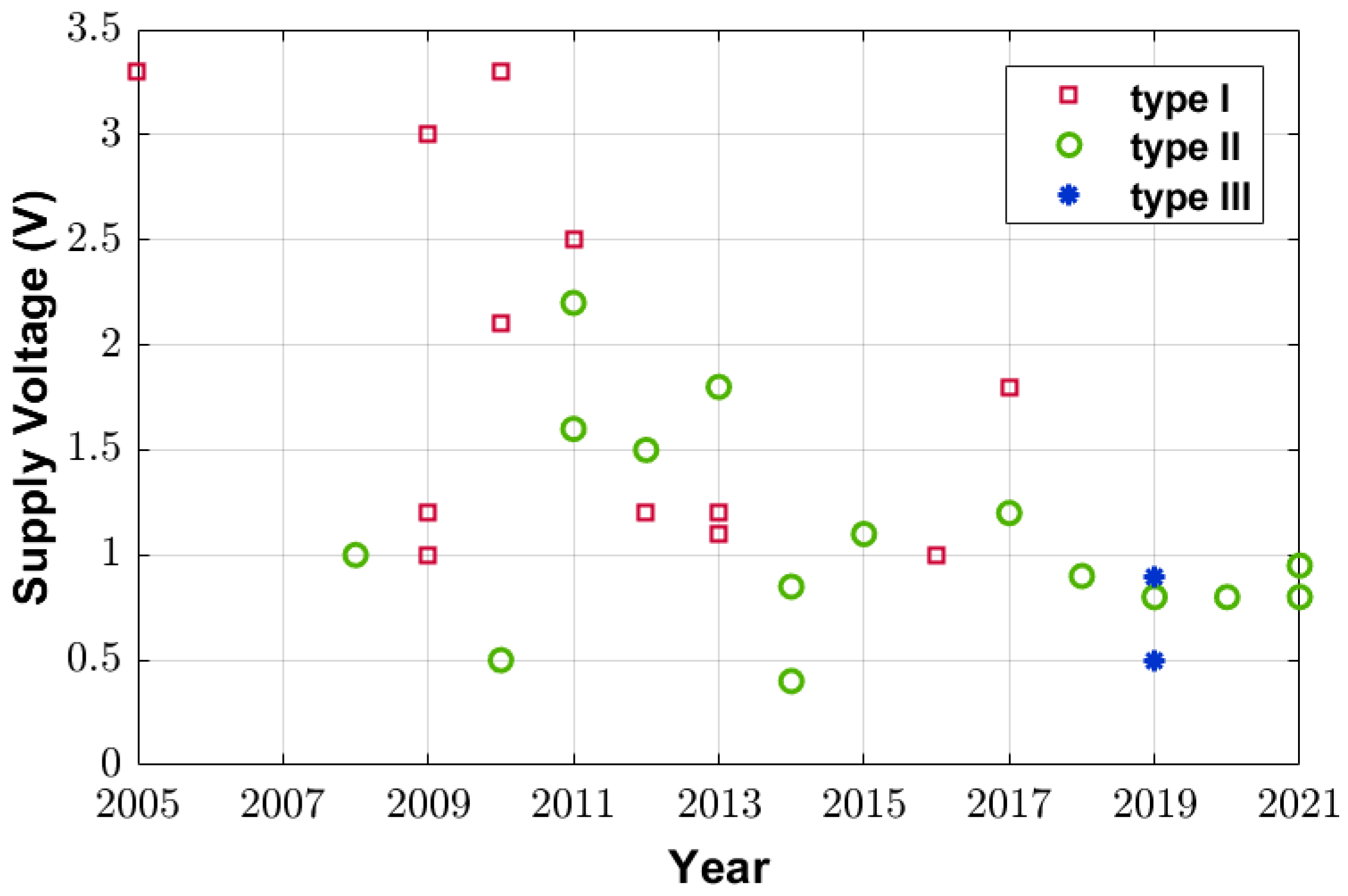
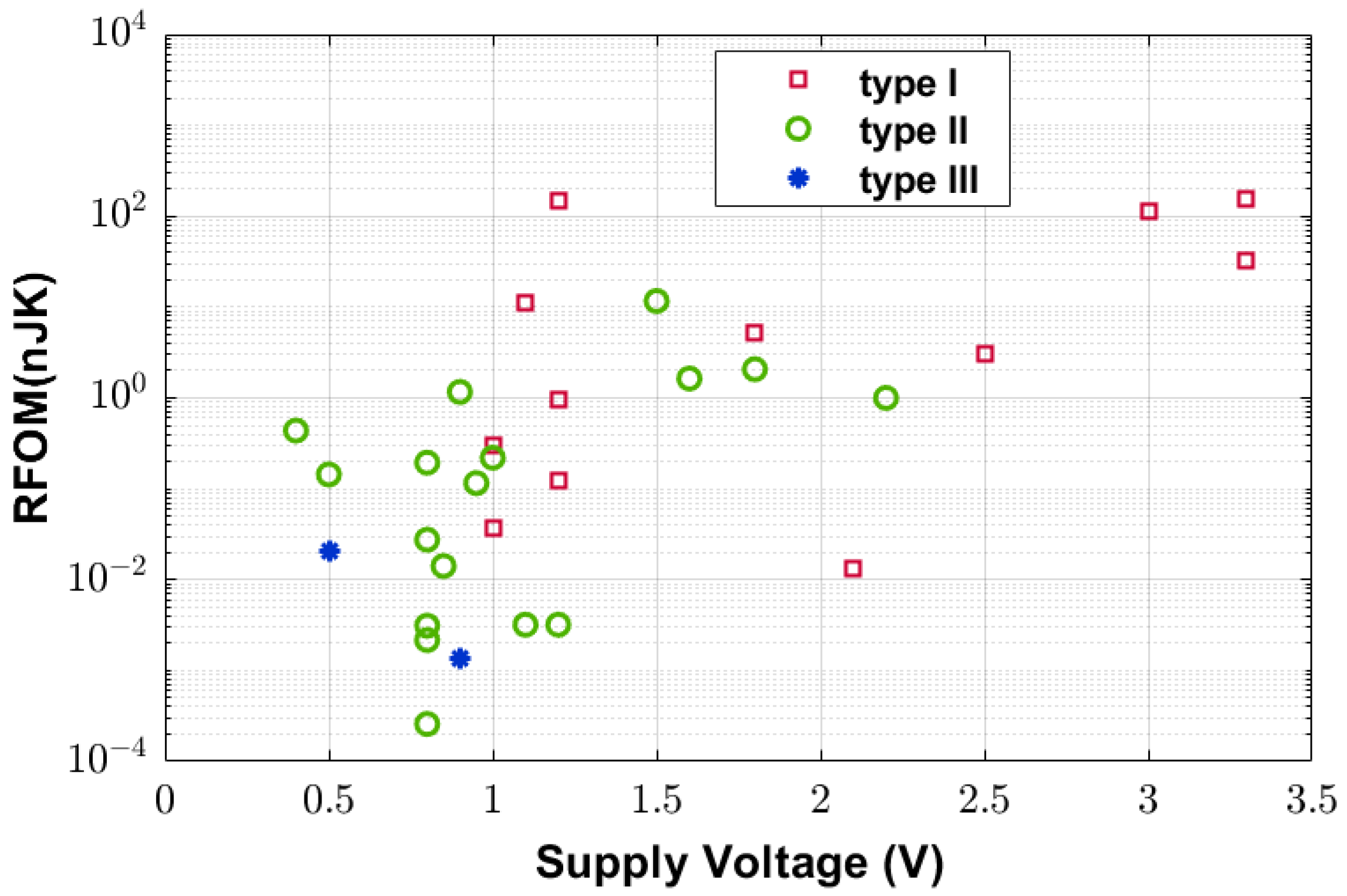
3.4. The Supply Voltage

Figure 12 shows the supply voltage level versus the year of publication. It indicates that, in general, the supply voltages for type II have been declining, during the last 10 years. It would be intuitive that RFOM are highly correlated with the supply voltage, as mentioned in the previous subsection, J = CV², as plotted in Figure 13. Another observation that could be made from Figure 13 is that the subthreshold MOS-based temperature sensor’s RFOM has a stronger correlation with the supply voltage, compared to type I, in general. In other words, the type II’s RFOM benefits more from voltage scaling.

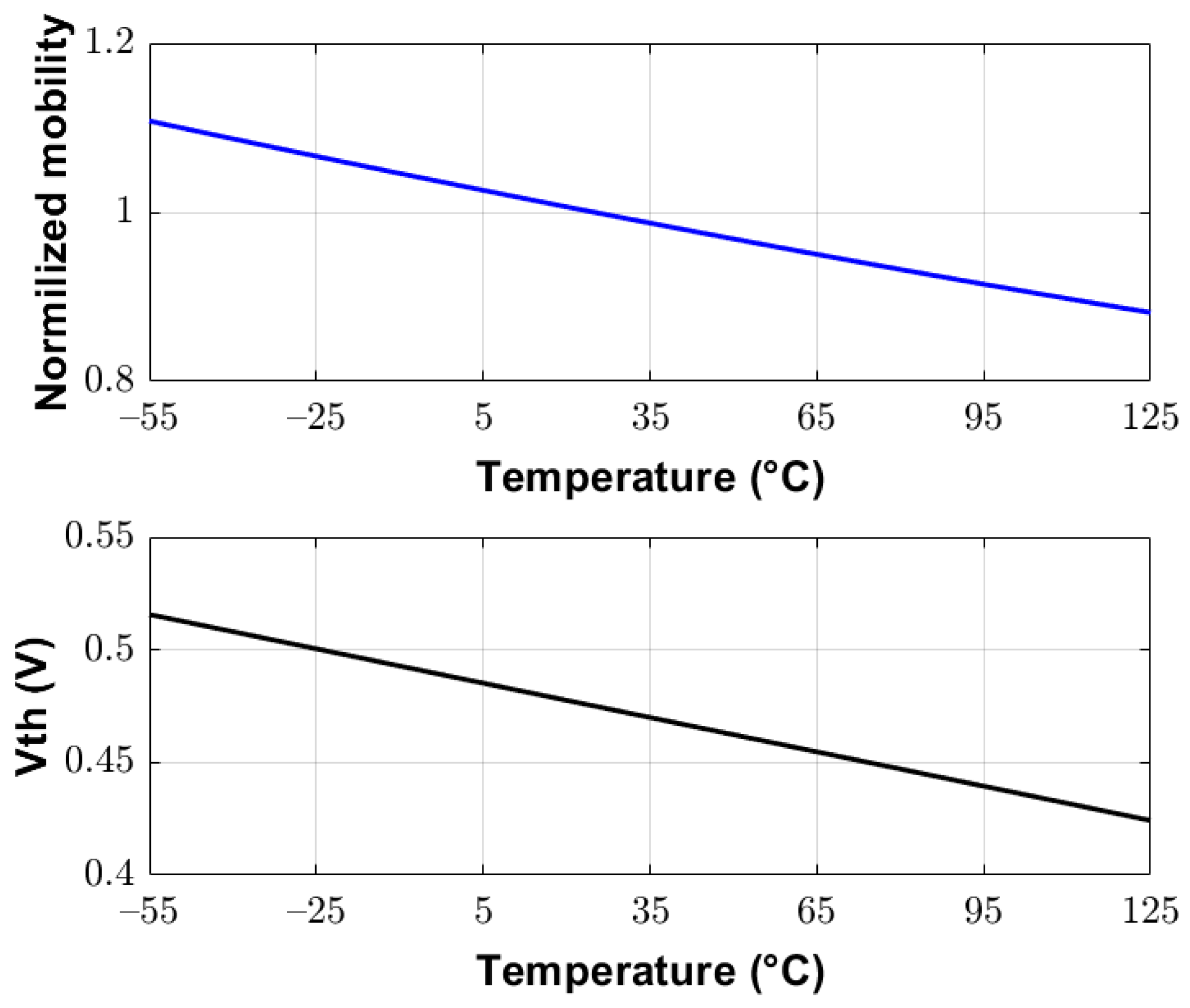
3.5. Inaccuracy vs. Area and Energy Efficiency

The relative inaccuracy (Rel. IA) was defined as 100×PP_IA/specified temperature range [106] where PP_IA is the worst-case inaccuracy (IA) over a specified temperature range. The Rel. IA for all three types is plotted against the year of publication in Figure 14, from which one can observe that the relative inaccuracy of the type II sensor has been getting better for the last 5 years. Figure 15 and Figure 16 show the Rel. IA versus the area and the RFOM, respectively, along with the constant product lines for the x and y axes for both figures. They indicate: (1) Among those sensors that have better trade-offs (or the smallest Rel. IA and area products, as well as Rel. IA and RFOM products) are references [20,22,28], which are all type II sensors. In Figure 14, the reference number is labelled next to the marker for type II. Those markers without any label either belong to the same publication but have a different trimming method, or, their inaccuracies are too high; (2) Other type II sensors, such as [24,27,30,31], also have relatively better trade-offs among area, power and accuracy, compared to the rest of the surveyed MOS-based temperature sensors. Among all the aforementioned references in this subsection, [20,22] rely on the subthreshold current-controlled ring oscillators’ temperature coefficient; the authors of [24,27,28] obtain the oscillation frequency ratio between two temperature-dependent ring oscillators either biased with proportional currents or with different V_TH levels. References [30,31] quantize their PTAT voltage front-end using voltage-domain delta-sigma ADCs. Among them, references [22,24,27,28,31] are powered by sub-1V (below 1V) power supplies. Therefore, the next subsection, Section 3.6 will focus on these five publications.

3.6. Process Variations, Number of Trims and Global Curve Fitting

This subsection focuses on the sub-1V designs that have better trade-offs among area, power and accuracy, mentioned in the last Section 3.5, namely, references [22,24,27,28,31], among which, [31] achieves a 3σ inaccuracy of ±0.4 °C, over the temperature range of −45 and 125 °C, with a one-point trim, while the rest of the references, [22,24,27,28] require at least two-point calibrations to achieve inaccuracies below ±0.5 °C, for their temperature ranges shown in Figure 17. The process variation is the reason. To mitigate the process variations, dynamic element matching (DEM) is employed in [31], along with a linearity calibration for each on-chip zoom ADC that quantizes the sensor’s PTAT front-end. In contrast, in [22,24,27,28] the temperature sensors work in the time domain and no DEM similar to that in [31] can be employed.

To better understand the effect of process variations on the temperature sensors, the block diagram showing the operating principle of the subthreshold MOS-based (type II) sensors [24,25,26,27] is drawn in Figure 18. The current-controlled oscillator may also be replaced by another type of delay cell [24]. The reference line, oscillator 1, is introduced for two purposes: to serve as the clock reference for oscillator 2 and to further remove the power supply sensitivity.

For the temperature sensor shown in Figure 18, the delay of oscillator 1 or 2 can be expressed as t_dis = C_L∙V_DD/I_dis. As the oscillator’s frequency is f = 1/(t_dis + t_cha), which is the inverse of the sum of the discharging time for nMOS and the charging time for pMOS. Assuming V_DD is identical for both oscillators at this moment, their current and oscillation frequency ratio can be obtained from Equation (5) as

$$\frac{f_{osc,1}}{f_{osc,2}}=\frac{I_{sub,1}}{I_{sub,2}}=exp\left(\frac{V_{gs,1}-V_{TH,1}-V_{gs,2}+V_{TH,2}}{n{V}_T}\right)$$

(9)

f_osc,1 and f_osc,2 refer to the oscillation frequency for oscillator 1 and 2, respectively. The thermal coefficient of $\frac{I_{sub,1}}{I_{sub,2}}$ can be obtained from the voltage difference either between V_gs,1 and V_gs,2, which is linked to series diode-connected bias [24], or between V_TH,1 and V_TH,2 voltage levels [27]. For a limited temperature range, Equation (9) can be quite linear [24,27] and can be obtained from counter 2′s outputs M in practical implementation, as

$$\frac{f_{osc,1}}{f_{osc,2}}=\frac{I_{sub,1}}{I_{sub,2}}=\frac{M}{N}$$

(10)

which indicates that when counter 1 counts 1 N numbers, which is a fixed number and it sends a stop/latch signal to counter 2, whose output M is the final digital representation of temperature.

When one applies the ln function to both sides of Equation (9), one gets

$$\ln \left(\frac{I_{sub,1}}{I_{sub,2}}\right)=\frac{V_{gs,1}-V_{TH,1}-V_{gs,2}+V_{TH,2}}{n{V}_T}$$

(11)

where V_T is the thermal voltage kT/q, and supposing V_gs,1 = V_gs,2 and V_TH,1 = β₁ − α₁T and V_TH,2 = β₂ − α₂T; α₁ ≠ α₂; β₁ ≠ β₂. Equation (11) can be expressed as a function of T

$$\ln \left(\frac{M}{N}\right)=\ln \left(\frac{I_{sub,1}}{I_{sub,2}}\right)=\frac{q}{nk}\left[\left({\alpha }_1-{\alpha }_2\right)+\frac{{\beta }_2-{\beta }_1}{T}\right]$$

(12)

where n, α₁, α₂, β₁, β₂ are all process dependent factors. Equation (12) indicates that the final digital representations of temperatures,$\frac{M}{N}$, contain an offset and a gain factor, respectively, and both are sensitive to process variations. Therefore, to remove the offset and the gain at the same time, the temperature sensors have to be calibrated at two temperature points (e.g., −25 and 100 °C), at least. In other words, if a temperature sensor having the characteristic as shown in Equation (12) is only calibrated at one point, either the gain or the offset can be removed, and therefore resulting in larger inaccuracies than when calibrated at two points, for the same sensor, as shown in Figure 17.

The one-point calibration concept was first proposed for the type I, logic and saturation MOS-based temperature sensor [4]. However, it may only be valid when the power supply level V_DD is much larger than V_TH, e.g., V_DD ≥ 1.1 V, as the basis for the one-point calibration proposed in [4] is to consider the carrier mobility µ for thermal dependency while neglecting that for V_TH, as expressed in Equation (1). In other words, as V_DD drops, the thermal dependency from V_TH cannot be ignored. Even when V_DD is larger than 1.1 V, e.g., 1.2 V in [4], the errors of ±4 °C after its one-point calibration are much larger than using a two-point calibration alternative. Nevertheless, the advantage of the one-point calibration is the reduction in high volume production costs. This advantage is meaningful for microprocessor thermal management, where lower calibration cost is desired and an inaccuracy of ±5 °C is acceptable.

After either a one-point or a two-point calibration that removes the process variations between different temperature sensors on the same or on different chips, a global master curve is applied to convert the digital outputs of each sensor into the temperatures. This master curve can be of third [4,28] or lower orders. In [28], the third order master curve, or, systematic error correction, is implemented off-chip. For mass production, a second or third master curve would mean extra cost and complexity and it is desirable that the master curve can be linear, or, of first order. In other words, the less inaccuracy between the sensor and the global linear master curve fitting, the better for mass production.

3.7. Noise

A sensor’s noise limits its resolution [12]. The noise, or the measurement uncertainties in the temperature sensor outputs are shown in [34], which also indicates when the conversion time is increased from 4 ms to 16 ms, the measured uncertainty-induced errors reduce from ±3 °C to ±1 °C. It is believed in [34] that the high frequency noise can be averaged out using a longer conversion time. In [27], the jitter or phase noise induced error is demonstrated to be proportional to its resolution (LSB) and is inversely proportional to a single cell’s propagation delay. When the ring oscillator or VCO’s delay line is long enough, or, when the sensor’s resolution is fine enough, the phase noise induced error can be kept small, e.g., around 0.02 °C in [27].

3.8. Power Supply Sensitivity

The power supply sensitivities of the temperature sensors [22,26,27,28,33] are listed in

Table 1. The performance summary of the selected MOS-based temperature sensors.

Reference.	Year	Technology (nm)	Area (mm2)	PP IA (°C) 1	Min (°C)	Max (°C)	Rel. IA (%) 1	Supply (V)	Conversion Time (ms)	µW	nJ	Resolution (°C)	RFOM 2	Power Supply Sensitivity (°C/V)	Type
[22]	2021	55	0.0024	0.5	−40	85	0.4	0.8	1.04	0.86	0.8944	0.017	0.000258	5.8	type II
[27]	2021	130	0.07	0.84	0	80	1.05	0.95	59	0.196	11.564	0.1	0.11564	13.7	type II
[28]	2020	55	0.00177	1.4	−40	125	0.85	0.8	1.31	9.8	12.838	0.013	0.00217	5.76	type II
[26]	2020	65	0.32	1.7	−30	70	1.7	0.8	765	0.0064	4.896	0.075	0.02754	2.8	type II
[33]	2019	65	0.63	1.56	0	100	1.56	0.5	300	0.000763	0.2289	0.3	0.020601	8.4	type III
[11]	2019	180	0.074	2.1	−20	80	2.1	0.8	839	0.011	9.2	0.145	0.194	3.8	type I
[32]	2019	65	0.013	4.5	−20	100	3.8	0.9	34	0.0006	0.022	0.25	0.00137	N/A	type III
[31]	2014	160	0.085	0.8	−40	125	0.5	0.85	6	0.6	3.6	0.063	0.01417	N/A	type II
[24]	2014	65	0.022	2.6	0	100	2.6	0.4	25	0.28	7	0.25	0.4375	N/A	type II
[12]	2016	65	0.004	1.8	0	100	1.8	1	0.022	154	3.4	0.3	0.30492	N/A	type I
[19]	2015	25	0.02	4	20	95	5.3	1.1	0.142	9	1.3	0.05	0.0032	N/A	type II
[20]	2017	180	0.0087	0.41	−20	100	0.34	1.2	8	0.1	0.6	0.073	0.0032	N/A	type II
[14]	2017	180	0.089	2	−20	80	2	1.8	800	0.8	660	0.09	5.3136	N/A	type I
[21]	2018	28	0.001	2.7	−5	85	3	0.9	0.036	56	2	0.76	1.16444	N/A	type II
[30]	2011	160	0.12	0.8	−55	125	0.4	1.6	200	7.5	1500	0.033	1.63786	N/A	type II
[30]	2011	160	0.12	0.2	−55	125	0.1	1.6	200	7.5	1500	0.033	1.63786	N/A	type II
[4]	2012	130	0.12	8	0	100	8	1.2	0.2	1200	240	0.78	146.016	N/A	type I
[29]	2012	180	0.475	1.6	−50	150	0.8	1.5	10	69	690	0.13	11.661	N/A	type II
[23]	2013	180	0.05	4.6	0	100	4.6	1.8	100	0.2	23	0.3	2.07	N/A	type II
[13]	2013	44	0.041	4.1	35	105	5.8	1.1	0.128	23.1	3	1.94	11.1	N/A	type I
[9]	2013	65	0.008	3	0	110	2.7	1.2	0.002	500	1.1	0.94	0.94103	N/A	type I

¹ The relative inaccuracy (Rel. IA) was defined as 100∙PP_IA/specified temperature range [106] where PP_IA is the worst-case inaccuracy (IA) over a specified temperature range. ² The RFOM is calculated as the energy/conversion∙resolution² and is a measure of energy efficiency in reference to its resolution.

, along with other performance parameters. For MOS-based temperature sensors working in their subthreshold regions, when their supply voltage level changes, the subthreshold current level deviates, as expressed in Equation (5), which is a function of V_ds, affected by the supply voltage level V_DD [27]. Similarly, when V_DD changes, the saturation current in Equation (3) changes, so does the propagation delay in Equation (1). When the supply voltage changes dynamically, the charging and discharging currents in the MOSFETs change accordingly and give rise to either increased or decreased propagation delay or oscillation frequency. This (rise or drop in the delay or the frequency) will eventually change the temperature sensors’ output readings (digital numbers) dynamically, as illustrated in Figure 19a, where the output codes rise 30 digital numbers (DN) within a 0.7 s interval, and the sensor mistakenly gives an information of −26 °C temperature change (at around 400 s), when the power supply changes suddenly [109]. Almost all types of temperature sensors, including the MOS-based ones, are sensitive to power supply level change. Currently, the methods to reduce the power supply sensitivities of the MOS-based temperature sensors are as follows: the first is to use a voltage regulator, as described in [9,20,21]; the second is to employ two oscillators which reduce the supply sensitivities by their oscillation frequency ratio [12,24,26,27]; the third is the subthreshold leakage-based delay cell proposed in [28], whose principle of reducing supply sensitivity is as follows. The power supply sensitivity of the propagation delay in the particular cell is a function of the voltage swing for charging. By adjusting the voltage swing, the supply sensitivity can be minimized for the delay cell. It is mentioned in [28] that this minimum supply sensitivity voltage swing shifts for different chips, due to process variations, but can be kept within a reasonable range, despite the process and temperature variations. The linear-region MOS-based temperature [15] is claimed to reduce power supply sensitivity despite no exact number of supply sensitivity being mentioned.

3.9. Self-Heating and Lifespan

The thermal resistance of silicon is around 14 °C/W, which means the temperature can rise by 14 °C from ambient when its power dissipation is 1 W. For the selected MOS-based temperature sensors in this review, the maximum power reported is 1200 µW (reference [4]), and accordingly, the temperature rise (from ambient) is 0.0168 °C (=14 × 1200 µW/1,000,000), which is 40× smaller than its resolution, 0.78 °C. For most MOS-based sensors listed in Table 1, their power dissipations are below 10 µW, and their self-heatings are less than 0.14 mK, which is almost 100× smaller, compared to the finest resolution of 13 mK in reference [28]. Therefore, the self-heating effect is negligible for the MOS-based temperature sensors.

A typical temperature sensor in industry is designed, e.g., to operate for 10 years at 105 °C, and in general, the higher the junction temperature, the shorter the lifespan of the temperature sensor.

4. Conclusions

This paper reviews the MOS-based temperature sensors and categorize them into three types: type I, the logic, saturation and linear MOS-based temperature sensors; type II, the subthreshold MOS-based temperature sensors; and type III, the gate leakage-based temperature sensors. In addition, it discusses the design considerations and challenges for the MOS-based temperature sensors, including: area, energy efficiency, accuracy, process variations, noise and power supply sensitivity. The future MOS-based temperature sensors may be based on the subthreshold MOSFET operation, which is the most popular design type among the three, currently. It should have better trade-offs between area, power efficiency and accuracy, likely having a differential architecture that reduces its power supply sensitivity, along with a lower-cost (e.g., one-point or self-calibrated) calibration method, powered at a supply voltage under 1 V.