Multi-Parameter Estimation for an S/S Compensated IPT Converter Based on the Phase Difference between Tx and Rx Currents
Abstract
:1. Introduction
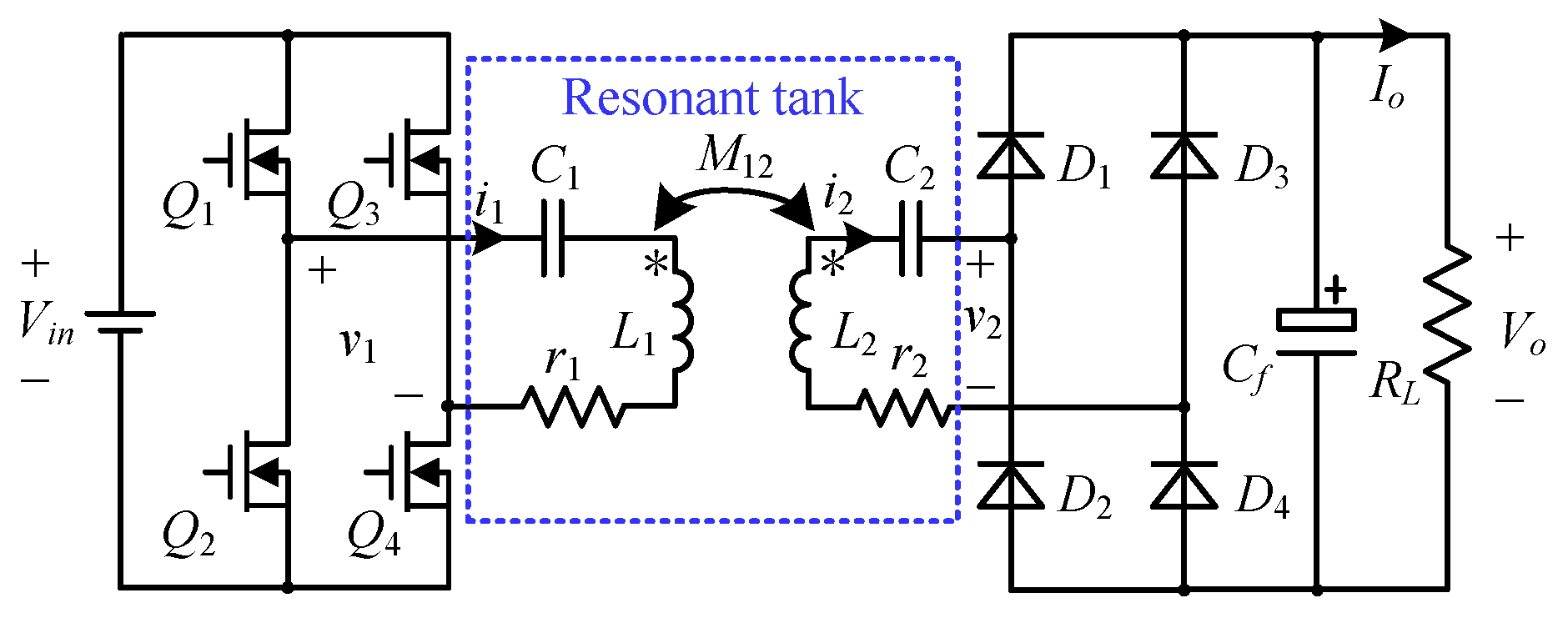
2. Parameter Estimation Method Based on the Phase Difference between Tx and Rx Current
2.1. Multi-Parameter Estimation Model
2.2. Parameter Estimation during Frequency Sweeping
2.3. Online Parameter Estimation
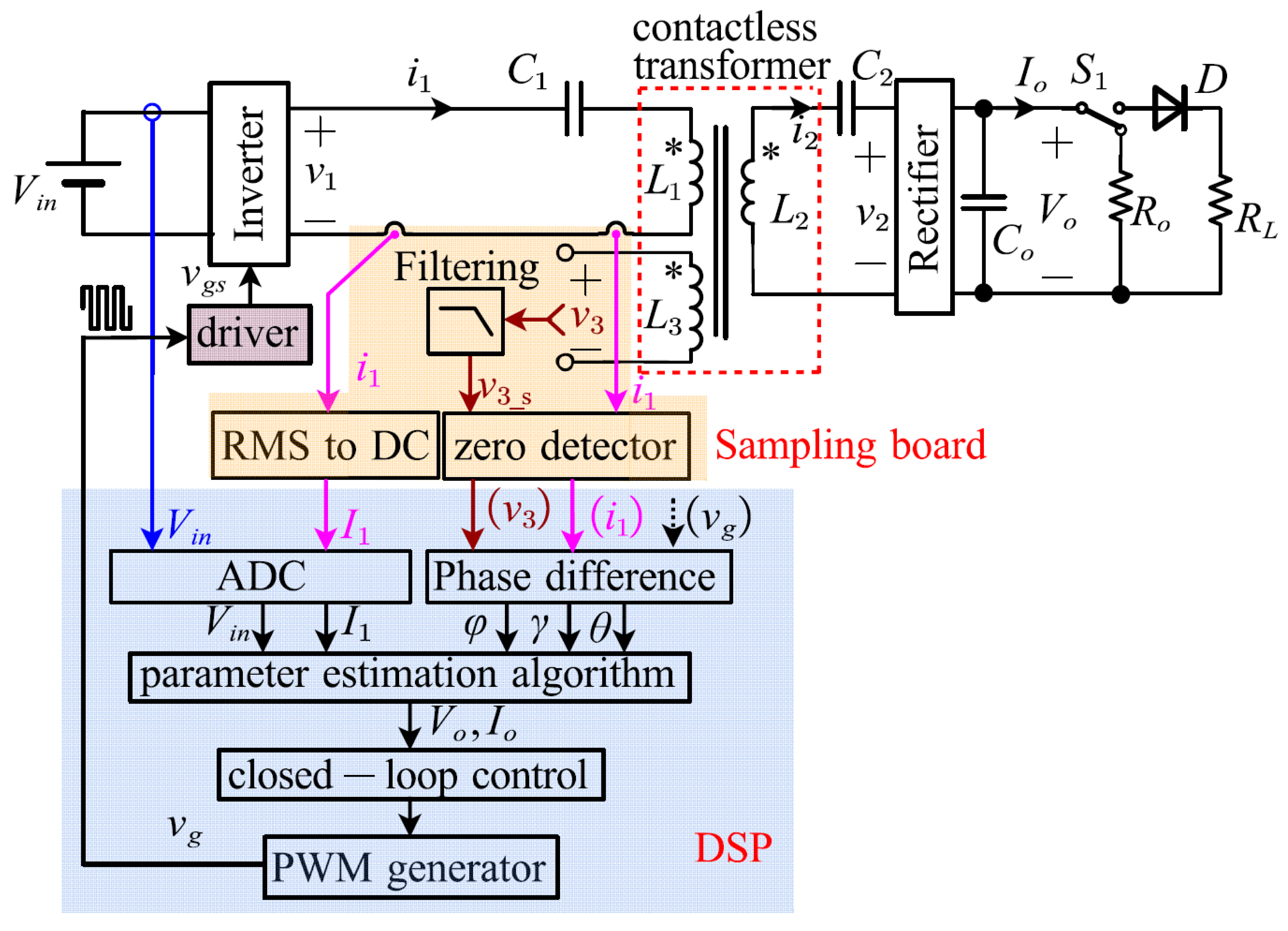
3. Implementation of the Proposed Estimation Method
3.1. Diagram of the IPT System
3.2. Flowchart of the Parameter Estimation
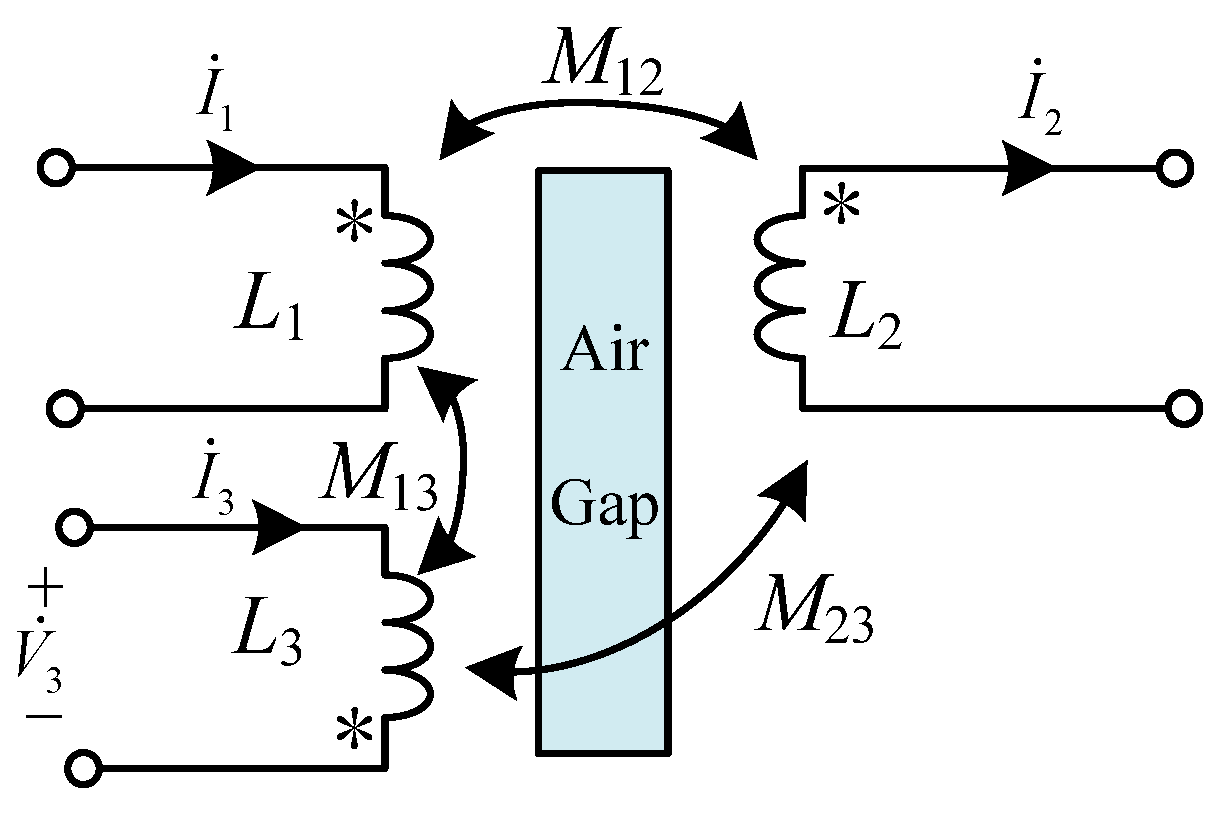
4. Configuration of the Magnetic Coupler
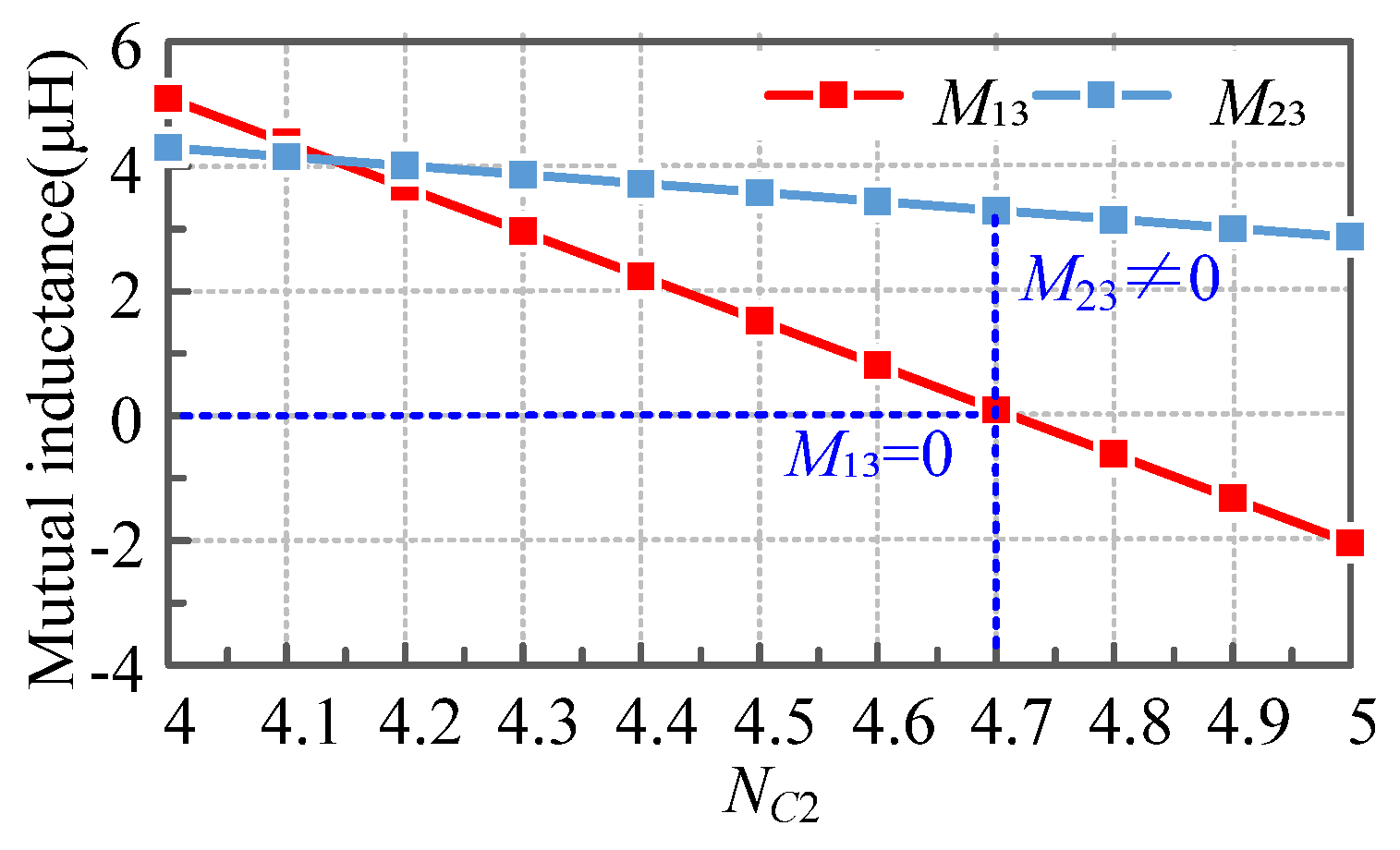
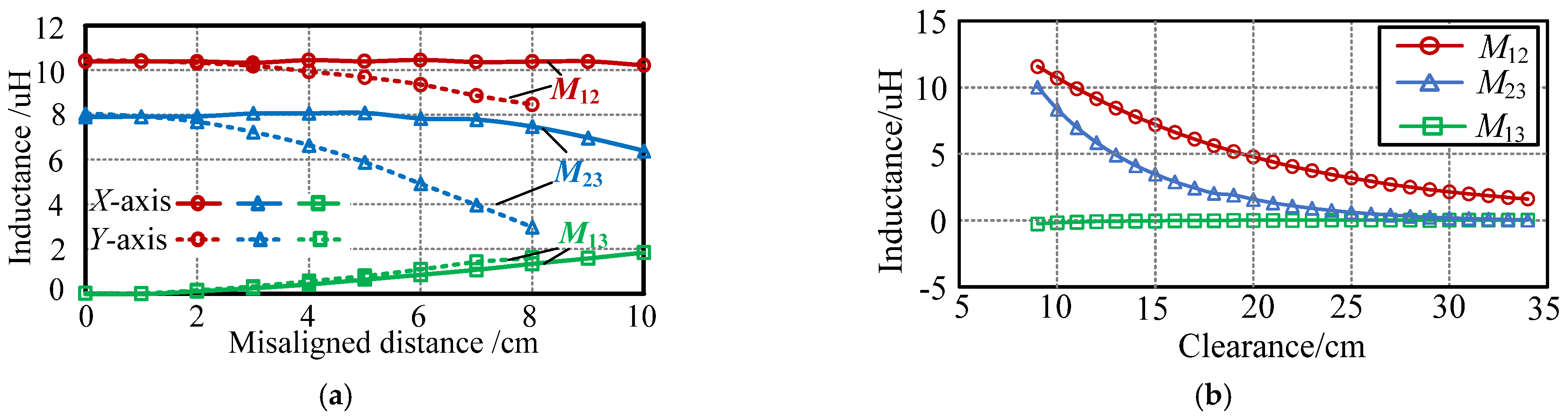
4.1. Proposed Asymmetrical Configuration
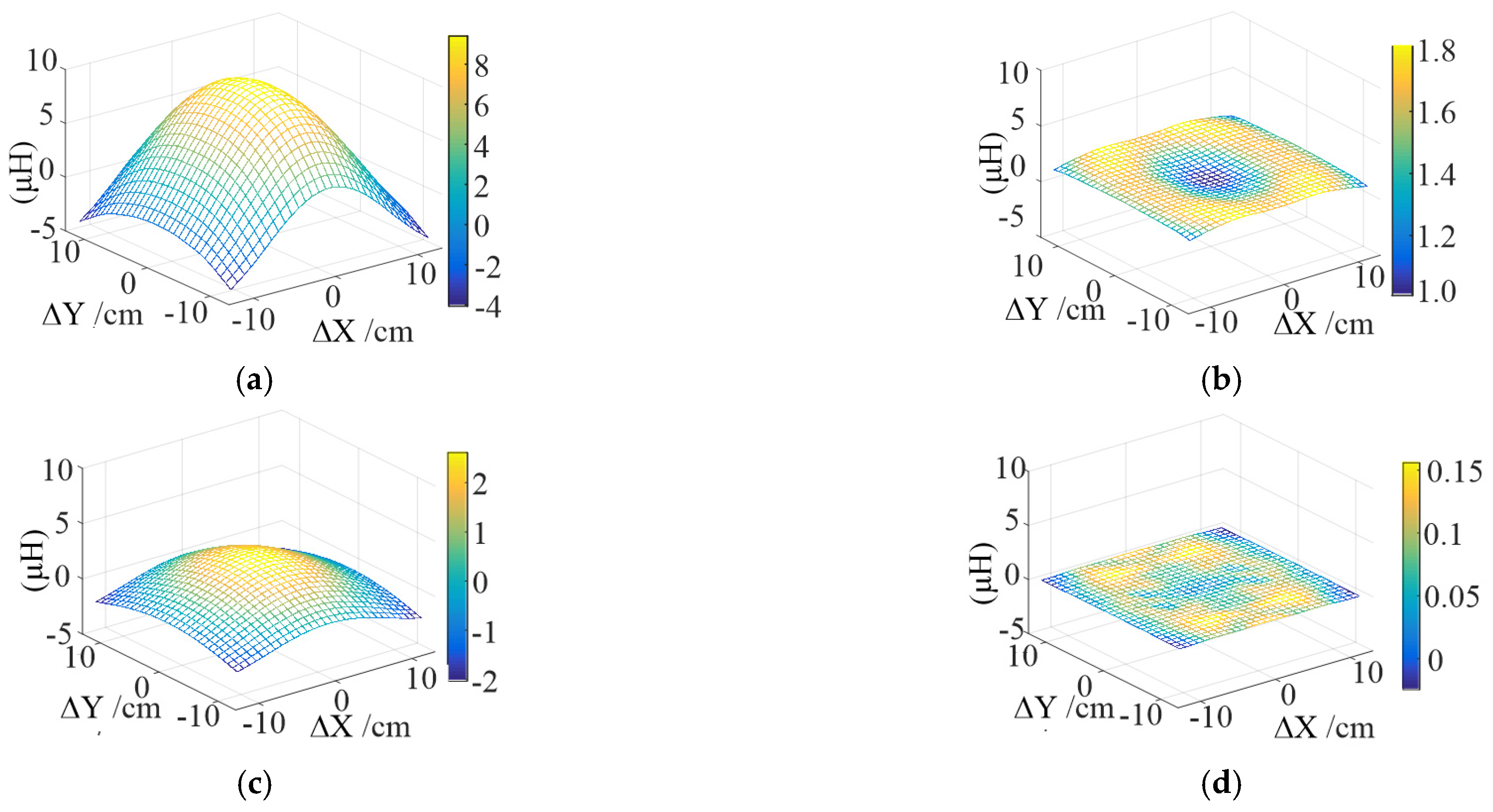
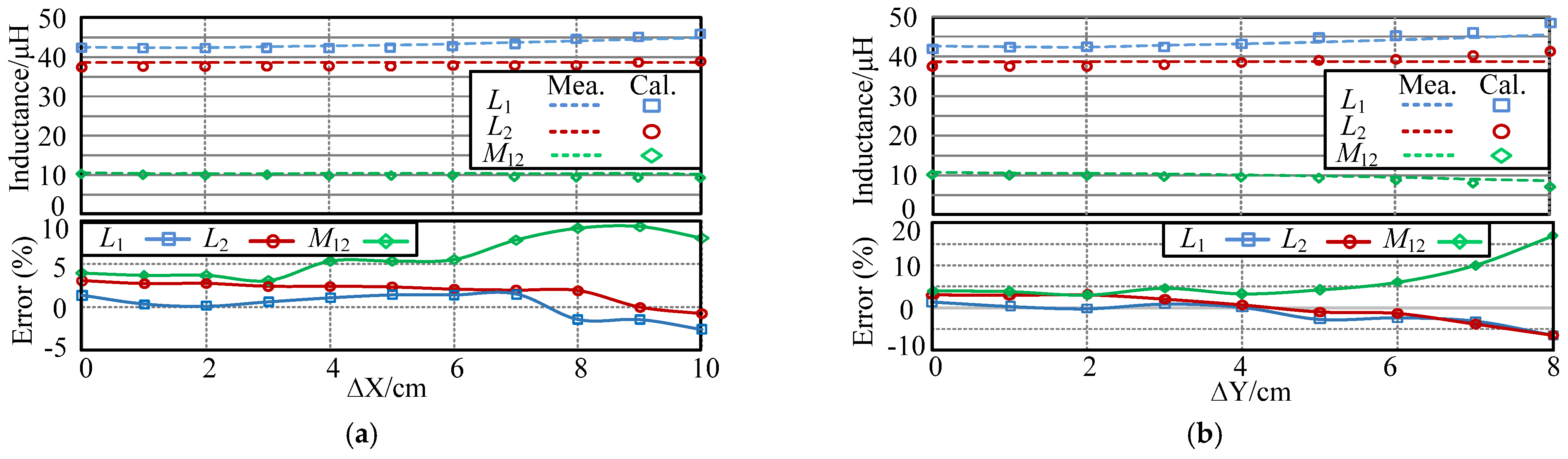
4.2. Simulation Results
5. Experimental Evaluation and Discussion
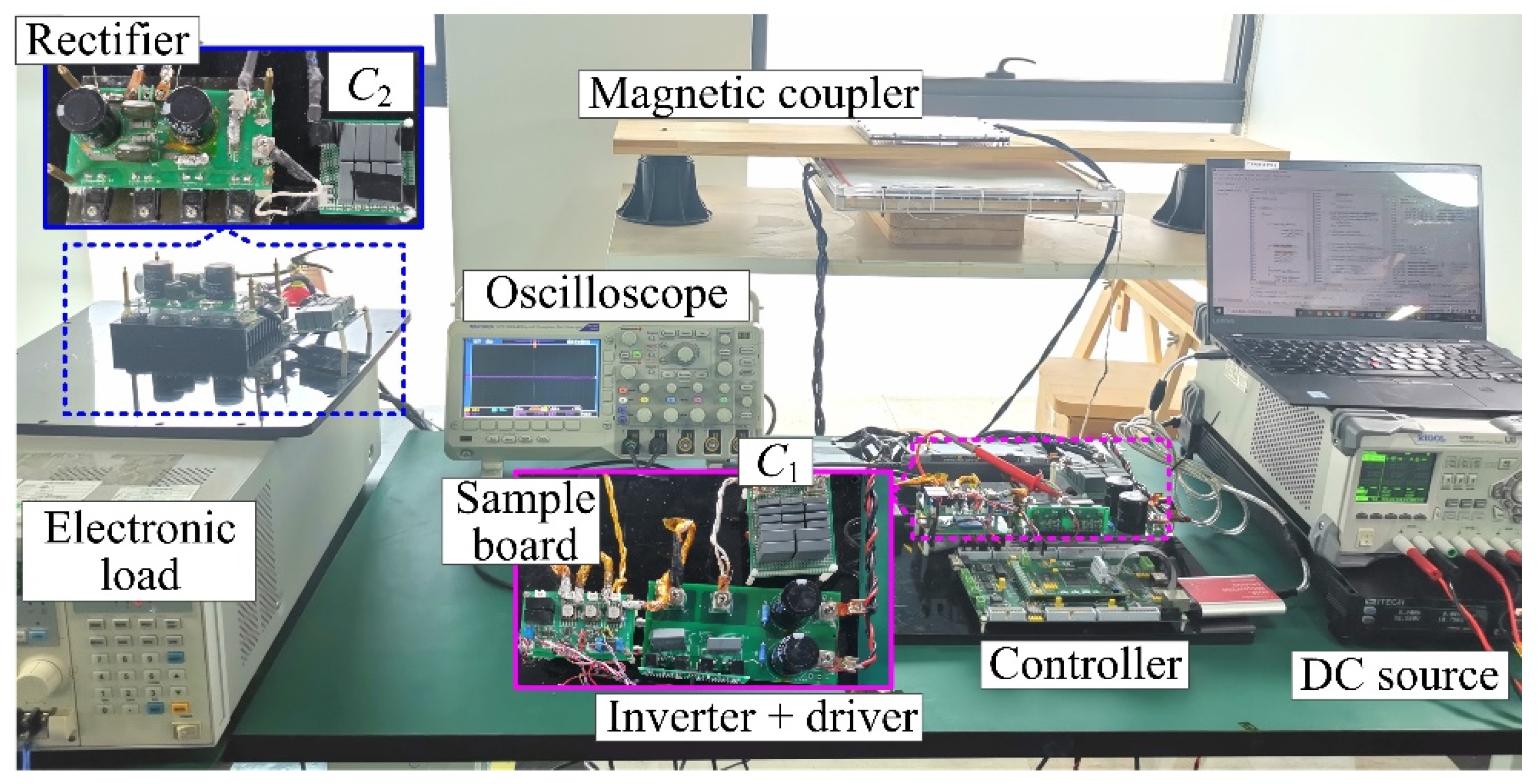
5.1. Experimental Prototype
5.2. Phase Detection of the Secondary Current
5.3. Parameter Estimation Results
5.3.1. Offline Parameter Estimation
5.3.2. Online Parameter Estimation
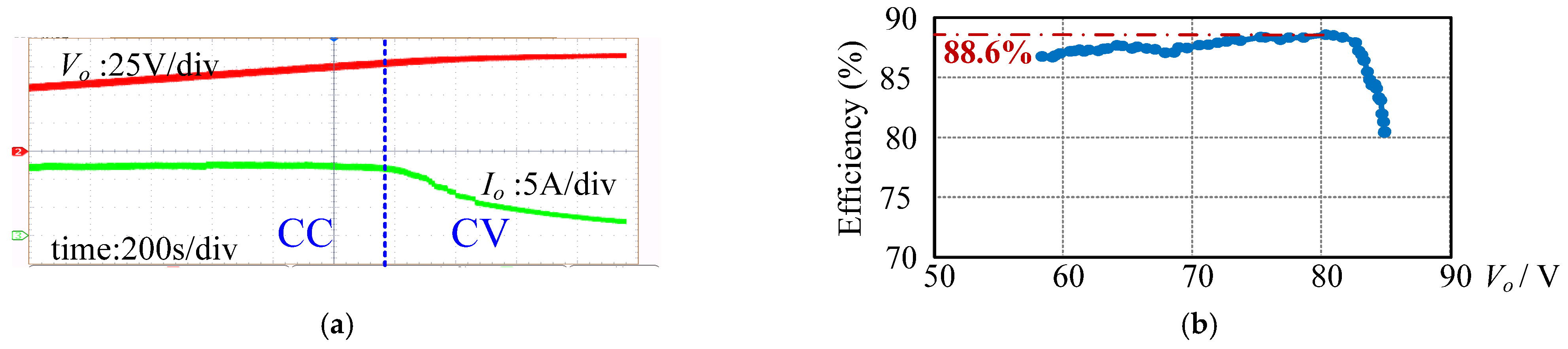
5.4. Closed-Loop Control Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Covic, G.A.; Boys, J.T. Inductive Power Transfer. Proc. IEEE 2013, 101, 1276–1289. [Google Scholar] [CrossRef]
- Cheng, Z.; Lei, Y.; Song, K.; Zhu, C. Design and Loss Analysis of Loosely Coupled Transformer for an Underwater High-Power Inductive Power Transfer System. IEEE Trans. Magn. 2015, 51, 1–10. [Google Scholar]
- Ho, J.S.; Kim, S.; Poon, A.S.Y. Midfield Wireless Powering for Implantable Systems. Proc. IEEE 2013, 101, 1369–1378. [Google Scholar] [CrossRef]
- Zhang, L.; Gu, S.J.S.; Huang, X.; Palmer, J.; Giewont, W.; Wang, F.; Tolbert, L.M. Design Considerations for High-Voltage Insulated Gate Drive Power Supply for 10-kV SiC MOSFET Applied in Medium-Voltage Converter. IEEE Trans. Ind. Electron. 2021, 68, 5712–5724. [Google Scholar] [CrossRef]
- Ahmad, A.; Alam, M.S.; Chabaan, R. A Comprehensive Review of Wireless Charging Technologies for Electric Vehicles. IEEE Trans. Transp. Electrification 2018, 4, 38–63. [Google Scholar] [CrossRef]
- Patil, D.; McDonough, M.K.; Miller, J.M.; Fahimi, B.; Wireless, P.T.B. Power Transfer for Vehicular Applications: Overview and Challenges. IEEE Trans. Transp. Electrification 2018, 4, 3–37. [Google Scholar] [CrossRef]
- Hsu, J.U.W.; Hu, A.P.; Swain, A. A Wireless Power Pickup Based on Directional Tuning Control of Magnetic Amplifier. IEEE Trans. Ind. Electron. 2009, 56, 2771–2781. [Google Scholar] [CrossRef]
- Beh, T.C.; Kato, M.; Imura, T.; Oh, S.; Hori, Y. Automated Impedance Matching System for Robust Wireless Power Transfer via Magnetic Resonance Coupling. IEEE Trans. Ind. Electron. 2013, 60, 3689–3698. [Google Scholar] [CrossRef]
- Huang, Z.; Lam, C.-S.; Mak, P.-I.; Martins, R.P.d.; Wong, S.-C.; Tse, C.K. A Single-Stage Inductive-Power-Transfer Converter for Constant-Power and Maximum-Efficiency Battery Charging. IEEE Trans. Power Electron. 2020, 35, 8973–8984. [Google Scholar] [CrossRef]
- Colak, K.; Asa, E.; Bojarski, M.; Czarkowski, D.; Onar, O.C. A Novel Phase-Shift Control of Semibridgeless Active Rectifier for Wireless Power Transfer. IEEE Trans. Power Electron. 2015, 30, 6288–6297. [Google Scholar] [CrossRef]
- Li, H.; Wang, K.; Fang, J.; Tang, Y. Pulse Density Modulated ZVS Full-Bridge Converters for Wireless Power Transfer Systems. IEEE Trans. Power Electron. 2019, 34, 369–377. [Google Scholar] [CrossRef]
- Li, H.; Fang, J.; Chen, S.; Wang, K.; Tang, Y. Pulse Density Modulation for Maximum Efficiency Point Tracking of Wireless Power Transfer Systems. IEEE Trans. Power Electron. 2018, 33, 5492–5501. [Google Scholar] [CrossRef]
- Jiang, Y.; Wang, L.; Wang, Y.; Wu, M.; Zeng, Z.; Liu, Y.; Sun, J. Phase-Locked Loop Combined With Chained Trigger Mode Used for Impedance Matching in Wireless High Power Transfer. IEEE Trans. Power Electron. 2020, 35, 4272–4285. [Google Scholar] [CrossRef]
- Yeo, T.D.; Kwon, D.; Khang, S.T.; Yu, J.W. Design of Maximum Efficiency Tracking Control Scheme for Closed-Loop Wireless Power Charging System Employing Series Resonant Tank. IEEE Trans. Power Electron. 2017, 32, 471–478. [Google Scholar] [CrossRef]
- Wang, Z.H.; Li, Y.P.; Sun, Y.; Tang, C.S.; Lv, X. Load Detection Model of Voltage-Fed Inductive Power Transfer System. IEEE Trans. Power Electron. 2013, 28, 5233–5243. [Google Scholar] [CrossRef]
- Hu, S.; Liang, Z.; Wang, Y.; Zhou, J.; He, X. Principle and Application of the Contactless Load Detection Based on the Amplitude Decay Rate in a Transient Process. IEEE Trans. Power Electron. 2017, 32, 8936–8944. [Google Scholar] [CrossRef]
- Thrimawithana, D.J.; Madawala, U.K. A primary side controller for inductive power transfer systems. In Proceedings of the 2010 IEEE International Conference on Industrial Technology, Via del Mar, Chile, 14–17 March 2010. [Google Scholar]
- Su, Y.G.; Zhang, H.Y.; Wang, Z.H.; Hu, A.P.; Chen, L.; Sun, Y. Steady-State Load Identification Method of Inductive Power Transfer System Based on Switching Capacitors. IEEE Trans. Power Electron. 2015, 30, 6349–6355. [Google Scholar] [CrossRef]
- Liu, Y.; Madawala, U.K.; Mai, R.; He, Z. Primary-Side Parameter Estimation Method for Bi-Directional Inductive Power Transfer Systems. IEEE Trans. Power Electron. 2021, 36, 68–72. [Google Scholar] [CrossRef]
- Liu, F.; Chen, K.; Zhao, Z.; Li, K.; Yuan, L. Transmitter-Side Control of Both the CC and CV Modes for the Wireless EV Charging System With the Weak Communication. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 6, 955–965. [Google Scholar] [CrossRef]
- Yin, J.; Lin, D.; Parisini, T.; Hui, S.Y. Front-End Monitoring of the Mutual Inductance and Load Resistance in a Series–Series Compensated Wireless Power Transfer System. IEEE Trans. Power Electron. 2016, 31, 7339–7352. [Google Scholar] [CrossRef]
- Dai, X.; Sun, Y.; Tang, C.; Wang, Z.; Su, Y.; Li, Y. Dynamic parameters identification method for inductively coupled power transfer system. In Proceedings of the 2010 IEEE International Conference on Sustainable Energy Technologies (ICSET), Kandy, Sri Lanka, 6–9 December 2010. [Google Scholar]
- Chow, J.P.-W.; Chung, H.-H.; Cheng, C.-S.; Wang, W. Use of Transmitter-Side Electrical Information to Estimate System Parameters of Wireless Inductive Links. IEEE Trans. Power Electron. 2017, 32, 7169–7186. [Google Scholar] [CrossRef]
- Chow, J.P.W.; Chung, H.S.H.; Cheng, C.S. Use of Transmitter-Side Electrical Information to Estimate Mutual Inductance and Regulate Receiver-Side Power in Wireless Inductive Link. IEEE Trans. Power Electron. 2016, 31, 6079–6091. [Google Scholar] [CrossRef]
- Xu, L.; Chen, Q.; Ren, X.; Wong, S.C.; Tse, C.K. Self-Oscillating Resonant Converter With Contactless Power Transfer and Integrated Current Sensing Transformer. IEEE Trans. Power Electron. 2017, 32, 4839–4851. [Google Scholar] [CrossRef]
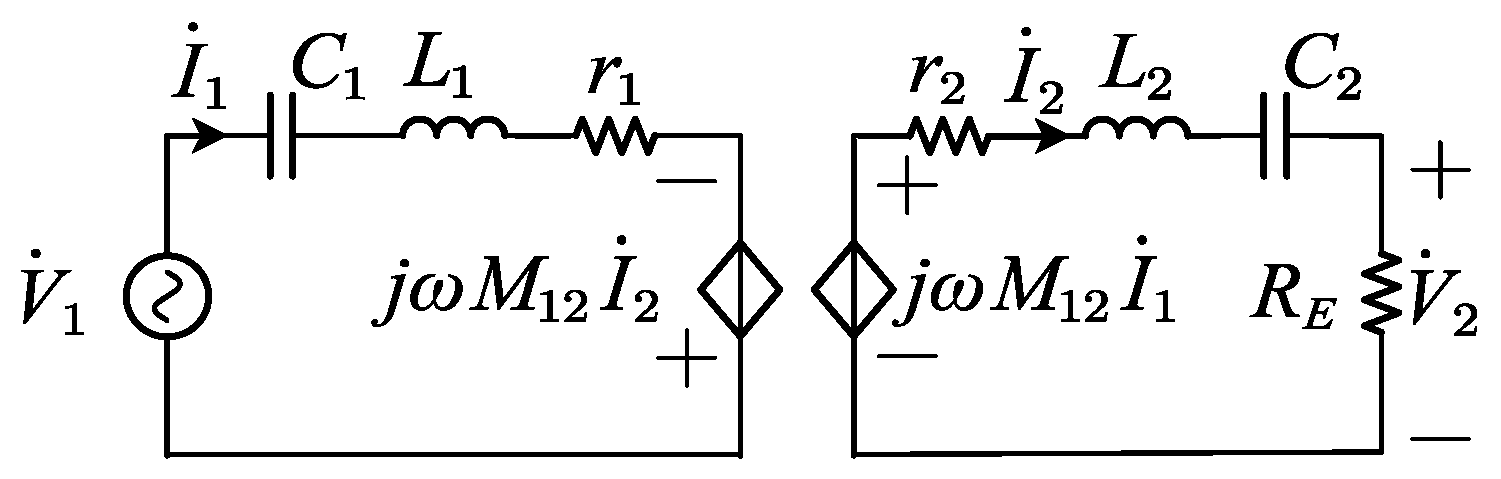








| Parameter Identification Methods | Compensations | Identified Variables | Operating Frequency | Ref. | |
|---|---|---|---|---|---|
| Transient model | Free oscillation damping model | S/S | RL (>50 Ω) | Self-oscillating frequency | [15] |
| RL (<25 Ω) | Self-oscillating frequency | [16] | |||
| Steady-state model | Phasor analysis | LCL/P | Vo and M | Fixed at resonant frequency | [17] |
| S/S | RL and M | Tracking primary resonant frequency | [18] | ||
| M | Frequency with zero input phase angle | [19] | |||
| M, r2 | Fixed at resonant frequency | [20] | |||
| RL and M | Different from ω2 | [21] | |||
| Energy conservation | S/S | Reflected impedance | Fixed at resonant frequency | [22] | |
| Curve fitting | S/S | M and equivalent load | Fixed at resonant frequency | [23] | |
| Q1, Q2, ω1, ω2, L1, L2, and k | / | [24] | |||
| Components | Value | Components | Value |
|---|---|---|---|
| Input voltage | 80 V | Output power | 1 kW |
| Resonant frequency | 85 kHz | Compensation | C1 = 88.1 nF, rC1 = 41.2 mΩ |
| Clearance range | 10–16 cm | C2 = 94.5 nF, rC1 = 27.4 mΩ |
| ∆Z | L1/μH | L2/μH | L3/μH | M12/μH | M13/μH | M23/μH | rL1/Ω | rL2/Ω | rL3/Ω |
|---|---|---|---|---|---|---|---|---|---|
| 10 cm | 42.56 | 38.66 | 47.26 | 10.62 | 0.165 | 8.36 | 0.065 | 0.06 | 0.28 |
| 13 cm | 44.07 | 37.52 | 46.5 | 8.455 | 0.06 | 4.92 | |||
| 16 cm | 44.97 | 36.7 | 46.25 | 6.635 | 0.015 | 2.915 |
| ∆Z | Estimated Results | Estimation Error ε | ||||||
|---|---|---|---|---|---|---|---|---|
| L1/μH | L2/μH | M12/μH | r1/Ω | L1/μH | L2/μH | M12/μH | r1/Ω | |
| 10 cm | 41.98 | 37.48 | 10.2 | 0.156 | −1.3% | −3.05% | −3.95% | 33.1% |
| 13 cm | 43.61 | 37.08 | 8.162 | 0.15 | −1.04% | −1.17% | −3.47% | 27.9% |
| 16 cm | 44.52 | 36.41 | 6.709 | 0.147 | −1% | −0.08% | −1.12% | 25.4% |
| Execution Cycle | Calculation Time | |
|---|---|---|
| Vo | 346 | 2.30667 μs |
| Io | 178 | 1.18667 μs |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, L.; Ke, G.; Chen, Q.; Zhang, B.; Ren, X.; Zhang, Z. Multi-Parameter Estimation for an S/S Compensated IPT Converter Based on the Phase Difference between Tx and Rx Currents. Electronics 2022, 11, 1023. https://doi.org/10.3390/electronics11071023
Xu L, Ke G, Chen Q, Zhang B, Ren X, Zhang Z. Multi-Parameter Estimation for an S/S Compensated IPT Converter Based on the Phase Difference between Tx and Rx Currents. Electronics. 2022; 11(7):1023. https://doi.org/10.3390/electronics11071023
Chicago/Turabian StyleXu, Ligang, Guangjie Ke, Qianhong Chen, Bin Zhang, Xiaoyong Ren, and Zhiliang Zhang. 2022. "Multi-Parameter Estimation for an S/S Compensated IPT Converter Based on the Phase Difference between Tx and Rx Currents" Electronics 11, no. 7: 1023. https://doi.org/10.3390/electronics11071023





