Efficient Architectures for Full Hardware Scrypt-Based Block Hashing System
Abstract
:1. Introduction
2. Background
2.1. Scrypt-Based Block Hashing for the Blockchain Network
| Algorithm 1 (block_hash, nonce) = Scrypt-based_block_hashing(block_header) |
| 1: nonce = 0 |
| 2: while nonce do |
| 3: block_hash = SHA256(SHA256(block_header)) |
| 4: scrypt_hash = Scrypt(block_header) |
| 5: if scrypt_hash < target then return (block_hash, nonce) |
| 6: else |
| 7: nonce = nonce + 1 |
| 8: end if |
| 9: end while |
2.2. Scrypt Algorithm
| Algorithm 2 Out = Scrypt (blockheader) |
| Scrypt variables and parameters for hashed block mining: |
| message = blockheader (640 bits) |
| salt = blockheader, padding (1024 bits) |
| Block size factor (r) = 1 |
| Number of iterations (c) = 1 |
| Parallelization parameter (p) = 1 |
| CPU/Memory cost parameter (N) = 1024 |
| Length of DK in bits (dklen) = 256 |
| Algorithm’s steps: |
| 1: p_out = PBKDF2(message, salt, c, 1024 × r × p) |
| 2: r_out = ROMix(p_out, N, r) |
| 3: scrypt_out = PBKDF2(message, r_out, c, dklen) |
| 4: return scrypt_out |
2.2.1. PBKDF2
| Algorithm 3 Out = PBKDF2(message, salt, c, dklen) |
| 1: Out = "" |
| 2: for i ← 1 to (dklen/256) do |
| 3: DK = HMAC({salt, i}, message) |
| 4: Out = {DK, DK} |
| 5: end for |
| 6: return Out |
| Algorithm 4 Out = HMAC(salti, message) |
| 1: IPAD = 36363636...36 (256 bits) |
| 2: OPAD = 5C5C5C5C...5C (256 bits) |
| 3: KHASH = SHA256(message) |
| 4: IXOR = {(KHASH ⊕ IPAD), IPAD} |
| 5: OXOR = {(KHASH ⊕ OPAD), OPAD} |
| 6: IHASH = SHA256({IXOR, salti}) |
| 7: OHASH = SHA256({OXOR, IHASH}) |
| 8: Out = OHASH |
| 9: return Out |
| Algorithm 5 digest = SHA256(message_in) |
| 1: M, N = Padding_Splitting (message_in) |
| 2: H = H_Constants |
| 3: for t ← 0 to (N-1) do |
| 4: W = BlockDecomposition(M) |
| 5: H = HashComputation(H, K_Constants, W) |
| 6: end for |
| 7: return digest = {H, H, H, H, H, H, H, H} |
2.2.2. ROMix
| Algorithm 6 block = ROMix (block, N, r) |
| 1: for i ← 0 to (N-1) do |
| 2: Mem = block |
| 3: block = BlockMix(block, r) |
| 4: end for |
| 5: for j ← 0 to (N-1) do |
| 6: j = block[489:480] (block’s 10-bit from 480 to 489) |
| 7: block = BlockMix(block ⊕ Mem, r) |
| 8: end for |
| 9: return block |
| Algorithm 7 block = BlockMix(block, r) |
| 1: X = block[1023:512] (block’s 512 high bits) |
| 2: for i ← 0 to (2 × r − 1) do |
| 3: X = X ⊕ block[511:0] (block’s 512 low bits) |
| 4: X = X + Salsa20/8(X) |
| 5: if (i == 0) then |
| 6: OutH = X |
| 7: else |
| 8: OutL = X |
| 9: end if |
| 10: end for |
| 11: block = {OutH, OutL} |
| 12: return block |
| Algorithm 8 Out = Salsa20/8(message) |
| 1: {x, x, …, x} = message |
| 2: for i ← 0 to 3 do |
| 3: {y, …, y} = ({x, …, x}) |
| 4: {x, …, x} = ({y, …, y}) |
| 5: end for |
| 6: Out = {x, x, …, x} |
| 7: return Out |
3. Proposed Scrypt Hardware Architecture
3.1. Low-Resource and High-Throughput Non-Pipelined Scrypt Architecture
3.2. Low-Resource and High-Throughput PBKDF2 Core Architectures
3.3. Proposed Architecture for ROMix Core
3.4. Shared Resources—Pipelined Scrypt Architecture
4. Results
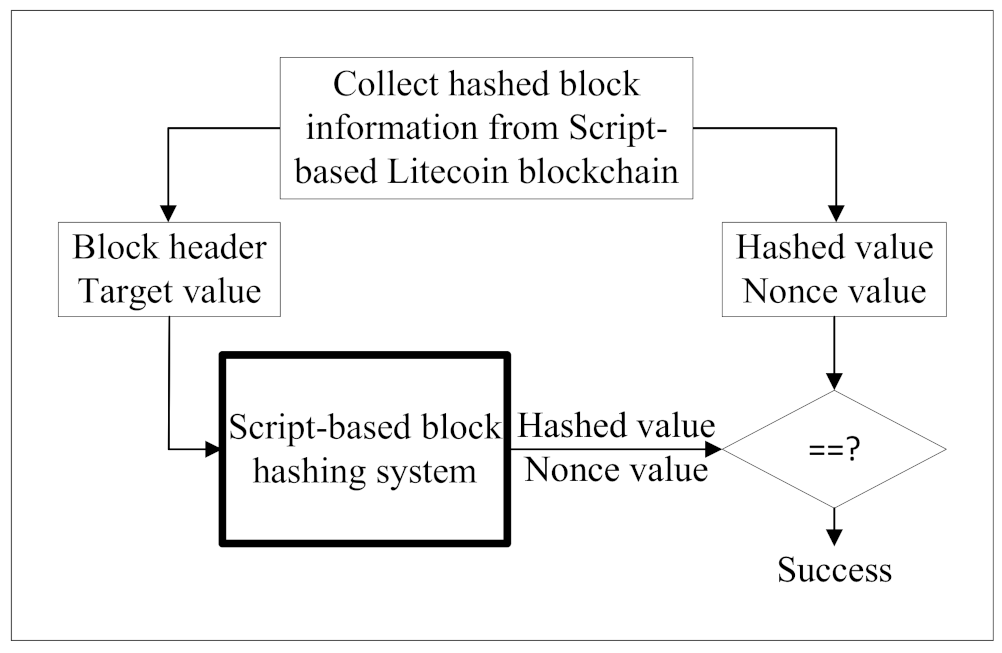
4.1. Function Verification Results
4.2. Implementation Performance Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Leible, S.; Schlager, S.; Schubotz, M.; Gipp, B. A Review on Blockchain Technology and Blockchain Projects Fostering Open Science. Front. Blockchain 2019, 2, 16. [Google Scholar] [CrossRef]
- Kshetri, N. Blockchain’s roles in strengthening cybersecurity and protecting privacy. Telecommun. Policy 2017, 41, 1027–1038. [Google Scholar] [CrossRef] [Green Version]
- Zhai, S.; Yang, Y.; Li, J.; Qiu, C.; Zhao, J. Research on the Application of Cryptography on the Blockchain. J. Phys. Conf. Ser. 2019, 1168, 32–77. [Google Scholar] [CrossRef]
- Fu, J.; Qiao, S.; Huang, Y.; Si, X.; Li, B.; Yuan, C. A Study on the Optimization of Blockchain Hashing Algorithm Based on PRCA. Secur. Commun. Netw. 2020, 2020, 8876317. [Google Scholar] [CrossRef]
- Wang, L.; Shen, X.; Li, J.; Shao, J.; Yang, Y. Cryptographic primitives in blockchains. J. Netw. Comput. Appl. 2019, 127, 43–58. [Google Scholar] [CrossRef]
- Martino, R.; Cilardo, A. Designing a SHA-256 processor for blockchain-based IoT applications. Internet Things 2020, 11, 100254. [Google Scholar] [CrossRef]
- Martino, R.; Cilardo, A. A Flexible Framework for Exploring, Evaluating, and Comparing SHA-2 Designs. IEEE Access 2019, 7, 72443–72456. [Google Scholar] [CrossRef]
- Wiemer, F.; Zimmermann, R. High-speed implementation of bcrypt password search using special-purpose hardware. In Proceedings of the 2014 International Conference on ReConFigurable Computing and FPGAs (ReConFig14), Cancun, Mexico, 8–10 December 2014; pp. 1–6. [Google Scholar] [CrossRef]
- Ertaul, L.; Kaur, M.; Gudise, V.A.K.R. Implementation and Performance Analysis of PBKDF2, Bcrypt, Scrypt Algorithms. In Proceedings of the 2016 International Conference on Wireless Network (ICWN’2016), Las Vegas, NV, USA, 25–28 July 2016; pp. 66–72. [Google Scholar]
- Hatzivasilis, G. Password-Hashing Status. Cryptography 2017, 1, 10. [Google Scholar] [CrossRef] [Green Version]
- Alwen, J.; Chen, B.; Pietrzak, K.; Reyzin, L.; Tessaro, S. Scrypt Is Maximally Memory-Hard. In Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques, Paris, France, 30 April–4 May 2017; Springer: Cham, Switzerland, 2017; pp. 33–62. [Google Scholar] [CrossRef]
- Jiwon, C.; Tali, M.; Iris, B.R.; Maurice, H. Attacking Memory-Hard Scrypt with near-Data-Processing. In Proceedings of the International Symposium on Memory Systems, MEMSYS ’19, Washington, DC, USA, 30 September–3 October 2019; Association for Computing Machinery: New York, NY, USA, 2019; pp. 33–37. [Google Scholar] [CrossRef]
- Percival, C.; Josefsson, S. The Scrypt Password-Based Key Derivation Function. Technical Report RFC 7914. Available online: https://doi.org/10.17487/RFC7914 (accessed on 8 March 2022). [CrossRef]
- Hatzivasilis, G.; Papaefstathiou, I.; Manifavas, C. Password Hashing Competition—Survey and Benchmark. IACR Cryptol. ePrint Arch. 2015, 2015, 265. [Google Scholar]
- Hatzivasilis, G. Password Management: How Secure Is Your Login Process? In Model-Driven Simulation and Training Environments for Cybersecurity; Hatzivasilis, G., Ioannidis, S., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 157–177. [Google Scholar]
- Padmavathi, M.; Suresh, R.M. Secure P2P Intelligent Network Transaction using Litecoin. Mob. Netw. Appl. 2019, 24, 318–326. [Google Scholar] [CrossRef]
- Ling, R.; Srinivas, D. Bandwidth Hard Functions for ASIC Resistance. In Theory of Cryptography; Yael, K., Leonid, R., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 466–492. [Google Scholar]
- Almeida, L.C.; Andrade, E.R.; Barreto, P.S.L.M.; Simplicio, M.A., Jr. Lyra: Password-based key derivation with tunable memory and processing costs. J. Cryptogr. Eng. 2014, 4, 75–89. [Google Scholar] [CrossRef] [Green Version]
- Alwen, J.; Chen, B.; Kamath, C.; Kolmogorov, V.; Pietrzak, K.; Tessaro, S. On the Complexity of Scrypt and Proofs of Space in the Parallel Random Oracle Model. In Advances in Cryptology—EUROCRYPT 2016; Fischlin, M., Coron, J.S., Eds.; Springer: Berlin/Heidelberg, Germany, 2016; pp. 358–387. [Google Scholar]
- Han, R.; Foutris, N.; Kotselidis, C. Demystifying Crypto-Mining: Analysis and Optimizations of Memory-Hard PoW Algorithms. In Proceedings of the 2019 IEEE International Symposium on Performance Analysis of Systems and Software (ISPASS), Madison, WI, USA, 24–26 March 2019; pp. 22–33. [Google Scholar] [CrossRef] [Green Version]
- Ntantogian, C.; Malliaros, S.; Xenakis, C. Evaluation of password hashing schemes in open source web platforms. Comput. Secur. 2019, 84, 206–224. [Google Scholar] [CrossRef]
- Dürmuth, M.; Kranz, T. On Password Guessing with GPUs and FPGAs. In Technology and Practice of Passwords; Mjølsnes, S.F., Ed.; Springer International Publishing: Cham, Switzerland, 2015; pp. 19–38. [Google Scholar]
- Litecoin Foundation. Litecoin Wiki, “Mining Hardware Comparision”. 2018. Available online: https://litecoin.info/index.php/Mining_hardware_comparison (accessed on 8 March 2022).
- Luca, P. Master Thesis: Hardware Implementation for Litecoin Mining; Technical Report; University in Leuven: Leuven, Belgium, 2015. [Google Scholar]
- Alpha Technology (INT) LTD. Scrypt ASIC Prototyping Preliminary Design Document; Technical Report; Alpha Technology (INT) LTD: Manchester, UK; London, UK, 2013. [Google Scholar]
- Duong, L.V.T.; Hieu, D.V.; Luan, P.H.; Hong, T.T.; Khai, L.D. Hardware Implementation For Fast Block Generator Of Litecoin Blockchain System. In Proceedings of the 2021 IEEE International Symposium on Electrical and Electronics Engineering (ISSE), Ho Chi Minh, Vietnam, 15–16 April 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Duong, L.V.T.; Thuy, N.T.T.; Khai, L.D. A fast approach for bitcoin blockchain cryptocurrency mining system. Integration 2020, 74, 107–114. [Google Scholar] [CrossRef]
- Litecoin. Block Hashing Algorithm. 2018. Available online: https://litecoin.info/index.php/Block_hashing_algorithm (accessed on 8 March 2022).
- Bitcoin. Block Hashing Algorithm. 2018. Available online: https://en.bitcoin.it/wiki/Block_hashing_algorithm (accessed on 8 March 2022).
- Kaliski, B. PKCS #5: Password-Based Cryptography Specification Version 2.0; Technical Report RFC 2898; The Internet Research Task Force Organization: USA, 2000; Available online: https://www.rfc-editor.org/info/rfc2898 (accessed on 8 March 2022). [CrossRef] [Green Version]
- Dang, Q.H. Secure Hash Standard; National Institute of Standards and Technology. Available online: https://doi.org/10.6028/nist.fips.180-4 (accessed on 8 March 2022). [CrossRef]
- Pham, H.L.; Tran, T.H.; Phan, T.D.; Le, V.T.D.; Lam, D.K.; Nakashima, Y. Double SHA-256 Hardware Architecture With Compact Message Expander for Bitcoin Mining. IEEE Access 2020, 8, 139634–139646. [Google Scholar] [CrossRef]
- Bernstein, D.J. The Salsa20 Family of Stream Ciphers. In New Stream Cipher Designs; Springer: Berlin/Heidelberg, Germany, 2008; pp. 84–97. [Google Scholar] [CrossRef] [Green Version]
- Cohen, D. On Holy Wars and a Plea for Peace. Computer 1981, 14, 48–54. [Google Scholar] [CrossRef]
- Litecoin Explorer. Available online: https://live.blockcypher.com/ltc/ (accessed on 8 March 2022).
- Bhatnagar, H. Advanced ASIC Chip Synthesis: Using Synopsys Design Compiler Physical Compiler and Prime Time; Kluwer Academic Publishers: New York, NY, USA, 2002. [Google Scholar] [CrossRef]
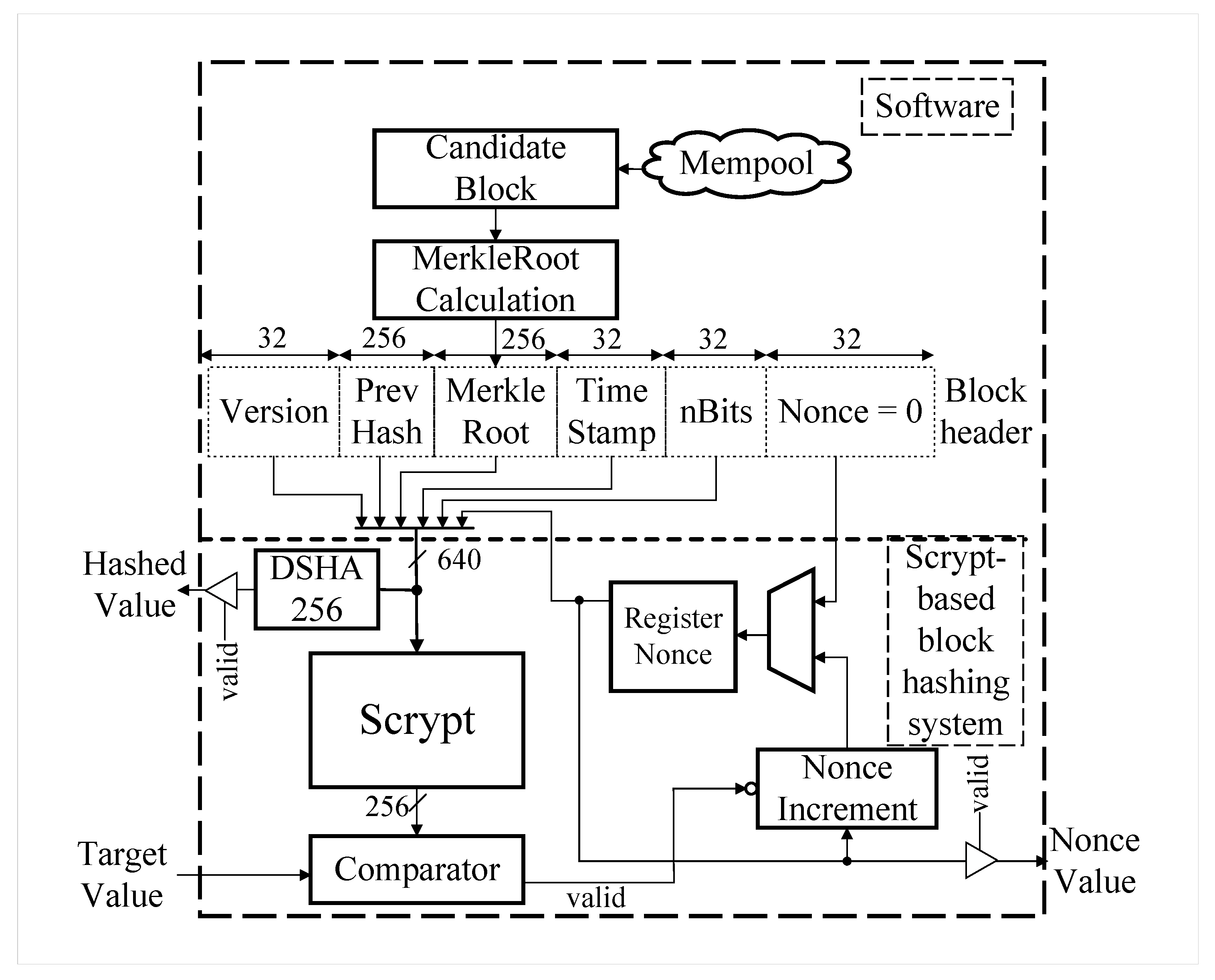







| Field | Length in Bit | Description |
|---|---|---|
| Version | 32 | Block version number |
| Previous Block Hash | 256 | 256-bit hash of the previous block header |
| Merkle Root | 256 | 256-bit hash based on all of the transactions in the block |
| Time Stamp | 32 | Current block timestamp as seconds since 1970-01-01T00:00 UTC |
| nBits | 32 | Current target in compact format |
| Nonce | 32 | 32-bit number (starts at 0) |
| Instances | Latency (No. Clocks) | HR Vertex 7 (No. Slices) | HR Aveo U280 (No. Slices) |
|---|---|---|---|
| PBKDF2_1 (P1) | 873 | 509 | 519 |
| PBKDF2_2 (P2) | 267 | 451 | 452 |
| ROMix | 55,872 | 965 | 949 |
| Design | Devices | No. Cores | No. BRAM | BRAM Utilization (%) |
|---|---|---|---|---|
| Proposed Non-pipelined | Virtex-7 VX485T | 1 | 28.5 | 28.5/1030 (2.8%) |
| Proposed Non-pipelined | Virtex-7 VX485T | 32 | 912 | 912/1030 (88.5%) |
| Proposed Pipelined 32 ROMix | Virtex-7 VX485T | 1 | 912 | 912/1030 (88.5%) |
| Proposed Pipelined 64 ROMix | Alveo U280 | 1 | 1824 | 1824/2016 (90.5%) |
| Design | Devices | No. Cores | HW. (Slice) | Freq. (MHz) | Hash Rate (kHash/s) | HW. Eff. (Hash/s/Slice) | Power (W) |
|---|---|---|---|---|---|---|---|
| [24] | Spartan-6 LX45 | 1 | 5859 | 50.00 | 6.90 | 1.18 | 2.25 |
| [25] | Virtex-6 LX240T | 1 | 4670 | 200.00 | 1.33 | 0.28 | NA |
| [26] | Virtex-7 VX485T | 1 | 52,298 | 355.05 | 5.33 | 0.10 | NA |
| Proposed Non-pipelined | Virtex-7 VX485T | 1 | 2347 | 156.05 | 2.74 | 1.17 | 0.55 |
| Proposed Non-pipelined | Virtex-7 VX485T | 32 | 75,104 | 156.05 | 87.68 | 1.17 | 17.6 |
| Proposed Pipelined 32 ROMix | Virtex-7 VX485T | 1 | 35,041 | 156.05 | 89.38 | 2.34 | 7.03 |
| Proposed Pipelined 64 ROMix | Alveo U280 | 1 | 68,431 | 259.94 | 229.1 | 3.35 | 14.45 |
| Design | Devices | No. Cores | Parameter (N, r, p) | Freq. (MHz) | Hash Rate (kHash/s) | Power (W) | Ener. Eff. (J/kHash) |
|---|---|---|---|---|---|---|---|
| [20] | NVDIA-CUDA 9.1 | 1 | (1024, 1, 1) | 2600.00 | 41.33 | NA | NA |
| [21] | NVIDIA-GTX 1070 | 1 | (8192, 1, 1) | 1683.00 | 0.12 | NA | NA |
| [22] | NVIDIA-GTX 480 | 1 | (4096, 1, 1) | 701.00 | 27.75 | NA | NA |
| [12] | ARMv7-Cortex A15 | 1 | (16,384, 8, 1) | 2500.00 | 0.01 | NA | NA |
| [23] | NVIDIA-GX TITAN | 1 | (1024, 1, 1) | 797.00 | 6.06 | 2.04 | 0.336 |
| [23] | AMD-AX 7990 | 1 | (1024, 1, 1) | 950.00 | 17.04 | 6.13 | 0.360 |
| Proposed Pipelined 64 ROMix | Alveo U280 | 1 | (1024, 1, 1) | 259.94 | 229.1 | 14.45 | 0.063 |
| Proposed Pipelined 64 ROMix | ROHM 180 nm ASIC | 1 | (1024, 1, 1) | 136.30 | 156.13 | 0.82 | 0.005 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lam, D.K.; Le, V.T.D.; Tran, T.H. Efficient Architectures for Full Hardware Scrypt-Based Block Hashing System. Electronics 2022, 11, 1068. https://doi.org/10.3390/electronics11071068
Lam DK, Le VTD, Tran TH. Efficient Architectures for Full Hardware Scrypt-Based Block Hashing System. Electronics. 2022; 11(7):1068. https://doi.org/10.3390/electronics11071068
Chicago/Turabian StyleLam, Duc Khai, Vu Trung Duong Le, and Thi Hong Tran. 2022. "Efficient Architectures for Full Hardware Scrypt-Based Block Hashing System" Electronics 11, no. 7: 1068. https://doi.org/10.3390/electronics11071068
APA StyleLam, D. K., Le, V. T. D., & Tran, T. H. (2022). Efficient Architectures for Full Hardware Scrypt-Based Block Hashing System. Electronics, 11(7), 1068. https://doi.org/10.3390/electronics11071068






