A Simple Method to Design a UWB Filter with a Notched Band Using Short-Circuit Step Impedance Stubs
Abstract
:1. Introduction
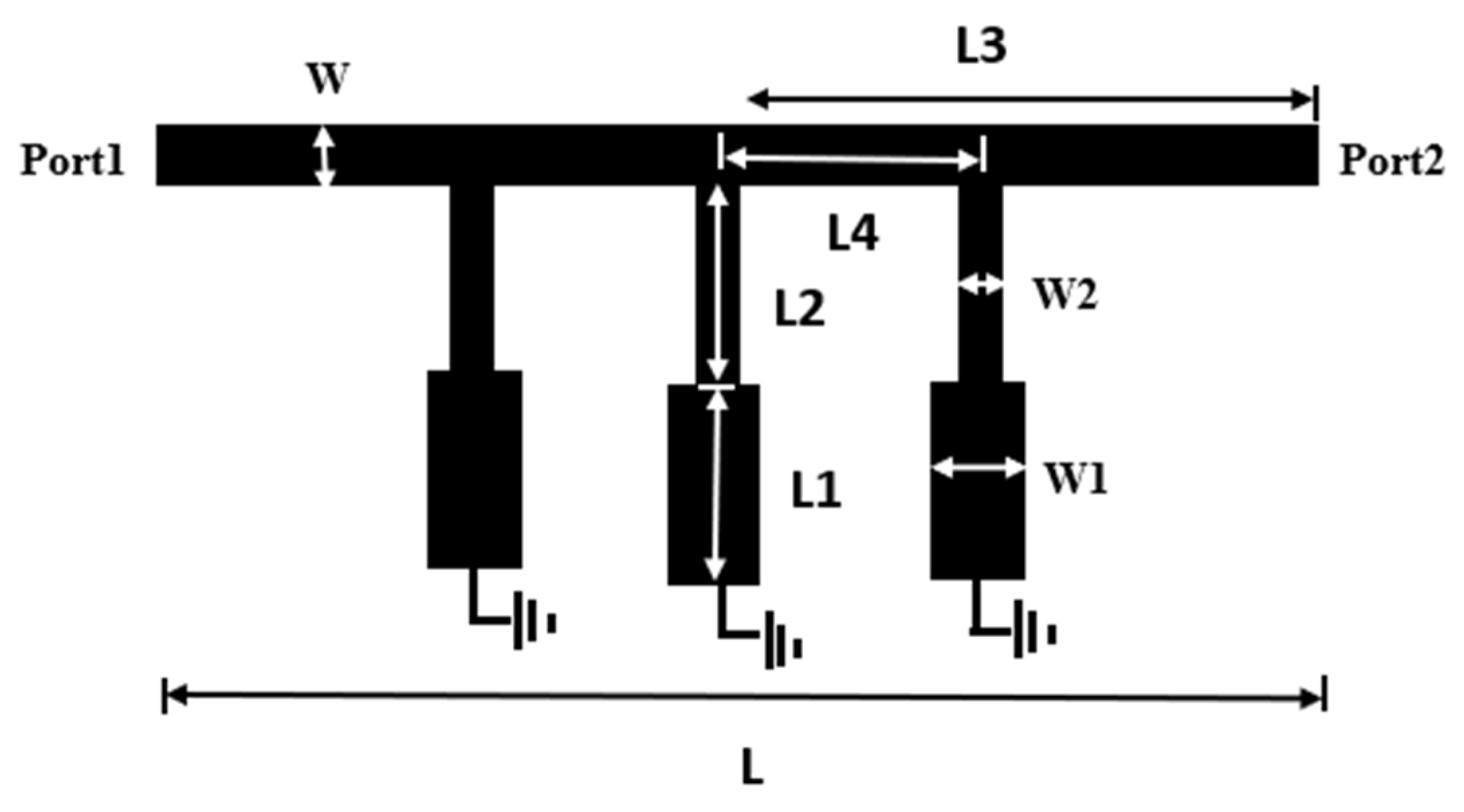
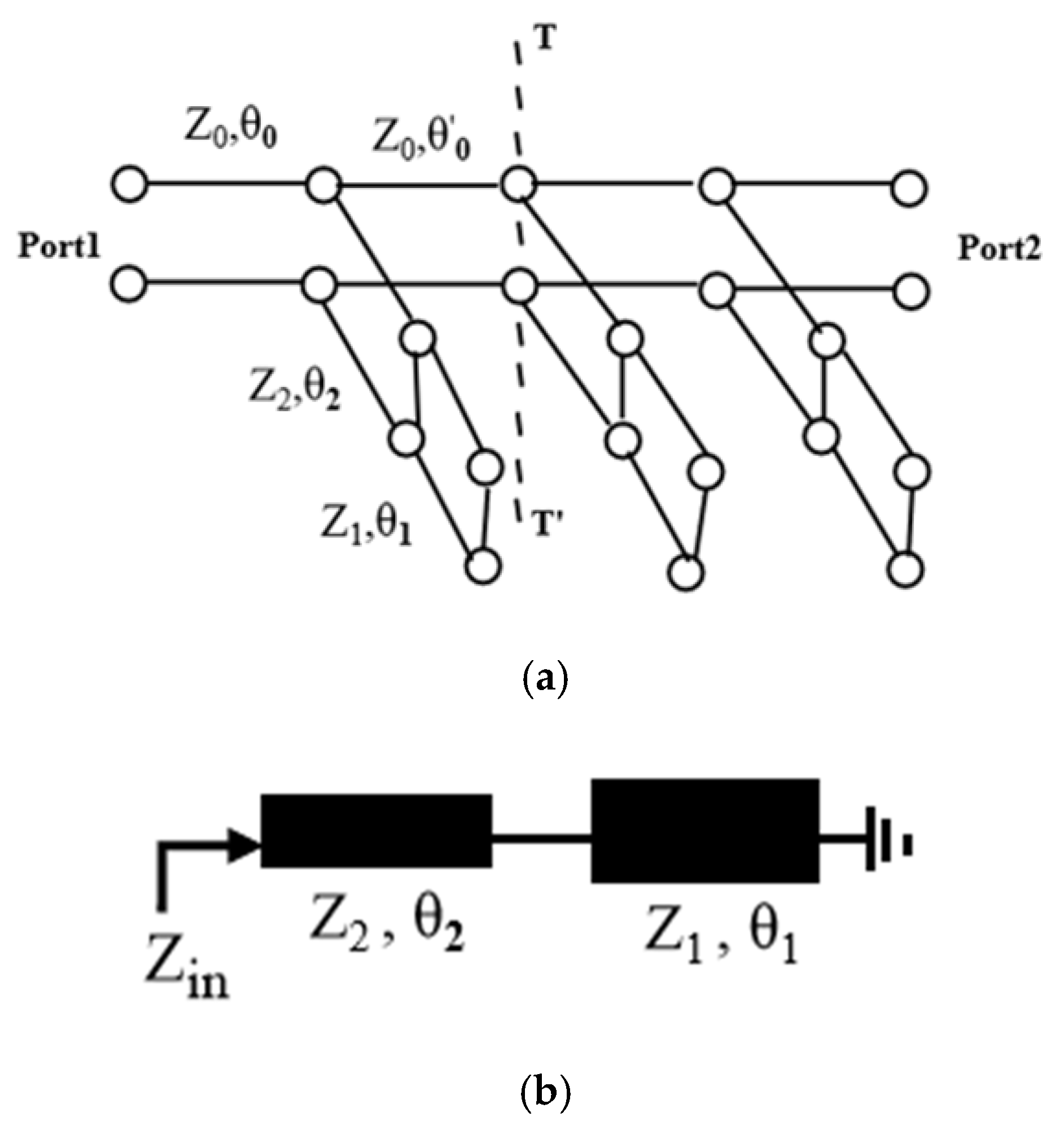
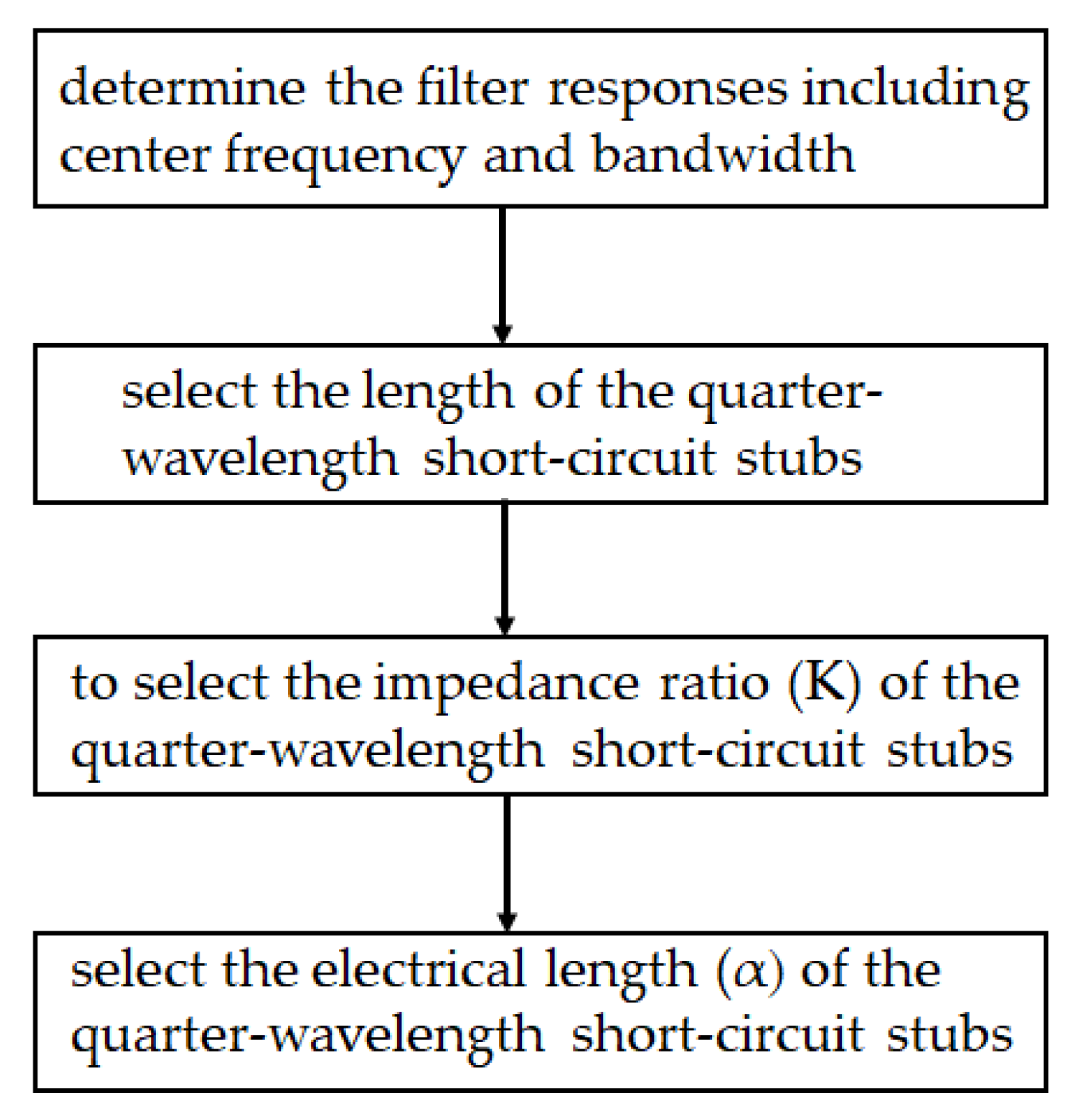
2. Design and Simulation
2.1. Equivalent Circuit
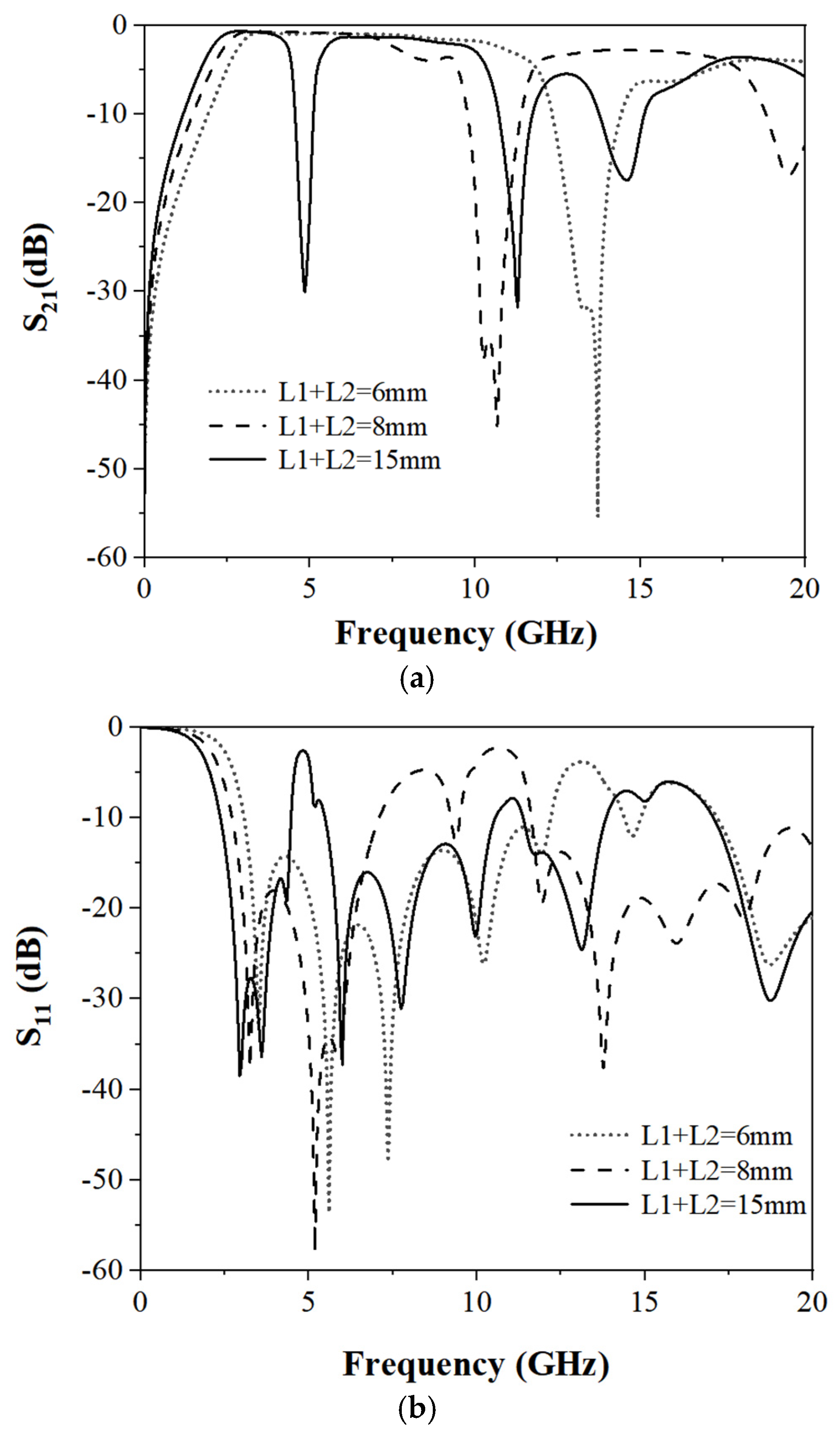
2.2. Parameter Analysis
2.3. UWB BPF with a Notched Band
3. Fabrication and Measurement
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hong, J.S. Microstrip Filters for RF/Microwave Applications, 2nd ed.; Wiley: New York, NY, USA, 2011. [Google Scholar]
- Revision of Part 15 of the Commission’s Rules Regarding Ultra-Wideband Transmission Systems; Federal Communication Commission: Washington, DC, USA, 2002.
- Chang, Y.-C.; Kao, C.-H.; Weng, M.-H.; Yang, R.-Y. Design of the Compact Wideband Bandpass Filter with Low Loss, High Selectivity and Wide Stopband. IEEE Microw. Wirel. Components Lett. 2008, 18, 770–772. [Google Scholar] [CrossRef]
- Yoon, K.; Kim, K. Design of Dual Ultra–Wideband Band–Pass Filter Using Stepped Impedance Resonator λg/4 Short Stubs and T–Shaped Band-Stop Filter. Electronics 2021, 10, 1951. [Google Scholar] [CrossRef]
- Fan, J.; Zhan, D.; Jin, C.; Luo, J. Wideband Microstrip Bandpass Filter Based on Quadruple Mode Ring Resonator. IEEE Microw. Wirel. Components Lett. 2012, 22, 348–350. [Google Scholar] [CrossRef]
- Yang, L.; Choi, W.W.; Tam, K.W.; Zhu, L. Novel wideband bandpass filter with dual notched bands using stub-loaded resonators. IEEE Microw. Wirel. Compon. Lett. 2017, 27, 25–27. [Google Scholar] [CrossRef]
- Feng, G.-X.; Wen, J.; Che, W.-Q. Compact Ultra-wideband bandpass filter with improved upper stopband using open/shorted stubs. IEEE Microw. Compon. Lett. 2017, 17, 123–125. [Google Scholar]
- Jankovi, N.; Niarchos, G.; Crnojević-Bengin, V. Compact UWB bandpass filter based on grounded square patch resonator. Electron. Lett. 2016, 52, 372–774. [Google Scholar] [CrossRef]
- Liu, J.; Ding, W.; Chen, J.; Zhang, A. New Ultra-Wideband Filter with Sharp Notched Band Using Defected Ground Structure. Prog. Electromagn. Res. Lett. 2019, 83, 99–105. [Google Scholar] [CrossRef] [Green Version]
- Ji, X.-C.; Ji, W.-S.; Feng, L.-Y.; Tong, Y.-Y.; Zhang, Z.-Y. Design of a Novel Multi-Layer Wideband Bandpass Filter with a Notched Band. Prog. Electromagn. Res. Lett. 2019, 82, 9–16. [Google Scholar] [CrossRef] [Green Version]
- Zhou, C.-X.; Guo, P.-P.; Zhou, K.; Wu, W. Design of a compact UWB filter with high selectivity and super wide stopband. IEEE Microw. Wirel. Compon. Lett. 2017, 27, 636–638. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, Y.-H.; Wan, X.; Jing, H.-S. Miniaturized dual-mode ultra-wideband filter using sector substrate integrated waveguide. Microw. Opt. Technol. Lett. 2021, 63, 2343–2347. [Google Scholar] [CrossRef]
- Jamshidi, M.-B.; Roshani, S.; Talla, J.; Roshani, S.; Peroutka, Z. Size reduction and performance improvement of a microstrip Wilkinson power divider using a hybrid design technique. Sci. Rep. 2021, 11, 7773. [Google Scholar] [CrossRef]
- Roshani, S.; Jamshidi, M.B.; Mohebi, F.; Roshani, S. Design and Modeling of a Compact Power Divider with Squared Resonators Using Artificial Intelligence. Wirel. Pers. Commun. 2021, 117, 2085–2096. [Google Scholar] [CrossRef]
- Pozar, D.-M. Microwave Engineering, 2nd ed.; Wiley: New York, NY, USA, 1998. [Google Scholar]
- Raman, S.; Soni, A. UWB bandpass filter with quarter wavelength short circuited stubs. Int. J. Sci. Eng. Res. 2013, 4, 1345–1348. [Google Scholar]
- Uikey, R.; Sangam, R.-S.; Prasadu, K.; Rakhesh, S.-K. Novel notched UWB filter using stepped impedance stub loaded microstrip resonator and spurlines. Int. J. Microw. Sci. Tech. 2015, 2015, 939521. [Google Scholar] [CrossRef]
- Parvez, S.; Sakib, N.; Mollah, M.-N. Chebyshev quarter wavelength wideband bandstop filter based on dumbbell annular ring resonator. In Proceedings of the IEEE International Conference on Electrical Computer and Communication Engineering (ECCE), Cox’s Bazar, Bangladesh, 16–18 February 2017; pp. 891–894. [Google Scholar]
- Sangam, R.-S.; Kshetrimayum, R.-S. Notched UWB filter using exponential tapered impedance line stub loaded microstrip resonator. J. Eng. 2018, 9, 768–772. [Google Scholar] [CrossRef]
- IE3D Simulator; Zeland Software. Available online: www.zeland.com (accessed on 10 September 2004).
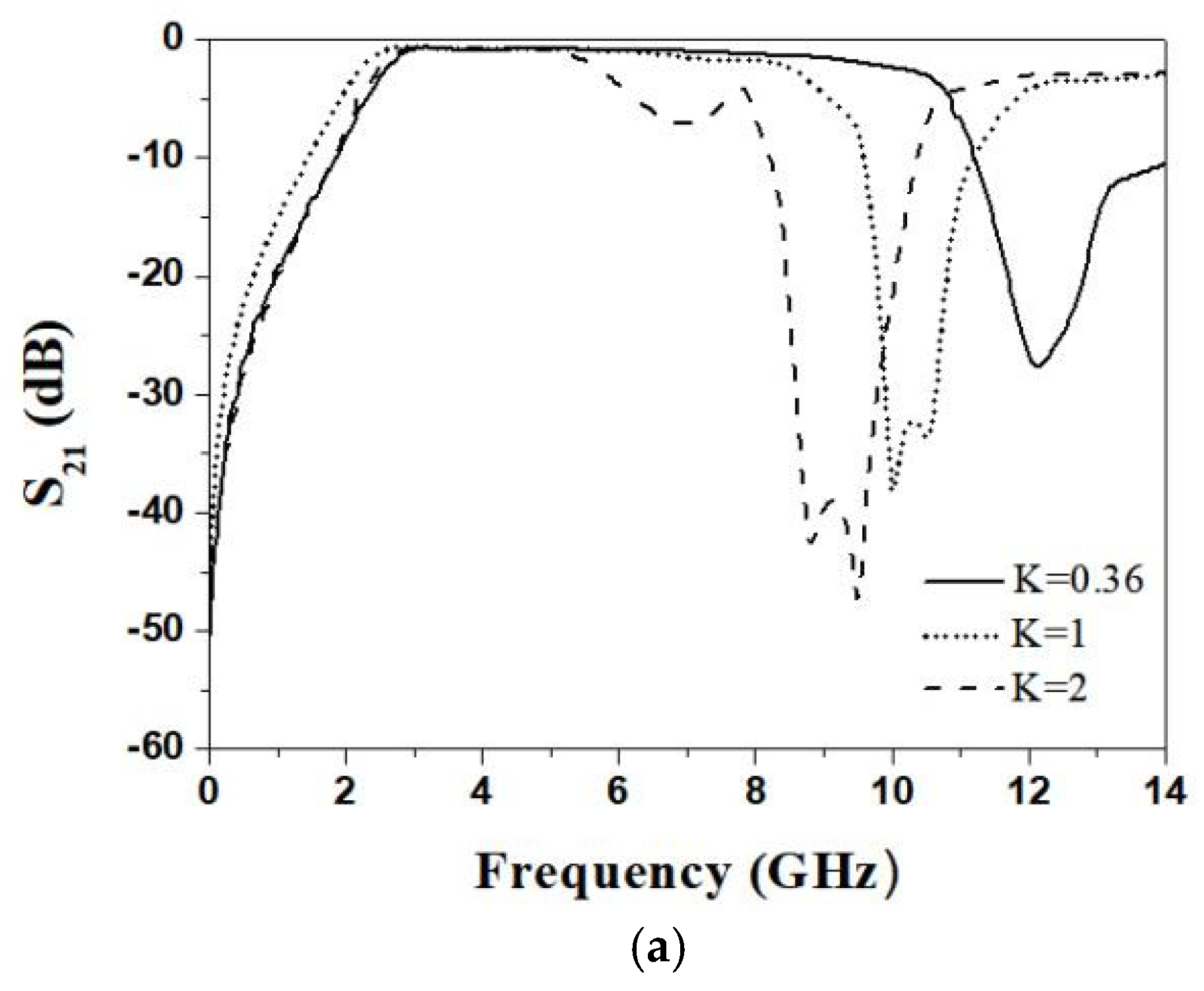
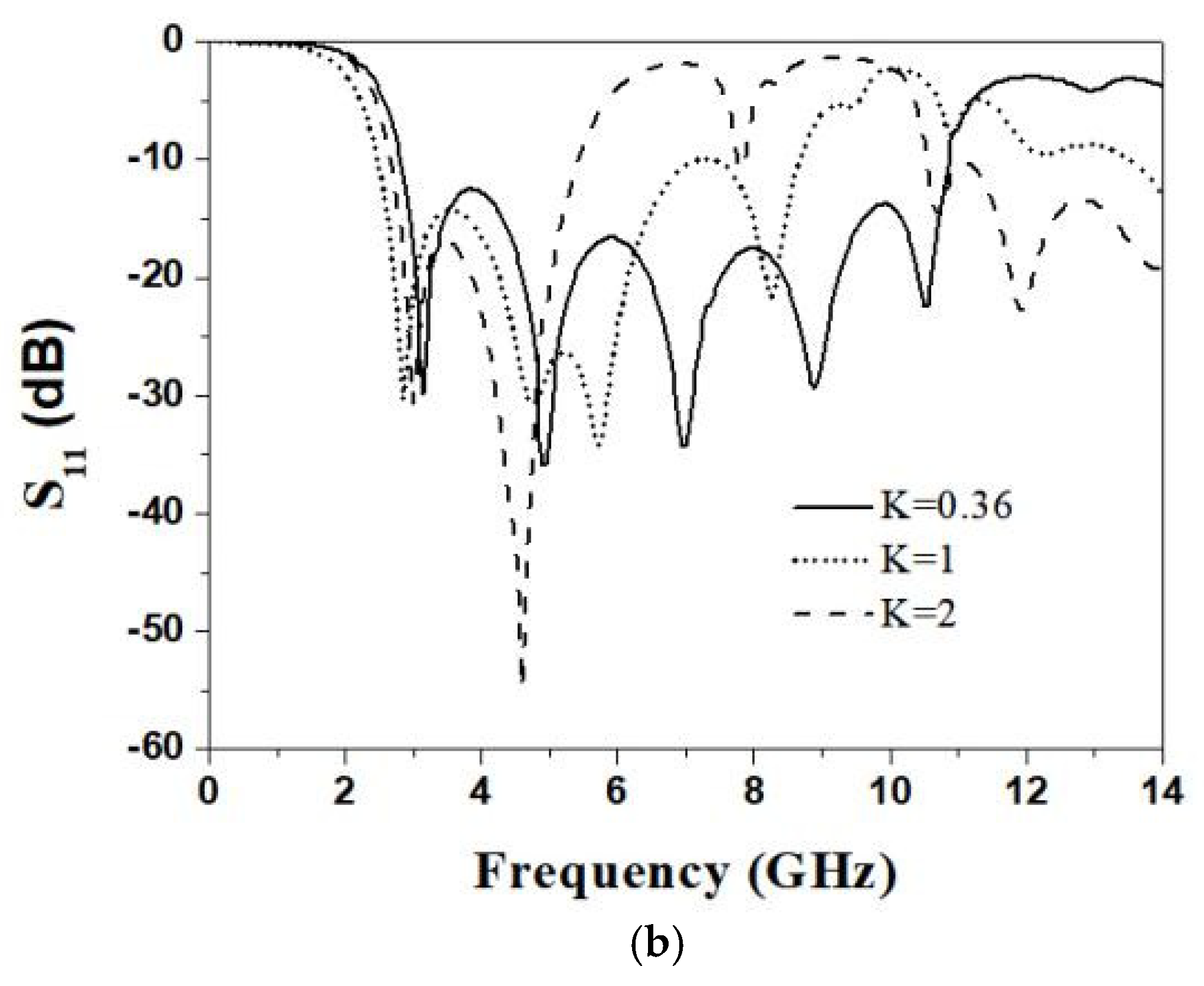
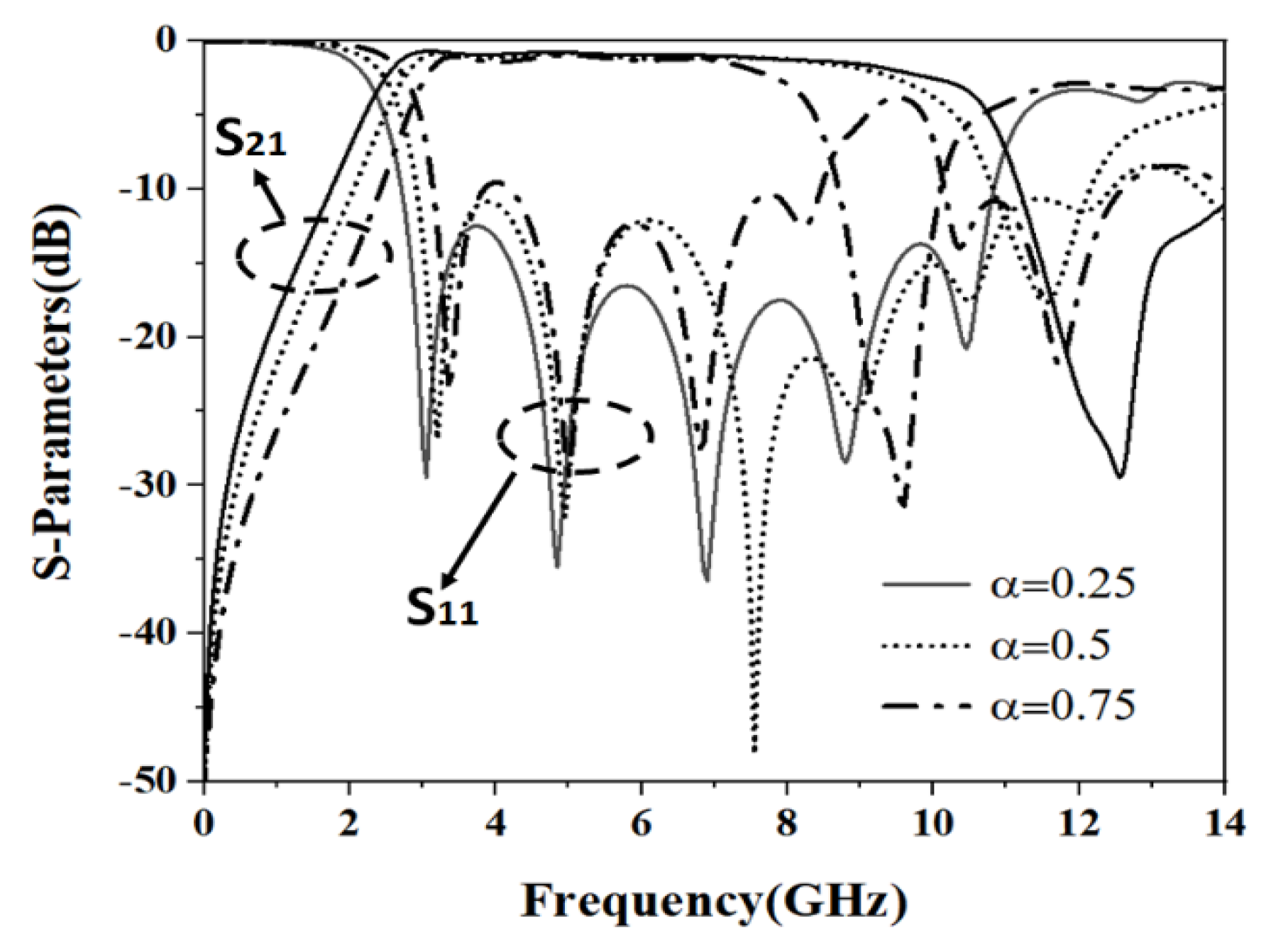
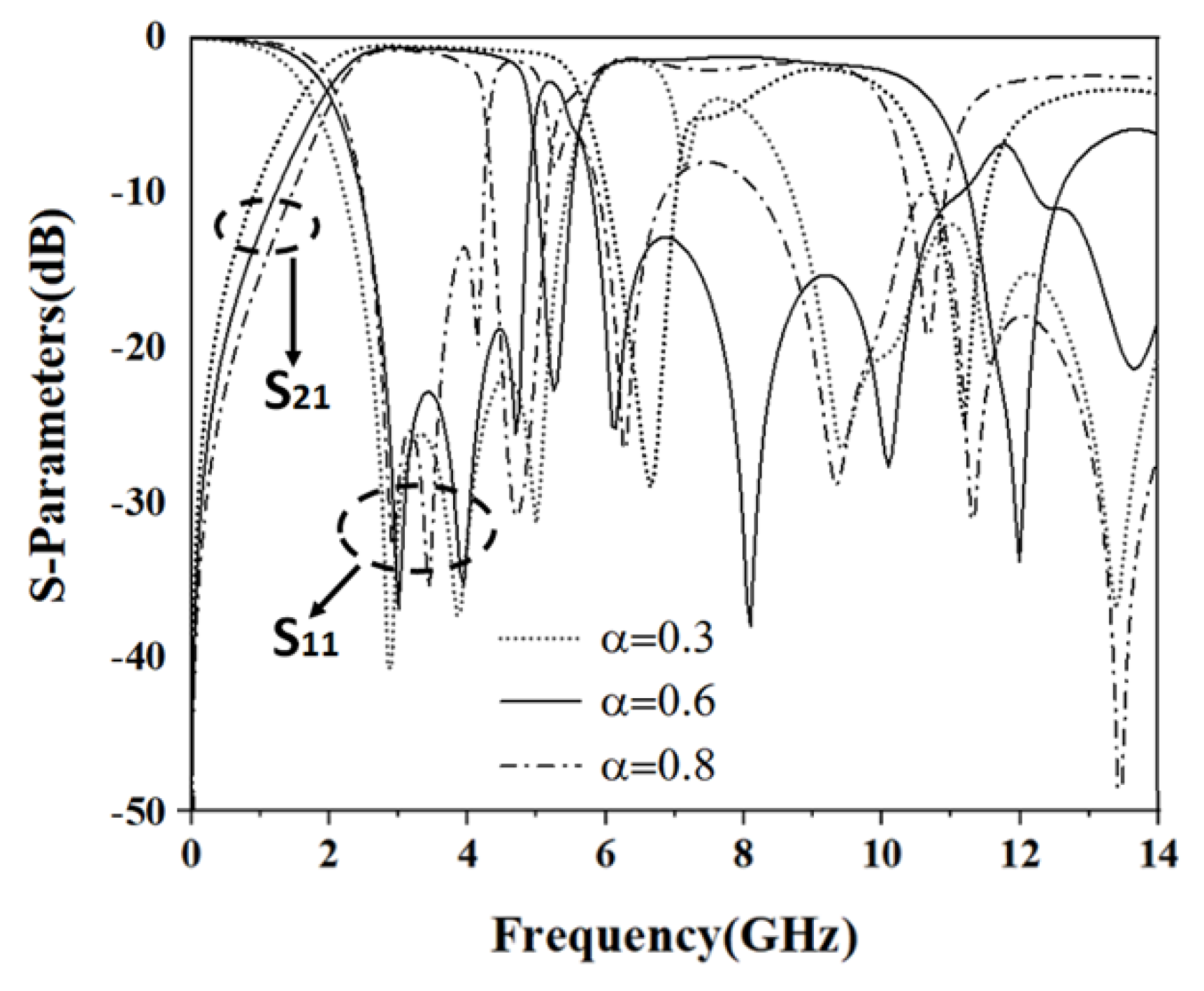


| Impedance Ratio K | Line Width of the High Impedance Line | Characteristic Impedance of the High Impedance Line | Line Width of the High Impedance Line | Characteristic Impedance of the High Impedance Line |
|---|---|---|---|---|
| 0.36 | w1 = 0.5 mm | 87 Ω | w2 = 3 mm | 32 Ω |
| 1 | w1 = 0.5 mm | 87 Ω | w2 = 0.5 mm | 87 Ω |
| 2 | w1 = 0.5 mm | 87 Ω | w2 = 0.04 mm | 174 Ω |
| Filter Performances | Ref. [15] | Ref. [16] | Ref. [17] | Ref. [18] | Ref. [19] | This Work |
|---|---|---|---|---|---|---|
| Stub type | open | short | open | open | short | short |
| Center frequency (GHz) | 4.0 | 7.23 | 7.25 | 2 | 6.85 | 6.65 |
| 3 dB FBW (%) | Low pass | 106 | 112 | 113 | 121 | 125 |
| Circuit Size (λg × λg) | - | 1.36 × 0.33 | - | 0.97 × 0.27 | - | 0.285 × 0.095 |
| Group delay (ns) | - | 0.26 | <0.7 | 0.45 | <0.35 | 0.3 |
| notch | No | No | Yes | No | Yes | Yes |
| Notch-band rejection level, dB | - | - | 39 | - | 32 | 45 |
| Notch band FBW, % | - | - | 15.6 | - | 9 | 5 |
| Notch frequency, GHz | - | - | 5.9 | - | ~5.5 | 5.1 |
| Extra structure | no | no | Defect ground | spurline | no | no |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, L.-Q.; Lai, H.-S.; Hu, H.-M.; Chen, J.-J.; Weng, M.-H.; Yang, R.-Y. A Simple Method to Design a UWB Filter with a Notched Band Using Short-Circuit Step Impedance Stubs. Electronics 2022, 11, 1124. https://doi.org/10.3390/electronics11071124
Liu L-Q, Lai H-S, Hu H-M, Chen J-J, Weng M-H, Yang R-Y. A Simple Method to Design a UWB Filter with a Notched Band Using Short-Circuit Step Impedance Stubs. Electronics. 2022; 11(7):1124. https://doi.org/10.3390/electronics11071124
Chicago/Turabian StyleLiu, Li-Qin, Huang-Sheng Lai, Hao-Ming Hu, Jun-Jie Chen, Min-Hang Weng, and Ru-Yuan Yang. 2022. "A Simple Method to Design a UWB Filter with a Notched Band Using Short-Circuit Step Impedance Stubs" Electronics 11, no. 7: 1124. https://doi.org/10.3390/electronics11071124
APA StyleLiu, L.-Q., Lai, H.-S., Hu, H.-M., Chen, J.-J., Weng, M.-H., & Yang, R.-Y. (2022). A Simple Method to Design a UWB Filter with a Notched Band Using Short-Circuit Step Impedance Stubs. Electronics, 11(7), 1124. https://doi.org/10.3390/electronics11071124







