Cooperative Automotive Radars with Multi-Aperture Multiplexing MIMO Sparse Array Design
Abstract
:1. Introduction
- Proposing a multi-aperture multiplexing MIMO sparse array for automotive radar, thus satisfying the multi-type detection demands simultaneous;
- Deriving the optimization model for the proposed sparse array design and adopting an improved genetic algorithm to achieve the optimized sparse array configuration.
2. Proposed Method
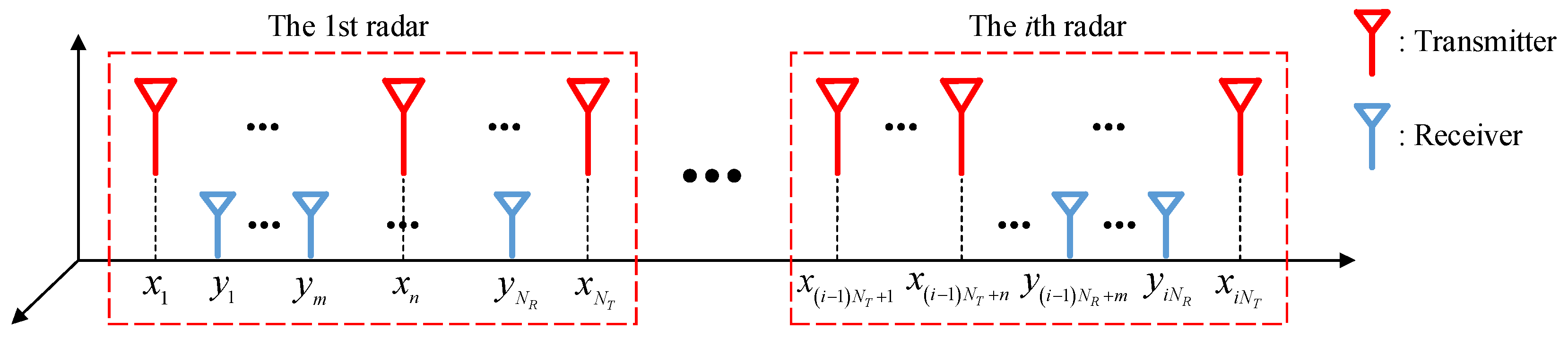
2.1. The MAM-MIMO Sparse Array for CARs
2.2. Sparse Array Optimization Model
2.2.1. Objective Functions
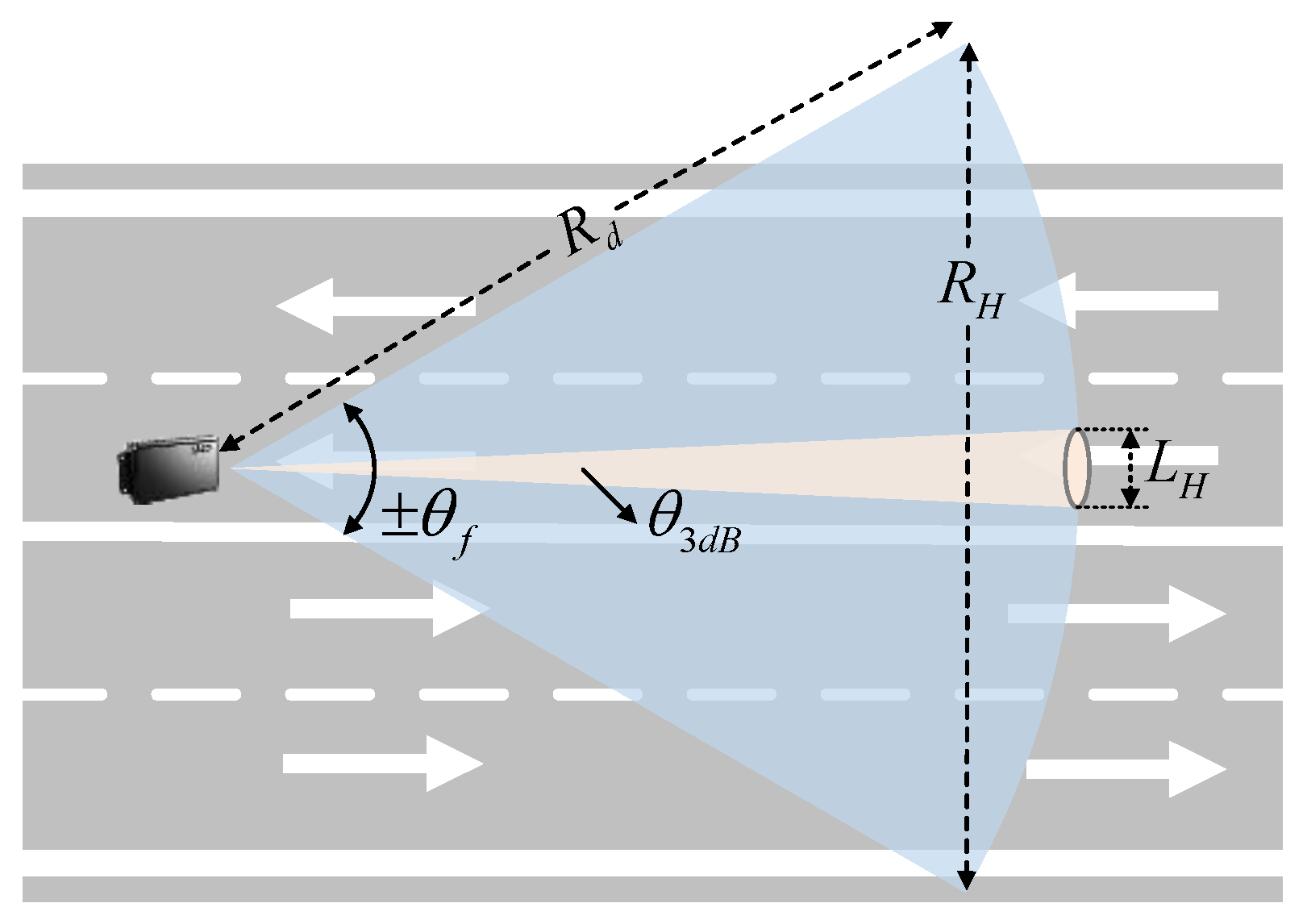
2.2.2. Constraints
- FOV (±θf);
- 2.
- Actual aperture (DA);
- 3.
- Virtual aperture (DV);
- 4.
- Physical limitations.
2.3. Optimization Algorithm
2.3.1. Processing Flow
- Initialization. Q subpopulations are generated as the upper genetic algorithm (GA) input, and each subpopulation with Z individuals is the lower GA input. Each individual consists of the array antenna spacing d, generated by binary coding rules.
- Evaluation at upper GA. The fitness of all individuals is calculated according to Equation (26), thus obtaining the average of each subpopulation as the evaluation metric at the upper GA.
- Selection, crossover, and mutation at upper GA. Multi-subpopulations are processed with selection, crossover, and mutation based on the evaluation metric calculated in step 2. Then the offspring subpopulations can be obtained.
- Evaluation at lower GA. Similar to step 2, the fitness of all individuals in each subpopulation is calculated as the evaluation metric at lower GA.
- Selection, crossover and mutation at lower GA. Similar to step 3, within the subpopulation, the operations of selection, crossover, and mutation are performed on the individuals.
- Termination at lower GA. If the individual fitness is stable for multiple iterations at the lower GA, the current multi-subpopulation can be output; otherwise, skip to step 4.
- Termination at upper GA. If the average fitness of the multi-subpopulation is stable for multiple iterations at the upper GA, the individual with the lowest fitness can be output as the optimized result; otherwise, output the multi-subpopulation and skip to step 3.
2.3.2. Computational Complexity Analysis
2.4. Sparse Array Assessment
3. Numerical Simulations
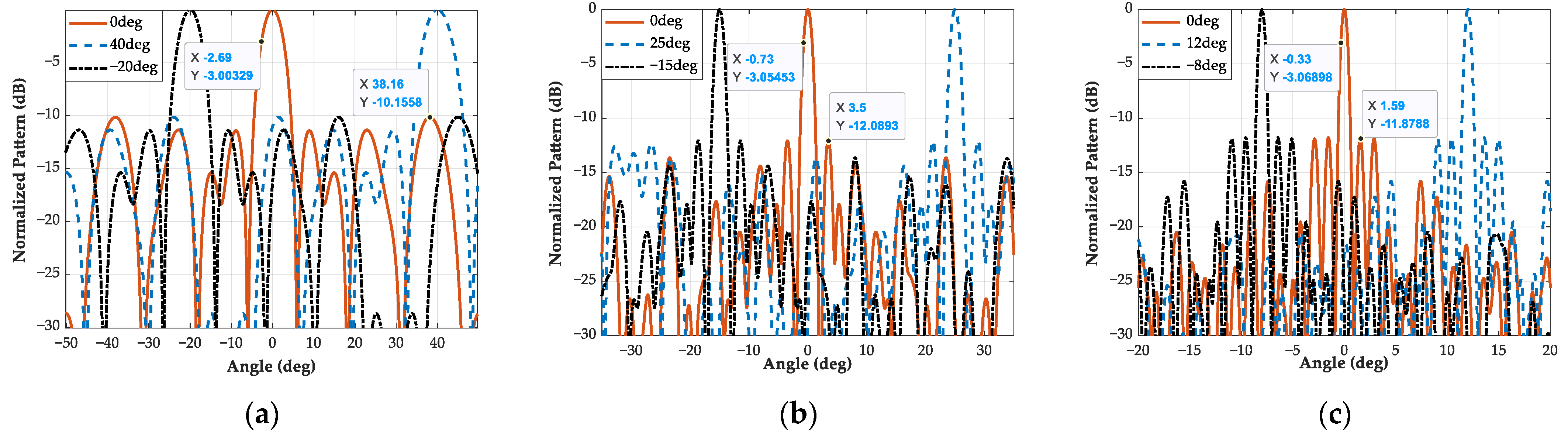
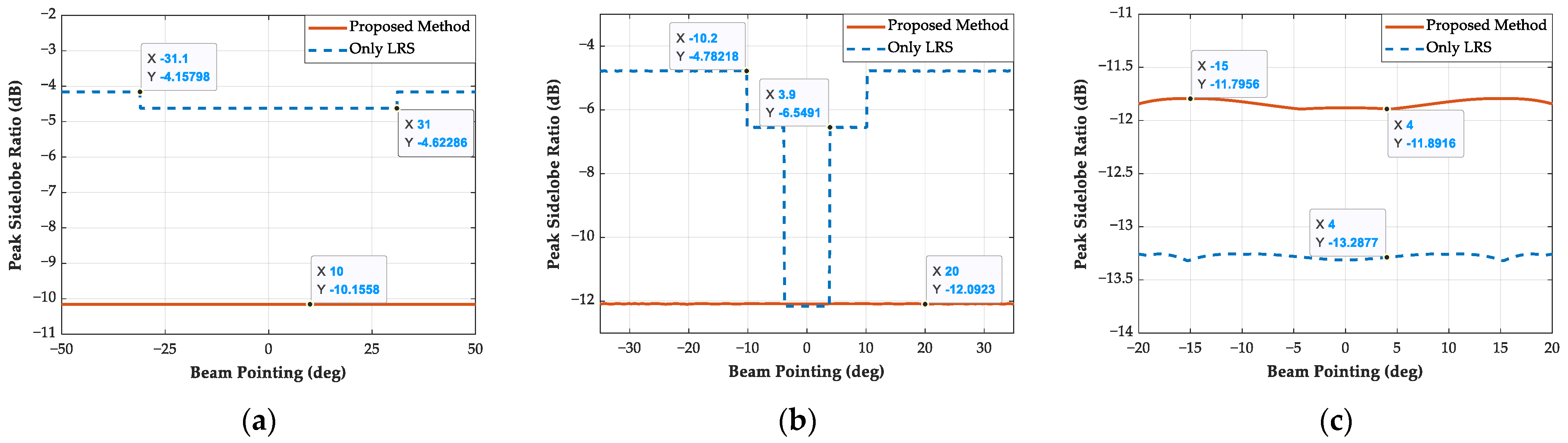
3.1. Optimized Sparse Array and Sidelobe Suppression
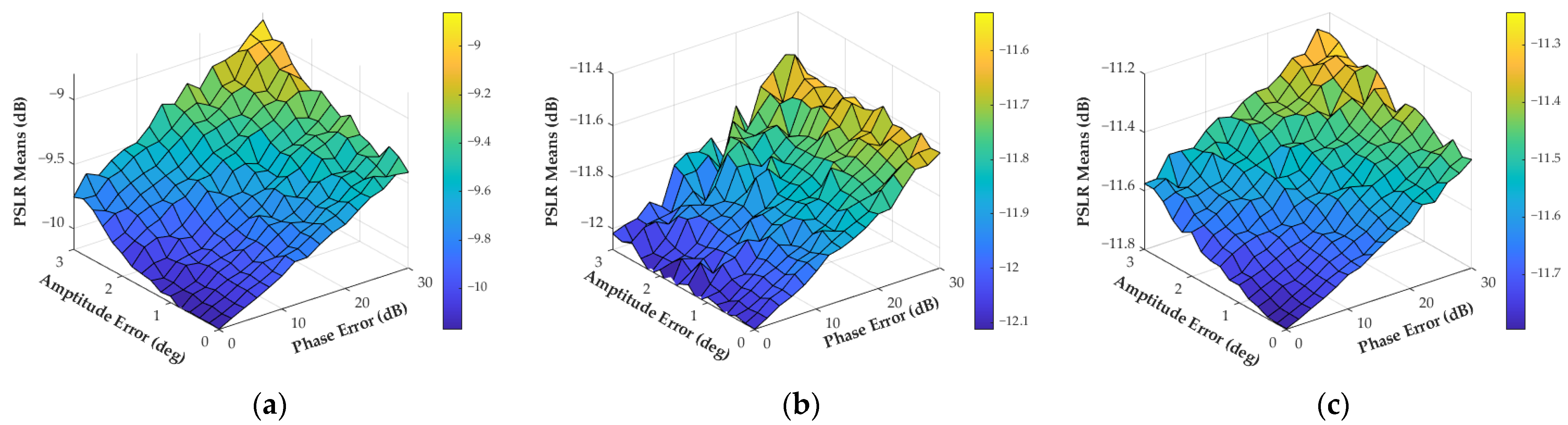
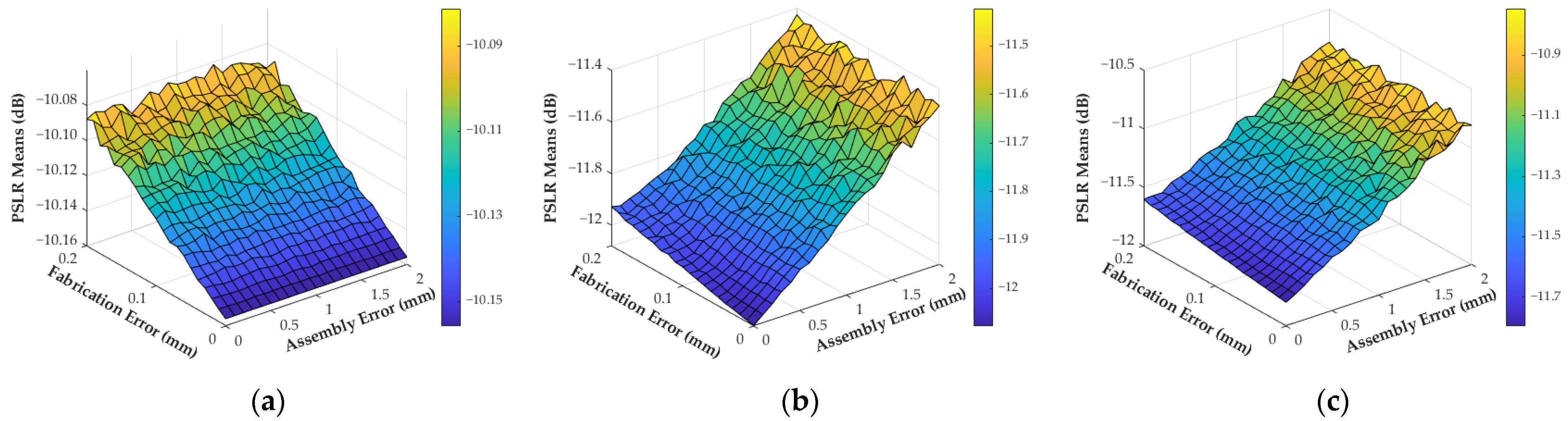
3.2. Imperfect Factors Adaptation Analysis
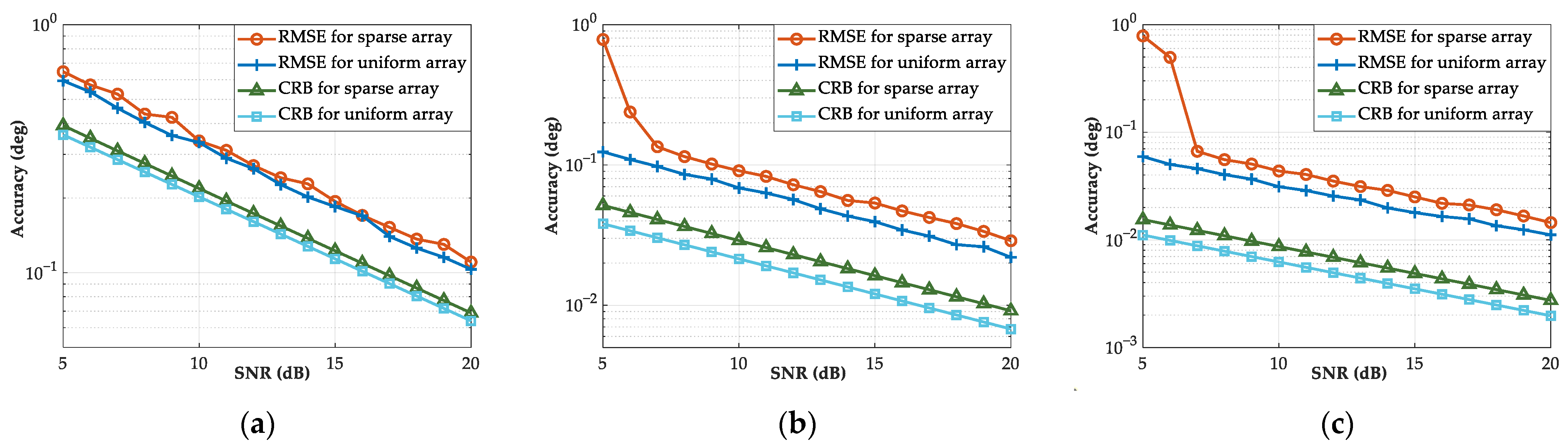
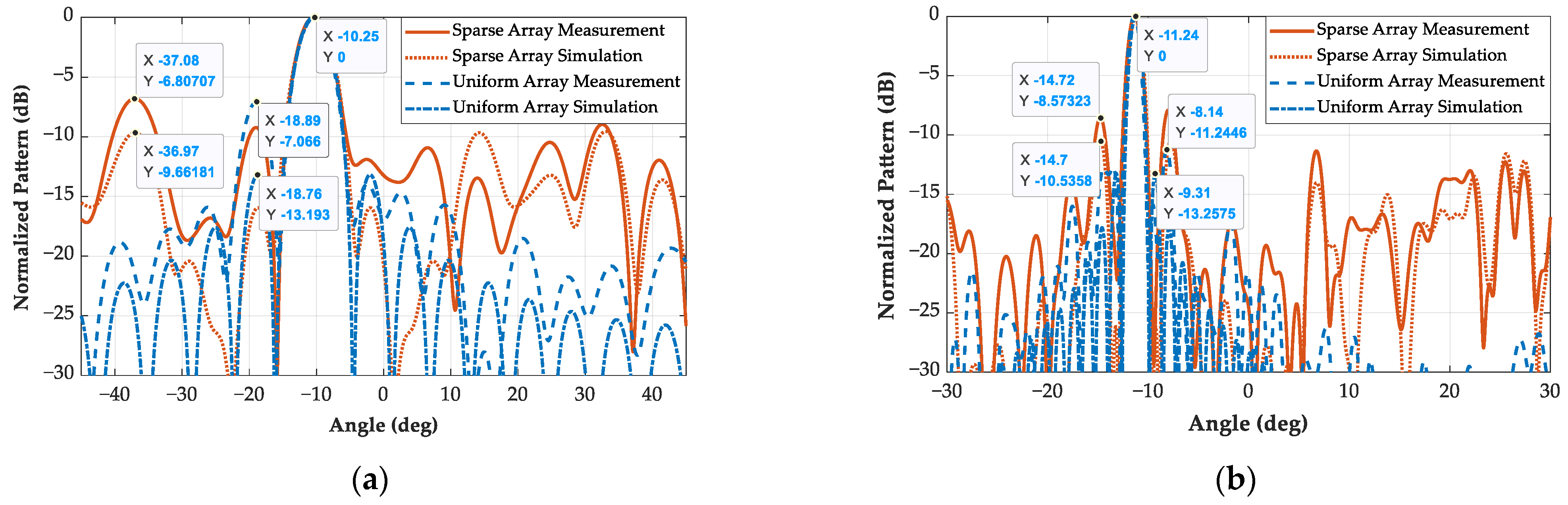
3.3. Angular Measurement Accuracy
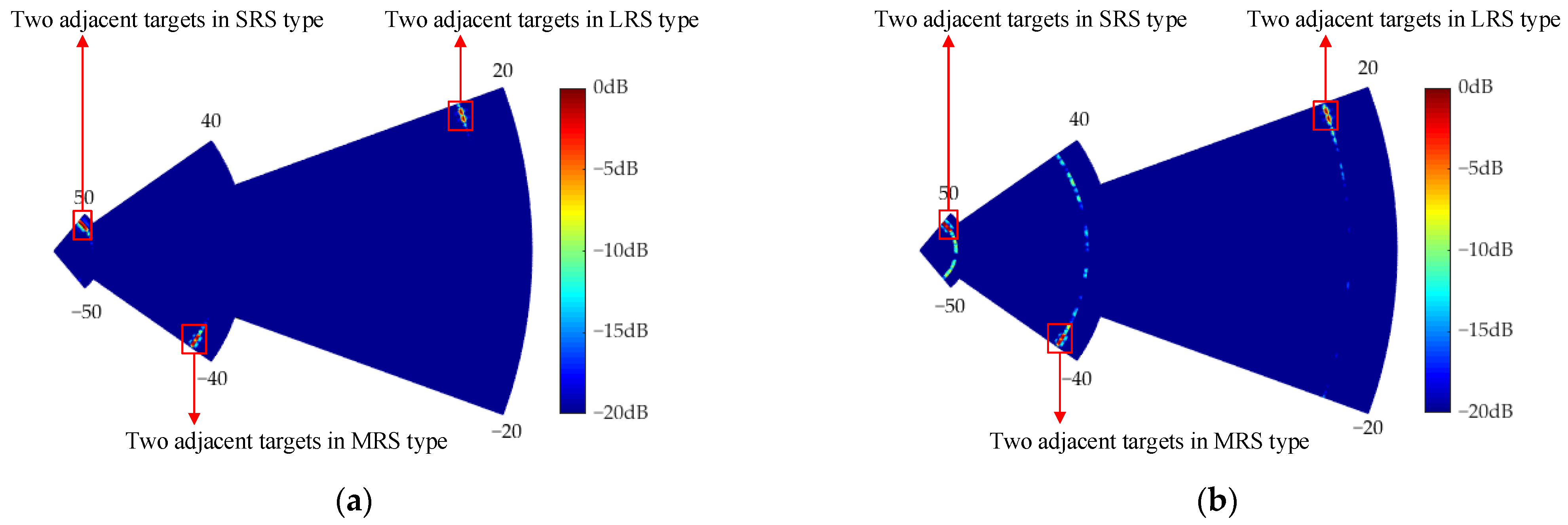
3.4. Detection Performance
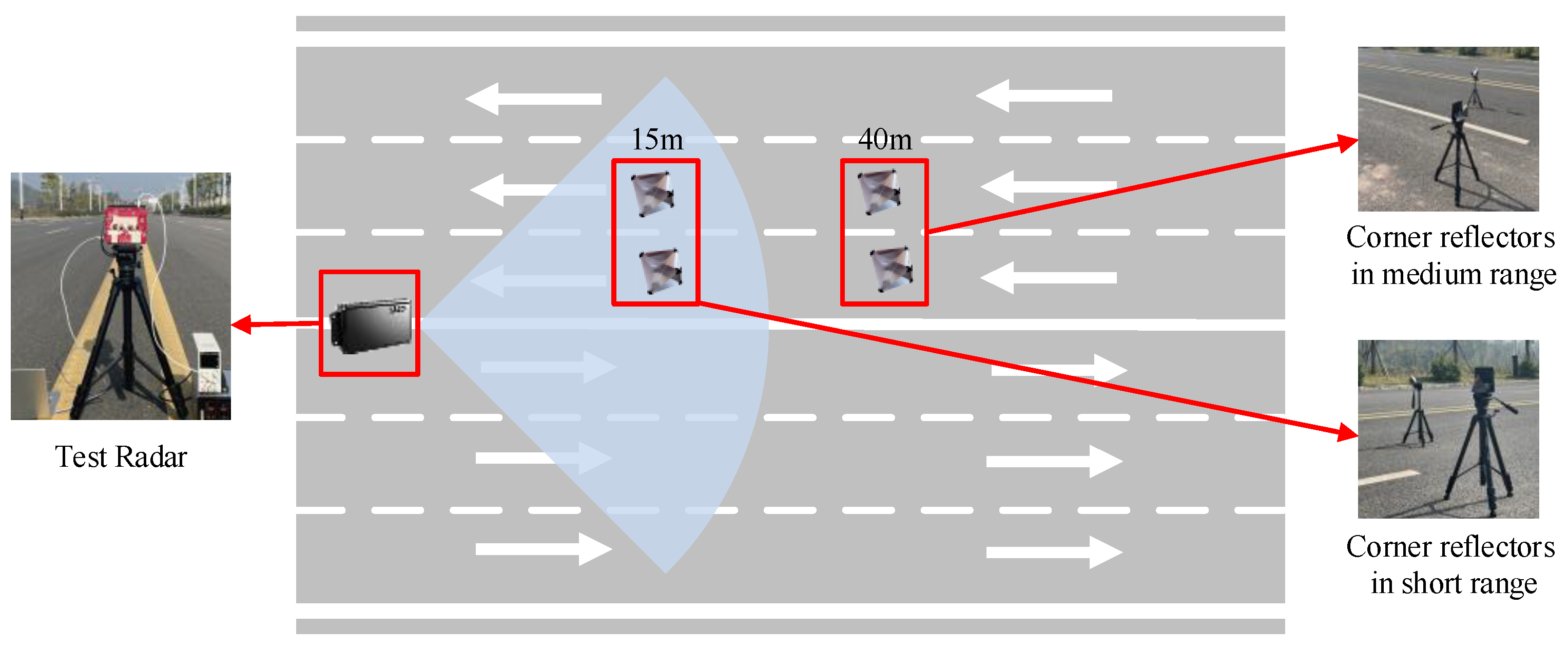
4. Real-Data Results
4.1. Simplified Optimized Sparse Array and Sidelobe Suppression
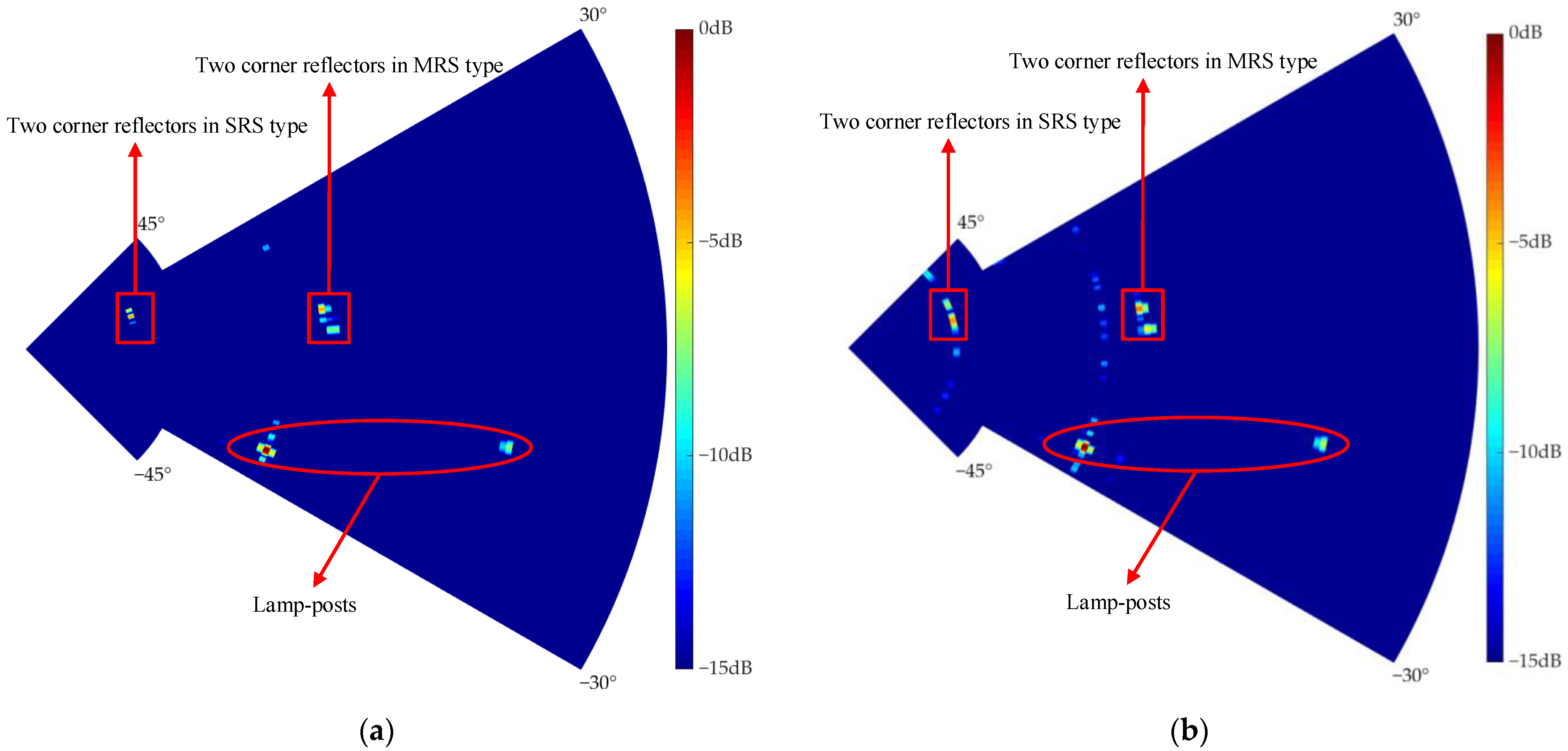
4.2. Detection Performance
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fleming, B. Recent Advancement in Automotive Radar Systems [Automotive Electronics]. IEEE Veh. Technol. Mag. 2012, 7, 4–9. [Google Scholar] [CrossRef]
- Harter, M.; Hildebrandt, J.; Ziroff, A.; Zwick, T. Self-Calibration of a 3-D-Digital Beamforming Radar System for Automotive Applications with Installation Behind Automotive Covers. IEEE Trans. Microw. Theory Tech. 2016, 64, 2994–3000. [Google Scholar] [CrossRef]
- Patole, S.M.; Torlak, M.; Wang, D.; Ali, M. Automotive radars: A review of signal processing techniques. IEEE Signal Process. Mag. 2017, 34, 22–35. [Google Scholar] [CrossRef]
- Engels, F.; Heidenreich, P.; Zoubir, A.M.; Jondral, F.K.; Wintermantel, M. Advances in Automotive Radar: A framework on computationally efficient high-resolution frequency estimation. IEEE Signal Process. Mag. 2017, 34, 36–46. [Google Scholar] [CrossRef]
- Hu, X.; Lu, M.; Li, Y.; Wang, Y. Motion Compensation for TDM MIMO Radar by Sparse Reconstruction. Electron. Lett. 2017, 53, 1604–1606. [Google Scholar] [CrossRef]
- Kim, G.; Mun, J.; Lee, J. A Peer-to-Peer Interference Analysis for Automotive Chirp Sequence Radars. IEEE Trans. Veh. Technol. 2018, 67, 8110–8117. [Google Scholar] [CrossRef]
- Roos, F.; Bechter, J.; Knill, C.; Schweizer, B.; Waldschmidt, C. Radar Sensors for Autonomous Driving: Modulation Schemes and Interference Mitigation. IEEE Microw. Mag. 2019, 20, 58–72. [Google Scholar] [CrossRef] [Green Version]
- Hu, X.; Li, Y.; Lu, M.; Wang, Y.; Yang, X. A Multi-Carrier-Frequency Random-Transmission Chirp Sequence for TDM MIMO Automotive Radar. IEEE Trans. Veh. Technol. 2019, 68, 3672–3685. [Google Scholar] [CrossRef]
- Uysal, F. Phase-Coded FMCW Automotive Radar: System Design and Interference Mitigation. IEEE Trans. Veh. Technol. 2020, 69, 270–281. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Jiang, W.; Huo, K.; Liu, Y.; Li, X. Robust Adaptive Beamforming Based on Linearly Modified Atomic-Norm Minimization with Target Contaminated Data. IEEE Trans. Signal Process. 2020, 68, 5138–5151. [Google Scholar] [CrossRef]
- Wang, J. CFAR-Based Interference Mitigation for FMCW Automotive Radar Systems. IEEE Trans. Intell. Transp. Syst. 2021. [Google Scholar] [CrossRef]
- Ciattaglia, G.; Santis, A.D.; Disha, D.; Spinsante, S.; Castellini, P.; Gambi, E. Performance Evaluation of Vibrational Measurements through mmWave Automotive Radars. Remote Sens. 2021, 13, 98. [Google Scholar] [CrossRef]
- Hasch, J.; Topak, E.; Schnabel, R.; Zwick, T.; Weigel, R.; Waldschmidt, C. Millimeter-Wave Technology for Automotive Radar Sensors in the 77 GHz Frequency Band. IEEE Trans. Microw. Theory Tech. 2012, 60, 845–860. [Google Scholar] [CrossRef]
- Schneider, M. Automotive Radar—Status and Trends. In Proceeding of the 2005 German Microwave Conference (GeMiC 2005), Ulm, Germany, 5–7 April 2005. [Google Scholar]
- Xu, J.; Hong, W.; Zhang, H.; Wang, G.; Yu, Y.; Jiang, Z.H. An Array Antenna for Both Long- and Medium-Range 77 GHz Automotive Radar Applications. IEEE Trans. Antennas Propag. 2017, 65, 7207–7216. [Google Scholar] [CrossRef]
- Yu, Y.; Hong, W.; Zhang, H.; Xu, J.; Jiang, Z.H. Optimization and Implementation of SIW Slot Array for Both Medium- and Long-Range 77 GHz Automotive Radar Application. IEEE Trans. Antennas Propag. 2018, 66, 3769–3774. [Google Scholar] [CrossRef]
- Guo, Z.J.; Hao, Z.C. A Compact Wideband Millimeter-Wave Substrate-Integrated Double-Line Slot Array Antenna. IEEE Trans. Antennas Propag. 2020, 69, 882–891. [Google Scholar] [CrossRef]
- Design Guide: TIDEP-01012 Imaging Radar Using Cascaded Mmwave Sensor Reference Design. Available online: https://www.ti.com/lit/ug/tiduen5a/tiduen5a.pdf (accessed on 16 April 2020).
- Abdullah, H.; Mabrouk, M.; Kabeel, A.E.; Hussein, A. High-Resolution and Large-Detection-Range Virtual Antenna Array for Automotive Radar Applications. Sensors 2021, 21, 1702. [Google Scholar] [CrossRef]
- Lee, S.; Kim, S.C. Logarithmic-Domain Array Interpolation for Improved Direction of Arrival Estimation in Automotive Radars. Sensors 2019, 19, 2410. [Google Scholar] [CrossRef] [Green Version]
- Yoo, S.; Milyakh, Y.; Kim, H.; Hong, C.; Choo, H. Patch Array Antenna Using a Dual Coupled Feeding Structure for 79 GHz Automotive Radar Applications. IEEE Antennas Wirel. Propag. Lett. 2020, 19, 676–679. [Google Scholar] [CrossRef]
- Sun, S.; Petropulu, A.P.; Poor, H.V. MIMO Radar for Advanced Driver-Assistance Systems and Autonomous Driving: Advantages and Challenges. IEEE Signal Process. Mag. 2020, 37, 98–117. [Google Scholar] [CrossRef]
- Sun, S.; Zhang, Y.D. 4D Automotive Radar Sensing for Autonomous Vehicles: A Sparsity-Oriented Approach. IEEE J. Sel. Top. Signal Process. 2021, 15, 879–891. [Google Scholar] [CrossRef]
- Yang, X.; Li, Y.; Liu, F.; Lan, T.; Long, T.; Sarkar, T.K. Antenna Position Optimization Method Based on Adaptive Genetic Algorithm with Self-Supervised Differential Operator for Distributed Coherent Aperture Radar. IET Radar Sonar Nav. 2021, 15, 677–685. [Google Scholar] [CrossRef]
- Dong, J.; Li, Q.; Guo, W. A Combinatorial Method for Antenna Array Design in Minimum Redundancy MIMO Radars. IEEE Antennas Wireless Propag. Lett. 2009, 8, 1150–1153. [Google Scholar] [CrossRef]
- Lange, O.; Yang, B. Antenna Geometry Optimization for 2D Direction-of-Arrival Estimation for Radar Imaging. In Proceedings of the International ITG Workshop on Smart Antennas, Aachen, Germany, 24–25 February 2011. [Google Scholar]
- Tan, K.; Wu, S.; Wang, Y.; Ye, S.; Chen, J.; Liu, X.; Fang, G.; Yan, S. On Sparse MIMO Planar Array Topology Optimization for UWB Near-Field High-Resolution Imaging. IEEE Trans. Antennas Propag. 2017, 65, 989–994. [Google Scholar] [CrossRef]
- Ma, Y.; Miao, C.; Zhao, Y.; Wu, W. An MIMO Radar System Based on the Sparse-Array and Its Frequency Migration Calibration Method. Sensors 2019, 19, 3580. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, J.; Aubry, P.; Yarovoy, A. 3-D Short-Range Imaging with Irregular MIMO Arrays Using NUFFT-Based Range Migration Algorithm. IEEE Trans. Geosci. Remote Sens. 2020, 58, 4730–4742. [Google Scholar] [CrossRef]
- Serio, A.D.; Hügler, P.; Roos, F.; Waldschmidt, C. 2-D MIMO Radar: A Method for Array Performance Assessment and Design of a Planar Antenna Array. IEEE Trans. Antennas Propag. 2020, 68, 4604–4616. [Google Scholar] [CrossRef]
- Bialer, O.; Jonas, A.; Tirer, T. Super Resolution Wide Aperture Automotive Radar. IEEE Sens. J. 2021, 21, 17846–17858. [Google Scholar] [CrossRef]
- Feger, R.; Pfeffer, C.; Scheiblhofer, W.; Schmid, C.M.; Lang, M.J.; Stelzer, A. A 77-GHz Cooperative Radar System Based on Multi-Channel FMCW Stations for Local Positioning Applications. IEEE Trans. Microw. Theory Tech. 2013, 61, 676–684. [Google Scholar] [CrossRef]
- Frischen, A.; Hasch, J.; Waldschmidt, C. A Cooperative MIMO Radar Network Using Highly Integrated FMCW Radar Sensors. IEEE Trans. Microw. Theory Tech. 2017, 65, 1355–1366. [Google Scholar] [CrossRef]
- Edstaller, S.; Mueller, D. A Cooperative Radar System with Active Reference Target Synchronization for Kinematic Target Analysis. IEEE Trans. Microw. Theory Tech. 2021, 69, 4118–4131. [Google Scholar] [CrossRef]
- Zhang, Y.; Bao, Z. Study of Optimum Thinning Arrays by Nonuniform Spacings. Electron. J. 1989, 17, 81–87. [Google Scholar]
- Kurup, D.G.; Himdi, M.; Rydberg, A. Synthesis of uniform amplitude unequally spaced antenna arrays using the differential evolution algorithm. IEEE Trans. Antennas Propag. 2003, 51, 2210–2217. [Google Scholar] [CrossRef]
- Deb, K.; Jain, H. An Evolutionary Many-Objective Optimization Algorithm Using Reference-Point-Based Nondominated Sorting Approach, Part I: Solving Problems with Box Constraints. IEEE Trans. Evol. Comput. 2014, 18, 577–601. [Google Scholar] [CrossRef]
- Jain, H.; Deb, K. An Evolutionary Many-Objective Optimization Algorithm Using Reference-Point Based Nondominated Sorting Approach, Part II: Handling Constraints and Extending to an Adaptive Approach. IEEE Trans. Evol. Comput. 2014, 18, 602–622. [Google Scholar] [CrossRef]
- Bray, M.G.; Werner, D.H.; Boeringer, D.W.; Machuga, D.W. Optimization of thinned aperiodic linear phased arrays using genetic algorithms to reduce grating lobes during scanning. IEEE Trans. Antennas Propag. 2002, 50, 1732–1742. [Google Scholar] [CrossRef]
- Chen, K.; Yun, X.; He, Z.; Han, C. Synthesis of Sparse Planar Arrays Using Modified Real Genetic Algorithm. IEEE Trans. Antennas Propag. 2007, 55, 1067–1073. [Google Scholar] [CrossRef]
- Cen, L.; Yu, Z.L.; Ser, W.; Cen, W. Linear Aperiodic Array Synthesis Using an Improved Genetic Algorithm. IEEE Trans. Antennas Propag. 2012, 60, 895–902. [Google Scholar] [CrossRef]
- Cheng, Y.F.; Shao, W.; Zhang, S.J.; Li, Y.P. An Improved Multi-Objective Genetic Algorithm for Large Planar Array Thinning. IEEE Trans. Magn. 2016, 52, 511–523. [Google Scholar] [CrossRef]
- Lin, Z.; Wen, F.; Wang, H.; Lin, G.; Mo, T.; Ye, X. CRITIC-Based Node Importance Evaluation in Skeleton-Network Reconfiguration of Power Grids. IEEE Trans. Circuits-II 2018, 65, 206–210. [Google Scholar] [CrossRef]
- Yu, S.; Liu, H.; Bai, L.; Han, F. Study on the Suitability of Passive Energy in Public Institutions in China. Energies 2019, 12, 2446. [Google Scholar] [CrossRef] [Green Version]
- Stoica, P.; Nehorai, A. Performance Study of Conditional and Unconditional Direction-of-Arrival Estimation. IEEE Trans. Acoust. Speech Signal Process. 1990, 38, 1783–1795. [Google Scholar] [CrossRef]
- Hu, X.; Tong, N.; Wang, J.; Ding, S.; Zhao, X. Matrix Completion-Based MIMO Radar Imaging with Sparse Planar Array. Signal Process. 2017, 131, 49–57. [Google Scholar] [CrossRef]
- Hu, X.; Zhang, L.; Long, J.; Liang, C.; Liu, J.; Wang, Y. High-Resolution Velocity-Azimuth Joint Estimation for Random-Time-Division-Multiplexing Multiple-Input-Multiple-Output Automotive Radar Using Matrix Completion. IET Radar Sonar Nav. 2021, 15, 1281–1296. [Google Scholar] [CrossRef]
- Lee, S.; Jung, Y.; Lee, M.; Lee, W. Compressive Sensing-Based SAR Image Reconstruction from Sparse Radar Sensor Data Acquisition in Automotive FMCW Radar System. Sensors 2021, 21, 7283. [Google Scholar] [CrossRef] [PubMed]
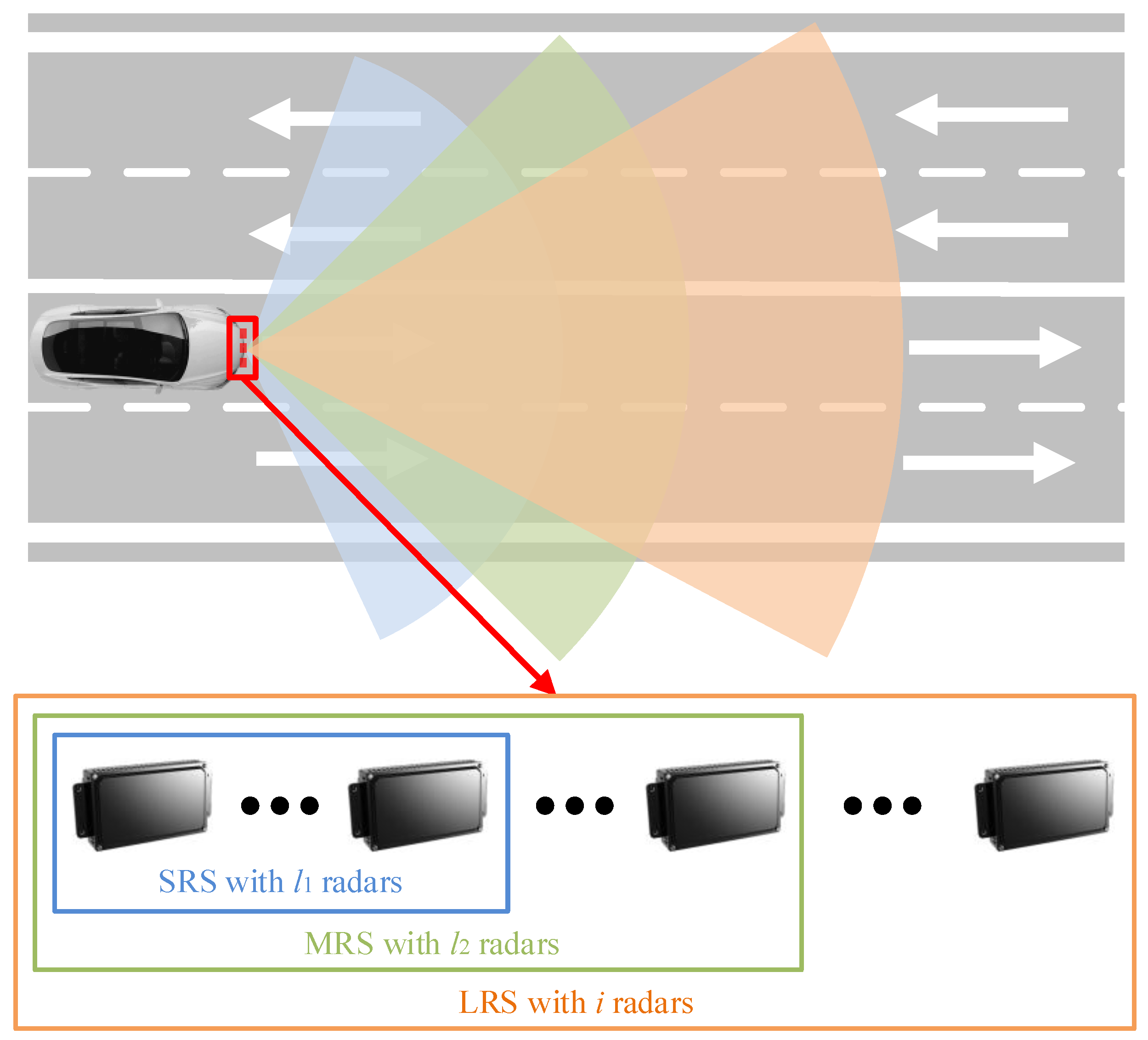




| Type | LRR | MRR | SRR |
|---|---|---|---|
| Detection range | 10–200 m | 1–100 m | 0.2–30 m |
| Azimuth beam width | 1.5° | 3° | 6° |
| Field-of-view | ±15° | ±30° | ±60° |
| Type | LRS | MRS | SRS | |
|---|---|---|---|---|
| Demands | Detection range | 0.2–20 m | 20–80 m | 80–200 m |
| Cross-range coverage | ±15 m (8 lanes) | |||
| Cross-range resolution | 2 m | |||
| Constraints | Beam width | ≤7° | ≤1.5° | ≤0.8° |
| Field-of-view | superior to ±45° | superior to ±30° | superior to ±15° | |
| Actual Aperture | ≤7λ | ≤30λ | ≤60λ | |
| Virtual Aperture | ≥8λ | ≥40λ | ≥80λ | |
| Subpopulation | 1 | 2 | 3 | 4 | 5 | 6 | Upper |
|---|---|---|---|---|---|---|---|
| individual number | 50 | 50 | 50 | 50 | 50 | 50 | 6 |
| crossover probability | 0.7 | 0.7 | 0.6 | 0.6 | 0.5 | 0.5 | 0.5 |
| mutation probability | 0.05 | 0.01 | 0.05 | 0.01 | 0.05 | 0.01 | 0.02 |
| crossover points number | 1 | 1 | 2 | 2 | 3 | 3 | 3 |
| mutation points number | 1 | 3 | 1 | 3 | 1 | 3 | 2 |
| xT,I and yR,I in λ | |||||||
|---|---|---|---|---|---|---|---|
| xT,1 | 0 | yR,1 | 0.6 | yR,7 | 13.4 | yR,13 | 38.6 |
| xT,2 | 4.8 | yR,2 | 1.2 | yR,8 | 14.4 | yR,14 | 39.6 |
| xT,3 | 12.4 | yR,3 | 2.4 | yR,9 | 15.4 | yR,15 | 40.3 |
| xT,4 | 19.7 | yR,4 | 3.0 | yR,10 | 16.6 | yR,16 | 41.3 |
| xT,5 | 37.9 | yR,5 | 3.6 | yR,11 | 17.8 | yR,17 | 42.3 |
| xT,6 | 43.7 | yR,6 | 4.2 | yR,12 | 18.8 | yR,18 | 43.2 |
| Target | Range | Azimuth | Velocity |
|---|---|---|---|
| 1 | 16 m | 45° | 0 m/s |
| 2 | 16 m | 39° | 0 m/s |
| 3 | 70 m | −33° | 5 m/s |
| 4 | 70 m | −31.5° | 5 m/s |
| 5 | 180 m | 18° | −10 m/s |
| 6 | 180 m | 18.8° | −10 m/s |
| xT,I and yR,I in λ | |||||||
|---|---|---|---|---|---|---|---|
| xT,1 | 4.5 | xT,4 | 16.5 | yR,1 | 0 | yR,5 | 16.5 |
| xT,2 | 6.0 | xT,5 | 18.5 | yR,2 | 3.0 | yR,6 | 19.5 |
| xT,3 | 7.0 | xT,6 | 20.0 | yR,3 | 5.0 | yR,7 | 22.5 |
| yR,4 | 7.0 | yR,8 | 25.5 | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, C.; Wang, Y.; Yang, Z.; Hu, X.; Pei, Q.; Gu, W.; Zhang, L. Cooperative Automotive Radars with Multi-Aperture Multiplexing MIMO Sparse Array Design. Electronics 2022, 11, 1198. https://doi.org/10.3390/electronics11081198
Liang C, Wang Y, Yang Z, Hu X, Pei Q, Gu W, Zhang L. Cooperative Automotive Radars with Multi-Aperture Multiplexing MIMO Sparse Array Design. Electronics. 2022; 11(8):1198. https://doi.org/10.3390/electronics11081198
Chicago/Turabian StyleLiang, Can, Yanhua Wang, Zhuxi Yang, Xueyao Hu, Qiubo Pei, Wei Gu, and Liang Zhang. 2022. "Cooperative Automotive Radars with Multi-Aperture Multiplexing MIMO Sparse Array Design" Electronics 11, no. 8: 1198. https://doi.org/10.3390/electronics11081198
APA StyleLiang, C., Wang, Y., Yang, Z., Hu, X., Pei, Q., Gu, W., & Zhang, L. (2022). Cooperative Automotive Radars with Multi-Aperture Multiplexing MIMO Sparse Array Design. Electronics, 11(8), 1198. https://doi.org/10.3390/electronics11081198






