Reinforcement-Learning-Based Decision and Control for Autonomous Vehicle at Two-Way Single-Lane Unsignalized Intersection
Abstract
:1. Introduction
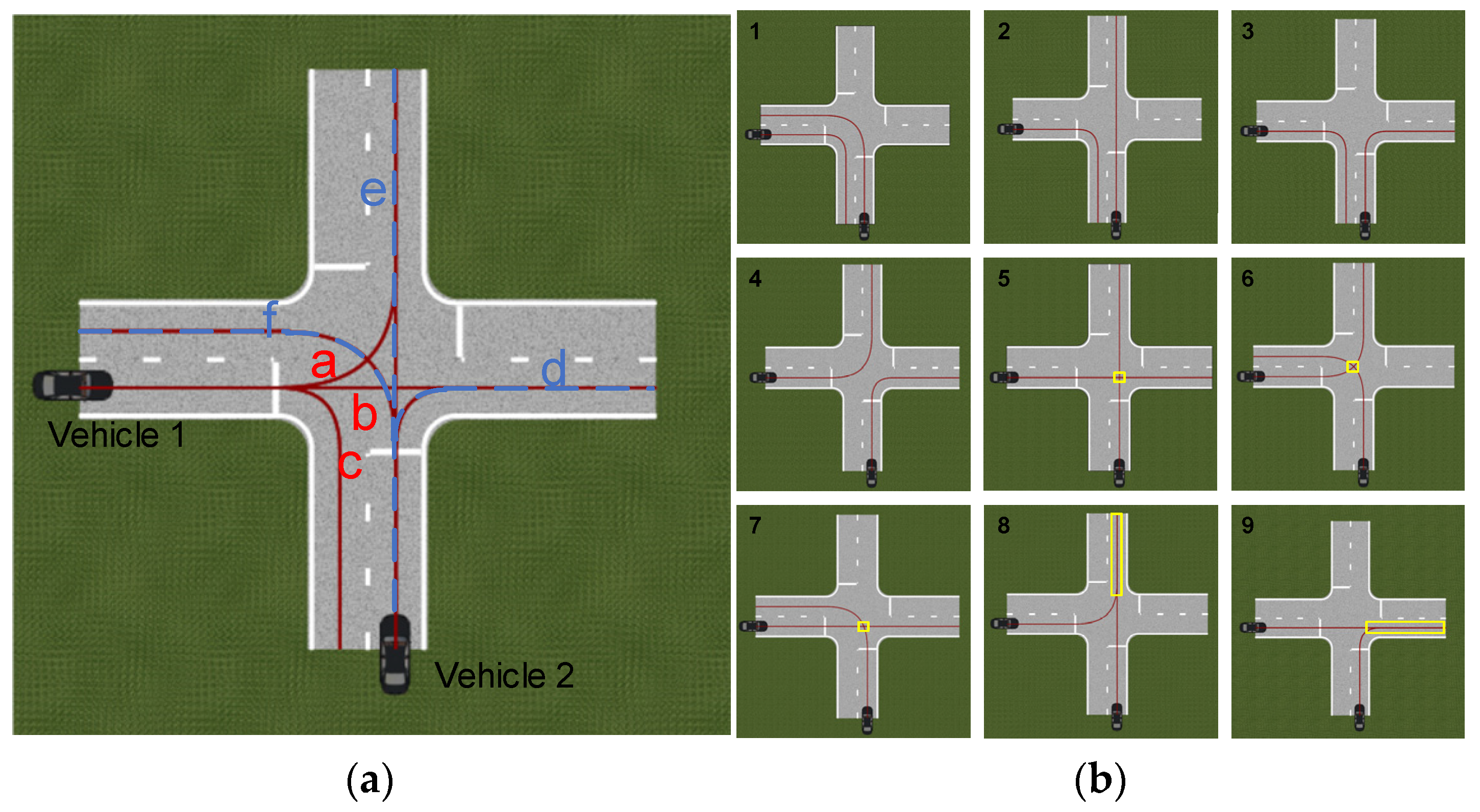
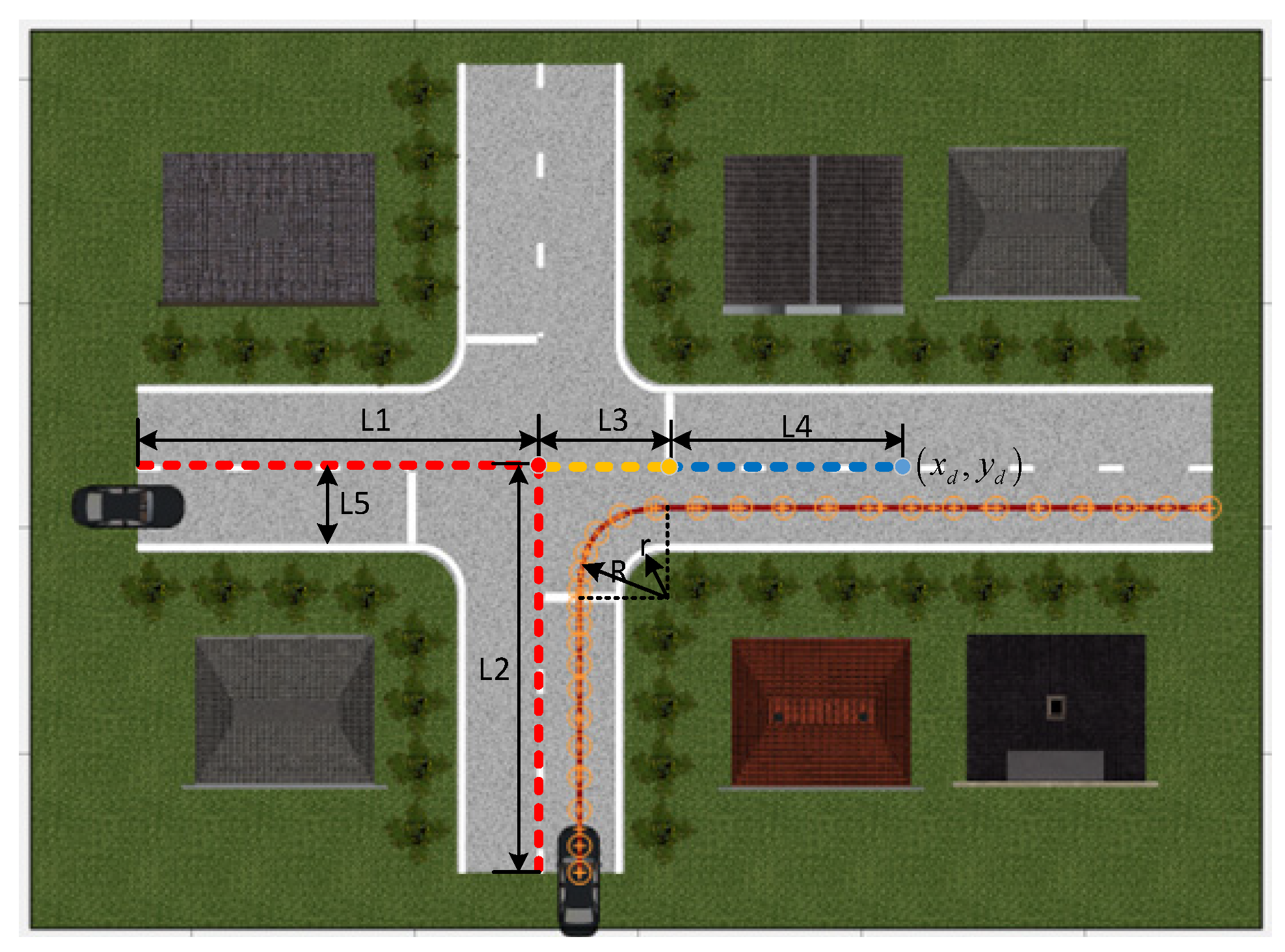
2. Intersection Confluence Condition Modeling
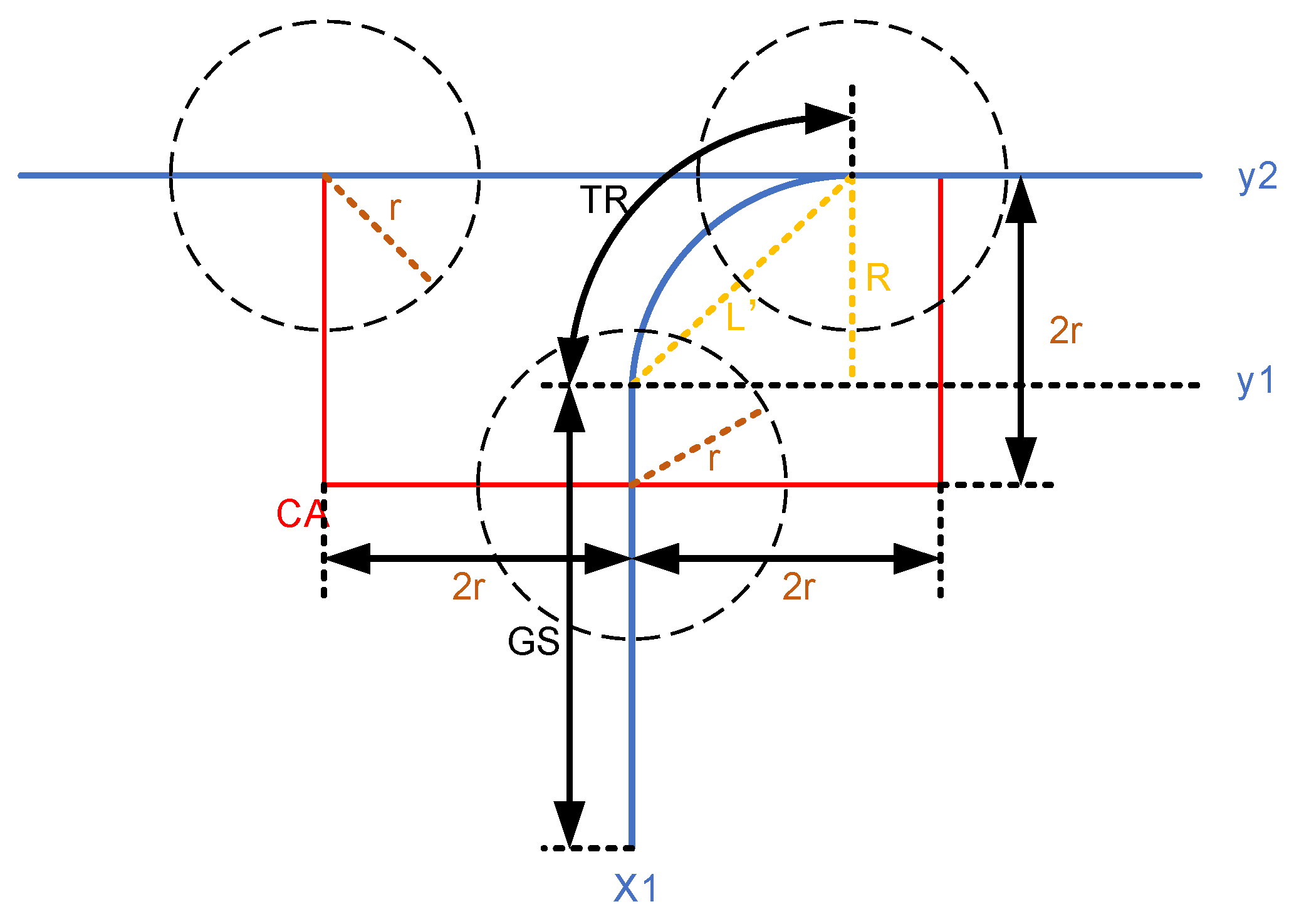
2.1. Circular Model of Vehicle Body
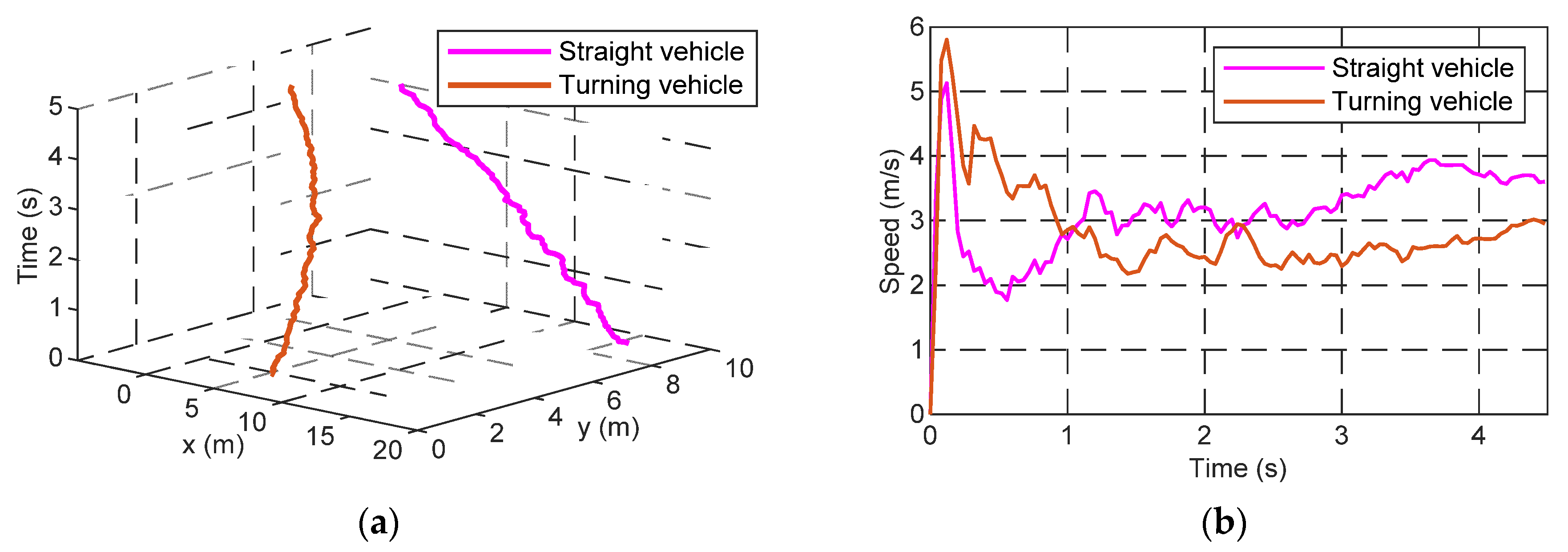
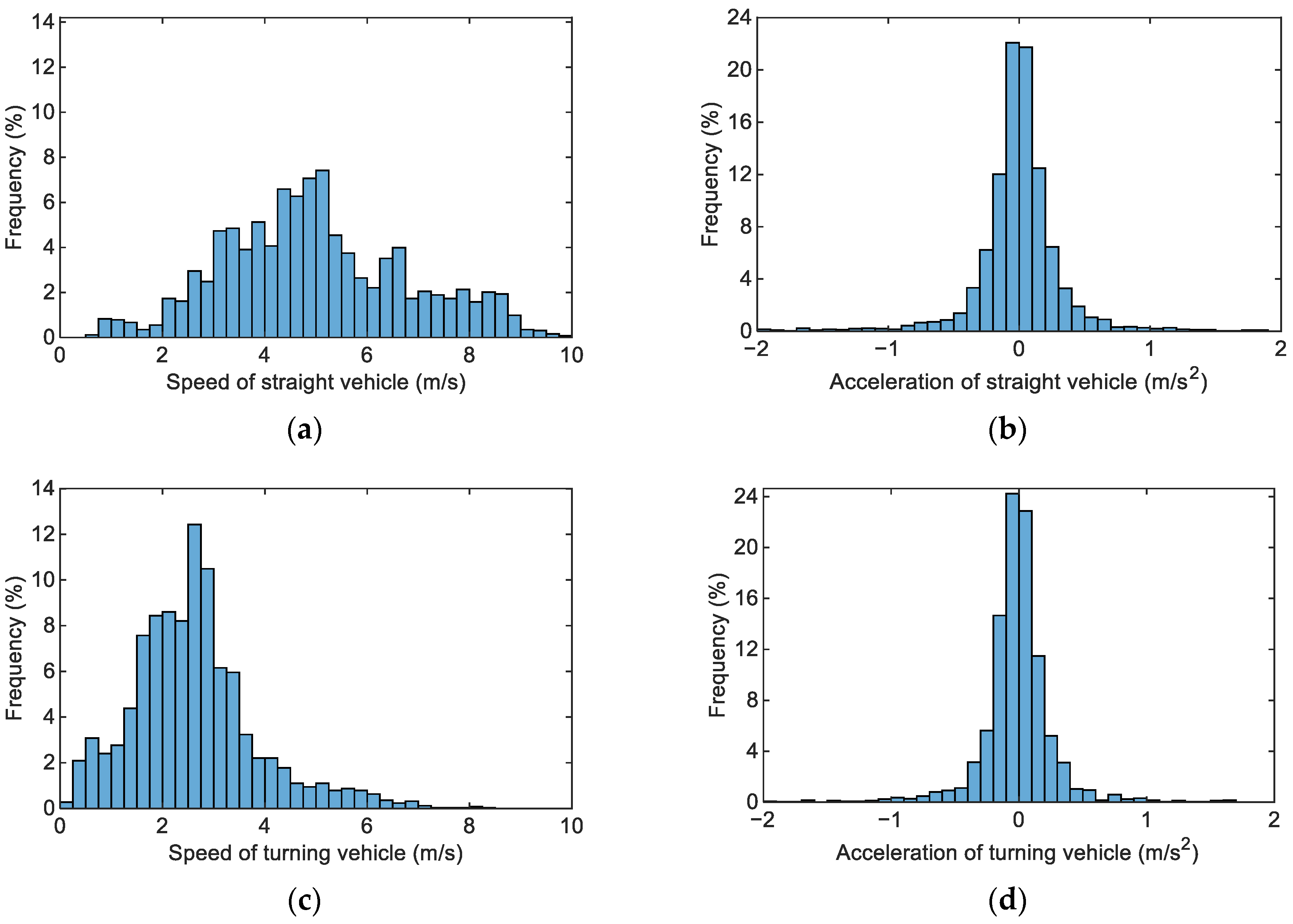
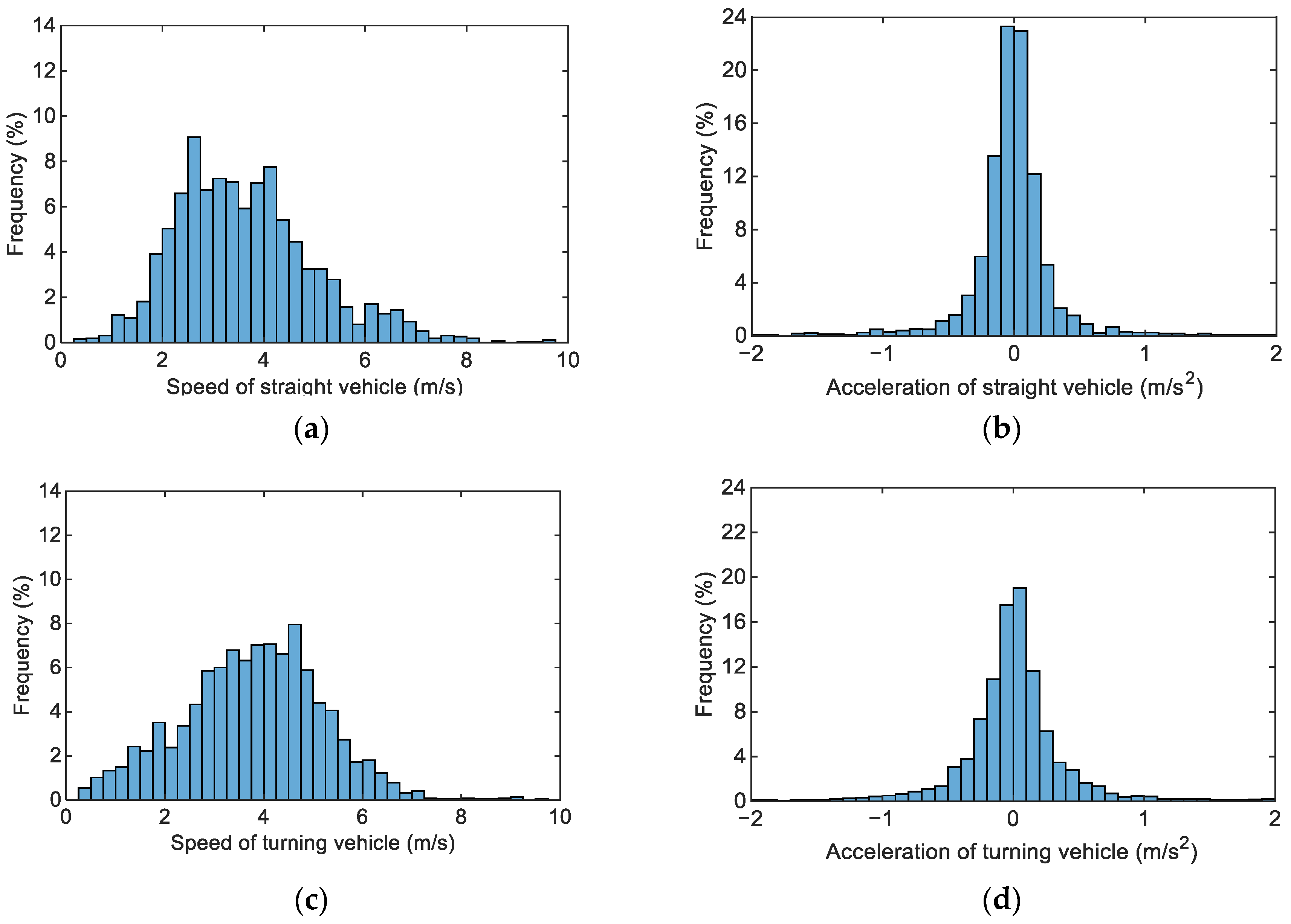
2.2. Statistical Analysis of Intersection Confluence Trajectory Data
3. Decision Making and Control Based on RL and ARIMA Prediction
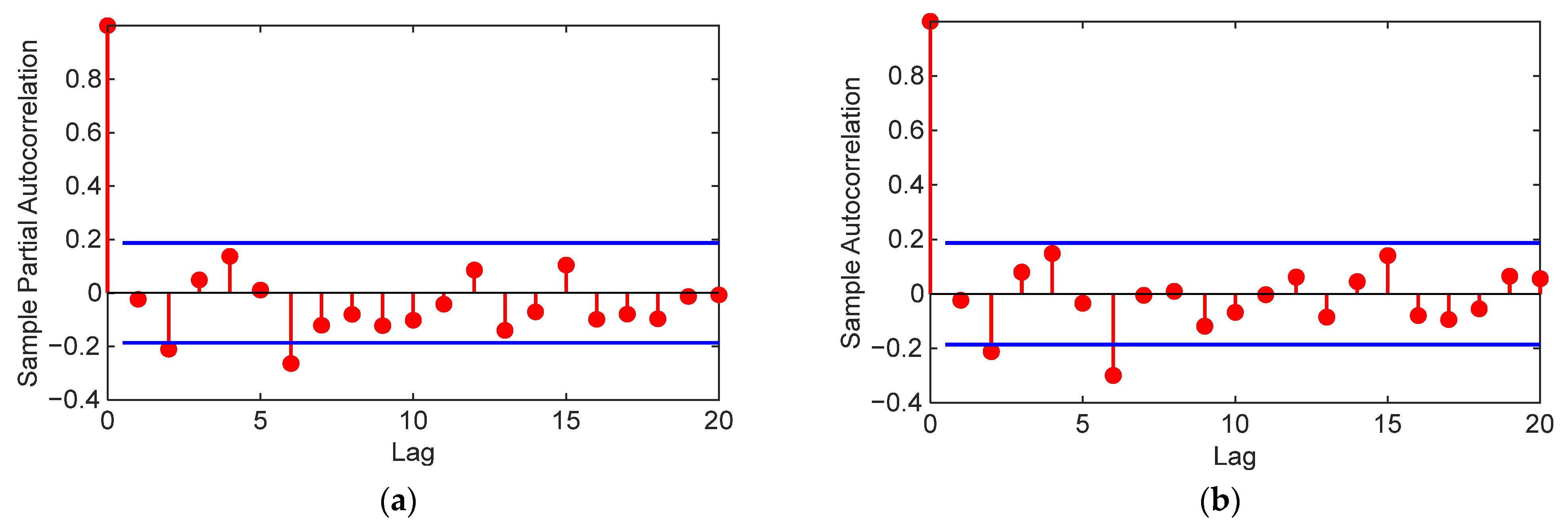
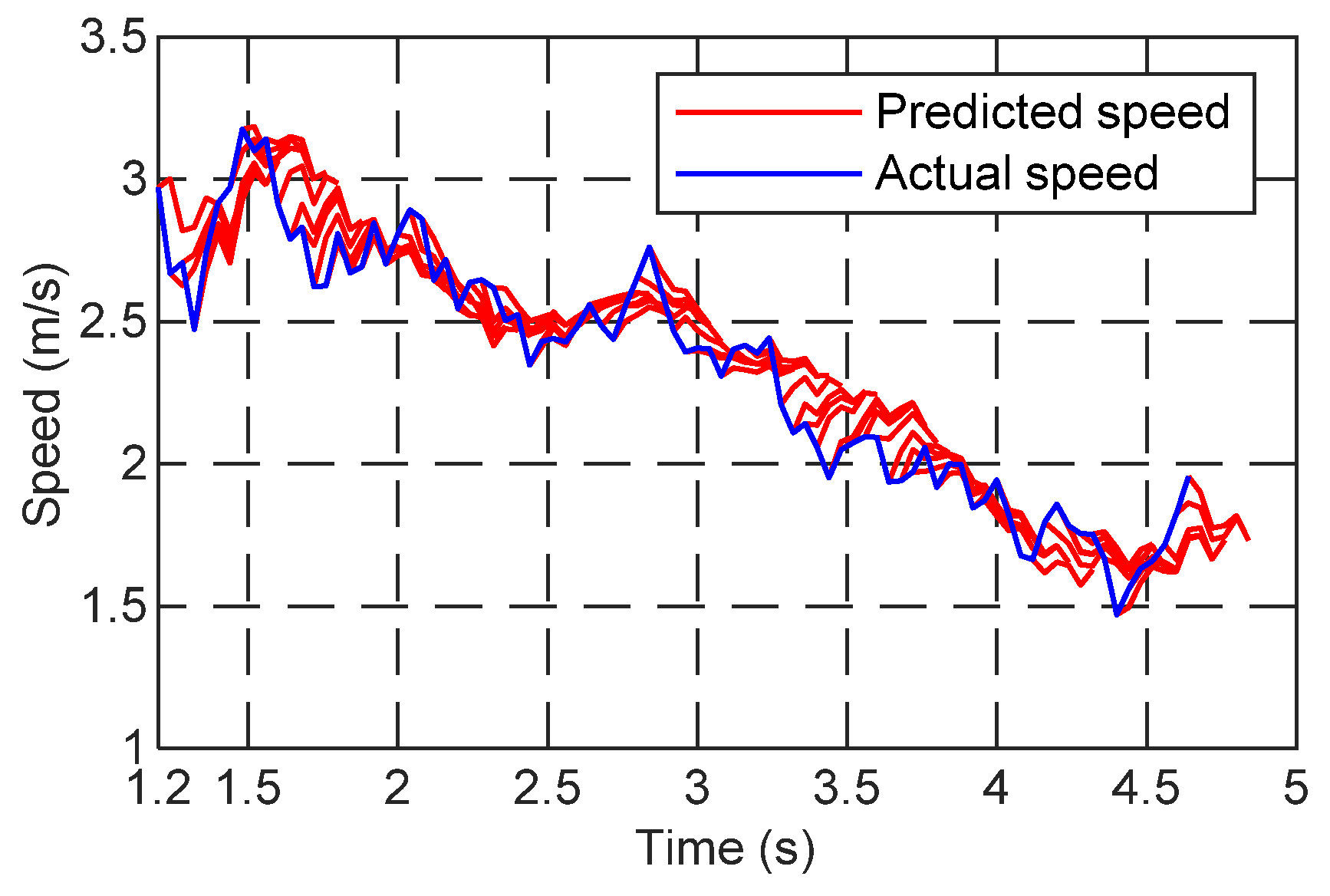
3.1. Turning-Vehicle Speed Prediction
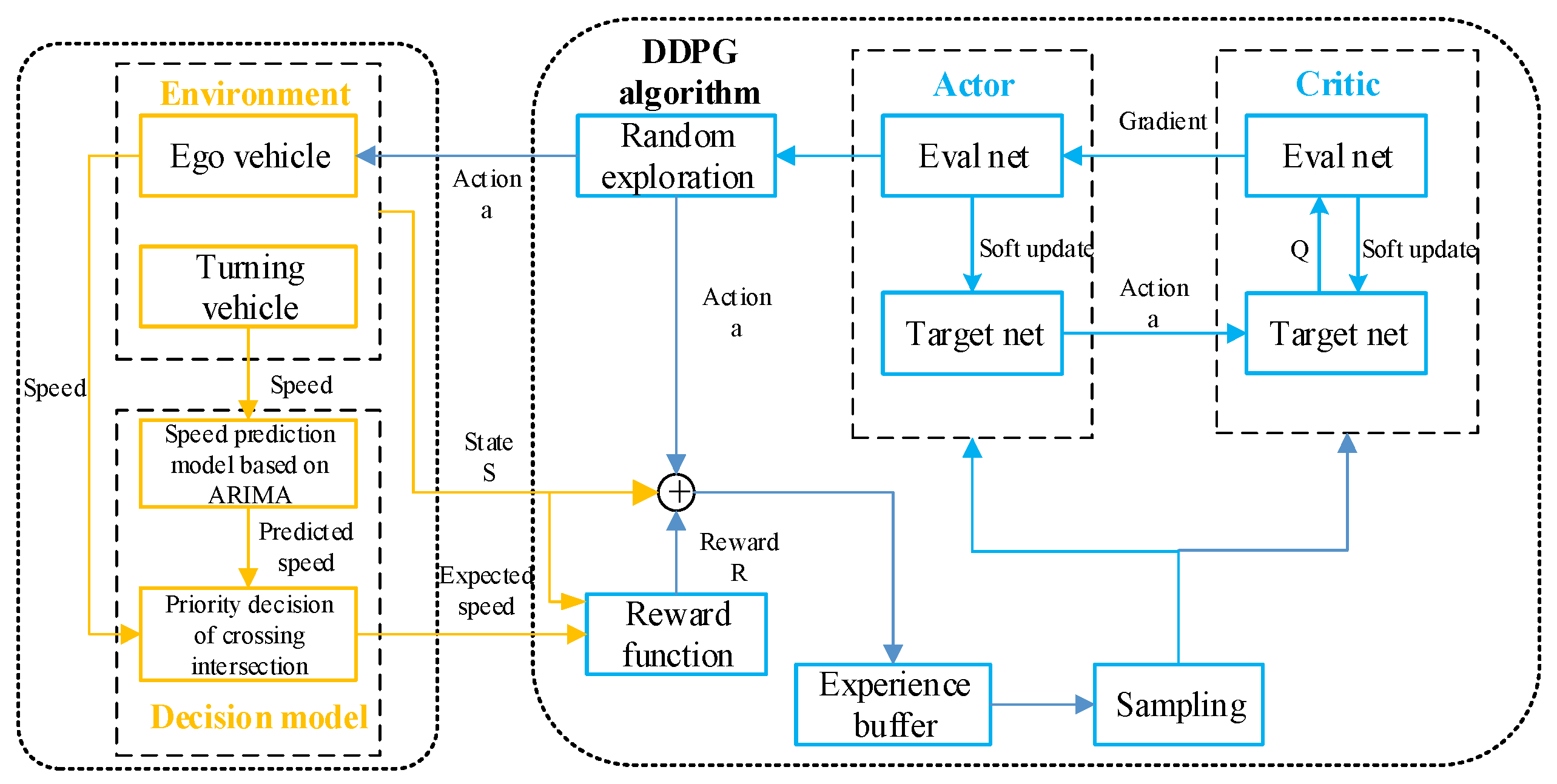
3.2. Decision and Control Based on RL
3.3. Model-Evaluation Method
4. Validation and Discussion
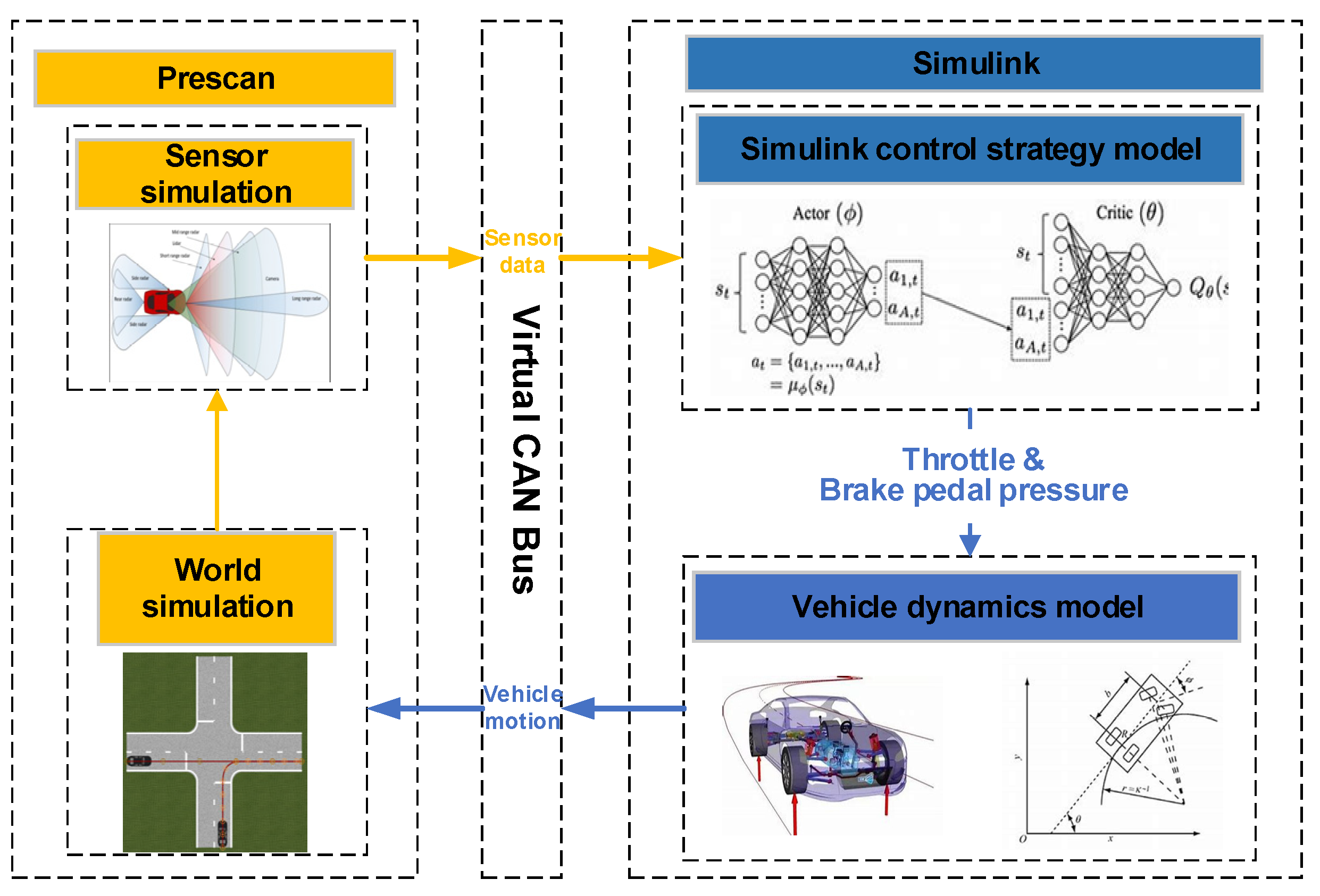
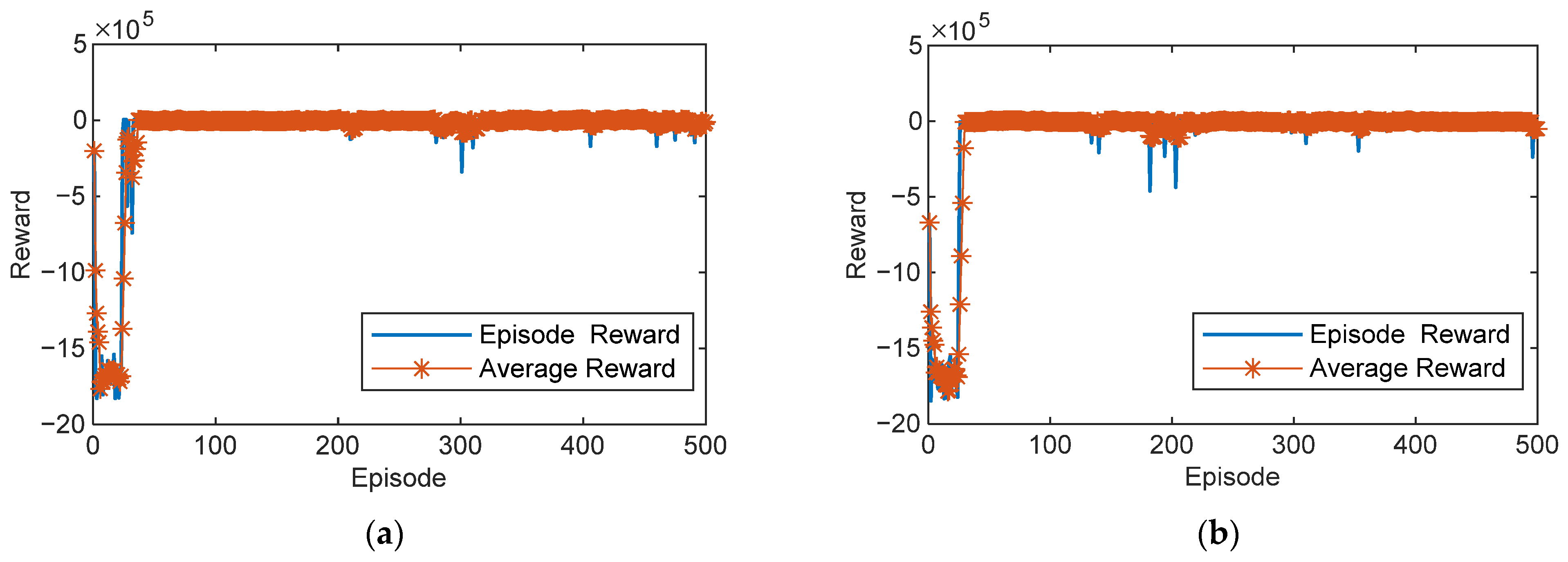
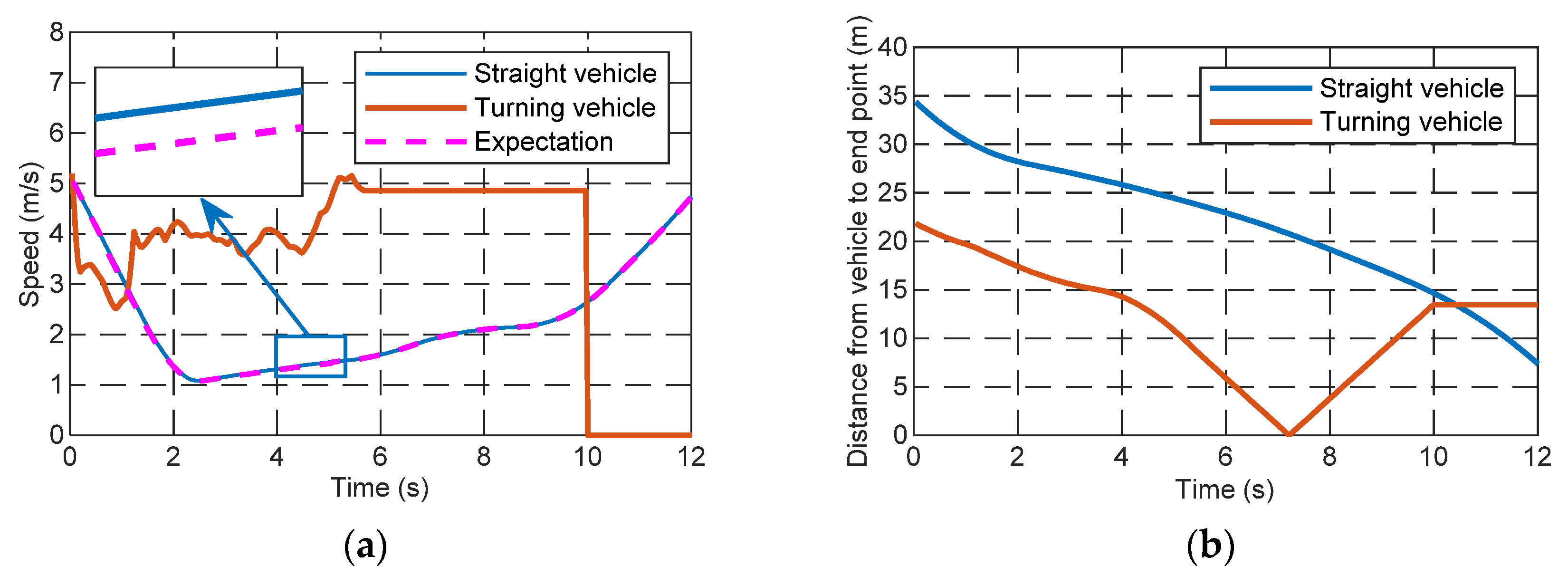
4.1. Simulation Validation
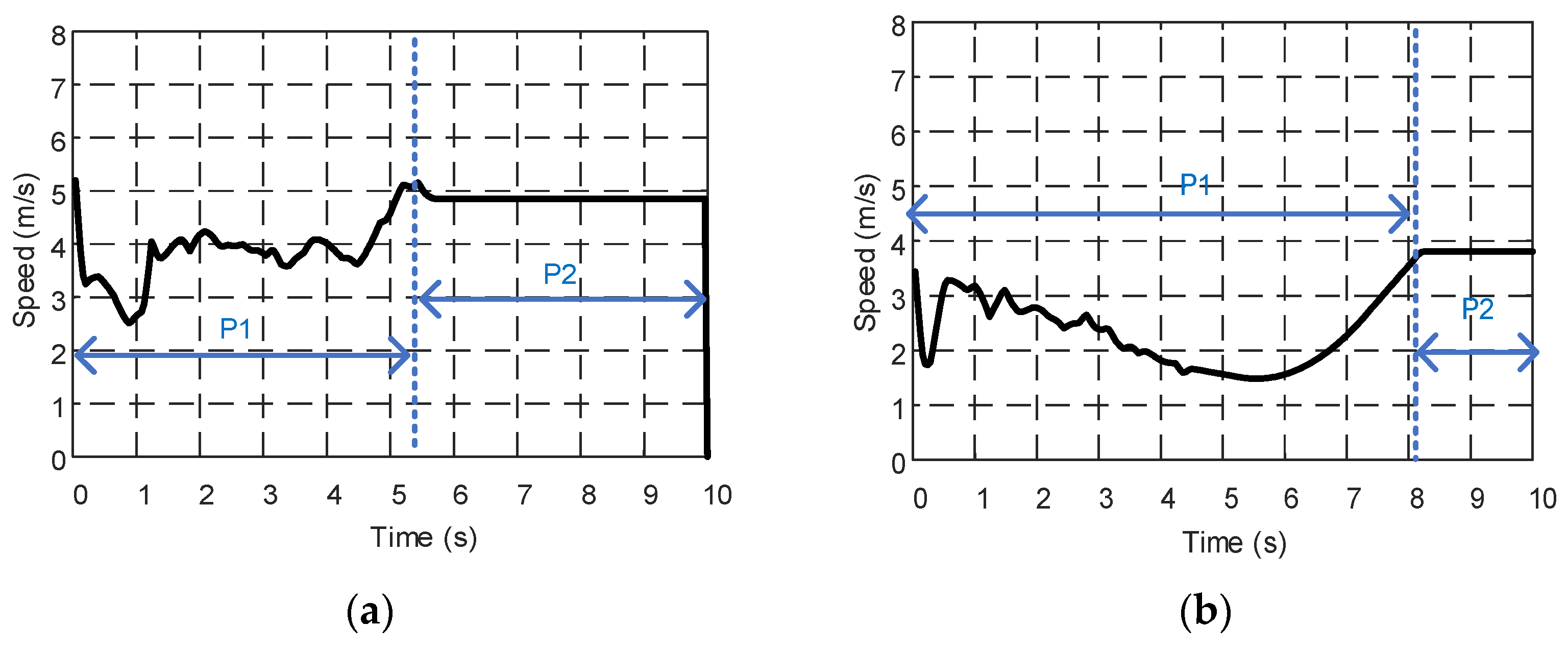
4.2. Effect Evaluation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shirazi, M.S.; Morris, B.T. Looking at Intersections: A Survey of Intersection Monitoring, Behavior and Safety Analysis of Recent Studies. IEEE Trans. Intell. Transp. Syst. 2017, 18, 4–24. [Google Scholar] [CrossRef]
- He, Y.; Yang, S.; Chan, C.Y.; Chen, L.; Wu, C. Visualization Analysis of Intelligent Vehicles Research Field Based on Mapping Knowledge Domain. IEEE Trans. Intell. Transp. Syst. 2021, 22, 5721–5736. [Google Scholar] [CrossRef]
- Zyner, A.; Worrall, S.; Ward, J.; Nebot, E. Long short term memory for driver intent prediction. In Proceedings of the 2017 IEEE Intelligent Vehicles Symposium (IV), Los Angeles, CA, USA, 11–14 July 2017; pp. 1484–1489. [Google Scholar]
- Noh, S. Decision-Making Framework for Autonomous Driving at Road Intersections: Safeguarding Against Collision, Overly Conservative Behavior, and Violation Vehicles. IEEE Trans. Ind. Electron. 2019, 66, 3275–3286. [Google Scholar] [CrossRef]
- Ma, L.; Xue, J.; Kawabata, K.; Zhu, J.; Ma, C.; Zheng, N. Efficient Sampling-Based Motion Planning for On-Road Autonomous Driving. IEEE Trans. Intell. Transp. Syst. 2015, 16, 1961–1976. [Google Scholar] [CrossRef]
- Ramyar, S.; Homaifar, A.; Anzagira, A.; Karimoddini, A.; Amsalu, S.; Kurt, A. Fuzzy modeling of drivers’ actions at intersections. In Proceedings of the 2016 World Automation Congress (WAC), Rio Grande, PR, USA, 31 July–4 August 2016; pp. 1–6. [Google Scholar]
- Hult, R.; Zanon, M.; Gros, S.; Falcone, P. Optimal Coordination of Automated Vehicles at Intersections: Theory and Experiments. IEEE Trans. Control Syst. Technol. 2019, 27, 2510–2525. [Google Scholar] [CrossRef]
- Zhao, X.; Wang, J.; Yin, G.; Zhang, K. Cooperative driving for connected and automated vehicles at non-signalized intersection based on model predictive control. In Proceedings of the 2019 IEEE Intelligent Transportation Systems Conference (ITSC), Auckland, New Zealand, 27–30 October 2019; pp. 2121–2126. [Google Scholar]
- Huang, L.X.; Panagou, D. Automated turning and merging for autonomous vehicles using a nonlinear model predictive control approach. In Proceedings of the 2017 American Control Conference (Acc), Seattle, WA, USA, 24–26 May 2017; pp. 5525–5531. [Google Scholar]
- Katriniok, A.; Kleibaum, P.; Josevski, M. Distributed Model Predictive Control for Intersection Automation Using a Parallelized Optimization Approach. IFAC Pap. 2017, 50, 5940–5946. [Google Scholar] [CrossRef]
- Schildbach, G.; Soppert, M.; Borrelli, F. A collision avoidance system at intersections using robust model predictive control. In Proceedings of the 2016 IEEE Intelligent Vehicles Symposium (IV), Gothenburg, Sweden, 19–22 June 2016; pp. 233–238. [Google Scholar]
- Bouton, M.; Cosgun, A.; Kochenderfer, M.J. Belief state planning for autonomously navigating urban intersections. In Proceedings of the 2017 IEEE Intelligent Vehicles Symposium (IV), Los Angeles, CA, USA, 11–14 June 2017; pp. 825–830. [Google Scholar]
- Shu, K.; Yu, H.; Chen, X.; Chen, L.; Wang, Q.; Li, L.; Cao, D. Autonomous driving at intersections: A critical-turning-point approach for left turns. In Proceedings of the 2020 IEEE 23rd International Conference on Intelligent Transportation Systems (ITSC), Rhodes, Greece, 20–23 September 2020; pp. 1–6. [Google Scholar]
- Kye, D.K.; Kim, S.W.; Seo, S.W. Decision making for automated driving at unsignalized intersection. In Proceedings of the 2015 15th International Conference on Control, Automation and Systems (Iccas), Busan, Korea, 13–16 October 2015; pp. 522–525. [Google Scholar]
- Hubmann, C.; Quetschlich, N.; Schulz, J.; Bernhard, J.; Althoff, D.; Stiller, C. A POMDP maneuver planner for occlusions in urban scenarios. In Proceedings of the 2019 IEEE Intelligent Vehicles Symposium (IV), Paris, France, 9–12 June 2019; pp. 2172–2179. [Google Scholar]
- Hubmann, C.; Schulz, J.; Becker, M.; Althoff, D.; Stiller, C. Automated Driving in Uncertain Environments: Planning With Interaction and Uncertain Maneuver Prediction. IEEE Trans. Intell. Veh. 2018, 3, 5–17. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Graves, A.; Antonoglou, I.; Wierstra, D.; Riedmiller, M. Playing Atari with Deep Reinforcement Learning. arXiv 2013, arXiv:1312.5602. [Google Scholar]
- Silver, D.; Huang, A.; Maddison, C.J.; Guez, A.; Sifre, L.; Van Den Driessche, G.; Schrittwieser, J.; Antonoglou, I.; Panneershelvam, V.; Lanctot, M.; et al. Mastering the game of Go with deep neural networks and tree search. Nature 2016, 529, 484–489. [Google Scholar] [CrossRef] [PubMed]
- Isele, D.; Rahimi, R.; Cosgun, A.; Subramanian, K.; Fujimura, K. Navigating occluded intersections with autonomous vehicles using deep reinforcement learning. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21–25 May 2018; pp. 2034–2039. [Google Scholar]
- Shi, Y.; Liu, Y.; Qi, Y.; Han, Q. A Control Method with Reinforcement Learning for Urban Un-Signalized Intersection in Hybrid Traffic Environment. Sensors 2022, 22, 779. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Lee, K.; Hsiung, P. Intersection crossing for autonomous vehicles based on deep reinforcement learning. In Proceedings of the 2019 IEEE International Conference on Consumer Electronics—Taiwan (ICCE-TW), Yilan, Taiwan, 20–22 May 2019; pp. 1–2. [Google Scholar]
- Zhou, M.; Yu, Y.; Qu, X. Development of an Efficient Driving Strategy for Connected and Automated Vehicles at Signalized Intersections: A Reinforcement Learning Approach. IEEE Trans. Intell. Transp. Syst. 2020, 21, 433–443. [Google Scholar] [CrossRef]
- Bucolo, M.; Buscarino, A.; Famoso, C.; Fortuna, L.; Frasca, M. Control of imperfect dynamical systems. Nonlinear Dyn. 2019, 98, 2989–2999. [Google Scholar] [CrossRef]
- Liu, Y.; Zhou, B.; Wang, X.; Li, L.; Cheng, S.; Chen, Z.; Li, G.; Zhang, L. Dynamic Lane-Changing Trajectory Planning for Autonomous Vehicles Based on Discrete Global Trajectory. IEEE Trans. Intell. Transp. Syst. 2021. [Google Scholar] [CrossRef]
- Xu, X.; Zuo, L.; Li, X.; Qian, L.; Ren, J.; Sun, Z. A Reinforcement Learning Approach to Autonomous Decision Making of Intelligent Vehicles on Highways. IEEE Trans. Syst. Man Cybern. Syst. 2020, 50, 3884–3897. [Google Scholar] [CrossRef]
- OpenITS. Available online: https://www.openits.cn/ (accessed on 13 January 2022).
- Tsay, R.S.; Tiao, G.C. Consistent estimates of autoregressive parameters and extended sample autocorrelation function for stationary and nonstationary ARMA models. J. Am. Stat. Assoc. 1984, 79, 84–96. [Google Scholar] [CrossRef]
- Method of Running Test—Automotive Ride Comfort. Available online: http://std.samr.gov.cn/gb (accessed on 13 January 2022).
- Yang, S.; Yoshitake, H.; Shino, M.; Shimosaka, M. Smooth and stopping interval aware driving behavior prediction at un-signalized intersection with inverse reinforcement learning on sequential MDPs. In Proceedings of the 2021 IEEE Intelligent Vehicles Symposium, Nagoya, Japan, 11–17 July 2021; pp. 586–593. [Google Scholar]








| RMS Value of Total Weighted Acceleration | Passenger Comfort Level |
|---|---|
| <0.315 | No discomfort |
| 0.315~0.63 | Little discomfort |
| 0.5~1 | Some discomfort |
| 0.8~1.6 | Uncomfortable |
| 1.25~2.5 | More uncomfortable |
| >2 | Extremely uncomfortable |
| Parameter | Description | Value (m) |
|---|---|---|
| Distance from the initial position of straight vehicle to the center of the intersection | 18 | |
| Distance from the initial position of the turning vehicle to the center of the intersection | 18 | |
| Distance from road center to confluence point | 5.5 | |
| Distance from the point of confluence to the end of the confluence | 10.5 | |
| Road width | 3.5 | |
| Radius of curvature at the turn of the road centerline | 4 | |
| Radius of curvature at road edge bends | 2.25 |
| Parameter | Value |
|---|---|
| Time duration of simulation | 16 s |
| Simulation step size | 0.04 s |
| Maximum number of training episodes | 500 |
| Input-layer size | 6 |
| Output-layer size | 1 |
| Number of neurons | 144 |
| Learning rate | 10−3 |
| Discount factor | 0.9 |
| Gradient threshold | 1 |
| Experience-pool size | 106 |
| Batch size | 64 |
| Period of Acceleration (s) | RMS of Weighted Acceleration | Passenger Comfort | Score |
|---|---|---|---|
| 0–1 | 0.8890 | Some discomfort | 60 |
| 1–2 | 0.8131 | Some discomfort | 60 |
| 2–3 | 0.1932 | No discomfort | 100 |
| 3–4 | 0.0642 | No discomfort | 100 |
| 4–5 | 0.0540 | No discomfort | 100 |
| 5–6 | 0.0641 | No discomfort | 100 |
| 6–7 | 0.1522 | No discomfort | 100 |
| 7–8 | 0.0822 | No discomfort | 100 |
| 8–9 | 0.0194 | No discomfort | 100 |
| 9–10 | 0.2068 | No discomfort | 100 |
| Period of Acceleration (s) | RMS of Weighted Acceleration | Passenger Comfort | Score |
|---|---|---|---|
| 0–1 | 0.5836 | Little discomfort | 80 |
| 1–2 | 0.6878 | Some discomfort | 60 |
| 2–3 | 0.8845 | Some discomfort | 60 |
| 3–4 | 0.5815 | Little discomfort | 80 |
| 4–5 | 0.4682 | Little discomfort | 80 |
| 5–6 | 0.3745 | Little discomfort | 80 |
| 6–7 | 0.2100 | No discomfort | 100 |
| 7–8 | 0.0510 | No discomfort | 100 |
| 8–9 | 0.6160 | Little discomfort | 80 |
| 9–10 | 0.2760 | No discomfort | 100 |
| Working Condition I | Working Condition II | |
|---|---|---|
| Success rate | 100 | 100 |
| Speed penalty | 100 | 100 |
| Security | 80.35 | 70.04 |
| Traffic efficiency | 65.65 | 95.80 |
| Passenger comfort | 92 | 82 |
| Comprehensive score | 87.60 | 89.57 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Liu, G.; Wu, Y.; He, W.; Zhang, Y.; Chen, Z. Reinforcement-Learning-Based Decision and Control for Autonomous Vehicle at Two-Way Single-Lane Unsignalized Intersection. Electronics 2022, 11, 1203. https://doi.org/10.3390/electronics11081203
Liu Y, Liu G, Wu Y, He W, Zhang Y, Chen Z. Reinforcement-Learning-Based Decision and Control for Autonomous Vehicle at Two-Way Single-Lane Unsignalized Intersection. Electronics. 2022; 11(8):1203. https://doi.org/10.3390/electronics11081203
Chicago/Turabian StyleLiu, Yonggang, Gang Liu, Yitao Wu, Wen He, Yuanjian Zhang, and Zheng Chen. 2022. "Reinforcement-Learning-Based Decision and Control for Autonomous Vehicle at Two-Way Single-Lane Unsignalized Intersection" Electronics 11, no. 8: 1203. https://doi.org/10.3390/electronics11081203
APA StyleLiu, Y., Liu, G., Wu, Y., He, W., Zhang, Y., & Chen, Z. (2022). Reinforcement-Learning-Based Decision and Control for Autonomous Vehicle at Two-Way Single-Lane Unsignalized Intersection. Electronics, 11(8), 1203. https://doi.org/10.3390/electronics11081203









