A Full Investigation of Terahertz Wave Power Transmission in Plasma from Theoretical, Numerical, and Experimental Perspectives
Abstract
:1. Introduction
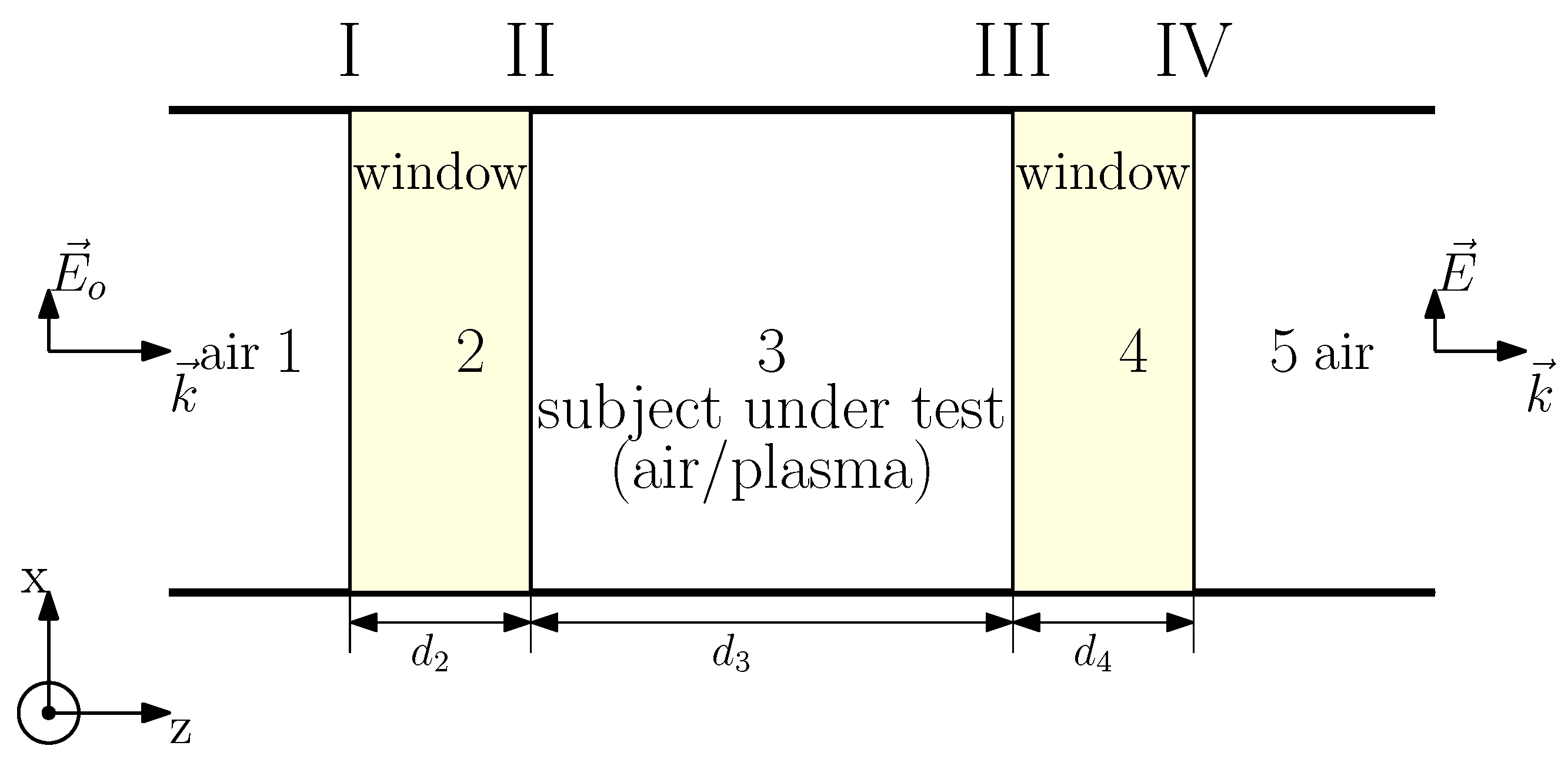
2. Measurement System Description
- The whole system with the shock-wave tube off-work was measured to obtain the reference parameters to calibrate the final data where the test area is just air.
- Then, the S parameters were measured with the shock-wave tube working to produce the plasma gas in the test area, recorded as .
- The whole transmission coefficient of the system can be obtained: , with the effects of the antenna windows.
3. Analytical Model and Numerical Model
3.1. Analytical Model
- In the calibration phase for the reference, area 3 was full of air; thus, the E field at Medium 5 can be obtained:where is the initial amplitude of the E field; stands for the transmission coefficient of the interface , while describes the wave propagation in the medium .
- After the calibration process, area 3 was filled with the non-magnetized plasma; thus, the E field at Medium 5 can be obtained:where is the initial amplitude of the E field; stands for the transmission coefficient of the interface , while describes the wave propagation in the medium .
- Finally, the transfer function can be obtained:because , , , and are the same as , , , and , respectively.
3.2. Numerical Model
- We assigned area 3 as air and ran the simulation to obtain the reference e-field at port 2;
- We changed medium 3 to plasma to obtain the ;
- The transmission coefficient could then be obtained: .
4. Results and Discussion
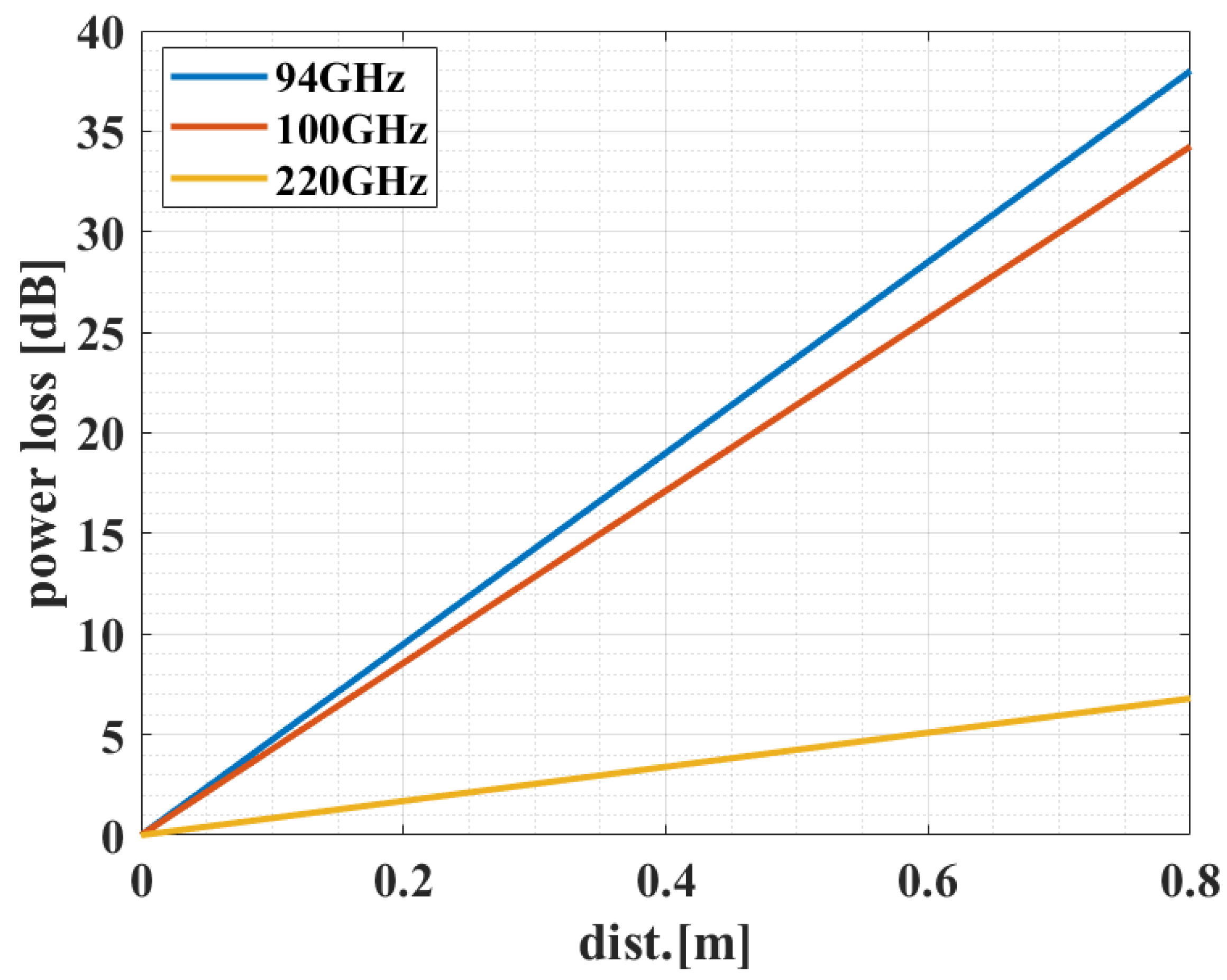
4.1. Comparison of Transmission Attenuation for Theoretical, Numerical, and Measured Results
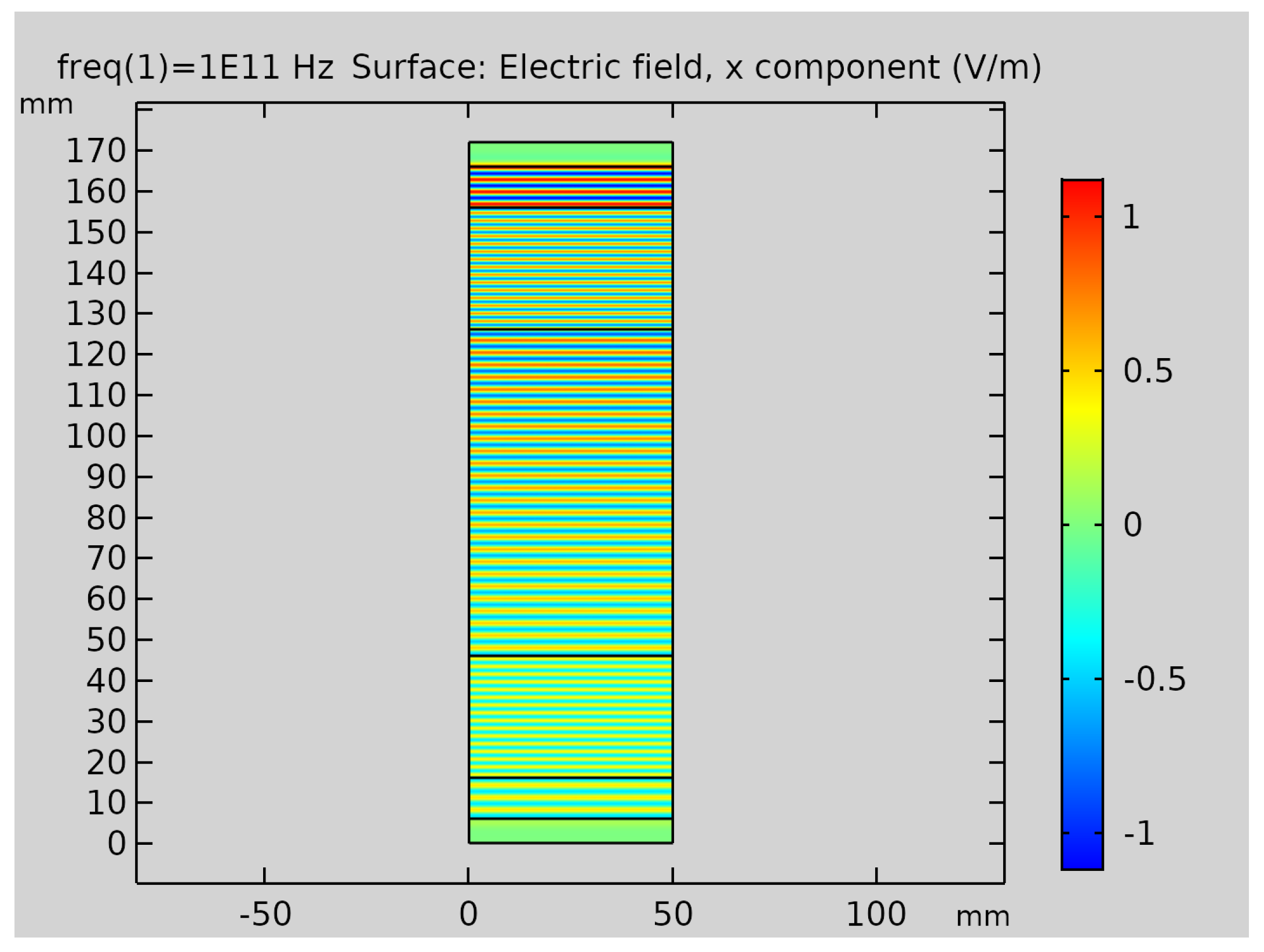
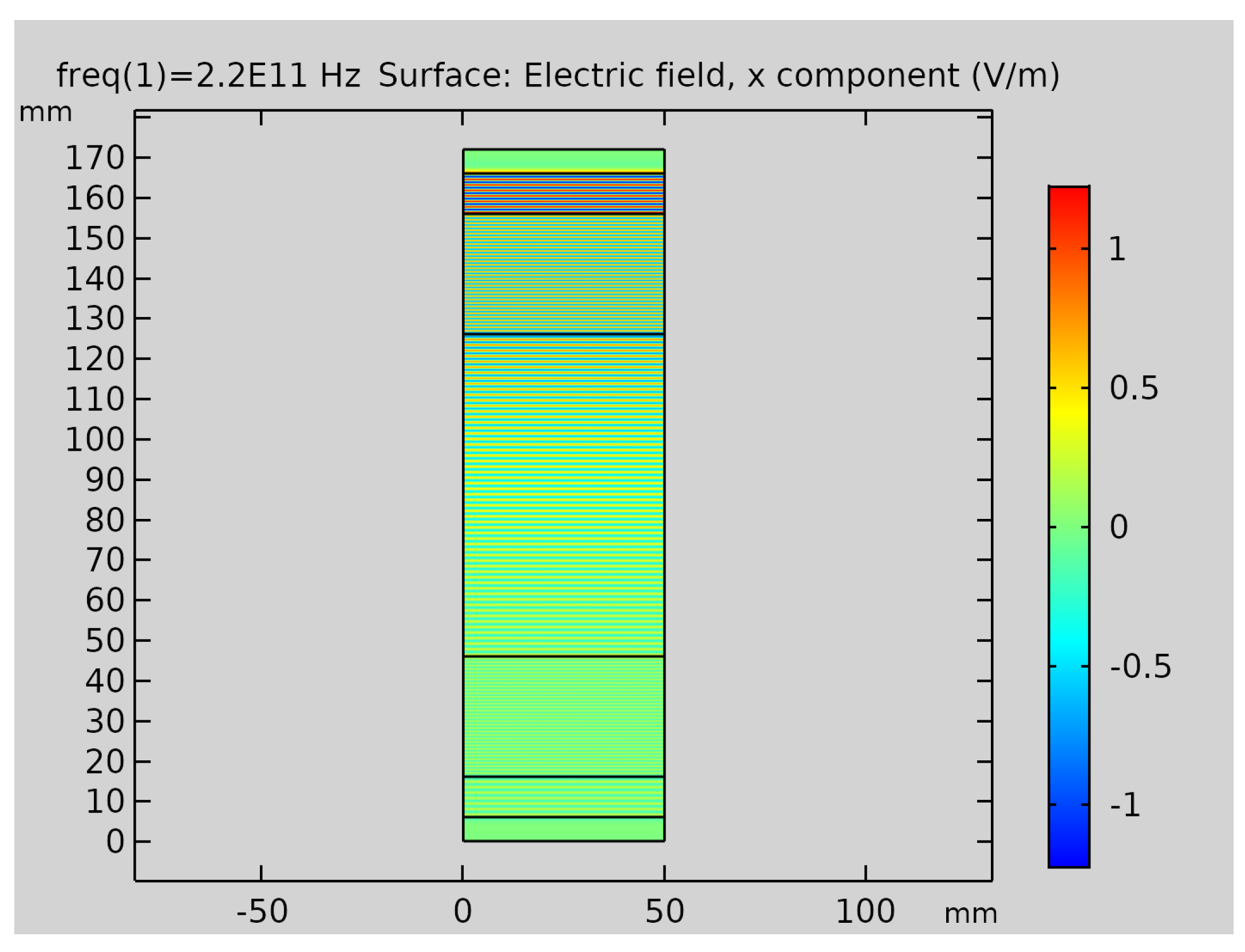
4.2. Field Distribution of the Full Wave Simulation
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Rybak, J.P.; Churchill, R. Progress in reentry communications. IEEE Trans. Aerosp. Electron. Syst. 1971, 5, 879–894. [Google Scholar] [CrossRef]
- Belov, I.; Borovoy, V.Y.; Gorelov, V.; Kireev, A.; Korolev, A.; Stepanov, E. Investigation of remote antenna assembly for radio communication with reentry vehicle. J. Spacecr. Rocket. 2001, 38, 249–256. [Google Scholar] [CrossRef]
- Mehra, N.; Singh, R.K.; Bera, S.C. Mitigation of communication blackout during re-entry using static magnetic field. Prog. Electromagn. Res. B 2015, 63, 161–172. [Google Scholar] [CrossRef] [Green Version]
- Kim, M.; Keidar, M.; Boyd, I.D. Analysis of an electromagnetic mitigation scheme for reentry telemetry through plasma. J. Spacecr. Rocket. 2008, 45, 1223. [Google Scholar] [CrossRef]
- Lin, T.; Sproul, L. Influence of reentry turbulent plasma fluctuation on EM wave propagation. Comput. Fluids 2006, 35, 703–711. [Google Scholar] [CrossRef]
- Song, H.J.; Nagatsuma, T. Present and future of terahertz communications. IEEE Trans. Terahertz Sci. Technol. 2011, 1, 256–263. [Google Scholar] [CrossRef]
- Tosun, Z.; Akbar, D.; Altan, H. The interaction of terahertz pulses with dc glow discharge plasma. In Proceedings of the 2009 34th International Conference on Infrared, Millimeter, and Terahertz Waves, Busan, Korea, 21–25 September 2009; pp. 1–2. [Google Scholar]
- Komerath, N.; Komerath, P. Implications of inter-satellite power beaming using a space power grid. In Proceedings of the Aerospace Conference, 2011 IEEE, Big Sky, MT, USA, 5–12 March 2011; pp. 1–11. [Google Scholar]
- Liu, J.F.; Xi, X.L.; Wan, G.B.; Wang, L.L. Simulation of electromagnetic wave propagation through plasma sheath using the moving-window finite-difference time-domain method. IEEE Trans. Plasma Sci. 2011, 39, 852–855. [Google Scholar] [CrossRef]
- Yuan, C.X.; Zhou, Z.X.; Zhang, J.W.; Xiang, X.L.; Yue, F.; Sun, H.G. FDTD analysis of terahertz wave propagation in a high-temperature unmagnetized plasma slab. IEEE Trans. Plasma Sci. 2011, 39, 1577–1584. [Google Scholar] [CrossRef]
- Yuan, C.; Zhou, Z.; Xiang, X.; Sun, H.; Wang, H.; Xing, M.; Luo, Z. Propagation properties of broadband terahertz pulses through a bounded magnetized thermal plasma. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms 2011, 269, 23–29. [Google Scholar] [CrossRef]
- Ping, M.; Xuejun, Z.; Anhua, S.; Shaoqing, B.; Zhefeng, Y. Experimental investigation on electromagnetic wave transmission characteristic in the plasma high temperature gas. J. Exp. Fluid Mech. 2010, 24, 51–56. [Google Scholar]
- Xiao, L.k.; Tang, P.; Chen, B.; Wan, L.l.; He, Z.y.; Ma, P. The Development and Application of Ka Band Transmission Measurement System for Plasma Diagnosis. J. Ordance Equip. Eng. 2017, 38, 44–50. [Google Scholar]
- Gregoire, D.; Santoru, J.; Schumacher, R. Electromagnetic-Wave Propagation in Unmagnetized Plasmas; Technical Report; HUGHES RESEARCH LABS: Malibu, CA, USA, 1992. [Google Scholar]
- Jackson, J.D. Classical Electrodynamics; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Dorney, T.D.; Baraniuk, R.G.; Mittleman, D.M. Material parameter estimation with terahertz time-domain spectroscopy. JOSA A 2001, 18, 1562–1571. [Google Scholar] [CrossRef] [PubMed] [Green Version]



| P [Pa] | T [K] | [Hz] | [cm] |
|---|---|---|---|
| 3.82 × | 3046.0 | 4.0 × 10 | 5.0 × 10 |
| 4.67 × | 3314.4 | 4.7 × | 3.8 × |
| 5.93 × | 3692.2 | 5.7 × | 9.0 × |
| 4.48 × | 3973.0 | 4.2 × | 1.6 × |
| 1.06 × | 4046.9 | 9.7 × | 6.9 × |
| P [Pa] | T [K] | [Hz] | [cm] |
|---|---|---|---|
| 9.61 × 10 | 3507.9 | 9.4 × 10 | 9.0 × 10 |
| 1.06 × | 3818.8 | 1.0 × | 3.2 × |
| 1.10 × | 4055.7 | 1.0 × | 7.3 × |
| 1.15 × | 4506.7 | 1.0 × | 2.4 × |
| 1 | 2.5 | Calculated form Equation (1) |
| [m] | [Hz] | [dB] | [dB] | [dB] |
|---|---|---|---|---|
| 5.0 × 10 | 4 × 10 | 0 | 0.12 | 0.1 |
| 3.8 × 10 | 4.7 × 10 | 0.44 | 0.99 | 0.85 |
| 9.0 × 10 | 5.7 × 10 | 1.21 | 2.63 | 2.27 |
| 1.6 × 10 | 4.2 × 10 | 2.04 | 3.89 | 3.36 |
| 6.9 × 1018 | 9.7 × 1010 | 19.17 | 23.6 | 20.52 |
| [m] | [Hz] | [dB] | [dB] | [dB] |
|---|---|---|---|---|
| 9.0 × 10 | 9.4 × 10 | 1.83 | 1.01 | 0.86 |
| 3.2 × 10 | 1.0 × 10 | 4.58 | 3.7 | 3.22 |
| 7.3 × 10 | 1.0 × 10 | 6.74 | 8.5 | 7.37 |
| 2.4 × 10 | 1.0 × 10 | 26.02 | 28.2 | 24.52 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, K.; Peng, D.; Wang, J.; Ma, P.; Li, B. A Full Investigation of Terahertz Wave Power Transmission in Plasma from Theoretical, Numerical, and Experimental Perspectives. Electronics 2022, 11, 1432. https://doi.org/10.3390/electronics11091432
Yang K, Peng D, Wang J, Ma P, Li B. A Full Investigation of Terahertz Wave Power Transmission in Plasma from Theoretical, Numerical, and Experimental Perspectives. Electronics. 2022; 11(9):1432. https://doi.org/10.3390/electronics11091432
Chicago/Turabian StyleYang, Ke, Di Peng, Jinhong Wang, Ping Ma, and Bin Li. 2022. "A Full Investigation of Terahertz Wave Power Transmission in Plasma from Theoretical, Numerical, and Experimental Perspectives" Electronics 11, no. 9: 1432. https://doi.org/10.3390/electronics11091432
APA StyleYang, K., Peng, D., Wang, J., Ma, P., & Li, B. (2022). A Full Investigation of Terahertz Wave Power Transmission in Plasma from Theoretical, Numerical, and Experimental Perspectives. Electronics, 11(9), 1432. https://doi.org/10.3390/electronics11091432







