BER Minimization by User Pairing in Downlink NOMA Using Laser Chaos Decision-Maker
Abstract
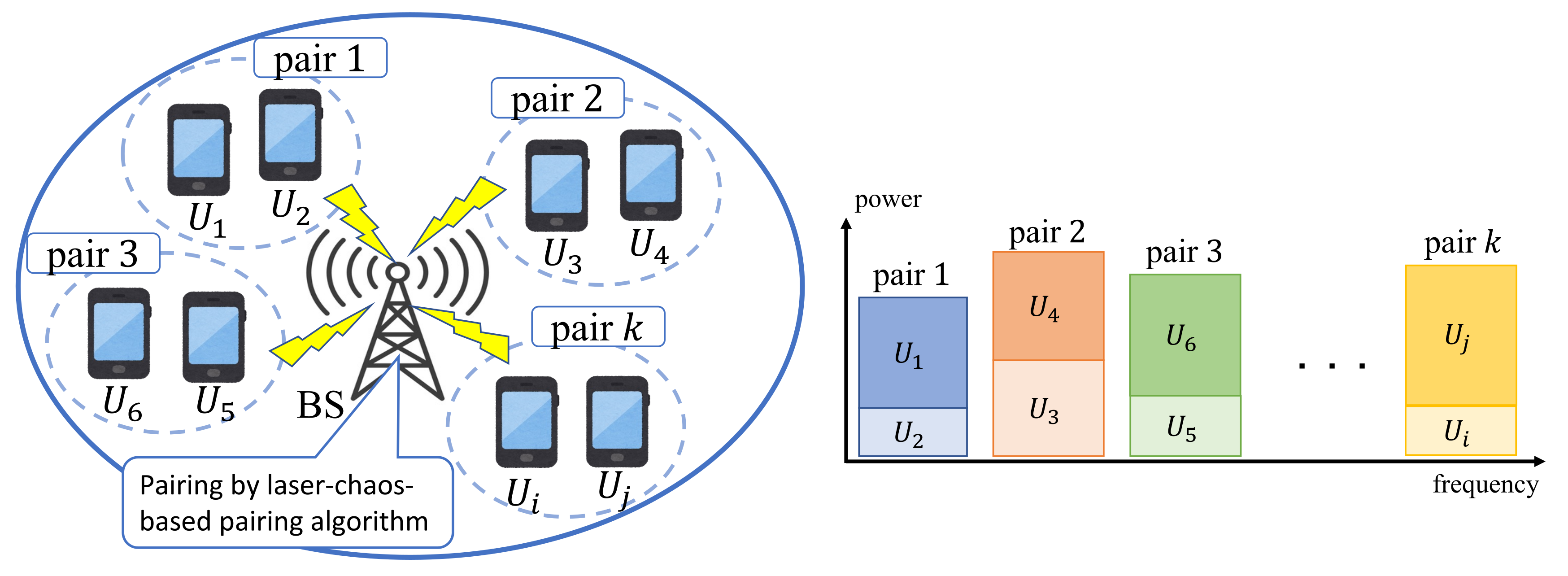
:1. Introduction
- We design a fast user-pairing scheme that can make real-time decisions for downlink NOMA systems based on the laser chaos decision-maker while considering the BER of the communications and user responses on the basis of a realistic system model.
- To improve the performance in terms of BER for our proposed scheme, error-correcting codes are introduced in the system. In addition, parameter dependencies in the user pairing by laser chaos decision-maker are investigated to minimize the BER of the NOMA system. Simulation results indicate that our proposed scheme can improve the BER of the NOMA system.
- To verify the effectiveness of the proposed scheme, we conduct a performance evaluation for our proposed scheme and compare it to several other conventional schemes. Simulation results demonstrate that our proposed scheme exhibits superior performances in BER compared to other conventional schemes. As the cell radius of the NOMA system gets smaller, the superior on the BER of our proposed scheme gets bigger. Specifically, our proposed scheme can decrease the BER from to compared to the conventional schemes when the cell radius is 400 m.
2. System Model and Problem Formulation
3. The Principle of Laser Chaos Decision-Maker
4. User Pairing in NOMA System with Laser Chaos Decision-Maker (LCDM-NOMA)
4.1. Operating Principle
4.2. Performance Evaluation
5. Parameter Optimization for NOMA System with Laser Chaos Decision-Maker and Error Correcting Codes
5.1. NOMA System with Error Correcting Codes
5.2. Performance Evaluation with ECC
5.3. Parameter Optimization
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Abrardo, A.; Moretti, M.; Saggese, F. Power and Subcarrier Allocation in 5G NOMA-FD Systems. IEEE Trans. Commun. 2020, 19, 8246–8260. [Google Scholar] [CrossRef]
- Chen, X.; Gong, F.; Li, G.; Zhang, H.; Song, P. User Pairing and Pair Scheduling in Massive MIMO-NOMA Systems. IEEE Commun. Lett. 2018, 22, 788–791. [Google Scholar] [CrossRef]
- Krishnamoorthy, A.; Schober, R. Uplink and Downlink MIMO-NOMA with Simultaneous Triangularization. IEEE Trans. Wirel. Commun. 2021, 20, 3381–3396. [Google Scholar] [CrossRef]
- Jia, M.; Gao, Q.; Guo, Q.; Gu, X. Energy-Efficiency Power Allocation Design for UAV-Assisted Spatial NOMA. IEEE Internet Things J. 2021, 8, 15205–15215. [Google Scholar] [CrossRef]
- Islam, S.M.R.; Avazov, N.; Dobre, O.A.; Kwak, K. Power-Domain Non-Orthogonal Multiple Access (NOMA) in 5G Systems: Potentials and Challenges. IEEE Commun. Surv. Tutor. 2017, 19, 721–742. [Google Scholar] [CrossRef] [Green Version]
- Yang, G.; Xu, X.; Liang, Y.-C.; Di Renzo, M. Reconfigurable Intelligent Surface-Assisted Non-Orthogonal Multiple Access. IEEE Trans. Wirel. Commun. 2021, 20, 3137–3151. [Google Scholar] [CrossRef]
- Abuajwa, O.; Roslee, M.B.; Yusoff, Z.B. Simulated Annealing for Resource Allocation in Downlink NOMA Systems in 5G Networks. Appl. Sci. 2021, 11, 4592. [Google Scholar] [CrossRef]
- Cai, D.; Ding, Z.; Fan, P.; Yang, Z. On the Performance of NOMA with Hybrid ARQ. IEEE Trans. Veh. Technol. 2018, 67, 10033–10038. [Google Scholar] [CrossRef] [Green Version]
- Xu, Y.; Cai, D.; Fang, F.; Ding, Z.; Shen, C.; Zhu, G. Outage Constrained Power Efficient Design for Downlink NOMA Systems with Partial HARQ. IEEE Trans. Commun. 2020, 68, 5188–5201. [Google Scholar] [CrossRef]
- Panchal, A.; Dutta, A.K. Performance Analysis and Design of MIMO Power NOMA with Estimated Parameters Error Statistics Along with SIC and Hardware Imperfections. IEEE Trans. Veh. Technol. 2021, 70, 1488–1500. [Google Scholar] [CrossRef]
- Kishore, R.; Gurugopinath, S.; Muhaidat, S.; Bouanani, F.E.; Dobre, O.A. Sum Rate Analysis of Generalized Space Shift Keying-Aided MIMO-NOMA Systems. IEEE Trans. Veh. Technol. 2021, 70, 7232–7236. [Google Scholar] [CrossRef]
- Shahab, M.B.; Kade, M.F.; Shin, S.Y. A Virtual User Pairing Scheme to Optimally Utilize the Spectrum of Unpaired Users in Non-orthogonal Multiple Access. IEEE Signal Process Lett. 2016, 23, 1766–1770. [Google Scholar] [CrossRef]
- Mouni, N.S.; Kumar, A.; Upadhyay, P.K. Adaptive User Pairing for NOMA Systems with Imperfect SIC. IEEE Wirel. Commun. Lett. 2021, 10, 1547–1551. [Google Scholar] [CrossRef]
- He, C.; Hu, Y.; Chen, Y.; Zeng, B. Joint Power Allocation and Channel Assignment for NOMA with Deep Reinforcement Learning. IEEE J. Sel. Areas Commun. 2019, 37, 2200–2210. [Google Scholar] [CrossRef]
- Mounchili, S.; Hamouda, S. Pairing Distance Resolution and Power Control for Massive Connectivity Improvement in NOMA Systems. IEEE Trans. Veh. Technol. 2020, 69, 4093–4103. [Google Scholar] [CrossRef]
- Duan, Z.; Li, A.; Okada, N.; Ito, Y.; Chauvet, N.; Naruse, M.; Hasegawa, M. User Pairing Using Laser Chaos Decision Maker for NOMA Systems. Nonlinear Theory Appl. 2022, 13, 72–83. [Google Scholar] [CrossRef]
- Zhu, L.; Zhang, J.; Cao, X.; Wu, D.O. Optimal User Pairing for Downlink Non-Orthogonal Multiple Access (NOMA). IEEE Wirel. Commun. Lett. 2019, 8, 328–331. [Google Scholar] [CrossRef]
- Chahab, M.B.; Irfan, M.; Kader, M.F.; Shin, S.Y. User pairing schemes for capacity maximization in non-orthogonal multiple access systems. Wirel. Commun. Mob. Comput. 2016, 16, 2884–2894. [Google Scholar]
- Mouchili, S.; Hamouda, S. New User Grouping Scheme for Better User Pairing in NOMA Systems. In Proceedings of the International Wireless Communications and Mobile Computing (IWCMC), Limassol, Cyprus, 15–19 June 2020; pp. 820–825. [Google Scholar]
- Lee, J.; So, J. Reinforcement Learning-Based Joint User Pairing and Power Allocation in MIMO-NOMA Systems. Sensors 2020, 20, 7094. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Lv, T.; Ni, W.; Beaulieu, N.C.; Guo, Y.J. Joint Resource Management for MC-NOMA: A Deep Reinforcement Learning Approach. IEEE Trans. Wirel. Commun. 2021, 20, 5672–5688. [Google Scholar] [CrossRef]
- Rezwan, S.; Choi, W. Priority-Based Joint Resource Allocation with Deep Q-Learning for Heterogeneous NOMA Systems. IEEE Access 2021, 9, 41468–41481. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, H.; Long, K.; Karagiannidis, G.K. Deep Learning Based Radio Resource Management in NOMA Networks: User Association, Subchannel and Power Allocation. IEEE Trans. Netw. Sci. Eng. 2020, 7, 2406–2415. [Google Scholar] [CrossRef]
- Gui, G.; Huang, H.; Song, Y.; Sari, H. Deep Learning for and Effective Nonorthogonal Multiple Access Scheme. IEEE Trans. Veh. Technol. 2018, 67, 8440–8450. [Google Scholar] [CrossRef]
- Shastri, B.J.; Tait, A.N.; de Lima, T.F.; Pernice, W.H.; Bhaskaran, H.; Wright, C.D.; Prucnal, P.R. Photonics for artificial intelligence and neuromorphic computing. Nat. Photonics 2021, 15, 102–114. [Google Scholar] [CrossRef]
- Chen, Z.; Segev, M. Highlighting photonics: Looking into the next decade. eLight 2021, 1, 2. [Google Scholar] [CrossRef]
- Genty, G.; Salmela, L.; Dudley, J.M.; Brunner, D.; Kokhanovskiy, A.; Kobtsev, S.; Turitsyn, S.K. Machine learning and applications in ultrafast photonics. Nat. Photonics 2021, 15, 91–101. [Google Scholar] [CrossRef]
- Kitayama, K.; Notomi, M.; Naruse, M.; Inoue, K.; Kawakami, S.; Uchida, A. Novel frontier of photonics for data processing—Photonic accelerator. APL Photonics 2019, 4, 090901. [Google Scholar] [CrossRef] [Green Version]
- Uchida, A. Optical Communication with Chaotic Lasers: Applications of Nonlinear Dynamics and Synchronization; Wiley-VCH: Weinheim, Germany, 2012. [Google Scholar]
- Naruse, M.; Terashima, Y.; Uchida, A.; Kim, S.-J. Ultrafast photonic reinforcement learning based on laser chaos. Sci. Rep. 2017, 7, 8772. [Google Scholar] [CrossRef] [Green Version]
- Naruse, M.; Mihana, T.; Hori, H.; Saigo, H.; Okamura, K.; Hasegawa, M.; Uchida, A. Scalable photonic reinforcement learning by time-division multiplexing of laser chaos. Sci. Rep. 2018, 8, 10890. [Google Scholar] [CrossRef] [Green Version]
- Naruse, M.; Chauvet, N.; Uchida, A.; Drezet, A.; Bachelier, G.; Huant, S.; Hori, H. Decision Making Photonics: Solving Bandit Problems Using Photons. IEEE J. Sel. Top. Quantum Electron. 2019, 26, 7700210. [Google Scholar] [CrossRef]
- Okada, N.; Hasegawa, M.; Chauvet, N.; Li, A.; Naruse, M. Analysis on Effectiveness of Surrogate Data-Based Laser Chaos Decision Maker. Complexity 2021, 2021, 8877660. [Google Scholar] [CrossRef]
- Furukawa, H.; Li, A.; Shoji, Y.; Watanabe, Y.; Kim, S.J.; Sato, K.; Andreopoulos, Y.; Hasegawa, M. A Channel selection algorithm using reinforcement learning for mobile devices in massive IoT system. In Proceedings of the 2021 IEEE 18th Annual Consumer Communications & Networking Conference (CCNC), Virtual, 9–12 January 2021. [Google Scholar]
- Takeuchi, S.; Hasegawa, M.; Kano, K.; Uchida, A.; Chauvet, N.; Naruse, M. Dynamic channel selection in wireless communications via a multi-armed bandit algorithm using laser chaos time series. Sci. Rep. 2020, 10, 1574. [Google Scholar] [CrossRef]
- Kanemasa, H.; Li, A.; Naruse, M.; Chauvet, N.; Hasegawa, M. Dynamic channel bonding in WLANs by hierarchical laser chaos decision maker. Nonlinear Theory Appl. 2022, 13, 84–100. [Google Scholar] [CrossRef]
- Li, A.; Fujisawa, M.; Urabe, I.; Kitagawa, R.; Kim, S.J.; Hasegawa, M. A lightweight decentralized reinforcement learning based channel selection approach for high-density LoRaWAN. In Proceedings of the 2021 IEEE International Symposium on Dynamic Spectrum Access Networks (DySPAN), Virtual, 13–15 December 2021. [Google Scholar]
- Yahya, H.; Alsusa, E.; Al-Dweik, A. Exact BER Analysis of NOMA with Arbitrary Number of Users and Modulation Orders. IEEE Trans. Commun. 2021, 69, 6330–6344. [Google Scholar] [CrossRef]
- Otsuka, T.; Kurasawa, K.; Duan, Z.; Li, A.; Sato, K.; Takesue, H.; Aihara, K.; Inaba, K.; Hasegawa, M. Coherent Ising Machine Based Optimal Channel Allocation and User Pairing in NOMA Networks. In Proceedings of the 2021 International Conference on Artificial Intelligence in Information and Communication (ICAIIC), Virtual, 13–16 April 2021. [Google Scholar]











| Cell Radius [m] | 100 | 200 | 300 | 400 | 500 | 600 | 700 | 800 | 900 | 1000 |
|---|---|---|---|---|---|---|---|---|---|---|
| SNR [dB] | 74.8 | 65.8 | 60.5 | 56.7 | 53.8 | 51.4 | 49.5 | 47.7 | 46.2 | 44.8 |
| Parameter | Value |
|---|---|
| Number of users | 10 |
| Cell shape | Circular |
| Deployment of users | Uniform distribution |
| Path-loss exponent | |
| Propagation condition | Non-line-of-sight propagation |
| Transmission power allocated to each pair | dBm |
| Power allocation factor for the pair | |
| Noise power spectral density | dBm |
| Total bandwidth | MHz |
| Reward criterion based on the number of receipt ACK information | (equal to the number of users) |
| Forgetting rate | |
| Number of bits sent to each user | bit, |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sugiyama, M.; Li, A.; Duan, Z.; Naruse, M.; Hasegawa, M. BER Minimization by User Pairing in Downlink NOMA Using Laser Chaos Decision-Maker. Electronics 2022, 11, 1452. https://doi.org/10.3390/electronics11091452
Sugiyama M, Li A, Duan Z, Naruse M, Hasegawa M. BER Minimization by User Pairing in Downlink NOMA Using Laser Chaos Decision-Maker. Electronics. 2022; 11(9):1452. https://doi.org/10.3390/electronics11091452
Chicago/Turabian StyleSugiyama, Masaki, Aohan Li, Zengchao Duan, Makoto Naruse, and Mikio Hasegawa. 2022. "BER Minimization by User Pairing in Downlink NOMA Using Laser Chaos Decision-Maker" Electronics 11, no. 9: 1452. https://doi.org/10.3390/electronics11091452
APA StyleSugiyama, M., Li, A., Duan, Z., Naruse, M., & Hasegawa, M. (2022). BER Minimization by User Pairing in Downlink NOMA Using Laser Chaos Decision-Maker. Electronics, 11(9), 1452. https://doi.org/10.3390/electronics11091452







