Small Defect Detection Based on Local Structure Similarity for Magnetic Tile Surface
Abstract
:1. Introduction
2. Related Work
3. Algorithm Design
3.1. Estimate Possible Defect Areas
3.2. Precise Locating of Defective Blocks
3.3. Improve Contrast of Defective Areas
3.4. Segment Defective Areas
3.5. Analysis of Computational Complexity
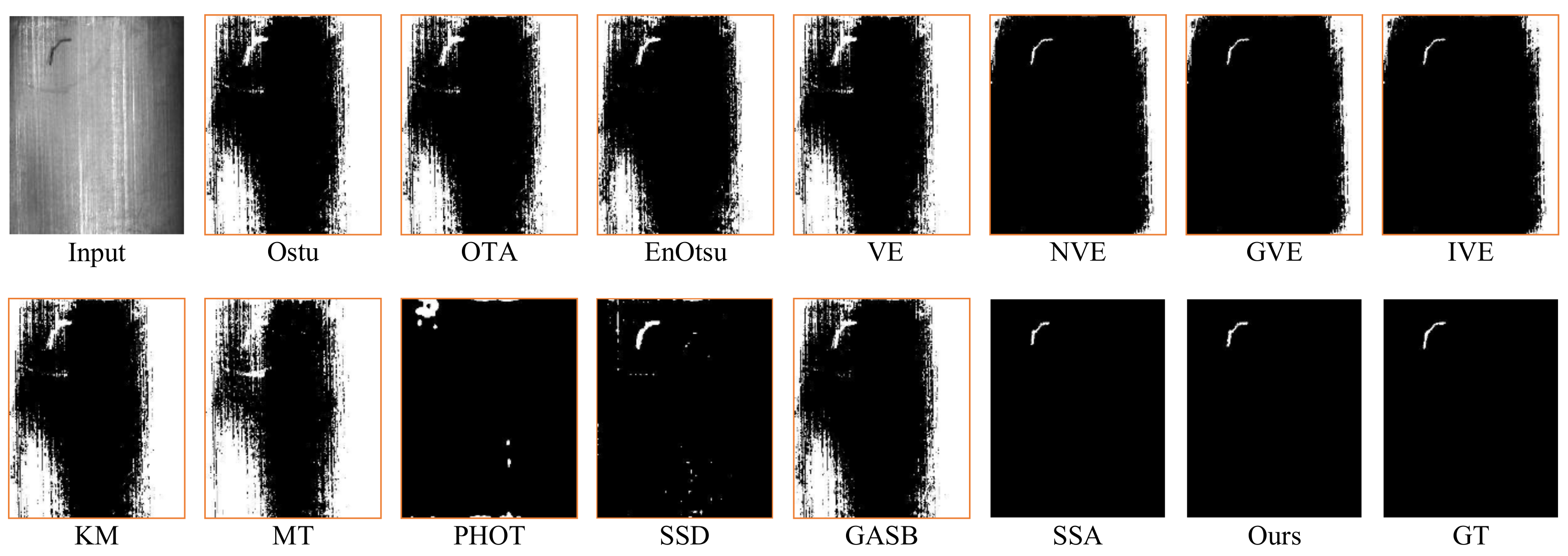
4. Experiments
4.1. Evaluation Metrics
4.2. Datasets
4.3. Performance Comparison with Related Method
4.3.1. Crack Defect Detect
4.3.2. Blowhole Defect Detection
4.3.3. Fabric Defect Detect
4.3.4. Effects of the Patch Size
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, Z.; Khajepour, A.; Song, J. A comprehensive review of the key technologies for pure electric vehicles. Energy 2019, 182, 824–839. [Google Scholar] [CrossRef]
- Salkuti, S.R. Energy storage and electric vehicles: Technology, operation, challenges, and cost-benefit analysis. Int. J. Adv. Comput. Sci. Appl. 2021, 12, 40–45. [Google Scholar] [CrossRef]
- Zarma, T.A.; Galadima, A.A.; Aminu, M.A. Review of motors for electrical vehicles. J. Sci. Res. Rep. 2019, 24, 1–6. [Google Scholar] [CrossRef]
- Cao, X.; Chen, B.; He, W. Unsupervised Defect Segmentation of Magnetic Tile Based on Attention Enhanced Flexible U-Net. IEEE Trans. Instrum. Meas. 2022, 71, 1–10. [Google Scholar] [CrossRef]
- Xie, L.; Xiang, X.; Xu, H.; Wang, L.; Lin, L.; Yin, G. FFCNN: A deep neural network for surface defect detection of magnetic tile. IEEE Trans. Ind. Electron. 2020, 68, 3506–3516. [Google Scholar] [CrossRef]
- Huang, Y.; Qiu, C.; Yuan, K. Surface defect saliency of magnetic tile. Vis. Comput. 2020, 36, 85–96. [Google Scholar] [CrossRef]
- Zhu, Z.; Zhu, P.; Zeng, J.; Qian, X. A Surface Fatal Defect Detection Method for Magnetic Tiles based on Semantic Segmentation and Object Detection: IEEE ITAIC(ISSN:2693-2865). In Proceedings of the 2022 IEEE 10th Joint International Information Technology and Artificial Intelligence Conference (ITAIC), Chongqing, China, 17–19 June 2022; Volume 10, pp. 2580–2586. [Google Scholar] [CrossRef]
- Adibhatla, V.A.; Huang, Y.C.; Chang, M.C.; Kuo, H.C.; Utekar, A.; Chih, H.C.; Abbod, M.F.; Shieh, J.S. Unsupervised Anomaly Detection in Printed Circuit Boards through Student–Teacher Feature Pyramid Matching. Electronics 2021, 10, 3177. [Google Scholar] [CrossRef]
- Yang, C.; Luo, J.; Liu, C.; Li, M.; Dai, S.L. Haptics Electromyography Perception and Learning Enhanced Intelligence for Teleoperated Robot. IEEE Trans. Autom. Sci. Eng. 2019, 16, 1512–1521. [Google Scholar] [CrossRef] [Green Version]
- Ying, H.; Chen, Y. A Neural Network Approach to Subjective Human Face Perception Classification based on Social Characteristics. In Proceedings of the 2021 IEEE 10th Data Driven Control and Learning Systems Conference (DDCLS), Suzhou, China, 14–16 May 2021; pp. 457–462. [Google Scholar] [CrossRef]
- Zhong, Z.; Ma, Z. A novel defect detection algorithm for flexible integrated circuit package substrates. IEEE Trans. Ind. Electron. 2022, 69, 2117–2126. [Google Scholar] [CrossRef]
- Wang, H.; Peng, J.; Yue, S. A directionally selective small target motion detecting visual neural network in cluttered backgrounds. IEEE Trans. Cybern. 2018, 50, 1541–1555. [Google Scholar] [CrossRef]
- Wang, H.; Peng, J.; Zheng, X.; Yue, S. A robust visual system for small target motion detection against cluttered moving backgrounds. IEEE Trans. Neural Netw. Learn. Syst. 2019, 31, 839–853. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Alzahrani, A.I.; Ayadi, M.; Asiri, M.M.; Al-Rasheed, A.; Ksibi, A. Detecting the Presence of Malware and Identifying the Type of Cyber Attack Using Deep Learning and VGG-16 Techniques. Electronics 2022, 11, 3665. [Google Scholar] [CrossRef]
- Li, L.; Xie, N.; Yuan, S. A Federated Learning Framework for Breast Cancer Histopathological Image Classification. Electronics 2022, 11, 3767. [Google Scholar] [CrossRef]
- Song, Z.; Wang, Y.; Fan, J.; Tan, T.; Zhang, Z. Self-Supervised Predictive Learning: A Negative-Free Method for Sound Source Localization in Visual Scenes. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 19–20 June 2022; pp. 3222–3231. [Google Scholar]
- Feng, G.; Jiang, Z.; Tan, X.; Cheng, F. Hierarchical Clustering-Based Image Retrieval for Indoor Visual Localization. Electronics 2022, 11, 3609. [Google Scholar] [CrossRef]
- Otsu, N. A threshold selection method from gray-level histograms. IEEE Trans. Syst. Man, Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef] [Green Version]
- Bradley, D.; Roth, G. Adaptive thresholding using the integral image. J. Graph. Tools 2007, 12, 13–21. [Google Scholar] [CrossRef]
- Vrochidou, E.; Sidiropoulos, G.K.; Ouzounis, A.G.; Lampoglou, A.; Tsimperidis, I.; Papakostas, G.A.; Sarafis, I.T.; Kalpakis, V.; Stamkos, A. Towards Robotic Marble Resin Application: Crack Detection on Marble Using Deep Learning. Electronics 2022, 11, 3289. [Google Scholar] [CrossRef]
- Aydin, I.; Akin, E.; Karakose, M. Defect classification based on deep features for railway tracks in sustainable transportation. Appl. Soft Comput. 2021, 111, 107706. [Google Scholar] [CrossRef]
- Bergmann, P.; Löwe, S.; Fauser, M.; Sattlegger, D.; Steger, C. Improving Unsupervised Defect Segmentation by Applying Structural Similarity to Autoencoders. In Proceedings of the VISIGRAPP (5: VISAPP), Prague, Czech Republic, 25–27 February 2019. [Google Scholar]
- Goldstein, T.; Bresson, X.; Osher, S. Geometric applications of the split Bregman method: Segmentation and surface reconstruction. J. Sci. Comput. 2010, 45, 272–293. [Google Scholar] [CrossRef] [Green Version]
- Oh, C.; Kim, H.; Cho, H. Rotation Estimation and Segmentation for Patterned Image Vision Inspection. Electronics 2021, 10, 3040. [Google Scholar] [CrossRef]
- Kanungo, T.; Mount, D.M.; Netanyahu, N.S.; Piatko, C.D.; Silverman, R.; Wu, A.Y. An efficient k-means clustering algorithm: Analysis and implementation. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 881–892. [Google Scholar] [CrossRef]
- Truong, M.T.N.; Kim, S. Automatic image thresholding using Otsu’s method and entropy weighting scheme for surface defect detection. Soft Comput. 2018, 22, 4197–4203. [Google Scholar] [CrossRef]
- Ng, H.F. Automatic thresholding for defect detection. Pattern Recognit. Lett. 2006, 27, 1644–1649. [Google Scholar] [CrossRef]
- Fan, J.L.; Lei, B. A modified valley-emphasis method for automatic thresholding. Pattern Recognit. Lett. 2012, 33, 703–708. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, J.; Zhao, Q.; Li, C. A fabric defect detection algorithm based on improved valley-emphasis method. Res. J. Appl. Sci. Eng. Technol. 2014, 7, 2427–2431. [Google Scholar] [CrossRef]
- Achanta, R.; Hemami, S.; Estrada, F.; Susstrunk, S. Frequency-tuned salient region detection. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 1597–1604. [Google Scholar]
- Dice, L.R. Measures of the amount of ecologic association between species. Ecology 1945, 26, 297–302. [Google Scholar] [CrossRef]
- Liu, Y.; Xu, J.; Wu, Y. A CISG Method for Internal Defect Detection of Solar Cells in Different Production Processes. IEEE Trans. Ind. Electron. 2022, 69, 8452–8462. [Google Scholar] [CrossRef]
- Luo, J.; Yang, Z.; Li, S.; Wu, Y. FPCB Surface Defect Detection: A Decoupled Two-Stage Object Detection Framework. IEEE Trans. Instrum. Meas. 2021, 70, 1–11. [Google Scholar] [CrossRef]
- Dong, H.; Song, K.; He, Y.; Xu, J.; Yan, Y.; Meng, Q. PGA-Net: Pyramid Feature Fusion and Global Context Attention Network for Automated Surface Defect Detection. IEEE Trans. Ind. Inform. 2020, 16, 7448–7458. [Google Scholar] [CrossRef]
- Liu, W.; Liu, Z.; Wang, H.; Han, Z. An Automated Defect Detection Approach for Catenary Rod-Insulator Textured Surfaces Using Unsupervised Learning. IEEE Trans. Instrum. Meas. 2020, 69, 8411–8423. [Google Scholar] [CrossRef]
- Mei, S.; Yang, H.; Yin, Z. An Unsupervised-Learning-Based Approach for Automated Defect Inspection on Textured Surfaces. IEEE Trans. Instrum. Meas. 2018, 67, 1266–1277. [Google Scholar] [CrossRef]
- Niu, M.; Song, K.; Huang, L.; Wang, Q.; Yan, Y.; Meng, Q. Unsupervised Saliency Detection of Rail Surface Defects Using Stereoscopic Images. IEEE Trans. Ind. Inform. 2021, 17, 2271–2281. [Google Scholar] [CrossRef]
- An, Y.; Lu, Y.; Wu, T. Segmentation Method of Magnetic Tile Surface Defects Based on Deep Learning. Int. J. Comput. Commun. Control 2022, 17, 4502. [Google Scholar] [CrossRef]
- Aiger, D.; Talbot, H. The phase only transform for unsupervised surface defect detection. In Proceedings of the 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010; pp. 295–302. [Google Scholar]
- Su, B.; Chen, H.; Zhu, Y.; Liu, W.; Liu, K. Classification of manufacturing defects in multicrystalline solar cells with novel feature descriptor. IEEE Trans. Instrum. Meas. 2019, 68, 4675–4688. [Google Scholar] [CrossRef]
- Peng, H.; Li, B.; Ling, H.; Hu, W.; Xiong, W.; Maybank, S.J. Salient object detection via structured matrix decomposition. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 39, 818–832. [Google Scholar] [CrossRef] [Green Version]
- Imamoglu, N.; Lin, W.; Fang, Y. A saliency detection model using low-level features based on wavelet transform. IEEE Trans. Multimed. 2012, 15, 96–105. [Google Scholar] [CrossRef]
- Song, G.; Song, K.; Yan, Y. Saliency detection for strip steel surface defects using multiple constraints and improved texture features. Opt. Lasers Eng. 2020, 128, 106000. [Google Scholar] [CrossRef]
- Xie, L.; Lin, L.; Yin, M.; Meng, L.; Yin, G. A novel surface defect inspection algorithm for magnetic tile. Appl. Surf. Sci. 2016, 375, 118–126. [Google Scholar] [CrossRef]
- Li, X.; Jiang, H.; Yin, G. Detection of surface crack defects on ferrite magnetic tile. Ndt E Int. 2014, 62, 6–13. [Google Scholar] [CrossRef]
- Yang, C.; Liu, P.; Yin, G.; Wang, L. Crack detection in magnetic tile images using nonsubsampled shearlet transform and envelope gray level gradient. Opt. Laser Technol. 2017, 90, 7–17. [Google Scholar] [CrossRef]
- Ben Gharsallah, M.; Ben Braiek, E. Defect identification in magnetic tile images using an improved nonlinear diffusion method. Trans. Inst. Meas. Control 2021, 43, 2413–2424. [Google Scholar] [CrossRef]
- Zhang, H.; Qian, J.; Zhang, B.; Yang, J.; Gong, C.; Wei, Y. Low-Rank Matrix Recovery via Modified Schatten- p Norm Minimization with Convergence Guarantees. IEEE Trans. Image Process. 2020, 29, 3132–3142. [Google Scholar] [CrossRef] [PubMed]
- Candès, E.J.; Li, X.; Ma, Y.; Wright, J. Robust principal component analysis? J. ACM (JACM) 2011, 58, 1–37. [Google Scholar] [CrossRef]
- Zhou, Z.; Li, X.; Wright, J.; Candes, E.; Ma, Y. Stable principal component pursuit. In Proceedings of the 2010 IEEE International Symposium on Information Theory, Austin, TX, USA, 13–18 June 2010; pp. 1518–1522. [Google Scholar]
- Gao, C.; Meng, D.; Yang, Y.; Wang, Y.; Zhou, X.; Hauptmann, A.G. Infrared patch-image model for small target detection in a single image. IEEE Trans. Image Process. 2013, 22, 4996–5009. [Google Scholar] [CrossRef] [PubMed]
- Lin, Z.; Ganesh, A.; Wright, J.; Wu, L.; Chen, M.; Ma, Y. Fast convex optimization algorithms for exact recovery of a corrupted low-rank matrix. In Coordinated Science Laboratory Report No. UILU-ENG-09-2214, DC-246; Coordinated Science Laboratory, University of Illinois at Urbana-Champaign: Urbana, IL, USA, 2009; Available online: https://core.ac.uk/download/pdf/158319805.pdf (accessed on 10 November 2022).
- Lin, Z.; Chen, M.; Ma, Y. The augmented lagrange multiplier method for exact recovery of corrupted low-rank matrices. arXiv 2010, arXiv:1009.5055. [Google Scholar]
- Petro, A.B.; Sbert, C.; Morel, J.M. Multiscale retinex. Image Process. Line 2014, 2014, 71–88. [Google Scholar] [CrossRef]
- Jobson, D.J.; Rahman, Z.u.; Woodell, G.A. A multiscale retinex for bridging the gap between color images and the human observation of scenes. IEEE Trans. Image Process. 1997, 6, 965–976. [Google Scholar] [CrossRef] [Green Version]
- Ng, H.F.; Jargalsaikhan, D.; Tsai, H.C.; Lin, C.Y. An improved method for image thresholding based on the valley-emphasis method. In Proceedings of the 2013 Asia-Pacific Signal and Information Processing Association Annual Summit and Conference, Kaohsiung, Taiwan, 29 October–1 November 2013; pp. 1–4. [Google Scholar]
- Yan, H.; Paynabar, K.; Shi, J. Anomaly detection in images with smooth background via smooth-sparse decomposition. Technometrics 2017, 59, 102–114. [Google Scholar] [CrossRef]








| (%) | (%) | (%) | (%) | |||||
|---|---|---|---|---|---|---|---|---|
| EnOtsu | 74.615 | 9.850 | 78.799 | 74.613 | 0.115 | 0.087 | 0.144 | 0.528 |
| NVE | 96.089 | 7.596 | 18.663 | 96.245 | 0.080 | 0.052 | 0.088 | 0.513 |
| GVE | 96.089 | 7.596 | 18.663 | 96.245 | 0.080 | 0.052 | 0.088 | 0.513 |
| IVE | 96.089 | 7.596 | 18.663 | 96.245 | 0.080 | 0.052 | 0.088 | 0.513 |
| SSA | 99.928 | 95.393 | 70.728 | 99.993 | 0.881 | 0.683 | 0.810 | 0.784 |
| Ours | 99.966 | 91.173 | 90.303 | 99.982 | 0.908 | 0.827 | 0.904 | 0.862 |
| (%) | (%) | (%) | (%) | |||||
|---|---|---|---|---|---|---|---|---|
| Ostu | 44.241 | 0.114 | 100.000 | 44.205 | 0.001 | 0.001 | 0.002 | 0.500 |
| OTA | 44.241 | 0.114 | 100.000 | 44.205 | 0.001 | 0.001 | 0.002 | 0.500 |
| EnOtsu | 35.388 | 0.102 | 100.000 | 35.347 | 0.001 | 0.001 | 0.002 | 0.500 |
| VE | 46.073 | 26.388 | 91.667 | 46.032 | 0.261 | 0.209 | 0.258 | 0.585 |
| NVE | 66.664 | 33.362 | 35.000 | 66.670 | 0.062 | 0.017 | 0.032 | 0.507 |
| GVE | 66.664 | 33.362 | 35.000 | 66.670 | 0.062 | 0.017 | 0.032 | 0.507 |
| IVE | 66.664 | 33.362 | 35.000 | 66.670 | 0.062 | 0.017 | 0.032 | 0.507 |
| kmeans | 44.141 | 0.113 | 100.000 | 44.104 | 0.001 | 0.001 | 0.002 | 0.500 |
| MT | 50.447 | 0.130 | 99.415 | 50.415 | 0.002 | 0.001 | 0.003 | 0.500 |
| PHOT | 99.231 | 0.612 | 26.667 | 99.288 | 0.008 | 0.006 | 0.012 | 0.502 |
| SSD | 99.336 | 39.233 | 50.117 | 99.373 | 0.367 | 0.248 | 0.360 | 0.592 |
| GASB | 45.611 | 0.117 | 100.000 | 45.575 | 0.002 | 0.001 | 0.002 | 0.500 |
| SSA | 99.911 | 45.788 | 76.111 | 99.932 | 0.453 | 0.326 | 0.487 | 0.628 |
| Ours | 99.946 | 63.156 | 64.865 | 99.974 | 0.597 | 0.419 | 0.583 | 0.661 |
| area | 21~40 | 51~80 | 81~110 | 111~140 | 141~180 | 181~223 | 21~223 |
| 33 | 70 | 102 | 129 | 160 | 206.8 | 98.6 | |
| 5.7 × 5.7 | 8.4 × 8.4 | 10.1 × 10.1 | 11.4 × 11.4 | 12.7 × 12.7 | 14.4 × 14.4 | 9.9 × 9.9 |
| height | 99.992 | 99.992 | 99.990 | 99.978 | 99.965 | 99.932 | 99.974 |
| height | 99.992 | 99.992 | 99.990 | 99.978 | 99.964 | 99.932 | 99.975 |
| height | 99.992 | 99.992 | 99.990 | 99.978 | 99.967 | 99.940 | 99.977 |
| height | 99.992 | 99.992 | 99.990 | 99.973 | 99.962 | 99.927 | 99.973 |
| height | 99.992 | 99.961 | 99.968 | 99.973 | 99.964 | 99.932 | 99.869 |
| height | 99.983 | 99.952 | 99.937 | 99.973 | 99.960 | 99.928 | 99.861 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhong, Z.; Wang, H.; Xiang, D. Small Defect Detection Based on Local Structure Similarity for Magnetic Tile Surface. Electronics 2023, 12, 185. https://doi.org/10.3390/electronics12010185
Zhong Z, Wang H, Xiang D. Small Defect Detection Based on Local Structure Similarity for Magnetic Tile Surface. Electronics. 2023; 12(1):185. https://doi.org/10.3390/electronics12010185
Chicago/Turabian StyleZhong, Zhiyan, Hongxin Wang, and Dan Xiang. 2023. "Small Defect Detection Based on Local Structure Similarity for Magnetic Tile Surface" Electronics 12, no. 1: 185. https://doi.org/10.3390/electronics12010185
APA StyleZhong, Z., Wang, H., & Xiang, D. (2023). Small Defect Detection Based on Local Structure Similarity for Magnetic Tile Surface. Electronics, 12(1), 185. https://doi.org/10.3390/electronics12010185





