A Novel Control Scheme Based on Exact Feedback Linearization Achieving Robust Constant Voltage for Boost Converter
Abstract
:1. Introduction
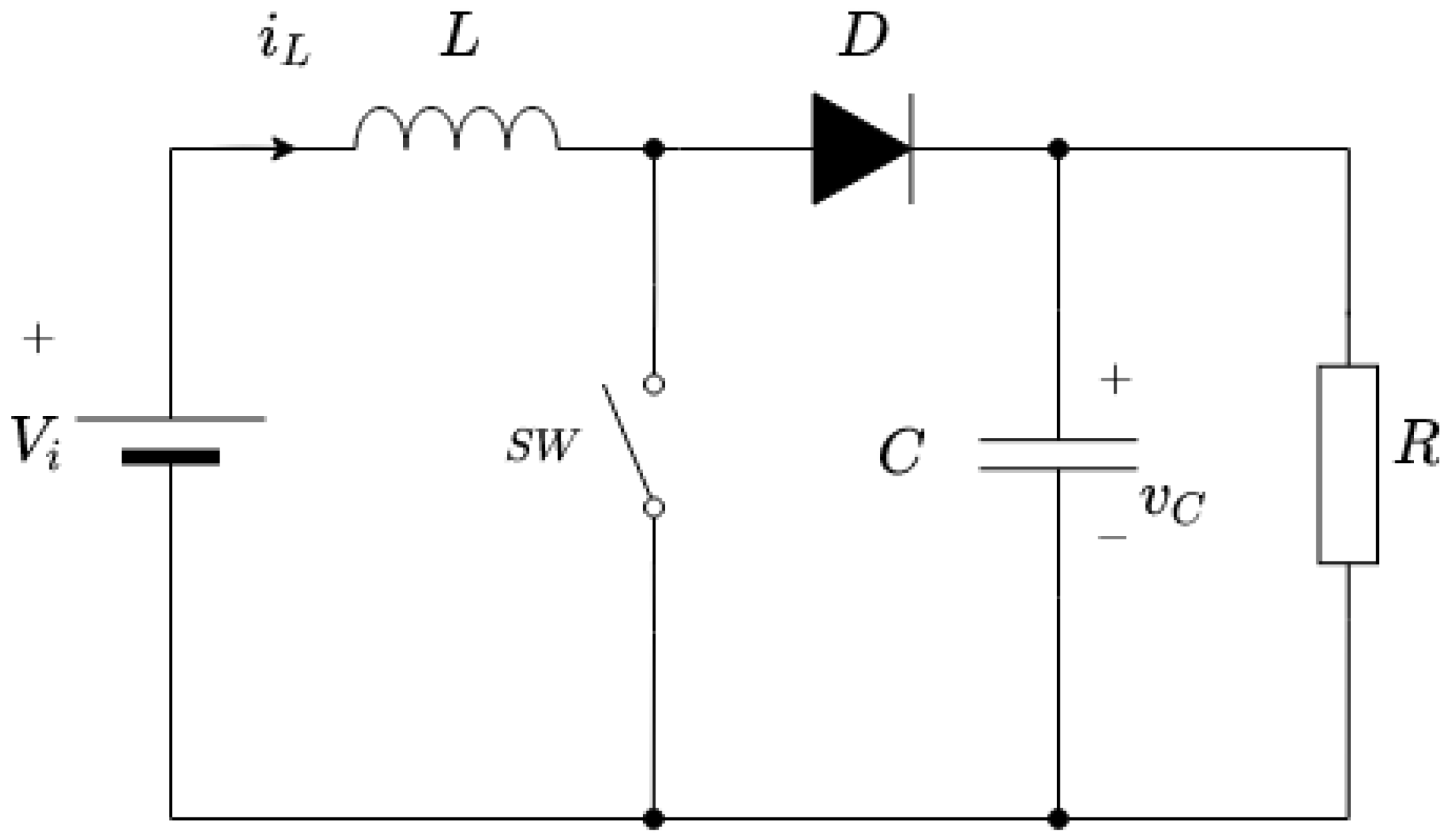
2. State Space Model of Nonlinear CCM Boost Converter
3. Principle of State Feedback Linearization
- the rank of system matrix should be equal with system dimension;
- The vector field is involutory in .
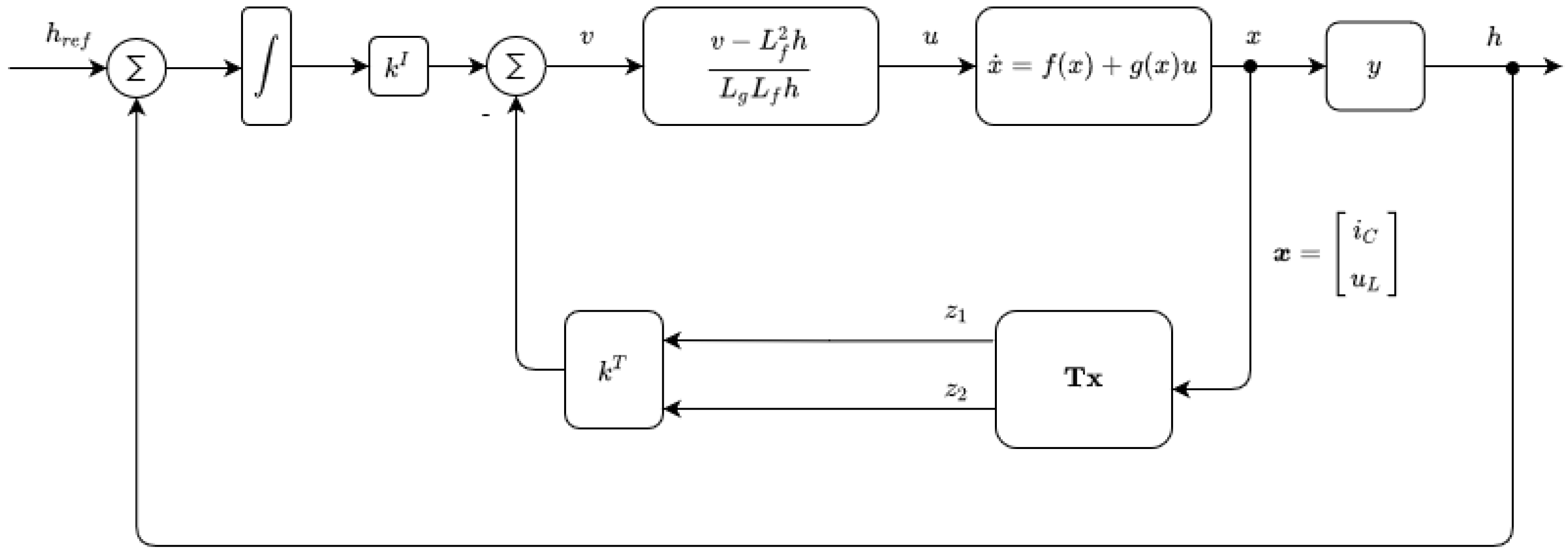
4. Controller Design Applying Exact Feedback Linearization with Integrator
Reference Value Calculation
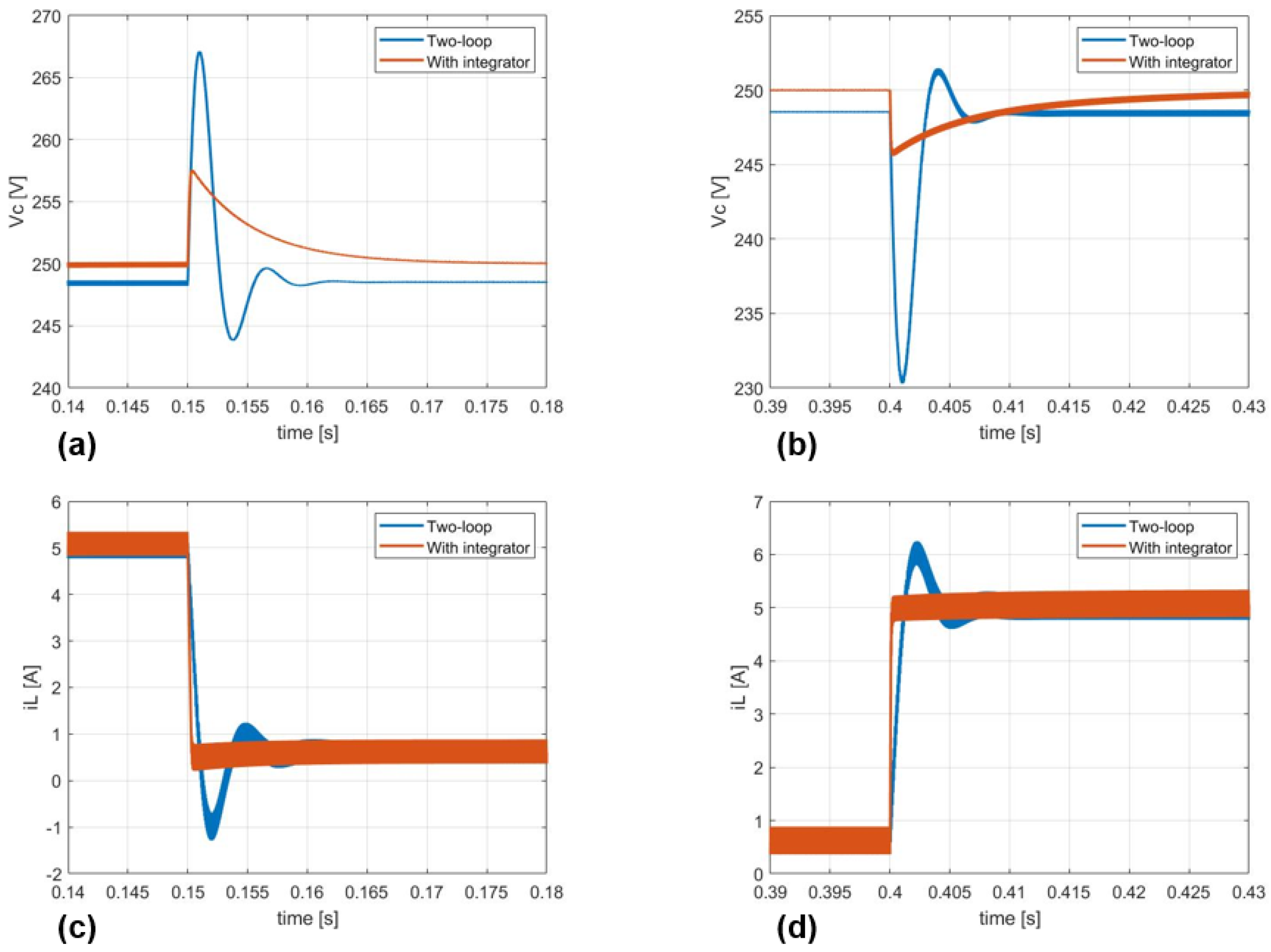
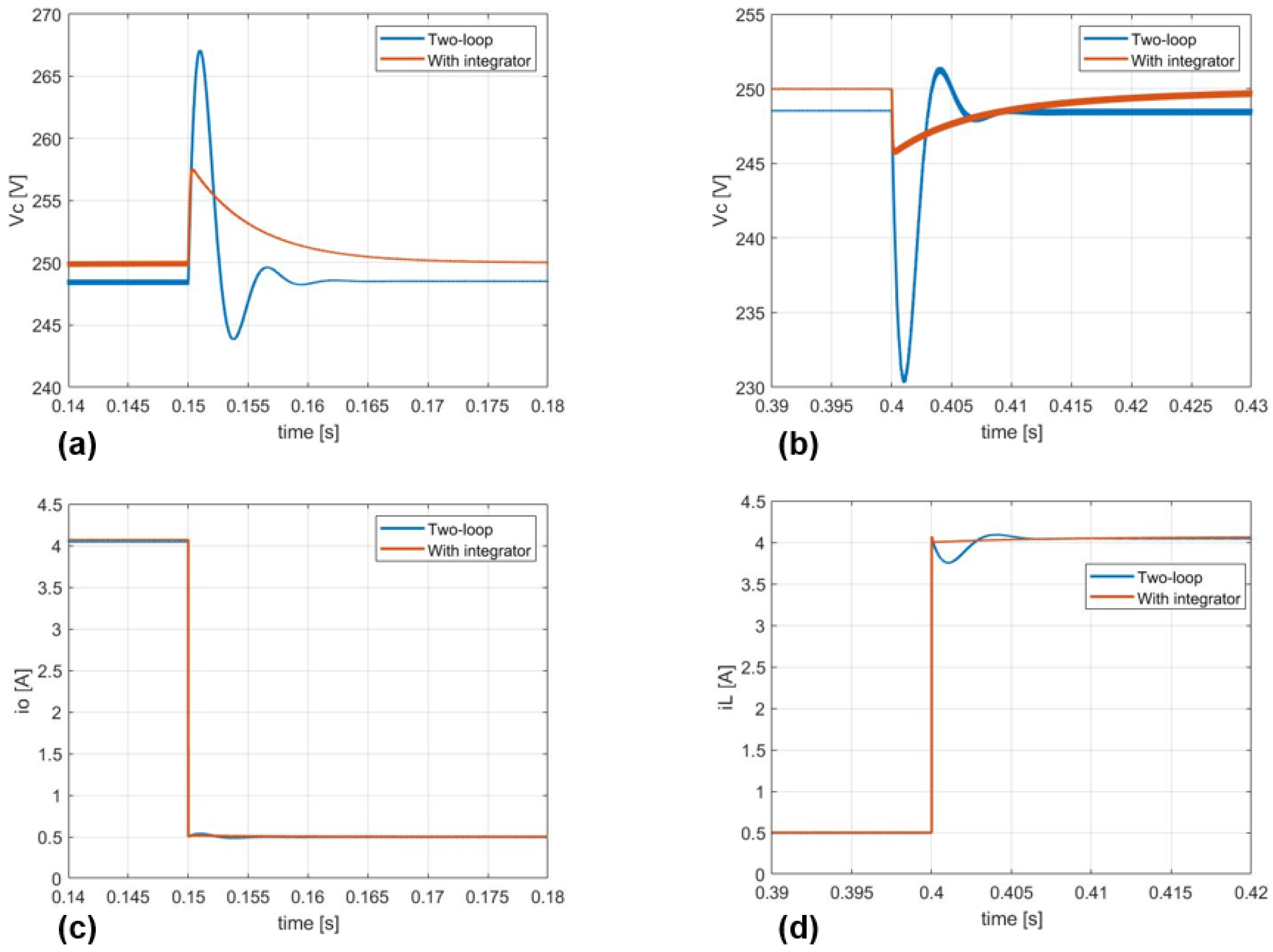
5. Simulation Results
5.1. Examined Scenario
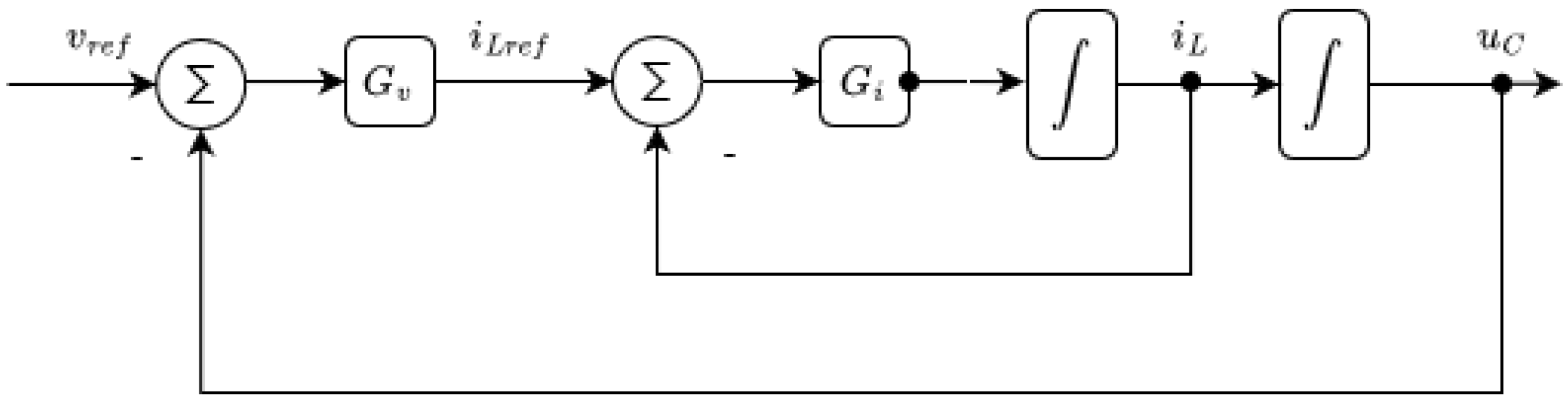
5.2. Linear Controller Design
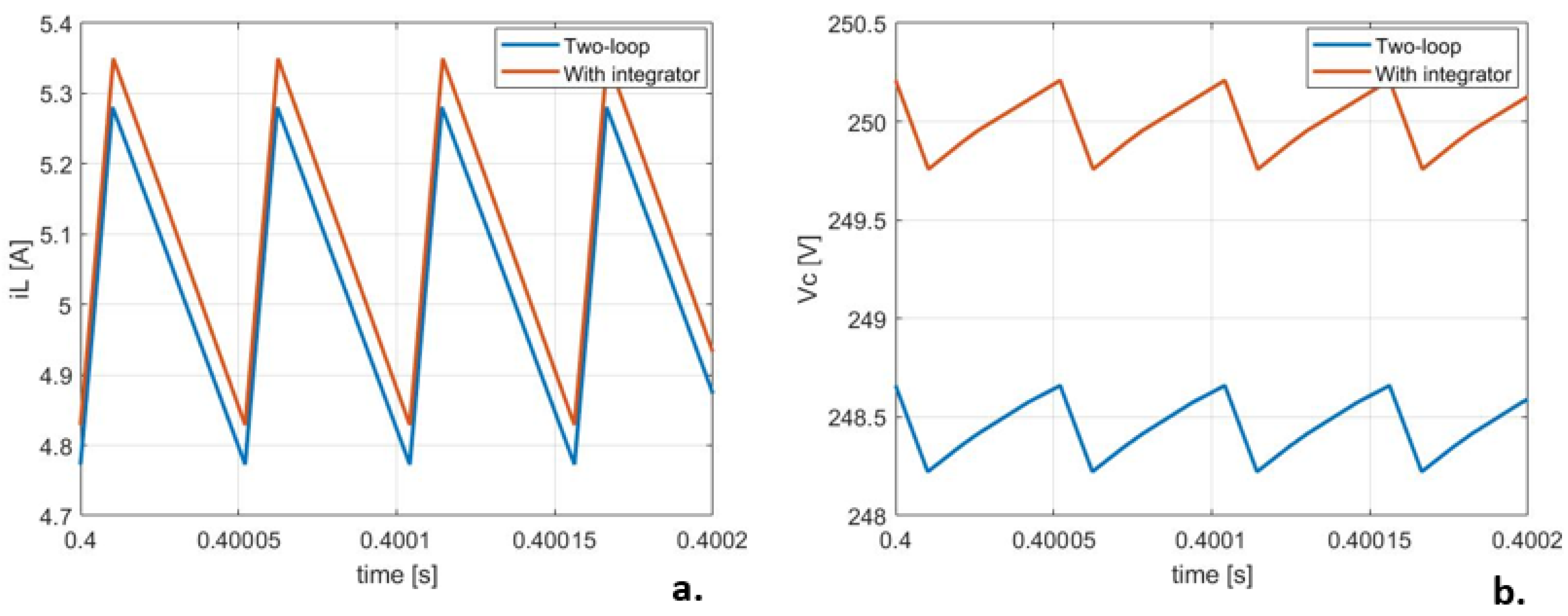
5.3. Steady-State Behavior
5.4. Dynamic Behavior
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shepherd, W.; Zhang, L. Power Converter Circuits; Marcel Dekker, Inc.: New York, NY, USA, 2004. [Google Scholar]
- Alatai, S.; Salem, M.; Ishak, D.; Das, H.S.; Alhuyi Nazari, M.; Bughneda, A.; Kamarol, M. A Review on State-of-the-Art Power Converters: Bidirectional, Resonant, Multilevel Converters and Their Derivatives. Appl. Sci. 2021, 11, 10172. [Google Scholar] [CrossRef]
- Mumtaz, F.; Yahaya, N.Z.; Meraj, S.T.; Singh, B.; Kannan, R.; Ibrahim, O. Review on non-isolated DC-DC converters and their control techniques for renewable energy applications. Ain Shams Eng. J. 2021, 12, 3747–3763. [Google Scholar] [CrossRef]
- Hemasuk, K.; Po-Ngam, S. The simplified regenerative boost converter for electric vehicle applications. In Proceedings of the 2017 International Electrical Engineering Congress (iEECON), Pattaya, Thailand, 8–10 March 2017; pp. 1–4. [Google Scholar]
- Prabhakar, S.; JL, F.D. A comparative study on the performance of interleaved converters for EV battery charging. In Proceedings of the 2016 IEEE 6th International Conference on Power Systems (ICPS), New Delhi, India, 4–6 March 2016; pp. 1–6. [Google Scholar]
- Mohanty, P.R.; Panda, A.K.; Das, D. An active PFC boost converter topology for power factor correction. In Proceedings of the 2015 Annual IEEE India Conference (INDICON), Online, 17–20 December 2015; pp. 1–5. [Google Scholar]
- Leoncini, M.; Levantino, S.; Ghioni, M. Design issues and performance analysis of CCM boost converters with RHP zero mitigation via inductor current sensing. J. Power Electron. 2021, 21, 285–295. [Google Scholar] [CrossRef]
- Almawlawe, M.D.H.; Kovandzic, M. A Modified Method for Tuning PID Controller for Buck-Boost Converter. Int. J. Adv. Eng. Res. Sci. 2016, 3, 20–26. [Google Scholar] [CrossRef]
- Bouziane, H.A.; Bouiadjra, R.B.; Debbat, M. Design of robust LQR control for DC-DC multilevel boost converter. In Proceedings of the 2015 4th International Conference on Electrical Engineering (ICEE), Boumerdes, Algeria, 13–15 December 2015; pp. 1–5. [Google Scholar]
- Prasad, G.; Kumar, A. A Comparison Between Sliding Mode Control and Feedback Linearization. In Proceedings of the 2018 5th IEEE Uttar Pradesh Section International Conference on Electrical, Electronics and Computer Engineering (UPCON), Gorakhpur, India, 2 November 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Mandal, S.; Mishra, D. Robust Control of Buck Converter using H-infinity Control Algorithm. In Proceedings of the 2018 IEEE Applied Signal Processing Conference (ASPCON), Kolkata, India, 7–9 December 2018; pp. 163–167. [Google Scholar] [CrossRef]
- Zheng, H.; Shuai, D. Nonlinear control of Boost converter by state feedback exact linearization. In Proceedings of the 2012 24th Chinese control and decision conference (CCDC), Taiyuan, China, 23–25 May 2012; pp. 3502–3506. [Google Scholar] [CrossRef]
- Csizmadia, M.; Kuczmann, M. Extended Feedback Linearisation Control of Non-ideal DCDC Buck Converter in Continuous-conduction Mode. Power Electron. Drives 2022, 7, 1–8. [Google Scholar] [CrossRef]
- Saraf, P.; Gupta, M.; Parimi, A.M. A Comparative Study Between a Classical and Optimal Controller for a Quadrotor. In Proceedings of the 2020 IEEE 17th India Council International Conference (INDICON), New Delhi, India, 10–13 December 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Huang, H.; Zhang, C.; Ding, W.; Xinke, Z.; Sun, G.; Wang, H. Design of the Depth Controller for a Floating Ocean Seismograph. J. Mar. Sci. Eng. 2020, 8, 166. [Google Scholar] [CrossRef]
- Utkin, V.; Lee, J. Chattering Problem in Sliding Mode Control Systems. In Proceedings of the International Workshop on Variable Structure Systems, Alghero, Italy, 5–7 June 2006; pp. 346–350. [Google Scholar] [CrossRef]
- Komurcugil, H.; Biricik, S.; Bayhan, S.; Zhang, Z. Sliding Mode Control: Overview of Its Applications in Power Converters. IEEE Ind. Electron. Mag. 2021, 15, 40–49. [Google Scholar] [CrossRef]
- Bevrani, H.; Abrishamchian, M.; Safari-Shad, N. Nonlinear and linear robust control of switching power converters. In Proceedings of the 1999 IEEE International Conference on Control Applications (Cat. No.99CH36328), Kohala Coast, HI, USA, 22–27 August 1999; Volume 1, pp. 808–813. [Google Scholar] [CrossRef] [Green Version]
- Implementing a PID Controller Using a PIC18 MCU, AN937, Microchip Technology Application Note. AN937, Application Note 2004. Available online: http://www.t-es-t.hu/download/microchip/an937a.pdf (accessed on 13 October 2022).
- Ming, W.; Liu, J. A new experimental study of input-output feedback linearization based control of Boost type DC/DC converter. In Proceedings of the 2010 IEEE International Conference on Industrial Technology, Vina del Mar, Chile, 14–17 March 2010; pp. 685–689. [Google Scholar]
- Accetta, A.; Cirrincione, M.; D’Ippolito, F.; Pucci, M.; Sferlazza, A. Input-Output Feedback Linearization Control with On-Line Inductances Estimation of Synchronous Reluctance Motors. In Proceedings of the 2021 IEEE Energy Conversion Congress and Exposition (ECCE), Vancouver, BC, Canada, 10–14 October 2021; pp. 4973–4978. [Google Scholar] [CrossRef]
- Khazaei, J.; Tu, Z.; Asrari, A.; Liu, W. Feedback Linearization Control of Converters with LCL Filter for Weak AC Grid Integration. IEEE Trans. Power Syst. 2021, 36, 3740–3750. [Google Scholar] [CrossRef]
- Dini, P.; Saponara, S. Cogging torque reduction in brushless motors by a nonlinear control technique. Energies 2019, 12, 2224. [Google Scholar] [CrossRef] [Green Version]
- Dini, P.; Saponara, S. Electro-Thermal Model-Based Design of Bidirectional On-Board Chargers in Hybrid and Full Electric Vehicles. Electronics 2021, 11, 112. [Google Scholar] [CrossRef]
- Dini, P.; Saponara, S. Model-Based Design of an Improved Electric Drive Controller for High-Precision Applications Based on Feedback Linearization Technique. Electronics 2021, 10, 2954. [Google Scholar] [CrossRef]
- Cervone, A.; Brando, G. Input-State Feedback Linearization of a Boost DC/DC Converter; ELECTRIMACS 2019 Selected Papers; Walter, Z., Giovanni, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2020; Volume 1, pp. 139–153. [Google Scholar] [CrossRef]
- Lucas, K.E.; Pagano, D.J.; Plaza, D.A.; Vaca-Benavides, D.A.; Ríos, S.J. Robust feedback linearization control for DAB converter feeding a CPL. IFAC-PapersOnLine 2020, 53, 13402–13409. [Google Scholar] [CrossRef]
- Wu, J.; Lu, Y. Feedback linearization adaptive control for a buck converter with constant power loads. In Proceedings of the 2018 IEEE International Power Electronics and Application Conference and Exposition (PEAC), Shenzhen, China, 4–7 November 2018; pp. 1–6. [Google Scholar]
- Bhattacharyya, D.; Padhee, S.; Pati, K.C. Modeling of DC–DC converter using exact feedback linearization method: A discussion. IETE J. Res. 2019, 65, 843–854. [Google Scholar] [CrossRef]
- Salimi, M.; Siami, S. Cascade nonlinear control of DC-DC buck/boost converter using exact feedback linearization. In Proceedings of the 2015 4th International Conference on Electric Power and Energy Conversion Systems (EPECS), Sharjah, United Arab Emirates, 24–26 November 2015; pp. 1–5. [Google Scholar]
- Liu, J.; Ming, W.; Gao, F. A new control strategy for improving performance of boost DC/DC converter based on input-output feedback linearization. In Proceedings of the 2010 8th World Congress on Intelligent Control and Automation, Jinan, China, 7–9 July 2010; pp. 2439–2444. [Google Scholar] [CrossRef]
- Liu, X.; Lin, X.; Xu, F.; Kang, Y. Research on Boost converter based on nonlinear control strategy. In Proceedings of the 2009 IEEE 6th International Power Electronics and Motion Control Conference, Wuhan, China, 17–20 May 2009; pp. 1329–1334. [Google Scholar] [CrossRef]
- Keviczky, L.; Bars, R.; Hetthéssy, J.; Bányász, C. Control Engineering; Advanced Textbooks in Control and Signal Processing; Springer: Singapore, 2018. [Google Scholar]

| Parameter | Symbol | Specification |
|---|---|---|
| Nominal load | R | 61.4 |
| Boost inductor | L | 4 mH |
| Boost filter capacitor | C | 94 F |
| Input voltage | 200 V | |
| Output voltage | 250 V | |
| Output current | 4 A | |
| Switching frequency | 19.2 kHz |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Csizmadia, M.; Kuczmann, M.; Orosz, T. A Novel Control Scheme Based on Exact Feedback Linearization Achieving Robust Constant Voltage for Boost Converter. Electronics 2023, 12, 57. https://doi.org/10.3390/electronics12010057
Csizmadia M, Kuczmann M, Orosz T. A Novel Control Scheme Based on Exact Feedback Linearization Achieving Robust Constant Voltage for Boost Converter. Electronics. 2023; 12(1):57. https://doi.org/10.3390/electronics12010057
Chicago/Turabian StyleCsizmadia, Miklós, Miklós Kuczmann, and Tamás Orosz. 2023. "A Novel Control Scheme Based on Exact Feedback Linearization Achieving Robust Constant Voltage for Boost Converter" Electronics 12, no. 1: 57. https://doi.org/10.3390/electronics12010057
APA StyleCsizmadia, M., Kuczmann, M., & Orosz, T. (2023). A Novel Control Scheme Based on Exact Feedback Linearization Achieving Robust Constant Voltage for Boost Converter. Electronics, 12(1), 57. https://doi.org/10.3390/electronics12010057








