Thirteen-Level Switching Capacitor Inverter with Six Times Boost and Self-Balancing Capability
Abstract
:1. Introduction
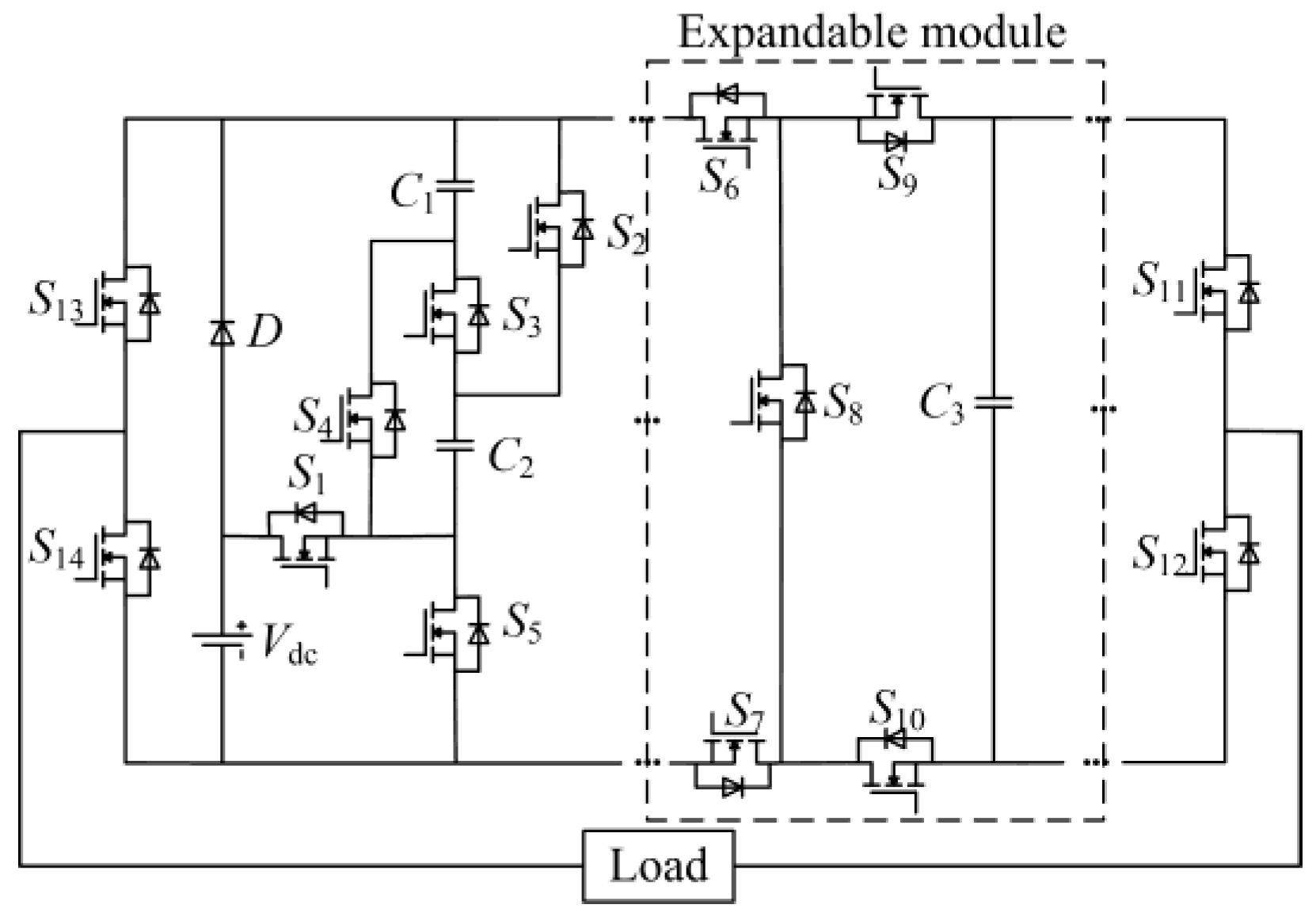
2. Proposed Topology
2.1. Description of the Proposed MLI
2.2. Steady-State Switching Analysis of the Proposed MLI
- (1)
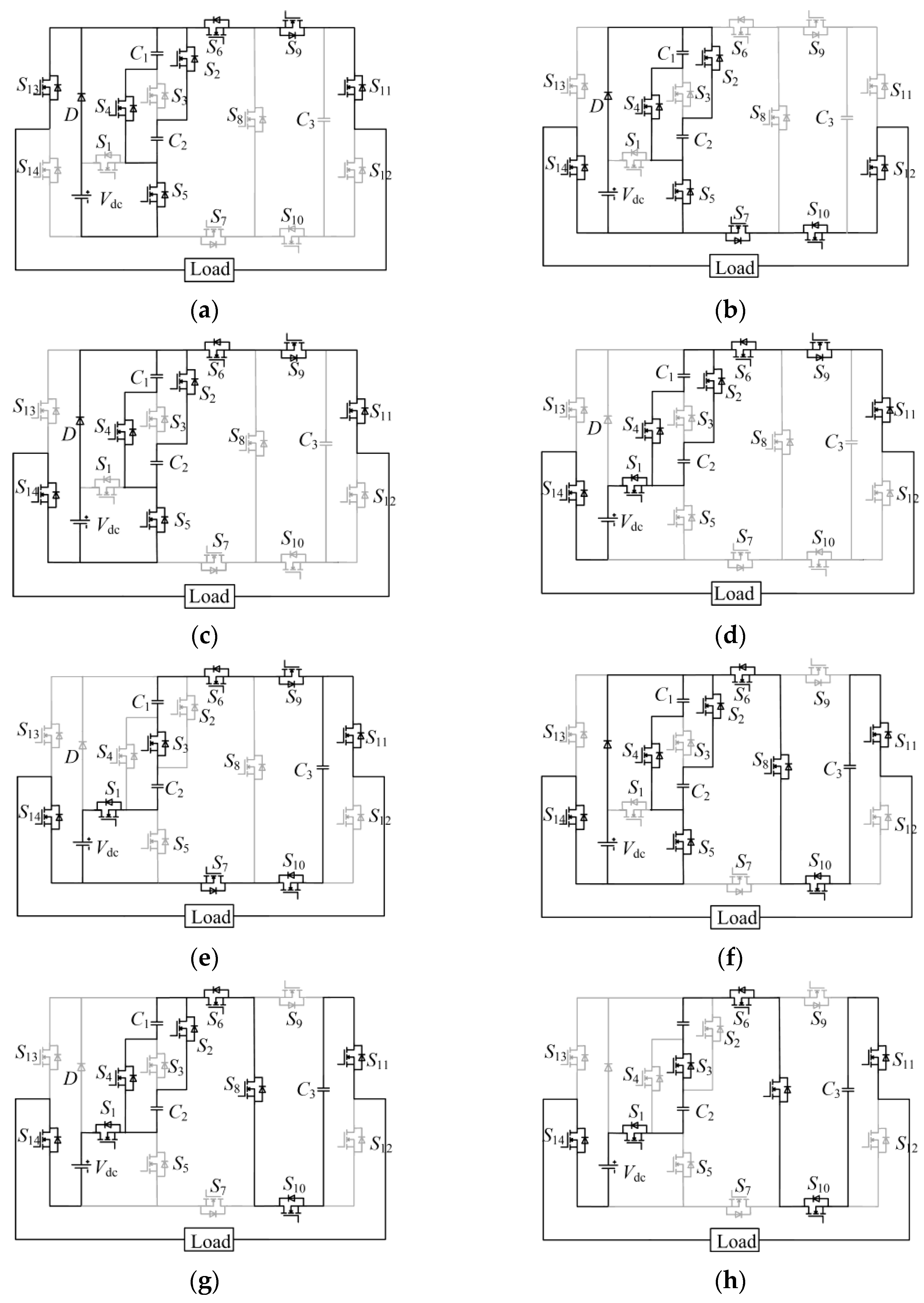
- Working mode 1 (Vo = 0), as shown in Figure 2a. In the dual-capacitor module, the switch tubes S2, S4 and S5 are turned on, the capacitors C1 and C2 are connected in parallel, and the DC power supply is connected in parallel with the capacitors C1 and C2 and charged to Vdc. In the expansion module, the switches S6 and S9 are turned on, and the dual-capacitor module discharges separately. In the half-bridge circuit structure, the switch tubes S11 and S13 are conductive. Similarly, the case of obtaining zero level in the negative half cycle is shown in Figure 2b.
- (2)
- Working mode 2 (Vo = +Vdc), as shown in Figure 2c. The state of each element in the dual capacitor module is the same as in Mode 1. In the expansion module, the switches S7 and S10 are turned on, and the dual-capacitor module discharges separately. In the half-bridge circuit structure, the switch tubes S12 and S14 are conductive.
- (3)
- Working mode 3 (Vo = +2Vdc), as shown in Figure 2d. In the dual-capacitor module, the capacitor C1 and C2 are connected in parallel and connected in series with the DC power supply to provide energy to the load. The switches S7 and S10 in the expansion module are conductive, and the double capacitor module discharges separately. In the half-bridge circuit structure, the switch tubes S12 and S13 are conductive.
- (4)
- Working mode 4 (Vo = +3Vdc), as shown in Figure 2e. In the double capacitor module, the switch tubes S1 and S3 are turned on, and the capacitor C1 and C2 are connected in series to provide energy to the load together with the DC power supply. The four switches S6, S7, S9 and S10 in the expansion module are switched on together, and the dual capacitor module charges the capacitor C3 to 3Vdc. In the half-bridge circuit structure, the switch tubes S11 and S14 are conductive.
- (5)
- Operating Mode 5 (Vo = +4Vdc), as shown in Figure 2f. In the dual-capacitor module, the switch tubes S2, S4 and S5 are turned on together. At this time, the capacitors C1 and C2 are connected in parallel, and then charged in parallel with the DC power supply to Vdc. The switches S7, S8 and S9 in the expansion module are turned on, and the dual-capacitor module discharges in series with the capacitor C3. In the half-bridge circuit structure, the switch tubes S11 and S14 are conductive.
- (6)
- Working mode 6 (Vo = +5Vdc), as shown in Figure 2g. In the dual-capacitor module, the switch tubes S1, S2 and S4 are turned on. After the capacitors C1 and C2 are connected in parallel, they are connected in series with the DC power supply to provide energy to the load. In the expansion module, the switch tubes S7, S8 and S9 are switched on, and the double capacitor module discharges in series with the capacitor C3. In the half-bridge circuit structure, the switch tubes S11 and S14 are conductive.
- (7)
- Working mode 7 (Vo = +6Vdc), as shown in Figure 2h. In the double capacitor module, the switch tubes S1 and S3 are connected, the capacitors C1 and C2 are connected in series, and the DC power supply is connected in series to provide energy to the load, and the diode D is cut off in reverse. In the expansion module, the switch tubes S7, S8 and S9 are turned on together, and the double capacitor module is discharged in series with the capacitor C3. In the half-bridge circuit structure, the switch tubes S11 and S14 are conductive. The working principle of the inverter working in the negative half cycle is consistent with that in the positive half cycle.
2.3. Proposed N-Level Topology
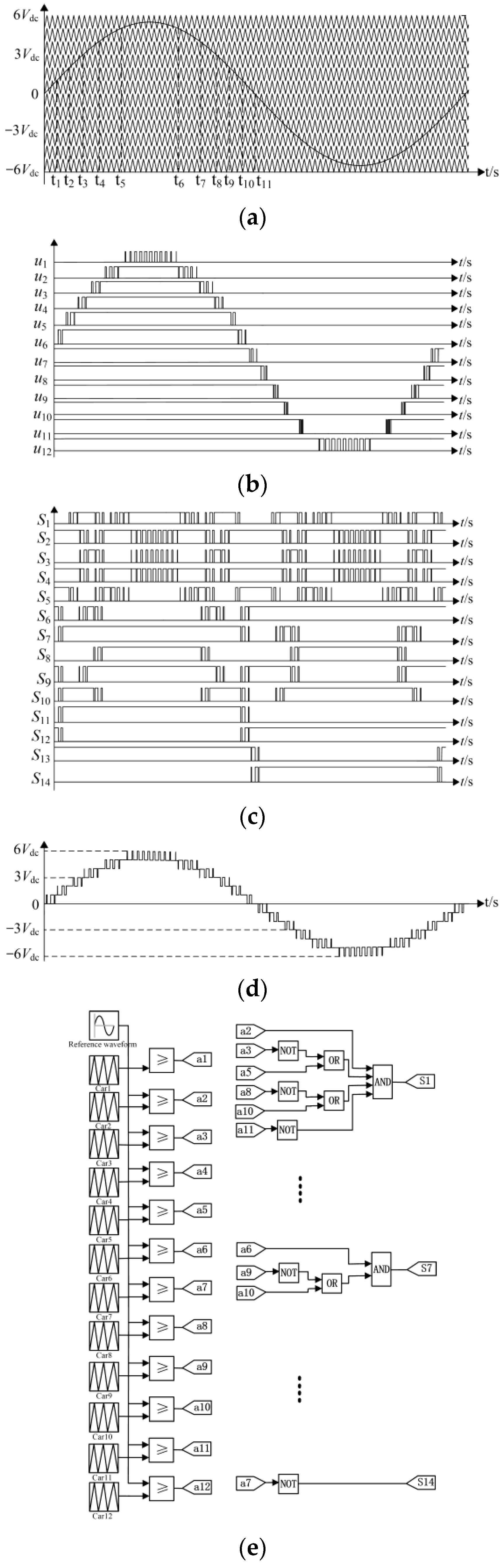
3. Modulation and Characteristic Strategy
3.1. Modulation Strategy
3.2. Analysis of Capacitor Balancing
3.3. Analysis of the Capacitors
3.4. Power Loss Calculation
4. Comparison Outcomes
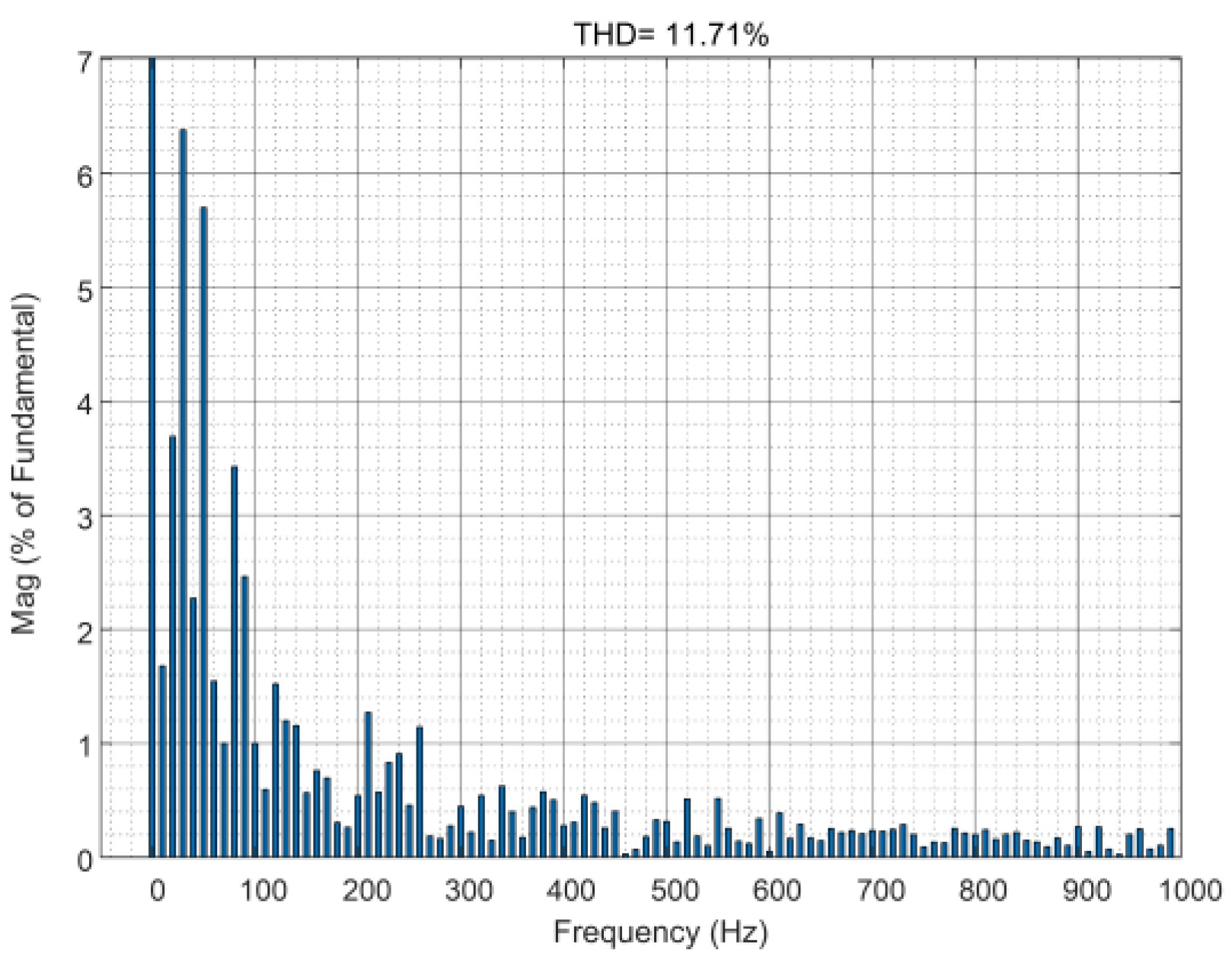
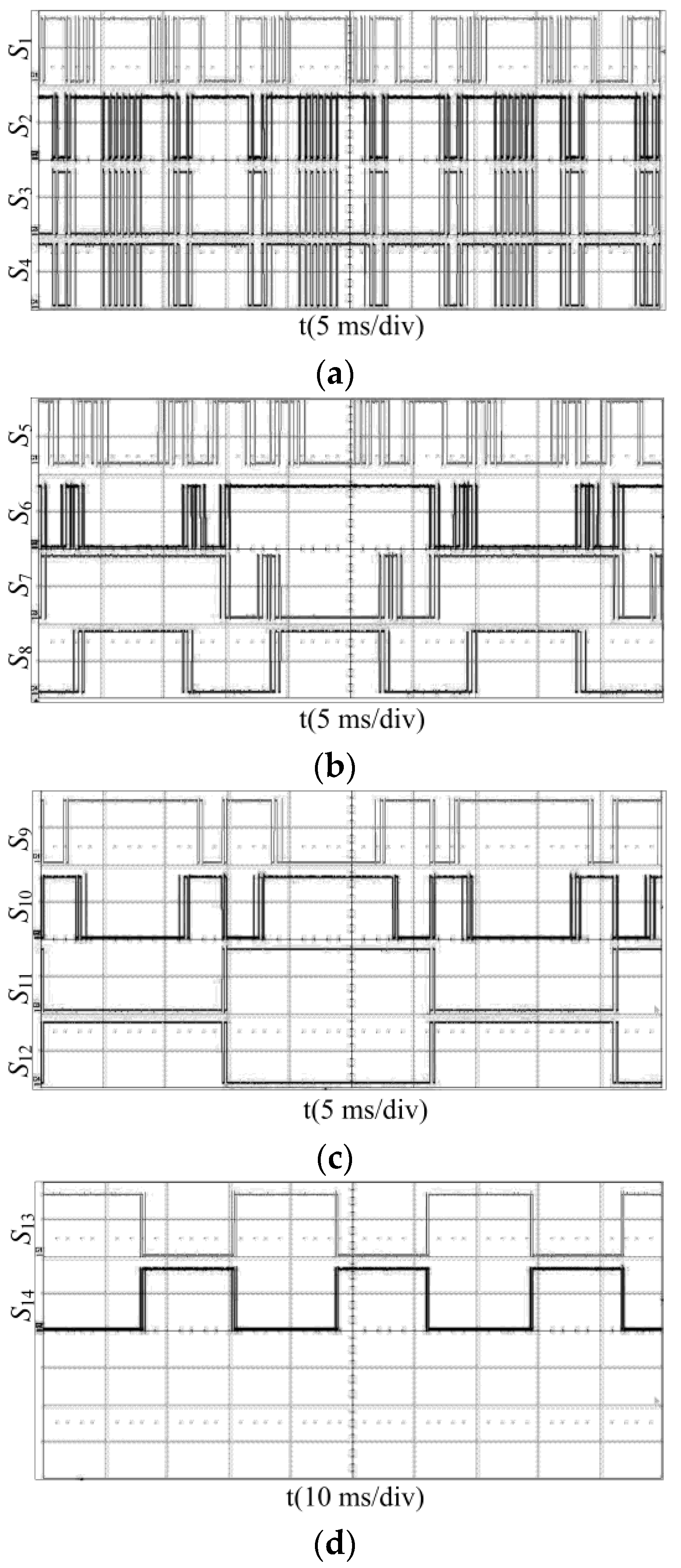
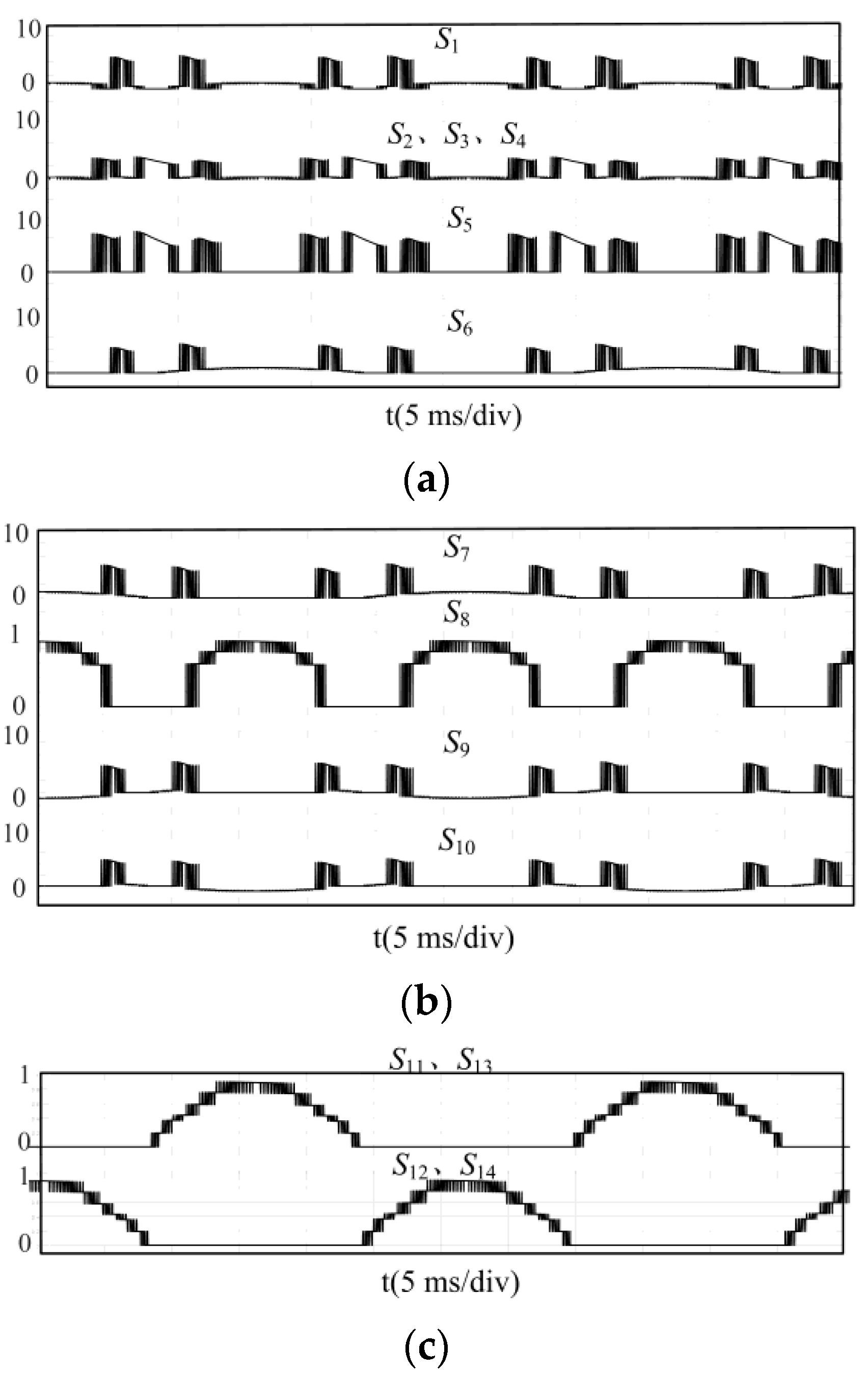
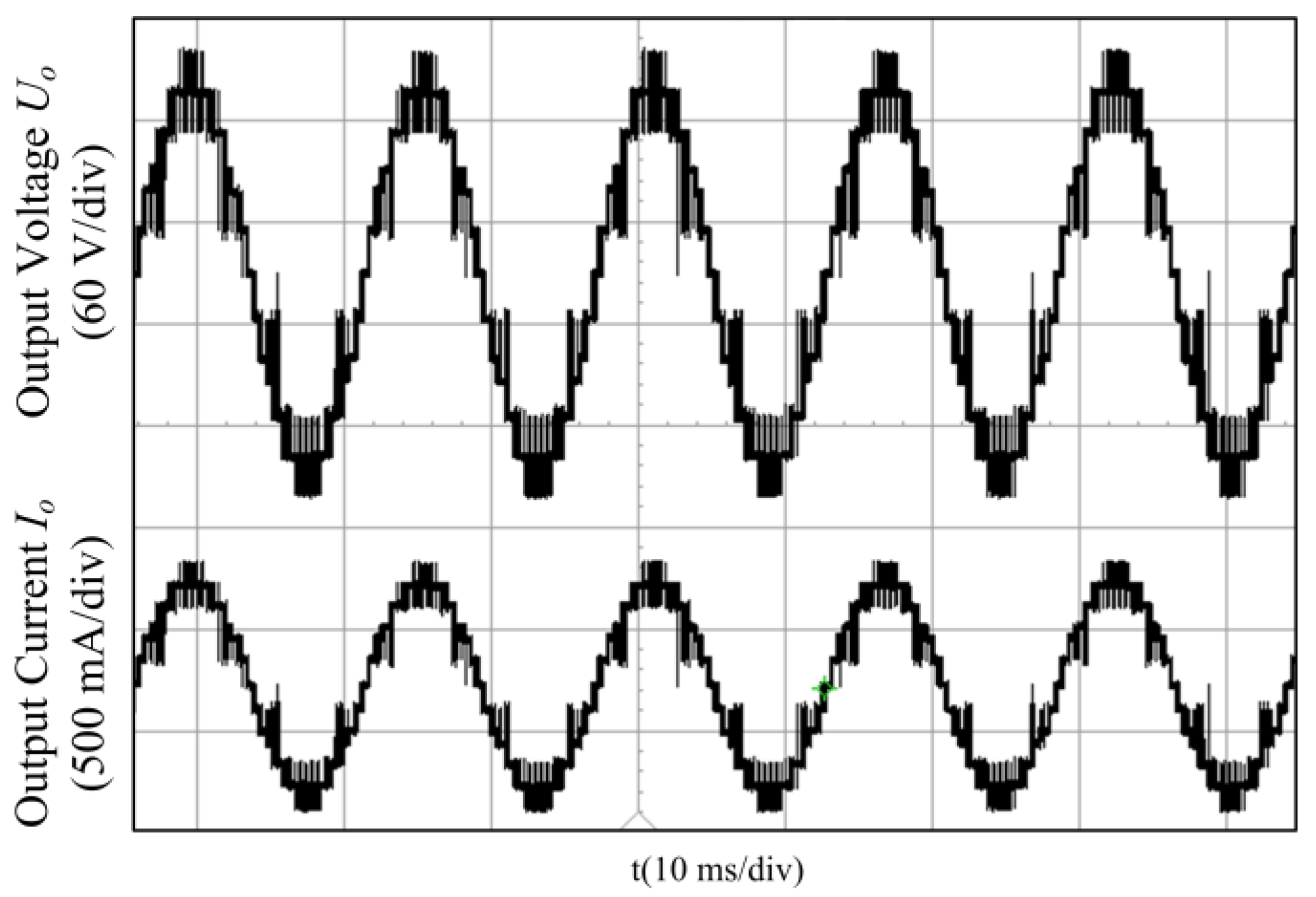
5. Simulation Verification and Experimental Verification
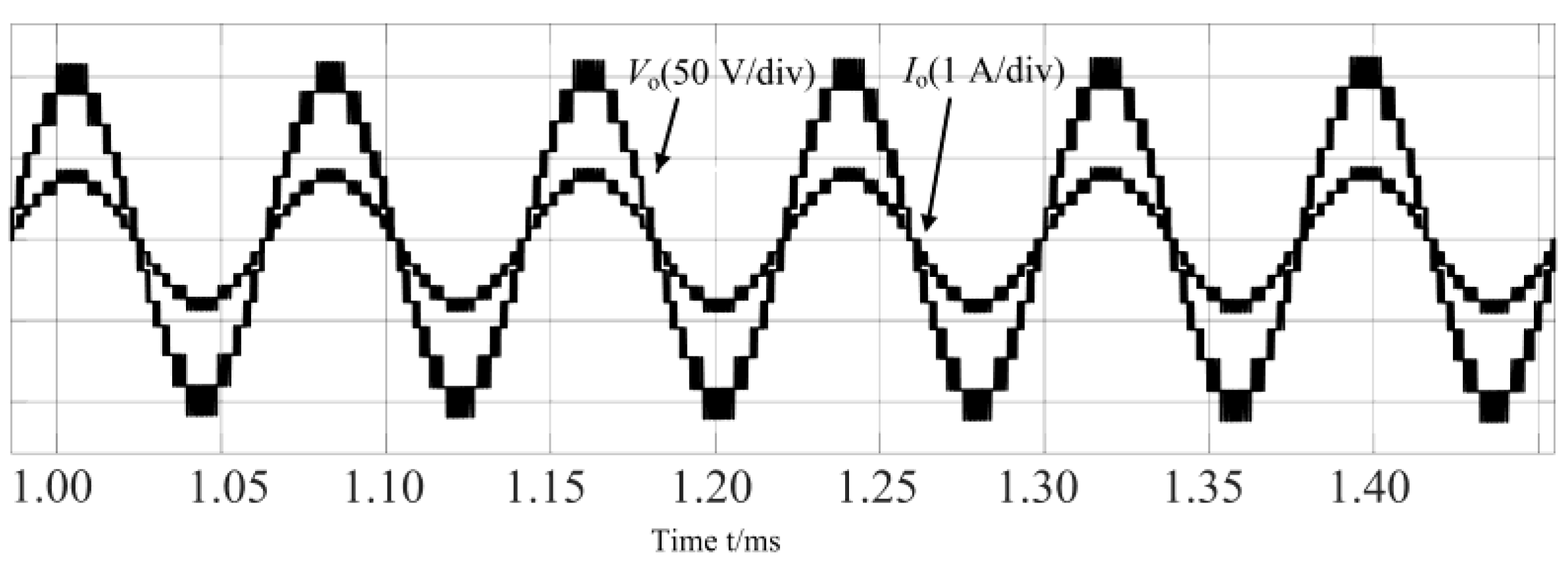
5.1. Simulation Verification
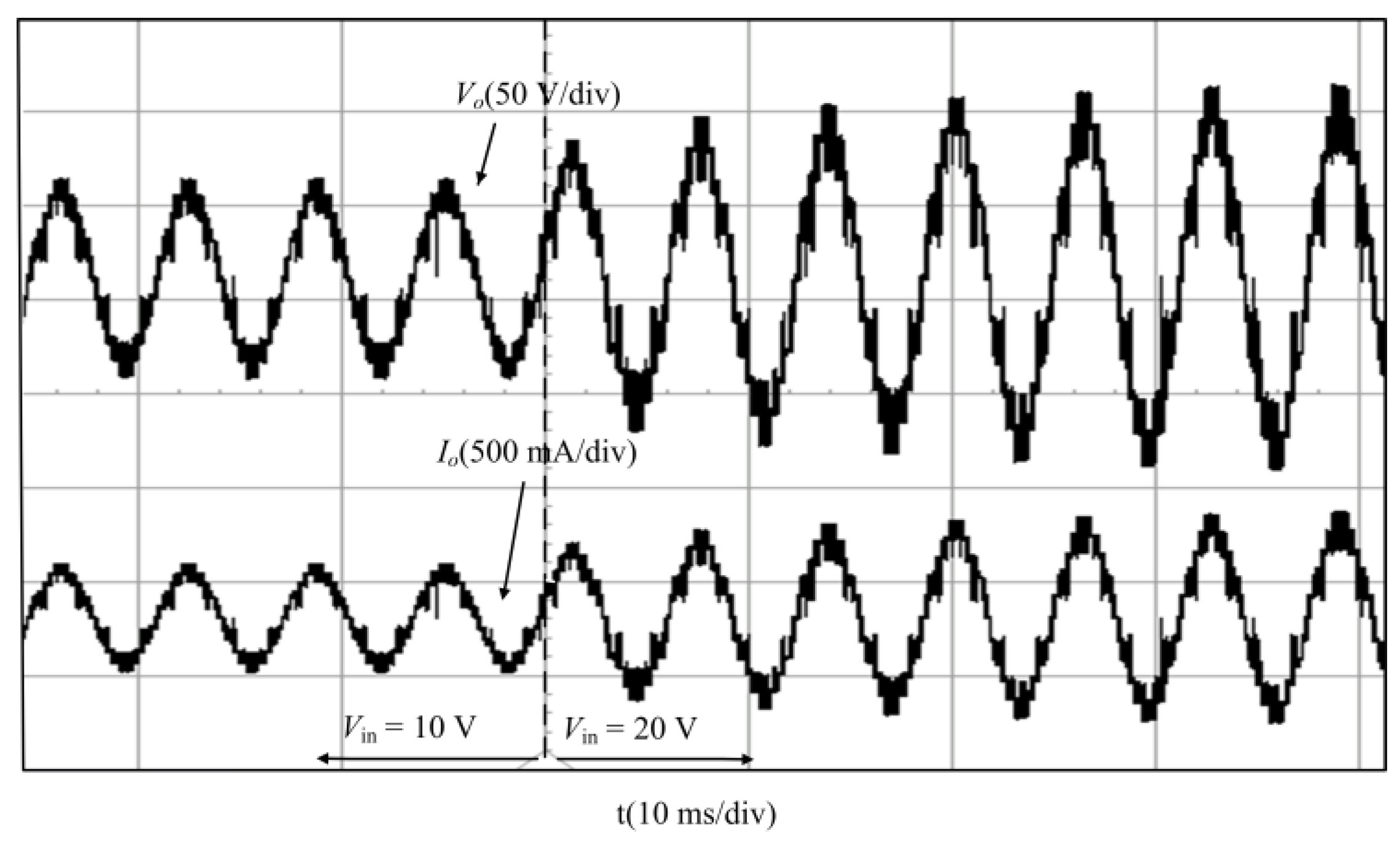
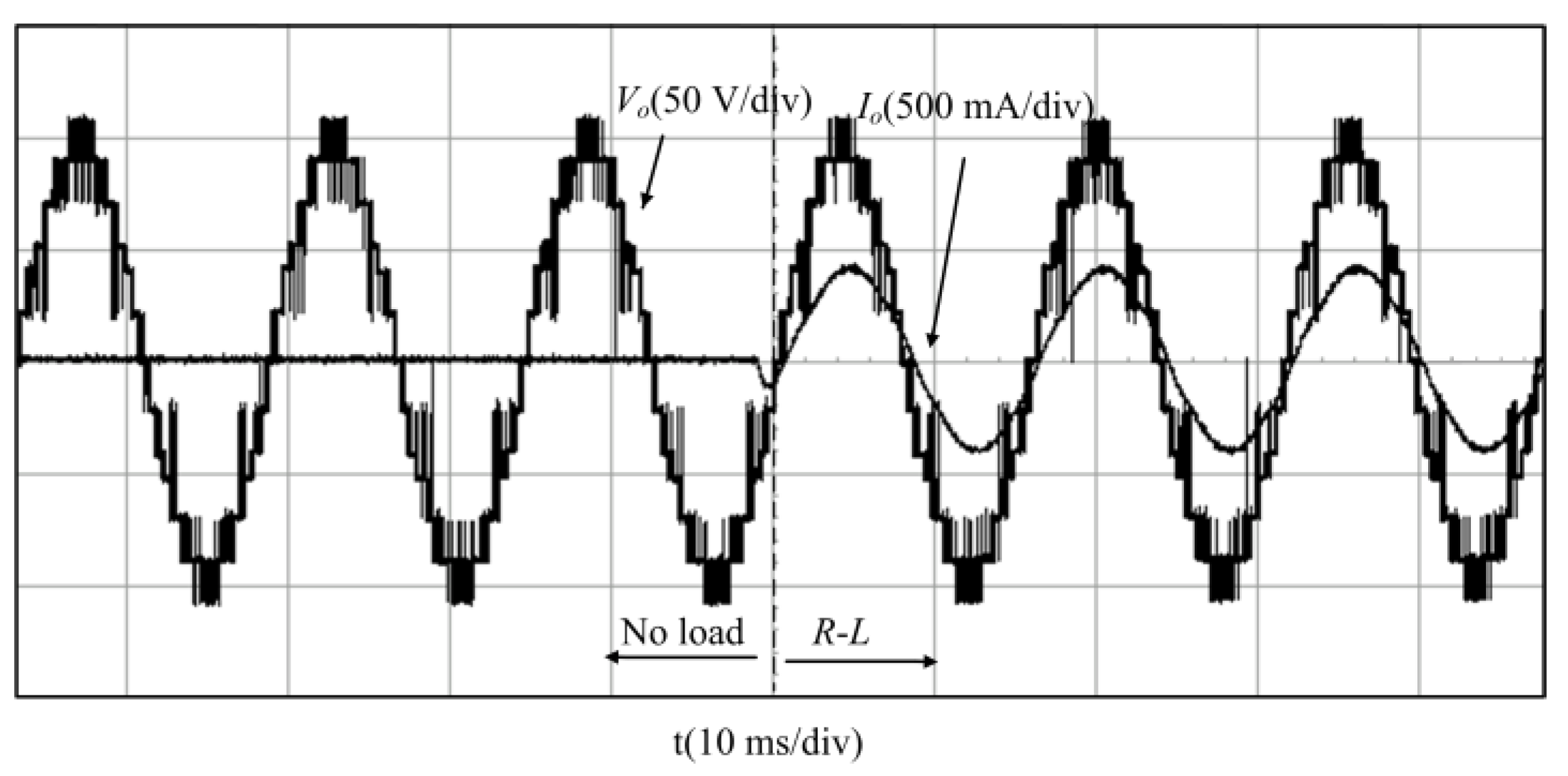
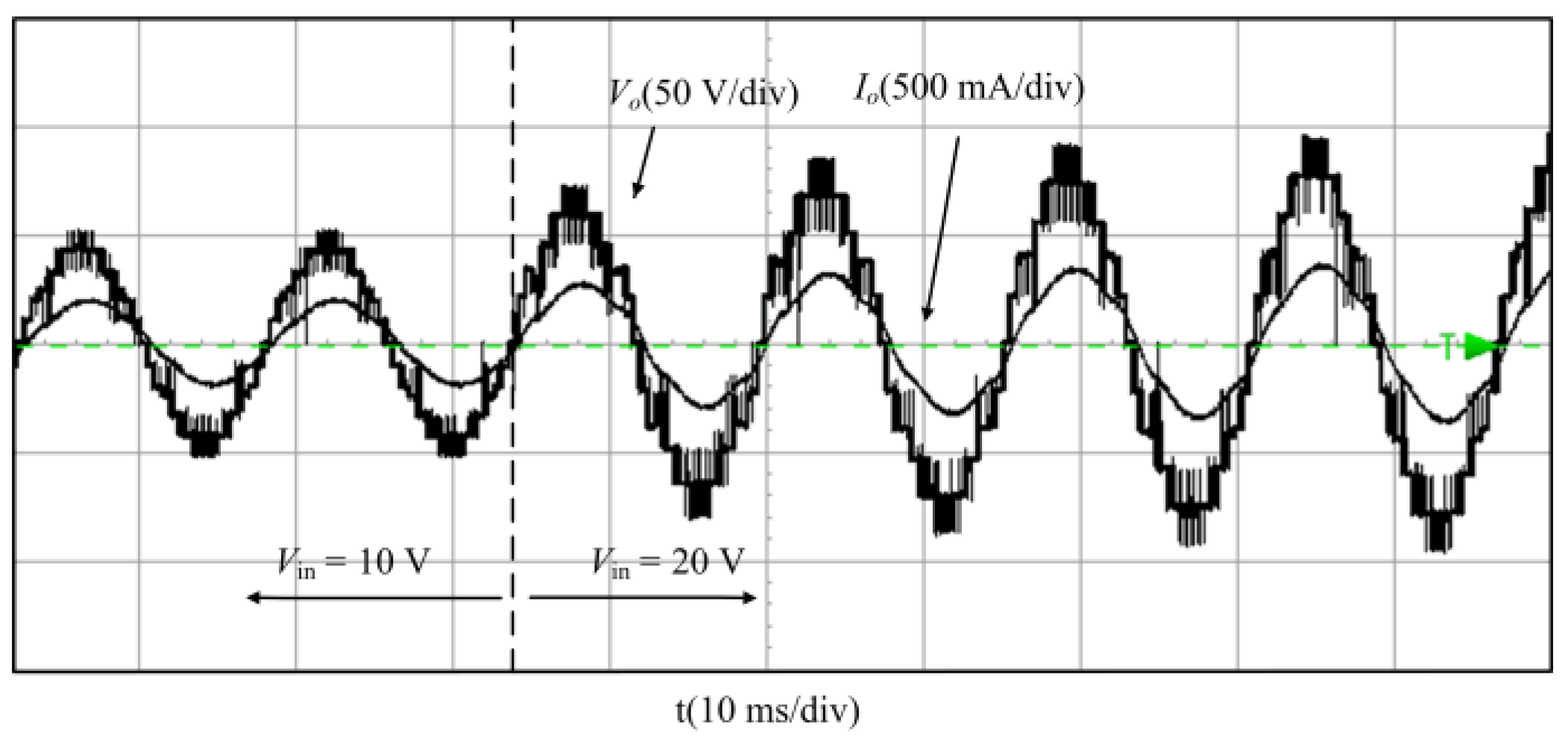
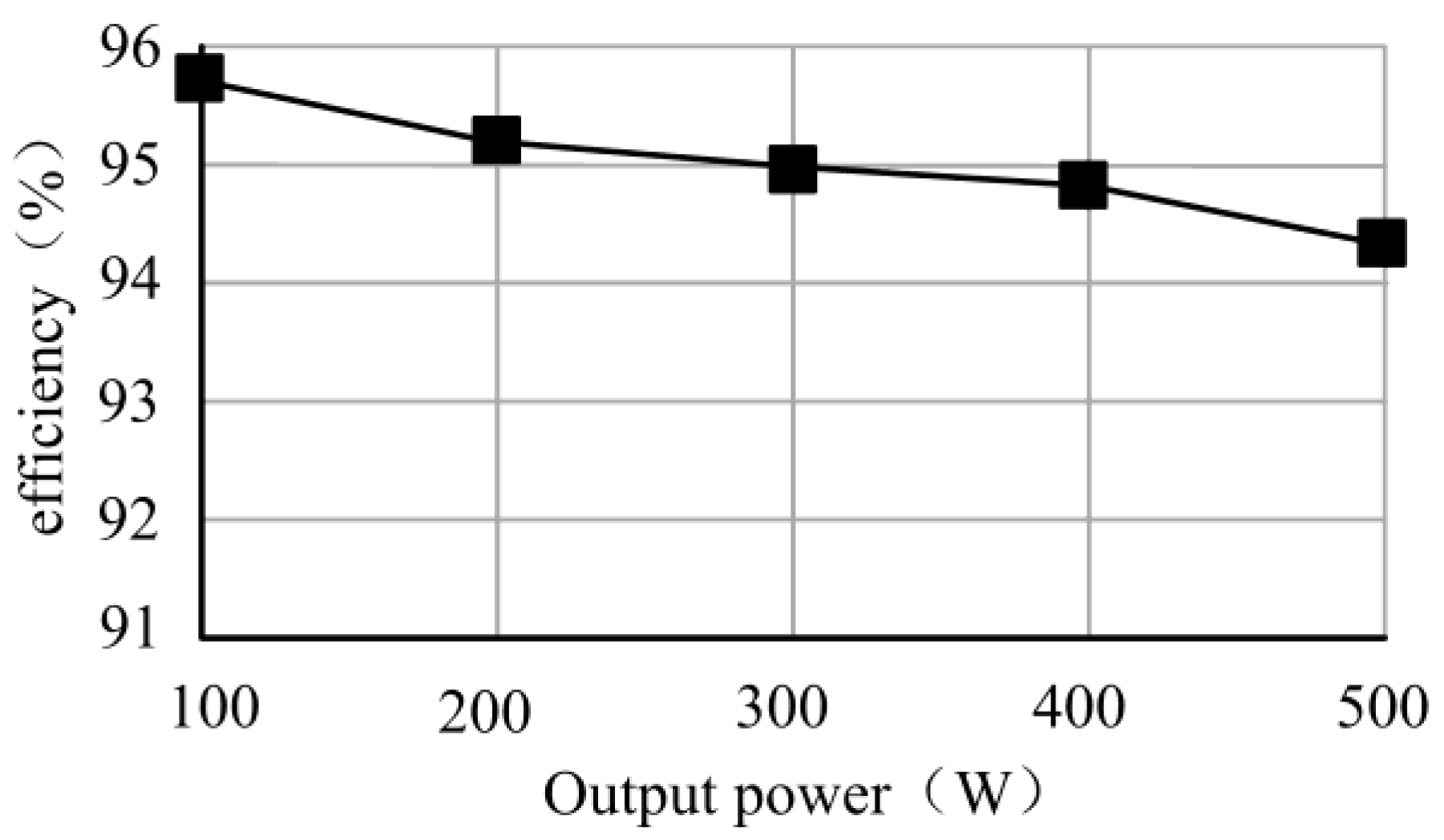
5.2. Experimental Validation
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ye, Y.; Zhang, G.; Wang, X.; Yi, Y.; Cheng, K.W.E. Self-Balanced Switched-Capacitor Thirteen-Level Inverters with Reduced Capacitors Count. IEEE Trans. Ind. Electron. 2022, 69, 1070–1076. [Google Scholar] [CrossRef]
- Tayyab, M.; Sarwar, A.; Hussan, M.R.; Murshid, S.; Tariq, M.; Alamri, B. A novel voltage boosting switched-capacitor 19-level inverter with reduced component count. Int. J. Circuit Theory Appl. 2022, 50, 2128–2149. [Google Scholar] [CrossRef]
- Chen, S.; Ye, Y.; Hua, T.; Wang, X. Self-balanced switched-capacitor multilevel inverter with asymmetric double-wing structure. Int. J. Electr. Power Energy Syst. 2021, 133, 107295. [Google Scholar] [CrossRef]
- Zamiri, E.; Vosoughi, N.; Hosseini, S.H.; Barzegarkhoo, R.; Sabahi, M. A new cascaded switched-capacitor multilevel inverter based on improved series–parallel conversion with less number of components. IEEE Trans. Ind. Electron. 2016, 63, 3582–3594. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, M.; Zhao, T.; Mao, W.; Hu, Y.; Cao, R. Topological comparison and analysis of medium-voltage and high-power direct-linked PV inverter. CES Trans. Electr. Mach. Syst. 2019, 3, 327–334. [Google Scholar] [CrossRef]
- Jena, K.; Kumar, D.; Janardhan, K.; Kumar, B.H.; Singh, A.R.; Nikolovski, S.; Bajaj, M. A Novel Three-Phase Switched-Capacitor Five-Level Multilevel Inverter with Reduced Components and Self-Balancing Ability. Appl. Sci. 2023, 13, 1713. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, K.; Li, G.; Wu, F.; Wang, K.; Liang, J. Generalized switched-capacitor step-up multilevel inverter employing single DC source. CSEE J. Power Energy Syst. 2021, 8, 439–451. [Google Scholar]
- Ye, Y.; Chen, S.; Wang, X.; Cheng, K.W.E. Self-balanced 13-level inverter based on switched capacitor and hybrid PWM algorithm. IEEE Trans. Ind. Electron. 2020, 68, 4827–4837. [Google Scholar] [CrossRef]
- Zheng, X.; Yao, J.; Xu, Z.; Ioinovici, A. Multioutput Switched-Capacitor Multilevel Inverter with Intrinsic Elimination of the Photovoltaics Induced Leakage Current and High Boost Factor. IEEE Trans. Ind. Electron. 2023, 70, 5850–5861. [Google Scholar] [CrossRef]
- Liu, J.; Zhu, X.; Zeng, J. A Seven-Level Inverter with SelfBalancing and Low-Voltage Stress. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 685–696. [Google Scholar] [CrossRef]
- Wang, Y.; Ye, J.; Ku, R.; Shen, Y.; Li, G.; Liang, J. A modular switched-capacitor multilevel inverter featuring voltage gain ability. J. Power Electron. 2023, 23, 11–22. [Google Scholar] [CrossRef]
- Ye, Y.; Chen, S.; Hua, T. Novel switched capacitor seven-level inverter with low voltage stress. Proc. CSEE 2021, 41, 4628–4636. [Google Scholar]
- Khodaparast, A.; Hassani, M.J.; Azimi, E.; Adabi, M.E.; Adabi, J.; Pouresmaeil, E. Circuit configuration and modulation of a seven-level switched-capacitor inverter. IEEE Trans. Power Electron. 2020, 36, 7087–7096. [Google Scholar] [CrossRef]
- Bana, P.R.; Panda, K.P.; Padmanaban, S.; Panda, G. Extendable switched-capacitor multilevel inverter with reduced number of components and self-balancing capacitors. IEEE Trans. Ind. Appl. 2020, 57, 3154–3163. [Google Scholar] [CrossRef]
- Hosseinzadeh, M.A.; Sarebanzadeh, M.; Garcia, C.F.; Babaei, E.; Rodriguez, J.; Kennel, R. Reduced Multisource Switched-Capacitor Multilevel Inverter Topologies. IEEE Trans. Power Electron. 2022, 37, 14647–14666. [Google Scholar] [CrossRef]
- Wang, Y.; Yuan, Y.; Li, G.; Ye, Y.; Wang, K.; Liang, J. A T-type switched-capacitor multilevel inverter with low voltage stress and self-balancing. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 68, 2257–2270. [Google Scholar] [CrossRef]
- Panda, K.P.; Bana, P.R.; Panda, G. A switched-capacitor self-balanced high-gain multilevel inverter employing a single DC source. IEEE Trans. Circuits Syst. II Express Briefs 2020, 67, 3192–3196. [Google Scholar] [CrossRef]
- Zeng, J.; Lin, W.; Liu, J. Switched-capacitor-based active-neutral-point-clamped seven-level inverter with natural balance and boost ability. IEEE Access 2019, 7, 126889–126896. [Google Scholar] [CrossRef]
- Kim, K.-M.; Han, J.-K.; Moon, G.-W. A High Step-Up Switched-Capacitor 13-Level Inverter with Reduced Number of Switches. IEEE Trans. Power Electron. 2021, 36, 2505–2509. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, C.; Wang, K.; Chen, T. Switched capacitor multilevel inverter with step-charging and self-balancing. J. Electr. Mach. Control 2021, 25, 90–101. [Google Scholar]
- Zhao, J.; Lei, W.; Lyu, G.; Qian, L. Multi-objective reliability optimization design of MMC based on sensitivity analysis. Power Electron. 2021, 55, 24–28. [Google Scholar]
- Wu, Z.; Xiao, L.; Yao, Z.; Qin, W. Double-grounded transformer-less buck-boost photovoltaic grid-connected inverter based on hysteresis current control. Proc. CSEE 2021, 41, 8097–8107. [Google Scholar]
- Yuya, N.; Hirotaka, K. A boost-type nine-level switched capacitor inverter. IEEE Trans. Power Electron. 2019, 34, 6522–6532. [Google Scholar]
- Siddique, M.D.; Mekhilef, S.; Shah, N.M.; Ali, J.S.M.; Blaabjerg, F. A new switched capacitor 7L inverter with triple voltage gain and low voltage stress. IEEE Trans. Circuits Syst. II Express Briefs 2020, 67, 1294–1298. [Google Scholar] [CrossRef]
- Ying, H.; You, F.; Lin, L.; Liu, C.; Pei, Z. High-frequency isolated bidirectional PSFB (B-PSFB) converter optimal design. Electr. Drive 2020, 50, 60–65. [Google Scholar]
- Barzegarkhoo, R.; Kojabadi, H.M.; Zamiry, E.; Vosoughi, N.; Chang, L. Generalized structure for a single phase switched-capacitor multilevel inverter using a new multiple DC link producer with reduced number of switches. IEEE Trans. Power Electron. 2016, 31, 5604–5617. [Google Scholar] [CrossRef]
- Peng, W.; Ni, Q.; Qiu, X.; Ye, Y. Seven-level inverter with selfbalanced switched-capacitor and its cascaded extension. IEEE Trans. Power Electron. 2019, 34, 889–896. [Google Scholar] [CrossRef]
- Ge, X.J.; Sun, Y.; Wang, Z.H.; Tang, C.S. A single-source switched-capacitor multilevel inverter for magnetic coupling wireless power transfer systems. Electr. Eng. 2019, 101, 1083–1094. [Google Scholar] [CrossRef]
- Li, Q.; Chen, J.; Jiang, D. Periodic variation in the effect of switching frequency on the harmonics of power electronic converters. Chin. J. Electr. Eng. 2020, 6, 35–45. [Google Scholar] [CrossRef]
- Lee, S.S. Single-stage switched-capacitor module (S3CM) topologyfor cascaded multilevel inverter. IEEE Trans. Power Electron. 2018, 33, 8204–8215. [Google Scholar] [CrossRef]
- IEEE Std. 1547-2018; IEEE Standard for Interconnection and Interoperability of Distributed Energy Resources with Associated Electric Power Systems Interfaces. IEEE: Piscataway, NJ, USA, 2018; pp. 1–138.





| Output Voltage | On-Off Switch Tube | C1 | C2 | C3 |
|---|---|---|---|---|
| 6Vdc | S1, S3, S7, S8, S9, S11, S14 | ▼ | ▼ | ▼ |
| 5Vdc | S1, S2, S4, S7, S8, S9, S11, S14 | ▼ | ▼ | ▼ |
| 4Vdc | S2, S4, S5, S7, S8, S9, S11, S14 | ▲ | ▲ | ▼ |
| 3Vdc | S1, S3, S6, S7, S9, S10, S11, S14 | ▼ | ▼ | ▲ |
| 2Vdc | S1, S2, S4, S7, S10, S11, S14 | ▼ | ▼ | — |
| Vdc | S2, S4, S5, S7, S10, S11, S14 | ▲ | ▲ | — |
| 0+ | S2, S4, S5, S6, S9, S11, S13 | ▲ | ▲ | — |
| 0− | S2, S4, S5, S7, S10, S12, S14 | ▲ | ▲ | — |
| −Vdc | S, S4, S5, S6, S9, S12, S13 | ▲ | ▲ | — |
| −2Vdc | S1, S2, S4, S6, S9, S12, S13 | ▼ | ▼ | — |
| −3Vdc | S1, S3, S6, S7, S9, S10, S12, S13 | ▼ | ▼ | ▲ |
| −4Vdc | S2, S4, S5, S6, S8, S10, S12, S13 | ▲ | ▲ | ▼ |
| −5Vdc | S1, S2, S4, S6, S8, S10, S12, S13 | ▼ | ▼ | ▼ |
| −6Vdc | S1, S3, S6, S8, S10, S12, S13 | ▼ | ▼ | ▼ |
| j | Uo | req |
|---|---|---|
| 0 | 0 | |
| 1 | Vdc | |
| 2 | 2Vdc | |
| 3 | 3Vdc | |
| 4 | 4Vdc | |
| 5 | 5Vdc | |
| 6 | 6Vdc |
| Topology | NCapacitor | NSwitch | NSource | MBV | TSV |
|---|---|---|---|---|---|
| [25] | 4 | 14 | 2 | 6 | 32 |
| [26] | 5 | 19 | 1 | 5 | 48 |
| [27] | 5 | 34 | 1 | 1 | 34 |
| [28] | 0 | 8 | 3 | 3 | 24 |
| [29] | 4 | 18 | 2 | 3 | 32 |
| [30] | 4 | 16 | 2 | 3 | 35 |
| Proposed | 3 | 14 | 1 | 3 | 32 |
| Components | Specifications (Parameters) |
|---|---|
| Controller | MK60FX512 |
| Switching Tube | IRF3205 |
| Diode | FR104, 1N5819 |
| Capacitance | 2200 uF, 4700 uF |
| Resistance | 100 Ω |
| Inductance | 40 mH |
| Switching frequency | 2 kHz |
| Output frequency | 50 Hz |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.; Liu, L.; Wu, Q.; He, W.; Deng, N. Thirteen-Level Switching Capacitor Inverter with Six Times Boost and Self-Balancing Capability. Electronics 2023, 12, 2259. https://doi.org/10.3390/electronics12102259
Li S, Liu L, Wu Q, He W, Deng N. Thirteen-Level Switching Capacitor Inverter with Six Times Boost and Self-Balancing Capability. Electronics. 2023; 12(10):2259. https://doi.org/10.3390/electronics12102259
Chicago/Turabian StyleLi, Shengqing, Li Liu, Qiang Wu, Weihua He, and Na Deng. 2023. "Thirteen-Level Switching Capacitor Inverter with Six Times Boost and Self-Balancing Capability" Electronics 12, no. 10: 2259. https://doi.org/10.3390/electronics12102259
APA StyleLi, S., Liu, L., Wu, Q., He, W., & Deng, N. (2023). Thirteen-Level Switching Capacitor Inverter with Six Times Boost and Self-Balancing Capability. Electronics, 12(10), 2259. https://doi.org/10.3390/electronics12102259







