Dual-Arm Cluster Tool Scheduling for Reentrant Wafer Flows

Abstract

Cluster tools are the key equipment in semiconductor manufacturing systems. They have been widely adopted for many wafer fabrication processes, such as chemical and physical vapor deposition processes. Reentrant wafer flows are commonly seen in cluster tool operations for deposition processes. It is very complicated to schedule cluster tools with reentrant processes. For a dual-arm cluster tool with two-time reentering, the existing studies point out that a one-wafer periodical (1-WP) schedule can be found, and it is optimal in terms of productivity. However, for some wafer fabrication processes, wafers should be processed at some PMs more than two times. This gives rise to a question of whether there still exists a 1-WP schedule for dual-arm cluster tools with the number of reentering times being more than two such that the cycle time of a tool can reach the lower bound. This problem is still open, and this is what this work wants to tackle. For a dual-arm cluster tool with the number of reentering times being k (>2) times, if there does not exist a value f ∈ {1, 2 …} such that k = 3f, theoretical proofs are given to show that a 1-WP schedule can be found, otherwise it does not exist. For cases with a 1-WP schedule, the cycle time can be obtained by analytical expressions. For the cases without a 1-WP schedule, two new methods for a three-wafer periodical schedule are proposed to improve the system productivity by comparing it with an existing three-wafer periodical schedule. The applications of the obtained results are demonstrated by examples. Wafer residency time constraints are required for some wafer fabrication processes. Note that the results obtained in this work cannot be directly applied to cluster tools with both reentrant wafer flows and wafer residency time constraints. Nevertheless, schedulablity and scheduling analyses for that applications can be conducted based on the obtained results in this work.

1. Introduction

In semiconductor manufacturing, cluster tools have been widely adopted for wafer fabrication. Such a tool compactly integrates several process modules (PMs), a robot, and two loadlocks (LLs). Moreover, it adopts a single-wafer processing technology such that wafers are processed one by one in a PM. With a single- or dual-arm robot, a tool is called a single-arm cluster tool (SACT) or dual-arm cluster tool (DACT), as shown in Figure 1a,b.

In an SACT or a DACT as shown in Figure 1, PMs are filled with chemicals for wafer processing, and the internal temperature in PMs is required to be high for some wafer fabrication processes. The robot in the center of a tool is used to transport wafers among the PMs. LLs have two doors. One faces the internal chamber in which there are several PMs, while the other faces outside. LLs are used to ensure the internal vacuum processing environment.

In semiconductor fabs, 25 wafers are grouped into a lot and held in a front opening unified pod (FOUP) [1]. FOUPs are transported to the right areas for wafer fabrication according to recipes. The recipes of wafers in a lot are identical. In a cluster tool, after a wafer lot is loaded into an LL, the LL is pumped into a vacuum environment. Then, the wafers can be delivered to PMs to be processed according to their recipes. After wafers in an LL are completed, then the raw wafers from the other LL are fed to PMs to be processed such that the tool can operate under a steady state without interruption [1,2].

For some wafer fabrication processes, wafers are required to visit some PMs for more than one time. Such a wafer fabrication process is called a reentering process. Atomic layer deposition (ALD) and plasma-enhanced chemical vapor deposition (PECVD) are such typical processes. For the ALD process, deposition processes should be repeatedly performed several times, even more than five. The first deposition layer requires three process steps: Al₂O₃ deposition, Ta₂O₅ deposition, and oxidation process. Each subsequent deposition layer repeats the last two process steps [3]. For a PECVD process, PECVD tools are used for depositing thin films onto silicon wafer substrates, which is one of the crucial steps in the manufacturing of microelectronic circuits and solar cells [4]. For reentering processes, the reentering operations should be performed under identical processing conditions. This presents a requirement that only one PM is configured to serve a processing step.

For a DACT with reentrant wafer flows, Qiao et al. [5] developed a one-wafer periodical (1-WP) scheduling method by adjusting the processing progresses of wafers at different steps such that a 1-WP schedule can be obtained. Moreover, theoretical proofs for its optimality are provided in [5]. However, the study is done for a 2-time reentering process, and it is not known if it is applicable to processes with the reentering times being more than two. In practice, for some reentering processes, wafers are required to visit some PMs for k (≥2) times. Recently, it has been found that a 1-WP schedule cannot be obtained for a DACT with k-time reentrant processes if there exists a value f ∈ ℕ = {1, 2 …} such that k = 3f holds. This implies that the method in [5] is not applicable to such cases, which motivates us to do this work. Further, this work aims at solving the scheduling problem of DACTs with k-time (k ≥ 3) reentrant processes such that the solutions to DACTs with reentrant processes are complete.

2. Literature Review

In SACTs and DACTs, the time taken for robot tasks, including placing, picking, and moving, is actually quite short in comparison with wafer processing time in PMs. Thus, for SACTs, a backward strategy is optimal in terms of productivity [6,7], while for DACTs, a swap strategy is optimal [8]. Further, studies on modeling and scheduling SACTs and DACTs were conducted in [8,9,10]. With two wafer types and one shared PM, the scheduling analysis was done for DACTs in [11]. The results obtained in the above-mentioned studies are based on the assumption that there are no wafer residency time constraints (WRTCs).

For some wafer fabrication processes, WRTCs are imposed, which requires that after a wafer is processed in a PM, it should be removed from the PM within a limited time interval, otherwise it would be damaged by the high temperature and chemical gas in the PM. In [12,13], methods were proposed to find optimal periodical schedules for DACTs with WRTCs. Further, based on Petri nets, a mixed integer programming (MIP) method was presented in [14] to get optimal cyclic schedules for both SACTs and DACTs with various wafer processing flows. To improve the computational efficiency in finding an optimal solution for SACTs and DACTs with WRTCs, schedulability conditions under which a feasible schedule exists were established in [15,16]. If schedulable checked by such conditions, the authors established analytical expressions to find optimal solutions. With multiple wafer types, wafer delay analysis and workload balancing of parallel PMs were conducted in [17]. Moreover, PM configuring problem of residency time-constrained DACTs was investigated, and a polynomial-complexity algorithm was developed to find optimal cyclic schedules in [18].

In practice, the time required for robot activities and wafer processing might be disturbed. Such a time variation may result in a feasible schedule obtained under the deterministic activity time assumption becoming infeasible. Thus, a robust scheduling method is necessary for cluster tools with activity time variation. To do so, in [19], based on Petri nets, a real-time control policy was proposed for DACTs with WRTCs and activity time variation to offset the activity time disturbance as much as possible by adjusting the robot waiting time in real-time. Then, an optimal real-time scheduling method consisting of an off-line schedule and a real-time control policy was presented in [20]. Since the robot task sequences for DACTs and SACTs are different, the methods for DACTs in [19,20] are not applicable to SACTs. Thus, in [21], for SACTs with a backward strategy, a real-time control policy was proposed to reduce the impact caused by activity time variation as much as possible and analytical expressions were given to calculate the upper bound of wafer sojourn time delay. Then, based on the results obtained in [21], an optimal real-time scheduling method was proposed in [22] for SACT with WRTCs and activity time variation. In [23], a class of schedules was proposed for cluster tools to keep timing patterns as steady as possible and adopt timing of tasks in response to process time variation so as to satisfy WRTCs robustly. To ensure the consistency of wafer sojourn time, ref. [24] examined the conditions under which a feedback controller proposed in their previous work can stabilize the wafer sojourn time in a stochastic processing environment with unexpected random time disturbances.

As the wafer size becomes larger, while the circuit width shrinks down, the wafer fabrication constraints are more and more strict. Periodical chamber cleaning operations are normally required for a PM in cluster tools after a PM processes a specified number of wafers so as to ensure the processing environment. Let h denote the number of wafers that a PM processes at most before it requires a chamber cleaning operation. When h = 1, the chamber cleaning operation is called a purge cleaning operation. To improve the productivity of SACTs and DACTs with purge operations, a backward(z) strategy is presented in [25] for SACTs based on the conventional backward strategy, while a swap(a, z) strategy is presented in [26,27] for DACTs based on the conventional swap strategy. By considering more general cases with h ≥ 1, Qiao et al. [28] presented a virtual wafer-based method for DACTs to deal with chamber cleaning requirements. Besides, in [29,30], efficient scheduling approaches were proposed to deal with the chamber cleaning operation issue caused by the processing environment detection.

All the above-mentioned studies were conducted for cluster tools without reentrant processes. In fact, for an SACT or a DACT without reentrant processes, it can be treated as a flow-shop system. However, with reentrant processes, it is not, therefore, the above-mentioned studies are not applicable. Thus, for cluster tools with reentrant processes, system behavior was modeled by Petri nets (PNs) in [31] for performance analysis without tackling their optimization problems. Then, in [3], these problems were addressed for SACTs based on a developed PN model and formulated by an MIP model. To improve the computational efficiency, based on a resource-oriented PN (ROPN) model, an analytical method was proposed to schedule the overall system with reentrant processes in [32]. For DACTs with reentrant processes, Wu et al. [33,34] pointed out that the tool may operate under a transient process for some cases all the time based on a three-wafer periodical (3-WP) scheduling method. This means that the obtained results under the steady state in [31] are not applicable. Further, ref. [35] presented the cycle time analysis for DACTs with k-time (k ≥ 3) reentrant processes based on the 3-WP scheduling method. Then, Qiao et al. [5] developed a 1-WP scheduling method by adjusting the processing progresses of wafers at different steps and theoretically proved its optimality. Furthermore, for time-constrained DACTs with reentrant processes, the schedulability and scheduling analysis was carried out in [36,37] based on such a 1-WP schedule. By taking the activity time variation into account, for time-constrained DACTs with reentrant processes, efficient algorithms were developed to calculate the upper bound of wafer sojourn time delay in [38] and an optimal real-time scheduling method was proposed in [31] to operate DACTs.

The existing studies for cluster tools with reentrant wafer flows are summarized in

Table 1. The existing studies for cluster tools with reentrant wafer flows.

References	Number of Reentrant Times	Other Constraints	The Addressed Problem	Methods	Results
[31]	k ≥ 2	None	Deadlock analysis	PNs	No optimality analysis
[3]	k ≥ 2	None	Scheduling	PNs and MIP	Optimal
[32]	k = 2	None	Scheduling	PNs	Optimal for SACTs
[33]	k = 2	None	Scheduling	PNs and 3-WP scheduling	Optimal for some cases
[34]	k = 2	None	Scheduling	PNs and 2-WP scheduling	Optimal for some cases
[5]	k = 2	None	Scheduling	PNs and 1-WP	Optimal
[36,37]	k = 2	WRTCs	Scheduling	1-WP	Optimal
[38,39]	k = 2	WRTCs, time variation	Control and Scheduling	PNs and 1-WP	Optimal
[35]	k ≥ 2	None	Cycle time analysis	PNs and 3-WP	Optimal for some cases

. In [31], it did not present a method to obtain optimal schedules. In [5], although the proposed MIP model can find optimal solutions, it would take a long time to solve the model as the number of reentering times increases. In [32], deadlock control policies were presented, and efficient scheduling methods were proposed for SACTs. In [5,33,34,36,37,38,39], the scheduling problem of DACTs with two-time reentrant processes was fully investigated. Moreover, by the swap strategy, a 1-WP scheduling method was found in [5] to achieve the lower bound of cycle time. However, as mentioned in the Introduction, in a case study for DACTs with three-time reentrant processes, it was found that a 1-WP schedule cannot be obtained by the swap strategy. Thus, it gives rise to a question of how to schedule DACTs with three-time reentrant processes so as to maximize productivity. With such motivation, this work is conducted.

In this work, if there does not exist a value f ∈ {1, 2 …} such that k = 3f, theoretical proofs are given to show that a 1-WP schedule can be found for DACTs with k-time reentrant processes. Furthermore, for cases with a 1-WP schedule, simple expressions are given to calculate the cycle time. For the cases without a 1-WP schedule, two new 3-WP scheduling methods are proposed to improve the system productivity by comparing it with an existing 3-WP scheduling method presented in [35]. In summary, compared with the existing studies, this work aims to tackle the open problem in this research field and makes significant improvements.

In the next section, the reentrant processes and the 1-WP schedule are introduced. Then, for k-time reentrant processes with k ≥ 3, Section 4 shows that a 1-WP schedule cannot be found if there exists a value f ∈ ℕ such that k = 3f holds. In Section 5, two novel methods are proposed to improve the productivity of DACTs for the cases where a 1-WP schedule cannot be found. The applications of the obtained results are demonstrated by examples in Section 6, and this work is concluded in Section 7.

3. The Reentrant Process and Periodical Schedules

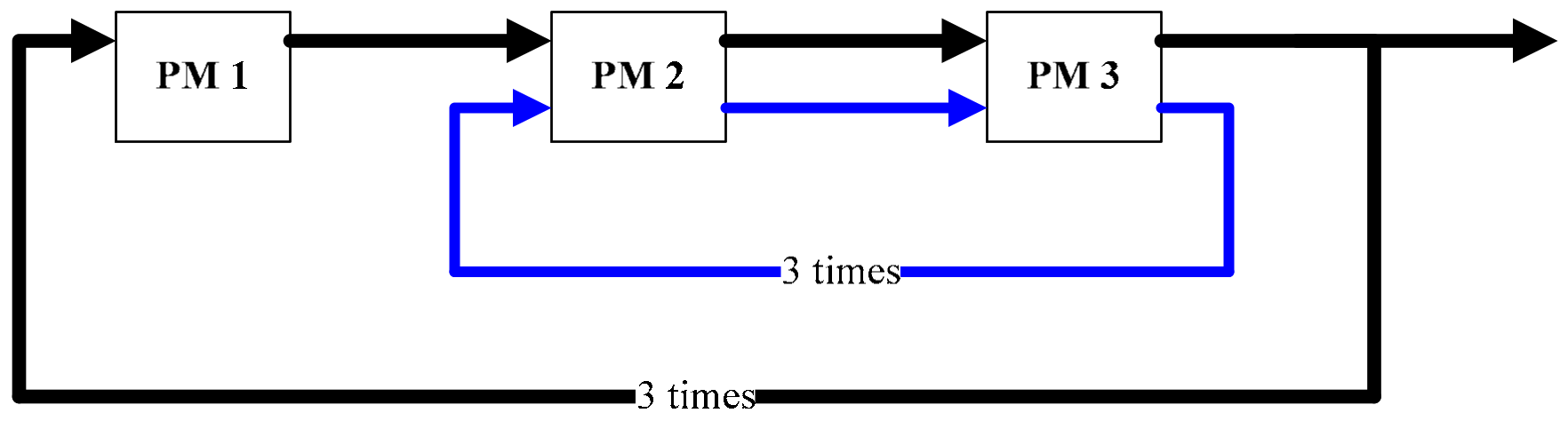
3.1. Reentrant Process

PMs in a cluster tool are divided into different groups. The PMs in the same group serve to perform the same fabrication operation called a step. For serial wafer flows, raw wafers sequentially visit several steps according to their processing recipes. For reentrant wafer flows (i.e., reentrant processes), wafers should revisit some steps multiple times. Notice that, for the steps involving reentrant processes, only one PM is configured so as to ensure processing consistency. For example, ALD and PECVD have such a requirement. Thus, if a wafer is repeatedly processed at a reentrant step, the processing environment is exactly identical such that the processing quality can be ensured.

There are three processing steps for the ALD process. After a raw wafer is moved out of an LL by the robot, the wafer is delivered to Step 1 to be processed, then Step 2, and followed by Step 3. When the processing of the wafer in Step 3 is completed, it revisits Steps 2 and 3 again such that a wafer visits Steps 2 and 3 totally k ≥ 2 times. Note that each step of Steps 2 and 3 has only one PM. In fact, the workloads at the reentrant steps are much greater than that in Step 1. Thus, more than one PM used for Step 1 cannot improve the productivity of a cluster tool. Therefore, only one PM is used to serve for Step 1 as well. Moreover, it can save cost to operate such a tool in this way since a PM (i.e., a chamber) is quite expensive. PM_i, i ∈ {1, 2, 3}, is used for Step i. Then, the wafer flow pattern is denoted as (PM₁, (PM₂, PM₃)^k), with (PM₂, PM₃)^k being the reentrant process.

Another commonly seen reentrant process is PECVD. For PECVD, it has two steps (i.e., Steps 1 and 2), and both are reentrant ones. PM₁ is used to complete plasma-enhanced chemical vapor deposition in Step 1, while PM₂ in Step 2 is used to complete a cure operation so as to ensure wafer quality. Then, (PM₁, PM₂)^k, k ≥ 2, is used to represent the wafer flow pattern of PECVD. By observing the wafer flow patterns of ALD and PECVD, the reentrant pattern of PECVD is a special case of ALD from the perspective of scheduling. Thus, this work focuses on the scheduling analysis of DACTs with (PM₁, (PM₂, PM₃)^k) with k ≥ 2, which is commonly seen in cluster tool scheduling with reentrant processes. Note that the results in [5] are conducted for DACTs with (PM₁, (PM₂, PM₃)^k) as well.

3.2. Activity Description

In a DACT, the two robot arms are named Arm-1 and Arm-2, respectively. Robot activities include picking a wafer from a PM, moving between two PMs, placing a wafer into a PM, rotating, and waiting. For a DACT, a swap strategy is efficient. At a state, assume that Arm-1 is empty and stays at PM_i, while Arm-2 carries a wafer. At this state, a swap operation at PM_i, i ∈ {1, 2, 3}, includes the following activities: Picking a processed wafer from PM_i by Arm-1 → rotating → placing the wafer held by Arm-2 into PM_i. The robot picking and placing activities at PM_i are denoted as PI_i and PL_i, respectively. A swap operation at PM_i is denoted as SWP_i. Thus, SWP_i includes PI_i, robot rotation, and PL_i. Besides, M_ij is used to denote the robot moving from Steps i to j. Note that LLs are denoted as Step 0.

To model the time aspect, we assume that the time needed to execute each of the above-mentioned robot activities is constant. The activities of executing PI_i, PL_i, and M_ij spend α, β, and μ time units, respectively. In practice, the time taken for SWP_i is often less than the sum of the time for performing PI_i, robot rotation, and PL_i. Thus, symbol λ is introduced to represent the time needed for SWP_i. Except for the robot activities, the wafer processing time at PM_i, i ∈ {1, 2, 3}, is denoted as ρ_i. The meanings of the notations are summarized in

Table 2. Robot and processing activities.

Notations	Robot Tasks	Time
PIi	Picking a wafer in Step i	α
PLi	Placing a wafer in Step i	β
Mij	Moving from Steps i to j	μ
SWPi	Swapping in Step i	λ

.

3.3. Periodical Schedules

In a cluster tool, raw wafers enter the system one by one. The d-th wafer entering the system is denoted as W_d, d ∈ ℕ. To find a periodical schedule, it is necessary to analyze the state evolution of the system. Let Θ_i = {W_d(q)}, i ∈ {1, 2, 3}, denote the state of PM_i (Step i), indicating that W_d is processed in PM_i for the q-th operation. Furthermore, let Θ₄ = {R_i(W_d(q)} denote the state of the robot, representing that the robot is staying at PM_i, i ∈ {1, 2, 3}, and at the same time, carrying W_d with its q-th operation to be processed in the PM. Then, the state of the system is denoted as S = {Θ₁, Θ₂, Θ₃, Θ₄}.

For a DACT with (PM₁, (PM₂, PM₃)²), by a swap strategy, Wu et al. [33] present a three-wafer periodical schedule called a 3-WP schedule in short. With a 3-WP schedule, starting from S₁ = {W₃(1), W₂(2), W₁(3), R₁(W₄(1))}, a DACT evolves as follows: S₁ = {W₃(1), W₂(2), W₁(3), R₁(W₄(1))} → S₂ = {W₄(1), W₃(2), W₁(3), R₃(W₂(3))} → S₃ = {W₄(1), W₁(4), W₂(3), R₃(W₃(3))} → S₄ = {W₄(1), W₂(4), W₃(3), R₃(W₁(5))} → S₅ = {W₄(1), W₃(4), W₁(5), R₃(W₂(5))} → S₆ = {W₄(1), W₃(4), W₂(5), R₁(W₅(1))} → S₇ = {W₅(1), W₄(2), W₃(5), R₁(W₆(1))} → S₈ = {W₆(1), W₅(2), W₄(3), R₁(W₇(1))} → S₉ = {W₇(1), W₆(2), W₄(3), R₃(W₅(3))}. Notice that S₁ and S₈ are equivalent. It implies that evolution from S₁ to S₈ forms a period.

Note that, to transfer S₁ to S₂ and S₈ to S₉, robot task sequence σ₁ = 〈SWP₁ → M₁₂ → SWP₂ → M₂₃〉 is performed, i.e., the robot sequentially performs the following robot tasks: Swaps at PM₁, moves to PM₂ from PM₁, swaps at PM₂, and moves to PM₃ from PM₂. To transfer S₂ to S₃, σ₂ = 〈SWP₃ → M₃₂ → SWP₂ → M₂₃〉 is performed, i.e., the robot sequentially performs the following robot tasks: Swaps at PM₃, moves to PM₂ from PM₃, swaps at PM₂, and moves to PM₃ from PM₂. σ₂ is repeated for S₃ to S₄ and S₄ to S₅. Note that σ₂ forms a robot task cycle involving the reentrant process (PM₂, PM₃)², and it is called a local cycle. σ₃ = 〈SWP₃ → M₃₀ → PL₀ → PI₀ → M₀₁〉 is for S₅ to S₆. This means that the robot sequentially performs the following robot tasks for σ₃: Swaps at PM₃, moves to an LL from PM₃, place a wafer into the LL, pick a wafer from the LL, and moves to PM₁ from the LL. σ₄ = 〈SWP₁ → M₁₂ → SWP₂ → M₂₃ → SWP₃ → M₃₀ → PL₀ → PI₀ → M₀₁〉 is for S₆ to S₇ and S₇ to S₈. This means that the robot sequentially performs the following robot tasks for σ₄: Swaps at PM₁, moves to PM₂ from PM₁, swaps at PM₂, moves to PM₃ from PM₂, swaps at PM₃, moves to an LL from PM₃, place a wafer into the LL, pick a wafer from the LL, and moves to PM₁ from the LL. Obviously, σ₄ is a robot cycle involving all PMs, and it is called a global cycle. Moreover, σ₁ and σ₃ together form a global cycle as well. Thus, as shown in Figure 2, a period from S₁ to S₈ (or S₂ to S₉) contains three local and three global cycles. Notice that, in each global cycle, one wafer with all operations being completed is returned to LLs. Thus, three wafers are returned to LLs in this period.

For a DACT with (PM₁, (PM₂, PM₃)²), by a 3-WP schedule, as shown in Figure 2, Wu et al. [33] point out that the tool may operate under a transient process in some cases all the time. In such cases, once the robot enters the global cycles from local cycles, there might be a time delay when the robot arrives at the PMs involving reentrant processes. Such time delay makes that the lower bound of the system cycle time cannot be reached, i.e., a 1-WP schedule may not be optimal in such cases. This also implies that productivity reduction is caused by multiple local and global cycles in a period. Thus, it raises the question of whether the performance of the system can be improved by reducing the number of local and global cycles. To answer this question, for a DACT with (PM₁, (PM₂, PM₃)²), Qiao et al. [5] present a 1-WP schedule.

By a 1-WP schedule, the tool should start to operate from a steady state, i.e., S₁ = {W₃(1), W₁(4), W₂(3), R₁(W₄(1))}. Then, by performing σ₁, the system enters state S₂ = {W₄(1), W₃(2), W₂(3), R₃(W₁(5))}. Further, by executing σ₂, it reaches S₃ = {W₄(1), W₂(4), W₁(5), R₃(W₃(3))}. Finally, by executing σ₃, S₄ = {W₄(1), W₂(4), W₃(3), R₁(W₅(1))} is reached. At this time, S₁ and S₄ are equivalent. Thus, as shown in Figure 3, a period with a local and a global cycle is formed. Moreover, during such a period, a wafer is returned to LLs.

For a DACT with (PM₁, (PM₂, PM₃)²), Qiao et al. [5] proved that the 1-WP schedule is optimal in terms of cycle time. However, in the cases where wafers are required to visit some PMs for k (>2) times, if there exists a value f ∈ ℕ = {1, 2 …} such that k = 3f holds, it is found that a 1-WP schedule cannot be obtained for a DACT, resulting in that the method in [5] is not applicable to such cases. It motivates us to conduct this work. Next, this work gives theoretical proofs for the above findings and provides the analytical expressions of the system cycle time if a 1-WP schedule exists for a DACT with (PM₁, (PM₂, PM₃)^k).

4. Scheduling Analysis by One-Wafer Cyclic Schedule

For a DACT with (PM₁, (PM₂, PM₃)^k), k ≥ 3, with a 3-WP schedule, the cycle time analysis has been conducted in [35]. It is found that there are (3k − 3) local cycles and three global cycles in a period. Thus, before a completed wafer goes back to LLs in a global cycle, it should undergo (3k − 3) local cycles to complete the reentrant process. Furthermore, when this wafer is returned to LLs, it has completed its (2k + 1)-th operation. Assume that a 1-WP schedule exists for a DACT with (PM₁, (PM₂, PM₃)^k). Then, the 1-WP schedule should result in a one-wafer period with multiple local cycles and a global cycle. Since only one completed wafer is returned to LLs in such a period, this wafer has already experienced (3k − 3) local cycles in fact. Notice that if (3k − 3) local cycles are consecutively performed, three wafers should be returned to LLs by three consecutive global cycles. This is a 3-WP schedule. If a 1-WP schedule exists, an obtained period should have (k − 1) local cycles first and then a global cycle such that a wafer is returned to LLs during each global cycle. Further, with a 1-WP schedule, there should be a state, i.e., S₁ = {W₁(1), W(ϑ₁), W(2k + 1), R₃(W(ϑ₂))} at which the last local cycle in a period is just completed.

Theorem 1. 

For a DACT with (PM₁, (PM₂, PM₃)^k), if there exists a value f ∈ ℕ ∪ {0} such that k = 3f + 2 holds, then the system can be scheduled by a 1-WP schedule.

Proof. 

Starting from S1 = {W₁(1), W(ϑ₁), W(2k + 1), R₃(W(ϑ₂))}, S₂ = {W₂(1), W₁(2), W(ϑ₂), R₃(W(ϑ₁ + 1))} is reached after a global cycle. Thus, the tool then evolves in local cycles. After (k − 1) local cycles, the robot stays at PM₃ and prepares to place W₁ into PM₃ for processing the (2f + 3)-th operation. Then, the tool undergoes a global cycle such that W₁ is processed at PM₃ for the (2f + 3)-th operation. Further, after (k − 1) local cycles, W₁ is processed at PM₂ for the (4f + 4)-th operation. In the next global cycle, the robot picks W₁ from PM₂ and moves to PM₃, implying that the robot is going to place W₁ into PM₃ for processing the (4f + 5)-th operation. The following evolution also undergoes (k − 1) local cycles. After that, W₁ is processed at PM₃ for the (6f + 5)-th operation. Note that, the robot is staying at PM₃ at this time. With k = 3f + 2, (6f + 5) = 2k + 1 holds. This means that W₁ can be returned to LLs in the next global cycle. Further, by repeatedly performing (k − 1) local cycles and a global cycle, wafers (i.e., W_d, d ∈ ℕ\{1}) are continuously completed and returned to LLs. Hence, the system can be scheduled by a 1-WP schedule. □

In this case, for a DACT with (PM₁, (PM₂, PM₃)^k), k ≥ 2, if k is known and there exists a value f ∈ ℕ ∪ {0} such that k = 3f + 2 holds, Theorem 1 provides a simple way to find a state (i.e., S₂ = {W₂(1), W₁(2), W(2f + 3), R₃(W(4f + 5))}) starting from which a 1-WP schedule exists.

Theorem 2. 

For a DACT with (PM₁, (PM₂, PM₃)^k), if there exists a value f ∈ ℕ such that k = 3f holds, then the system cannot be scheduled by a 1-WP schedule.

Proof. 

Starting from marking S₁ = {W₁(1), W(ϑ₁), W(2k + 1), R₃(W(ϑ₂))}, S₂ = {W₂(1), W₁(2), W(ϑ₂), R₃(W(ϑ₁ + 1))} is reached after a global cycle. Thus, the tool then evolves in local cycles. After (k − 1) local cycles, the robot is at PM₃, and wafer W₁ is just being processed at the PM for the (2f + 1)-th operation. By a 1-WP schedule, a global cycle should be performed next. In this global cycle, W₁ should be delivered to LLs without completing all operations. Hence, the theorem holds. □

In this case, a 1-WP schedule is not applicable. Thus, this work presents two novel scheduling methods for this case in the next section to improve the system productivity.

Theorem 3. 

For a DACT with (PM₁, (PM₂, PM₃)^k), if there exists a value f ∈ ℕ such that k = 3f +1 holds, then the system can be scheduled by a 1-WP schedule.

Proof. 

Starting from S₁ = {W₁(1), W(ϑ₁), W(2k + 1), R₃(W(ϑ₂))}, S₂ = {W₂(1), W₁(2), W(ϑ₂), R₃(W(ϑ₁ + 1))} is reached after a global cycle. Thus, the tool then evolves in local cycles. After (k − 1) local cycles, wafer W₁ is just being processed at PM₂ for the (2f + 2)-th operation. Then, after a global cycle, the robot picks W₁ from PM₂, moves to PM₃, and stays there. By a 1-WP schedule, the following state evolution is for local cycles. After (k − 1) local cycles, the robot is at PM₃ with W₁ being held to be placed into the PM for the (4f + 3)-th operation. After the wafer is placed into the PM, W₁ is processed in PM₃ for the (4f + 3)-th operation, and then the system just enters the next global cycle. Then, after a global cycle, the system evolves for (k − 1) local cycles. After that, W₁ is processed at PM₃ for the (6f + 3)-th operation. Due to k = 3f + 1, (6f + 3) = 2k + 1 holds, implying that W₁ can be returned to LLs in the next global cycle. Further, by repeatedly performing (k − 1) local cycles and a global cycle, wafers (i.e., W_d, d ∈ ℕ\{1}) are continuously completed and returned to LLs. Hence, the system can be scheduled by a 1-WP schedule. □

In this case, for a DACT with (PM₁, (PM₂, PM₃)^k), k ≥ 2, if k is known and there exists a value f ∈ ℕ such that k = 3f + 1 holds, Theorem 3 provides a simple way to find a state (i.e., S₂ = {W₂(1), W₁(2), W(4f + 3), R₃(W(2f + 3))}) starting from which a 1-WP schedule exists. Then, for the cases where a 1-WP schedule is applicable to a DACT with (PM₁, (PM₂, PM₃)^k), k ≥ 2, the cycle time is analyzed next.

For DACTs, in Step i (PM_i), a swap operation makes a processed wafer removed from the PM and a new wafer placed into the PM. Then, the PM starts to process the wafer. When the robot comes to the PM again to perform a swap operation, the wafer in the PM is picked up, and a new wafer is placed into the PM again. Thus, the time taken to complete a wafer in Step i (i.e., the workload) is

Π_i = ρ_i + λ, i ∈ {1, 2, 3}

(1)

Let φ and ψ denote the time taken for a local and a global cycle without considering the robot waiting time, respectively. Then, they can be calculated as follows.

φ = 2λ + 2μ

(2)

ψ = α + β + 3λ + 4μ

(3)

Further, let Π_local = max{Π₂, Π₃, φ} and Π_1-WP be the cycle time of a DACT with (PM₁, (PM₂, PM₃)^k), k ≥ 2, if a 1-WP schedule exists. Then, according to the cycle time analysis for a 1-WP schedule in [5], if Π₁ ≤ (k − 1)Π_local + ψ, Corollaries 1 and 2 are given below.

Corollary 1. 

For a DACT with (PM₁, (PM₂, PM₃)^k), when there does not exist a value f ∈ ℕ such that k = 3f holds, by a 1-WP schedule, if Π₁ ≤ (k − 1)Π_local + ψ and max{Π₂, Π₃} ≤ ψ, the cycle time is

Π_1-WP = (k − 1)Π_local + ψ

(4)

In fact, the time taken for the (k − 1) local cycles is (k − 1)Π_local. In this case, due to Π₁ ≤ (k − 1)Π_local + ψ and max{Π₂, Π₃} ≤ ψ, when the robot comes to PM_i, i ∈ {1, 2, 3}, the PM has completed the wafer processing. Thus, the robot can perform a swap operation immediately such that there is no robot waiting in the global cycle. Therefore, the time taken for the global cycle is ψ. Hence, in this case, (4) holds.

Corollary 2. 

For a DACT with (PM₁, (PM₂, PM₃)^k), when there does not exist a value f ∈ ℕ such that k = 3f holds, by a 1-WP schedule, if Π₁ ≤ (k − 1)Π_local + ψ and max{Π₂, Π₃} > ψ, the cycle time is

Π_1-WP = kΠ_local

(5)

In this case, due to Π₁ ≤ (k − 1)Π_local + ψ, it implies that when the robot comes to PM₁, PM₁ has completed the wafer processing. Thus, the robot can perform a swap operation immediately. However, due to max{Π₂, Π₃} > ψ, it implies that the time taken for the global cycle is max{Π₂, Π₃}. Therefore, (5) holds. Further, if Π₁ > (k − 1)Π_local + ψ, according to the cycle time analysis for a 1-WP schedule in [5], Corollaries 3–5 are given below.

Corollary 3. 

For a DACT with (PM₁, (PM₂, PM₃)^k), when there does not exist a value f ∈ ℕ such that k = 3f holds, by a 1-WP schedule, if kΠ_local ≥ Π₁ > (k − 1)Π_local +ψ and max{Π₂, Π₃} > ψ, the cycle time is

Π_1-WP = kΠ_local

(6)

In this case, due to Π₁ > (k − 1)Π_local + ψ, it implies that when the robot comes to PM₁, the robot has to wait for some time since the PM has not completed the wafer processing yet at this time. The robot waiting time at PM₁ should be Π₁ − [(k − 1)Π_local + ψ]. Without loss of generality, in this case, let Π₃ = max{Π₂, Π₃} = Π_local > ψ. This means that in a global cycle, the total robot waiting time should be Π_local − ψ at least. Note that Π₁ − [(k − 1)Π_local + ψ] ≤ kΠ_local − [(k − 1)Π_local + ψ] = Π_local − ψ, indicating that, in a global cycle, although the robot has waited at PM₁ for Π₁ − [(k − 1)Π_local + ψ] time units, it still needs to wait at PM₃ such that the time taken for the global cycle is Π_local. Therefore, (6) holds.

Corollary 4. 

For a DACT with (PM₁, (PM₂, PM₃)^k), when there does not exist a value f ∈ ℕ such that k = 3f holds, by a 1-WP schedule, if Π₁ > kΠ_local and max{Π₂, Π₃} > ψ, the cycle time is

Π_1-WP = Π₁

(7)

Corollary 5. 

For a DACT with (PM₁, (PM₂, PM₃)^k), when there does not exist a value f ∈ ℕ such that k = 3f holds, by a 1-WP schedule, if Π₁ > (k − 1)Π_local + ψ and max{Π₂, Π₃} ≤ ψ, the cycle time is

Π_1-WP = Π₁

(8)

For the cases given by Corollaries 4 and 5, in a global cycle, when the robot comes to PM₁, the robot must wait there since the PM has not completed the wafer processing yet. However, when the robot comes to PM_i, i ∈ {2, 3}, the wafer in the PM has been completed, meaning that the workload at PM₁ dominates the system cycle time. Therefore, (7) and (8) for Corollaries 4 and 5 hold, respectively.

Besides, in the cases given by Corollaries 1–5, a 1-WP schedule can achieve the lower bound of the cycle time, i.e., it is optimal in terms of productivity. Up to now, the cycle time analysis has been done in all cases where a 1-WP schedule is applicable to a DACT with (PM₁, (PM₂, PM₃)^k). Based on the above analysis, to apply a 1-WP schedule, the key is to get the desired state of the system shown above, then, by starting from this state, the system can evolve with the 1-WP schedule.

5. Two Novel Scheduling Methods

As above-discussed, given the number k of revisiting times, if there is an f ∈ ℕ such that k = 3f, then no 1-WP schedule can be found. Thus, in this case, there is an issue of how to schedule the system so as to improve productivity. This section aims to tackle this issue by proposing two novel scheduling methods.

For a DACT with (PM₁, (PM₂, PM₃)^k), k ≥ 2, when the system evolves from local cycles to a global cycle, there might be wafer delay time in PMs involved in the reentrant process in the global cycle such that the system cycle time cannot reach its lower bound [33]. Thus, after the local cycles, if the number of global cycles can be decreased, the system cycle time can be improved. With this idea, the first scheduling method is proposed.

5.1. Scheduling Method One

Without loss of generality, the scheduling analysis is conducted for a DACT with (PM₁, (PM₂, PM₃)³). Then, by the proposed method, a DACT with (PM₁, (PM₂, PM₃)³) evolves as follows: S₁ = {W₄(1), W₃(2), W₁(5), R₃(W₂(5))} → S₂ = {W₄(1), W₁(6), W₂(5), R₃(W₃(3))} → S₃ = {W₄(1), W₂(6), W₃(3), R₃(W₁(7))} → S₄ = {W₄(1), W₃(4), W₁(7), R₃(W₂(7))} → S₅ = {W₅(1), W₄(2), W₂(7), R₃(W₃(5))} → S₆ = {W₆(1), W₅(2), W₃(5), R₃(W₄(3))} → S₇ = {W₆(1), W₃(6), W₄(3), R₃(W₅(3))} → S₈ = {W₆(1), W₄(4), W₅(3), R₃(W₃(7))} → S₉ = {W₆(1), W₅(4), W₃(7), R₃(W₄(5))} → S₁₀ = {W₇(1), W₆(2), W₄(5), R₃(W₅(5))} with S₁ and S₁₀ being equivalent. Thus, a period from S₁ to S₁₀ is formed. Note that to reach S₂ from S₁, S₃ from S₂, S₄ from S₃, S₇ from S₆, S₈ from S₇, and S₉ from S₈, robot task sequence σ₂ for a local cycle is performed, respectively. To reach S₅ from S₄, S₆ from S₅, and S₁₀ from S₉, σ₅ = 〈SWP₃ → M₃₀ → PL₀ → PI₀ → M₀₁ → SWP₁ → M₁₂ → SWP₂ → M₂₃〉 is executed, respectively. Note that σ₅ is a global cycle.

During a period from S₁ to S₁₀, before two global cycles (i.e., the first global cycle from S₄ to S₅ and the second one from S₅ to S₆), three local cycles are performed at first. Then, there are three local cycles again, and they are followed by one global cycle (i.e., the third global cycle from S₉ to S₁₀). Thus, after the local cycles, the number of global cycles followed is decreased by comparing with the 3-WP schedule presented in [33,35]. Moreover, in each global cycle, one wafer is returned to LLs. Totally, three wafers are returned to LLs in a period. Therefore, it is also a 3-WP schedule. However, it is different from the 3-WP schedule presented in [33,35], by which three wafers are completed in three consecutive global cycles in a period. Thus, it is a new 3-WP schedule, called an N3-WP1 schedule in short. Let Π_N3-WP1 denote the system cycle time by an N3-WP1 schedule.

Theorem 4. 

For a DACT with (PM₁, (PM₂, PM₃)³), by an N3-WP1 schedule, if Π₁ ≤ 3Π_local + ψ and max{Π₂, Π₃} ≤ ψ, the cycle time is

$${\Pi }_{\mathrm{N}3-\mathrm{WP}1}=\left\{\begin{array}{c}2{\Pi }_{local}+\psi , if \psi \ge {\Pi }_1\\ \frac{6{\Pi }_{local}+2\psi +{\Pi }_1}{3}, if \psi <{\Pi }_1\end{array}\right.$$

(9)

Proof. 

From S₁ to S₄, there are three local cycles that take 3Π_local time units. After that, the system performs two global cycles. Due to Π₁ ≤ 3Π_local + ψ and max{Π₂, Π₃} ≤ ψ, when the robot arrives at PM_i, i ∈ {1, 2, 3}, to pick up a wafer in the first global cycle from S₄ to S₅, the wafer should have been processed and can be picked up from the PM immediately. Therefore, the robot does not need to wait at PM_i, i ∈ {1, 2, 3}, such that ψ time units are needed for the first global cycle. Then, if ψ < Π₁, the next global cycle from S₅ to S₆ takes Π₁ time units, and otherwise, it takes ψ time units. From S₆ to S₉, the three local cycles take 3Π_local time units. For the global cycle from S₉ to S₁₀, ψ time units are required due to Π₁ ≤ 3Π_local + ψ. Thus, by an N3-WP1 schedule, if ψ ≥ Π₁, a period takes 6Π_local + 3ψ time units, and otherwise it takes 6Π_local + 2ψ + Π₁ time units. Therefore, (9) holds. □

In this case, when ψ < Π₁, the result obtained by a 3-WP schedule is improved. Let ω_1i, ω_2i, and ω_3i, i ∈ {1, 2, 3}, denote the robot waiting time before a swap operation at PM₁, PM₂ and PM₃ in the i-th global cycle in a period, respectively. Moreover, let χ = Π₁ − Π_local. The following result is achieved.

Theorem 5. 

For a DACT with (PM₁, (PM₂, PM₃)³), by an N3-WP1 schedule, if Π₁ ≤ 3Π_local + ψ and max{Π₂, Π₃} > ψ, the cycle time is

$${\Pi }_{N3-WP1}=\left\{\begin{array}{c}3{\Pi }_{local}, if {\Pi }_{local}-\psi \ge \chi \hfill \\ 3{\Pi }_{local}+\frac{\chi +\psi -{\Pi }_{local}}{3}, if {\Pi }_{local}-\psi <\chi \hfill \end{array}\right.$$

(10)

Proof. 

By Theorem 4, for the three local cycles from S₁ to S₄, 3Π_local time units are required. After that, the system undergoes two global cycles. Due to Π₁ ≤ 3Π_local + ψ, when the robot arrives at PM₁ to pick up a wafer in the first global cycle from S₄ to S₅, the wafer should have been processed and can be picked up from the PM immediately. Therefore, ω₁₁ = 0. Further, due to max{Π₂, Π₃} > ψ, ω₂₁ + ω₃₁ = Π_local − ψ. In this way, the wafer in a PM with a higher workload of PM₂ and PM₃ can be picked up once it is processed. Thus, Π_local time units are needed for the first global cycle. In the second global cycle from S₅ to S₆, when the robot comes to PM₁, there are two cases: (1) Π_local − ψ ≥ χ and (2) Π_local − ψ < χ. In the first case, before the robot can pick a wafer up from PM₁, it should wait at the PM for ω₁₂ = Π₁ − (ψ + ω₂₁ + ω₃₁) = Π₁ − Π_local = χ time units if χ ≥ 0, or ω₁₂ = 0 if χ < 0. Then, due to max{Π₂, Π₃} > ψ, ω₂₂ + ω₃₂ = Π_local − ψ − ω₁₂ = Π_local − ψ − max(χ, 0) ≥ 0, implying that a wafer in a PM with the higher workload of PM₂ and PM₃ can be picked up once it is processed. Thus, the time taken for the second global cycle is Π_local in this case. In Case (2), before the robot can pick a wafer up from PM₁, it should wait at the PM for ω₁₂ = Π₁ − (ψ + ω₂₁ + ω₃₁) = Π₁ − Π_local = χ > Π_local − ψ > 0 time units. Further, when the robot comes to PM₂ or PM₃ to pick up a wafer, the wafer has already been processed due to Π_local − ψ < χ = ω₁₂ (i.e., Π_local < ω₁₂ + ψ). Thus, for the second global cycle, it spends ω₁₂ + ψ = χ + ψ time units. Similarly, the time taken for the process from S₆ to S₁₀ is 4Π_local. Hence, (10) holds. □

In this case, when Π_local − ψ ≥ χ, the cycle time is optimal. Furthermore, when Π_local − ψ < χ, the result obtained by a 3-WP schedule is improved.

Theorem 6. 

For a DACT with (PM₁, (PM₂, PM₃)³), by an N3-WP1 schedule, if 4Π_local ≥ Π₁ > 3Π_local + ψ and max{Π₂, Π₃} > ψ, the cycle time is

Π_N3-WP1 = (Π₁ + 7Π_local + ψ + max{2Π₁ − ψ − 7Π_local, 0})/3

(11)

Proof. 

Note that in the second global cycle from S₅ to S₆, due to Π₁ > 3Π_local + ψ, ω₂₂ + ω₃₂ = 0 should hold. Thus, from S₆ to S₁₀, it takes 4Π_local time units due to 4Π_local ≥ Π₁ > 3Π_local + ψ and max{Π₂, Π₃} > ψ. Further, in the third global cycle, ω₁₃ = Π₁ − (3Π_local + ψ) and ω₂₃ + ω₃₃ = Π_local − ω₁₃ − ψ = 4Π_local − Π₁.

By Theorem 4, from S₁ to S₄, it takes 3Π_local time units. Further, with ω₂₃ + ω₃₃ = 4Π_local − Π₁, during the first global cycle from S₄ to S₅, ω₁₁ = max(Π₁ − (3Π_local + ψ) − (ω₂₃ + ω₃₃), 0) = max(Π₁ − (3Π_local + ψ) − (4Π_local − Π₁), 0) = max{2Π₁ − ψ − 7Π_local, 0} and ω₂₁ + ω₃₁ = Π_local − ψ − max{2Π₁ − ψ − 7Π_local, 0}. If 2Π₁ − ψ − 7Π_local > 0, then Π_local − ψ − max{2Π₁ − ψ − 7Π_local, 0} = Π_local − ψ − 2Π₁ + ψ + 7Π_local = 8Π_local − 2Π₁ ≥ 0, i.e., ω₂₁ + ω₃₁ ≥ 0. Therefore, the time taken for the first global cycle is ψ + ω₁₁ + ω₂₁ + ω₃₁ = Π_local.

In the second global cycle from S₅ to S₆, ω₁₂ = Π₁ − Π_local + max{2Π₁ − ψ − 7Π_local, 0} > 2Π_local + ψ + max{2Π₁ − ψ − 7Π_local, 0} holds due to Π₁ > 3Π_local + ψ. Thus, ω₂₂ + ω₃₂ = 0. Therefore, the time taken for this global cycle is ω₁₂ + ψ = Π₁ − Π_local + max{2Π₁ − ψ − 7Π_local, 0} + ψ.

Thus, the time taken for a period from S₁ to S₁₀ is Π₁ + 7Π_local + ψ + max{2Π₁ − ψ − 7Π_local, 0}. With three wafers being completed in a period, the cycle time can be obtained by (11). □

Similar to Corollaries 4 and 5, the following two theorems are presented. Due to the space limit, their proofs are omitted.

Theorem 7. 

For a DACT with (PM₁, (PM₂, PM₃)³), by an N3-WP1 schedule, if Π₁ > 4Π_local and max{Π₂, Π₃} > ψ, the cycle time is

Π_N3-WP1 = Π₁

(12)

Theorem 8. 

For a DACT with (PM₁, (PM₂, PM₃)³), by an N3-WP1 schedule, if Π₁ > 3Π_local + ψ and max{Π₂, Π₃} ≤ ψ, the cycle time is

Π_N3-WP1 = Π₁

(13)

Note that in the cases presented by Theorems 7 and 8, the cycle time is optimal.

5.2. Scheduling Method Two

Up to now, the cycle time analysis for a DACT with (PM₁, (PM₂, PM₃)³) by an N3-WP1 schedule has been done. With the N3-WP1 schedule, in some cases, the productivity of the system is improved over the existing 3-WP schedule. However, in some other cases, the optimal cycle time cannot be achieved. Thus, we present another scheduling method by which a DACT with (PM₁, (PM₂, PM₃)³) evolves as follows: S₁ = {W₄(1), W₃(2), W₂(3), R₃(W₁(7))} → S₂ = {W₄(1), W₂(4), W₁(7), R₃(W₃(3))} → S₃ = {W₅(1), W₄(2), W₃(3), R₃(W₂(5))} → S₄ = {W₅(1), W₃(4), W₂(5), R₃(W₄(3))} → S₅ = {W₅(1), W₂(6), W₄(3), R₃(W₃(5))} → S₆ = {W₅(1), W₄(4), W₃(5), R₃(W₂(7))} → S₇ = {W₅(1), W₃(6), W₂(7), R₃(W₄(5))} → S₈ = {W₆(1), W₅(2), W₄(5), R₃(W₃(7))} → S₉ = {W₆(1), W₄(6), W₃(7), R₃(W₅(3))} → S₁₀ = {W₇(1), W₆(2), W₅(3), R₃(W₄(7))}. Since S₁ and S₁₀ are equivalent, a period is formed by this state evolution. In the above state evolution, to realize the process from S₁ to S₂, S₃ to S₄, S₄ to S₅, S₅ to S₆, S₆ to S₇, and S₈ to S₉, robot task sequence σ₁ for a local cycle is executed, respectively, while to reach S₃ from S₂, S₈ from S₇, and S₁₀ from S₉, robot task sequence σ₅ for a global cycle is executed, respectively.

During the period from S₁ to S₁₀, at first, there is a local cycle followed by a global cycle (i.e., the first global cycle from S₂ to S₃). Then, there are four local cycles and then a global cycle (i.e., the second global cycle from S₇ to S₈) is followed. After that, there is a local cycle followed by a global cycle (i.e., the third global cycle from S₉ to S₁₀) again. In each global cycle, one wafer is completed. Thus, during the period, it is also a 3-WP schedule that is different from the one presented in [33,35]. In this work, the second scheduling method is called an N3-WP2 schedule in short. Let Π_N3-WP2 denote the system cycle time under an N3-WP2 schedule. Based on Corollary 1 and Theorem 4, we present Theorem 9, while based on Corollary 2 and Theorem 5, we can get Theorem 10. The proofs of Theorems 9 and 10 are omitted due to the space limit.

Theorem 9. 

For a DACT with (PM₁, (PM₂, PM₃)³), by an N3-WP2 schedule, if Π₁ ≤ Π_local + ψ and max{Π₂, Π₃} ≤ ψ, the cycle time is

Π_N3-WP2 = 2Π_local + ψ

(14)

Theorem 10. 

For a DACT with (PM₁, (PM₂, PM₃)³), by an N3-WP2 schedule, if Π₁ ≤ Π_local + ψ and max{Π₂, Π₃} > ψ, the cycle time is

Π_N3-WP2 = 3Π_local

(15)

In these two cases, as presented in Theorems 9 and 10, the cycle time cannot be shortened anymore, implying that this is the lower bound. For an N3-WP2 schedule, ω_1i, ω_2i, and ω_3i, I ∈ {1, 2, 3}, are also used to denote the robot waiting time before a swap operation at PM₁, PM₂, and PM₃ in the i-th global cycle during a period, respectively. Then, the following result is presented.

Theorem 11. 

For a DACT with (PM₁, (PM₂, PM₃)³), by an N3-WP2 schedule, if 2Π_local ≥ Π₁ > Π_local + ψ and max{Π₂, Π₃} > ψ, the cycle time is

Π_N3-WP2 = 3Π_local

(16)

Proof. 

Due to 2Π_local ≥ Π₁ > Π_local + ψ, the time taken for the state evolution from S₃ to S₈ is 5Π_local. Further, ω₂₂ + ω₃₂ = 0 holds. For the local cycle from S₈ to S₉, it takes Π_local time units. In the global cycle from S₉ to S₁₀, when the robot comes to PM₁, due to Π₁ > Π_local + ψ, it has to wait there for ω₁₃ = Π₁ − (Π_local + ψ) time units. Further, we have ω₂₃ + ω₃₃ = Π_local − ψ − ω₁₃ = 2Π_local − Π₁ ≥ 0. Then, the time taken for the global cycle from S₉ to S₁₀ is ψ + ω₁₃ + ω₂₃ + ω₃₃ = Π_local. Similarly, for the local cycle from S₁ to S₂, it takes Π_local time units. For the global cycle from S₂ to S₃, when the robot comes to PM₁, due to Π₁ > Π_local + ψ, it has to wait there for ω₁₁ = max(Π₁ − (Π_local + ψ) − (ω₂₃ + ω₃₃), 0) = max(Π₁ − (Π_local + ψ) − (2Π_local − Π₁), 0) = max(2Π₁ − 3Π_local − ψ, 0) time units. Then, there are two cases: (1) ω₁₁ = 0 and (2) ω₁₁ = 2Π₁ − 3Π_local − ψ. In Case (1), ω₂₁ + ω₃₁ = Π_local − ψ, leading to that the time taken for the global cycle from S₂ to S₃ is ψ + ω₁₁ + ω₂₁ + ω₃₁ = Π_local. In Case (2), ω₂₁ + ω₃₁ = Π_local − ψ − ω₁₁ = Π_local − ψ − (2Π₁ − 3Π_local − ψ) = 4Π_local − 2Π₁ ≥ 0 due to 2Π_local ≥ Π₁. Thus, in this case, the time taken for the global cycle from S₂ to S₃ is ψ + ω₁₁ + ω₂₁ + ω₃₁ = Π_local as well. Therefore, it takes 9Π_local time units for the period from S₁ to S₁₀. With three wafers completed in the period, (16) holds. □

The cycle time cannot be shortened in this case either, i.e., it is optimal. Further, the following result for another case can be obtained.

Theorem 12. 

For a DACT with (PM₁, (PM₂, PM₃)³), by an N3-WP2 schedule, if 4Π_local ≥ Π₁ > 2Π_local and max{Π₂, Π₃} > ψ, the cycle time is

$${\Pi }_{N3-WP2}=\left\{\begin{array}{c}3{\Pi }_{local}, if 5{\Pi }_{local}-2{\Pi }_1-\psi \ge 0\hfill \\ \frac{4{\Pi }_{local}+\psi +2{\Pi }_1}{3}, if 5{\Pi }_{local}-2{\Pi }_1-\psi <0\hfill \end{array}\right.$$

(17)

Proof. 

For the four local cycles from S₃ to S₇, it takes 4Π_local time units. With 4Π_local ≥ Π₁ > 2Π_local, 4Π_local + ψ > Π₁ holds. Thus, during the global cycle from S₇ to S₈, when the robot comes to PM₁, the robot does not need to wait before swapping at the PM, i.e., ω₁₂ = 0. Further, ω₂₂ + ω₃₂ = Π_local − ψ, resulting in that the time taken for the global cycle from S₇ to S₈ is ψ + ω₁₂ + ω₂₂ + ω₃₂ = Π_local. For the local cycle from S₈ to S₉, it takes Π_local time units. In the global cycle from S₉ to S₁₀, when the robot comes to PM₁, it has to wait there for ω₁₃ = Π₁ − Π_local − ψ − (ω₂₂ + ω₃₂) = Π₁ − 2Π_local > 0 time units due to 4Π_local ≥ Π₁ > 2Π_local. Further, we have ω₂₃ + ω₃₃ = max(Π_local − (ω₁₃ + ψ), 0) = max(Π_local − (Π₁ − 2Π_local + ψ), 0) = max(3Π_local − Π₁ − ψ, 0). Then, there are two cases as follows.

Case 1: max(3Π_local − Π₁ − ψ, 0) = 3Π_local − Π₁ − ψ. In this case, the time taken for the global cycle from S₉ to S₁₀ is ψ + ω₁₃ + ω₂₃ + ω₃₃ = ψ + Π₁ − 2Π_local + 3Π_local − Π₁ − ψ = Π_local. Then, the time taken for the local cycle from S₁ to S₂ is Π_local. Furthermore, in the global cycle from S₂ to S₃, when the robot arrives at PM₁, it has to wait there for ω₁₁ = Π₁ − Π_local − ψ − (ω₂₃ + ω₃₃) = Π₁ − Π_local − ψ − (3Π_local − Π₁ − ψ) = 2Π₁ − 4Π_local > 0 time units due to 4Π_local ≥ Π₁ > 2Π_local. Thus, ω₂₁ + ω₃₁ = max(Π_local − (ω₁₁ + ψ), 0) = max(Π_local − (2Π₁ − 4Π_local + ψ), 0) = max(5Π_local − 2Π₁ − ψ, 0). Then, there are two cases as follows again. Case 1.1: max(5Π_local − 2Π₁ − ψ, 0) = 5Π_local − 2Π₁ − ψ. In this case, the time taken for the global cycle S₂ to S₃ is ψ + ω₁₁ + ω₂₁ + ω₃₁ = ψ + 2Π₁ − 4Π_local + 5Π_local − 2Π₁ − ψ = Π_local. Hence, the time taken for a period from S₁ to S₁₀ is 9Π_local in this case. Case 1.2: max(5Π_local − 2Π₁ − ψ, 0) = 0. In this case, the time taken for the global cycle from S₂ to S₃ is ψ + ω₁₁ + ω₂₁ + ω₃₁ = ψ + 2Π₁ − 4Π_local. Hence, the time taken for a period from S₁ to S₁₀ is 4Π_local + ψ + 2Π₁ in this case.

Case 2: max(3Π_local − Π₁ − ψ, 0) = 0. In this case, the time taken for the global cycle from S₉ to S₁₀ is ψ + ω₁₃ + ω₂₃ + ω₃₃ = ψ + Π₁ − 2Π_local. Then, the time taken for the local cycle from S₁ to S₂ is Π_local. Furthermore, in the global cycle from S₂ to S₃, when the robot arrives at PM₁, it has to wait there for ω₁₁ = Π₁ − Π_local − ψ − (ω₂₃ + ω₃₃) = Π₁ − Π_local − ψ > 0 time units. Thus, ω₂₁ + ω₃₁ = max(Π_local − (ω₁₁ + ψ), 0) = max(2Π_local − Π₁, 0) = 0. Therefore, the time taken for the global cycle from S₂ to S₃ is ψ + ω₁₁ + ω₂₁ + ω₃₁ = Π₁ − Π_local. Hence, the time taken for a period from S₁ to S₁₀ is 4Π_local + ψ + 2Π₁ in this case.

In summary, we conclude that the theorem holds. □

Therefore, by an N3-WP2 schedule, we ensure that, in the case with 5Π_local − 2Π₁ − ψ ≥ 0, the cycle time is optimal. Further, by Theorem 12, the following result can be obtained.

Theorem 13. 

For a DACT with (PM₁, (PM₂, PM₃)³), by an N3-WP2 schedule, if 3Π_local + ψ ≥ Π₁ > Π_local + ψ and max{Π₂, Π₃} ≤ ψ, the cycle time is

Π_N3-WP2 = (4Π_local + 2Π₁ + ψ)/3

(18)

Proof. 

For the four local cycles from S₃ to S₇, it takes 4Π_local time units. With 3Π_local + ψ ≥ Π₁, 4Π_local + ψ > Π₁ holds. Thus, during the global cycle from S₇ to S₈, when the robot comes to PM₁, the robot does not need to wait before swapping at the PM, i.e., ω₁₂ = 0. Further, ω₂₂ + ω₃₂ = 0 due to max{Π₂, Π₃} ≤ ψ. Therefore, the time taken for the global cycle from S₇ to S₈ is ψ. For the local cycle from S₈ to S₉, it takes Π_local time units. During the global cycle from S₉ to S₁₀, when the robot comes to PM₁, it has to wait there for ω₁₃ = Π₁ − Π_local − ψ − (ω₂₂ + ω₃₂) = Π₁ − Π_local − ψ > 0 time units. Further, ω₂₃ + ω₃₃ = 0 due to max{Π₂, Π₃} ≤ ψ. Thus, the time taken for the global cycle from S₉ to S₁₀ is ψ + ω₁₃ + ω₂₃ + ω₃₃ = Π₁ − Π_local. Similarly, the time taken for the local cycle from S₁ to S₂ and the global cycle from S₂ to S₃ is Π_local and Π₁ − Π_local, respectively. Thus, the time taken for the period from S₁ to S₁₀ is 4Π_local + ψ + 2Π₁. Therefore, with three wafers being completed in such a period, the cycle time can be obtained by (18), or the theorem holds. □

Based on the above development, Algorithm 1 is presented to determine one of the schedules N3-WP1 and N3-WP2 to be applied to the system to maximize productivity.

Algorithm 1: For a DACT with (PM1, (PM2, PM3)3), the following algorithm is applied to choose one of the N3-WP1 and N3-WP2 schedules for the tool.
Input: ρ1, ρ2, ρ3, α, μ, β, and λ Output: The adopted schedule
1.	Calculate ψ, Π1, Π2, Π3, and Πlocal;
2.	If max{Π2, Π3} ≤ ψ
3.	If Π1 ≤ Πlocal + ψ
4.	The N3-WP2 schedule is applied, and the cycle time is calculated by Theorem 9;
5.	If Πlocal + ψ < Π1 ≤ 3Πlocal + ψ
6.	Calculate ΠN3-WP1 by Theorem 4 and ΠN3-WP2 by Theorem 13;
7.	If ΠN3-WP1 < ΠN3-WP2
8.	The N3-WP1 schedule is applied;
9.	Else
10.	The N3-WP2 schedule is applied;
11.	If Π1 > 3Πlocal + ψ
12.	The N3-WP1 schedule is applied, and the cycle time is calculated by Theorem 8;
13.	Else
14.	If Π1 ≤ Πlocal + ψ
15.	The N3-WP2 schedule is applied, and the cycle time is calculated by Theorem 10;
16.	If Πlocal + ψ < Π1 ≤ 2Πlocal
17.	The N3-WP2 schedule is applied, and the cycle time is calculated by Theorem 11;
18.	If 2Πlocal < Π1 ≤ 2.5Πlocal − 0.5ψ
19.	The N3-WP2 schedule is applied, and the cycle time is calculated by Theorem 12;
20.	If 2.5Πlocal − 0.5ψ < Π1 ≤ 3Πlocal + ψ
21.	Calculate ΠN3-WP1 by Theorem 5 and ΠN3-WP2 by Theorem 12;
22.	If ΠN3-WP1 < ΠN3-WP2
23.	The N3-WP1 schedule is applied;
24.	Else
25.	The N3-WP2 schedule is applied;
26.	If 3Πlocal + ψ < Π1 ≤ 4Πlocal
27.	Calculate ΠN3-WP1 by Theorem 6 and ΠN3-WP2 by Theorem 12.
28.	If ΠN3-WP1 < ΠN3-WP2
29.	The N3-WP1 schedule is applied;
30.	Else
31.	The N3-WP2 schedule is applied;
32.	If Π1 > 4Πlocal
33.	The N3-WP1 schedule is applied, and the cycle time can be obtained by Theorem 7;

Note that, in the case with 4Π_local < Π₁ and max{Π₂, Π₃} > ψ, by Theorem 7, an N3-WP1 schedule can achieve the minimum system cycle time, while in the case with Π₁ > 3Π_local + ψ and max{Π₂, Π₃} ≤ ψ, by Theorem 8, an N3-WP1 schedule can achieve the minimum system cycle time as well. Thus, we do not present the cycle time analysis in both cases under an N3-WP2 schedule. Now, we have completed the cycle time analysis for a DACT with (PM₁, (PM₂, PM₃)³) by the N3-WP1 and N3-WP2 schedules.

Based on Theorems 10–12, in the case with 2.5Π_local − 0.5ψ ≥ Π₁ and max{Π₂, Π₃} > ψ, an N3-WP2 schedule is optimal. Based on Theorem 7, in the case with Π₁ > 4Π_local and max{Π₂, Π₃} > ψ, an N3-WP1 schedule is optimal. Based on Theorem 9, in the case with Π₁ ≤ Π_local + ψ and max{Π₂, Π₃} ≤ ψ, an N3-WP2 schedule is optimal. Based on Theorem 8, in the case with Π₁ > 3Π_local + ψ and max{Π₂, Π₃} ≤ ψ, an N3-WP1 schedule is optimal. In other cases, for the N3-WP1 and N3-WP2 schedule, the one with the minimum cycle time can be applied to a DACT with (PM₁, (PM₂, PM₃)³). This is what Algorithm 1 does. Besides, in such cases, the adopted scheduling method cannot ensure optimality in terms of the cycle time. This is also the limitation of this work.

Note that by extending the N3-WP1 and N3-WP2 schedules, similar schedules can be developed for a DACT with (PM₁, (PM₂, PM₃)^k), k ∈ {3f| f ∈ ℕ\{1}}. Furthermore, the cycle time can be analyzed in a similar way. Besides, according to the investigation from enterprises of integrated circuit high-end technological equipment, for DACTs with k-time reentrant processes, k is normally no greater than five. Therefore, the obtained results in this work match the practical demand well.

6. Implementation of the Proposed Methods and Illustrative Examples

6.1. Implementation of the Proposed Methods

For a DACT with (PM₁, (PM₂, PM₃)^k), k ≥ 2 and k ≠ 3f, f ∈ {1, 2 …}, based on Theorems 1 and 3, a 1-WP schedule exists for the tool such that the lower bound of the system cycle time can be achieved. Let W₀ denote a virtual wafer and assume that a tool starts from its idle state. To implement the 1-WP schedule for a DACT, virtual wafers are introduced into the tool, and we assume that at the initial state, each PM is processing a virtual wafer and also the robot is holding a wafer.

For the case that a DACT with (PM₁, (PM₂, PM₃)^k), k = 3f +2 and f ∈ ℕ ∪ {0}, Theorem 1 provides a simple way to find a state (i.e., {W₂(1), W₁(2), W(2f + 3), R₃(W(4f + 5))}) starting from which a 1-WP schedule exists. By introducing virtual wafers into the tool, let S₀ = {W₀(1), W₀(2), W₀(3), R₃(W₀(5))} be the initial (idle) state of the tool. Then, by the swap strategy, the tool can evolve into a state in which all virtual wafers are removed from the tool. At this time, the wafers in the tool are all real ones. In this way, the 1-WP schedule is implemented.

For the case that a DACT with (PM₁, (PM₂, PM₃)^k), k = 3f +1 and f ∈ ℕ, Theorem 3 provides a simple way to find a state (i.e., {W₂(1), W₁(2), W(4f + 3), R₃(W(2f + 3))}) starting from which a 1-WP schedule exists. By introducing virtual wafers into the tool, let S₀ = {W₀(1), W₀(2), W₀(7), R₃(W₀(5))} be the initial (idle) state of the tool. Then, by the swap strategy, the tool can evolve into a state in which all virtual wafers are removed from the tool, and the wafers in the tool are all real ones. In this way, the 1-WP schedule is implemented.

For a DACT with (PM₁, (PM₂, PM₃)^k), k = 3f and f ∈ ℕ, based on Theorem 2, a 1-WP schedule does not exist. In this case, this work presents two methods (an N3-WP1 schedule and an N3-WP2 schedule) to operate the tool for productivity improvement. To implement the N3-WP1 schedule, by introducing virtual wafers, let S₀ = {W₀(1), W₀(2), W₀(5), R₃(W₀(5))} be the initial (idle) state of the tool. Then, by the swap strategy, the tool can evolve into a state in which all virtual wafers are removed from the tool, and the wafers in the tool are all real ones. To implement the N3-WP2 schedule, by introducing virtual wafers, let S₀ = {W₀(1), W₀(2), W₀(3), R₃(W₀(7))} be the initial (idle) state of the tool. Then, by the swap strategy, the tool can evolve into a state in which all virtual wafers are removed from the tool, and the wafers in the tool are all real ones. In this way, the N3-WP1 schedule and N3-WP2 schedule are implemented.

6.2. Illustrative Examples

Now, several examples are presented to demonstrate the obtained results in this work. Among them, Examples 2–4 come from [35]. Note that Π_3-WP represents the system cycle time obtained by a 3-WP schedule.

Example 1. 

For a DACT with (PM₁, (PM₂, PM₃)⁵), the wafer processing time at PM₁, PM₂, and PM₃ is 80 s, 35 s, and 50 s (i.e., ρ₁ = 80 s, ρ₂ = 35 s, and ρ₃ = 50 s), respectively, and α = μ = β = 3 s and λ = 8 s.

For this example, k = 3 × 1 + 2 with f = 1, Π₁ = 88 s, Π₂ = 43 s, Π₃ = 58 s, and ψ = 42 s. By applying a 3-WP schedule, Π_3-WP = (290 + 44/3) s ≈ 304.67 s. However, if a 1-WP schedule is applied, it follows from Corollary 2 that Π_1-WP = 5Π₃ = 290 s. Obviously, the 1-WP schedule outperforms the 3-WP schedule.

Example 2. 

For a DACT with (PM₁, (PM₂, PM₃)³), ρ₁ = 37 s, ρ₂ = 22 s, ρ₃ = 32 s, α = μ = β = 4 s, and λ = 8 s.

For this example, Π₁ = 45 s, Π₂ = 30 s, Π₃ = 40 s, and ψ = 48 s. By using a 3-WP schedule, we get Π_3-WP = 128 s. If an N3-WP1 schedule is applied, by Theorem 4, we get Π_N3-WP1 = 128 s, while if an N3-WP2 schedule is applied, by Theorem 9, we also get Π_N3-WP2 = 128 s. Thus, the three scheduling methods can obtain the same results.

Example 3. 

For a DACT with (PM₁, (PM₂, PM₃)³), ρ₁ = 50 s, ρ₂ = 22 s, ρ₃ = 32 s, α = μ = β = 4 s, and λ = 8 s.

For this example, Π₁ = 58 s, Π₂ = 30 s, Π₃ = 40 s, and ψ = 48 s. By using a 3-WP schedule, Π_3-WP = 404/3 s ≈ 134.67 s. However, if an N3-WP1 schedule is applied, by Theorem 4, Π_N3-WP1 = 394/3 s ≈ 131.33 s. If an N3-WP2 schedule is applied, by Theorem 9, Π_N3-WP2 = 128 s. Thus, in this case, an N3-WP2 schedule should be applied since it can achieve the best performance among the three schedules.

Example 4. 

For a DACT with (PM₁, (PM₂, PM₃)³), ρ₁ = 450 s, ρ₂ = 200 s, ρ₃ = 250 s, α = μ = β = 3 s, and λ = 8 s.

For this example, Π₁ = 458 s, Π₂ = 208 s, Π₃ = 258 s, and ψ = 42 s. By using a 3-WP schedule, Π_3-WP = (774 + 184/3) s ≈ 835.33 s. However, if an N3-WP1 schedule is applied, by Theorem 5, Π_N3-WP1 = 774 s. If an N3-WP2 schedule is applied, by Theorem 11, Π_N3-WP2 = 774 s. Thus, in this case, we can choose either N3-WP1 or N3-WP2 to improve the cycle time by 7.34% in comparison with a 3-WP schedule.

Example 5. 

For a DACT with (PM₁, (PM₂, PM₃)³), ρ₁ = 200 s, ρ₂ = 45 s, ρ₃ = 50 s, α = μ = β = 2 s, and λ = 5 s.

In this example, Π₁ = 205 s, Π₂ = 50 s, Π₃ = 55 s, and ψ = 27 s. By using a 3-WP schedule, we have Π_3-WP = (165 + 272/3) s ≈ 255.67 s. However, if an N3-WP1 schedule is applied, by Theorem 6, Π_N3-WP1 = 617/3 s ≈ 205.67 s. If an N3-WP2 schedule is applied, by Theorem 12, Π_N3-WP2 = 219 s. Thus, in this case, the N3-WP1 schedule should be applied, and it improves the cycle time by 19.56% in comparison with a 3-WP schedule.

In Examples 1–5, with the parameters of the cluster tool provided, we can quickly obtain the cycle time of the system under any one of the 3-WP schedule, N3-WP1 schedule, N3-WP2 schedule, and 1-WP schedule (if existing). With the system cycle time obtained, one can determine the best scheduling method to be applied to DACTs with reentrant wafer flows.

Besides, more examples are given in

Table 3. Comparison results.

No.	ρ1	ρ2	ρ3	N3-WP1		N3-WP2		3-WP	The Adopted Scheduling Method	Improvement
				ΠN3-WP1	Theorem	ΠN3-WP2	Theorem	Π3-WP
1	250	35	50	258	7	/	/	302	N3-WP1	14.57%
2	150	25	30	158	8	/	/	195(1/3)	N3-WP1	19.11%
3	70	25	30	130	4	118	9	142	N3-WP2	16.90%
4	70	25	35	140(1/3)	5	129	10	152	N3-WP2	15.13%
5	95	40	50	183(2/3)	5	174	11	198(2/3)	N3-WP2	12.42%
6	110	40	50	188(2/3)	5	174	12	208(2/3)	N3-WP2	16.61%
7	140	25	30	153(1/3)	4	163(1/3)	13	188(2/3)	N3-WP1	18.73%
8	100	25	30	140	4	136(2/3)	13	162	N3-WP2	15.64%
9	210	35	50	222	6	236(2/3)	12	275(1/3)	N3-WP1	19.37%
10	200	35	50	218(2/3)	5	230	12	268(2/3)	N3-WP1	18.61%
11	120	35	50	192	5	176(2/3)	12	215(1/3)	N3-WP2	17.96%

to show the superiority of the proposed methods by comparing them with the 3-WP schedule in terms of the system cycle time. In the cases in Table 3, the time for the robot activities and wafer processing is set according to real applications in a semiconductor equipment vendor in China. With these given parameters of cluster tools, Algorithm 1 can be used to obtain the best scheduling method immediately in the cases shown in Table 3. Furthermore, by using the best one of the N3-WP1 and N3-WP2 schedules, the cycle time of the system is improved by 16.8% on average by comparing with the 3-WP schedule. Besides, in Cases 1–6, the adopted scheduling method can achieve a minimal cycle time. However, in Cases 7–11, the optimality of the adopted scheduling method cannot be ensured. Nevertheless, the adopted method significantly outperforms the existing 3-WP schedule.

7. Conclusions

Wafer reentrant flows normally exist for some processes, such as chemical vapor and physical vapor deposition. Moreover, cluster tools are widely applied to wafer fabrication for such processes. Such a tool compactly integrates several PMs, a wafer transport robot, and two LLs. It can provide a highly precise vacuum environment for wafer fabrication. Since there is no buffer between PMs, it is important to effectively schedule such a tool with reentrant processes. For a DACT with two-time reentrant processes, it is found that a 1-WP schedule can achieve the optimal cycle time. However, for some wafer fabrication processes, wafers should be processed at some processing steps more than two times. Up to now, the problem is open for the issue if a 1-WP schedule exists for a DACT with wafer reentrant processes for more than two times. If not, it raises the question of whether a better schedule exists by comparing it with an existing 3-WP schedule. This motivates us to do this work to answer this question.

In this work, theorical analysis is conducted on it. In Section 4, it is shown that if there exists a value f ∈ ℕ such that k = 3f holds, then a 1-WP schedule does not exist, and otherwise, the system can be scheduled by a 1-WP schedule. Further, analytical expressions are given to calculate the system cycle time if a 1-WP schedule exists. In the cases where a 1-WP schedule is not applicable, this work presents two novel scheduling methods in Section 5 to improve the cycle time by comparing it with an existing 3-WP schedule. Meanwhile, by these two scheduling methods, analytical expressions are given to obtain the system cycle time. Further, an algorithm is given to display the conditions under which one of the two novel scheduling methods can be used to operate cluster tools. Besides, this work presents the conditions under which the two novel scheduling methods may not achieve the minimal cycle time, i.e., the limitation of the methods. Thus, given a case, by simply calculating the cycle time, one can decide which method should be applied to the system. In Section 6, by introducing virtual wafers, a way to implement the proposed scheduling methods is given, and the application of the proposed scheduling methods is demonstrated by examples.

In the future, we aim to deal with the scheduling problems of cluster tools handling multi-wafer types with different wafer flow patterns as well as multi-cluster tools. Moreover, the proposed scheduling methods cannot achieve the minimal system cycle time in some cases. Thus, another future work needs to be done for optimal scheduling of such cases.