Sawtooth V-Trough Cavity for Low-Concentration Photovoltaic Systems Based on Small-Scale Linear Fresnel Reflectors: Optimal Design, Verification, and Construction
Abstract
:1. Introduction
- (i)
- The use of non-concentrated solar energy has significantly increased its presence in the electricity sector, mainly due to the lower costs. Based on a recent report from the International Renewable Energy Agency () [2], the levelized cost of energy () from non-concentrated photovoltaic () systems is expected to decrease by (USD/kWh) by 2050. The lower cost of modules is one of the main reasons for this decrease [3]. In this regard, the International Renewable Energy Agency () presented a report in 2017 predicting a drop in the cost of modules over the following 10 years [4]. The spot price of a module is currently USD 0.266/ [5]. Concentrated systems replace the large surface area of photovoltaic cells used in non-concentrated photovoltaic systems with cheaper optical materials (e.g., lenses or mirrors), which thus reduces the cost of these systems.
- (ii)
- As with any other technology, non-concentrated solar power ages and degrades over time. Manufacturers of silicon-based modules estimate their lifetime to be about 20–25 years. After that, the module components need to be dismantled and properly recycled. In 2016, the International Renewable Energy Agency () and the International Energy Agency Photovoltaic Power Systems () [6] presented the first global projections for future module waste volumes up to 2050. Annual module waste accounted for 250,000 tons in 2016. However, the contribution of global waste from modules is expected to considerably increase in the coming years. Waste generation from solar modules is estimated to reach million tons by 2030 and will continue to increase to around 60 million tons by 2050 [6]. The significant decrease in the large surface area of cells used in non-concentrated systems and thus in the resulting waste is one of the main advantages of concentrated systems.
- (iii)
- The conversion efficiency of cells used in non-concentrated systems is relatively low, typically around 10–20% for commercially available silicon cells [2]. This figure can be up to for more sophisticated multijunction cells used in systems [2]. Hasan et al. [7] demonstrated that a with p-Si solar cells improved the Pmax by more than a non-concentrated p-Si solar panel.
- (iv)
- (v)
- The temperature of a cell increases with the increase in solar irradiance concentration, thus leading to a loss in solar cell efficiency. For this reason, concentrated systems are equipped with a cooling system. In addition to reducing the cell temperature, cooling systems can also be used to heat water in household applications if a low-concentration photovoltaic system is used. This dual use increases the energy efficiency of the system. Kandilli [10] evaluated the overall efficiency of a system at over .
- (vi)
- (vii)
- The installation cost of an system can be more than double ( times) the cost of a non-concentrated system [13]. However, under suitable conditions of high direct irradiation (>2.5 (MWh/m2 year)) and at utility scale, technologies have proven to be competitive with non-concentrated photovoltaic systems [14].
- (i)
- The optimal design of a sawtooth V-trough cavity, which ensures uniform illumination of the photovoltaic cells;
- (ii)
- The verification of the designed sawtooth V-cavity to confirm that the derived equations are correct;
- (iii)
- The manufacture of the designed sawtooth V-cavity, in order to identify any manufacturing difficulties;
- (iv)
- Experimental tests to show that the manufactured sawtooth cavity meets the specifications.
- (i)
- A methodology for designing a new sawtooth V-cavity;
- (ii)
- A significant reduction in the cavity height of the proposed sawtooth V-trough cavity;
- (iii)
- After (ii), a considerable reduction in the cost of manufacturing an ;
- (iv)
- A comparison between the proposed sawtooth V-cavity and the standard V-cavity, considering that both cavities have the same cavity opening and the same cell width;
- (v)
- The presentation of a novel graphical system to design the primary reflector system for the .
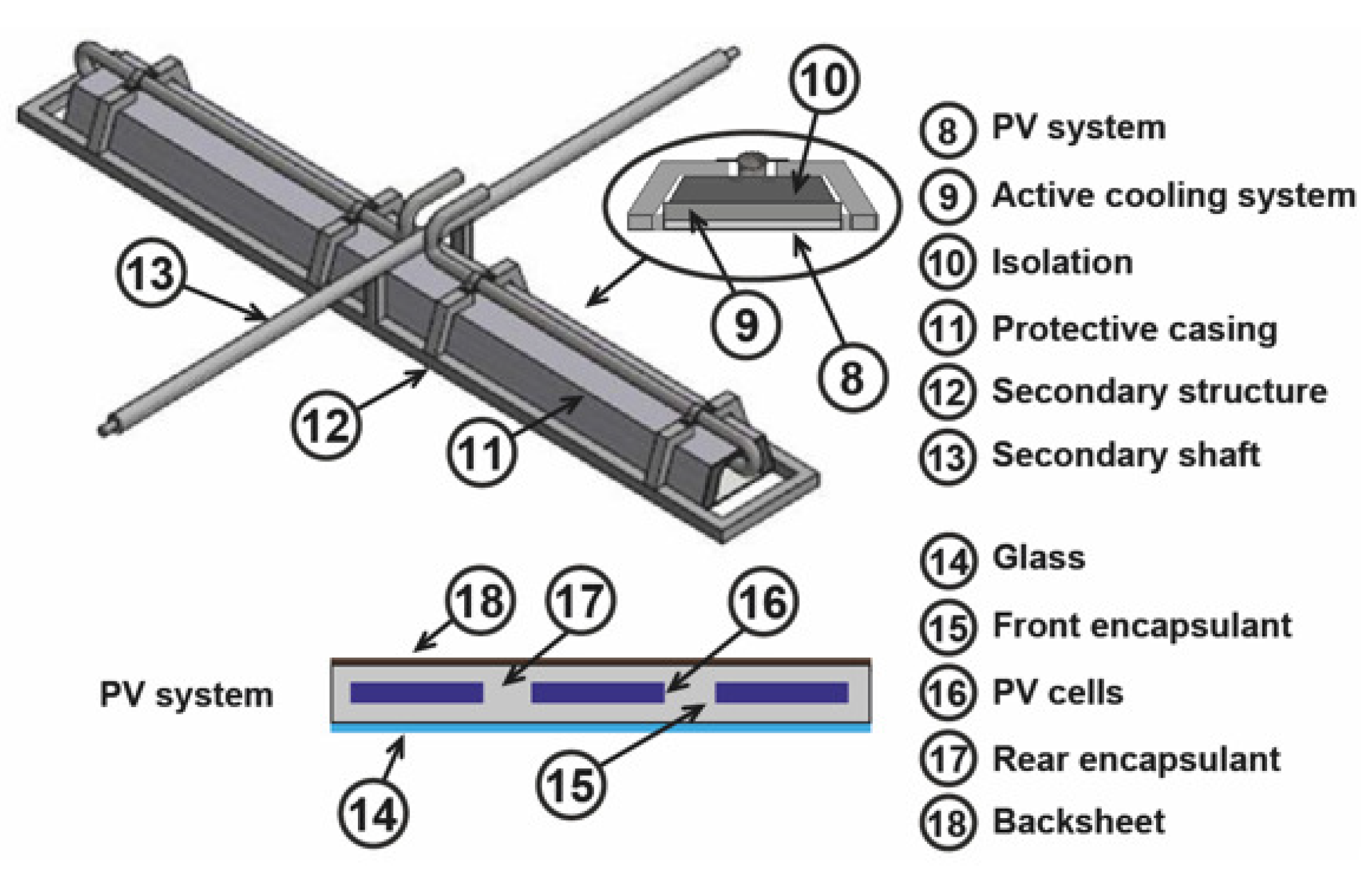
2. Overview of an SSLFR
- (i)
- The primary reflector system (see Figure 1).
- (ii)
- The secondary system (see Figure 3).
3. Methodology
3.1. The Main Elements of a Concentrator
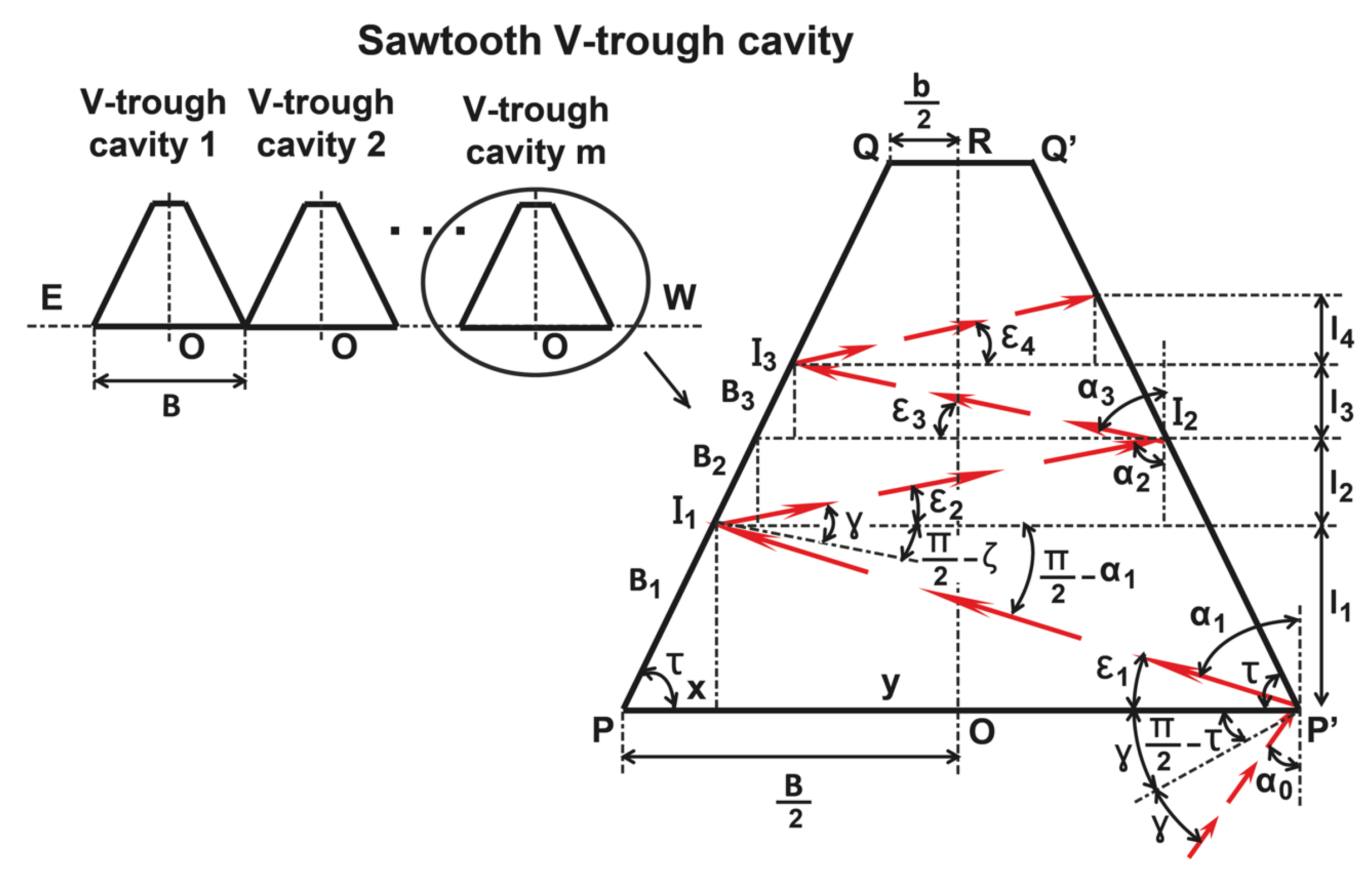
3.2. The Optimal Design of a Sawtooth V-Trough Cavity
- (i)
- The sawtooth V-trough cavity is symmetrical to the central mirror in the primary system.
- (ii)
- The sidewalls ( and ) are assumed to be perfectly specular.
- (iii)
- The width of the cells, b, is standardized by the cell manufacturers.
- (iv)
- The V-trough cavity is east–west aligned.
- (v)
- The trough wall angle () is the complement of [39].
- (vi)
- The trough wall angle () is fixed.
- (vii)
- The axis is the reference axis for the angles of the sun’s incident rays. is considered positive for the solar rays coming from the mirrors on the left side and negative for those coming from the mirrors on the right.
- (viii)
- The angle between the solar ray reaching the cavity and is denoted as (i.e., ). In addition, each successive reflection of the sun’s ray inside the cavity is denoted as , for
3.3. Uniform Distribution of Flux on PV Cells
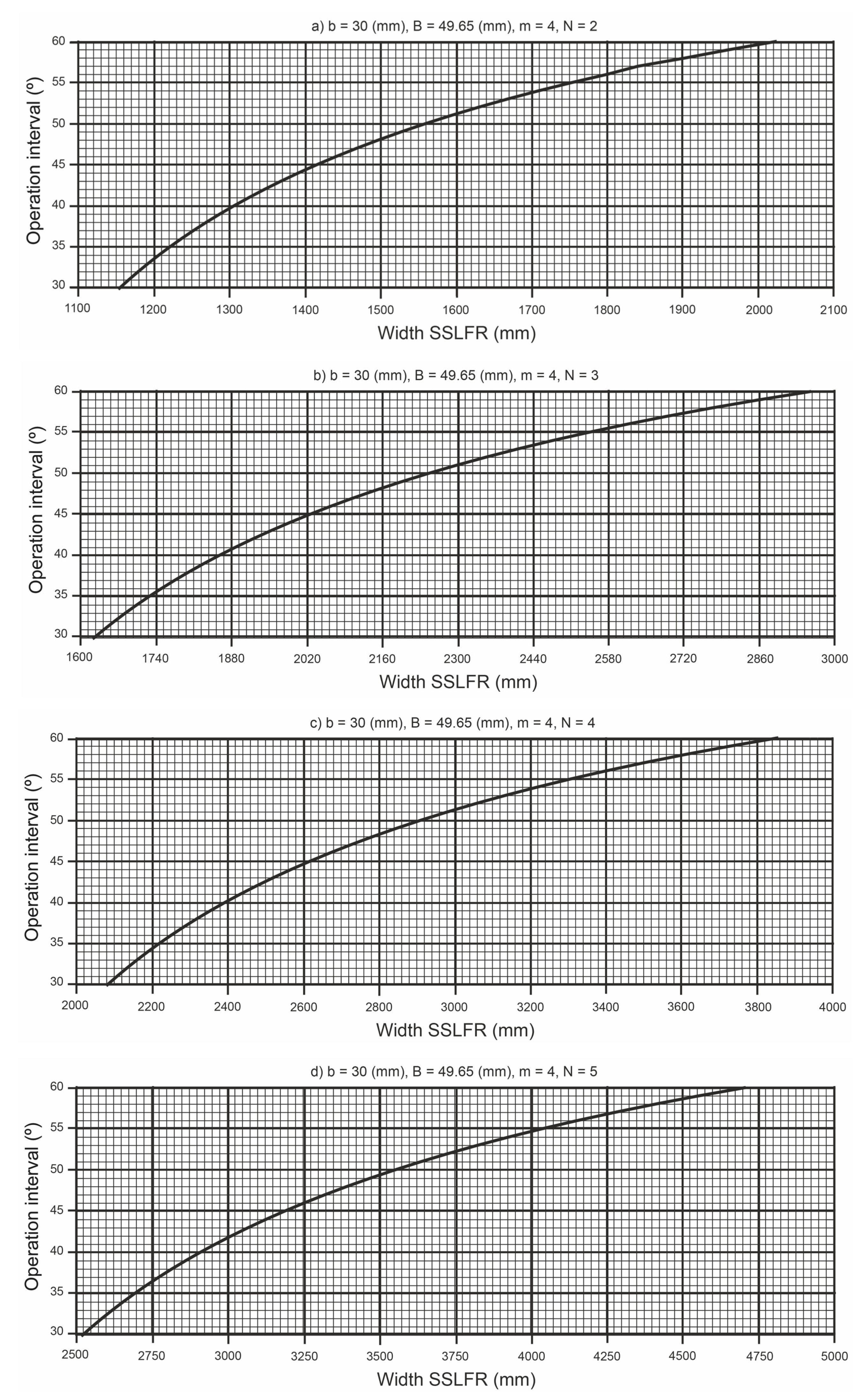
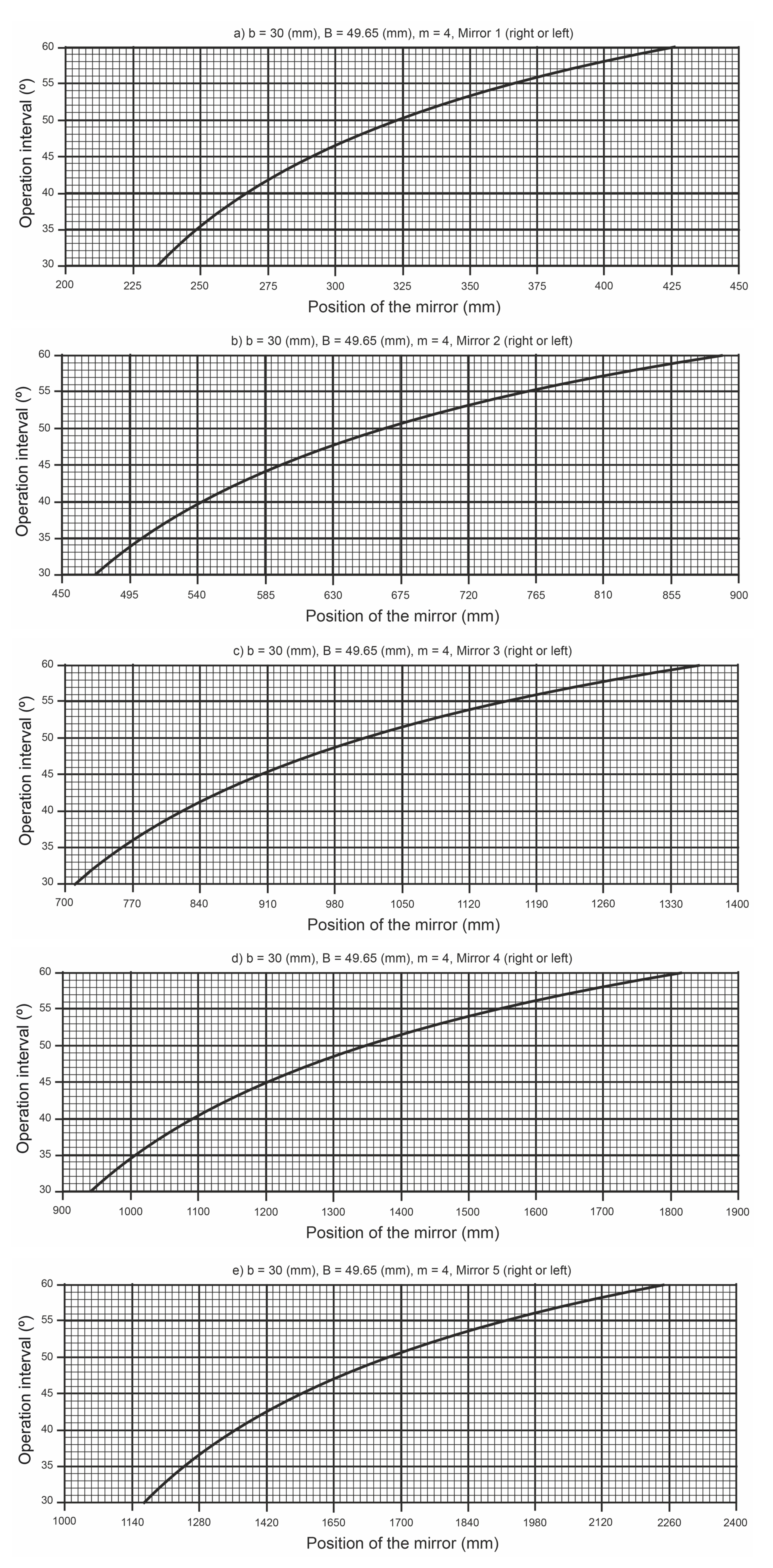
- (i)
- Parameter (small ). Shading (one mirror creates a shadow on an adjacent mirror) and blocking (one mirror blocks the reflected rays of an adjacent mirror) obviously depend on the distance between consecutive mirrors (). This distance is not fixed and depends on the width of each mirror.
- (ii)
- Parameter (large ). Increasing the value of the parameter prevents the occurrence of the shading and blocking phenomena, but an excessive value of also leads to the nonuniform illumination of the cells [18].
- (iii)
- Parameter N. As each mirror has a different , using a large number of mirrors in the design increases the probability of a nonuniform flux distribution in the cells [18].
- (iv)
- Parameter . The ratio between the width of each mirror and the width of the cells also influences the uniform illumination of the cells [18].
3.4. Verification
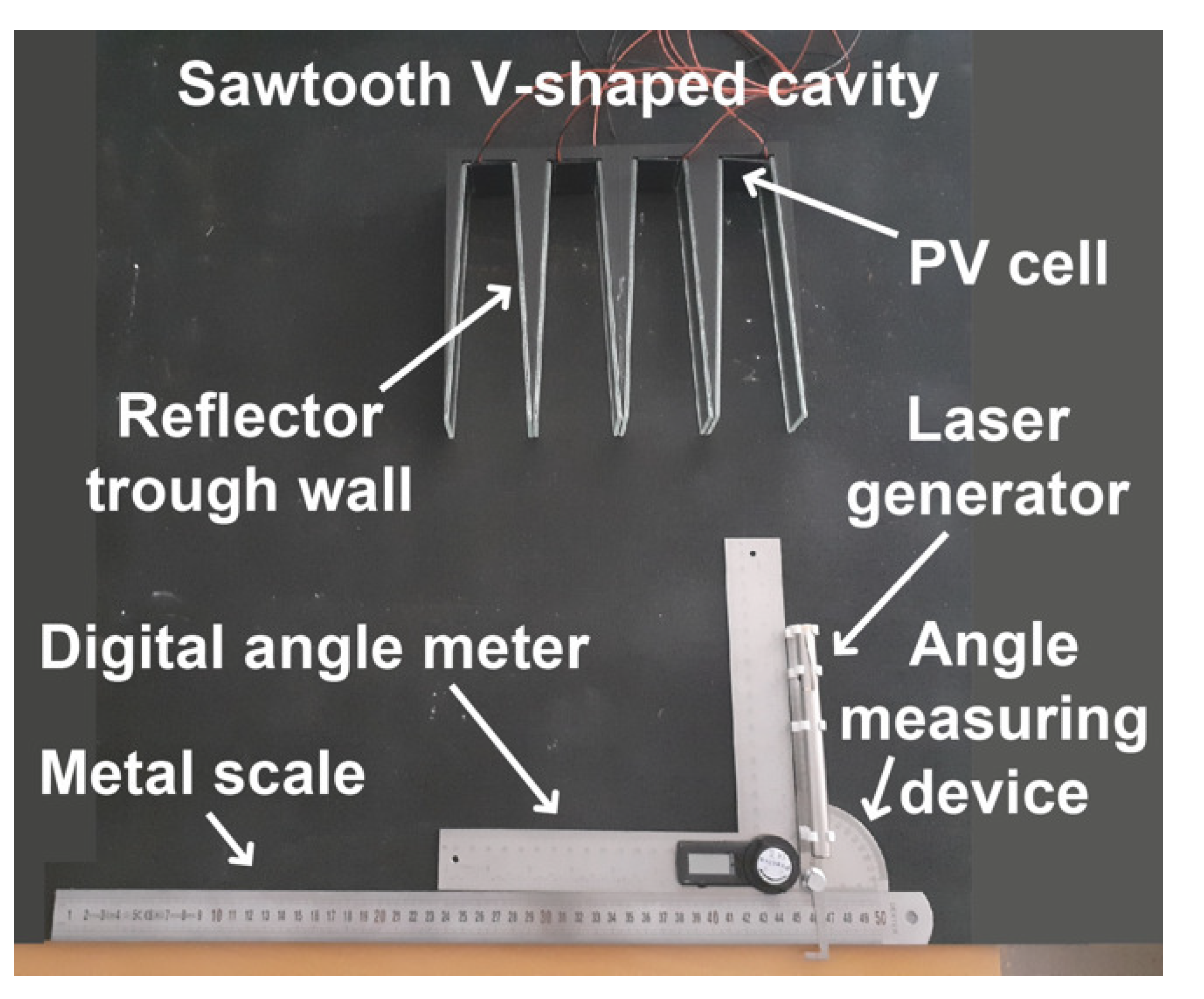
3.5. The Manufacture of the Sawtooth V-Trough Cavity and the Laser Experiment
4. Application of the Methodology and Analysis of the Results
- (i)
- Available roof surface area. The available roof area was considered to be able to accommodate an with the following dimensions: width 2244 mm and length 2000 mm.
- (ii)
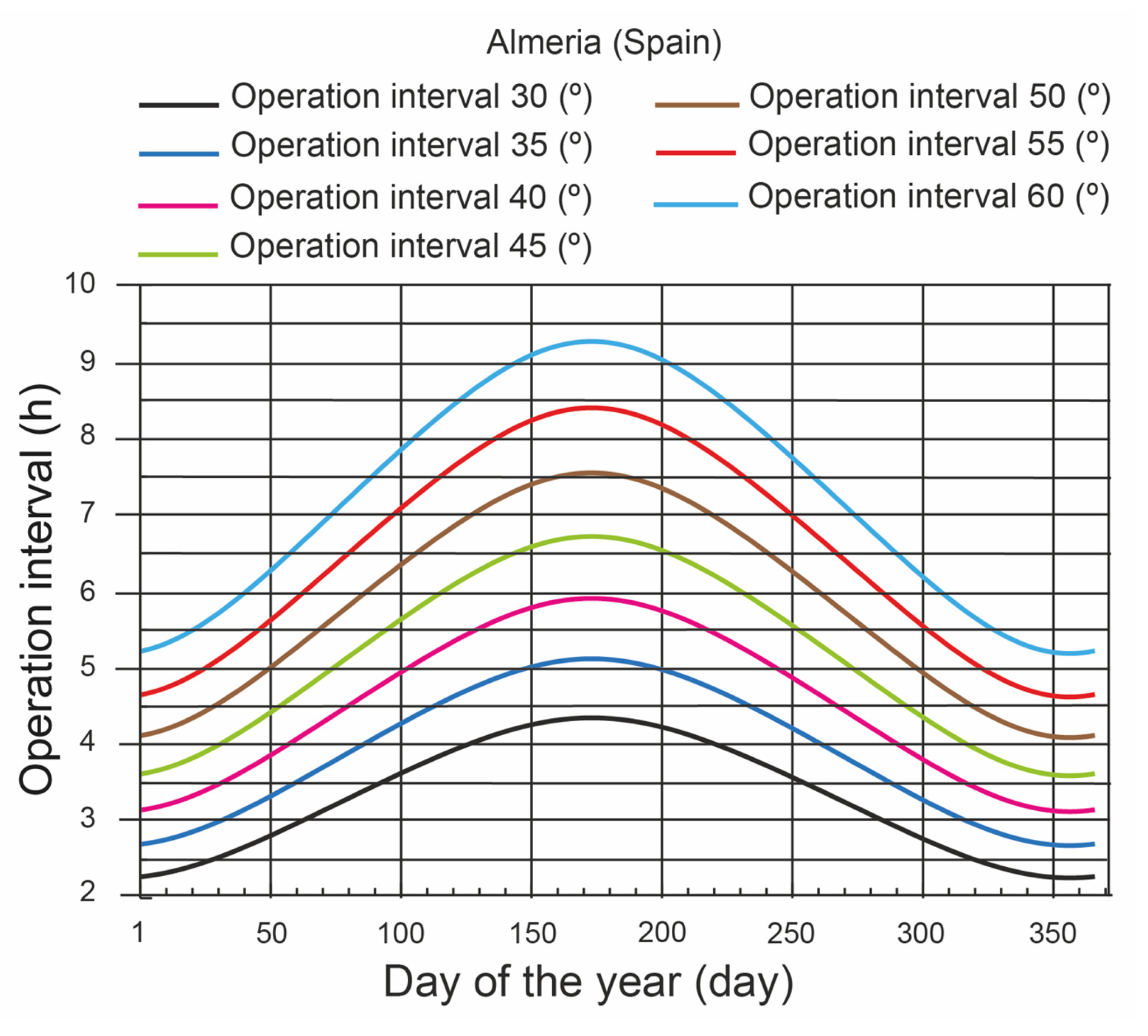
- Study location. The rooftop was located in Almería (Spain), for which the geographical data were: latitude 36° N, longitude 02° W, and altitude 22 m.
- (iii)
- Width of the commercial cells (). A commercial cell width of 30 mm was considered. The assumption of this value does not limit the application of the methodology.
- (iv)
- Acceptance angle (). A (°) was considered. It is a plausible value for the typical dimensions of an [18].
- (v)
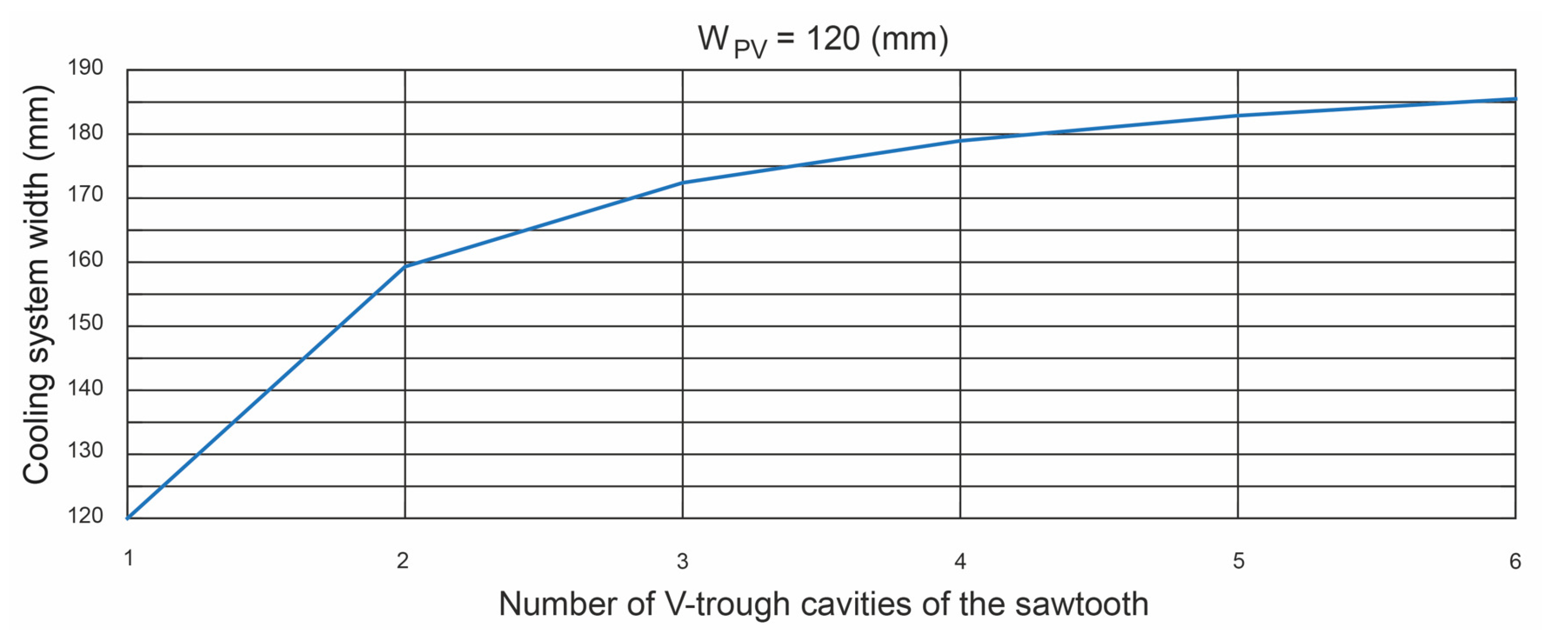
- Number of V-trough cavities in the sawtooth (m). This m was equal to 4 to limit the number of mirrors as well as any increase in the cost of the [28]. Any other value of this parameter can be used.
- (vi)
- (vii)
- Number of mirrors of the . The number of mirrors of the was considered to be equal to seven so that the cost of the was not too high [28]. Therefore, .
- (viii)
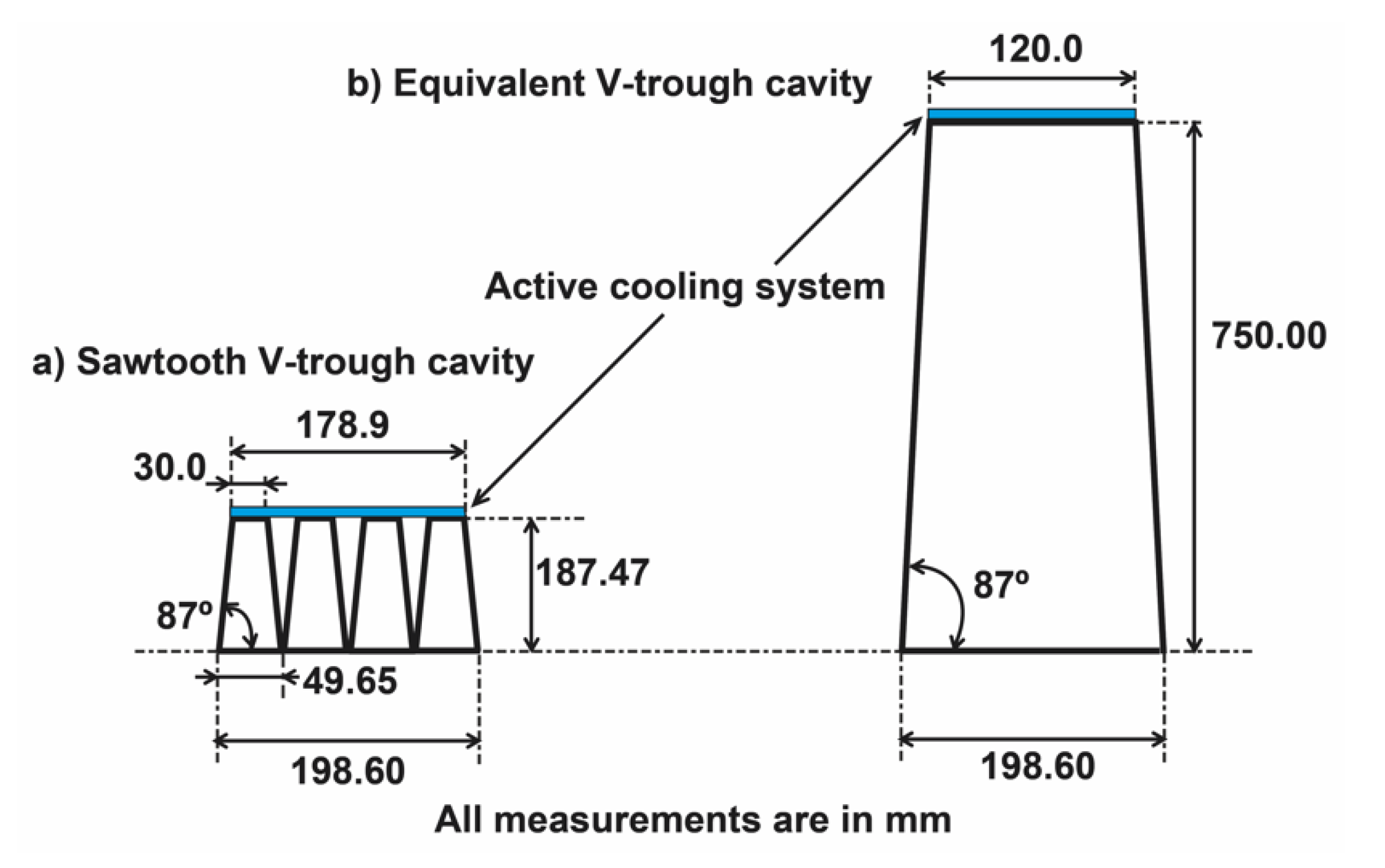
4.1. Comparison between the Proposed Sawtooth V-Cavity and the Standard V-Cavity
4.1.1. Mechanical Aspects
- (i)
- Reduction in the cost of the fixed structure. As the height of the proposed cavity is much lower, the fixed structure of the is smaller, which lowers the cost thereof.
- (ii)
- Reduction in the cost of the fixed structure and secondary system structures. By reducing the height of the cavity, the surface area exposed to wind loads is smaller, which lowers the cost of the fixed structure and the secondary system structures.
4.1.2. Thermal Aspects
4.1.3. Other Beneficial Aspects
- (i)
- The same reflective surface for both cavities. The multiple reflective walls of the new cavity, however, are used in combination to replace the two reflective surfaces of the V-trough cavity, which could reduce the difficulty of manufacturing, maintaining, and transporting the large glasses. This would also decrease the total cost of the .
- (ii)
- The connection of the cells. The connection of the photovoltaic cells is facilitated due to the separation between the photovoltaic cells in the new cavity.
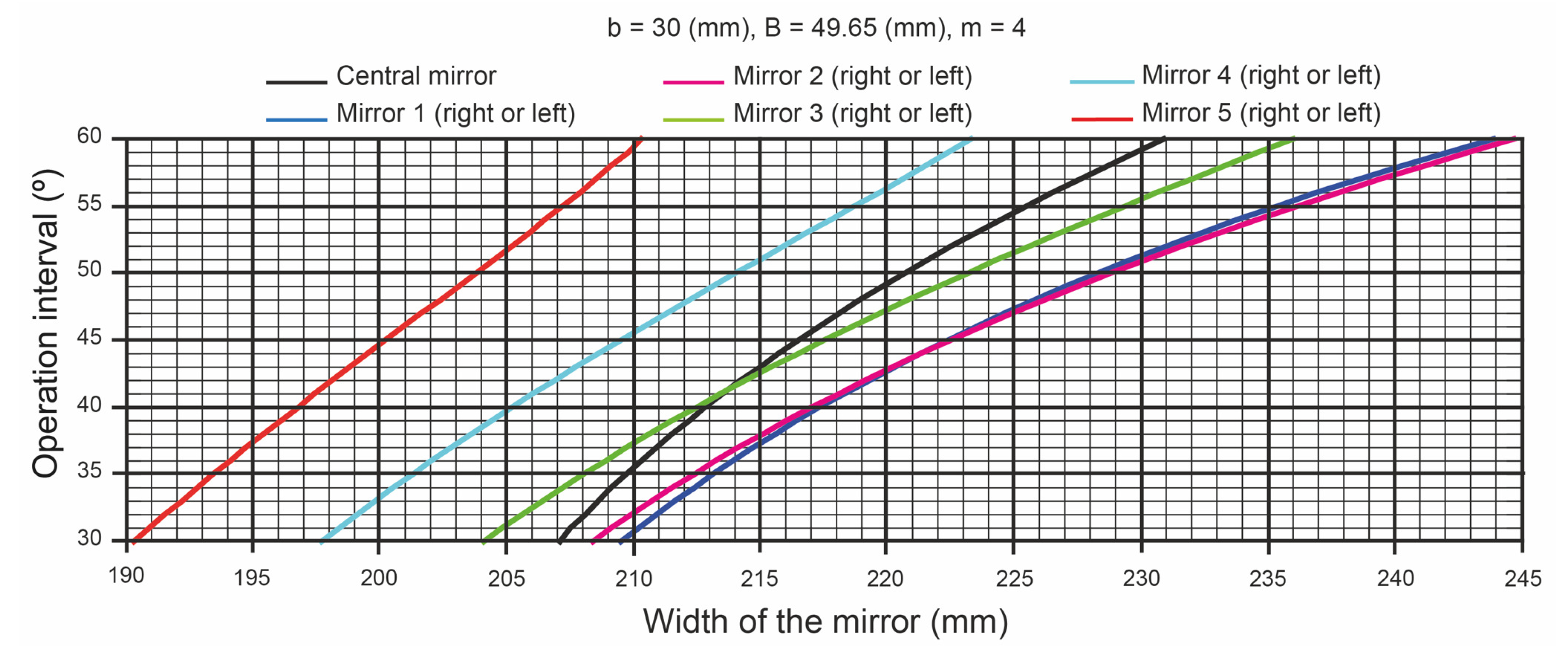
4.2. The Application of the Graphic System When Designing the Primary Reflector System
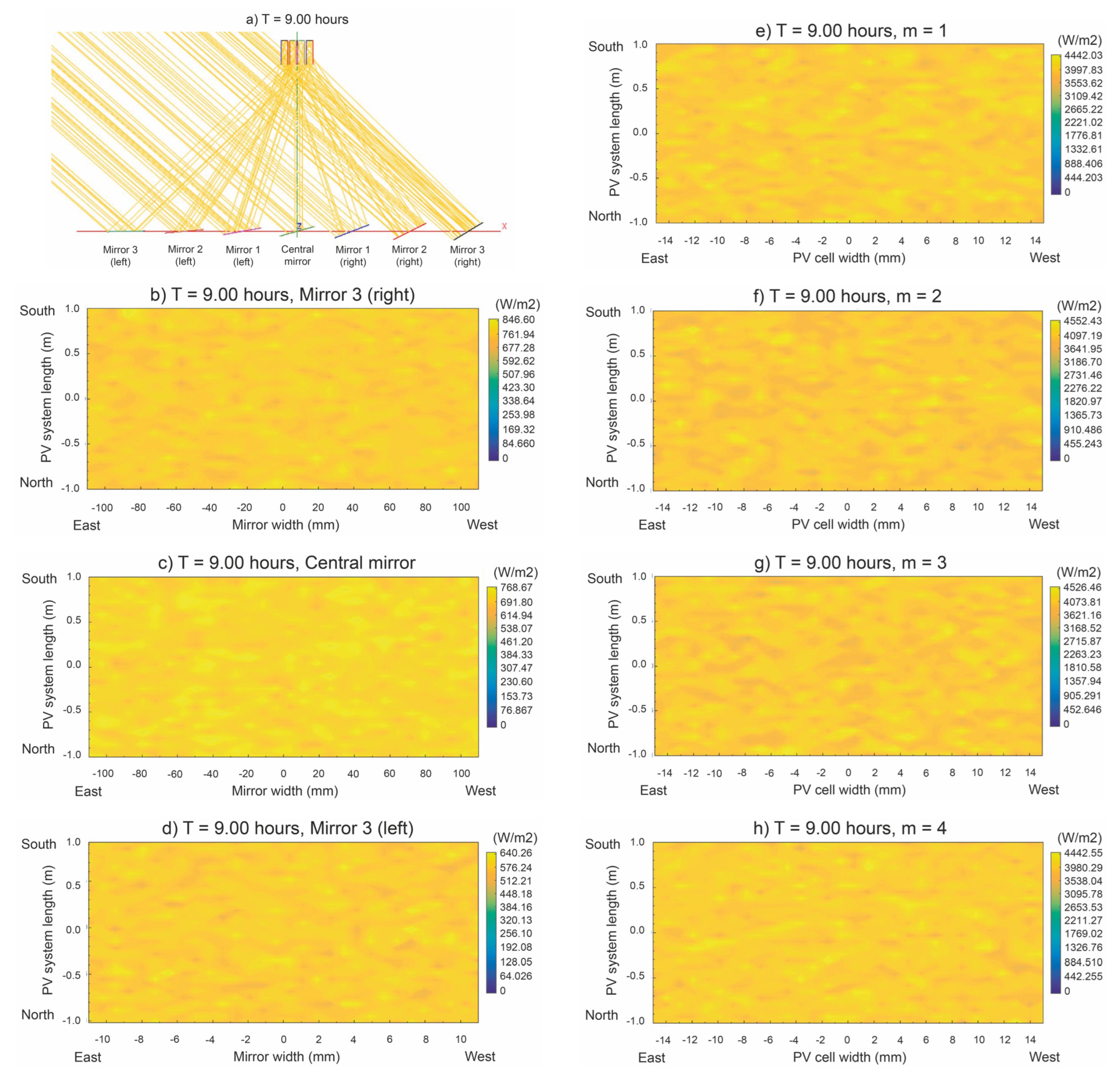
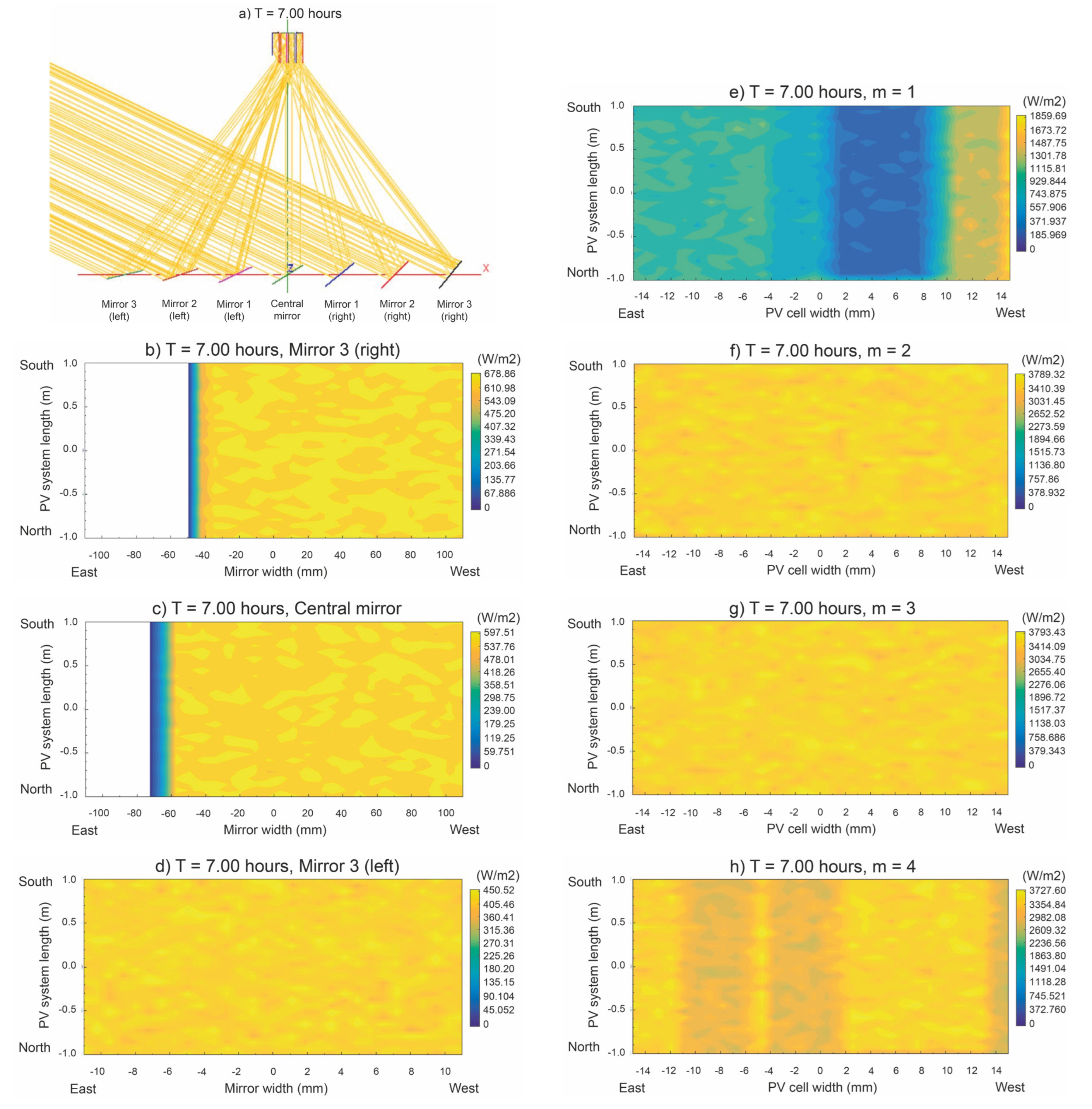
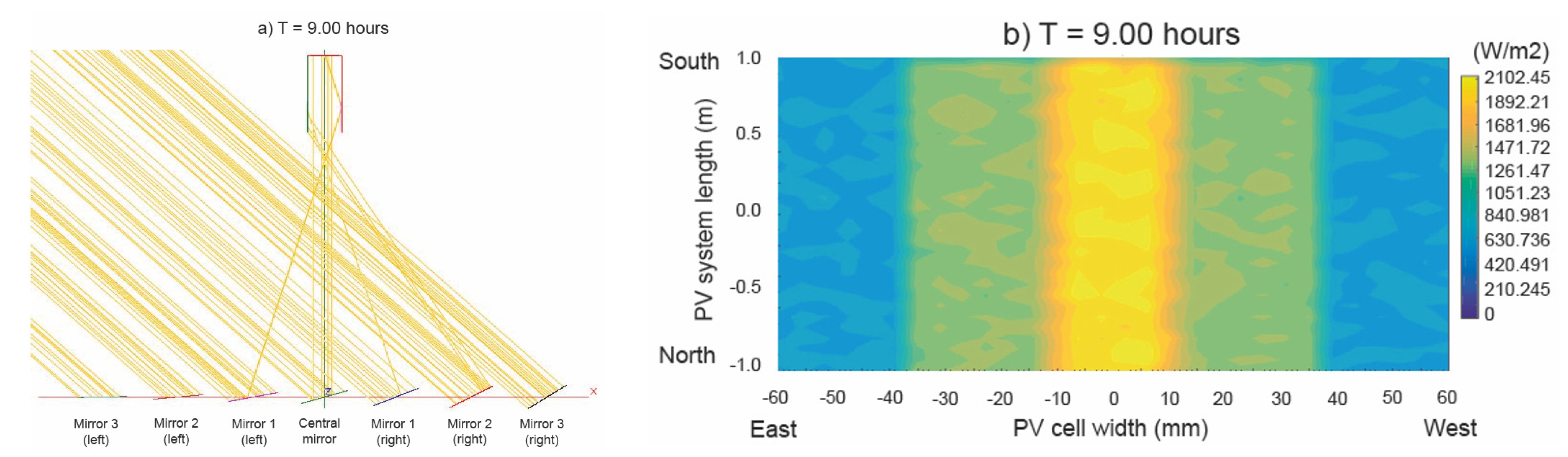
4.3. Verification through a Monte Carlo Simulation
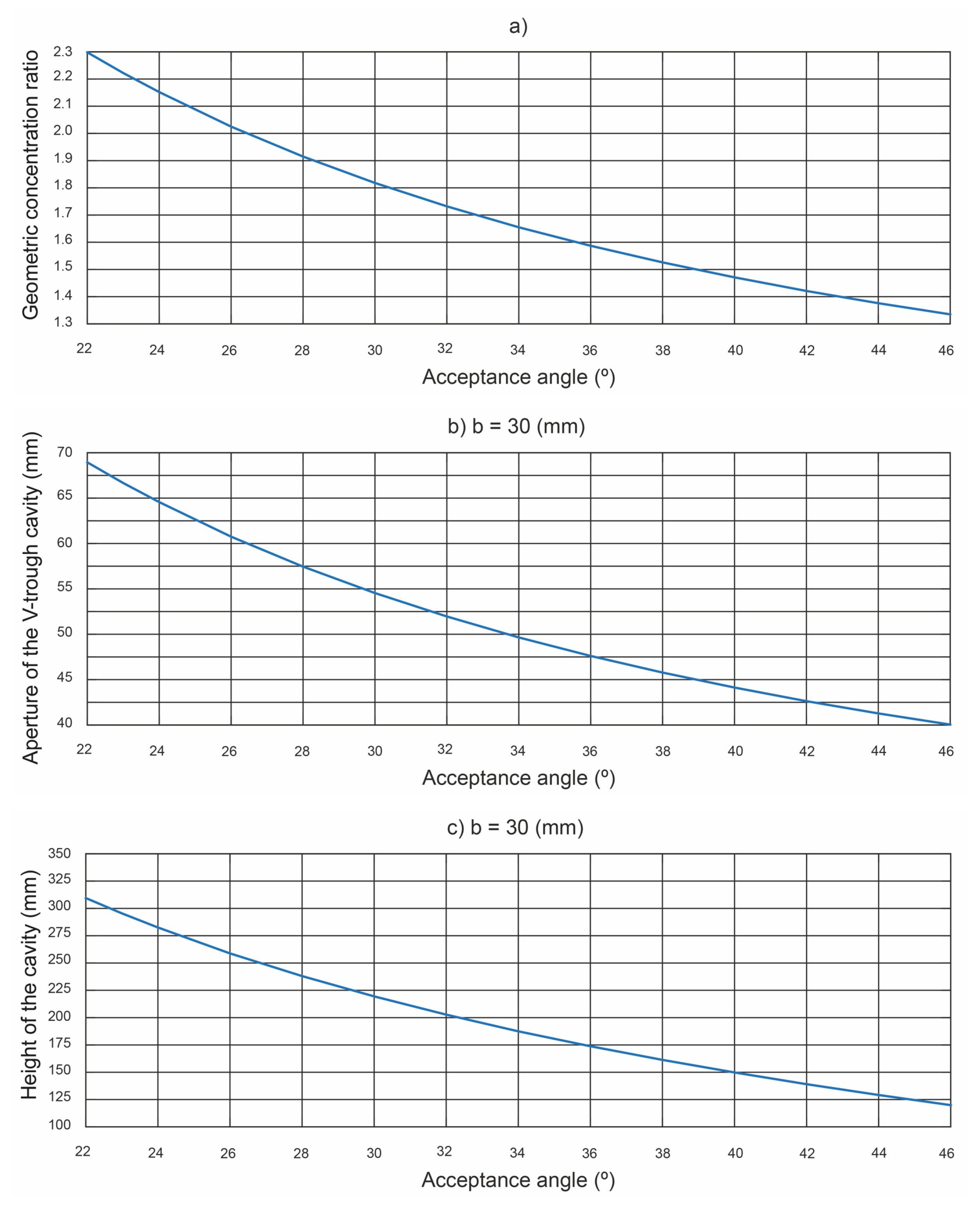
4.4. Influence of the Acceptance Angle of the V-Trough Cavity
4.5. The Manufacture of the Sawtooth V-Trough Cavity and the Laser Experiment
5. Conclusions
- (i)
- Since the height of the proposed cavity is much lower, in this case four times lower, the fixed structure of the small-scale linear Fresnel reflectors are smaller; therefore, the cost is lower.
- (ii)
- The wind-exposed area of the sawtooth V-trough cavity is four times less than in the case of the standard V-trough cavity, which reduces the cost of the fixed structure and secondary system structures. This is essential considering that the optimal installation location for small-scale linear Fresnel reflectors is on the roofs of buildings.
- (iii)
- The cooling surface in the case of the sawtooth V-cavity is times larger, and the in the case of the sawtooth V-cavity is times the in the case of the standard V-cavity. Hence, the temperature of the cells with the sawtooth V-cavity is always lower than that of cells with a standard V-cavity, which increases the electrical efficiency.
- (iv)
- Although both cavities have the same reflective surface, the multiple reflective walls of the new cavity are used in combination to replace the two reflective surfaces of the standard V-trough cavity, which could reduce the difficulty in manufacturing, maintaining, and transporting the large glasses. Furthermore, the overall cost of the small-scale linear Fresnel reflector may also decrease.
- (v)
- Although the surface area of the photovoltaic cells is the same, the spacing between the photovoltaic cells that characterizes the designed cavity facilitates cooling between the photovoltaic cells and the use of cooling systems with a larger surface area, which improves the efficiency of the cooling system.
- (vi)
- Due to the separation between the photovoltaic cells in the new cavity, the connection between the photovoltaic cells is easier.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Area of the active cooling system (m) | |
| Total area of the cells (m) | |
| B | Aperture of the V-trough cavity (m) |
| b | Absorber width of the V-trough cavity (m) |
| Area or geometric concentration ratio (dimensionless) | |
| Optical concentration ratio (dimensionless) | |
| Cleanliness factor of the glass (dimensionless) | |
| Cleanliness factor of the mirror (dimensionless) | |
| Direct normal irradiance (W/m) | |
| Separation between -th and -th mirrors (m) | |
| Blocking and shading coefficient (dimensionless) | |
| f | Height of the receiver (m) |
| H | Height of the V-trough cavity (m) |
| Optimum operation time (h) | |
| k | Thermal conductivity (W/m °C) |
| Position of -th mirror (m) | |
| Effectively illuminated length (m) | |
| Vertical length (m) | |
| m | Number of V-trough cavities of the sawtooth |
| N | Number of mirrors on each side of the SSLFR |
| Ordinal of the day | |
| n | Number of reflections |
| Internal heat generation in cells (W) | |
| Reflector-to-aperture area ratio (dimensionless) | |
| T | Solar time (h) |
| Temperature of the active cooling system (°C) | |
| Temperature of the cells (°C) | |
| Reference temperature (°C) | |
| W | Width of the (m) |
| Width of the active cooling system (m) | |
| Width of the of the cells (m) | |
| Width of the cells illuminated by the -th mirror (m) | |
| Width of the -th mirror (m) | |
| Width of the cells (m) | |
| Angle between the solar ray reaching the cavity and (°) | |
| Solar altitude (°) | |
| Angle that mirror i forms with the horizontal (°) | |
| Temperature coefficient (1/°C) | |
| Solar azimuth (°) | |
| Declination (°) | |
| Wall thickness of the cooling system (m) | |
| Angle between and the -th reflection (°) | |
| Electrical efficiency of the system (dimensionless) | |
| Optical efficiency (dimensionless) | |
| Ray acceptance rate (dimensionless) | |
| Reference electrical efficiency (dimensionless) | |
| Acceptance angle of the V-trough cavity (°) | |
| Angle between the vertical at the focal point and the line connecting the center point | |
| of each mirror to the focal point (°) | |
| Longitudinal angle (°) | |
| Transversal incidence angle (°) | |
| Operation interval (°) | |
| Zenith angle (°) | |
| Latitude (°) | |
| Reflectivity of the primary mirrors (dimensionless) | |
| Reflectivity of the mirror (dimensionless) | |
| Trough wall angle (°) | |
| Transmissivity of glass (dimensionless) | |
| Hour angle (°) |
References
- Yadav, P.; Tripathi, B.; Lokhande, M.; Kumar, M. Estimation of steady state and dynamic parameters of low concentration photovoltaic system. Sol. Energy Mater. Sol. Cells 2013, 112, 65–72. [Google Scholar]
- IRENA. Future of Solar Photovoltaic: Deployment, Investment, Technology, Grid Integration and Socio-Economic Aspects; International Renewable Energy Agency: Abu Dhabi, United Arab Emirates, 2019; Available online: https://irena.org/-/media/Files/IRENA/Agency/Publication/2019/Nov/IRENA_Future%_of_Solar_PV_2019.pdf (accessed on 11 June 2023).
- Barbose, G.; Darghouth, N.; O’Shaughnessy, E.; Forrester, S. Tracking the Sun: Pricing and Design Trends for Distributed Photovoltaic Systems in the United States; Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 2021.
- IRENA. Solar Costs To Fall Further, Powering Global Demand; International Renewable Energy Agency: Abu Dhabi, United Arab Emirates, 2017; Available online: https://www.reuters.com/article/singapore-energy-solar-idUSL4N1MY2F8 (accessed on 11 June 2023).
- Pvinsights. Available online: http://pvinsights.com/ (accessed on 11 June 2023).
- IRENA; IEA. End-of-Life Management: Solar Photovoltaic Panels; International Renewable Energy Agency: Abu Dhabi, United Arab Emirates; International Energy Agency Photovoltaic Power Systems: Paris, France, 2016; Available online: https://www.irena.org/publications/2016/Jun/End-of-life-management-Solar-Photovoltaic-Panels (accessed on 11 June 2023).
- Hasan, H.A.; Sopian, K.; Jaaz, A.H.; Al-Shamani, A.N. Experimental investigation of jet array nanofluids impingement in photovoltaic/thermal collector. Sol. Energy 2017, 144, 321–334. [Google Scholar] [CrossRef]
- Barbón, A.; Bayón-Cueli, C.; Bayón, L.; Fortuny Ayuso, P. Influence of solar tracking error on the performance of a small-scale linear Fresnel reflector. Renew. Energy 2020, 162, 43–54. [Google Scholar] [CrossRef]
- Barbón, A.; Fernández-Rubiera, J.A.; Martínez-Valledor, L.; Pérez-Fernández, A.; Bayón, L. Design and construction of a solar tracking system for small-scale linear Fresnel reflector with three movements. Appl. Energy 2021, 285, 116477. [Google Scholar]
- Kandilli, C. Performance analysis of a novel concentrating photovoltaic combined system. Energy Convers. Manag. 2013, 67, 186–196. [Google Scholar]
- Barbón, A.; Ghodbane, M.; Bayón, L.; Said, Z. A general algorithm for the optimization of photovoltaic modules layout on irregular rooftop shapes. J. Clean. Prod. 2022, 365, 132774. [Google Scholar] [CrossRef]
- Silva, R.M.; Fernandes, J.L.M. Hybrid photovoltaic/thermal (PV/T) solar systems simulation with Simulink/Matlab. Sol. Energy 2010, 84, 1985–1996. [Google Scholar] [CrossRef]
- Kamath, H.G.; Ekins-Daukes, N.J.; Araki, K.; Ramasesha, S.K. The potential for concentrator photovoltaics: A feasibility study in India. Prog. Photovoltaics Res. Appl. 2018, 27, 316–327. [Google Scholar] [CrossRef]
- Moreno, A.; Chemisana, D.; Fernández, E.F. Hybrid high-concentration photovoltaic-thermal solar systems for building applications. Appl. Energy 2021, 304, 117647. [Google Scholar] [CrossRef]
- Bamroongkhan, P.; Lertsatitthanakorn, C.; Soponronnarit, S. Experimental performance study of a solar parabolic dish photovoltaic-thermoelectric generator. Energy Procedia 2019, 158, 528–533. [Google Scholar] [CrossRef]
- Brahim Kechiche, O.B.H.; Hamza, M. Enhancement of a commercial PV module performance under low concentrated photovoltaic (LCPV) conditions: A numerical study. Renew. Energy Focus 2022, 41, 258–267. [Google Scholar]
- Xu, N.; Ji, J.; Sun, W.; Huang, W.; Li, J.; Jin, Z. Numerical simulation and experimental validation of a high concentration photovoltaic/thermal module based on point-focus Fresnel lens. Appl. Energy 2016, 168, 269–281. [Google Scholar]
- Barbón, A.; Fortuny Ayuso, P.; Bayón, L.; Fernández-Rubiera, J.A. Non-uniform illumination in low concentration photovoltaic systems based on small-scale linear Fresnel reflectors. Energy 2022, 239, 122217. [Google Scholar]
- Wang, G.; Wang, F.; Shen, F.; Jiang, T.; Chen, Z.; Hu, P. Experimental and optical performances of a solar CPV device using a linear Fresnel reflector concentrator. Renew. Energy 2020, 146, 2351–2361. [Google Scholar] [CrossRef]
- Said, Z.; Ghodbane, M.; Kumar Tiwari, A.; Muhammad Ali, H.; Boumeddane, B.; Ali, Z.M. 4E (Energy, Exergy, Economic, and Environment) examination of a small LFR solar water heater: An experimental and numerical study. Case Stud. Therm. Eng. 2021, 27, 101277. [Google Scholar]
- Vihari Parupudi, R.; Singh, H.; Kolokotroni, M. Low Concentrating Photovoltaics (LCPV) for buildings and their performance analyses. Appl. Energy 2020, 279, 115839. [Google Scholar]
- Xu, J.; Chen, F.; Xia, E.; Gao, C.; Deng, C. An optimization design method and optical performance analysis on multi-sectioned compound parabolic concentrator with cylindrical absorber. Energy 2020, 197, 117212. [Google Scholar]
- Ustaoglu, A.; Ozbey, U.; Torlaklı, H. Numerical investigation of concentrating photovoltaic/thermal (CPV/T) system using compound hyperbolic–trumpet, V-trough and compound parabolic concentrators. Renew. Energy 2020, 152, 1192–1208. [Google Scholar]
- Otanicar, T.P.; Wingert, R.; Orosz, M.; McPheeters, C. Concentrating photovoltaic retrofit for existing parabolic trough solar collectors: Design, experiments, and levelized cost of electricity. Appl. Energy 2020, 265, 11475. [Google Scholar]
- Al-Shohani, W.A.M.; Al-Dadah, R.; Mahmoud, S.; Algareu, A. Optimum design of V-trough concentrator for photovoltaic applications. Sol. Energy 2016, 140, 241–254. [Google Scholar]
- Barbón, A.; Sánchez Rodríguez, J.A.; Bayón, L.; Barbón, N. Development of a fiber daylighting system based on a small scale linear Fresnel reflector: Theoretical elements. Appl. Energy 2018, 212, 733–745. [Google Scholar] [CrossRef]
- Pardellas, A.; Fortuny Ayuso, P.; Bayón, L.; Barbón, A. A new two-foci V-trough concentrator for small-scale linear Fresnel reflectors. Energies 2023, 16, 1597. [Google Scholar] [CrossRef]
- Barbón, A.; Sánchez-Rodríguez, J.A.; Bayón, L.; Bayón-Cueli, C. Cost estimation relationships of a small scale linear Fresnel reflector. Renew. Energy 2019, 134, 1273–1284. [Google Scholar] [CrossRef]
- Li, G.; Xuan, Q.; Pei, G.; Su, Y.; Ji, J. Effect of non-uniform illumination and temperature distribution on concentrating solar cell—A review. Energy 2018, 144, 1119–1136. [Google Scholar] [CrossRef]
- Guerriero, P.; Tricoli, P.; Daliento, S. A bypass circuit for avoiding the hot spot in PV modules. Sol. Energy 2019, 181, 430–438. [Google Scholar] [CrossRef]
- Ustaoglu, A.; Kandilli, C.; Cakmak, M.; Torlaklı, H. Experimental and economical performance investigation of V-trough concentrator with different reflectance characteristic in photovoltaic applications. J. Clean. Prod. 2020, 272, 123072. [Google Scholar] [CrossRef]
- Ghodbane, M.; Said, Z.; Amine Hachicha, S.; Boumeddane, B. Performance assessment of linear Fresnel solar reflector using MWCNTs/DW nanofluids. Renew. Energy 2020, 151, 43–56. [Google Scholar] [CrossRef]
- Barbón, A.; Barbón, N.; Bayón, L.; Sánchez-Rodríguez, J.A. Parametric study of the small-scale linear Fresnel reflector. Renew. Energy 2018, 116, 64–74. [Google Scholar] [CrossRef]
- Duffie, J.A.; Beckman, W.A. Solar Engineering of Thermal Processes; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Zhu, Y.; Shi, J.; Li, Y.; Wang, L.; Huang, Q.; Xu, G. Design and thermal performances of a scalable linear Fresnel reflector solar system. Energy Convers. Manag. 2017, 146, 174–181. [Google Scholar] [CrossRef]
- Zhu, Y.; Shi, J.; Li, Y.; Wang, L.; Huang, Q.; Xu, G. Design and experimental investigation of a stretched parabolic linear Fresnel reflector collecting system. Energy Convers. Manag. 2016, 126, 89–98. [Google Scholar] [CrossRef]
- Shoeibi, H.; Jarrahian, A.; Mehrpooya, M.; Assaerh, E.; Izadi, M.; Pourfayaz, F. Mathematical modeling and simulation of a compound parabolic concentrators collector with an absorber tube. Energies 2023, 16, 287. [Google Scholar] [CrossRef]
- Jaaz, A.H.; Abdulrasool Hasan, H.; Sopian, K.; Haji Ruslan, M.H.B.; Hussain Zaidi, S. Design and development of compound parabolic concentrating for photovoltaic solar collector: Review. Renew. Sustain. Energy Rev. 2017, 76, 1108–1121. [Google Scholar] [CrossRef]
- Tina, G.M.; Scandura, P.F. Case study of a grid connected with a battery photovoltaic system: V-trough concentration vs. single-axis tracking. Energy Convers. Manag. 2012, 64, 569–578. [Google Scholar] [CrossRef]
- Hadavinia, H.; Harjit, S. Modelling and experimental analysis of low concentrating solar panels for use in building integrated and applied photovoltaic (BIPV/BAPV) systems. Renew. Energy 2019, 139, 815–829. [Google Scholar] [CrossRef]
- Madala, S.; Boehm, R.F. A review of nonimaging solar concentrators for stationary and passive tracking applications. Renew. Sustain. Energy Rev. 2017, 71, 309–322. [Google Scholar] [CrossRef]
- Oprea, R.; Istrate, M.; Machidon, D. Analysis of V-trough reflector’s geometry influence on low concentration photovoltaic systems. In Proceedings of the 8th International Conference on Modern Power Systems, Cluj-Napoca, Romania, 21–23 May 2019. [Google Scholar]
- Tang, R.; Liu, X. Optical performance and design optimization of V-trough concentrators for photovoltaic applications. Sol. Energy 2011, 85, 2154–2166. [Google Scholar] [CrossRef]
- Fernández-Rubiera, J.A.; Barbón, A.; Bayón, L.; Díaz, G.; Bayón-Cueli, C. Low concentration photovoltaic systems based on small-scale linear Fresnel reflectors: Development of a new sawtooth V-trough concentrator. In Proceedings of the IEEE International Conference on Environmental and Electrical Engineering (EEEIC2022), Prague, Czech Republic, 8 June–1 July 2022; pp. 1–6. [Google Scholar]
- Barbón, A.; Barbón, N.; Bayón, L.; Sánchez-Rodríguez, J.A. Optimization of the distribution of small scale linear Fresnel reflectors on roofs of urban buildings. Appl. Math. Model. 2018, 59, 233–250. [Google Scholar] [CrossRef]
- Mishra, P.; Pandey, M.; Tamaura, Y.; Tiwari, S. Numerical analysis of cavity receiver with parallel tubes for cross-linear concentrated solar system. Energy 2021, 220, 119609. [Google Scholar] [CrossRef]
- Gong, J.H.; Wang, J.; Lund, P.D.; Zhao, D.D.; Hu, E.Y. Improving the performance of large-aperture parabolic trough solar concentrator using semi-circular absorber tube with external fin and flat-plate radiation shield. Renew. Energy 2022, 159, 1215–1223. [Google Scholar] [CrossRef]
- Xu, J.; Chen, F.; Deng, C. Design and analysis of a novel multi-sectioned compound parabolic concentrator with multi-objective genetic algorithm. Energy 2021, 225, 120216. [Google Scholar] [CrossRef]
- Tan, L.J.; Zhu, W.; Zhou, K. Recent progress on polymer materials for additive manufacturing. Adv. Funct. Mater. 2020, 30, 2003062. [Google Scholar] [CrossRef]
- Chen, F.; Liu, Y. Model construction and performance investigation of multi-section compound parabolic concentrator with solar vacuum tube. Energy 2022, 250, 123887. [Google Scholar] [CrossRef]
- Sharma, V.M.; Nayak, J.K.; Kedare, S.B. Effects of shading and blocking in linear Fresnel reflector field. Sol. Energy 2015, 113, 114–138. [Google Scholar] [CrossRef]
- Theunissen, P.H.; Beckman, W.A. Solar transmittance characteristics of evacuated tubular collectors with diffuse back reflectors. Sol. Energy 1985, 35, 311–320. [Google Scholar] [CrossRef]
- Barbón, A.; Fortuny Ayuso, P.; Bayón, L.; Fernández-Rubiera, J.A. Predicting beam and diffuse horizontal irradiance using Fourier expansions. Renew. Energy 2020, 154, 46–57. [Google Scholar] [CrossRef]
- PVGIS. Joint Research Centre (JRC). Available online: http://re.jrc.ec.europa.eu/pvg_tools/en/tools.html#PVP (accessed on 11 June 2023).
- ESTIF. Spanish Technical Building Code Royal Decree 314/2006, 17 March 2006; European Solar Thermal Industry Federation (ESTIF): Brussels, Belgium, 2006. [Google Scholar]
- Aly, S.P.; Ahzi, S.; Barth, N.; Abdallah, A. Using energy balance method to study the thermal behavior of PV panels under time-varying field conditions. Energy Convers. Manag. 2018, 175, 246–262. [Google Scholar] [CrossRef]
- Cengel, Y.A. Heat Transfer and Mass Transfer: A Practical Approach, 3rd ed.; McGraw Hill Book Company: New York, NY, USA, 2006. [Google Scholar]
- Evans, D.L. Simplified method for predicting photovoltaic array output. Sol. Energy 1981, 27, 555–560. [Google Scholar] [CrossRef]







| Parameters | Value | |
|---|---|---|
| Area concentration ratio | ||
| Trough wall angle | ° | |
| B | Aperture of the V-trough cavity | mm |
| H | Height of the V-trough cavity | m |
| Parameters | Value | |
|---|---|---|
| Area concentration ratio | ||
| Trough wall angle | (°) | |
| B | Aperture of the V-trough cavity | mm |
| H | Height of the V-trough cavity | (m) |
| Mirror | (mm) | (mm) |
|---|---|---|
| Central mirror | 0 | |
| Mirror 1 (right or left) | ||
| Mirror 2 (right or left) | ||
| Mirror 3 (right or left) |
| Surface | Max. Irradiance W/m2 | Min. Irradiance W/m2 | Avg. Irradiance W/m2 | Uniformity |
|---|---|---|---|---|
| Mirror 3 (right) | ||||
| Mirror 2 (right) | ||||
| Mirror 1 (right) | ||||
| Central mirror | ||||
| Mirror 1 (left) | ||||
| Mirror 2 (left) | ||||
| Mirror 3 (left) | ||||
| cell () | ||||
| cell () | ||||
| cell () | ||||
| cell () |
| Surface | Max. Irradiance W/m2 | Min. Irradiance W/m2 | Avg. Irradiance W/m2 | Uniformity |
|---|---|---|---|---|
| Mirror 3 (right) | 0 | |||
| Mirror 2 (right) | 0 | |||
| Mirror 1 (right) | 0 | |||
| Central mirror | 0 | |||
| Mirror 1 (left) | 0 | |||
| Mirror 2 (left) | ||||
| Mirror 3 (left) | ||||
| cell () | ||||
| cell () | ||||
| cell () | ||||
| cell () |
| Surface | Max. Irradiance W/m2 | Min. Irradiance W/m2 | Avg. Irradiance W/m2 | Uniformity |
|---|---|---|---|---|
| Mirror 3 (right) | ||||
| Mirror 2 (right) | ||||
| Mirror 1 (right) | ||||
| Central mirror | ||||
| Mirror 1 (left) | ||||
| Mirror 2 (left) | ||||
| Mirror 3 (left) | ||||
| cell |
| Secondary Reflector System | Primary Reflector System | |||||
|---|---|---|---|---|---|---|
| (°) | (mm) | (mm) | (°) | |||
| 23 | 3 | 2 | 640 | 49 | ||
| 34 | 50 | 4 | 3 | 1010 | 50 | |
| 46 | 40 | 5 | 5 | 1550 | 47 | |
| Mirror | (mm) | (mm) | (°) |
|---|---|---|---|
| Central mirror | 0 | 0 | |
| Mirror 1 (right or left) | |||
| Mirror 2 (right or left) | |||
| Mirror 3 (right or left) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fernández-Rubiera, J.Á.; Barbón, A.; Bayón, L.; Ghodbane, M. Sawtooth V-Trough Cavity for Low-Concentration Photovoltaic Systems Based on Small-Scale Linear Fresnel Reflectors: Optimal Design, Verification, and Construction. Electronics 2023, 12, 2770. https://doi.org/10.3390/electronics12132770
Fernández-Rubiera JÁ, Barbón A, Bayón L, Ghodbane M. Sawtooth V-Trough Cavity for Low-Concentration Photovoltaic Systems Based on Small-Scale Linear Fresnel Reflectors: Optimal Design, Verification, and Construction. Electronics. 2023; 12(13):2770. https://doi.org/10.3390/electronics12132770
Chicago/Turabian StyleFernández-Rubiera, José Ángel, Arsenio Barbón, Luis Bayón, and Mokhtar Ghodbane. 2023. "Sawtooth V-Trough Cavity for Low-Concentration Photovoltaic Systems Based on Small-Scale Linear Fresnel Reflectors: Optimal Design, Verification, and Construction" Electronics 12, no. 13: 2770. https://doi.org/10.3390/electronics12132770
APA StyleFernández-Rubiera, J. Á., Barbón, A., Bayón, L., & Ghodbane, M. (2023). Sawtooth V-Trough Cavity for Low-Concentration Photovoltaic Systems Based on Small-Scale Linear Fresnel Reflectors: Optimal Design, Verification, and Construction. Electronics, 12(13), 2770. https://doi.org/10.3390/electronics12132770









