Abstract
This paper proposes a new algorithm for adaptive deep image compression (DIC) that can compress images for different purposes or contexts at different rates. The algorithm can compress images with semantic awareness, which means classification-related semantic features are better protected in lossy image compression. It builds on the existing conditional encoder-based DIC method and adds two features: a model-based rate-distortion-classification-perception (RDCP) framework to control the trade-off between rate and performance for different contexts, and a mechanism to generate coding conditions based on image complexity and semantic importance. The algorithm outperforms the QMAP2021 benchmark on the ImageNet dataset. Over the tested rate range, it improves the classification accuracy by and the perceptual quality by , , and on average for NIQE, LPIPS, and FSIM metrics, respectively.
1. Introduction
Image compression is widely required in vision-related processing, storage, and transmission over the Internet [1,2,3]. Deep image compression (DIC) is a learning-based approach that outperforms traditional image-coding algorithms, such as JPEG, JPEG2000, and BPG [2,4]. DIC uses deep neural networks to implement and optimize the image coding framework in an end-to-end manner. This approach has two main advantages. First, it can jointly optimize the performance of signal-processing modules that are traditionally separated. Second, DIC can customize the codec to optimize for specific applications, such as various downstream computer vision tasks [5].
The context of image coding refers to the external environment where image coding is used. Among the various factors that contribute to the context, the most important factors are resource constraint and intent, i.e., the compression rate requirement (bits used to encode an image) and the intended purpose of the image application. The intended purpose can be further divided into three categories: reconstruction, high-level tasks, and perception [6]. Reconstruction aims for pixel-level fidelity, and its performance is measured by pixel-level distortion. High-level tasks aim to support downstream tasks, such as image classification, object detection, and semantic segmentation. The focus is on encoding features that are most relevant to a task instead of treating every pixel equally. Perception aims to present an image that has close statistics (thus being perceived similarly) compared to a given image dataset (e.g., a natural image dataset).
In practice, image coding usually needs to serve multiple purposes. For example, in surveillance applications, an image should, on the one hand, support proper reconstruction for human-oriented perception and verification, and, on the other hand, support machine-oriented detection and classification algorithms. Coding for multiple purposes is also called hybrid-context image coding [7]. In this paper, we study a type of hybrid-context DIC focused on image reconstruction and classification. In the deep learning literature, it is well-established that classification-driven learning can effectively encode high-level image features that are useful and transferable to a wide range of other computer vision tasks [8]. The classification-relevant, high-level features are also called the “semantics” of an image [5]. It is important to note that different purposes have distinct rate requirements. Reconstruction typically demands a much higher bit rate than classification and perception [4,8,9]. More importantly, there are complex performance trade-offs among encoded rates and multiple purposes. This is formulated as the rate-distortion-perception-classification (RDPC) trade-off problem [7]. Our paper will explore the RDPC trade-off framework for image codec design.
In a communications scenario, hybrid-context DIC should be able to perform fast rate and context adaptation to accommodate variations in channel capacity and changes in user application. A common way to do this is to train different DIC models for different bitrates and contexts [10]. However, this method can only achieve discrete adaptation, and it needs significant storage and computation resources to cover different combinations of contexts and rates. The conditional encoder-based, rate-adaptive DIC uses a single deep model and implements variable-rate image coding by generating different latent vectors according to the input conditions [11,12]. However, these encoding mechanisms are mainly optimized for image reconstruction, and they can degrade the image quality at low bitrates, leading to negative performance impacts on downstream machine tasks. To solve this problem, researchers have proposed an algorithm in [13], that uses a quality map (Qmap) to control the coding quality of each pixel at different bitrates and provide context-adaptive coding. This approach prioritizes the high-quality reconstruction of semantic salient regions at low bitrates to preserve the computer vision task’s performance, while also ensuring the high-quality reconstruction of the whole image at high bitrates. This adaptive DIC mainly relies on a variable-rate regions of interest (ROI)-based coding scheme, which balances the classification and reconstruction contexts in the allocation of bits.
This paper proposes an efficient conditional encoder-based adaptive DIC method for hybrid contexts that can satisfy both human visual perception and downstream classification task requirements. The method aims to produce reconstructed images that have low distortion and high perceptual and classification quality. To achieve this, we define the optimization objective of hybrid context DIC as a joint optimization of distortion, classification, and perception. Three loss functions are applied to train the DIC model: the mean squared error (MSE), semantic feature matching (SFM), and generative adversarial network (GAN) loss [14,15]. We use the weighted sum of these three loss terms to control the trade-off between DCP at different bitrates. A three-stage DIC model training procedure is proposed to generate visually pleasing images while retaining relevant information for downstream tasks. During adaptive coding, we propose a Qmap generation mechanism based on image complexity and semantic importance to control the reconstruction quality of each pixel at different rates. At lower rates, the Qmap generation mechanism prioritizes the reconstruction quality of semantic important regions. As the rate increases, the mechanism also allocates some bits to improve the visual quality of large regions with low complexity while improving classification accuracy.
This paper makes the following main contributions:
- First, we extend the conditional encoder-based rate-adaptive DIC to hybrid contexts scenarios. We propose a rate-distortion-perception-classification (RDPC) joint optimization framework to train the neural network model for hybrid contexts.
- Second, we propose a Qmap generation mechanism based on image complexity and semantic importance, which allows variable-rate encoding within the rate range and controls the trade-off between classification and reconstruction contexts during bit allocation.
- Third, we evaluate the proposed DIC using performance metrics that correspond to DCP objectives. We show that the proposed DIC can generalize to different datasets and downstream classifiers and achieve superior RDCP trade-off performance.
2. Related Work
2.1. DIC for Single Context
DIC for contex of Image reconstruction. The goal of image reconstruction context DIC is to balance the compression rate and distortion of the reconstructed image with the original image [3]. Many studies have tried to improve this trade-off by optimizing the backbone network structure, quantization, and entropy model. The backbone network is usually based on the autoencoder architecture, and techniques such as generalized dividing normalization (GDN) [16], multi-stacked residual blocks [17], pyramid decomposition [18], attention [19], and vision transformer (ViT) [20] have been used to improve the efficiency of representation learning. For quantization, methods such as multi-level, soft, and non-uniform quantization have been explored to deal with the differentiability problem in DIC model training and to enhance encoding efficiency [21,22,23]. Entropy models are used to estimate the distribution of quantized vectors and reduce redundancy in the encoding process. The hyperprior model is currently the most popular entropy model in DIC, and researchers are still investigating correlations of the spatial and channel dimensions to develop more effective entropy models [24,25,26]. GAN is used to generate images that resemble a given distribution. Therefore, the reconstructed images obtained from GAN-based DIC have a similar distribution to the original image and show better perceptual quality [27,28,29].
DIC for context of high-level tasks. In high-level task context DIC, DNN models are optimized for a specific task, such as classification or semantic segmentation. In this approach, the decoder directly outputs the task result without generating a reconstructed image. This allows only task-relevant information to be encoded, resulting in high task accuracy and compression rates. For example, studies such as [30,31] have used classification and semantic segmentation loss functions to optimize the decoder for task accuracy that is similar to the original image.
2.2. DIC for Hybrid Contexts
The hybrid contexts DIC is designed to optimize both image reconstruction and specific high-level tasks, while catering to both human and machine perception. This DIC can be classified into two types: compression feature-based and reconstruction image-based hybrid contexts DIC, depending on the input at the receiver performing the computer vision task [4,32,33,34,35,36]. In this paper, we focus on the latter, as it only requires one image reconstruction network to achieve both high-quality reconstructed images and accurate machine task results, while the former needs multiple decoders for different machine tasks. This can lead to higher model complexity and limited scalability.
To improve the accuracy of specific machine tasks in reconstruction image-based hybrid contexts DIC, there are two common techniques. First, the loss term related to the machine task is added to the objective function of the DIC model training. Second, more bits are allocated to regions relevant to the machine task during bit allocation. For example, several papers, such as [36,37,38], have adopted the first technique. Moreover, ref. [36] uses class activation mapping (CAM) to obtain semantic information about the image and integrates it with the attention mechanism as prior knowledge to assign more bits to semantic salient regions.
2.3. Adaptive DIC
DIC that can support rate adaptation using a single DNN model can be divided into three types: conditional encoder-based, quantization-based, and latent vector-based rate-adaptive DIC. In conditional encoder-based rate-adaptive DIC, the encoder generates different latent vectors for different bitrates, usually using Lagrange multipliers or pre-mapped Lagrange multipliers [11,12]. Quantization techniques, which are widely used in traditional source coding, have been adapted and applied in DIC [19,39,40]. In these DIC, the elements of the latent vector are scaled using different coefficients and assigned to different quantization intervals. Latent vector-based rate-adaptive DIC, on the other hand, generates a single latent vector that can be encoded to produce a bitstream for various bitrates. For example, [21,41,42] transformed the original image into layered latent vectors with ordered dependencies using a residual network, while [43] used a spatial mask to modulate the channel and achieve the desired rate.
However, all these rate-adaptive DIC are focused on image reconstruction and cannot achieve context adaptation. To address this, a conditional encoder-based adaptive DIC is proposed in [13], which uses an encoding quality map as a conditional input to control the encoding quality of each pixel. This adaptive DIC can perform ROI encoding at different bitrates, prioritizing the reconstruction quality of relevant pixels important for machine tasks. However, it only uses MSE as the distortion term during model training. Another latent vector-based adaptive DIC proposed in [7] uses the weighted sum of MSE, SFM, and GAN losses as the distortion term during training. This DIC uses a mask for bit allocation, which causes an overhead that limits fine-grained bit allocation.
3. Conditional Encoder-Based Adaptive DIC in Hybrid Contexts
3.1. The RDCP Trade-Off
This study proposes an adaptive DIC algorithm for hybrid contexts, which aims to achieve high classification accuracy and good visual quality of reconstructed images at variable rates. Good visual quality includes low distortion and high perceptual quality, as defined in previous works [44,45]. To jointly optimize rate, distortion, classification, and perception, we use the definitions of the corresponding metrics in [6,46]. Specifically, the distortion metric measures the pixel-wise difference between the original and reconstructed image using various full-reference loss functions, while the perceptual metric measures the distributional divergence between the original and reconstructed image. The classification metric measures the classification error rate of the reconstructed image using a pre-trained classifier. The RDCP optimization problem in hybrid contexts is formulated as follows:
where E and G are the encoder and decoder of the DIC, respectively. Specifically, the encoder maps an input image to a latent vector , i.e., . Subsequently, the decoder reconstructs the image using the latent vector, i.e., . The rate of encoding is determined by the mutual information between the original and reconstructed images, which measures the amount of information needed to represent the image.
Designing optimal codecs for achieving optimal bounds for the RDCP trade-off in hybrid contexts DIC is a highly challenging task. To simplify the problem, we adopt the approach from our previous work [7] and reduce the problem to finding the optimal parameters in the proposed DIC model to achieve the RDCP trade-off. Moreover, we consider the trade-off between distortion and classification in the design of the bit allocation strategy.
3.2. Framework of Proposed DIC
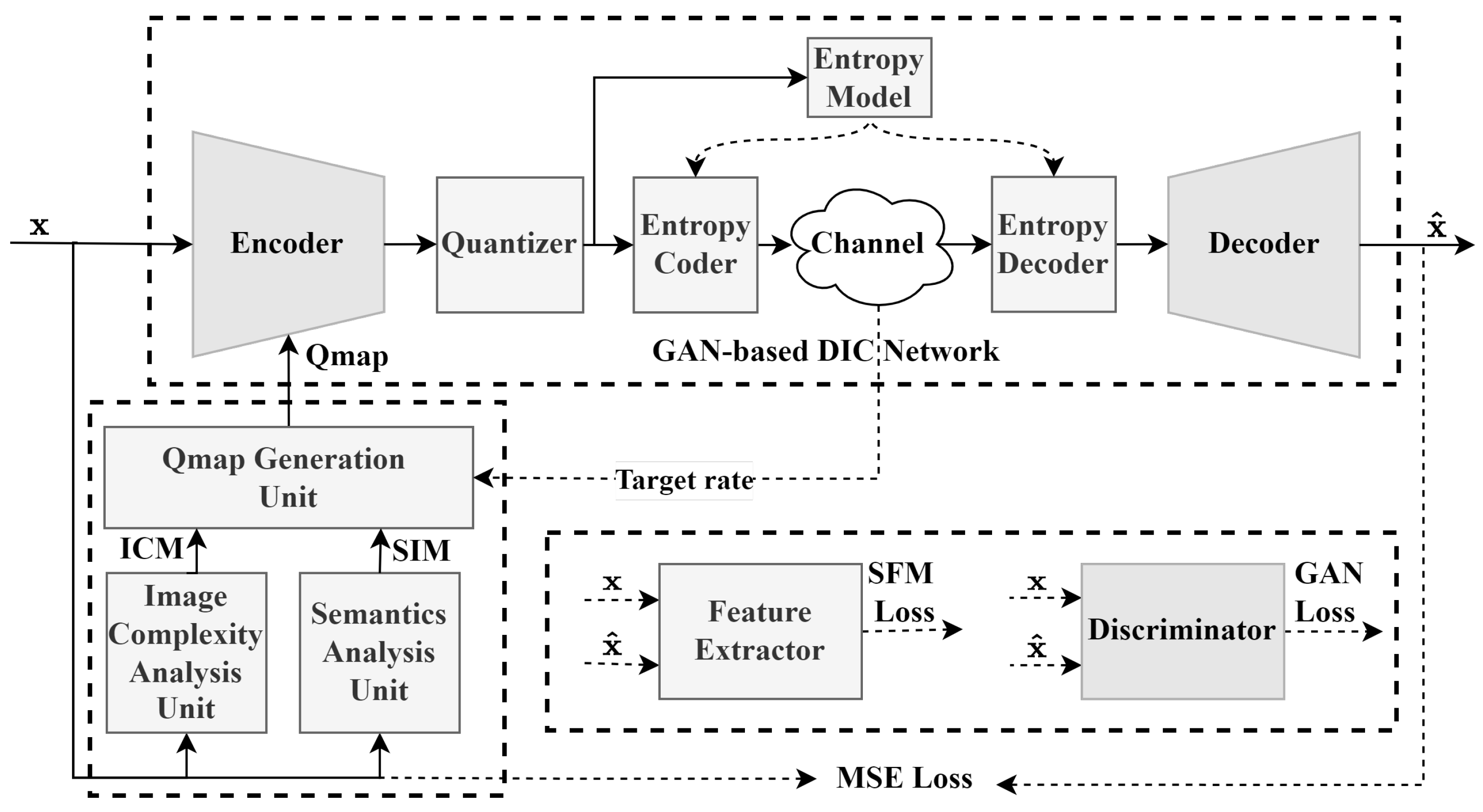
Figure 1 shows the proposed DIC framework, which has two main modules: a coding quality assignment module and a GAN-based deep coding network. The coding quality assignment module generates a Qmap for an input image based on the target rate and the contextual importance of each pixel. The Qmap vector is , . The coding quality assignment module analyzes the image by the semantic analysis unit and the image complexity analysis unit to obtain the semantic importance map (SIM) and the image complexity map (ICM), respectively. The SIM measures the importance of each pixel for classification, and the ICM measures the compression complexity of pixels [47,48]. The Qmap generation unit generates the Qmap based on the SIM, ICM, and target rate, where the target rate is determined by the underlying channel. Here, the channel is a conceptual model of rate-limited channels that can correspond to various real physical channels. The Qmap and the original image are then used as inputs to the encoder to generate the latent vector . The latent vector is quantized using a uniform scalar quantizer, and the entropy model extracts contextual information from the quantized vector to generate parameters for estimating its distribution. The entropy encoder calculates its distribution based on the entropy model and performs entropy encoding to generate the code stream, which is sent to the receiver. The entropy decoder estimates its distribution based on the entropy model and decodes the received stream to obtain the quantized vector. Finally, the GAN-based decoder generates the reconstructed image from the quantized vector.
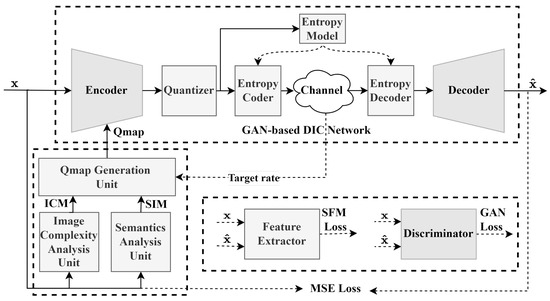
Figure 1.
Framework of proposed encoder-based adaptive DIC.
3.3. Loss Function Design
This paper formulates designing adaptive DIC for hybrid contexts as an RDCP performance trade-off control problem, where the distortion, classification, and perception performances should be simultaneously optimized at different rates.
For the distortion performance, the most common distortion metric for reconstructed images is the pixel MSE, which is computed as
For classification performance, we use the SFM loss, which measures the similarity between classification features extracted from the original image and the reconstructed image, respectively. The SFM loss is computed as
where is the size of the feature extracted from and , and is a pre-trained feature extractor in the semantic analysis network.
For perceptual performance, it is defined as the measurement of the distributional divergence between the original and reconstructed image. Therefore, we adopt the GAN loss to bring the statistical distribution of the reconstructed image closer to that of the input image. Specifically, we use the conditional GAN [14,15] and choose the unsaturated GAN [14] as the optimal loss for GAN training. The loss functions of the generator and discriminator are as follows:
where D is the discriminator and is the conditional vector.
As illustrated in Figure 1, the input image is encoded into the latent vector with the Qmap’s control. The rate of the quantized latent vector is
where P is the entropy model conditioned on the vector .
In summary, the proposed DIC loss function is
where , and are the weights of MSE, SFM, and GAN losses, respectively. These weights globally control the three objectives of hybrid contexts DIC at different rates and balance the RDCP trade-off.
3.4. Method for Training the Proposed DIC
In [13], a variable rate codec network controlled by Qmap is trained using pixel-by-pixel rate-distortion optimization. The optimization process aims to minimize the sum of the rate term R and a weighted MSE term , where is a vector composed of Lagrange multipliers corresponding to each pixel, and is a vector composed of each pixel’s MSE. The element of is obtained by mapping the element of the Qmap through a pre-defined monotonic increasing function , i.e., . This enables pixel-wise control of the encoding quality, with higher values of leading to higher values of , resulting in higher encoding rates and better reconstruction quality at that pixel.
The distortion loss is calculated pixel-by-pixel, while the classification and perception losses are computed after feature extraction for the entire image. To control the coding quality for each pixel, we propose a stepwise optimization training method. First, the rate-distortion optimization method used in [13] is employed to obtain the variable rate encoding for DIC in the reconstruction context. Then, the encoder and decoder are trained with distortion and classification losses by adding the term. Finally, the network parameters at the encoding end are frozen, and the decoder network based on the conditional GAN generator is alternately and iteratively trained using the loss functions (7) and (5) to optimize distortion, classification, and perception at the same time.
3.5. Qmap-Based Bits Assignment
The proposed conditional encoder-based rate adaptation mechanism can balance the trade-off between different objectives in hybrid contexts in the spatial domain. The Qmap can adjust the encoding rates and the encoding quality of different image regions according to their semantic importance and complexity.
Figure 2 shows how different Qmap generation strategies affect bit allocation and reconstructed images at the same rate, using a lighthouse photo from the Kodak dataset as an example. The bit allocation map shows the negative log-likelihood of each element of the quantized latent vector, where lower rates correspond to darker regions and vice versa. By comparing the bit allocation maps, we can see that complex regions need more bits to encode. However, giving more bits to complex regions may not improve the reconstruction quality much. A Qmap that considers image complexity gradually distributes limited bits to more regions to enhance the overall reconstruction quality. On the other hand, the strategy of allocating bits based on SIM achieves high reconstruction quality for semantic salient regions, but it may ignore the background regions. We combine the advantages of different allocation strategies and propose a coding quality generation mechanism that considers both image complexity and semantic importance to improve the overall reconstruction quality while prioritizing the semantic salient regions.

Figure 2.
Illustration of Qmap generation strategies.
4. Implementation of the Proposed DIC
4.1. Network Structure
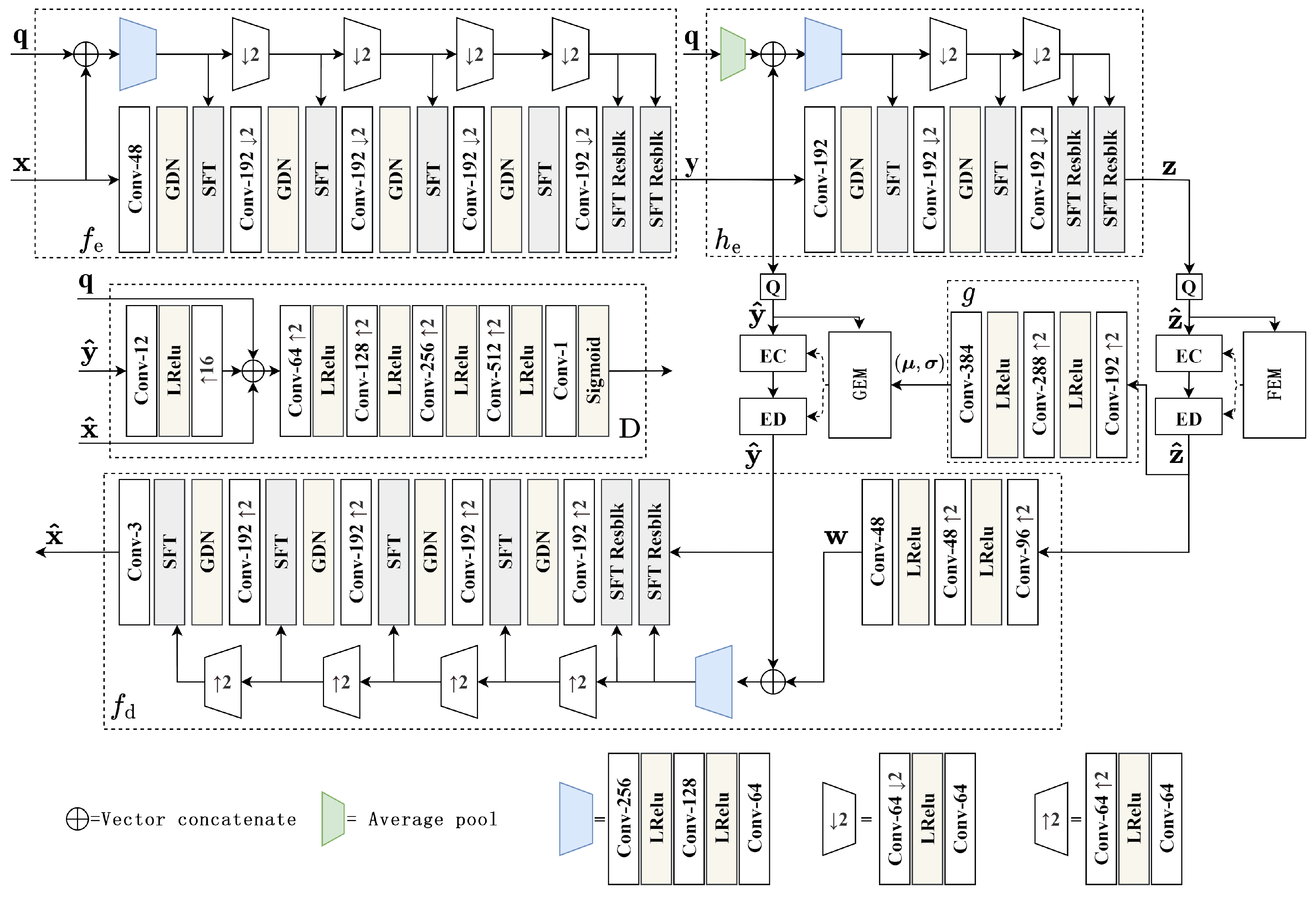
Figure 3 illustrates the network structure of this implementation, which consists of an encoder , a decoder , an entropy model side information encoder , an entropy model parameter generator g, and a discriminator D. The variable rate codec backbone network is similar to [13], except that we use conditional GAN to train the decoder. During training, the coding quality vector and the quantized latent vector serve as the conditional input for the conditional GAN. The codec process of the proposed algorithm can be written as follows:
where is the quantization operation during coding, while uniform noise is used to approximate this operation during training to overcome the non-derivability of quantization. The side information encoder takes the quantized latent vector and the Qmap as inputs to generate the hyper-prior vector , which is used to generate the mean and variance parameters to estimate the latent vector distribution. The quantized latent vector is further coded by an entropy codec.
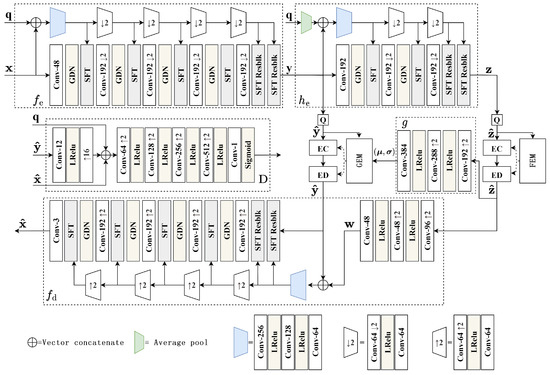
Figure 3.
The network structure of the proposed adaptive DIC.
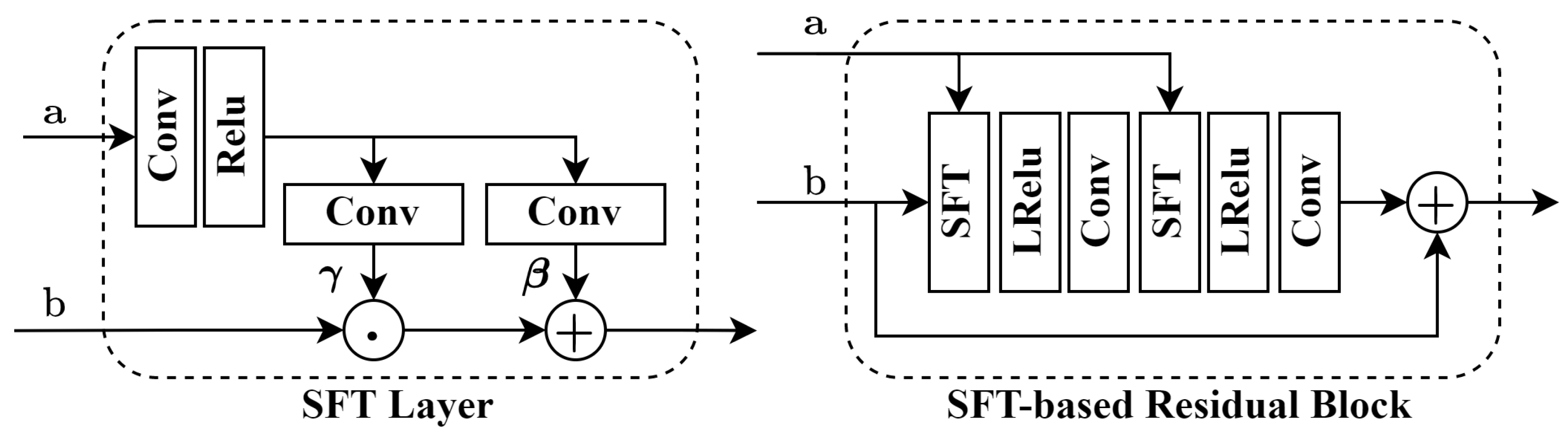
We adopt the spatial feature transform (SFT) layer [49] to generate a pair of parameters based on the input conditions , and use to affine transform the input feature vectors to obtain the features for a certain context and rate. The affine transform is defined as
where the symbol ∘ represents the Hadamard product, which is an element-wise multiplication between vector and vector . To learn better latent space representations with deeper networks, our model also uses residual blocks based on the SFT layer, as shown in Figure 4.
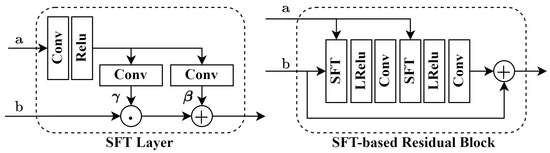
Figure 4.
The SFT layer and SFT-based residual block. and are the input condition vector and the feature from the former layer, respectively.
4.2. Deep Codec Model Training
To achieve adaptive DIC, a deep model training method with objective-by-objective incremental optimization is proposed. First, a pixel-by-pixel rate-distortion optimization is used to train whole network parameters to obtain a variable rate coding model controlled by Qmap. The training loss function is
where is the rate estimate of the compressed stream, which includes the quantized latent vector and the side information vector. Following the variable rate mechanism in [13], we set , where and adjust the interval of the variable rate.
where is the conditional Gaussian model and is the factorized entropy model.
Second, after obtaining the variable-rate DIC model trained by the MSE loss, the SFM loss term is added to further fine-tune the model’s parameters. The optimization loss function of this step is
Finally, the parameters of , , and g are frozen and the parameters of are fine-tuned using a generative adversarial approach. This step alternately trains and the discriminator D, with the following loss functions:
4.3. Qmap Generation
SIM generation. The semantic analysis unit generates the SIM and consists of a classification network and a CAM analysis operation. First, the original image is fed into the classification network to obtain the category. A pre-trained VGG16 [50] model is used as the classification network, which was pre-trained on the ImageNet dataset with 1000 categories. Next, the CAM method is used to analyze the semantic importance of each pixel in the image. The obtained semantic importance mapping is further normalized to [0,1], yielding the SIM. The SIM is a two-dimensional vector denoted as , where higher values indicate that the corresponding pixel is more important for the classification result. The gradient-based CAM method is used as a semantic importance analysis tool because it can be applied to any CNN-based classifier for semantic analysis [51].
ICM generation. We proposed a calculation method based on the image’s spatial information to obtain the ICM, which measures the image’s complexity, in [48]. The detailed ICM calculation process is as follows:
First, the Sobel operator [52] in the horizontal and vertical directions is used to calculate the spatial information matrix . The calculation process is
where , , , , , and are matrices obtained by applying the Sobel operator to the red, green, and blue channels, respectively, in both horizontal and vertical directions.
Second, the obtained is partitioned into blocks of size , and the mean value of each block is calculated. The mean value of each block is taken as the complexity of that block, and these mean values form the matrix . Here, K is the number of times the encoder downsamples the original image, and H and W are the height and width of the original image, respectively.
Third, nearest neighbor adaptive interpolation is applied to to obtain a matrix of the same size as the image, and the elements of this matrix are normalized to [0,1]; the resulting matrix is the ICM, which is noted as .
Qmap generation. The Qmap generation unit generates a Qmap for each pixel in an image that assigns a specific encoding quality level based on the target rate, SIM, and ICM. A Qmap with all elements set to 0 generates a stream with the lowest possible rate, resulting in the lowest-quality reconstructed image. Conversely, a Qmap with all elements set to 1 generates a stream with the highest possible rate, resulting in the highest-quality reconstructed image. However, when the target rate is lower than the highest possible rate, we cannot achieve the best reconstruction quality for every pixel in the image. Therefore, the Qmap generation unit prioritizes certain pixel regions based on contextual targets and available rates in the Qmap generation process. According to Section 3.5, the priority order for bit allocation is: semantic salient regions, low complexity regions, and high complexity regions. The Qmap generation process is as follows:
The first step is generating the importance map of each pixel based on SIM and ICM according to the proposed priority order for bit allocation. To begin with, elements of the semantic importance vector are binarized to either 0 or 1. This operation divides the image into semantic salient and non-salient regions. The OTSU algorithm [53] is adopted to determine the binarization threshold. For the semantic non-salient regions, the pixel importance is inversely proportional to the complexity, and the relative importance of this region can be expressed as , where is the ICM. The importance map of each pixel is represented as a vector , which is calculated as follows:
where normalizes all elements in the input vector between 0 and the minimum of the non-zero elements of . ensures that the semantic non-salient regions are less important than the semantic salient regions.
The second step is mapping vector to vector to get the Qmap corresponding to the target rate using the mapping function , , . In this mapping, the elements of these two vectors are mapped one-by-one according to , where is defined as
where is the target rate and is the rate of the quantized latent vector obtained by encoding the input image with the condition vector .
The principle of bit assignment is to make as close to the as possible while maintaining pixel priority order. Since the vector for an image is fixed, the coding quality assignment at the target rate becomes selecting the appropriate variable or of the function to obtain . However, since involves non-linear operation, it is impossible to directly solve for or from . It is stated that is a monotonically increasing function concerning the variables and in its domain, and that is also an increasing function concerning . Therefore, is an increasing function with respect to and , and a search algorithm is used to determine or . When , is always 0. To allocate more bits to each pixel when the bitrate is sufficient, the value of is set to the minimum non-zero element in .
Therefore, the process of generating Qmap according to the importance map of each pixel includes determining the mapping function based on , using the golden section search algorithm to obtain or that results in a bitrate close to , and finally mapping to according to the determined mapping function.
5. Experimental Results
5.1. Experimental Setup
The proposed DIC model is trained on the COCO [54] dataset with data augmentation by randomly cropping images without resizing. Random Qmaps are generated using methods described in [13]. The performance of the DIC model is evaluated on the Kodak [55] and ImageNet [56] datasets compared to other image compression algorithms. For the Kodak dataset, 23 original images are used for algorithm performance evaluation. For the ImageNet dataset, 100 categories are randomly selected from the ImageNet validation set, and then 5 images are randomly selected from each category separately; finally, the 500 selected images are used to evaluate the algorithm’s performance.
The DIC model is implemented based on Pytorch [57] and the CompreAI library [58], and then trained in three stages. In the first stage, the model is trained iteratively for 2 million steps with the loss function (10). In the second stage, 300,000 steps of training are performed with the loss function (12). In the third stage, the decoder and discriminator are trained alternately with 300,000 steps using the loss functions (13) and (14), respectively. The Adam optimizer [59] is used with a learning rate of . initially and adjusted to after 1.4 million steps. The batch size is set to 8 and the gradient clipping is used for stable training. Default hyperparameters include , , and . The coding rate range is controlled by and , and the average rate range on the Kodak dataset varies from 0.05 bpp to 0.35 bpp using default settings. The VGG16 with pre-training parameters published on the official Tensorflow website is used as the classifier to compute the classification accuracy, and its feature extraction network is used to compute the SFM loss and SIM.
Several metrics are used to evaluate the proposed DIC model and other baseline models, such as the classification accuracy, peak signal-to-noise ratio (PSNR) [60], structural similarity index measure (SSIM) [61], feature similarity index measure (FSIM) [62], learned perceptual image patch similarity (LPIPS) [63], and natural image quality evaluator (NIQE) [64]. SSIM, FSIM, LPIPS, and NIQE are all perceptual metrics, but they have different characteristics and applications. SSIM, FSIM, and LPIPS are referential metrics that measure the perceptual similarity between two images (e.g., original and reconstructed images) using different image features. SSIM evaluates the distortion in luminance, contrast, and structure; FSIM considers perceptually sensitive local features, such as phase congruency and gradient magnitude; and LPIPS uses higher-level “deep features” that are also significant for semantic tasks (such as classification). In short, SSIM, FSIM, and LPIPS estimate the feature-level distortions in a particular domain. Conversely, NIQE is a non-referential metric that assesses how natural an image appears by comparing its statistics with those of natural images. This matches the theoretical formulation of the DCP trade-off, which defines perceptual quality as the divergence between image distributions. Minimizing such a divergence is also the motivation for using GAN in our proposed DIC method. It is important to note that smaller values of the LPIPS and NIQE metrics indicate better performance, while larger values of the other metrics indicate better performance.
5.2. Comparison of Loss Terms’ Weights Settings
We use the loss terms corresponding to distortion, classification, and perception to optimize the codec network parameters simultaneously, and their weights have clear impacts on the RDCP tradeoff. This section discusses the impact of different weight settings on the DCP metrics through experiments. The proposed DIC achieves variable rate compression based on pixel-by-pixel RD optimization, and, therefore, we fix the weights of the rate and distortion loss terms. We set the weight of the rate to the weights of the rate and the distortion loss terms are fixed. The weight of the rate is set to 1 and and , which determine the variable rate range. The different settings of and are as follows:
(A) ;
(B) ;
(C) ;
(D) ;
(E) ;
(F) .
We train different DIC models according to the above settings, and then use 500 images extracted from the ImageNet dataset to evaluate the performance of the six different DIC models.
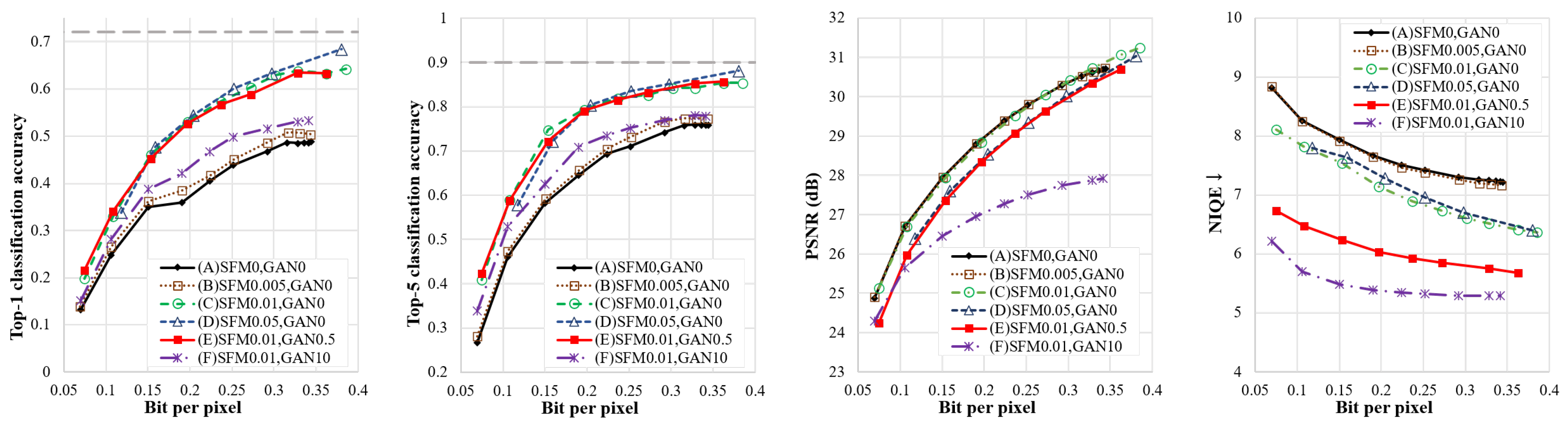
Figure 5 shows a performance comparison of all six cases in terms of classification accuracy, PSNR, and NIQE. Comparing the performance metrics under cases (A), (B), (C) and (D), the following phenomena can be observed: First, as increases, both top-1 and top-5 classification accuracy improve, but the improvement shows a decreasing trend. Second, increasing the within a certain range does not affect the PSNR. Third, increasing also improves the NIQE, but the improvement is not monotonically increasing with . The comparison of cases (C), (E), and (F) shows that raising the increases the NIQE metrics while lowering the PSNR metrics. When is modest, classification accuracy is hardly impacted. When is set too high, classification accuracy suffers dramatically.
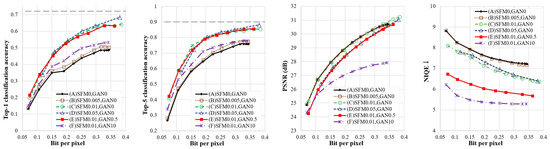
Figure 5.
Impacts of and .
In conclusion, perception-distortion is a strict trade-off, while classification-perception and classification-distortion are not strict trade-offs. The relationship between distortion, classification, and perception can be balanced by reasonable and settings, and the degradation in distortion performance can be reduced while improving classification and perception performance.
5.3. Comparison of Qmap Generation Policies
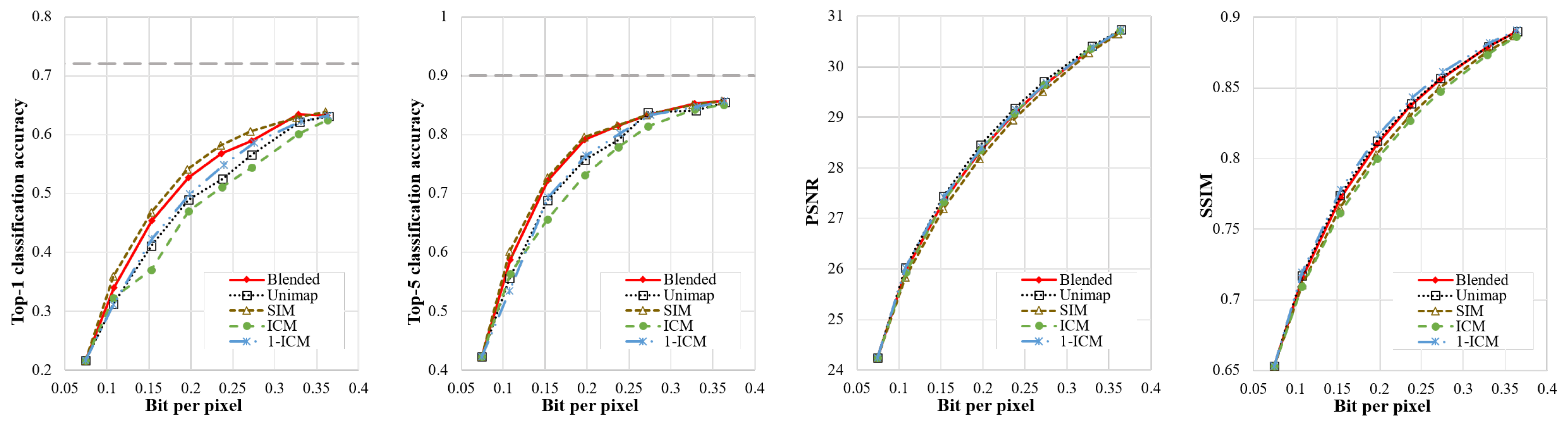
The Qmap generation strategies provide control mechanisms for the reconstruction and classification trade-off at different rates under the proposed coding framework. Five Qmap generation strategies are introduced for specific rate coding, as follows: (A) all elements in the Qmap have the same values; (B) elements corresponding to the more complex regions in the Qmap have larger values; (C) elements corresponding to the regions of lower complexity in the Qmap have larger values; (D) elements corresponding to the region of higher semantic importance in the Qmap are larger; (E) the higher the semantic importance in the semantic salient region of the Qmap, the higher the value, while the lower the image complexity in the semantic non-salient regions, the higher the values. Strategies (A), (B), and (C) are optimized for the reconstruction; strategy (D) is optimized for the classification; and strategy (E) prioritizes ensuring the reconstruction quality in semantic salient regions and allocates limited bits to more pixels in semantic non-significant regions, thus improving the overall reconstruction quality. To compare the impacts of the Qmap generation strategies on classification and the reconstruction metrics, we first train the proposed DIC model according to the default hyperparameter configuration. Then, we use the above five Qmap generation strategies to encode images at different rates on the ImageNet dataset. Finally, we compare the classification accuracy, PSNR, and SSIM performance metrics of the reconstructed images obtained under different Qmap generation strategies. PSNR and SSIM measure the pixel-wise and structural similarity of the image to the original image, respectively.
Figure 6 shows a comparison of the classification accuracy, PSNR, and SSIM metrics of the reconstructed images with varied rates under different Qmap generation strategies. We use Unimap, ICM, 1-ICM, SIM, and Blended to denote the results obtained using strategies (A), (B), (C), (D), and (E), respectively. According to the comparison results, we can observe the following phenomena: First, in strategies (D) and (E), the pixels with high semantic importance have higher priority and better reconstruction quality at different rates, thus obtaining better classification accuracy than those obtained from other strategies. Second, strategies (A), (B), and (C) are all reconstruction-based allocation strategies but obtain different results. Among them, ICM favors complex pixel regions, which are difficult to compress, and raising the same bits brings a lower reconstruction gain; therefore, it has the worst performance among them. Unimap is oriented toward global average reconstruction optimization, so it has the best PSNR metrics. The strategy 1-ICM reduces the coding quality of complex regions and allocates the saved bits to more pixels, so the 1-ICM achieves the best SSIM metric, and the PSNR metric is also close to that of Unimap. Third, the blended strategy, which combines SIM and 1-ICM, achieves classification performance that is similar to that of the SIM-based strategy. Additionally, the PSNR and SSIM metrics for this strategy are close to those of the Unimap-based and 1-ICM-based strategies. The three phenomena mentioned above demonstrate that different strategies for generating Qmaps represent a trade-off between distortion and classification. The proposed blended Qmap generation strategy strikes a better balance between distortion and classification and performs well in both classification and distortion metrics. Therefore, the blended Qmap generation strategy, which combines SIM and ICM, is adopted as the Qmap generation strategy for different rate coding in subsequent sections.
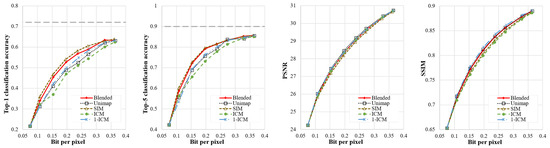
Figure 6.
Performance of different Qmap generation strategies.
5.4. Performance Evaluation and Comparison
In this subsection, we use evaluation metrics, including PSNR, SSIM, FSIM, LPIPS, NIQE, and classification accuracy, to assess the performance of the encoder-based variable rate image coding algorithm implemented for hybrid contexts. To evaluate classification accuracy, the VGG16 classifier is used to classify the original images in the ImageNet test set, achieving a Top-1 accuracy of and a Top-5 accuracy of . The DIC model is first trained with default settings, and then the Qmap generation strategy based on a mixture of SIM and ICM is used to generate the Qmap and reconstruct images at different rates. Finally, the algorithm’s performance is evaluated on the ImageNet and Kodak datasets.
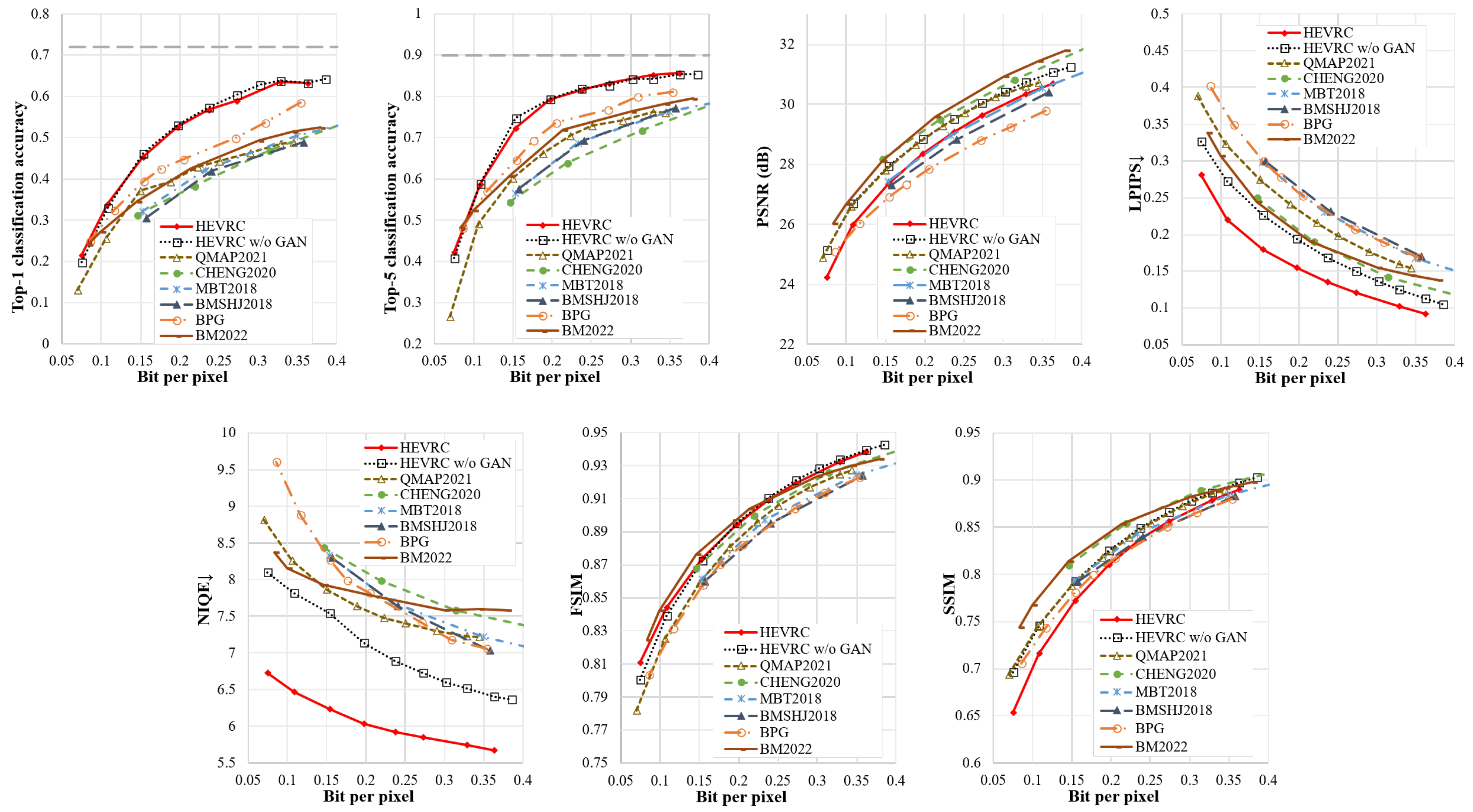
Ablation analysis. The model implemented in [13] is denoted as QMAP2021, the model trained with and is denoted as , the decoder of the model is fine-tuned with the , and the final model is denoted as HEVRC. Our approach improves QMAP2021 in three ways: First, is added to optimize the classification objective. Second, a mechanism for generating Qmap based on pixel context importance is designed to achieve encoding at any bitrate within the rate range. Third, both SIM and ICM are considered during the Qmap generation process. HEVRC introduced a GAN loss term on the basis of to optimize the perceptual objective. In order to achieve image encoding at any bitrate within the bitrate range, QMAP2021 generated Qmap according to the mechanism proposed in this paper based on SIM.
As shown in Figure 7, and QMAP2021 have similar PSNR, but outperforms QMAP2021 for other metrics. The most significant improvement is in classification accuracy, with average increases of and in the Top-1 and Top-5 classification accuracy, respectively, within the rate range. For NIQE, LPIPS, FSIM, and SSIM, the relative performance average improvements are about , , , and , respectively. These results demonstrate that appropriate weighting of can simultaneously improve classification and perception performance. HEVRC has a comparable performance in classification accuracy to , but the superiority of HEVRC is mainly in the perception performance, with relative performance improvement values of and for NIQE and LPIPS, respectively. In terms of PSNR and SSIM performance, HEVRC has a 0.95 dB lower PSNR and a relative decrease of in SSIM metrics compared to . The comparison between HEVRC and further confirms the trade-off between perception and distortion.
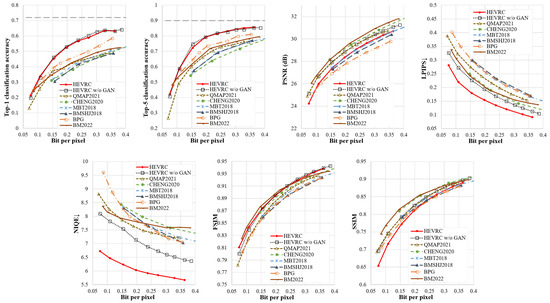
Figure 7.
Performance of different compression coding algorithms on the ImageNet dataset.
RDCP trade-off performance analysis. The above ablation analysis shows that the proposed encoding framework and rate-adaptive mechanism can improve the performance of DIC for hybrid contexts of classification and reconstruction. To further evaluate its performance, this section selects three other DIC algorithms, and one traditional image compression algorithm, to compare with the two algorithms implemented in this paper, HEVRC and . The algorithms for comparison include: BMSHJ2018 [24], MBT2018 [25], CHENG2020 [10], BM2022 [40] and BPG [65]. Among them, BMSHJ2018, MBT2018, and CHENG2020 train DIC models at different bit rates by changing Lagrange multipliers, and they are single-context DIC algorithms aimed for reconstruction. BM2022 is a state-of-the-art variable-rate DIC algorithm for image reconstruction context.
In terms of classification accuracy, the performance of HEVRC and is superior to other algorithms in the rate range. The average Top-1 and Top-5 classification accuracy of the two proposed algorithms is approximately higher than that of the BPG algorithm, and about higher than other DIC algorithms. The superior performance of these two algorithms in classification accuracy is mainly due to two factors. First, the loss term is added in model training. This loss term can better preserve semantic relevant information during the encoding and decoding. Second, a strategy of using a combination of SIM and ICM is adopted to generate Qmap, which better protects the pixel reconstruction of semantic salient regions at different bit rates.
In terms of PSNR performance, HEVRC and are approximately 0.6 dB and 0.3 dB worse than BM2022, respectively. The main reason is that BM2022 is a quantization-based variable-rate DIC and its backbone model uses the autoregressive entropy model to further eliminate redundancy between pixels. Moreover, during the training process of HEVRC, a GAN loss term is added, which encourages the joint distribution of decoded image pixels to resemble the training dataset. This is different from aiming for high fidelity of each pixel. Therefore, the PSNR performance of HEVRC is worse than BM2022. Due to the superior performance of the backbone network compared to MBT2018, BMSHJ2018, and BPG, the PSNR performance of the two proposed DIC models is better than all three algorithms.
In terms of perceptual metrics, both HEVRC and achieve better performance in FSIM, LPIPS, and NIQE, indicating that both and can improve these perceptual metrics. The results show that adding further improves all three metrics. The main purpose of using GAN is to make the reconstructed image more realistic, which is consistent with NIQE. Therefore, HEVRC with achieves the best NIQE performance.
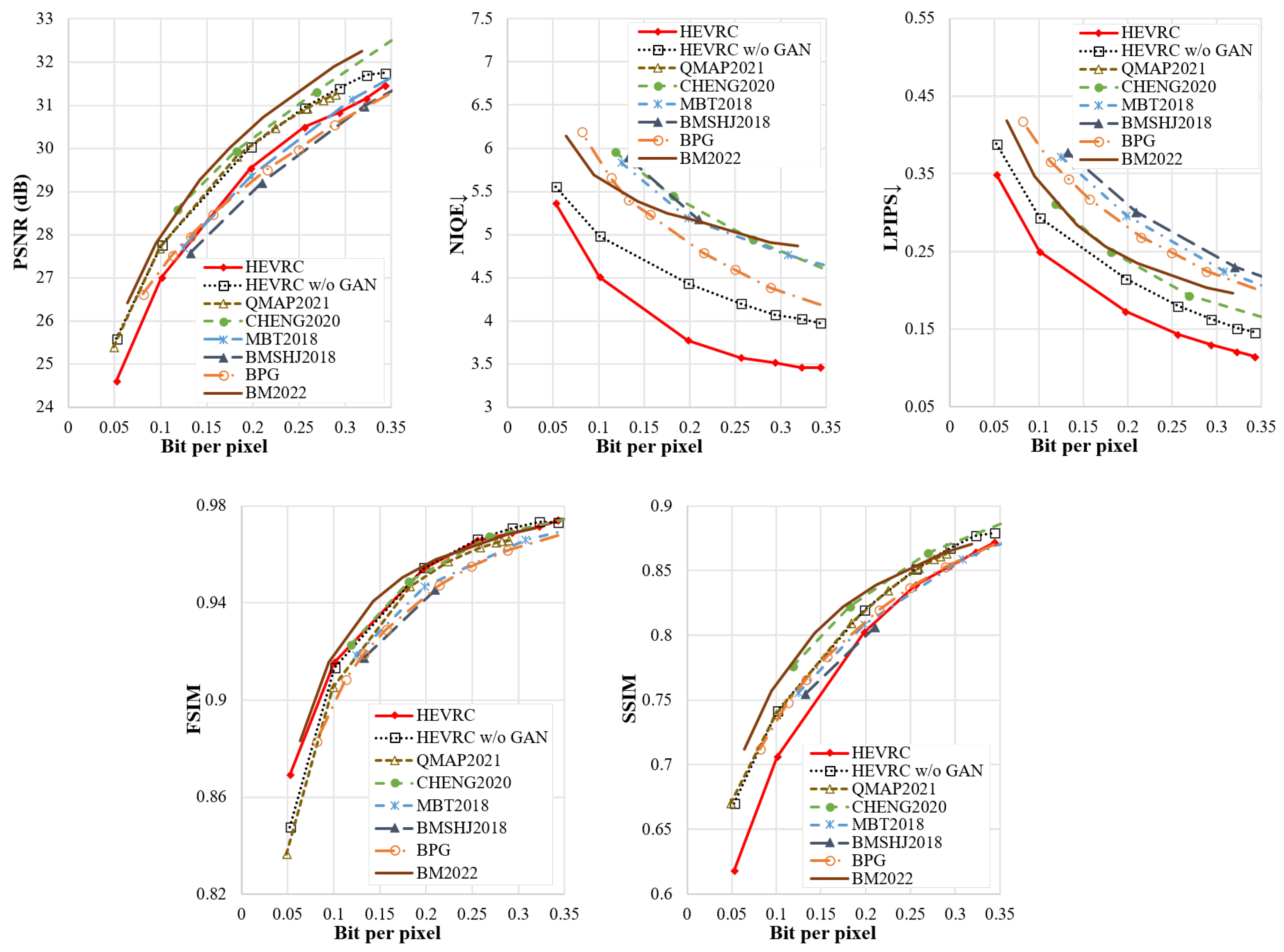
Generalization to other datasets. All algorithms implemented in this section use the COCO dataset for training and are tested on the ImageNet dataset in comparison with other algorithms. The results show that the proposed algorithm still performs well when the training and test datasets are different. To further test the generalizability of the proposed DIC models to different datasets, we use the Kodak dataset to evaluate the performance of the proposed algorithms in terms of the PSNR, SSIM, FSIM, LPIPS, and NIQE metrics. Figure 8 shows the performance comparison. The results indicate that the performance of our proposed algorithms on the Kodak dataset is consistent with that on the ImageNet dataset.
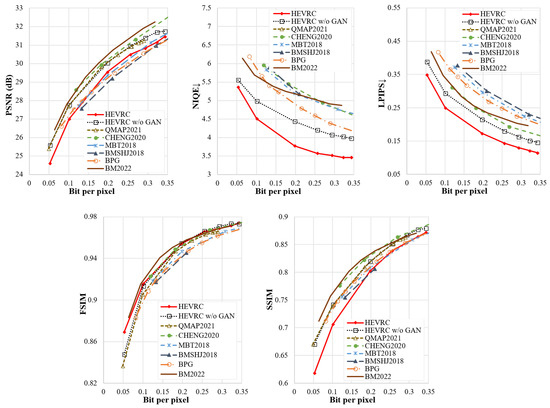
Figure 8.
Performance of different compression coding algorithms on the Kodak dataset.
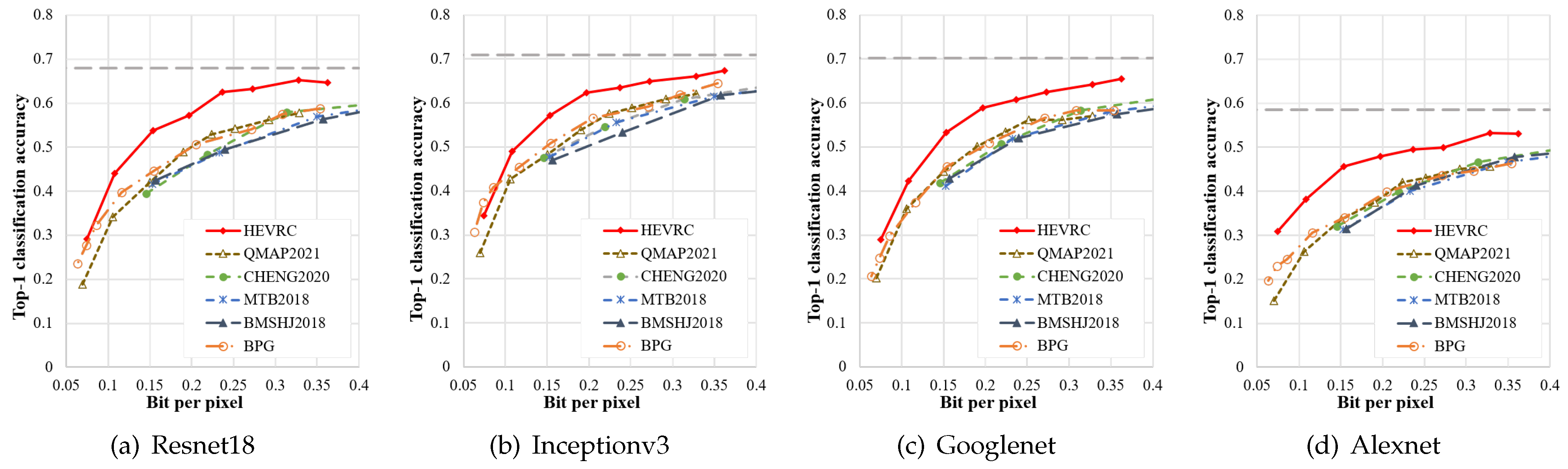
Adaptation analysis of different classification models. In the experiments above, the same feature extractor network is used for both semantic analysis and SFM loss calculation in HEVRC. To validate the adaptability of our proposed method to different downstream classifiers, we further evaluated the classification performance of HEVRC using four other pre-trained classification models. Figure 9 shows the results of classifying the reconstructed images using Resnet18 [66], Inceptionv3 [67], Googlenet [68], and Alexnet [69] on the ImageNet dataset. The results show that HEVRC achieves the best classification performance in different classification models, and the classification accuracy is close to the original image’s accuracy at higher bitrates. These results demonstrate that the proposed SFM loss-based method for improving the classification accuracy of reconstructed images has a certain generality and can adapt to multiple different classification models. In addition, the Qmap generation mechanism based on the fusion of SIM and ICM also shows generality in protecting semantic information at different bitrates across different classification models.
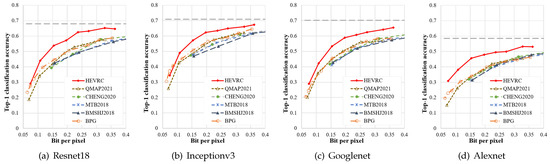
Figure 9.
Variation in classification accuracy with the rate for different compression algorithms with different classification networks.
Visual effects. The proposed DIC framework uses SFM and GAN loss terms to optimize the similarity of high-level semantic features and the distribution similarity between the reconstructed image and the original image, respectively. The high-level semantic similarity makes the reconstructed image easier to recognize, while the distribution similarity makes the reconstructed image look more realistic and perceptually better. In Qmap-based rate-adaptive coding, a Qmap generation mechanism combines SIM and ICM to ensure priority reconstruction of semantic salient regions while also considering the reconstruction of semantic non-salient regions. In the previous sections, we showed that the HEVRC algorithm achieved the best performance in both classification accuracy and perceptual quality in the quantitative performance comparison analysis. In this section, we select two typical images from the Kodak dataset and compare the visual effects of HEVRC with QMAP2021, BM2022 and BPG to demonstrate the superior visual performance of HEVRC.
Figure 10 shows the reconstructed images produced by four different algorithms at various bitrates. The following observations can be made: First, at lower bitrates, BPG’s reconstructed images show block artifacts, while QMAP2021, BM2022, and HEVRC do not. This is because BPG uses block coding, such that differences between blocks at low bitrates can cause block artifacts. In contrast, DIC algorithms encode the whole image. Second, the reconstructed images produced by BPG, BM2022, and QMAP2021 look blurry, especially at low bitrates, while those produced by HEVRC look sharper and more realistic. This is because BPG, BM2022, and QMAP2021 are optimized with MSE loss, while HEVRC adds the GAN loss, which is known to yield perceptually sharper and more realistic images. Third, in HEVRC and QMAP2021, the pixels in the regions most relevant to the classification category have better reconstruction quality (e.g., the parrot’s head and lighthouse top), even at lower bit rates. Moreover, when comparing the non-salient regions of the reconstructed images generated by HEVRC, BM2022, and QMAP2021, HEVRC has better visual quality for objects such as clouds, grass, and road signs in the background. This is mainly due to the GAN loss and SFM loss, which can better preserve the contour information in the entire image. Furthermore, during the Qmap generation process, HEVRC improves the overall coding quality by suppressing the coding quality of complex regions, providing higher reconstruction quality for a larger range of pixels at the same bitrate.





Figure 10.
The visual comparison on the Kodak dataset.
6. Conclusions
This paper proposes an encoder-based DIC with classification-driven semantic awareness. The proposed algorithm expands the conditional encoder-based rate-adaptive DIC to hybrid contexts in three ways. First, the loss function is designed for RDCP optimization, which is the weighted sum of rate, MSE loss, SFM loss, and GAN loss. Second, the objective-by-objective optimization training approach is introduced to train DIC models in hybrid contexts. Third, the Qmap generation mechanism, which takes into account both image complexity and semantic importance, is designed to control the distortion-classification trade-off during bits assignment. The experimental results obtained on multiple open datasets show that, compared with the benchmark algorithm QMAP2021, the proposed DIC can achieve an average improvement in classification accuracy of , along with other improvements in the LPIPS, NIQE, and FSIM metrics, ranging from to . However, the improvement comes with a reasonable cost in PSNR reduction around 0.5 dB, and degradation in SSIM performance around . In summary, the proposed DIC can flexibly control the RDCP trade-off performance, such that the reconstructed images have good visual perception and superior accuracy in downstream classification tasks.
In this paper, adaptive coding in hybrid contexts is achieved by conditional encoders. However, the adaptive process involves repeated calls to the encoder, which increases computational complexity and processing delay. In the future, distillation learning methods can be explored to obtain encoders with lower complexity but similar performance. In addition, the encoding quality of each pixel is assigned based on the relative values of SIM and ICM in the proposed algorithm. We note that this assignment policy is essentially a heuristic policy instead of an optimal one. To further improve the trade-off performance of RDCP, one may formulate a multi-objective optimization problem to explore the Pareto-front of the performance trade-off. Some initial efforts towards a theoretical understanding of this trade-off can be found in [6].
Author Contributions
Methodology, Z.L. and X.H.; software, Z.L. and W.Z.; validation, W.Z., J.S., M.S. and C.L.; investigation, Z.L., W.Z., M.S. and C.L.; writing—original draft preparation, Z.L. and X.H.; writing—review and editing, Z.L., X.H. and W.Z.; funding acquisition, J.S., M.S. and C.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Science and Technology Key Project of Xiamen under grant 3502Z20221027.
Data Availability Statement
The data and source code can be obtained by contacting the first author upon reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hu, Y.; Yang, W.; Ma, Z.; Liu, J. Learning end-to-end lossy image compression: A benchmark. IEEE Trans. Pattern Anal. 2021, 44, 4194–4211. [Google Scholar] [CrossRef] [PubMed]
- Mishra, D.; Singh, S.K.; Singh, R.K. Deep architectures for image compression: A critical review. Signal Process. 2022, 191, 108346. [Google Scholar] [CrossRef]
- Ma, S.; Zhang, X.; Jia, C.; Zhao, Z.; Wang, S.; Wang, S. Image and video compression with neural networks: A review. IEEE Trans. Circuits Syst. Video Technol. 2019, 30, 1683–1698. [Google Scholar] [CrossRef]
- Binglin, L.; Linwei, Y.; Jietao, L.; Yang, W.; Jingning, H. Region-of-interest and channel attention-based joint optimization of image compression and computer vision. Neurocomputing 2022, 500, 13–25. [Google Scholar]
- Gündüz, D.; Qin, Z.; Aguerri, I.E.; Dhillon, H.S.; Yang, Z.; Yener, A.; Wong, K.K.; Chae, C.B. Beyond transmitting bits: Context, semantics, and task-oriented communications. IEEE J. Sel. Areas Commun. 2022, 41, 5–41. [Google Scholar] [CrossRef]
- Liu, D.; Zhang, H.; Xiong, Z. On the classification-distortion-perception tradeoff. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 8 December 2019. [Google Scholar]
- Lei, Z.; Duan, P.; Hong, X.; Mota, J.F.; Shi, J.; Wang, C.X. Progressive Deep Image Compression for Hybrid Contexts of Image Classification and Reconstruction. IEEE J. Sel. Areas Commun. 2022, 41, 72–89. [Google Scholar] [CrossRef]
- Singh, S.; Abu-El-Haija, S.; Johnston, N.; Ballé, J.; Shrivastava, A.; Toderici, G. End-to-end learning of compressible features. In Proceedings of the IEEE International Conference on Image Processing, Abu Dhabi, United Arab Emirates, 25 October 2020. [Google Scholar]
- Borkar, T.S.; Karam, L.J. DeepCorrect: Correcting DNN models against image distortions. IEEE Trans. Image Process. 2019, 28, 6022–6034. [Google Scholar] [CrossRef]
- Cheng, Z.; Sun, H.; Takeuchi, M.; Katto, J. Learned image compression with discretized gaussian mixture likelihoods and attention modules. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13 June 2020. [Google Scholar]
- Sun, Z.; Tan, Z.; Sun, X.; Zhang, F.; Qian, Y.; Li, D.; Li, H. Interpolation variable rate image compression. In Proceedings of the ACM International Conference on Multimedia, Virtual Event, China, 20 October 2021. [Google Scholar]
- Yang, F.; Herranz, L.; Van De Weijer, J.; Guitián, J.A.I.; López, A.M.; Mozerov, M.G. Variable rate deep image compression with modulated autoencoder. IEEE Signal Process. Lett. 2020, 27, 331–335. [Google Scholar] [CrossRef]
- Song, M.; Choi, J.; Han, B. Variable-rate deep image compression through spatially-adaptive feature transform. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10 October 2021. [Google Scholar]
- Goodfellow, I.J.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.C.; Bengio, Y. Generative Adversarial Nets. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 8 December 2014. [Google Scholar]
- Agustsson, E.; Tschannen, M.; Mentzer, F.; Timofte, R.; Gool, L.V. Generative adversarial networks for extreme learned image compression. In Proceedings of the the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October 2019. [Google Scholar]
- Ballé, J.; Laparra, V.; Simoncelli, E.P. End-to-end optimization of nonlinear transform codes for perceptual quality. In Proceedings of the Picture Coding Symposium, Nuremberg, Germany, 4 December 2016. [Google Scholar]
- Mentzer, F.; Agustsson, E.; Tschannen, M.; Timofte, R.; Van Gool, L. Conditional probability models for deep image compression. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18 June 2018. [Google Scholar]
- Nakanishi, K.M.; Maeda, S.I.; Miyato, T.; Okanohara, D. Neural multi-scale image compression. In Proceedings of the Asian Conference on Computer Vision, Perth, Australia, 2 December 2018. [Google Scholar]
- Chen, T.; Liu, H.; Ma, Z.; Shen, Q.; Cao, X.; Wang, Y. End-to-end learnt image compression via non-local attention optimization and improved context modeling. IEEE Trans. Image Process. 2021, 30, 3179–3191. [Google Scholar] [CrossRef]
- Lu, M.; Guo, P.; Shi, H.; Cao, C.; Ma, Z. Transformer-based image compression. arXiv 2021, arXiv:2111.06707. [Google Scholar]
- Toderici, G.; Vincent, D.; Johnston, N.; Jin Hwang, S.; Minnen, D.; Shor, J.; Covell, M. Full resolution image compression with recurrent neural networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21 July 2017. [Google Scholar]
- Gong, R.; Liu, X.; Jiang, S.; Li, T.; Hu, P.; Lin, J.; Yu, F.; Yan, J. Differentiable soft quantization: Bridging full-precision and low-bit neural networks. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October 2019. [Google Scholar]
- Cai, J.; Zhang, L. Deep image compression with iterative non-uniform quantization. In Proceedings of the IEEE International Conference on Image Processing, Athens, Greece, 7 October 2018. [Google Scholar]
- Ballé, J.; Minnen, D.; Singh, S.; Hwang, S.J.; Johnston, N. Variational image compression with a scale hyperprior. arXiv 2018, arXiv:1802.01436. [Google Scholar]
- Minnen, D.; Ballé, J.; Toderici, G.D. Joint autoregressive and hierarchical priors for learned image compression. In Proceedings of the Advances in Neural Information Processing Systems, Montréal, QC, Canada, 3 December 2018. [Google Scholar]
- Minnen, D.; Singh, S. Channel-wise autoregressive entropy models for learned image compression. In Proceedings of the IEEE International Conference on Image Processing, Abu Dhabi, United Arab Emirates, 25 October 2020. [Google Scholar]
- Huang, C.; Liu, H.; Chen, T.; Shen, Q.; Ma, Z. Extreme image coding via multiscale autoencoders with generative adversarial optimization. In Proceedings of the IEEE Visual Communications and Image Processing, Sydney, Australia, 1 December 2019. [Google Scholar]
- Wu, L.; Huang, K.; Shen, H. A gan-based tunable image compression system. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Snowmass Village, CO, USA, 2 March 2020. [Google Scholar]
- Minnen, D.; Toderici, G.; Covell, M.; Chinen, T.; Johnston, N.; Shor, J.; Hwang, S.J.; Vincent, D.; Singh, S. Spatially adaptive image compression using a tiled deep network. In Proceedings of the IEEE International Conference on Image Processing, Beijing, China, 17 September 2017. [Google Scholar]
- Torfason, R.; Mentzer, F.; Agustsson, E.; Tschannen, M.; Timofte, R.; Van Gool, L. Towards image understanding from deep compression without decoding. arXiv 2018, arXiv:1803.06131. [Google Scholar]
- Mei, Y.; Li, F.; Li, L.; Li, Z. Learn A Compression for Objection Detection-VAE with a Bridge. In Proceedings of the International Conference on Visual Communications and Image Processing, Munich, Germany, 5 December 2021. [Google Scholar]
- Chamain, L.D.; Qi, S.; Ding, Z. End-to-End Image Classification and Compression with variational autoencoders. IEEE Internet Things J. 2022, 9, 21916–21931. [Google Scholar] [CrossRef]
- Liu, L.; Chen, T.; Liu, H.; Pu, S.; Wang, L.; Shen, Q. 2C-Net: Integrate image compression and classification via deep neural network. Multimed. Syst. 2023, 29, 945–959. [Google Scholar] [CrossRef]
- Zhang, Q.; Liu, D.; Li, H. Deep network-based image coding for simultaneous compression and retrieval. In Proceedings of the IEEE International Conference on Image Processing, Beijing, China, 17 September 2017. [Google Scholar]
- Le, N.; Zhang, H.; Cricri, F.; Ghaznavi-Youvalari, R.; Tavakoli, H.R.; Rahtu, E. Learned image coding for machines: A content-adaptive approach. In Proceedings of the IEEE International Conference on Multimedia and Expo, Shenzhen, China, 5 July 2021. [Google Scholar]
- Wang, Q.; Shen, L.; Shi, Y. Recognition-driven compressed image generation using semantic-prior information. IEEE Signal Process. Lett. 2020, 27, 1150–1154. [Google Scholar] [CrossRef]
- Xiao, J.; Aggarwal, L.; Banerjee, P.; Aggarwal, M.; Medioni, G. Identity Preserving Loss for Learned Image Compression. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 19 June 2022. [Google Scholar]
- Le, N.; Zhang, H.; Cricri, F.; Ghaznavi-Youvalari, R.; Rahtu, E. Image coding for machines: An end-to-end learned approach. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Toronto, ON, Canada, 6 June 2021. [Google Scholar]
- Cui, Z.; Wang, J.; Gao, S.; Guo, T.; Feng, Y.; Bai, B. Asymmetric gained deep image compression with continuous rate adaptation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Virtual, 19 June 2021. [Google Scholar]
- Yin, S.; Li, C.; Bao, Y.; Liang, Y.; Meng, F.; Liu, W. Universal Efficient Variable-Rate Neural Image Compression. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Singapore, 22 May 2022. [Google Scholar]
- Cai, C.; Chen, L.; Zhang, X.; Gao, Z. Efficient variable rate image compression with multi-scale decomposition network. IEEE Trans. Circuits Syst. 2018, 29, 3687–3700. [Google Scholar] [CrossRef]
- Sinha, A.K.; Moorthi, S.M.; Dhar, D. Self-Supervised Variable Rate Image Compression Using Visual Attention. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 21 June 2022. [Google Scholar]
- Han, C.; Duan, Y.; Tao, X.; Xu, M.; Lu, J. Toward variable-rate generative compression by reducing the channel redundancy. IEEE Trans. Circuits Syst. 2020, 30, 1789–1802. [Google Scholar] [CrossRef]
- Blau, Y.; Michaeli, T. The perception-distortion tradeoff. In Proceedings of the IEEE conference on Computer Vision and Rattern Recognition, Salt Lake City, UT, USA, 18 June 2018. [Google Scholar]
- Blau, Y.; Michaeli, T. Rethinking lossy compression: The rate-distortion-perception tradeoff. In Proceedings of the International Conference on Machine Learning, Long Beach, CA, USA, 9 June 2019. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Mishra, S.; Chen, D.Z.; Hu, X.S. Image complexity guided network compression for biomedical image segmentation. ACM J. Emerg. Technol. Comput. Syst. 2021, 18, 1–23. [Google Scholar] [CrossRef]
- Yu, H.; Winkler, S. Image complexity and spatial information. In Proceedings of the International Workshop on Quality of Multimedia Experience, Klagenfurt am Wórthersee, Austria, 3 July 2013. [Google Scholar]
- Wang, X.; Yu, K.; Dong, C.; Loy, C.C. Recovering realistic texture in image super-resolution by deep spatial feature transform. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18 June 2018. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Chattopadhay, A.; Sarkar, A.; Howlader, P.; Balasubramanian, V.N. Grad-CAM++: Generalized gradient-based visual explanations for deep convolutional networks. In Proceedings of the IEEE Winter Conference on Applications of Computer Vision, Lake Tahoe, UT, USA, 12 March 2018. [Google Scholar]
- Ding, L.; Goshtasby, A. On the Canny edge detector. Pattern Recognit. 2001, 34, 721–725. [Google Scholar] [CrossRef]
- Otsu, N. A threshold selection method from gray-level histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Lin, T.Y.; Maire, M.; Belongie, S.; Hays, J.; Perona, P.; Ramanan, D.; Dollár, P.; Zitnick, C.L. Microsoft coco: Common objects in context. In Proceedings of the European Conference on Computer Vision, Zurich, Switzerland, 6 September 2014. [Google Scholar]
- Franzen, R. Kodak Lossless True Color Image Suite. Available online: http://r0k.us/graphics/kodak/ (accessed on 3 March 2023).
- Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Fei-Fei, L. Imagenet: A large-scale hierarchical image database. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20 June 2009. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. Pytorch: An imperative style, high-performance deep learning library. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 8 December 2019. [Google Scholar]
- Bégaint, J.; Racapé, F.; Feltman, S.; Pushparaja, A. Compressai: A pytorch library and evaluation platform for end-to-end compression research. arXiv 2020, arXiv:2011.03029. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
- Hore, A.; Ziou, D. Image quality metrics: PSNR vs. SSIM. In Proceedings of the International Conference on Pattern Recognition, Istanbul, Turkey, 23 August 2010. [Google Scholar]
- Zhang, L.; Zhang, L.; Mou, X.; Zhang, D. FSIM: A feature similarity index for image quality assessment. IEEE Trans. Image Process. 2011, 20, 2378–2386. [Google Scholar] [CrossRef]
- Zhang, R.; Isola, P.; Efros, A.A.; Shechtman, E.; Wang, O. The unreasonable effectiveness of deep features as a perceptual metric. In Proceedings of the IEEE Conference on Computer Vision and Rattern Recognition, Salt Lake City, UT, USA, 18 June 2018. [Google Scholar]
- Mittal, A.; Soundararajan, R.; Bovik, A.C. Making a “completely blind” image quality analyzer. IEEE Signal Process. Lett. 2012, 20, 209–212. [Google Scholar] [CrossRef]
- Bellard, F. BPG Image Format. Available online: https://bellard.org/bpg/ (accessed on 3 March 2023).
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27 June 2016. [Google Scholar]
- Szegedy, C.; Vanhoucke, V.; Ioffe, S.; Shlens, J.; Wojna, Z. Rethinking the inception architecture for computer vision. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27 June 2016. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 8 June 2015. [Google Scholar]
- Krizhevsky, A. One weird trick for parallelizing convolutional neural networks. arXiv 2014, arXiv:1404.5997. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).