PEM Fuel Cell Emulators: A Review
Abstract
1. Introduction
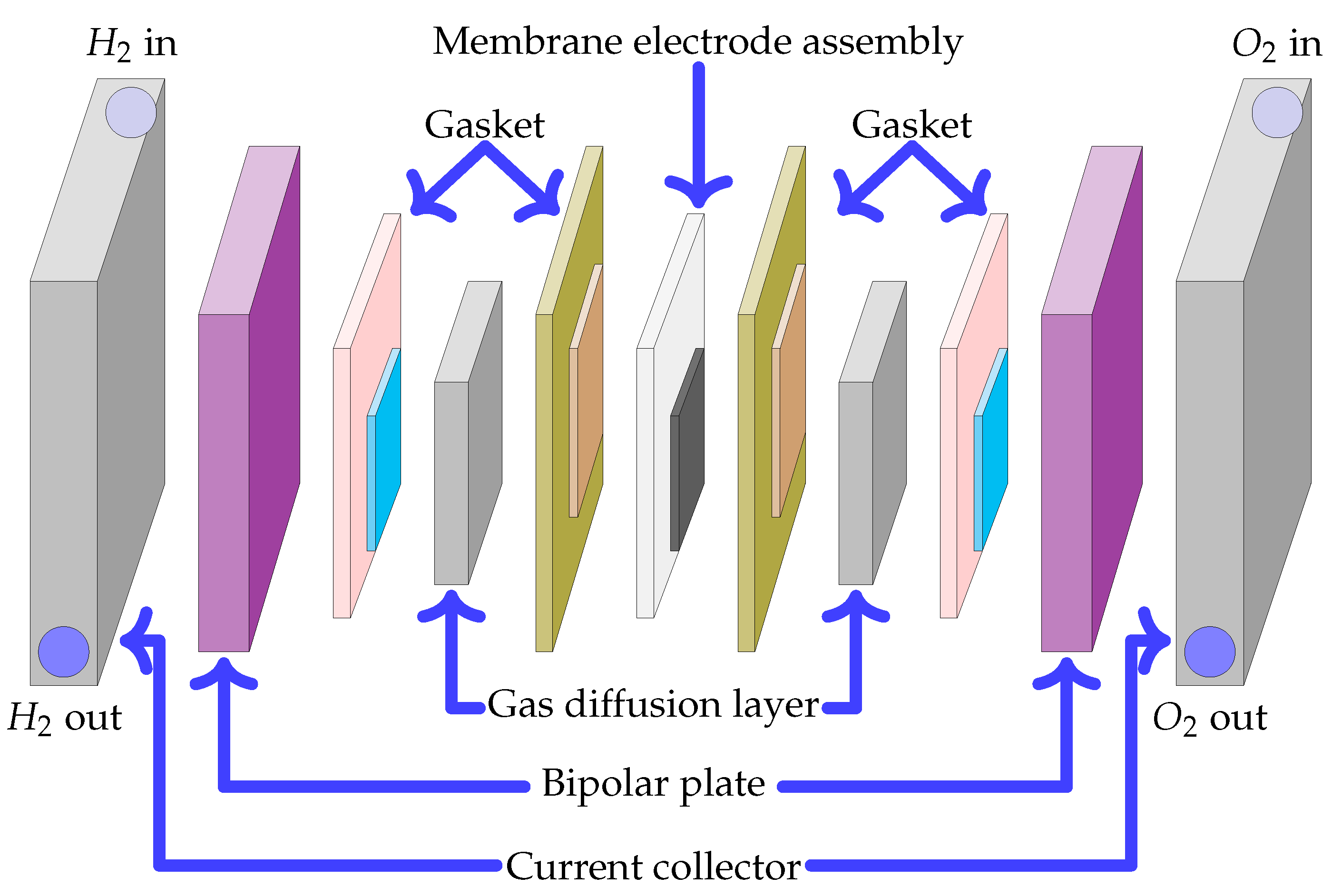
2. The Basic Operation of PEMFCs
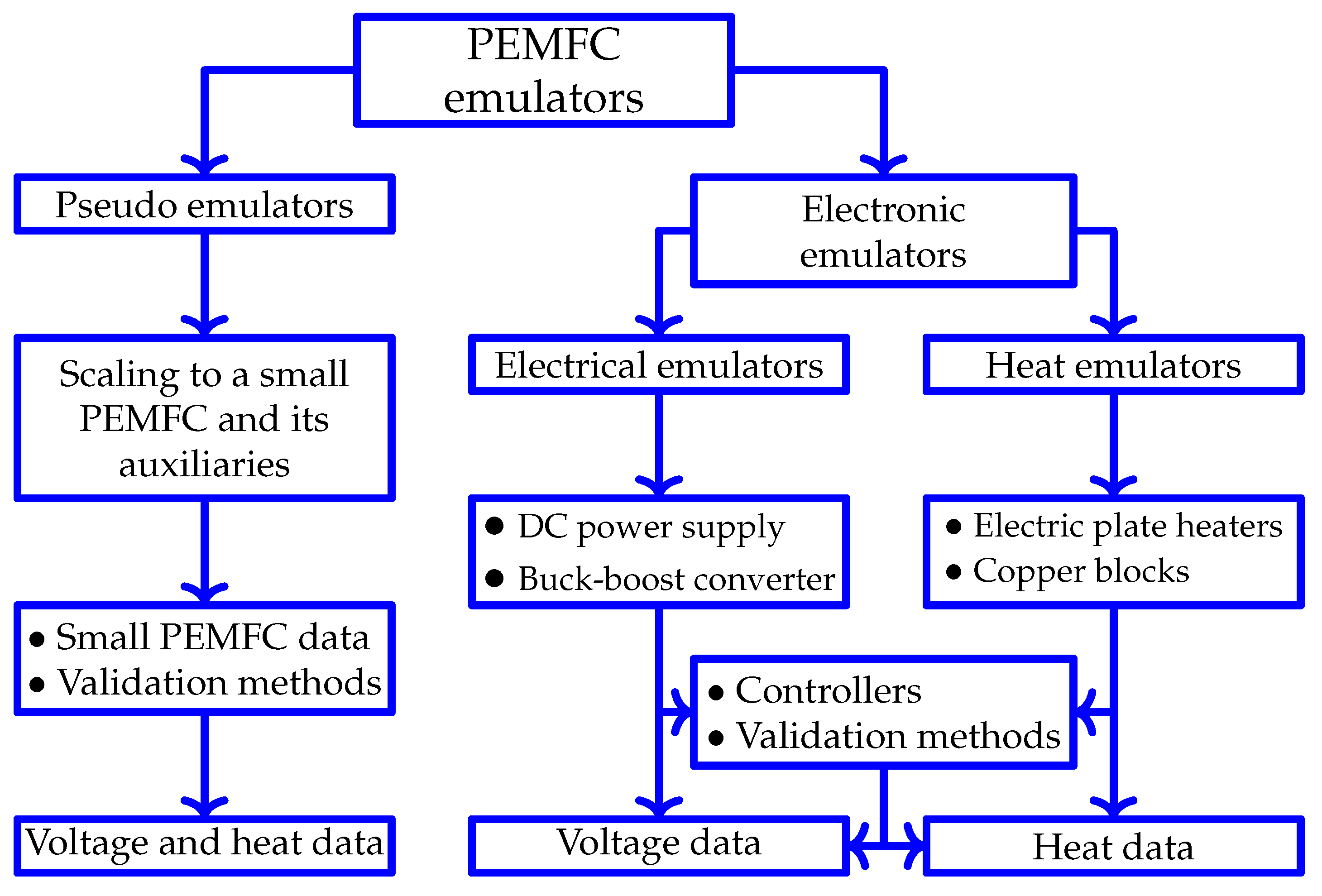
3. Types of PEMFC Emulators
3.1. Pseudo Emulators
3.2. Electrical Emulators
Control Strategies and Implementation Methods for Electric Emulators
3.3. Heat Emulators
3.4. HIL Method
4. Mathematical Model
4.1. Voltage–Current Models
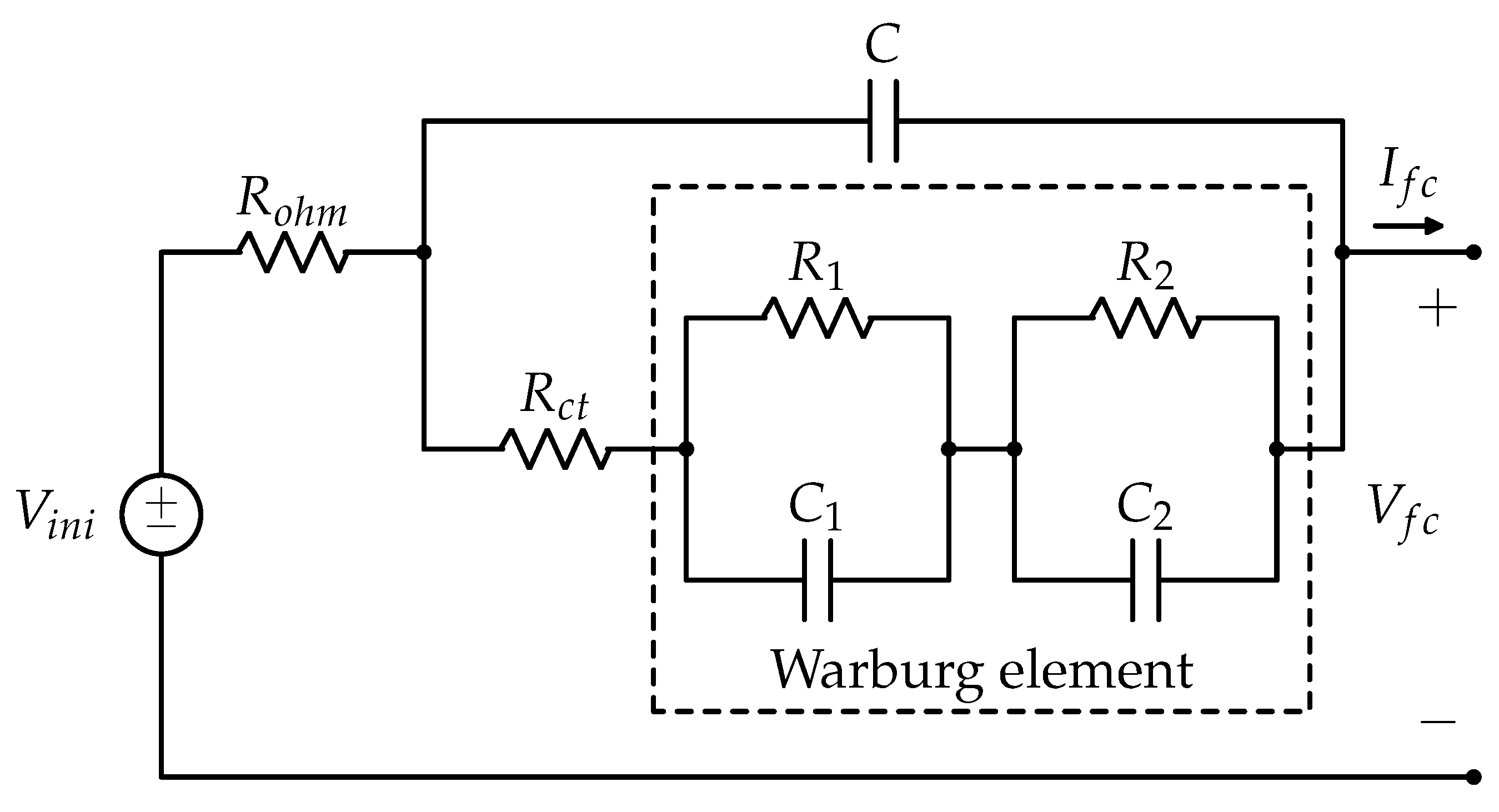
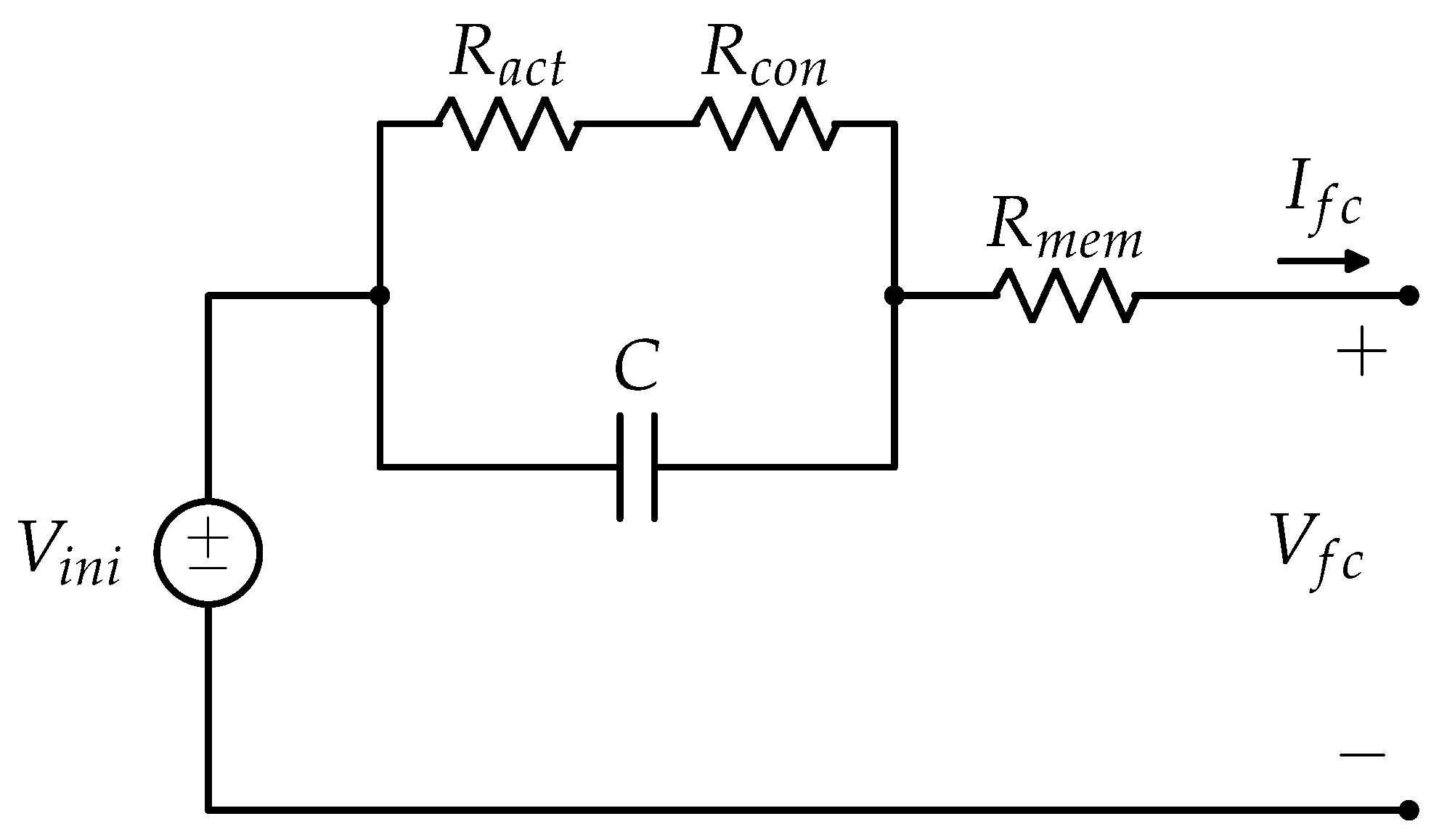
4.2. Voltage–Current ECMs
4.3. Heat and Temperature Models
4.4. Heat and Temperature ECMs
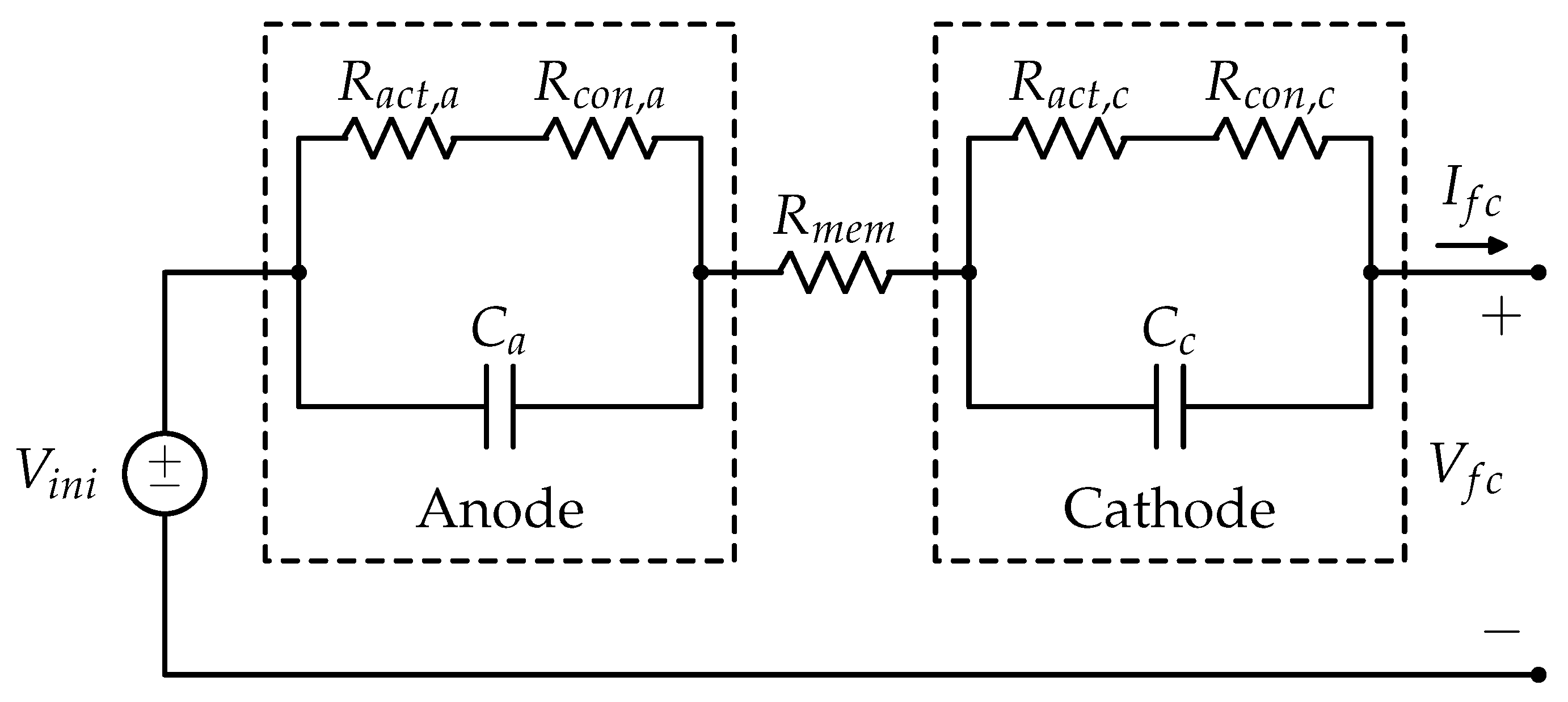
4.5. Electrochemical Models
5. Electronic Circuit Designs for Electronic Emulators
5.1. Design of Electronic Circuits for Electrical Emulators
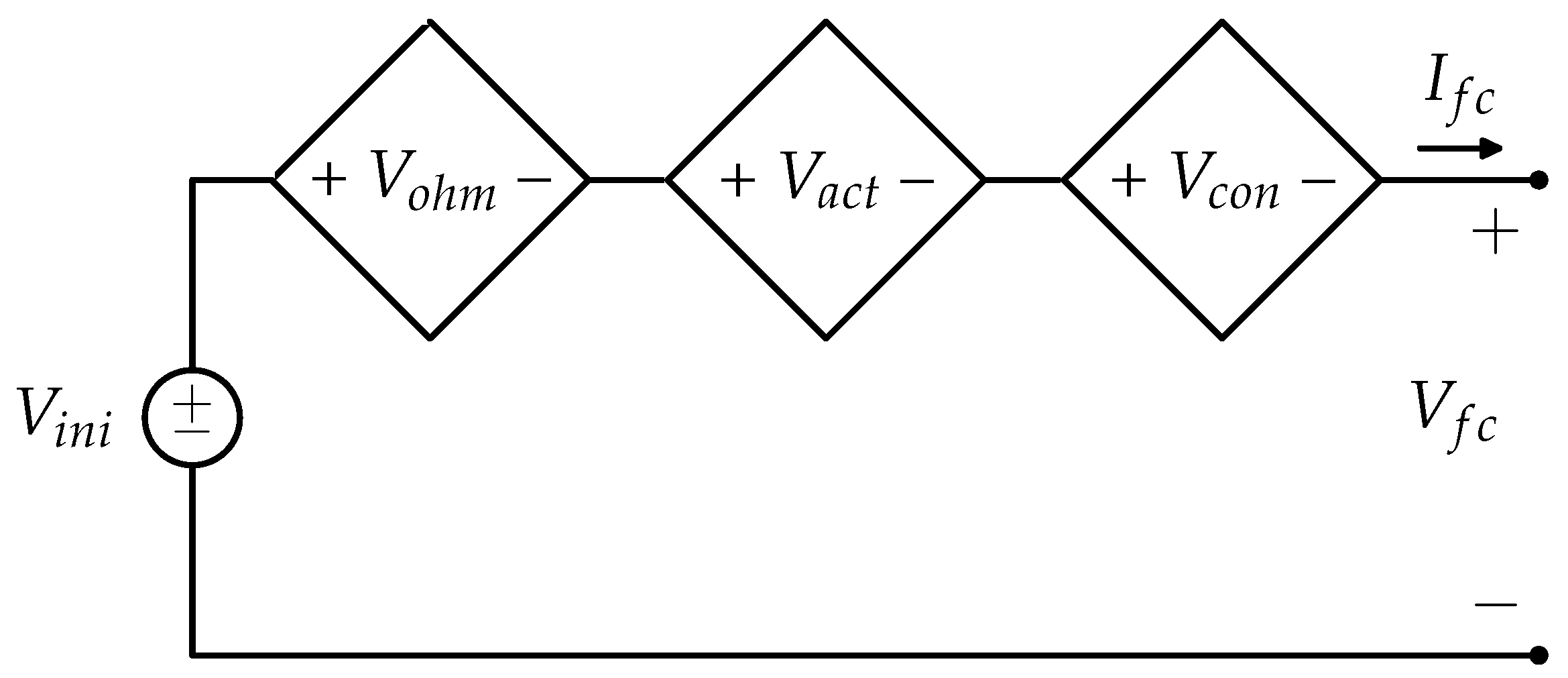
5.1.1. Design of Electronic Circuit Equation Based Electronic Circuits
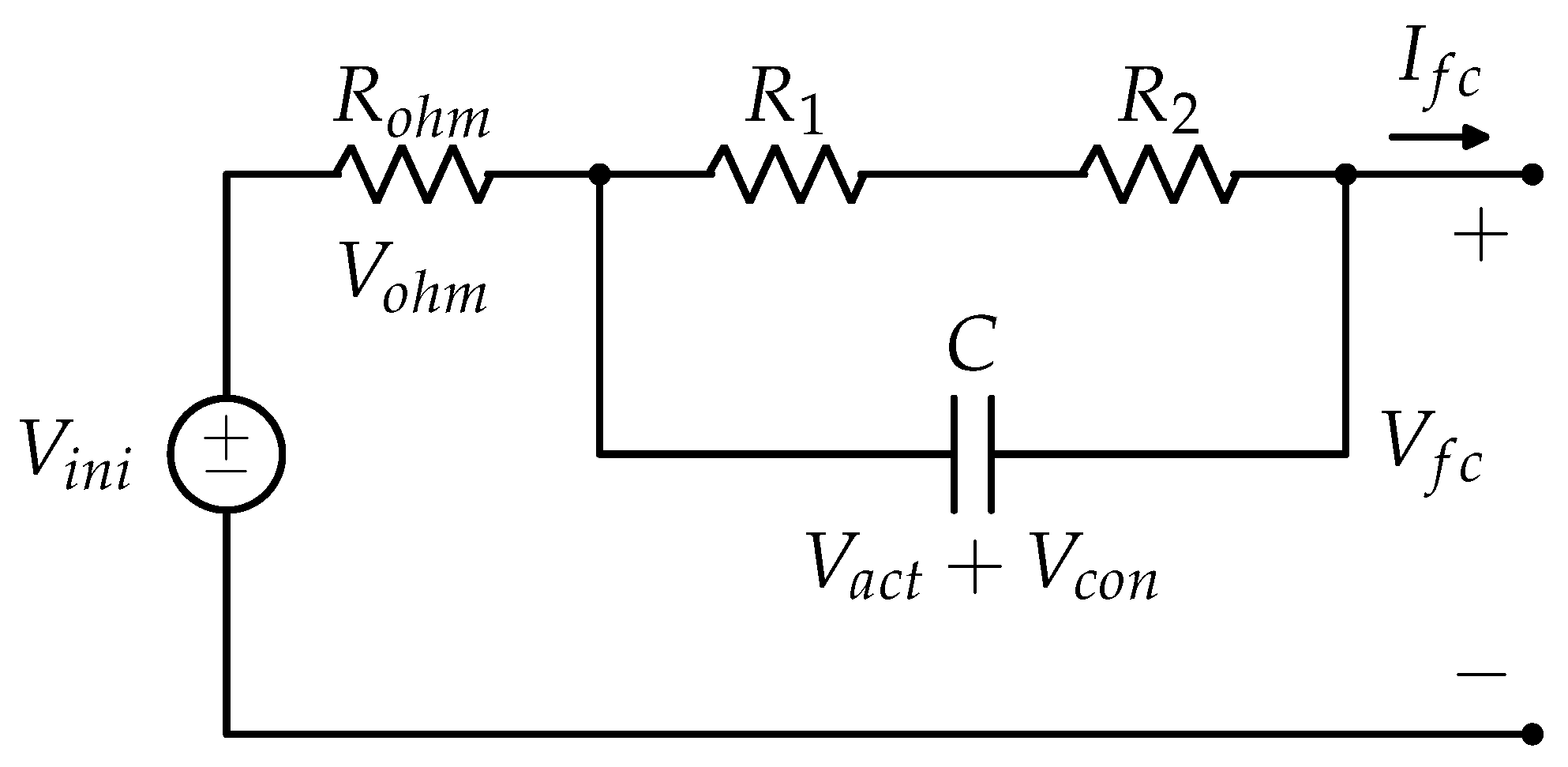
5.1.2. Design of a Components-Based Electronic Circuit
5.2. Design of Electronic Circuits for Heat Emulators
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DSP | Digital Signal Processor |
| ECM | Electronic Circuit Model |
| FC | Fuel Cell |
| FPGA | Field-Programmable Gate Array |
| HIL | Hardware-in-a-Loop |
| MDPI | Multidisciplinary Digital Publishing Institute |
| PEMFC | Proton Exchange Membrane Fuel Cell |
| PI | Proportional-Integral |
| PWM | Pulse Width Modulator |
References
- Zhang, H.; Sun, C.; Ge, M. Review of the Research Status of Cost-Effective Zinc–Iron Redox Flow Batteries. Batteries 2022, 8, 202. [Google Scholar] [CrossRef]
- Albarbar, A.; Alrweq, M. Introduction and Background; Springer International Publishing: Cham, Switzerland, 2018; Chapter 1; pp. 1–8. [Google Scholar] [CrossRef]
- Sopian, K.; Wan Daud, W.R. Challenges and future developments in proton exchange membrane fuel cells. Renew. Energy 2006, 31, 719–727. [Google Scholar] [CrossRef]
- Larminie, J.; Dicks, A. Introduction, Fuel Cell Systems Explained, 2nd ed.; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2003; Chapter 1; pp. 1–24. [Google Scholar] [CrossRef]
- Barhate, S.; Mudhalwadkar, R. Portable fuel cell system emulator as a hardware-in-loop setup. In Proceedings of the International Conference on Communication & Information Processing (ICCIP) 2020, Tokyo, Japan, 27–29 November 2020; pp. 1–8. [Google Scholar] [CrossRef]
- Daud, W.; Rosli, R.; Majlan, E.; Hamid, S.; Mohamed, R.; Husaini, T. Pem fuel cell system control: A review. Renew. Energy 2017, 113, 620–638. [Google Scholar] [CrossRef]
- Jawad, N.H.; Yahya, A.A.; Al-Shathr, A.R.; Salih, H.G.; Rashid, K.T.; Al-Saadi, S.; AbdulRazak, A.A.; Salih, I.K.; Zrelli, A.; Alsalhy, Q.F. Fuel cell types, properties of membrane, and operating conditions: A review. Sustainability 2022, 14, 14653. [Google Scholar] [CrossRef]
- Mao, L.; Jackson, L.; Huang, W.; Li, Z.; Davies, B. Polymer electrolyte membrane fuel cell fault diagnosis and sensor abnormality identification using sensor selection method. J. Power Sources 2020, 447, 227394. [Google Scholar] [CrossRef]
- Tongroon, M.; Putrasari, Y.; Thongchai, S. Influence of engine operating conditions on effect of ethanol combined with biodiesel in ternary blends on combustion behavior in a compression ignition engine. J. Mech. Sci. Technol. 2023, 37, 1. [Google Scholar] [CrossRef]
- Marsala, G.; Pucci, M.; Vitale, G.; Cirrincione, M.; Miraoui, A. A prototype of a fuel cell pem emulator based on a buck converter. Appl. Energy 2009, 86, 2192–2203. [Google Scholar] [CrossRef]
- Kwan, T.H.; Yao, Q. A cost effective experimental emulator for fuel cell based combined heat and power systems. Energy Procedia 2019, 158, 1437–1448. [Google Scholar] [CrossRef]
- Cirrincione, M.; Piazza, M.C.D.; Marsala, G.; Pucci, M.; Vitale, G. Real time simulation of renewable sources by model-based control of dc/dc converters. In Proceedings of the 2008 IEEE International Symposium on Industrial Electronics, Cambridge, UK, 30 June–2 July 2008; pp. 1548–1555. [Google Scholar] [CrossRef]
- Gao, F.; Blunier, B.; Bouquain, D.; Miraoui, A.; Moudni, A.E. Polymer electrolyte fuel cell stack emulator for automotive hardware-in-the-loop applications. In Proceedings of the 2009 IEEE Vehicle Power and Propulsion Conference, Dearborn, MI, USA, 7–11 September 2009; pp. 998–1004. [Google Scholar] [CrossRef]
- Gebregergis, A.; Pillay, P. Implementation of fuel cell emulation on dsp and dspace controllers in the design of power electronic converters. IEEE Trans. Ind. Appl. 2010, 46, 285–294. [Google Scholar] [CrossRef]
- Voottipruex, K.; Sangswang, A.; Naetiladdanon, S.; Mujjalinvimut, E.; Wongyoa, N. Pem fuel cell emulator based on dynamic model with relative humidity calculation. In Proceedings of the 2017 14th International Conference on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology (ECTI-CON), Phuket, Thailand, 27–30 June 2017; pp. 529–532. [Google Scholar] [CrossRef]
- Kartal, F.; Özveren, U. Investigation of an integrated circulating fluidized bed gasifier/steam turbine/proton exchange membrane (pem) fuel cell system for torrefied biomass and modeling with artificial intelligence approach. Energy Convers. Manag. 2022, 263, 115718. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, J.; Hu, S.; Zhang, T. An effective equivalent stiffness model combined with equivalent beam model to predict the contact pressure distribution for a large pem fuel cell stack. Int. J. Hydrogen Energy 2022, 48, 11431–11441. [Google Scholar] [CrossRef]
- Gößling, S.; Nickig, N.; Bahr, M. 2-d + 1-d pem fuel cell model for fuel cell system simulations. Int. J. Hydrogen Energy 2021, 46, 34874–34882. [Google Scholar] [CrossRef]
- Bernhard, D.; Kadyk, T.; Kirsch, S.; Scholz, H.; Krewer, U. Model-assisted analysis and prediction of activity degradation in pem-fuel cell cathodes. J. Power Sources 2023, 562, 232771. [Google Scholar] [CrossRef]
- Kulikovsky, A. A model–based analysis of pem fuel cell distribution of relaxation times. Electrochim. Acta 2022, 429, 141046. [Google Scholar] [CrossRef]
- Bagherabadi, K.B.; Skjong, S.; Pedersen, E. Dynamic modelling of pem fuel cell system for simulation and sizing of marine power systems. Int. J. Hydrogen Energy 2022, 47, 17699–17712. [Google Scholar] [CrossRef]
- Kulikovsky, A. Analytical model for pem fuel cell concentration impedance. J. Electroanal. Chem. 2021, 899, 115672. [Google Scholar] [CrossRef]
- Omran, A.; Lucchesi, A.; Smith, D.; Alaswad, A.; Amiri, A.; Wilberforce, T.; Sodré, J.R.; Olabi, A. Mathematical model of a proton-exchange membrane (pem) fuel cell. Int. J. Thermofluids 2021, 11, 100110. [Google Scholar] [CrossRef]
- Li, Y.; Zhou, Z.; Liu, X.; Wu, W.-T. Modeling of pem fuel cell with thin mea under low humidity operating condition. Appl. Energy 2019, 242, 1513–1527. [Google Scholar] [CrossRef]
- Qin, Y.; Ma, S.; Chang, Y.; Liu, Y.; Yin, Y.; Zhang, J.; Liu, Z.; Jiao, K.; Du, Q. Modeling the membrane/cl delamination with the existence of cl crack under rh cycling conditions of pem fuel cell. Int. J. Hydrogen Energy 2021, 46, 8722–8735. [Google Scholar] [CrossRef]
- Runtz, K.; Lyster, M. Fuel cell equivalent circuit models for passive mode testing and dynamic mode design. In Proceedings of the Canadian Conference on Electrical and Computer Engineering, Saskatoon, SK, Canada, 1–4 May 2005; pp. 794–797. [Google Scholar] [CrossRef]
- Yu, D.; Yuvarajan, S. Electronic circuit model for proton exchange membrane fuel cells. J. Power Sources 2005, 142, 238–242. [Google Scholar] [CrossRef]
- Garnier, J.; Pera, M.; Hissel, D.; Harel, F.; Candusso, D.; Glandut, N.; Diard, J.; Bernardinis, A.D.; Kauffmann, J.; Coquery, G. Dynamic pem fuel cell modeling for automotive applications. In Proceedings of the 2003 IEEE 58th Vehicular Technology Conference. VTC 2003-Fall (IEEE Cat. No.03CH37484), Orlando, FL, USA, 6–9 October 2003; Volume 5, pp. 3284–3288. [Google Scholar] [CrossRef]
- Choi, W.; Howze, J.; Enjeti, P. Development of an equivalent circuit model of a fuel cell to evaluate the effects of inverter ripple current. J. Power Sources 2006, 158, 1324–1332, papers from the 6th International Conference on Lead-Acid Batteries (LABAT 2005, Varna, Bulgaria) and the 11th Asian Battery Conference (11 ABC, Ho Chi Minh City, Vietnam) together with regular papers. [Google Scholar] [CrossRef]
- Zhang, Z.; Huang, X.; Jiang, J.; Wu, B. An improved dynamic model considering effects of temperature and equivalent internal resistance for pem fuel cell power modules. J. Power Sources 2006, 161, 1062–1068. [Google Scholar] [CrossRef]
- Choi, W.; Enjeti, P.; Howze, J. Development of an equivalent circuit model of a fuel cell to evaluate the effects of inverter ripple current. In Proceedings of the Nineteenth Annual IEEE Applied Power Electronics Conference and Exposition, 2004. APEC ‘04, Anaheim, CA, USA, 22–26 February 2004; Volume 1, pp. 355–361. [Google Scholar] [CrossRef]
- Parker-Allotey, N.; Bryant, A.; Palmer, P. The application of fuel cell emulation in the design of an electric vehicle powertrain. In Proceedings of the 2005 IEEE 36th Power Electronics Specialists Conference, Dresden, Germany, 16 June 2005; pp. 1869–1874. [Google Scholar] [CrossRef]
- Lee, T.-W.; Kim, S.-H.; Yoon, Y.-H.; Jang, S.-J.; Won, C.-Y. A 3 kw fuel cell generation system using the fuel cell simulator. In Proceedings of the 2004 IEEE International Symposium on Industrial Electronics, Scottsdale, AZ, USA, 10–13 May 2004; Volume 2, pp. 833–837. [Google Scholar] [CrossRef]
- Rezzak, D.; Khoucha, F.; Benbouzid, M.; Kheloui, A.; Mamoune, A. A dc-dc converter-based pem fuel cell system emulator. In Proceedings of the 2011 International Conference on Power Engineering, Energy and Electrical Drives, Malaga, Spain, 11–13 May 2011; pp. 1–6. [Google Scholar] [CrossRef]
- García-Vite, P.M.; Reyes-García, B.L.; Valdez-Hernández, C.L.; Martínez-Salazar, A. Microcontroller-based emulation of a pem fuel cell. Int. J. Hydrogen Energy 2020, 45, 13767–13776. [Google Scholar] [CrossRef]
- Restrepo, C.; Konjedic, T.; Garces, A.; Calvente, J.; Giral, R. Identification of a proton-exchange membrane fuel cell’s model parameters by means of an evolution strategy. IEEE Trans. Ind. Inform. 2015, 11, 548–559. [Google Scholar] [CrossRef]
- Sanchez, V.M.; Barbosa, R.; Arriaga, L.; Ramirez, J.M. Real time control of air feed system in a pem fuel cell by means of an adaptive neural-network. Int. J. Hydrogen Energy 2014, 39, 16750–16762. [Google Scholar] [CrossRef]
- Paja, C.A.R.; Nevado, A.R.; Castillón, R.G.; Martinez-Salamero, L.; Saenz, C.I.S. Switching and linear power stages evaluation for pem fuel cell emulation. Int. J. Circuit Theory Appl. 2011, 39, 475–499. [Google Scholar] [CrossRef]
- Marsala, G.; Bouquin, D.; Pukrushpan, J.T.; Pucci, M.; Cirrincione, G.; Vitale, G.; Miraoui, A. A neural inverse control of a pem-fc system by the generalized mapping regressor (gmr). In Proceedings of the 2008 IEEE Industry Applications Society Annual Meeting, Edmonton, AB, Canada, 5–9 October 2008; pp. 1–12. [Google Scholar] [CrossRef]
- Pinto, F.R.P.; Vega-Leal, A.P. A test of hil cots technology for fuel cell systems emulation. IEEE Trans. Ind. Electron. 2010, 57, 1237–1244. [Google Scholar] [CrossRef]
- Sanchez, V.; Chan, F.; Ramírez, J.M.; Rosas-Caro, J.C. Fuel cell emulator based on interleaved synchronous buck converter. In Proceedings of the 2012 IEEE Energy Conversion Congress and Exposition (ECCE), Raleigh, NC, USA, 15–20 September 2012; pp. 4464–4470. [Google Scholar] [CrossRef]
- Gauchia, L.; Sanz, J. A per-unit hardware-in-the-loop simulation of a fuel cell/battery hybrid energy system. IEEE Trans. Ind. Electron. 2010, 57, 1186–1194. [Google Scholar] [CrossRef]
- Lim, J.-G.; Kim, S.-H.; Seo, E.-K.; Shin, H.-B.; Chung, S.-K.; Lee, H.-W. Implementation of fuel cell dynamic simulator. In Proceedings of the 2006 37th IEEE Power Electronics Specialists Conference, Jeju, Republic of Korea, 18–22 June 2006; pp. 1–5. [Google Scholar] [CrossRef]
- Gao, F.; Blunier, B.; Simões, M.G.; Miraoui, A. Pem fuel cell stack modeling for real-time emulation in hardware-in-the-loop applications. IEEE Trans. Energy Convers. 2011, 26, 184–194. [Google Scholar] [CrossRef]
- Gao, F.; Chrenko, D.; Blunier, B.; Bouquain, D.; Miraoui, A. Multi-rates fuel cell emulation with spatial reduced real-time fuel cell modelling. In Proceedings of the 2011 IEEE Industry Applications Society Annual Meeting, Orlando, FL, USA, 9–13 October 2011; pp. 1–8. [Google Scholar] [CrossRef]
- Liu, J.; Laghrouche, S.; Ahmed, F.-S.; Wack, M. Pem fuel cell air-feed system observer design for automotive applications: An adaptive numerical differentiation approach. Int. J. Hydrogen Energy 2014, 39, 17210–17221. [Google Scholar] [CrossRef]
- Lemeš, Z.; Vath, A.; Hartkopf, T.; Mäncher, H. Dynamic fuel cell models and their application in hardware in the loop simulation. J. Power Sources 2006, 154, 386–393. [Google Scholar] [CrossRef]
- Restrepo, C.; Ramos-Paja, C.; Giral, R.; Calvente, J.; Romero, A. Fuel cell emulator for oxygen excess ratio estimation on power electronics applications. Comput. Electr. Eng. 2012, 38, 926–937. [Google Scholar] [CrossRef]
- Das, H.S.; Tan, C.W.; Yatim, A.; Muhamad, N.D.b. Proton exchange membrane fuel cell emulator using pi controlled buck converter. Int. J. Power Electron. Drive Syst. (IJPEDS) 2017, 8, 462–469. [Google Scholar] [CrossRef]
- Samosir, A.S.; Anwari, M.; Yatim, A.H.M. A simple pem fuel cell emulator using electrical circuit model. In Proceedings of the 2010 Conference Proceedings IPEC, Singapore, 27–29 October 2010; pp. 881–885. [Google Scholar] [CrossRef]
- Karami, N.; Outbib, R.; Moubayed, N. A low-cost microcontroller based 500-watt pem fuel cell emulator. In Proceedings of the 2012 IEEE International Systems Conference SysCon, Vancouver, BC, Canada, 19–22 March 2012; pp. 1–4. [Google Scholar] [CrossRef]
- Ramos-Paja, C.; Jaramillo-Matta, A.; Pérez-Rojas, A.; Antonio, E. Design and implementation of a pem fuel cell emulator for static and dynamic behavior. Dyna 2011, 78, 1–12. Available online: https://www.redalyc.org/articulo.oa?id=49622401013 (accessed on 23 March 2023).
- Premkumar, K.; Vishnupriya, M.; Thamizhselvan, T.; Sanjeevikumar, P.; Manikandan, B. Pso optimized pi controlled dc-dc buck converter-based proton-exchange membrane fuel cell emulator for testing of mppt algorithm and battery charger controller. Int. Trans. Electr. Energy Syst. 2021, 31, e12754. [Google Scholar] [CrossRef]
- Ramos-Paja, C.; Romero, A.; Giral, R.; Vidal-Idiarte, E.; Martinez-Salamero, L. Fuzzy-based modelling technique for pemfc electrical power generation systems emulation. IET Power Electron. 2009, 2, 241–255. Available online: https://digital-library.theiet.org/content/journals/10.1049/iet-pel.2008.0008 (accessed on 23 March 2023). [CrossRef]
- de Beer, C.; Barendse, P.; Khan, A. Development of an ht pem fuel cell emulator using a multiphase interleaved dc–dc converter topology. IEEE Trans. Power Electron. 2013, 28, 1120–1131. [Google Scholar] [CrossRef]
- Lindahl, P.A.; Shaw, S.R.; Leeb, S.B. Fuel cell stack emulation for cell and hardware-in-the-loop testing. IEEE Trans. Instrum. Meas. 2018, 67, 2143–2152. [Google Scholar] [CrossRef]
- Benyahia, N.; Rekioua, T.; Benamrouche, N.; Bousbaine, A. Fuel cell emulator for supercapacitor energy storage applications. Electr. Power Components Syst. 2013, 41, 569–585. [Google Scholar] [CrossRef]
- Jung, J.-H.; Ahmed, S.; Enjeti, P. Pem fuel cell stack model development for real-time simulation applications. IEEE Trans. Ind. Electron. 2011, 58, 4217–4231. [Google Scholar] [CrossRef]
- Boscaino, V.; Miceli, R.; Capponi, G. Matlab-based simulator of a 5 kw fuel cell for power electronics design. Int. J. Hydrogen Energy 2013, 38, 7924–7934. [Google Scholar] [CrossRef]
- Bojoi, R.; Tenconi, A.; Vaschetto, S.; Colasante, L.; Delmastro, A. Power electronics of a real-time emulator of pem fuel cell systems. In Proceedings of the 2009 International Conference on Clean Electrical Power, Capri, Italy, 9–11 June 2009; pp. 338–343. [Google Scholar] [CrossRef]
- Boscaino, V.; Capponi, G.; Marino, F. Fpga implementation of a fuel cell emulator. SPEEDAM 2010, 2010, 1297–1301. [Google Scholar] [CrossRef]
- Sirisukprasert, S.; Saengsuwan, T. The modeling and control of fuel cell emulators. In Proceedings of the 2008 5th International Conference on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology, Krabi, Thailand, 14–17 May 2008; Volume 2, pp. 985–988. [Google Scholar] [CrossRef]
- Flores-Bahamonde, F.; Rivera, M.; Baier, C.; Calvente, J.; Giral, R.; Restrepo, C. Dc transformer based on the versatile dc-dc noninverting buck-boost converter for fuel cell emulation. In Proceedings of the 2017 IEEE Southern Power Electronics Conference (SPEC), Puerto Varas, Chile, 4–7 December 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Alberro, M.; Marzo, F.; Manso, A.; Domínguez, V.; Barranco, J.; Garikano, X. Electronic modeling of a pemfc with logarithmic amplifiers. Int. J. Hydrogen Energy 2015, 40, 3708–3718. [Google Scholar] [CrossRef]
- Correa, J.; Farret, F.; Gomes, J.; Simoes, M. Simulation of fuel-cell stacks using a computer-controlled power rectifier with the purposes of actual high-power injection applications. IEEE Trans. Ind. Appl. 2003, 39, 1136–1142. [Google Scholar] [CrossRef]
- Lee, T.-W.; Lee, B.-K.; Jang, S.-J.; Kim, S.-H.; Won, C.-Y. Development of a 3 kw fuel cell generation system with an active fuel cell simulator: Topology, control, and design. In Proceedings of the 2004 IEEE 35th Annual Power Electronics Specialists Conference (IEEE Cat. No.04CH37551), Aachen, Germany, 20–25 June 2004; Volume 6, pp. 4743–4748. [Google Scholar] [CrossRef]
- Kwan, T.H.; Wu, X.; Yao, Q. Integrated teg-tec and variable coolant flow rate controller for temperature control and energy harvesting. Energy 2018, 159, 448–456. [Google Scholar] [CrossRef]
- Albarbar, A.; Alrweq, M. Proton Exchange Membrane Fuel Cells: Review; Springer International Publishing: Cham, Switzerland, 2018; Chapter 2; pp. 9–29. [Google Scholar] [CrossRef]
- Pukrushpan, J.T.; Stefanopoulou, A.G.; Peng, H. Background and Introduction; Springer: London, UK, 2004; Chapter 1; pp. 1–13. [Google Scholar] [CrossRef]
- Sun, C.; Negro, E.; Vezzu, K.; Pagot, G.; Cavinato, G.; Nale, A.; Bang, Y.H.; Noto, V.D. Hybrid inorganic-organic proton-conducting membranes based on SPEEK doped with WO3 nanoparticles for application in vanadium redox flow batteries. Electrochim. Acta 2019, 309, 311–325. [Google Scholar] [CrossRef]
- Sun, C.-Y.; Zhang, H. Investigation of Nafion series membranes on the performance of iron-chromium redox flow battery. Int. J. Energy Res. 2019, 43, 8739–8752. [Google Scholar] [CrossRef]
- Puranik, S.V.; Keyhani, A.; Khorrami, F. State-space modeling of proton exchange membrane fuel cell. IEEE Trans. Energy Convers. 2010, 25, 804–813. [Google Scholar] [CrossRef]
- Acharya, P.; Enjeti, P.; Pitel, I. An advanced fuel cell simulator. In Proceedings of the Nineteenth Annual IEEE Applied Power Electronics Conference and Exposition, APEC ‘04, Anaheim, CA, USA, 22–26 February 2004; Volume 3, pp. 1554–1558. [Google Scholar] [CrossRef]
- Ordonez, M.; Iqbal, M.; Quaicoe, J. Dev elopment of a fuel cell simulator based on an experimentally derived model. In Proceedings of the Canadian Conference on Electrical and Computer Engineering, Saskatoon, SK, Canada, 1–4 May 2005; pp. 1449–1452. [Google Scholar] [CrossRef]
- Ordonez, M.; Iqbal, M.; Quaicoe, J. A novel fuel cell simulator. In Proceedings of the 2005 IEEE 36th Power Electronics Specialists Conference, Dresden, Germany, 16 June 2005; pp. 178–184. [Google Scholar] [CrossRef]
- Yang, F.; Zhu, X.-J.; Cao, G.-Y. Nonlinear fuzzy modeling of a mcfc stack by an identification method. J. Power Sources 2007, 166, 354–361. [Google Scholar] [CrossRef]
- Pukrushpan, J.T.; Stefanopoulou, A.G.; Peng, H. Fuel Cell System Model: Fuel Cell Stack; Springer: London, UK, 2004; Chapter 3; pp. 31–56. [Google Scholar] [CrossRef]
- Musio, F.; Tacchi, F.; Omati, L.; Stampino, P.G.; Dotelli, G.; Limonta, S.; Brivio, D.; Grassini, P. Pemfc system simulation in matlab-simulink® environment. Int. J. Hydrogen Energy 2011, 36, 8045–8052. [Google Scholar] [CrossRef]
- Sankar, K.; Aguan, K.; Jana, A.K. A proton exchange membrane fuel cell with an airflow cooling system: Dynamics, validation and nonlinear control. Energy Convers. Manag. 2019, 183, 230–240. [Google Scholar] [CrossRef]
- Buasri, P.; Salameh, Z. An electrical circuit model for a proton exchange membrane fuel cell (pemfc). In Proceedings of the 2006 IEEE Power Engineering Society General Meeting, Montreal, QC, Canada, 18–22 June 2006; p. 6. [Google Scholar] [CrossRef]
- San Martin, J.; Zamora, I.; San Martin, J.; Aperribay, V.; Torres, E.; Eguia, P. Influence of the rated power in the performance of different proton exchange membrane (pem) fuel cells. Energy 2010, 35, 1898–1907. [Google Scholar] [CrossRef]
- Larminie, J. Current interrupt techniques for circuit modelling. In Proceedings of the IEE Colloquium on Electrochemical Measurement, London, UK, 17 March 1994; pp. 1–6. [Google Scholar]
- Fardoun, A.A.; Hejase, H.A.; Al-Marzouqi, A.; Nabag, M. Electric circuit modeling of fuel cell system including compressor effect and current ripples. Int. J. Hydrogen Energy 2017, 42, 1558–1564. [Google Scholar] [CrossRef]
- Mohammadi, A.; Cirrincione, G.; Djerdir, A.; Khaburi, D. A novel approach for modeling the internal behavior of a pemfc by using electrical circuits. Int. J. Hydrogen Energy 2018, 43, 11539–11549. [Google Scholar] [CrossRef]
- Ferrero, R.; Marracci, M.; Prioli, M.; Tellini, B. Simplified model for evaluating ripple effects on commercial pem fuel cell. Int. J. Hydrogen Energy 2012, 37, 13462–13469. [Google Scholar] [CrossRef]
- Wang, C.; Nehrir, M.; Shaw, S. Dynamic models and model validation for pem fuel cells using electrical circuits. IEEE Trans. Energy Convers. 2005, 20, 442–451. [Google Scholar] [CrossRef]
- Rubio, M.; Urquia, A.; Dormido, S. Diagnosis of pem fuel cells through current interruption. J. Power Sources 2007, 171, 670–677. [Google Scholar] [CrossRef]
- Famouri, P.; Gemmen, R. Electrochemical circuit model of a pem fuel cell. In Proceedings of the 2003 IEEE Power Engineering Society General Meeting (IEEE Cat. No.03CH37491), Toronto, ON, Canada, 13–17 July 2003; Volume 3, pp. 1436–1440. [Google Scholar] [CrossRef]
- Yu, D.; Yuvarajan, S. A novel circuit model for pem fuel cells. In Proceedings of the Nineteenth Annual IEEE Applied Power Electronics Conference and Exposition, APEC ‘04, Anaheim, CA, USA, 22–26 February 2004; Volume 1, pp. 362–366. [Google Scholar] [CrossRef]
- Adzakpa, K.P.; Agbossou, K.; DubÉ, Y.; Dostie, M.; Fournier, M.; Poulin, A. Pem fuel cells modeling and analysis through current and voltage transient behaviors. IEEE Trans. Energy Convers. 2008, 23, 581–591. [Google Scholar] [CrossRef]
- Khan, M.J.; Iqbal, M.T. Modelling and analysis of electro-chemical, thermal, and reactant flow dynamics for a pem fuel cell system. Fuel Cells 2005, 5, 463–475. [Google Scholar] [CrossRef]
- Correa, J.; Farret, F.; Popov, V.; Simoes, M. Sensitivity analysis of the modeling parameters used in simulation of proton exchange membrane fuel cells. IEEE Trans. Energy Convers. 2005, 20, 211–218. [Google Scholar] [CrossRef]
- Qingshan, X.; Nianchun, W.; Ichiyanagi, K.; Yukita, K. Pem fuel cell modeling and parameter influences of performance evaluation. In Proceedings of the 2008 Third International Conference on Electric Utility Deregulation and Restructuring and Power Technologies, Nanjing, China, 6–9 April 2008; pp. 2827–2832. [Google Scholar] [CrossRef]
- Lee, D.-J.; Wang, L. Dynamic and steady-state performance of pem fuel cells under various loading conditions. In Proceedings of the 2007 IEEE Power Engineering Society General Meeting, Tampa, FL, USA, 24–28 June 2007; pp. 1–8. [Google Scholar] [CrossRef]
- Lazarou, S.; Pyrgioti, E.; Alexandridis, A.T. A simple electric circuit model for proton exchange membrane fuel cells. J. Power Sources 2009, 190, 380–386. [Google Scholar] [CrossRef]
- Andujar, J.; Segura, F.; Vasallo, M. A suitable model plant for control of the set fuel cell–dc/dc converter. Renew. Energy 2008, 33, 813–826. [Google Scholar] [CrossRef]
- Laffly, E.; Pera, M.-C.; Hissel, D. Dynamic model of a polymer electrolyte fuel cell power device. In Proceedings of the IECON 2006—32nd Annual Conference on IEEE Industrial Electronics, Paris, France, 7–10 November 2006; pp. 466–471. [Google Scholar] [CrossRef]
- Brunetto, C.; Moschetto, A.; Tina, G. Pem fuel cell testing by electrochemical impedance spectroscopy. Electr. Power Syst. Res. 2009, 79, 17–26. [Google Scholar] [CrossRef]
- Restrepo, C.; Torres, C.; Calvente, J.; Giral, R.; Leyva, R. Simulator of a pem fuel-cell stack based on a dynamic model. In Proceedings of the 2009 35th Annual Conference of IEEE Industrial Electronics, Porto, Portugal, 3–5 November 2009; pp. 2796–2801. [Google Scholar] [CrossRef]
- Lan, T.; Strunz, K. Modeling of multi-physics transients in pem fuel cells using equivalent circuits for consistent representation of electric, pneumatic, and thermal quantities. Int. J. Electr. Power Energy Syst. 2020, 119, 105803. [Google Scholar] [CrossRef]
- Page, S.; Krumdieck, S.; Al-Anbuky, A. Testing procedure for passive fuel cell state of health. In Proceedings of the Australasian Universities Power Engineering Conference (AUPEC 2004), Brisbane, Australia, 26–29 September 2004; pp. 1–6. [Google Scholar]
- Forde, T.; Eriksen, J.; Pettersen, A.G.; Vie, P.J.S.; Ulleberg, O. Thermal integration of a metal hydride storage unit and a PEM fuel cell stack. Int. J. Hydrogen Energy 2009, 34, 6730–6739. [Google Scholar] [CrossRef]
- Yiotis, A.G.; Kainourgiakis, M.E.; Charalambopoulou, G.C.; Stubos, A.K. A generic physical model for a thermally integrated high-temperature PEM fuel cell and sodium alanate tank system. Int. J. Hydrogen Energy 2015, 40, 14551–14561. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hernández-Gómez, Á.; Langarica-Cordoba, D.; Martinez-Rodriguez, P.R.; Guilbert, D.; Ramirez, V.; Saldivar, B. PEM Fuel Cell Emulators: A Review. Electronics 2023, 12, 2812. https://doi.org/10.3390/electronics12132812
Hernández-Gómez Á, Langarica-Cordoba D, Martinez-Rodriguez PR, Guilbert D, Ramirez V, Saldivar B. PEM Fuel Cell Emulators: A Review. Electronics. 2023; 12(13):2812. https://doi.org/10.3390/electronics12132812
Chicago/Turabian StyleHernández-Gómez, Ángel, Diego Langarica-Cordoba, Panfilo R. Martinez-Rodriguez, Damien Guilbert, Victor Ramirez, and Belem Saldivar. 2023. "PEM Fuel Cell Emulators: A Review" Electronics 12, no. 13: 2812. https://doi.org/10.3390/electronics12132812
APA StyleHernández-Gómez, Á., Langarica-Cordoba, D., Martinez-Rodriguez, P. R., Guilbert, D., Ramirez, V., & Saldivar, B. (2023). PEM Fuel Cell Emulators: A Review. Electronics, 12(13), 2812. https://doi.org/10.3390/electronics12132812








