A FL-Based Radio Map Reconstruction Approach for UAV-Aided Wireless Networks
Abstract
:1. Introduction
1.1. Related Works
1.2. Motivations
1.3. Contribution
- We propose a federal learning architecture for radio map reconstruction in UAV-aided communication based on training with feedback. This architecture reduces the risk of privacy breach, mitigates client drift [36] by incorporating non-sensitive global information and speeds up the convergence.
- We propose a lightweight and efficient client model to reduce communication overhead between the FL server (UAVs) and clients (users) while maintaining a high level of accuracy in pathloss prediction despite the limited storage and computing resources.
2. System Model
2.1. Preliminaries
2.2. Problem Formulation
3. Proposition
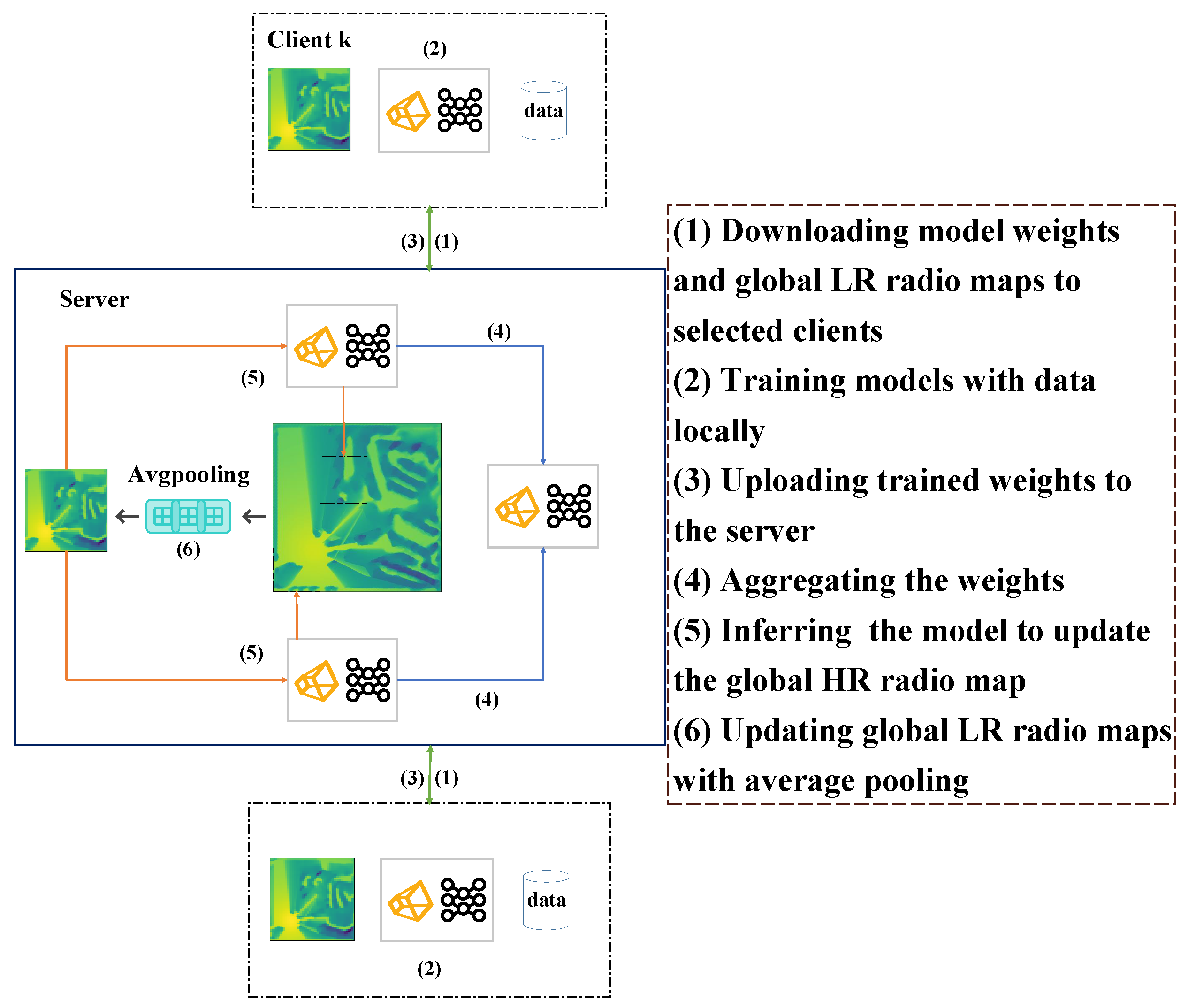
3.1. Methodology and Architecture
3.1.1. FL Clients
3.1.2. FL Server
| Algorithm 1: FL-based radio map reconstruction with training feedback strategy |
 |
3.2. Design of Models
3.2.1. RadioSRNet
3.2.2. RadioSRCNet
4. Experiment and Results
4.1. Dataset and Parameter Setting
4.2. Baseline and Metrics
4.3. Results
4.3.1. Impact of Client Model Architectures
4.3.2. Impact of Training with Feedback
4.3.3. Comparison with FL Models
4.3.4. Comparison with Non-FL Model
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| UAV | Unmanned aerial vehicle |
| SR | Super-resolution |
| APP | Arbitrary position prediction |
| TX | Transmitter |
| RX | Receiver |
| FL | Federated learning |
| LIIF | Local implicit image function |
| FLOPs | Floating-point Operations |
| FF | Feature fusion |
| HR | High-resolution |
| LR | Low-resolution |
| CNN | Convolutional neural network |
| FC | Fully connected |
| MLP | Multi-layer perceptron |
| MAE | Mean absolute error |
| NMSE | Normalized mean squared error |
References
- Yuan, X.; Hu, Y.; Gross, J.; Schmeink, A. Radio-Map-Based UAV Placement Design for UAV-Assisted Relaying Networks. In Proceedings of the 2021 IEEE Statistical Signal Processing Workshop (SSP), Rio de Janeiro, Brazil, 11–14 July 2021; pp. 286–290. [Google Scholar] [CrossRef]
- Wang, Y.; Feng, W.; Wang, J.; Quek, T.Q.S. Hybrid Satellite-UAV-Terrestrial Networks for 6G Ubiquitous Coverage: A Maritime Communications Perspective. IEEE J. Sel. Areas Commun. 2021, 39, 3475–3490. [Google Scholar] [CrossRef]
- Li, X.; Feng, W.; Wang, J.; Chen, Y.; Ge, N.; Wang, C.X. Enabling 5G on the Ocean: A Hybrid Satellite-UAV-Terrestrial Network Solution. IEEE Wirel. Commun. 2020, 27, 116–121. [Google Scholar] [CrossRef]
- Fang, X.; Feng, W.; Wang, Y.; Chen, Y.; Ge, N.; Ding, Z.; Zhu, H. NOMA-Based Hybrid Satellite-UAV-Terrestrial Networks for 6G Maritime Coverage. IEEE Trans. Wirel. Commun. 2023, 22, 138–152. [Google Scholar] [CrossRef]
- Zeng, Y.; Wu, Q.; Zhang, R. Accessing From the Sky: A Tutorial on UAV Communications for 5G and Beyond. Proc. IEEE 2019, 107, 2327–2375. [Google Scholar] [CrossRef]
- Fan, R.; Cui, J.; Jin, S.; Yang, K.; An, J. Optimal Node Placement and Resource Allocation for UAV Relaying Network. IEEE Commun. Lett. 2018, 22, 808–811. [Google Scholar] [CrossRef]
- Ouamri, M.A.; Oteşteanu, M.E.; Barb, G.; Gueguen, C. Coverage Analysis and Efficient Placement of Drone-BSs in 5G Networks. Eng. Proc. 2022, 14, 18. [Google Scholar] [CrossRef]
- Ouamri, M.A.; Singh, D.; Muthanna, M.A.; Bounceur, A.; Li, X. Performance Analysis of UAV Multiple Antenna-Assisted Small Cell Network with Clustered Users. Wirel. Netw. 2023, 29, 1859–1872. [Google Scholar] [CrossRef]
- Li, P.; Xu, J. Fundamental Rate Limits of UAV-Enabled Multiple Access Channel with Trajectory Optimization. IEEE Trans. Wirel. Commun. 2020, 19, 458–474. [Google Scholar] [CrossRef]
- Zeng, Y.; Xu, J.; Zhang, R. Energy Minimization for Wireless Communication with Rotary-Wing UAV. IEEE Trans. Wirel. Commun. 2019, 18, 2329–2345. [Google Scholar] [CrossRef]
- Ouamri, M.A.; Alkanhel, R.; Singh, D.; El-kenawy, E.S.; Ghoneim, S. Double Deep Q-Network Method for Energy Efficiency and Throughput in a UAV-Assisted Terrestrial Network. Comput. Syst. Sci. Eng. 2022, 46, 73–92. [Google Scholar] [CrossRef]
- Chen, J.; Mitra, U.; Gesbert, D. Optimal UAV Relay Placement for Single User Capacity Maximization over Terrain with Obstacles. In Proceedings of the 2019 IEEE 20th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Cannes, France, 2–5 July 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Li, H.; Li, P.; Xu, J.; Chen, J.; Zeng, Y. Derivative-Free Placement Optimization for Multi-UAV Wireless Networks with Channel Knowledge Map. In Proceedings of the 2022 IEEE International Conference on Communications Workshops (ICC Workshops), Seoul, Republic of Korea, 16–20 May 2022; pp. 1029–1034. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, R. Radio Map-Based 3D Path Planning for Cellular-Connected UAV. IEEE Trans. Wirel. Commun. 2021, 20, 1975–1989. [Google Scholar] [CrossRef]
- Chen, J.; Yatnalli, U.; Gesbert, D. Learning radio maps for UAV-aided wireless networks: A segmented regression approach. In Proceedings of the 2017 IEEE International Conference on Communications (ICC), Paris, France, 21–25 May 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Levie, R.; Yapar, Ç.; Kutyniok, G.; Caire, G. RadioUNet: Fast Radio Map Estimation with Convolutional Neural Networks. IEEE Trans. Wirel. Commun. 2021, 20, 4001–4015. [Google Scholar] [CrossRef]
- Mo, X.; Huang, Y.; Xu, J. Radio-Map-Based Robust Positioning Optimization for UAV-Enabled Wireless Power Transfer. IEEE Wirel. Commun. Lett. 2020, 9, 179–183. [Google Scholar] [CrossRef]
- Utkovski, Z.; Agostini, P.; Frey, M.; Bjelakovic, I.; Stanczak, S. Learning Radio Maps for Physical-Layer Security in the Radio Access. In Proceedings of the 2019 IEEE 20th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Cannes, France, 2–5 July 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Grimoud, S.; Ben Jemaa, S.; Sayrac, B.; Moulines, E. A REM enabled soft frequency reuse scheme. In Proceedings of the 2010 IEEE Globecom Workshops, Seoul, Republic of Korea, 16–20 May 2010; pp. 819–823. [Google Scholar] [CrossRef]
- Zugno, T.; Drago, M.; Giordani, M.; Polese, M.; Zorzi, M. Toward Standardization of Millimeter-Wave Vehicle-to-Vehicle Networks: Open Challenges and Performance Evaluation. IEEE Commun. Mag. 2020, 58, 79–85. [Google Scholar] [CrossRef]
- Rizk, K.; Wagen, J.F.; Gardiol, F. Two-dimensional ray-tracing modeling for propagation prediction in microcellular environments. IEEE Trans. Veh. Technol. 1997, 46, 508–518. [Google Scholar] [CrossRef]
- Kermani, M.; Kamarei, M. A ray-tracing method for predicting delay spread in tunnel environments. In Proceedings of the 2000 IEEE International Conference on Personal Wireless Communications, Conference Proceedings (Cat. No.00TH8488), Hyderabad, India, 17–20 December 2000; pp. 538–542. [Google Scholar] [CrossRef]
- Wahl, R.; Wölfle, G.; Wertz, P.; Wildbolz, P.; Landstorfer, F.M. Dominant Path Prediction Model for Urban Scenarios. In Proceedings of the IST Mobile and Wireless Communications Summit, Dresden, Germany, 19–23 June 2005. [Google Scholar]
- Boccolini, G.; Hernández-Peñaloza, G.; Beferull-Lozano, B. Wireless sensor network for Spectrum Cartography based on Kriging interpolation. In Proceedings of the 2012 IEEE 23rd International Symposium on Personal, Indoor and Mobile Radio Communications—(PIMRC), Sydney, NSW, Australia, 9–12 September 2012; pp. 1565–1570. [Google Scholar] [CrossRef]
- Li, J.; Heap, A.D. A review of comparative studies of spatial interpolation methods in environmental sciences: Performance and impact factors. Ecol. Inform. 2011, 6, 228–241. [Google Scholar] [CrossRef]
- Redondi, A.E.C. Radio Map Interpolation Using Graph Signal Processing. IEEE Commun. Lett. 2018, 22, 153–156. [Google Scholar] [CrossRef]
- Malkova, A.; Amini, M.R.; Denis, B.; Villien, C. Deep Learning with Partially Labeled Data for Radio Map Reconstruction. arXiv 2023, arXiv:2306.05294. [Google Scholar] [CrossRef]
- Suto, K.; Bannai, S.; Sato, K.; Inage, K.; Adachi, K.; Fujii, T. Image-Driven Spatial Interpolation with Deep Learning for Radio Map Construction. IEEE Wirel. Commun. Lett. 2021, 10, 1222–1226. [Google Scholar] [CrossRef]
- Saito, K.; Jin, Y.; Kang, C.; Takada, J.I.; Leu, J.S. Two-step path loss prediction by artificial neural network for wireless service area planning. IEICE Commun. Express 2019, 8, 611–616. [Google Scholar] [CrossRef]
- Li, K.; Chen, J.; Yu, B.; Shen, Z.; Li, C.; He, S. Supreme: Fine-grained Radio Map Reconstruction via Spatial-Temporal Fusion Network. In Proceedings of the 2020 19th ACM/IEEE International Conference on Information Processing in Sensor Networks (IPSN), Sydney, NSW, Australia, 21–24 April 2020; pp. 1–12. [Google Scholar] [CrossRef]
- Tonchev, K.; Ivanov, A.; Neshov, N.; Manolova, A.; Poulkov, V. Learning Graph Convolutional Neural Networks to Predict Radio Environment Maps. In Proceedings of the 2022 25th International Symposium on Wireless Personal Multimedia Communications (WPMC), Herning, Denmark, 30 October–2 November 2022; pp. 392–395. [Google Scholar] [CrossRef]
- Teganya, Y.; Romero, D. Deep Completion Autoencoders for Radio Map Estimation. IEEE Trans. Wirel. Commun. 2022, 21, 1710–1724. [Google Scholar] [CrossRef]
- Liu, Y.; Yuan, X.; Xiong, Z.; Kang, J.; Wang, X.; Niyato, D. Federated learning for 6G communications: Challenges, methods, and future directions. China Commun. 2020, 17, 105–118. [Google Scholar] [CrossRef]
- Islam, A.; Al Amin, A.; Shin, S.Y. FBI: A Federated Learning-Based Blockchain-Embedded Data Accumulation Scheme Using Drones for Internet of Things. IEEE Wirel. Commun. Lett. 2022, 11, 972–976. [Google Scholar] [CrossRef]
- Do, Q.V.; Pham, Q.V.; Hwang, W.J. Deep Reinforcement Learning for Energy-Efficient Federated Learning in UAV-Enabled Wireless Powered Networks. IEEE Commun. Lett. 2022, 26, 99–103. [Google Scholar] [CrossRef]
- Karimireddy, S.P.; Kale, S.; Mohri, M.; Reddi, S.; Stich, S.; Suresh, A.T. SCAFFOLD: Stochastic Controlled Averaging for Federated Learning. In Proceedings of the 37th International Conference on Machine Learning, PMLR, Vienna, Austria, 13–18 July 2020; Volume 119, pp. 5132–5143. [Google Scholar]
- McMahan, B.; Moore, E.; Ramage, D.; Hampson, S.; Arcas, B.A.Y. Communication-Efficient Learning of Deep Networks from Decentralized Data. In Proceedings of the 20th International Conference on Artificial Intelligence and Statistics, PMLR, Jakarta, Indonesia, 20–22 April 2017; Volume 54, pp. 1273–1282. [Google Scholar]
- Woo, S.; Park, J.; Lee, J.Y.; Kweon, I.S. CBAM: Convolutional Block Attention Module. In Proceedings of the Computer Vision—ECCV 2018, Munich, Germany, 8–14 September 2018; pp. 3–19. [Google Scholar]
- Chen, Y.; Liu, S.; Wang, X. Learning Continuous Image Representation with Local Implicit Image Function. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 8624–8634. [Google Scholar] [CrossRef]
- Graziosi, F.; Santucci, F. A general correlation model for shadow fading in mobile radio systems. IEEE Commun. Lett. 2002, 6, 102–104. [Google Scholar] [CrossRef]
- Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K.Q. Densely Connected Convolutional Networks. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 2261–2269. [Google Scholar] [CrossRef]
- Dumoulin, V.; Visin, F. A guide to convolution arithmetic for deep learning. arXiv 2016, arXiv:1603.07285. [Google Scholar] [CrossRef]
- Huangfu, Y.; Wang, J.; Dai, S.; Li, R.; Wang, J.; Huang, C.; Zhang, Z. WAIR-D: Wireless AI Research Dataset. arXiv 2022, arXiv:2212.02159. [Google Scholar]





| Dataset | |
|---|---|
| Size of area (m) | |
| Coordinates of base stations (m) | |
| Size of area for each group (m) | |
| Centroidal coordinates for each group (m) | |
| Training set | |
| Testing set | |
| Federated Learning | |
| FL server | 1 |
| Number of clients | 90 |
| Clients used in federated updates | 5 |
| Local training epochs | 10 |
| Communication rounds | 180 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tan, Z.; Xiao, L.; Tang, X.; Zhao, M.; Li, Y. A FL-Based Radio Map Reconstruction Approach for UAV-Aided Wireless Networks. Electronics 2023, 12, 2817. https://doi.org/10.3390/electronics12132817
Tan Z, Xiao L, Tang X, Zhao M, Li Y. A FL-Based Radio Map Reconstruction Approach for UAV-Aided Wireless Networks. Electronics. 2023; 12(13):2817. https://doi.org/10.3390/electronics12132817
Chicago/Turabian StyleTan, Zhiqiang, Limin Xiao, Xinyi Tang, Ming Zhao, and Yunzhou Li. 2023. "A FL-Based Radio Map Reconstruction Approach for UAV-Aided Wireless Networks" Electronics 12, no. 13: 2817. https://doi.org/10.3390/electronics12132817
APA StyleTan, Z., Xiao, L., Tang, X., Zhao, M., & Li, Y. (2023). A FL-Based Radio Map Reconstruction Approach for UAV-Aided Wireless Networks. Electronics, 12(13), 2817. https://doi.org/10.3390/electronics12132817







