Joint Packet Length and Power Optimization for Covert Short-Packet D2D Communications
Abstract
:1. Introduction
- Through the uncertainty of the background noise power of the warden and the interference of CUE in the detection process, the warden cannot accurately judge whether the changes in the received signal come from the occurrence of the D2D communication behavior. We construct a short-packet D2D communication scene assisted by covert communication. In this model, the ECT is proposed to quantitatively characterize the tradeoff between the covertness and reliability of the D2D pair under the short packet communication. We consider the process of obtaining CSI under covert conditions, comprehensively considering the average decoding error and channel estimation error of the short packet communication receiver, and analyze the transmission performance of the system.
- In the covert short-packet D2D communication scenario, we derive a strict covert constraint lower bound based on the KL divergence of the observed signal probability, and analyze the factors affecting the covert performance such as the allocation factor and pilot packet length. On this basis, the analysis of the existing equal power distribution scheme between the pilot and data signal can ensure the best covert performance of D2D communication, but it damages the reliability of D2D communication.
- To ensure both communication covertness and reliability, we aim to maximize the ECT of D2D pairs and construct a joint optimization problem for the pilot transmission power, data transmission power, and packet length. Furthermore, we propose a 2D numerical search algorithm to obtain the optimal solution of the established optimization problem. The simulation results demonstrate that compared with the scheme of the equal power transmission for the pilot and data, under the general model, the transmission performance of the system has been improved to a certain extent while ensuring covertness.
2. System Model
2.1. Channel Estimation Modeling
2.2. Communication Link Quality Assessment
3. Covert Performance Analysis
3.1. Willie’s Detection Strategy
3.2. Covert Constraints
4. Communication Performance Analysis
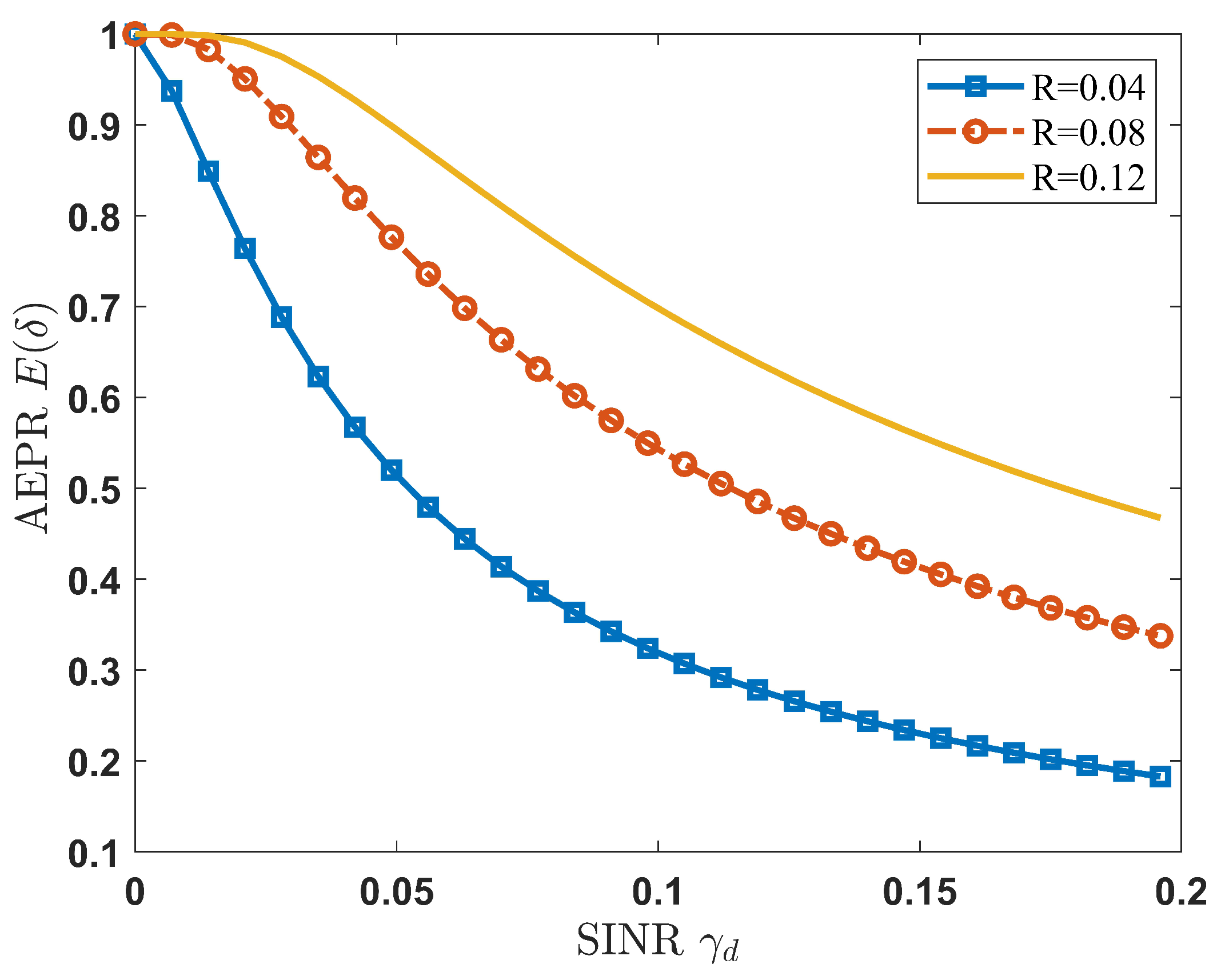
4.1. D2D Receiver Error Packet Rate
4.2. Effective Covert Throughput
| Algorithm 1 The 2D search algorithm for maximizing throughput |
|
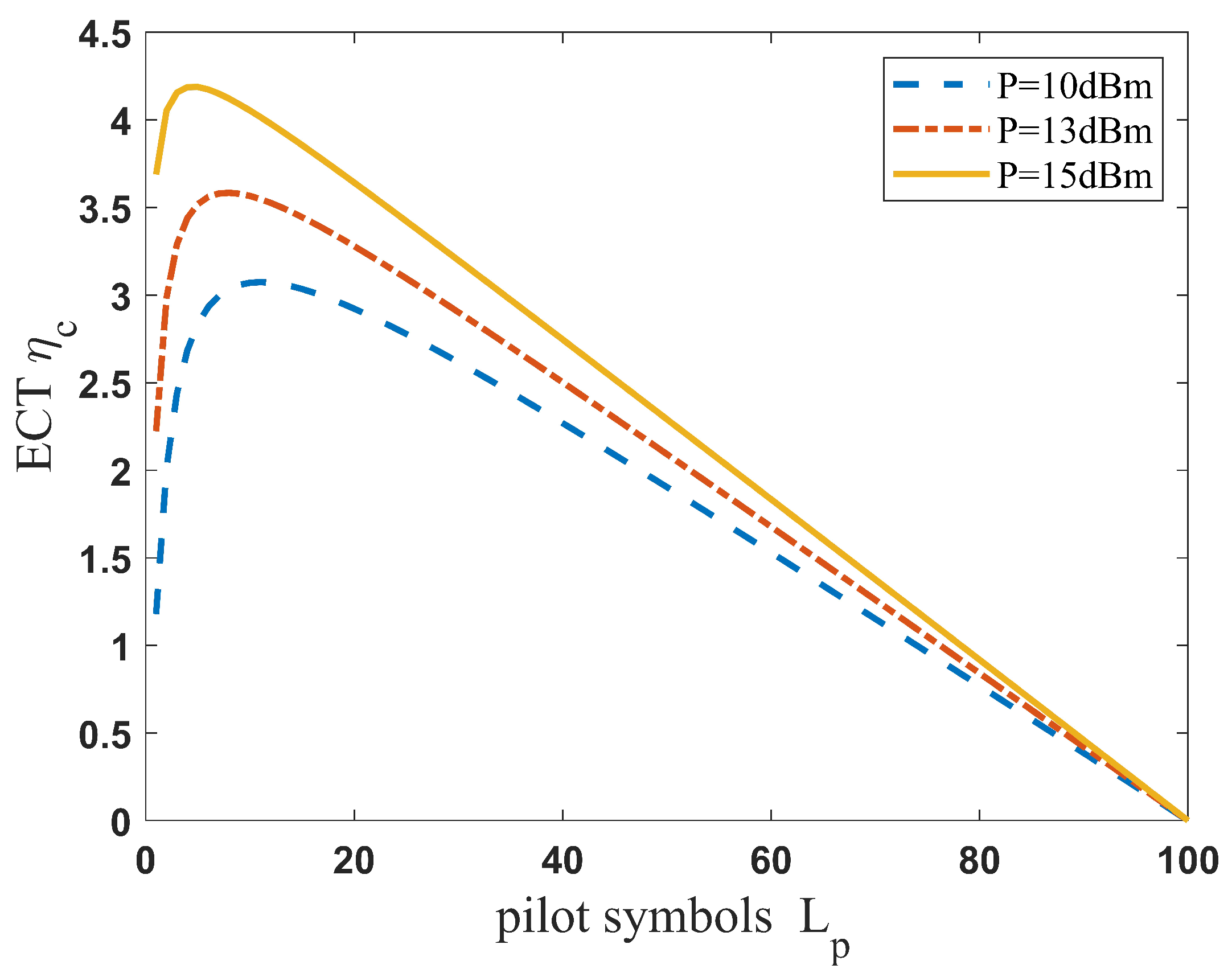
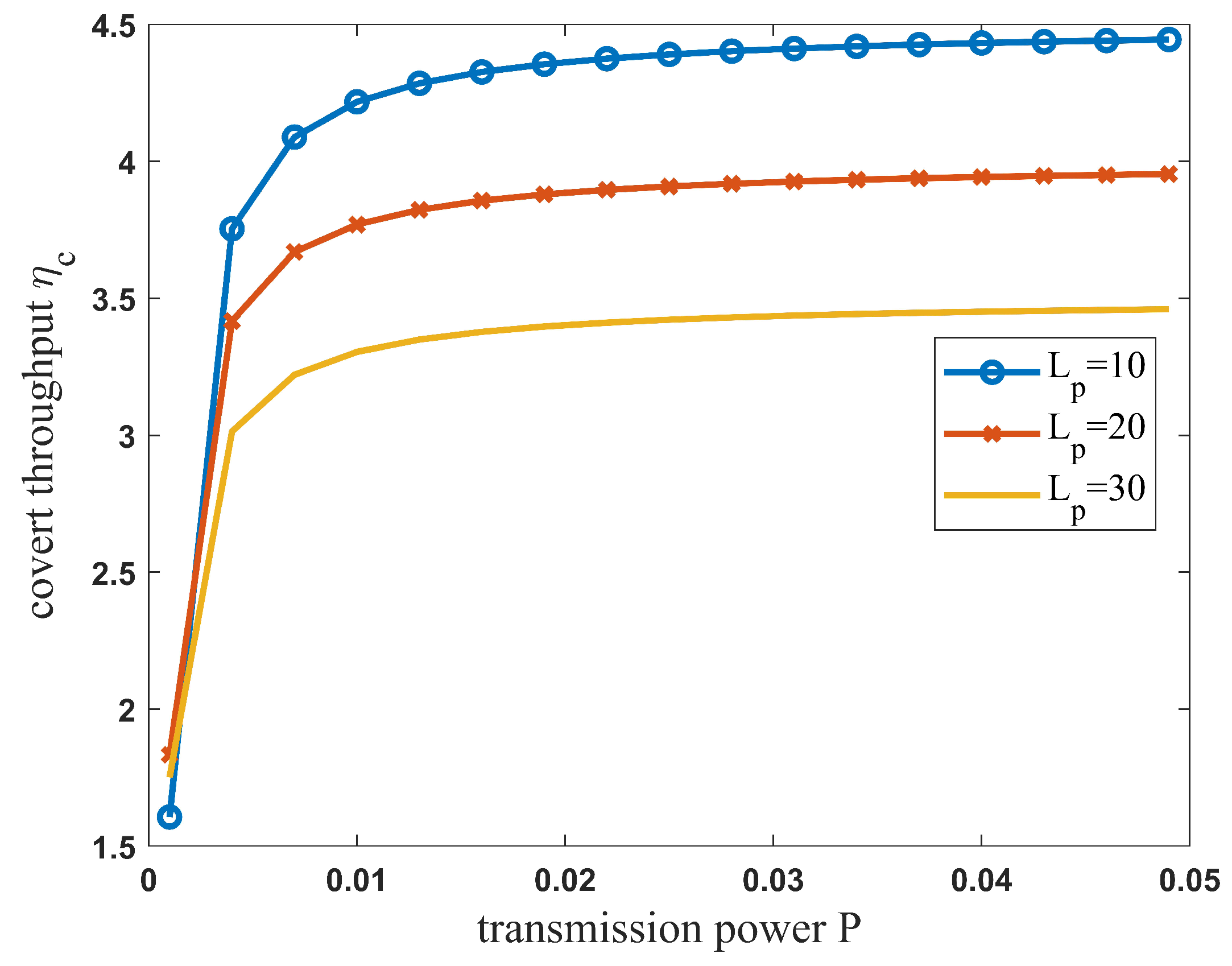
5. Simulation Results and Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ansari, R.I.; Chrysostomou, C.; Hassan, S.A.; Guizani, M.; Mumtaz, S.; Rodriguez, J.; Rodrigues, J.J. 5G D2D networks: Techniques, challenges, and future prospects. IEEE Syst. 2018, 12, 3970–3984. [Google Scholar] [CrossRef]
- Salim, M.M.; Wang, D.; Elsayed, H.A.E.A.; Liu, Y.; Abd Elaziz, M. Joint optimization of energy-harvesting-powered two-way relaying D2D communication for IoT: A rate–energy efficiency tradeoff. IEEE Internet Things J. 2020, 7, 11735–11752. [Google Scholar] [CrossRef]
- Wu, D.; Zhou, L.; Cai, Y.; Qian, Y. Collaborative caching and matching for D2D content sharing. IEEE Wirel. Commun. 2018, 25, 43–49. [Google Scholar] [CrossRef]
- Wu, D.; Zhou, L.; Cai, Y.; Hu, R.Q.; Qian, Y. The role of mobility for D2D communications in LTE-Advanced networks: Energy vs. bandwidth efficiency. IEEE Wirel. Commun. 2014, 21, 66–71. [Google Scholar] [CrossRef]
- Yang, W.; Durisi, G.; Koch, T.; Polyanskiy, Y. Quasi-static multiple-antenna fading channels at finite blocklength. IEEE Trans. Inf. Theory 2014, 60, 4232–4265. [Google Scholar] [CrossRef] [Green Version]
- Durisi, G.; Koch, T.; Popovski, P. Toward massive, ultrareliable, and low-latency wireless communication with short packets. Proc. IEEE 2016, 104, 1711–1726. [Google Scholar] [CrossRef] [Green Version]
- Durisi, G.; Koch, T.; Östman, J.; Polyanskiy, Y.; Yang, W. Short-packet communications over multiple-antenna rayleigh-fading channels. IEEE Trans. Commun. 2016, 64, 618–629. [Google Scholar] [CrossRef]
- Lee, B.; Park, S.; Love, D.J.; Ji, H.; Shim, B. Packet structure and receiver design for low latency wireless communications with ultra-short packets. IEEE Trans. Commun. 2018, 66, 796–807. [Google Scholar] [CrossRef]
- Tang, A.; Wang, X.; Zhang, C. Cooperative full duplex Device to Device communication underlaying cellular networks. IEEE Trans. Wirel. Commun. 2017, 16, 7800–7815. [Google Scholar] [CrossRef]
- Li, J.; Wu, D.; Yue, C.; Yang, Y.; Wang, M.; Yuan, F. Energy-efficient transmit probability-power control for covert D2D communications with age of information constraints. IEEE Trans. Veh. Technol. 2022, 71, 9690–9704. [Google Scholar] [CrossRef]
- Jamil, S.; Fawad; Rahman, M.; Ullah, A.; Badnava, S.; Forsat, M.; Mirjavadi, S.S. Malicious UAV detection using integrated audio and visual features for public safety applications. Sensors 2020, 20, 3923. [Google Scholar] [CrossRef] [PubMed]
- Bash, B.A.; Goeckel, D.; Towsley, D. Hiding information in noise: Fundamental limits of covert wireless communication. IEEE Commun. Mag. 2015, 53, 26–31. [Google Scholar] [CrossRef] [Green Version]
- Bash, B.A.; Goeckel, D.; Towsley, D. Limits of reliable communication with low probability of detection on AWGN channels. IEEE J. Sel. Areas Commun. 2013, 31, 1921–1930. [Google Scholar] [CrossRef] [Green Version]
- Yan, S.; He, B.; Cong, Y.; Zhou, X. Covert communication with finite blocklength in AWGN channels. In Proceedings of the 2017 IEEE International Conference on Communications (ICC), Paris, France, 21–25 May 2017; pp. 1–6. [Google Scholar]
- Yan, S.; Zhou, X.; Hu, J.; Hanly, S.V. Low probability of detection communication: Opportunities and challenges. IEEE Wirel. Commun. 2019, 26, 19–25. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Wornell, G.; Zheng, L. Fundamental limits of communication with low probability of detection. IEEE Trans. Inf. Theory 2016, 62, 3493–3503. [Google Scholar] [CrossRef] [Green Version]
- Wan, C.; Wu, D.; Wang, M.; Shi, X.; Guan, X. Covert communication with power uncertainty for D2D content sharing. In Proceedings of the 2019 11th International Conference on Wireless Communications and Signal Processing (WCSP), Xi’an, China, 23–25 October 2019; pp. 1–6. [Google Scholar]
- Rao, H.; Wu, M.; Wang, J.; Tang, W.; Xiao, S.; Li, S. D2D covert communications with safety area. IEEE Syst. J. 2021, 15, 2331–2341. [Google Scholar] [CrossRef]
- Jiang, Y.E.; Wang, L.; Zhao, H.; Chen, H.H. Covert communications in D2D underlaying cellular networks with power domain NOMA. IEEE Syst. J. 2020, 14, 3717–3728. [Google Scholar] [CrossRef]
- Jiang, Y.; Wang, L.; Chen, H. Covert communications in D2D underlaying cellular networks with antenna array assisted artificial noise transmission. IEEE Trans. Veh. Technol. 2020, 69, 2980–2992. [Google Scholar] [CrossRef]
- Yan, S.; He, B.; Zhou, X.; Cong, Y.; Swindlehurst, A.L. Delay-intolerant covert communications with either fixed or random transmit power. IEEE Trans. Inf. Forensics Secur. 2019, 14, 129–140. [Google Scholar] [CrossRef] [Green Version]
- Yu, B.; Cai, Y.; Wu, D.; Xiang, Z. Average age of information in Short packet based machine type communication. IEEE Trans. Veh. Technol. 2020, 69, 10306–10319. [Google Scholar] [CrossRef]
- Lu, X.; Yang, W.; Yan, S.; Tao, L.; Ng, D.W.K. Joint packet generation and covert communication in delay-intolerant status update systems. IEEE Trans. Veh. Technol. 2022, 71, 2170–2175. [Google Scholar] [CrossRef]
- Sun, L.; Xu, T.; Yan, S.; Hu, J.; Yu, X.; Shu, F. On resource allocation in covert wireless communication with channel estimation. IEEE Trans. Commun. 2020, 68, 6456–6469. [Google Scholar] [CrossRef]
- Ma, R.; Yang, X.; Pan, G.; Guan, X.; Zhang, Y.; Yang, W. Covert communications with channel inversion power control in the finite blocklength regime. IEEE Wirel. Commun. Lett. 2021, 10, 835–839. [Google Scholar] [CrossRef]
- Gursoy, M.C. On the capacity and energy efficiency of training-based transmissions over fading channels. IEEE Trans. Inf. Theory 2009, 55, 4543–4567. [Google Scholar] [CrossRef] [Green Version]
- Yang, W.; Lu, X.; Yan, S.; Shu, F.; Li, Z. Age of information for short-packet covert communication. IEEE Wirel. Commun. Lett. 2021, 10, 1890–1894. [Google Scholar] [CrossRef]
- Ma, R.; Yang, W.; Tao, L.; Lu, X.; Xiang, Z.; Liu, J. Covert communications with randomly distributed wardens in the finite blocklength regime. IEEE Trans. Veh. Technol. 2022, 71, 533–544. [Google Scholar] [CrossRef]
- Ma, R.; Yang, W.; Hu, J.; Lu, X. Covert mmWave communication when the warden locates in the beam direction. IEEE Wirel. Commun. Lett. 2022, 11, 2595–2599. [Google Scholar] [CrossRef]
- Lu, X.; Yan, S.; Yang, W.; Li, M.; Ng, D.W.K. Covert communication with time uncertainty in time-critical wireless networks. IEEE Trans. Wirel. Commun. 2023, 22, 1116–1129. [Google Scholar] [CrossRef]


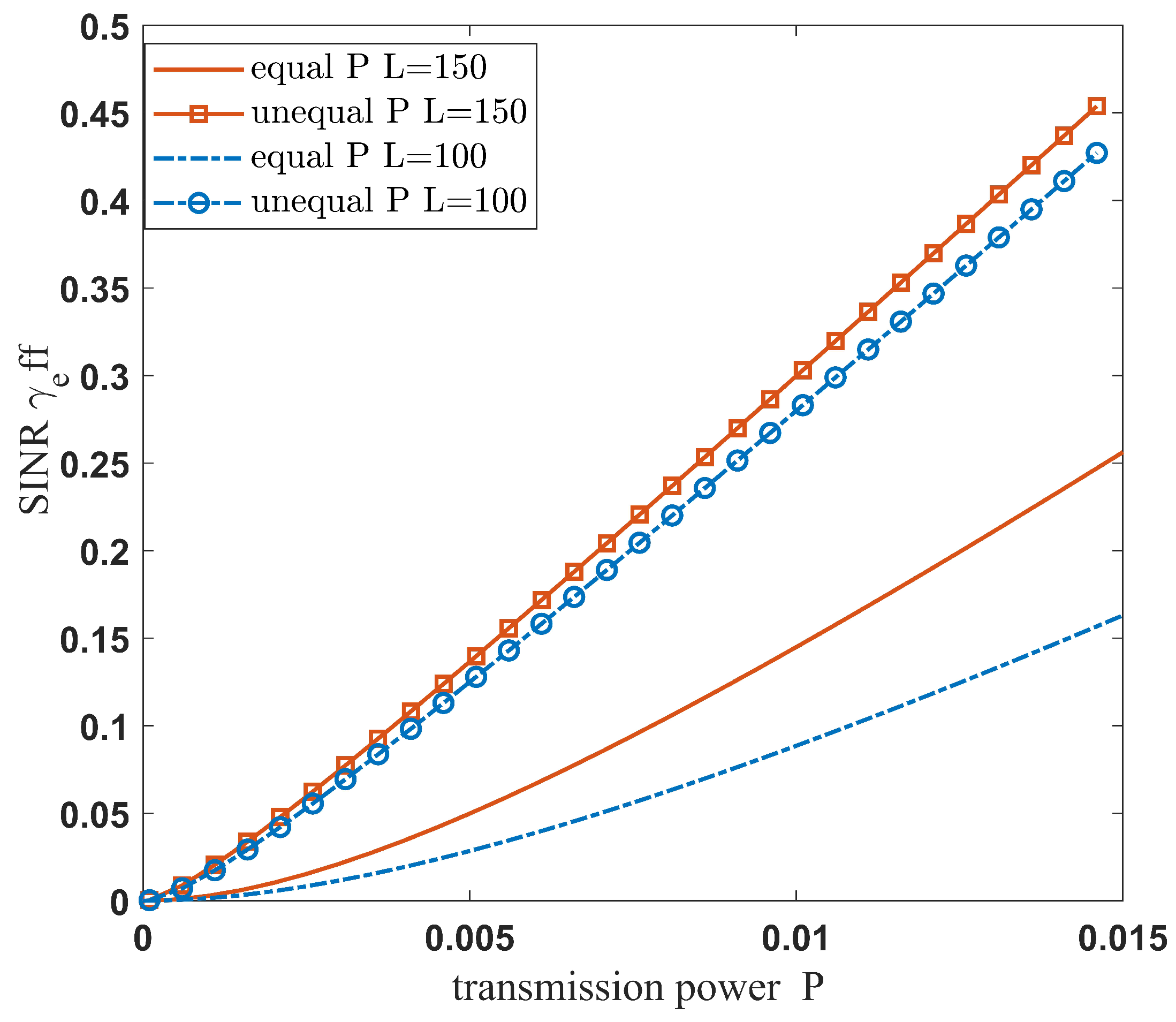
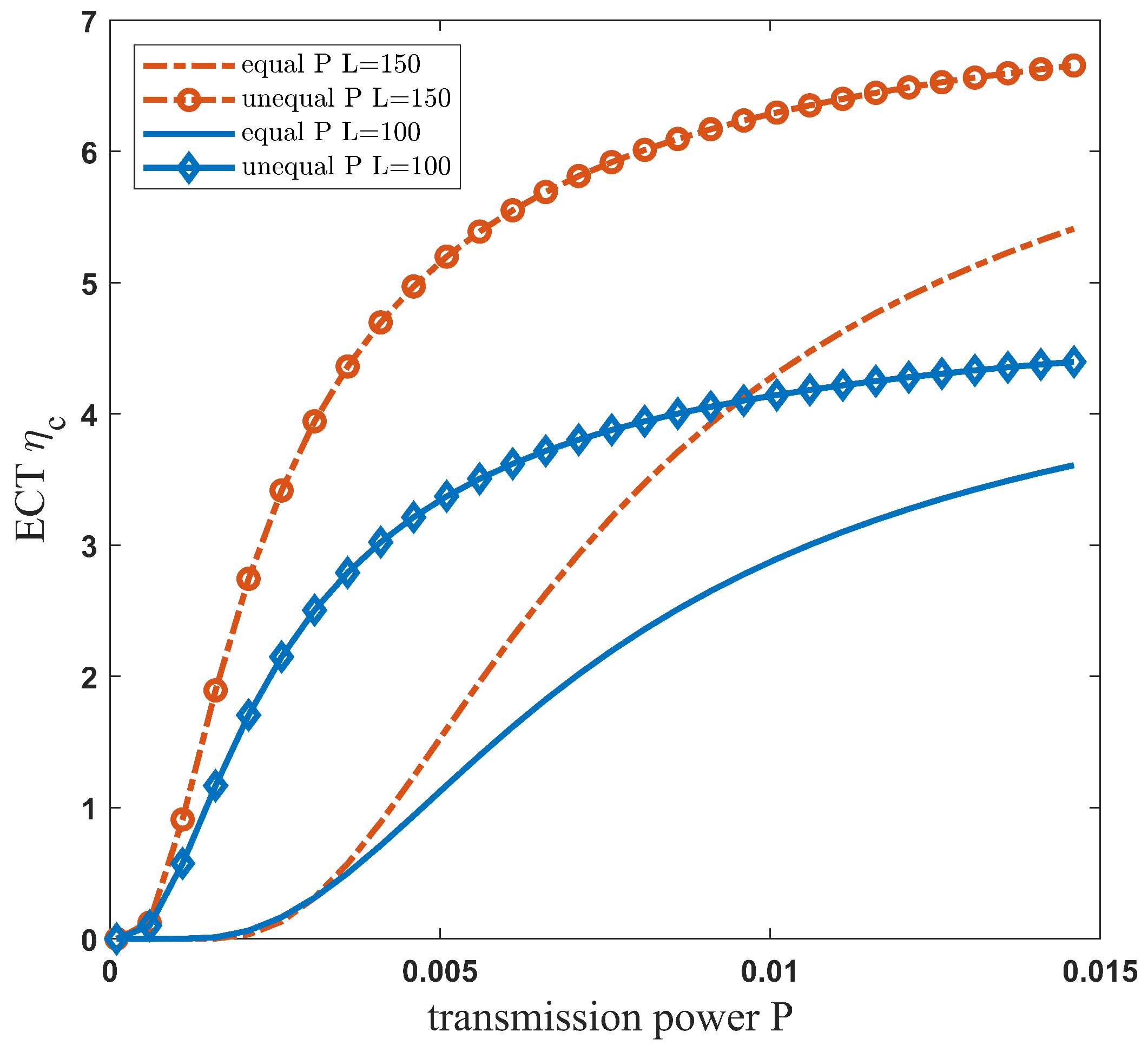
| Parameter | Value |
|---|---|
| The minimum distance between CUE and BS | 30 m |
| The maximum distance of D2D users | 50 m |
| The distance between DT and CUE | 80 m |
| The distance between DT and Willie | 80 m |
| The distance between CUEs and DR | 150 m |
| Cell radius of CUEs | 1000 m |
| D2D user’s maximum transmit power | 24 dBm |
| The noise power at the receiver of Willie and DR | −80 dBm |
| The user’s minimum SINR | 0∼10 dB |
| The transmitted power of CUEs | 17∼23 dBm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Liu, J.; Huang, Y. Joint Packet Length and Power Optimization for Covert Short-Packet D2D Communications. Electronics 2023, 12, 2822. https://doi.org/10.3390/electronics12132822
Zhang X, Liu J, Huang Y. Joint Packet Length and Power Optimization for Covert Short-Packet D2D Communications. Electronics. 2023; 12(13):2822. https://doi.org/10.3390/electronics12132822
Chicago/Turabian StyleZhang, Xiaolong, Jie Liu, and Yuzhen Huang. 2023. "Joint Packet Length and Power Optimization for Covert Short-Packet D2D Communications" Electronics 12, no. 13: 2822. https://doi.org/10.3390/electronics12132822




