Broad Stopband, Low-Loss, and Ultra-Compact Dual-Mode Bandpass Filter Based on HMSIRC
Abstract
:1. Introduction
- (i)
- It occupies a footprint area of only 0.028 λg2, which is extremely small compared to the dual-mode BPFs that have previously been reported;
- (ii)
- Its insertion loss is 0.41 dB;
- (iii)
- It exhibits a passband of 15.9%, a broad stopband response of 4.36 f0, and a rejection level of 20 dB.
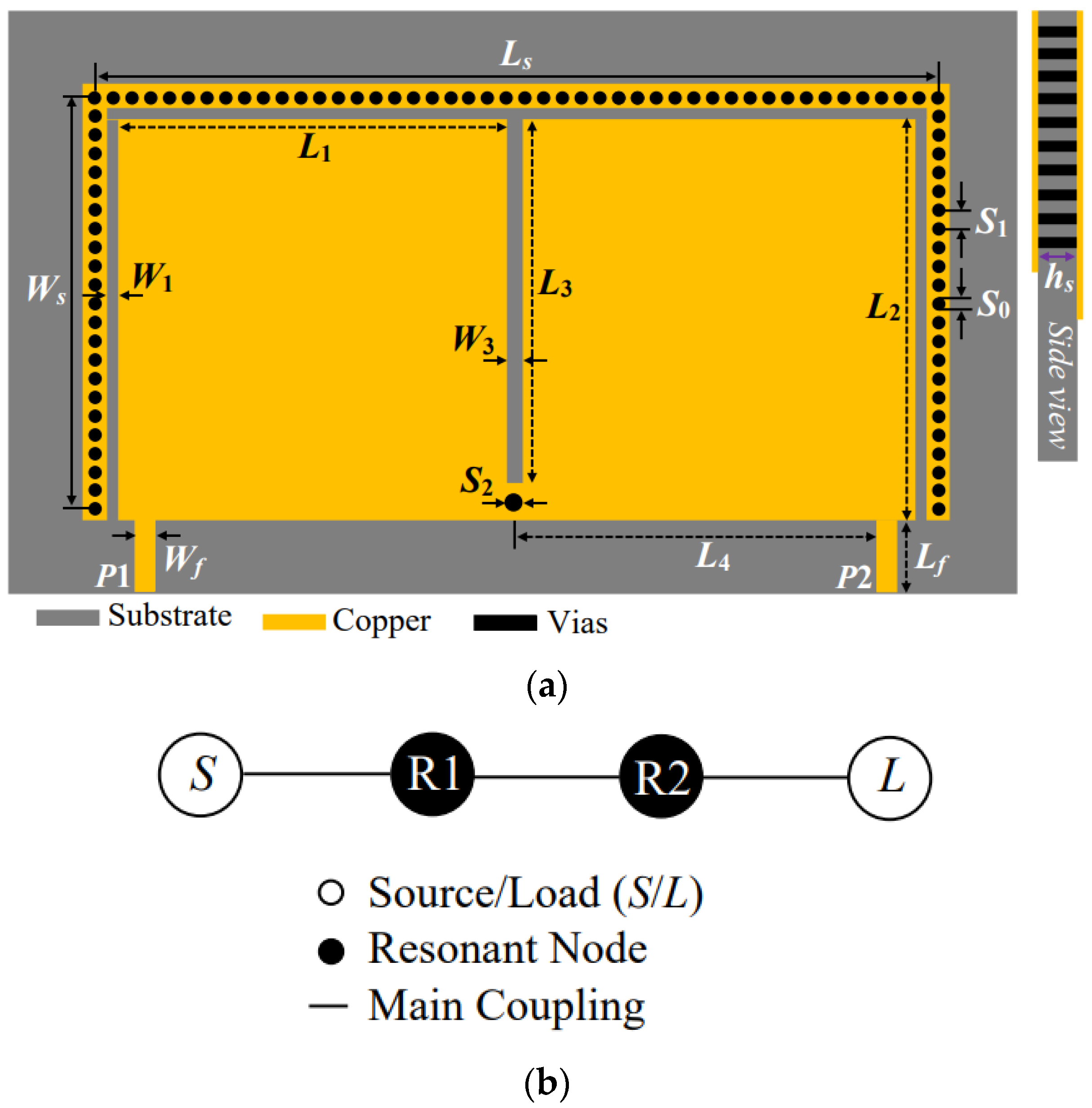
2. Design and Analysis of the HMSIRC-Based Bandpass Filter
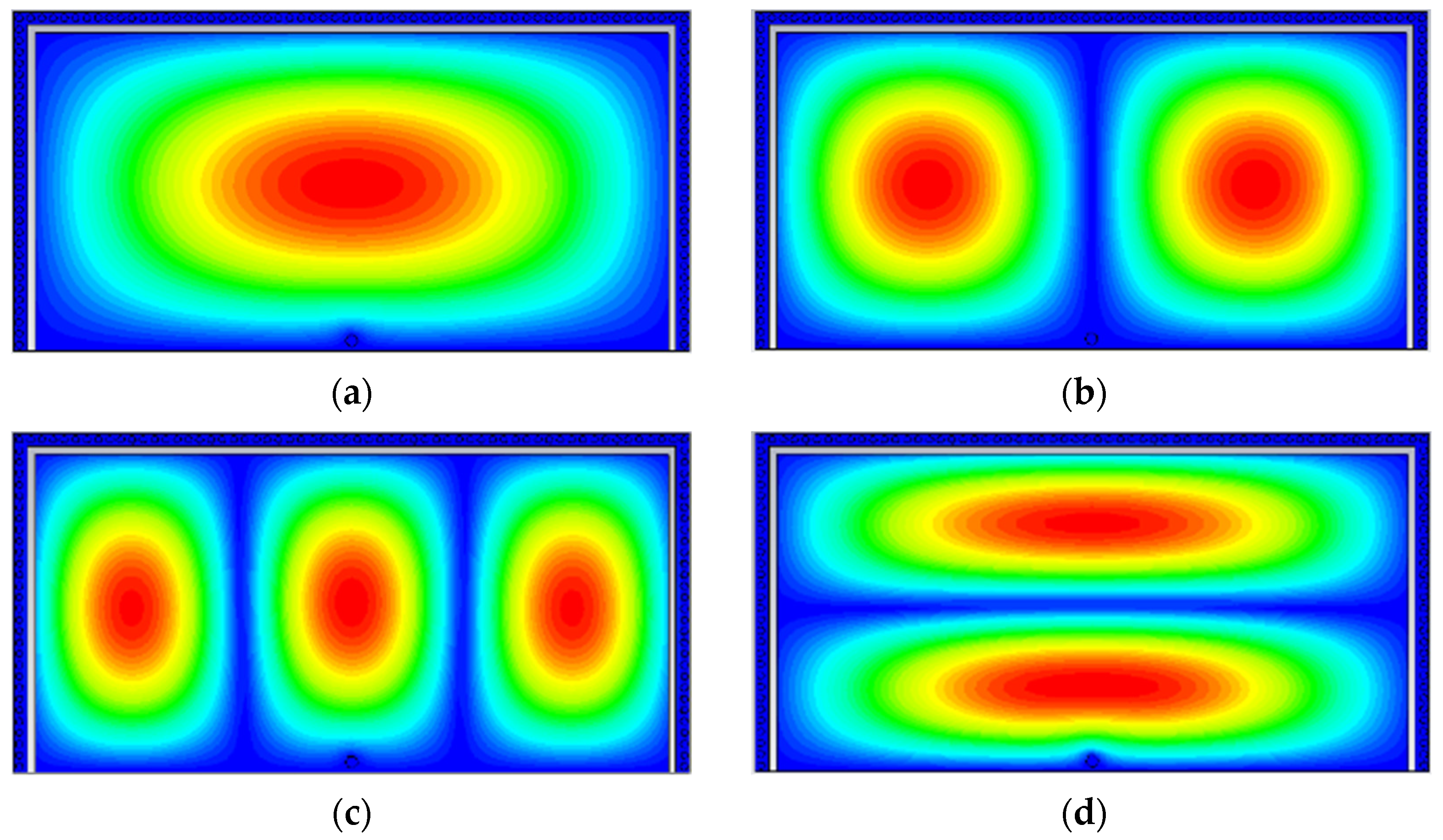
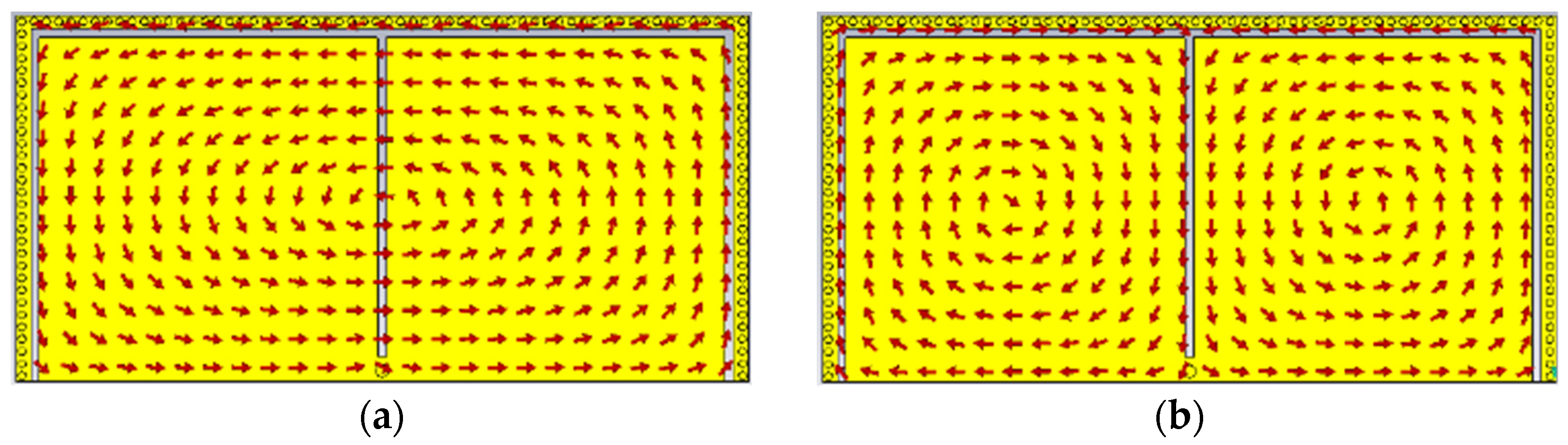
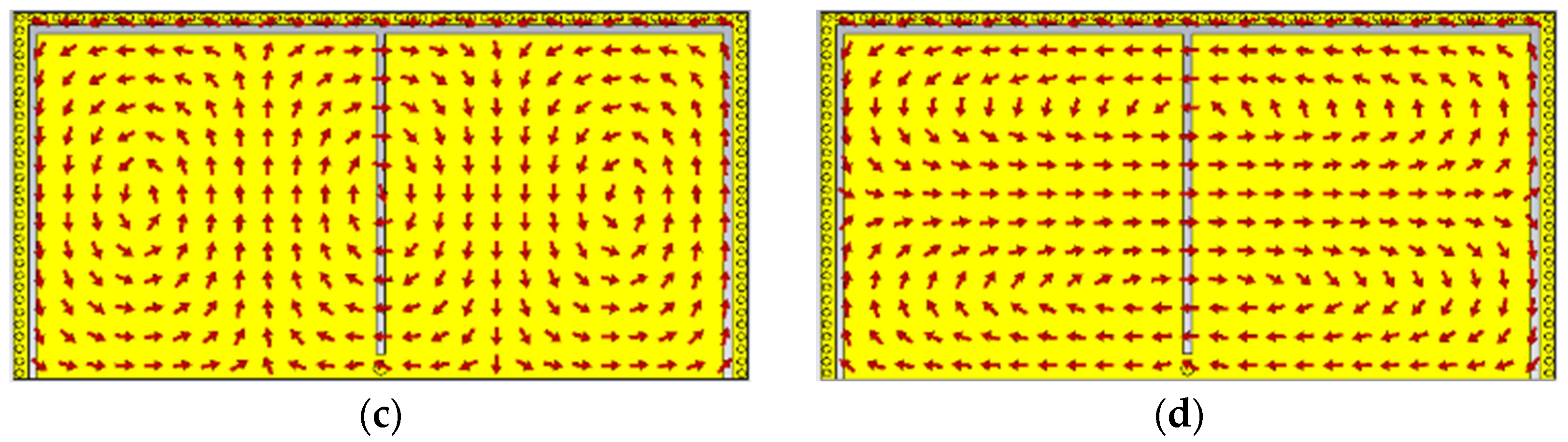
2.1. Configuration and Working Principles
2.2. Synthesis of a Dual-Mode Bandpass Filter
2.3. Analysis of Insertion Loss
2.4. Analogous Circuit Model of a Second-Order Bandpass Filter
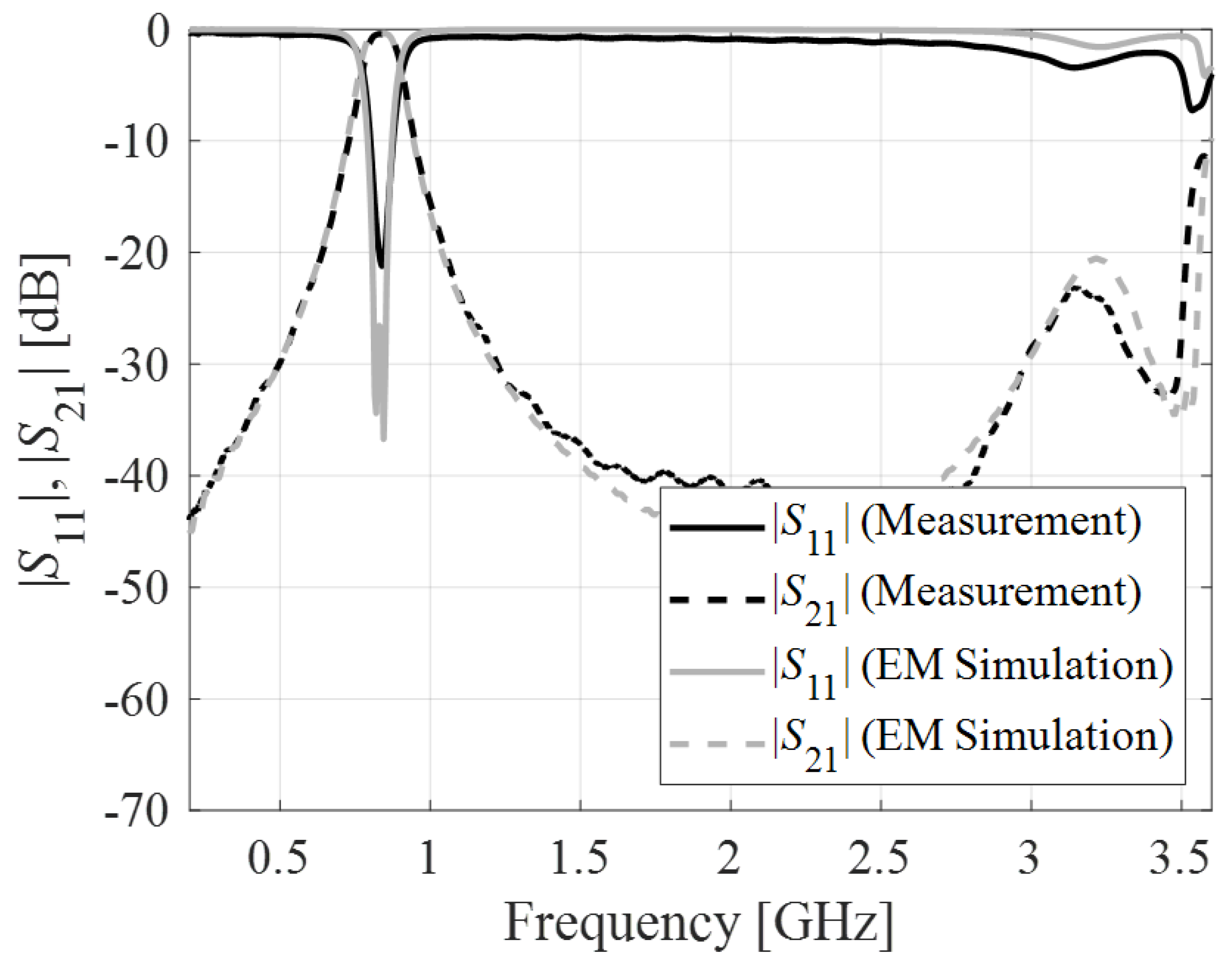
3. Fabrication, Measurement, and Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Deslandes, D.; Wu, K. Single-substrate integration technique of planar circuits and waveguide filters. IEEE Trans. Microw. Theory Tech. 2003, 51, 593–596. [Google Scholar] [CrossRef]
- Bozzi, M.; Georgiadis, A.; Wu, K. Review of substrate-integrated waveguide circuits and antennas. IET Microw. Antennas Propag. 2011, 5, 909–920. [Google Scholar] [CrossRef]
- Hong, J.S.; Lancaster, M.J. Microstrip Filters for RF/Microwave Applications; Wiley: New York, NY, USA, 2001. [Google Scholar]
- Sánchez-Soriano, M.A.; Sirci, S.; Martínez, J.D.; Boria, V.E. Compact dual-mode substrate integrated waveguide coaxial cavity for bandpass filter design. IEEE Microw. Wirel. Compon. Lett. 2016, 26, 386–388. [Google Scholar] [CrossRef] [Green Version]
- Cheng, F.; Lin, X.Q.; Lancaster, M.J.; Song, K.; Fan, Y. A dual-mode substrate integrated waveguide filter with controllable transmission zeros. IEEE Microw. Wirel. Compon. Lett. 2015, 25, 576–578. [Google Scholar] [CrossRef]
- Xie, H.W.; Zhou, K.; Zhou, C.X.; Wu, W. Wide-stopband SIW filters using modified multi-spurious modes suppression technique. IEEE Trans. Circuits Syst. II Exp. Briefs 2020, 67, 2883–2887. [Google Scholar] [CrossRef]
- Moscato, S.; Tomassoni, C.; Bozzi, M.; Perregrini, L. Quarter-mode cavity filters in substrate integrated waveguide technology. IEEE Trans. Microw. Theory Tech. 2016, 64, 2538–2547. [Google Scholar] [CrossRef]
- Lee, B.; Nam, S.; Jeong, S.; Lee, J. Post-loaded substrate-integrated waveguide bandpass filter with wide upper stopband and reduced electric field intensity. IEEE Microw. Wirel. Compon. Lett. 2020, 30, 371–374. [Google Scholar] [CrossRef]
- Liu, Z.; Xiao, G.; Zhu, L. Triple-mode bandpass filters on CSRR-loaded substrate integrated waveguide cavities. IEEE Trans. Compon. Packag. Manuf. Tech. 2016, 6, 1099–1105. [Google Scholar] [CrossRef]
- Chu, P.; Hong, W.; Tuo, M.; Zheng, K.L.; Yang, W.W.; Xu, F.; Wu, K. In-line ports dual-mode substrate integrated waveguide filter with flexible responses. IEEE Microw. Wirel. Compon. Lett. 2018, 28, 882–884. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, D.; Zhang, Y.; Qing, L.; Zhou, D. Novel dual-mode bandpass filters based on SIW resonators under different boundaries. IEEE Microw. Wirel. Compon. Lett. 2017, 27, 28–30. [Google Scholar] [CrossRef]
- Kim, P.; Jeong, Y. Compact and wide stopband substrate integrated waveguide bandpass filter using mixed quarter- and one-eighth modes cavities. IEEE Microw. Wirel. Compon. Lett. 2020, 30, 16–19. [Google Scholar] [CrossRef]
- Chu, P.; Hong, W.; Tuo, M.; Zheng, K.L.; Yang, W.W.; Xu, F.; Wu, K. Dual-mode substrate integrated waveguide filter with flexible response. IEEE Trans. Microw. Theory Tech. 2017, 65, 824–830. [Google Scholar] [CrossRef]
- Liu, Q.; Zhou, D.; Wang, S.; Zhang, Y. Highly-selective pseudo-elliptic filters based on dual-mode substrate integrated waveguide resonators. Electron. Lett. 2016, 52, 1233–1235. [Google Scholar] [CrossRef]
- Zhu, F.; Luo, G.Q.; Liao, Z.; Dai, X.W.; Wu, K. Compact dual-mode bandpass filters based on half-mode substrate-integrated waveguide cavities. IEEE Microw. Wirel. Compon. Lett. 2021, 31, 441–444. [Google Scholar] [CrossRef]
- Liu, Q.; Zhang, D.; Tang, M.; Deng, H.; Zhou, D. A class of box-like bandpass filters with wide stopband based on new dual-mode rectangular SIW cavities. IEEE Trans. Microw. Theory Tech. 2021, 69, 101–110. [Google Scholar] [CrossRef]
- Zhu, F.; Luo, G.Q.; You, B.; Zhang, X.H.; Wu, K. Planar dual-mode bandpass filters using perturbed substrate-integrated waveguide rectangular cavities. IEEE Trans. Microw. Theory Tech. 2021, 69, 3048–3057. [Google Scholar] [CrossRef]
- Zhu, Y.; Dong, Y. A novel compact wide-stopband filter with hybrid structure by combining SIW and microstrip technologies. IEEE Microw. Wirel. Compon. Lett. 2021, 31, 841–844. [Google Scholar] [CrossRef]
- Weng, M.-H.; Tsai, C.-Y.; Chen, D.-L.; Chung, Y.-C.; Yang, R.-Y. A Bandpass Filter Using Half Mode SIW Structure with Step Impedance Resonator. Electronics 2021, 10, 51. [Google Scholar] [CrossRef]
- Huang, L.; Yuan, N. A Compact Wideband SIW Bandpass Filter with Wide Stopband and High Selectivity. Electronics 2019, 8, 440. [Google Scholar] [CrossRef] [Green Version]
- Xie, H.Y.; Wu, B.; Xia, L.; Chen, J.Z.; Su, T. Miniaturized half-mode fan-shaped SIW filter with extensible order and wide stopband. IEEE Microw. Wirel. Compon. Lett. 2020, 30, 749–752. [Google Scholar] [CrossRef]
- Liu, D.; Dong, Y. Compact Low-Loss Half-Mode Substrate Integrated Waveguide Filter with Controllable Transmission Zeros. IEEE Trans. Circuits Syst. II Exp. Briefs 2022, 69, 4248–4252. [Google Scholar] [CrossRef]
- Chen, K.F.; Yang, X.; Zhou, L.; Mao, J.F. Miniaturized half-mode T-septum SIW bandpass filter with an ultrawide stopband. IEEE Microw. Wirel. Compon. Lett. 2021, 31, 853–856. [Google Scholar] [CrossRef]
- Khan, A.A.; Mandal, M.K. Narrowband substrate integrated waveguide bandpass filter with high selectivity. IEEE Microw. Wirel. Compon. Lett. 2018, 28, 416–418. [Google Scholar] [CrossRef]
- Praveena, N.; Gunavathi, N. High Selectivity SIW Cavity Bandpass Filter Loaded CSRR with Perturbing Vias for Sub-6 GHz Applications. Prog. Electromagn. Res. Lett. 2023, 109, 103–110. [Google Scholar] [CrossRef]
- Howe, G.W.O. Coupling and coupling coefficients. Wirel. Eng. 1932, 9, 485. [Google Scholar]
- Qin, P.Y.; Liang, C.H.; Wu, B.; Su, T. Novel dual-mode bandpass filter with transmission zeros using substrate integrated waveguide cavity. J. Electromag. Waves Appl. 2008, 22, 723–730. [Google Scholar] [CrossRef]
- You, B.; Chen, L.; Luo, G. The novel reconfigurable double-layer half-mode SIW filter with tunable DMS structure. J. Electromag. Waves Appl. 2018, 32, 1816–1823. [Google Scholar] [CrossRef]
- Tharani, D.; Barik, R.K.; Cheng, Q.S.; Selvajyothi, K.; Karthikeyan, S.S. Compact dual-band SIW filters loaded with double ring D-shaped resonators for sub-6 GHz applications. J. Electromag. Waves Appl. 2021, 35, 923–936. [Google Scholar] [CrossRef]
- Li, R.; Du, G. A SIW filter with asymmetric frequency response by non-resonating node. J. Electromag. Waves Appl. 2013, 27, 1550–1556. [Google Scholar] [CrossRef]
- Kurudere, S.; Ertürk, V.B. SIW-based interdigital bandpass filter with harmonic suppression. Microw. Opt. Technol. Lett. 2015, 57, 66–69. [Google Scholar] [CrossRef]
- Li, D.; Yu, Y.; Tang, M.C.; Shi, T. Design of compact wideband bandpass filter with broad stopband using hybrid HMSIW and open-circuit tri-section stepped impedance resonators. Microw. Opt. Technol. Lett. 2018, 60, 2998–3003. [Google Scholar] [CrossRef]
- Pelluri, S.; MV, K. A narrow band and high selectivity half-mode substrate integrated waveguide bandpass filter with interdigital slots. Microw. Opt. Technol. Lett. 2021, 63, 1180–1186. [Google Scholar] [CrossRef]
- Tharani, D.; Barik, R.K.; Cheng, Q.S.; Selvajyothi, K.; Karthikeyan, S.S. Miniaturized SIW filter using D-shaped resonators with wide out-of-band rejection for 5G applications. J. Electromag. Waves Appl. 2020, 34, 2397–2409. [Google Scholar]
- Che, W.; Li, C.; Deng, K.; Yang, L. A novel bandpass filter based on complementary split rings resonators and substrate integrated waveguide. Microw. Opt. Technol. Lett. 2008, 50, 699–701. [Google Scholar] [CrossRef]
- Liu, C.; An, X. A SIW-DGS wideband bandpass filter with a sharp roll-off at upper stopband. Microw. Opt. Technol. Lett. 2017, 59, 789–792. [Google Scholar] [CrossRef]
- Zhao, Q.; Chen, Z.; Huang, J.; Li, G.; Zhang, Z.; Dang, W. Compact dual-band bandpass filter based on composite right/left-handed substrate integrated waveguide loaded by complementary split-ring resonators defected ground structure. J. Electromag. Waves Appl. 2014, 28, 1807–1814. [Google Scholar] [CrossRef]
- Xu, Z.Q.; Shi, Y.; Wang, P.; Liao, J.X.; Wei, X.B. Substrate integrated waveguide (SIW) filter with hexagonal resonator. J. Electromag. Waves Appl. 2012, 26, 1521–1527. [Google Scholar] [CrossRef]
- Alhzzoury, A.I.; Raveu, N.; Prigent, G.; Pigaglio, O.; Baudrand, H.; Al-Abdullah, K. Substrate integrated waveguide filter design with wave concept iterative procedure. Microw. Opt. Technol. Lett. 2011, 53, 2939–2942. [Google Scholar] [CrossRef]
- Rhbanou, A.; Bri, S.; Sabbane, M. Design of X-band substrate integrated waveguide bandpass filter with dual high rejection. Microw. Opt. Technol. Lett. 2015, 57, 1744–1752. [Google Scholar] [CrossRef]
- Chu, H.; Shi, X.Q. Compact ultra-wideband bandpass filter based on SIW and DGS technology with a notch band. J. Electromag. Waves Appl. 2011, 25, 589–596. [Google Scholar] [CrossRef]
- Mahant, K.; Mewada, H. A novel substrate integrated waveguide (SIW) based highly selective filter for radar applications. J. Electromag. Waves Appl. 2019, 33, 1718–1725. [Google Scholar] [CrossRef]
- Mahan, A.; Pourjafari, S.M.; Tayarani, M.; Mahani, M.S. A novel compact dual-mode SIW filter with wide rejection band and selective response. Microw. Opt. Technol. Lett. 2019, 61, 573–577. [Google Scholar] [CrossRef]
- Song, S.; Guo, Y.; Wang, Y. Compact quasi-elliptic SIR-SIW filter with multiple transmission zeros. Microw. Opt. Technol. Lett. 2021, 63, 2348–2354. [Google Scholar] [CrossRef]
- Hu, G.; Liu, C.; Yan, L.; Huang, K.; Menzel, W. Novel dual mode substrate integrated waveguide band-pass filters. J. Electromag. Waves Appl. 2010, 24, 1661–1672. [Google Scholar] [CrossRef]
- Li, R.; Du, G. Substrate integrated waveguide filter with high-design flexibility. J. Electromag. Waves Appl. 2013, 27, 1751–1758. [Google Scholar] [CrossRef]
- Jiang, W.; Shen, W.; Zhou, L.; Yin, W.Y. Miniaturized and high-selectivity substrate integrated waveguide (SIW) bandpass filter loaded by complementary split-ring resonators (CSRRs). J. Electromag. Waves Appl. 2012, 26, 1448–1459. [Google Scholar] [CrossRef]


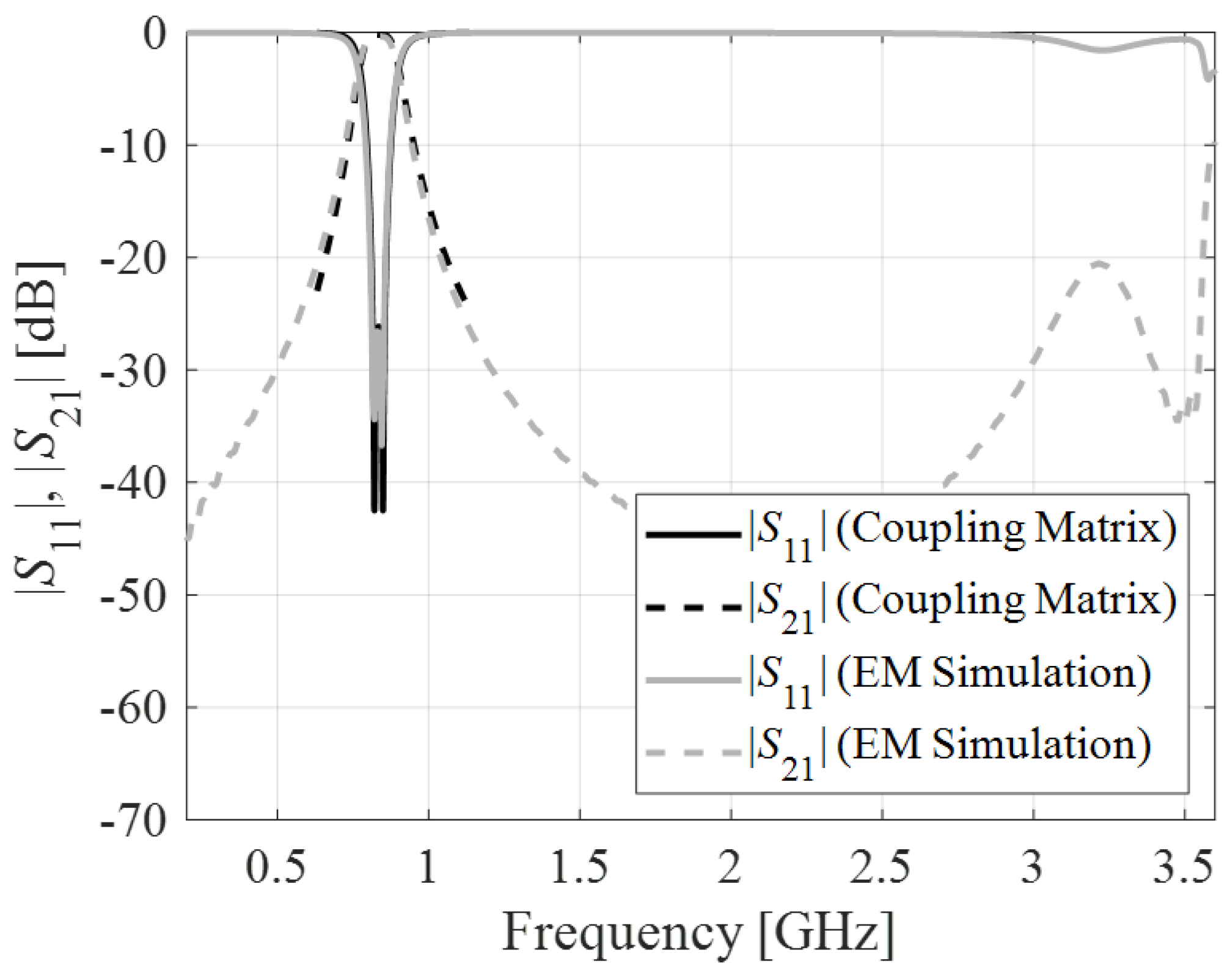
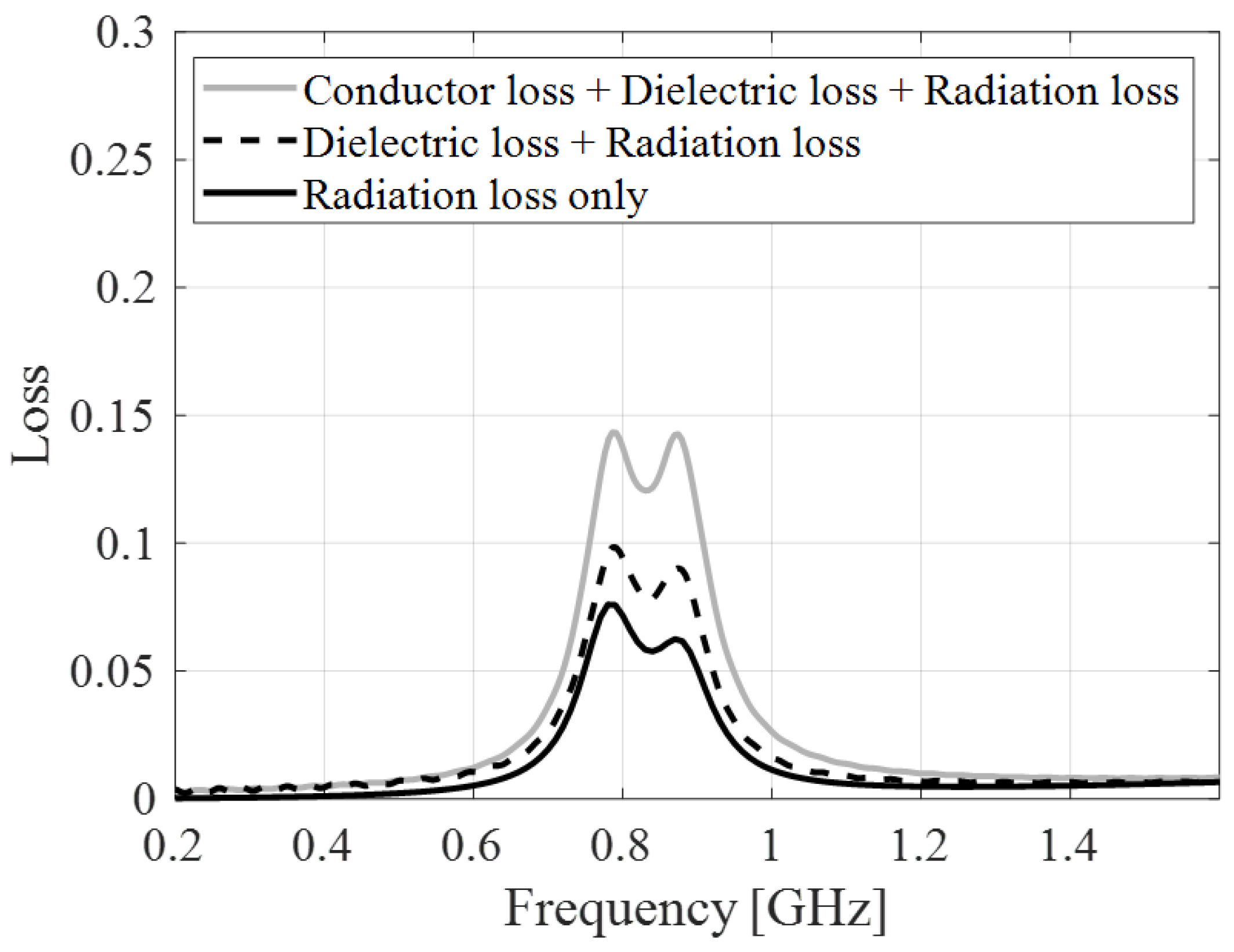
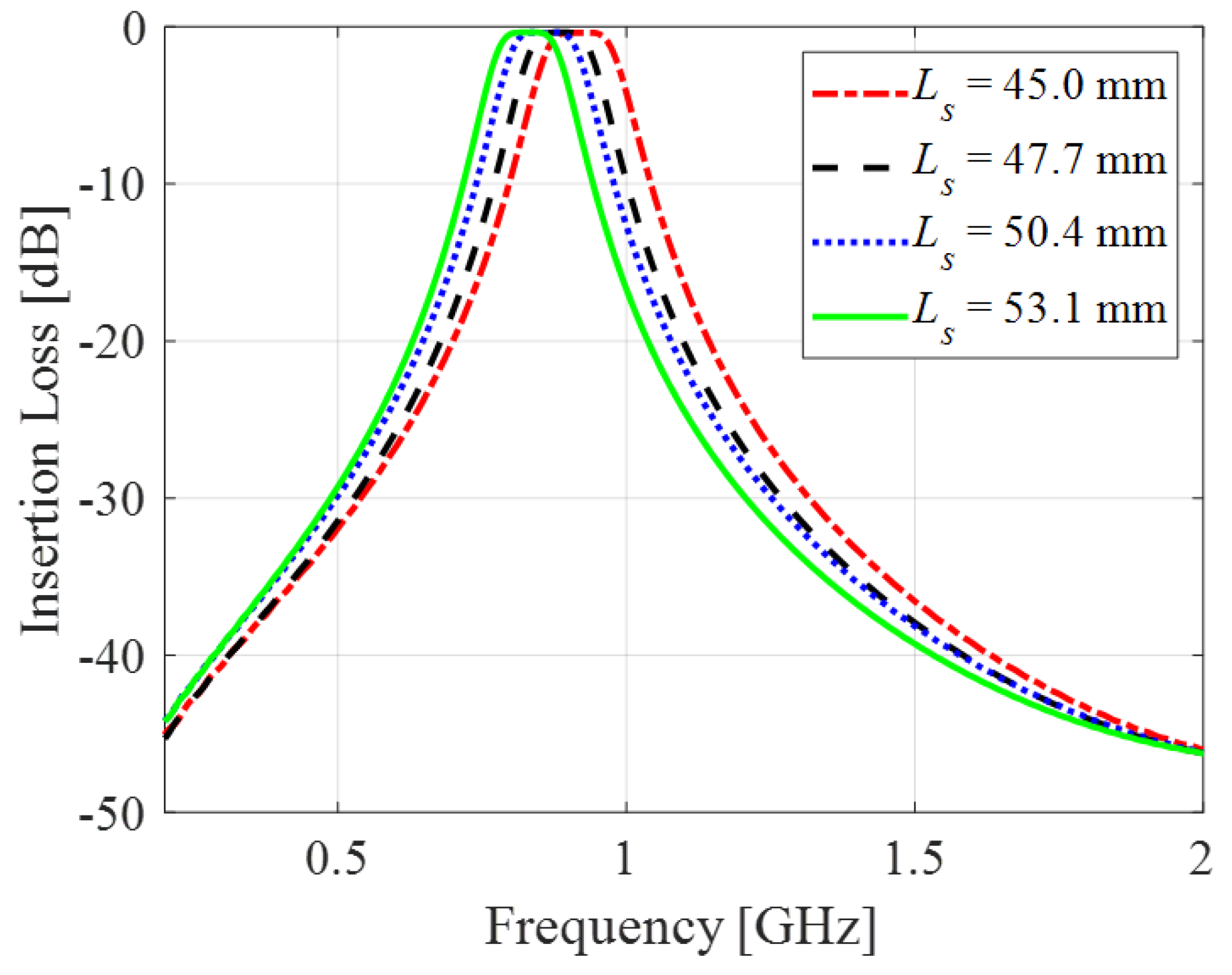
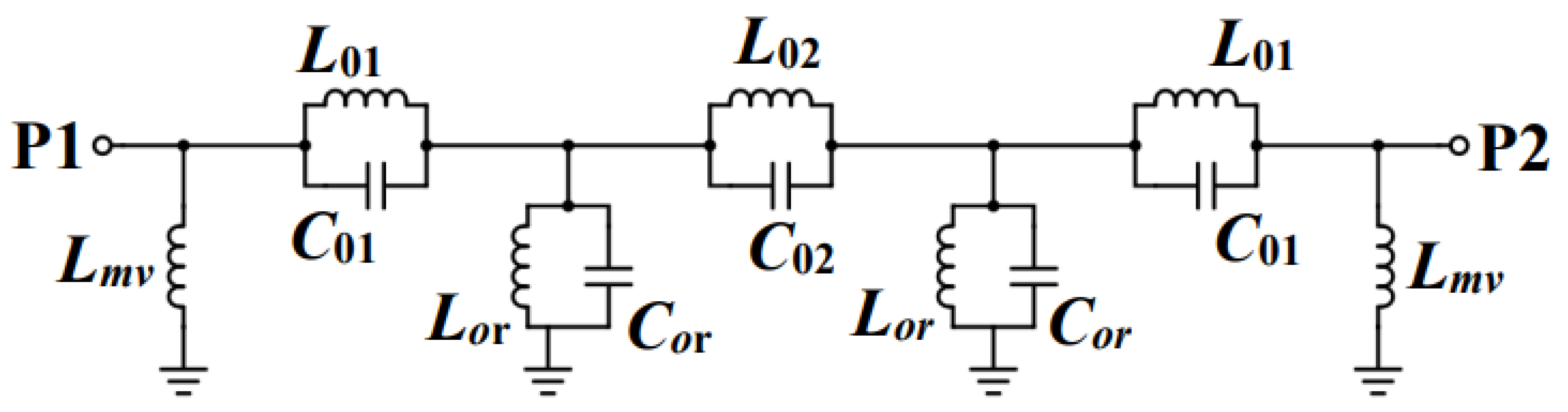


| Ls (mm) | f0 (GHz) | IL (dB) |
|---|---|---|
| 53.1 | 0.839 | 0.362 |
| 50.4 | 0.86 | 0.367 |
| 47.7 | 0.891 | 0.364 |
| 45 | 0.938 | 0.37 |
| Ref | fc (GHz) | FBW (%) | IL (dB) | N | Upper Stopband | Size (λg2) | SF (%) |
|---|---|---|---|---|---|---|---|
| [4] | 8 | 20 | 0.7 | 2 | 14 [email protected] f0 | 0.176 | 32.9 $ |
| [5] | 8 | 3.51 | 2.15 | 3 | 20 [email protected] f0 | 0.804 | 28.53 |
| [6] | 7.55 | 1.84 | 3.22 | 3 | 20 [email protected] f0 | 1.61 | 22.2 |
| [7] | 4 | 16 | 1.02 | 3 | 15 [email protected] f0 | 0.0625 | 40.9 |
| [8] | 5 | 6.6 | 0.9 | 3 | 30 [email protected] f0 | NR | 30.2 |
| [9] | 10.8 | 16.5 | 1.5 | 3 | 20 [email protected] f0 | 1.09 | 62.2 |
| [12] | 8 | 11 | 0.9 | 3 | 23 [email protected] f0 | 0.147 | 25.3 |
| [14] | 5.22 | - | 1.62 | 4 | 20 [email protected] f0 | - | 51.47 |
| [15] | 10 | 5.3 | 2.4 | 4 | 30 [email protected] f0 | 1.75 | 36.6 |
| [16] | 10.01 | 3.98 | 1.52 | 4 | 20 [email protected] f0 | 1.978 | 38.3 |
| [17] | 10 | 3.3 | 1.55 | 4 | 30 [email protected] f0 | 2 | 49.27 |
| [18] | 10.11 | 11.7 | 1.22 | 4 | 20 [email protected] f0 | 0.5 | 41.9 |
| [19] | 3.25 | 4.62 | 2.5 | 2 | NA | 0.051 | 19.85 |
| [21] | 1 | 12 | 0.83 | 2 | 20 [email protected] f0 | 0.038 | 30.6 $ |
| [22] | 4.51 | 26 | 0.57 | 4 | 20 [email protected] f0 | 0.159 | 43.7 |
| [23] | 10.6 | 17.77 | 2.61 | 3 | 20 [email protected] f0 | 0.016 | 26.45 $ |
| This work | 0.835 | 15.8 | 0.41 | 2 | 20 [email protected] f0 | 0.028 | 32.51 $ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barik, R.K.; Koziel, S.; Pietrenko-Dabrowska, A. Broad Stopband, Low-Loss, and Ultra-Compact Dual-Mode Bandpass Filter Based on HMSIRC. Electronics 2023, 12, 2831. https://doi.org/10.3390/electronics12132831
Barik RK, Koziel S, Pietrenko-Dabrowska A. Broad Stopband, Low-Loss, and Ultra-Compact Dual-Mode Bandpass Filter Based on HMSIRC. Electronics. 2023; 12(13):2831. https://doi.org/10.3390/electronics12132831
Chicago/Turabian StyleBarik, Rusan Kumar, Slawomir Koziel, and Anna Pietrenko-Dabrowska. 2023. "Broad Stopband, Low-Loss, and Ultra-Compact Dual-Mode Bandpass Filter Based on HMSIRC" Electronics 12, no. 13: 2831. https://doi.org/10.3390/electronics12132831








