Parkinson’s Disease Detection Using Hybrid LSTM-GRU Deep Learning Model
Abstract
:1. Introduction
- To balance the highly imbalanced Parkinson’s disease dataset, this study adopted undersampling and oversampling techniques to accurately detect the disease in its early stages. Moreover, with these techniques, the problem of model overfitting is solved and performance increases.
- A hybrid LSTM-GRU model is proposed that automatically detects the PD in time. In addition, the performance of single models and hybrid models is also investigated and compared to evaluate the proposed model results.
- The true positive rate (TPR) and the false positive rate (FPR) are calculated and displayed against one another on the ROC curve for different threshold values to assess the performance of hybrid models.
- The comparison of different sampling techniques with hybrid models and other state-of-the-art studies is explored.
2. Literature Review
State-of-the-Art DL Models
| Methods | Sampling | Advantages | Drawbacks |
|---|---|---|---|
| CNN+LSTM [20] | - | Early detection of Parkinson’s disease was essential for its prevention. DL techniques have been used to detect PD in limited time. | There is no particular cure for PD, but the impact can be reduced through early detection and the right medication. |
| DNN [24] | - | A deep neural network with 42 preprocessed voice recordings was used for the prediction of Parkinson’s disease. | Their approach attained only 81% accuracy and does not used any augmentation technique. |
| BiLSTM [25] | - | They utilized dynamic features of speech for Parkinson’s disease detection using BiLSTM model. | The results achieved are not very accurate. |
| CNN [26] | - | CNN with a 13-layer architecture was developed by the authors to accurately predict the disease in 40 patients. Moreover, their approach was implemented for clinical practice. | The results were not accurate, and the 13-layer design was very expensive. |
| RNN [21] | SMOTE | The authors employed three DL methods for the prediction of Parkinson’s disease with extensive preprocessing techniques. An oversampling SMOTE technique was deployed to enhance the model results. | They do not describe whether they used oversampling on the whole dataset or only for training. |
| CNN-LSTM [31] | - | They used CNN for feature extraction and LSTM for prediction. The main objective of this study is to detect Parkinson’s disease. | Authors first used CNN model to extract relevant features from the voices and then employed LSTM for prediction that leads to high computation cost. |
| CNN [32] | Oversampling | The authors utilised explainable DL architecture for disease detection in PD datasets. In order to improve the overall detection results, they also increased the number of data samples by utilising oversampling methods. | Few features are selected from the entire dataset, resulting in an overfitting issue. |
| ResNet [27] | Augmentation | This study used a modified version of the ResNet model to predict disease using the PD dataset. The authors used augmentation to balance the class samples because the dataset only comprises small samples of audio recordings. | This study utilized augmentation on test set to increase the results but score is not good for the accurate detection of Parkinson’s disease. |
| Proposed Method | Random oversampling and SMOTE | The authors employed various Dl models with extensive preprocessing, scaling and sampling techniques that enhanced the overall results. The proposed LSTM+GRU model attained superior results compared to previous models. It detected Parkinson’s disease in its early stage with the help of hybrid Dl models. | This study has a limited dataset, which is a drawback and leaves space for others to do more research. |
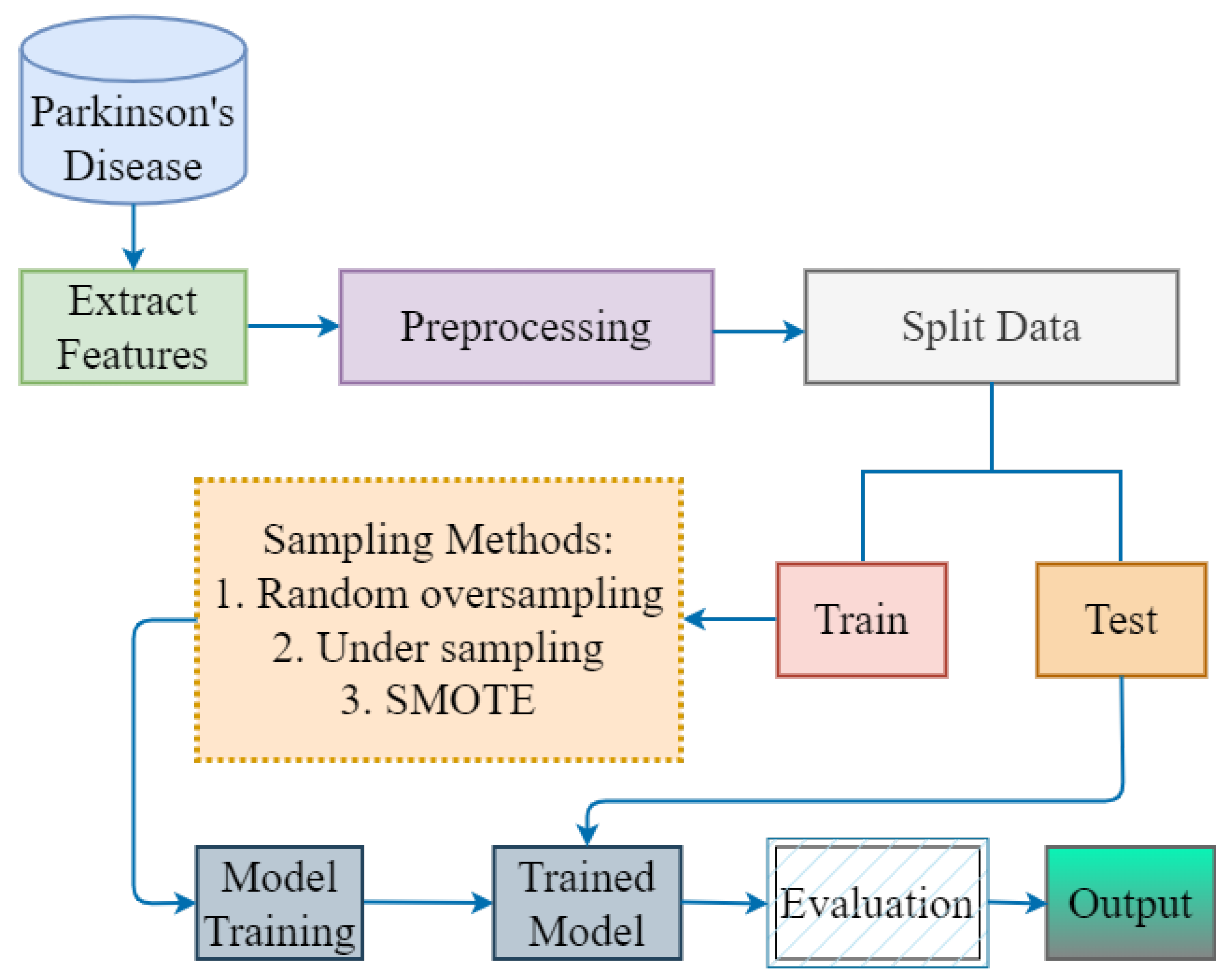
3. Proposed Methodology
3.1. Parkinson’s Disease Dataset
3.2. Extract Features and Sampling Methods
| Algorithm 1 Proposed Methodology for Parkinson’s disease detection |
| Input: Parkinson’s disease Dataset |
| Output: PD or Healthy |
| Start: |
|
| End |
3.3. Data Splitting
3.4. Proposed Hybrid Model
3.5. Performance Metrics
- True Positive (TP): positive cases, correctly identified.
- True Negative (TN): negative cases, correctly identified.
- False Negative (FN): cases in which a negative result is predicted incorrectly.
- False Positive (FP):cases in which a positive result is predicted incorrectly.
4. Results and Discussion
4.1. Performance of DL Models Using Different Sampling Techniques
4.2. Performance of Hybrid Models Using Different Sampling Techniques on % (70:30) Dataset
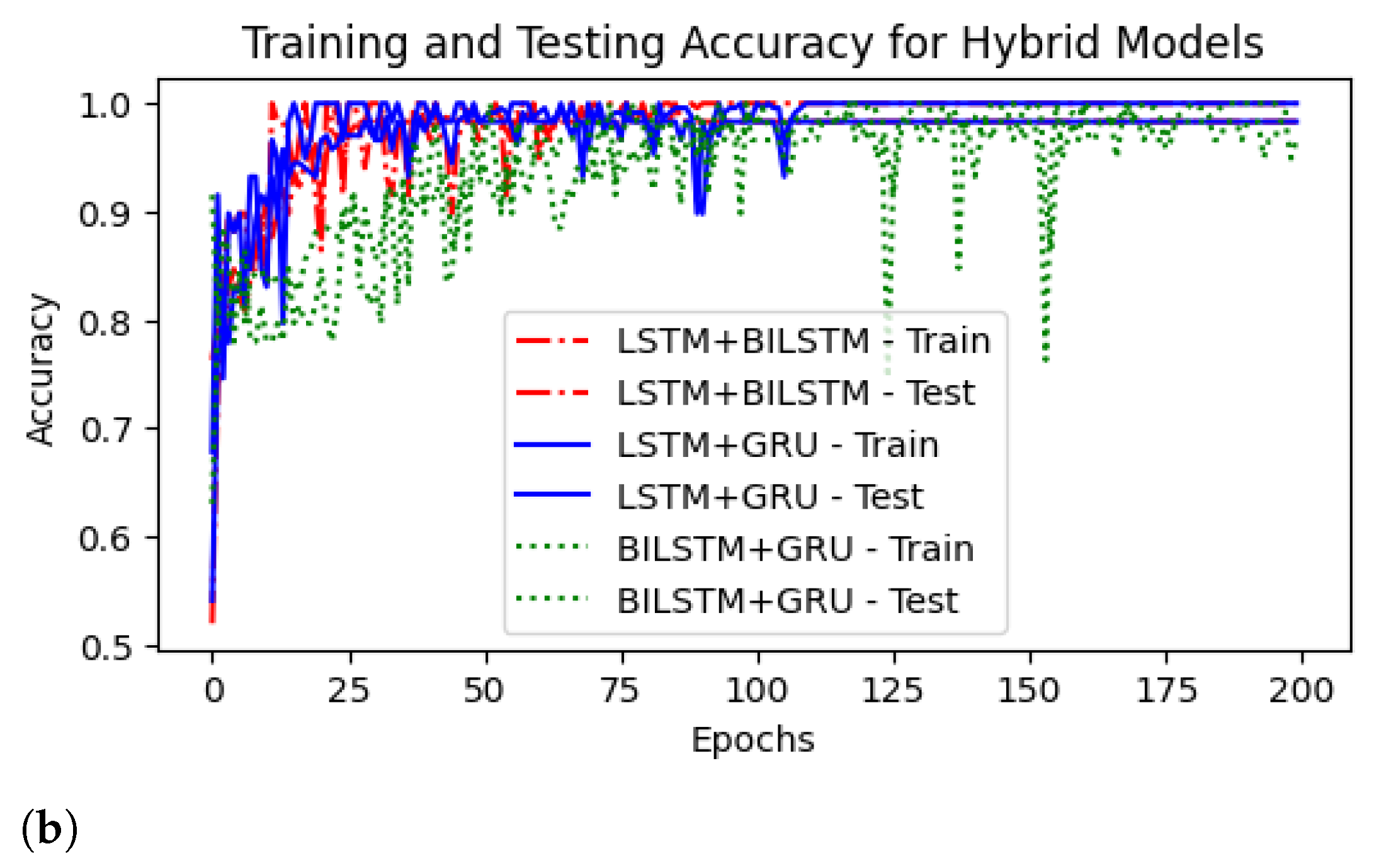
4.3. ROC Curves
4.4. Comparison Results of Hybrid Models Using Different Sampling Techniques
4.5. Comparative Results of Proposed Hyrbrid Model with the State-of-the-Art Studies
4.6. Discussion and Limitations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Poewe, W.; Seppi, K.; Tanner, C.; Halliday, G.; Brundin, P.; Volkmann, J.; Schrag, A.; Lang, A. Parkinson disease. Nat. Rev. Dis. Prim. 2017, 3, 17013. [Google Scholar] [CrossRef] [PubMed]
- Hopes, L.; Grolez, G.; Moreau, C.; Lopes, R.; Ryckewaert, G.; Carrière, N.; Auger, F.; Laloux, C.; Petrault, M.; Devedjian, J.C.; et al. Magnetic resonance imaging features of the nigrostriatal system: Biomarkers of Parkinson’s disease stages? PLoS ONE 2016, 11, e0147947. [Google Scholar] [CrossRef] [Green Version]
- Chaudhuri, K.R.; Schapira, A.H. Non-motor symptoms of Parkinson’s disease: Dopaminergic pathophysiology and treatment. Lancet Neurol. 2009, 8, 464–474. [Google Scholar] [CrossRef]
- Cheng, H.C.; Ulane, C.M.; Burke, R.E. Clinical progression in Parkinson disease and the neurobiology of axons. Ann. Neurol. 2010, 67, 715–725. [Google Scholar] [CrossRef] [PubMed]
- Pringsheim, T.; Jette, N.; Frolkis, A.; Steeves, T.D. The prevalence of Parkinson’s disease: A systematic review and meta-analysis. Mov. Disord. 2014, 29, 1583–1590. [Google Scholar] [CrossRef]
- Shivangi; Johri, A.; Tripathi, A. Parkinson disease detection using deep neural networks. In Proceedings of the 2019 Twelfth International Conference on Contemporary Computing (IC3), Noida, India, 8–10 August 2019; pp. 1–4. [Google Scholar]
- Singh, N.; Pillay, V.; Choonara, Y.E. Advances in the treatment of Parkinson’s disease. Prog. Neurobiol. 2007, 81, 29–44. [Google Scholar] [CrossRef] [PubMed]
- Sakar, C.O.; Kursun, O. Telediagnosis of Parkinson’s disease using measurements of dysphonia. J. Med. Syst. 2010, 34, 591–599. [Google Scholar] [CrossRef]
- Ali, N.A.; Abbassi, A.E.; Cherradi, B. The performances of iterative type-2 fuzzy C-mean on GPU for image segmentation. J. Supercomput. 2022, 78, 1583–1601. [Google Scholar] [CrossRef]
- Ali, N.A.; Cherradi, B.; El Abbassi, A.; Bouattane, O.; Youssfi, M. New parallel hybrid implementation of bias correction fuzzy C-means algorithm. In Proceedings of the 2017 International Conference on Advanced Technologies for Signal and Image Processing (ATSIP), Fez, Morocco, 22–24 May 2017; pp. 1–6. [Google Scholar]
- Aitali, N.; Cherradi, B.; El Abbassi, A.; Bouattane, O.; Youssfi, M. GPU based implementation of spatial fuzzy c-means algorithm for image segmentation. In Proceedings of the 2016 4th IEEE International Colloquium on Information Science and Technology (CiSt), Tangier, Morocco, 24–26 October 2016; pp. 460–464. [Google Scholar]
- Ait Ali, N.; Cherradi, B.; El Abbassi, A.; Bouattane, O.; Youssfi, M. GPU fuzzy c-means algorithm implementations: Performance analysis on medical image segmentation. Multimed. Tools Appl. 2018, 77, 21221–21243. [Google Scholar] [CrossRef]
- Aitali, N.; Cherradi, B.; Bouattane, O.; Youssfi, M.; Raihani, A. New fine-grained clustering algorithm on GPU architecture for bias field correction and MRI image segmentation. In Proceedings of the 2015 27th International Conference on Microelectronics (ICM), Casablanca, Morocco, 20–23 December 2015; pp. 118–121. [Google Scholar]
- Dolz, J.; Desrosiers, C.; Ayed, I.B. 3D fully convolutional networks for subcortical segmentation in MRI: A large-scale study. NeuroImage 2018, 170, 456–470. [Google Scholar] [CrossRef] [Green Version]
- Ghafoorian, M.; Karssemeijer, N.; Heskes, T.; van Uden, I.W.; Sanchez, C.I.; Litjens, G.; de Leeuw, F.E.; van Ginneken, B.; Marchiori, E.; Platel, B. Location sensitive deep convolutional neural networks for segmentation of white matter hyperintensities. Sci. Rep. 2017, 7, 5110. [Google Scholar] [CrossRef]
- Wang, S.H.; Phillips, P.; Sui, Y.; Liu, B.; Yang, M.; Cheng, H. Classification of Alzheimer’s disease based on eight-layer convolutional neural network with leaky rectified linear unit and max pooling. J. Med. Syst. 2018, 42, 85. [Google Scholar] [CrossRef]
- Younis Thanoun, M.; Yaseen, M.T. A comparative study of Parkinson disease diagnosis in machine learning. In Proceedings of the 2020 the 4th International Conference on Advances in Artificial Intelligence, London, UK, 9–11 October 2020; pp. 23–28. [Google Scholar]
- Elhassan, T.; Aljurf, M. Classification of imbalance data using tomek link (t-link) combined with random under-sampling (rus) as a data reduction method. Glob. J. Technol. Optim. S 2016, 1, 2016. [Google Scholar]
- Fan, S.; Sun, Y. Early Detection of Parkinson’s Disease using Machine Learning and Convolutional Neural Networks from Drawing Movements. Comput. Sci. Inf. Technol. 2022, 12, 291–301. [Google Scholar]
- Aşuroğlu, T.; Oğul, H. A deep learning approach for parkinson’s disease severity assessment. Health Technol. 2022, 12, 943–953. [Google Scholar] [CrossRef]
- Chintalapudi, N.; Battineni, G.; Hossain, M.A.; Amenta, F. Cascaded Deep Learning Frameworks in Contribution to the Detection of Parkinson’s Disease. Bioengineering 2022, 9, 116. [Google Scholar] [CrossRef] [PubMed]
- Polat, K. A hybrid approach to Parkinson disease classification using speech signal: The combination of smote and random forests. In Proceedings of the 2019 Scientific Meeting on Electrical-Electronics & Biomedical Engineering and Computer Science (EBBT), Istanbul, Turkey, 24–26 April 2019; pp. 1–3. [Google Scholar]
- Caliskan, A.; Badem, H.; Basturk, A.; Yuksel, M. Diagnosis of the parkinson disease by using deep neural network classifier. IU-J. Electr. Electron. Eng. 2017, 17, 3311–3318. [Google Scholar]
- Grover, S.; Bhartia, S.; Yadav, A.; Seeja, K. Predicting severity of Parkinson’s disease using deep learning. Procedia Comput. Sci. 2018, 132, 1788–1794. [Google Scholar] [CrossRef]
- Quan, C.; Ren, K.; Luo, Z. A deep learning based method for Parkinson’s disease detection using dynamic features of speech. IEEE Access 2021, 9, 10239–10252. [Google Scholar] [CrossRef]
- Oh, S.L.; Hagiwara, Y.; Raghavendra, U.; Yuvaraj, R.; Arunkumar, N.; Murugappan, M.; Acharya, U.R. A deep learning approach for Parkinson’s disease diagnosis from EEG signals. Neural Comput. Appl. 2020, 32, 10927–10933. [Google Scholar] [CrossRef]
- Wodzinski, M.; Skalski, A.; Hemmerling, D.; Orozco-Arroyave, J.R.; Nöth, E. Deep learning approach to Parkinson’s disease detection using voice recordings and convolutional neural network dedicated to image classification. In Proceedings of the 2019 41st Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Berlin, Germany, 23–27 July 2019; pp. 717–720. [Google Scholar]
- Little, M.; McSharry, P.; Hunter, E.; Spielman, J.; Ramig, L. Suitability of dysphonia measurements for telemonitoring of Parkinson’s disease. Nat. Preced. 2008. [Google Scholar] [CrossRef]
- Quan, C.; Ren, K.; Luo, Z.; Chen, Z.; Ling, Y. End-to-end deep learning approach for Parkinson’s disease detection from speech signals. Biocybern. Biomed. Eng. 2022, 42, 556–574. [Google Scholar] [CrossRef]
- Yasar, A.; Saritas, I.; Sahman, M.; Cinar, A. Classification of Parkinson disease data with artificial neural networks. IOP Conf. Ser. Mater. Sci. Eng. 2019, 675, 012031. [Google Scholar] [CrossRef]
- Li, K.; Ao, B.; Wu, X.; Wen, Q.; Ul Haq, E.; Yin, J. Parkinson’s disease detection and classification using EEG based on deep CNN-LSTM model. Biotechnol. Genet. Eng. Rev. 2023. [Google Scholar] [CrossRef] [PubMed]
- Ma, Y.W.; Chen, J.L.; Chen, Y.J.; Lai, Y.H. Explainable deep learning architecture for early diagnosis of Parkinson’s disease. Soft Comput. 2023, 27, 2729–2738. [Google Scholar] [CrossRef]
- Staudemeyer, R.C.; Morris, E.R. Understanding LSTM–a tutorial into long short-term memory recurrent neural networks. arXiv 2019, arXiv:1909.09586. [Google Scholar]
- Dey, R.; Salem, F.M. Gate-variants of gated recurrent unit (GRU) neural networks. In Proceedings of the 2017 IEEE 60th International Midwest Symposium on Circuits and Systems (MWSCAS), Boston, MA, USA, 6–9 August 2017; pp. 1597–1600. [Google Scholar]
- Shelke, M.S.; Deshmukh, P.R.; Shandilya, V.K. A review on imbalanced data handling using undersampling and oversampling technique. Int. J. Recent Trends Eng. Res. 2017, 3, 444–449. [Google Scholar]
- Fernández, A.; Garcia, S.; Herrera, F.; Chawla, N.V. SMOTE for learning from imbalanced data: Progress and challenges, marking the 15-year anniversary. J. Artif. Intell. Res. 2018, 61, 863–905. [Google Scholar] [CrossRef]
- Abunadi, I. Deep and hybrid learning of MRI diagnosis for early detection of the progression stages in Alzheimer’s disease. Connect. Sci. 2022, 34, 2395–2430. [Google Scholar] [CrossRef]
- Eltahir, M.M.; Abunadi, I.; Al-Wesabi, F.N.; Hilal, A.M.; Yousif, A.; Motwakel, A.; Al Duhayyim, M.; Hamza, M.A. Optimal Hybrid Feature Extraction with Deep Learning for COVID-19. Comput. Mater. Contin. 2022, 71, 6257–6273. [Google Scholar] [CrossRef]
- Abdullah, S.M.; Abbas, T.; Bashir, M.H.; Khaja, I.A.; Ahmad, M.; Soliman, N.F.; El-Shafai, W. Deep Transfer Learning Based Parkinson’s Disease Detection Using Optimized Feature Selection. IEEE Access 2023, 11, 3511–3524. [Google Scholar] [CrossRef]








| Name and Features | Description of Features |
|---|---|
| MDVP; Fo (Hz) | [Average Vocal Fundamental Frequency] |
| MDVP; Fhi (Hz | [Maximum Vocal Fundamental Frequency] |
| MDVP; Flo (Hz) | [Minimum Vocal Fundamental Frequency] |
| MDVP; Jitter (%) | [Several Measures of Variation in Fundamental Frequency, Kay pentax multi-dimensional voice program as (%)] |
| MDVP; Jitter (Abs) | [Kay pentax Multi-dimensional voice program Absolute in Microseconds] |
| MDVP; RAP | [Kay pentax Multi-dimensional voice program relative amplitude perturbation] |
| MDVP; PPQ | [Kay pentax Multi-dimensional voice program Five point period perturbation] |
| Jitter; DDP | [Difference of differences between Cycles and period] |
| MDVP; Shimmer, | [Kay pentax Multi-dimensional voice program shimmer local] |
| MDVP; Shimmer (dB) | [Kay pentax Multi-dimensional voice program shimmer in decibel’s] |
| Shimmer; APQ3 | [Kay pentax Multi-dimensional voice program amplitude perturbation quotient with three points] |
| MDVP; APQ | [Eleven point Kay pentax Multi-dimensional voice program amplitude perturbation quotient] |
| Shimmer; APQ5 | [Five point Kay pentax Multi-dimensional voice program amplitude perturbation quotient] |
| Shimmer; DDA | [Difference of differences between amplitude and period] |
| NHR, HNR | [Noise to harmonic ratio, Harmonic to noise ratio] |
| Status | [Healthy (0) and Parkinson’s disease (1)] |
| RPDE | [Re-currence period density Entropy] |
| DFA | [Detrended fluctuation analysis] |
| spread1, spread2, PPE | [Pitch period Entropy, the fundamental frequency can be quantified in three nonlinear ways]. |
| Model | Class | Accuracy Score | Precision Score | Recall Score | F1 Score |
|---|---|---|---|---|---|
| NN | PD | 0.87 | 0.80 | 0.57 | 0.67 |
| Healthy | 0.91 | 0.97 | 0.94 | ||
| LSTM | PD | 0.89 | 0.80 | 0.57 | 0.67 |
| Healthy | 0.91 | 0.97 | 0.94 | ||
| BILSTM | PD | 0.92 | 0.83 | 0.71 | 0.77 |
| Healthy | 0.94 | 0.97 | 0.92 | ||
| GRU | PD | 0.92 | 0.83 | 0.71 | 0.77 |
| Healthy | 0.94 | 0.97 | 0.95 |
| Model | Class | Accuracy Score | Precision Score | Recall Score | F1 Score |
|---|---|---|---|---|---|
| NN | PD | 0.98 | 0.97 | 1.00 | 0.98 |
| Healthy | 1.00 | 0.97 | 0.98 | ||
| LSTM | PD | 0.97 | 0.97 | 0.97 | 0.97 |
| Healthy | 0.96 | 0.96 | 0.96 | ||
| BILSTM | PD | 0.97 | 0.94 | 1.00 | 0.97 |
| Healthy | 1.00 | 0.93 | 0.96 | ||
| GRU | PD | 0.93 | 0.91 | 0.97 | 0.94 |
| Healthy | 0.96 | 0.89 | 0.92 |
| Model | Class | Accuracy Score | Precision Score | Recall Score | F1 Score |
|---|---|---|---|---|---|
| NN | PD | 0.98 | 1.00 | 0.97 | 0.98 |
| Healthy | 0.97 | 1.00 | 0.98 | ||
| LSTM | PD | 0.97 | 0.94 | 1.00 | 0.97 |
| Healthy | 1.00 | 0.93 | 0.96 | ||
| BILSTM | PD | 0.90 | 0.91 | 0.91 | 0.91 |
| Healthy | 0.89 | 0.89 | 0.89 | ||
| GRU | PD | 0.95 | 0.94 | 0.97 | 0.95 |
| Healthy | 0.96 | 0.93 | 0.94 |
| Original Dataset | Balanced Dataset (With Random Oversampling Technique) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Model | Class | Accuracy | Precision | Recall | F1 Score | Accuracy | Precision | Recall | F1 Score |
| LSTM+GRU | PD | 0.95 | 0.95 | 0.92 | 0.96 | 0.98 | 0.96 | 1.00 | 0.98 |
| Healthy | 0.94 | 0.91 | 0.95 | 1.00 | 0.95 | 0.97 | |||
| BILSTM+GRU | PD | 0.93 | 0.92 | 0.93 | 0.93 | 0.98 | 0.98 | 0.98 | 0.98 |
| Healthy | 0.93 | 0.92 | 0.92 | 0.98 | 0.98 | 0.98 | |||
| LSTM+BILSTM | PD | 0.91 | 0.91 | 0.92 | 0.91 | 0.94 | 0.93 | 0.95 | 0.94 |
| Healthy | 0.91 | 0.93 | 0.92 | 0.96 | 0.95 | 0.94 | |||
| Balanced Dataset (With Random Undersampling Technique) | Balanced Dataset (With SMOTE Oversampling Technique) | ||||||||
| LSTM+GRU | PD | 0.96 | 1.00 | 0.93 | 0.96 | 0.98 | 0.98 | 0.98 | 0.98 |
| Healthy | 0.94 | 1.00 | 0.97 | 0.98 | 0.98 | 0.98 | |||
| BILSTM+GRU | PD | 0.93 | 0.93 | 0.93 | 0.93 | 0.96 | 0.93 | 0.97 | 0.95 |
| Healthy | 0.93 | 0.93 | 0.93 | 0.98 | 0.94 | 0.96 | |||
| LSTM+BILSTM | PD | 0.93 | 0.93 | 0.93 | 0.93 | 0.94 | 0.90 | 0.97 | 0.94 |
| Healthy | 0.93 | 0.93 | 0.93 | 0.98 | 0.92 | 0.95 | |||
| Original Dataset | Balanced Dataset (With Random Oversampling Technique) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Model | Class | Accuracy | Precision | Recall | F1 Score | Accuracy | Precision | Recall | F1 Score |
| LSTM+GRU | PD | 0.95 | 1.00 | 0.71 | 0.83 | 1.00 | 1.00 | 1.00 | 1.00 |
| Healthy | 0.94 | 1.00 | 0.97 | 1.00 | 1.00 | 1.00 | |||
| BILSTM+GRU | PD | 0.92 | 0.83 | 0.71 | 0.77 | 1.00 | 1.00 | 1.00 | 1.00 |
| Healthy | 0.94 | 0.97 | 0.95 | 1.00 | 1.00 | 1.00 | |||
| LSTM+BILSTM | PD | 0.92 | 0.83 | 0.71 | 0.77 | 0.95 | 0.91 | 1.00 | 0.95 |
| Healthy | 0.94 | 0.97 | 0.95 | 1.00 | 0.90 | 0.95 | |||
| Balanced Dataset (With Random Undersampling Technique) | Balanced Dataset (With SMOTE Oversampling Technique) | ||||||||
| LSTM+GRU | PD | 0.95 | 0.92 | 1.00 | 0.96 | 0.98 | 1.00 | 0.97 | 0.98 |
| Healthy | 1.00 | 0.89 | 0.94 | 0.97 | 1.00 | 0.98 | |||
| BILSTM+GRU | PD | 0.95 | 0.92 | 1.00 | 0.96 | 0.98 | 1.00 | 0.97 | 0.98 |
| Healthy | 1.00 | 0.89 | 0.94 | 0.97 | 1.00 | 0.98 | |||
| LSTM+BILSTM | PD | 0.90 | 0.91 | 0.91 | 0.91 | 0.97 | 1.00 | 0.93 | 0.97 |
| Healthy | 0.89 | 0.89 | 0.89 | 0.94 | 1.00 | 0.97 | |||
| Original Dataset | Balanced Dataset (With Random Oversampling Technique) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Model | Class | Accuracy | Precision | Recall | F1 Score | Accuracy | Precision | Recall | F1 Score |
| LSTM+GRU | PD | 0.94 | 1.00 | 0.79 | 0.86 | 0.98 | 0.97 | 0.97 | 0.98 |
| Healthy | 0.91 | 0.97 | 0.93 | 0.96 | 1.00 | 0.96 | |||
| BILSTM+GRU | PD | 0.91 | 0.87 | 0.74 | 0.72 | 0.97 | 0.94 | 0.97 | 0.97 |
| Healthy | 0.90 | 0.95 | 0.92 | 0.97 | 0.93 | 0.97 | |||
| LSTM+BILSTM | PD | 0.90 | 0.83 | 0.75 | 0.88 | 0.95 | 0.96 | 0.97 | 0.95 |
| Healthy | 0.91 | 0.97 | 0.92 | 0.96 | 0.95 | 0.96 | |||
| Balanced Dataset (With Random Undersampling Technique) | Balanced Dataset (With SMOTE Oversampling Technique) | ||||||||
| LSTM+GRU | PD | 0.95 | 1.00 | 0.90 | 0.95 | 0.97 | 0.97 | 1.00 | 0.98 |
| Healthy | 0.91 | 1.00 | 0.95 | 1.00 | 0.96 | 0.98 | |||
| BILSTM+GRU | PD | 0.95 | 0.92 | 1.00 | 0.96 | 0.97 | 0.97 | 0.97 | 0.98 |
| Healthy | 1.00 | 0.89 | 0.94 | 0.96 | 0.95 | 0.96 | |||
| LSTM+BILSTM | PD | 0.91 | 0.91 | 0.91 | 0.91 | 0.96 | 0.96 | 0.97 | 0.96 |
| Healthy | 0.89 | 0.89 | 0.89 | 0.96 | 0.95 | 0.96 | |||
| Random Oversampling | SMOTE | ||
|---|---|---|---|
| Model | Time consumption | Model | Time consumption |
| LSTM | 110 s | LSTM | 120 s |
| GRU | 135 s | GRU | 150 s |
| BILSTM | 140 s | BILSTM | 130 s |
| LSTM+GRU | 150 s | LSTM+GRU | 170 s |
| BILSTM+GRU | 165 s | BILSTM+GRU | 185 s |
| LSTM+BILSTM | 211 s | LSTM+BILSTM | 203 s |
| Authors | Dataset | Model | Accuracy |
|---|---|---|---|
| Grover et al. [24] | 42 patients | DNN | 81% |
| Quan et al. [25] | 45 patients | RNN | 84% |
| Oh et al. [26] | 20 patients | CNN | 88% |
| Wodzinski et al. [27] | 100 patients | ResNet | 90% |
| Abdullah et al. [39] | - | CNN | 95% |
| Yasir et al. [30] | 80 patients | ANN | 95% |
| Caliskan et al. [23] | 31 patients | DNN | 94% |
| Yasir et al. | 80 patients | ANN | 95% |
| Our Study | 31 patients | Hybrid LSTM+GRU | 98% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rehman, A.; Saba, T.; Mujahid, M.; Alamri, F.S.; ElHakim, N. Parkinson’s Disease Detection Using Hybrid LSTM-GRU Deep Learning Model. Electronics 2023, 12, 2856. https://doi.org/10.3390/electronics12132856
Rehman A, Saba T, Mujahid M, Alamri FS, ElHakim N. Parkinson’s Disease Detection Using Hybrid LSTM-GRU Deep Learning Model. Electronics. 2023; 12(13):2856. https://doi.org/10.3390/electronics12132856
Chicago/Turabian StyleRehman, Amjad, Tanzila Saba, Muhammad Mujahid, Faten S. Alamri, and Narmine ElHakim. 2023. "Parkinson’s Disease Detection Using Hybrid LSTM-GRU Deep Learning Model" Electronics 12, no. 13: 2856. https://doi.org/10.3390/electronics12132856
APA StyleRehman, A., Saba, T., Mujahid, M., Alamri, F. S., & ElHakim, N. (2023). Parkinson’s Disease Detection Using Hybrid LSTM-GRU Deep Learning Model. Electronics, 12(13), 2856. https://doi.org/10.3390/electronics12132856










