Improvement of DBSCAN Algorithm Based on K-Dist Graph for Adaptive Determining Parameters
Abstract
:1. Introduction
2. Preliminary Knowledge
2.1. Related Definition
2.2. DBSCAN Algorithm Steps
3. X-DBSCAN
3.1. The Basic Idea of X-DBSCAN
3.2. Selection of X-DBSCAN Parameters
3.2.1. Adaptively Generate Eps Parameter List
3.2.2. Adaptively Generate MinPts Parameter List
3.2.3. Adaptively Determine the Optimal Parameters
3.2.4. Verify the Optimal Parameters
3.3. The Overall Steps of X-DBSCAN
3.4. The Pseudocode of X-DBSCAN
| Algorithm 1: Generate parameter list | |
| Input: Dataset D Output: Eps parameter list Epslist, MinPts parameter list MinPtslist | |
| 1 | S = read(D) // Read data into S |
| 2 | Zscore(S) // data normalization |
| 3 | for s0 to sn |
| 4 | Calculate the distance of each point to other points dist(si,sj) |
| 5 | Generate a distance matrix matrix |
| 6 | Matrix[i].sort() // Sort the elements in the distance matrix in //ascending row order |
| 7 | end for |
| 8 | for k to n |
| 9 | KList.append(Matrix[i][k]) // Add the kth column elements of all //rows of the matrix to the KList list |
| 10 | KList.sort() // Sort the elements in the KList list to generate a K-dist //curve |
| 11 | Y_pred = Polyfit(KList) // Fitting a K-dist curve |
| 12 | Calculate the point with the largest curvature in the abrupt region after the fitted K- dist smooth curve rises steadily, denoted as the curve inflection point q |
| 13 | The ordinate of q as the Eps parameter EpsK |
| 14 | Epslist.append(EpsK) // Add the parameter EpsK to the Eps //parameter list |
| 15 | end for |
| 16 | for s0 to sn |
| 17 | Calculate the mathematical expectation of the number of objects in the Eps neighborhood of each object in the dataset D as the MinPts undetermined parameter M |
| 18 | MinPtsK = M × β // Add a noise reduction threshold to the MinPts //pending parameter to generate the parameter //MinPtsK |
| 19 | MinPtslist.append(MinPtsK) // Add the parameter MinPtsK to the //MinPts parameter list |
| 20 | end for |
| 21 | return Epslist, MinPtslist |
| Algorithm 2: X-DBSCAN Clustering | |
| Input: Eps parameter list Epslist, MinPts parameter list MinPtslist Output: Clustering results | |
| 1 | for i to n |
| 2 | Cluster.append(DBSCAN(Epslist[i], MinPtslist[i])) |
| 3 | Generate a relationship curve with the abscissa as ClusterNumber and the ordinate as K Value |
| 4 | end for |
| 5 | While(y >= 2) // y = 5 |
| 6 | if ClusterNumber is X consecutively y times then |
| 7 | When the number of clusters is selected as X, the maximum K value is the optimal parameter K |
| 8 | break |
| 9 | else if y = 2 |
| 10 | The maximum K value in the interval where the fluctuation range of the number of clusters is within 1 is selected as the optimal parameter K |
| 11 | else |
| 12 | y = y − 1 |
| 13 | continue |
| 14 | end if |
| 15 | DBSCAN(EpsK, MinPtsK) |
| 16 | return clusters |
3.5. The Time Complexity Analysis of X-DBSCAN
4. Experiment and Result Analysis
4.1. Dataset
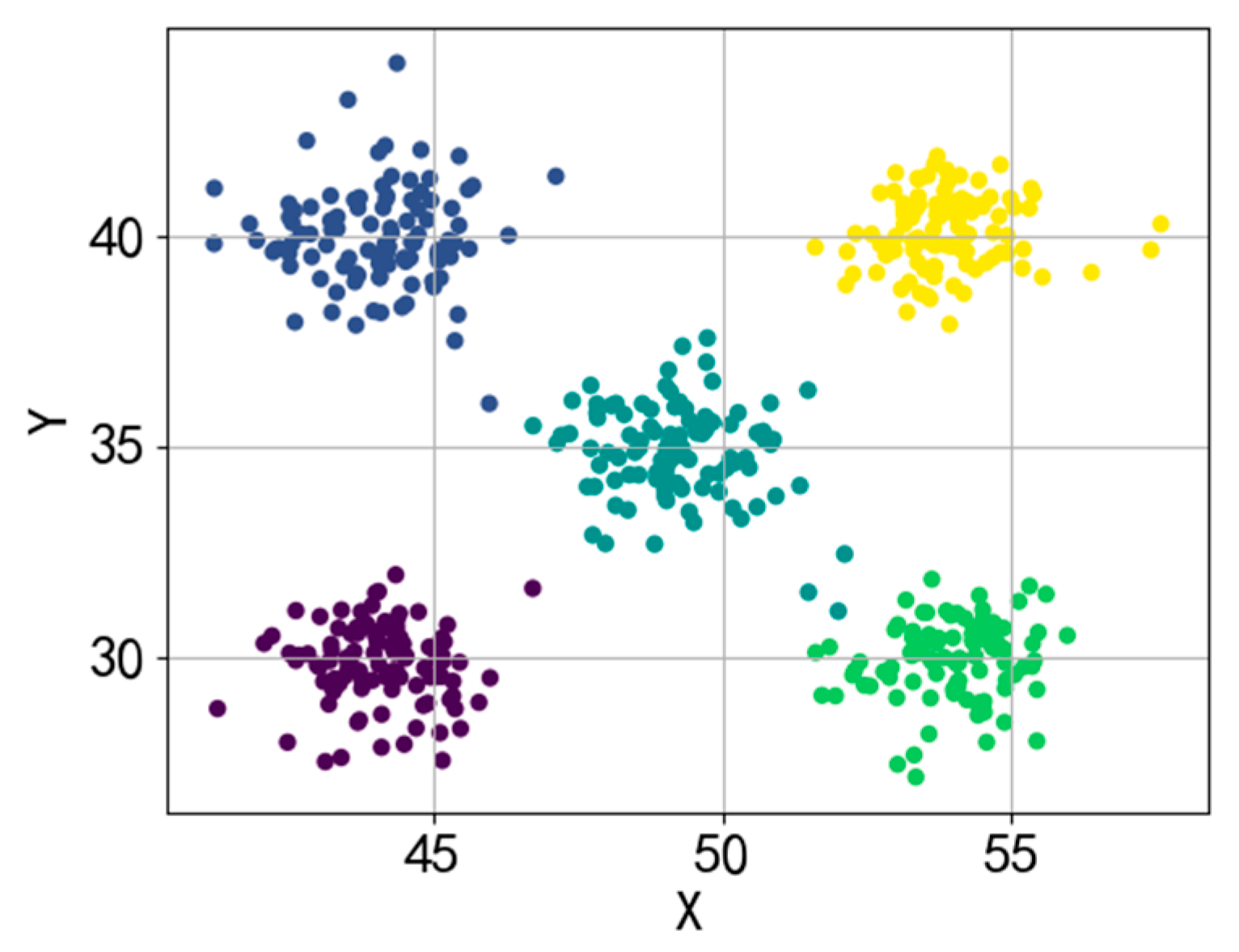
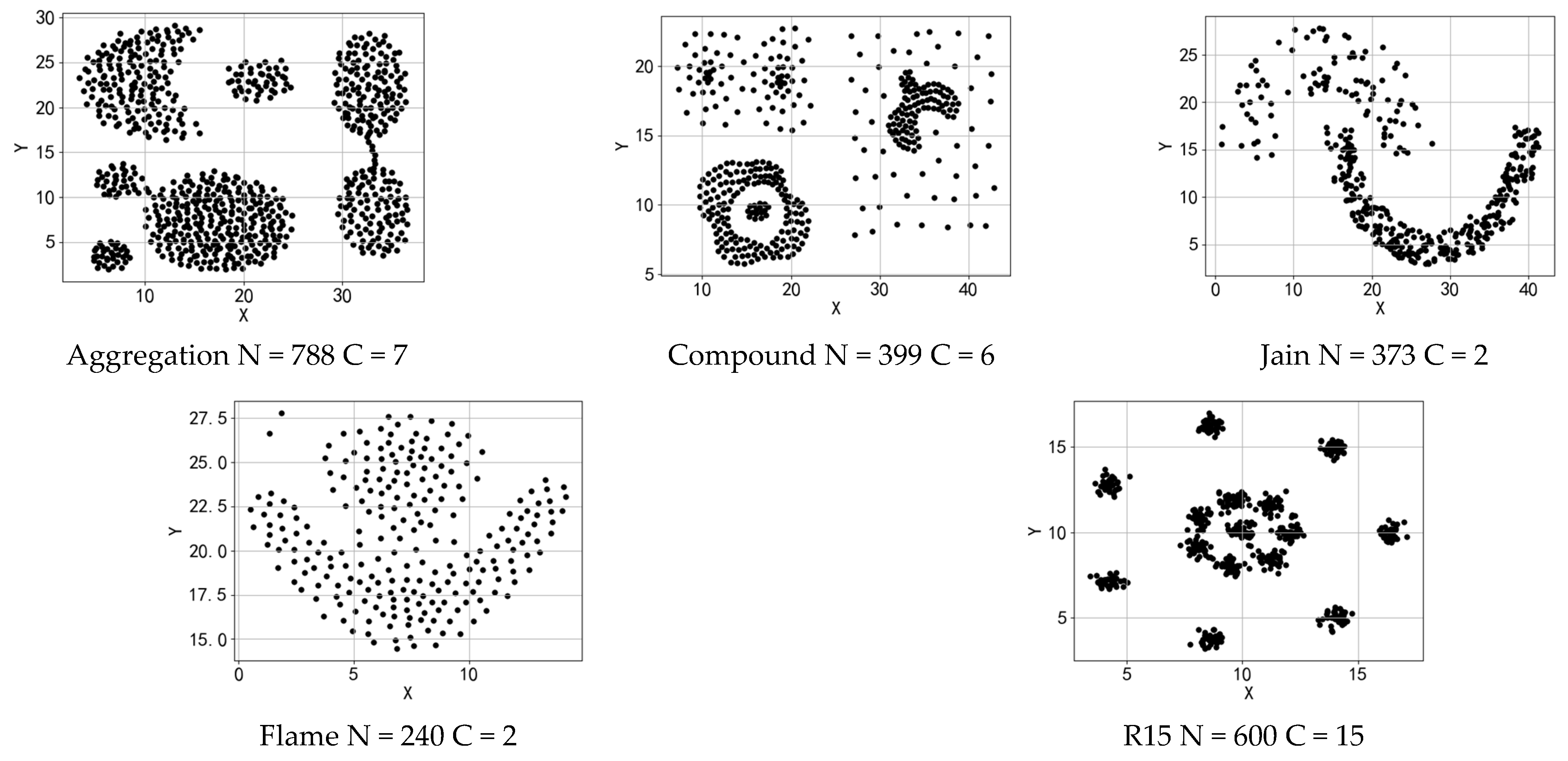
4.1.1. Two-Dimensional Artificial Dataset
4.1.2. UCI Real Dataset
4.1.3. Synthetic Datasets of Different Dimensions Constructed Using Gaussian Distribution
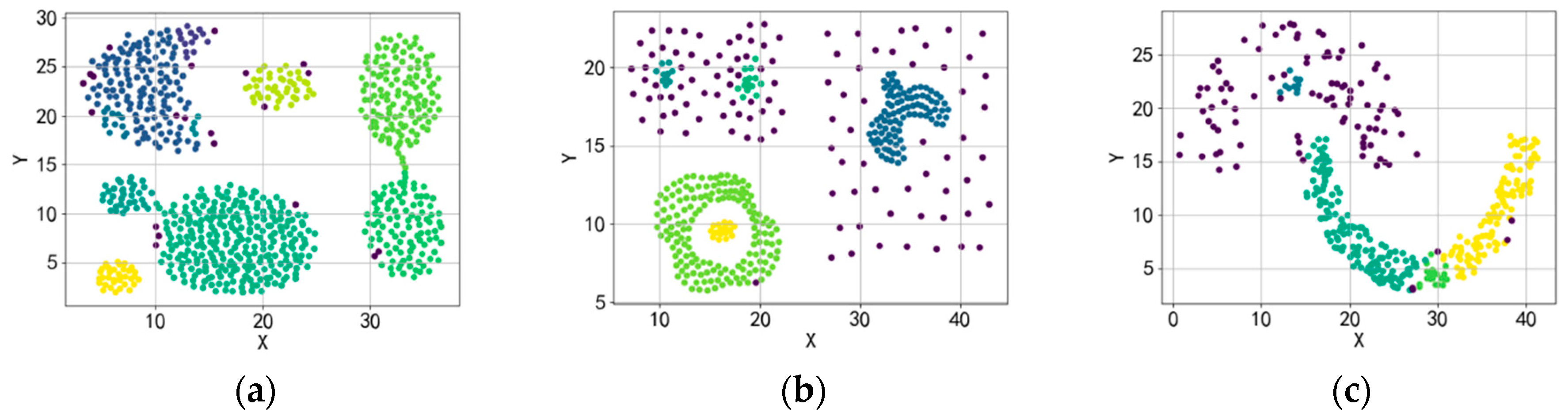
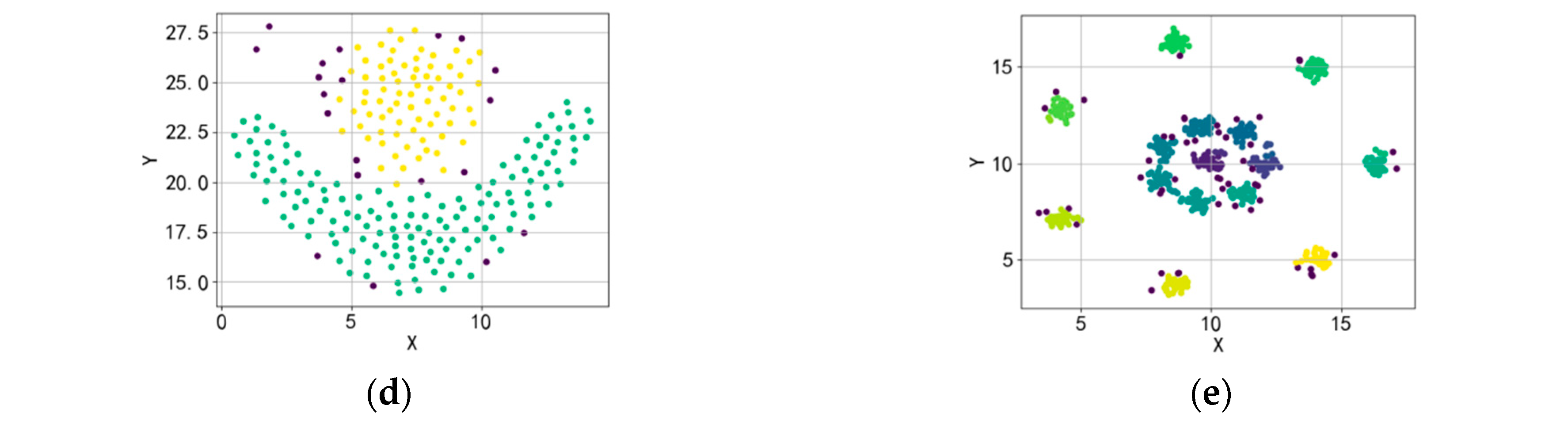
4.2. Experiment on Artificial Two-Dimensional Datasets
4.3. Experiment on UCI Real Dataset
4.4. Synthetic Dataset Experiment: Gaussian-Distributed Dimensions
5. Conclusions
- (1)
- The clustering results of the X-DBSCAN algorithm on datasets with large density differences and multiple densities still have certain errors, and the idea of data partitioning can be used to solve this problem. Firstly, data blocks with the same density can be divided into one area, and, after the different density areas in the dataset are effectively separated, each area can be clustered and merged.
- (2)
- The X-DBSCAN algorithm has high time complexity. On the one hand, we can improve the data structure of the X-DBSCAN algorithm by using the KD tree structure to retrieve all points within a given distance of a specific point. On the other hand, we can use the distributed big data platform to parallelize the X-DBSCAN algorithm. This method can effectively and reasonably reduce the time complexity of the algorithm and improve the execution efficiency of the algorithm.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tan, P.-N.; Steinbach, M.S.; Kumar, V. Introduction to Data Mining. In Data Mining and Machine Learning Applications; Wiley: Hoboken, NJ, USA, 2022. [Google Scholar]
- Han, J.; Kamber, M. Data Mining: Concepts and Technology; China Machine Press: Beijing, China, 2012. [Google Scholar]
- Chen, Y.; Tang, S.; Bouguila, N.; Wang, C.; Du, J.; Li, H. A fast clustering algorithm based on pruning unnecessary distance computations in DBSCAN for high-dimensional data. Pattern Recognit. 2018, 83, 375–387. [Google Scholar] [CrossRef]
- Rodriguez, A.; Laio, A. Clustering by fast search and find of density peaks. Science 2014, 344, 1492–1496. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bensmail, H.; Celeux, G.; Raftery, A.E.; Robert, C.P. Inference in model-based cluster analysis. Stat. Comput. 1997, 7, 1–10. [Google Scholar] [CrossRef]
- Ester, M.; Kriegel, H.-P.; Sander, J.; Xu, X. A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise. In Proceedings of the KDD’96: Proceedings of the Second International Conference on Knowledge Discovery and Data Mining, Portland, OR, USA, 2–4 August 1996; pp. 226–231. [Google Scholar]
- Bechini, A.; Marcelloni, F.; Renda, A. TSF-DBSCAN: A Novel Fuzzy Density-Based Approach for Clustering Unbounded Data Streams. IEEE Trans. Fuzzy Syst. 2022, 30, 623–637. [Google Scholar] [CrossRef]
- Chen, H.; Wang, T.; Chen, T.; Deng, W. Hyperspectral Image Classification Based on Fusing S3-PCA, 2D-SSA and Random Patch Network. Remote Sens. 2023, 15, 3402. [Google Scholar] [CrossRef]
- Li, M.; Bi, X.; Wang, L.; Han, X. A method of two-stage clustering learning based on improved DBSCAN and density peak algorithm. Comput. Commun. 2021, 167, 75–84. [Google Scholar] [CrossRef]
- Chen, H.; Chen, Y.; Wang, Q.; Chen, T.; Zhao, H. A New SCAE-MT Classification Model for Hyperspectral Remote Sensing Images. Sensors 2022, 22, 8881. [Google Scholar] [CrossRef]
- Xu, J.J.; Zhao, Y.L.; Chen, H.Y.; Deng, W. ABC-GSPBFT: PBFT with grouping score mechanism and optimized consensus process for flight operation data-sharing. Inform. Sci. 2023, 624, 110–127. [Google Scholar] [CrossRef]
- Zhou, D.; Liu, P. VDBSCAN: Variable Density Clustering Algorithm. Comput. Eng. Appl. 2009, 45, 137–141. [Google Scholar]
- Li, W.; Yan, S.; Jiang, Y. Algorithm Research on Adaptive Determination of DBSCAN Algorithm Parameters. Comput. Eng. Appl. 2019, 55, 1–7. [Google Scholar]
- Wan, J.; Hu, D.; Jiang, Y. Algorithm Research on Multi-density Adaptive Determination of DBSCAN Algorithm Parameters. Comput. Eng. Appl. 2022, 58, 78–85. [Google Scholar]
- Zhou, Z.; Wang, J.; Zhu, S. An Improved Adaptive Fast AF-DBSCAN Clustering Algorithm. J. Intell. Syst. 2016, 11, 93–98. [Google Scholar]
- Wang, Z.; Ye, Z.; Du, Y.; Mao, Y.; Liu, Y.; Wu, Z.; Wang, J. AMD-DBSCAN: An Adaptive Multi-density DBSCAN for datasets of extremely variable density. In Proceedings of the 2022 IEEE 9th International Conference on Data Science and Advanced Analytics (DSAA), Shenzhen, China, 13–16 October 2022; pp. 1–10. [Google Scholar]
- Latifi-Pakdehi, A.; Daneshpour, N. DBHC: A DBSCAN-based hierarchical clustering algorithm. Data Knowl. Eng. 2021, 135, 101922. [Google Scholar] [CrossRef]
- Wang, G.; Lin, G. Improved adaptive parameter DBSCAN clustering algorithm. Comput. Eng. Appl. 2020, 56, 45–51. [Google Scholar]
- Gholizadeh, N.; Saadatfar, H.; Hanafi, N. K-DBSCAN: An improved DBSCAN algorithm for big data. J. Supercomput. 2020, 77, 6214–6235. [Google Scholar] [CrossRef]
- Bryant, A.; Cios, K. RNN-DBSCAN: A Density-Based Clustering Algorithm Using Reverse Nearest Neighbor Density Estimates. IEEE Trans. Knowl. Data Eng. 2018, 30, 1109–1121. [Google Scholar] [CrossRef]
- Falahiazar, Z.; Bagheri, A.; Reshadi, M. Determining the Parameters of DBSCAN Automatically Using the Multi-Objective Genetic Algorithm. J. Inf. Sci. Eng. 2021, 37, 157–183. [Google Scholar]
- Hou, J.; Lv, C.; Zhang, A.; Xu, E. Merging DBSCAN and Density Peak for Robust Clustering; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Chen, W.; Shi, H. Improved DBSCAN clustering algorithm based on KD tree. Comput. Syst. Appl. 2022, 31, 305–310. [Google Scholar]
- Kim, J.-H.; Choi, J.-H.; Yoo, K.-H.; Nasridinov, A. AA-DBSCAN: An approximate adaptive DBSCAN for finding clusters with varying densities. J. Supercomput. 2018, 75, 142–169. [Google Scholar] [CrossRef]
- Ros, F.; Guillaume, S.; Riad, R.; Hajji, M.E. Detection of natural clusters via S-DBSCAN a Self-tuning version of DBSCAN. Knowl.-Based Syst. 2022, 241, 108288. [Google Scholar] [CrossRef]
- Ros, F.; Guillaume, S.; Riad, R. Path-scan: A novel clustering algorithm based on core points and connexity. Expert Syst. Appl. 2022, 210, 118316. [Google Scholar] [CrossRef]
- Zhang, X.; Shen, X.; Ouyang, T. Extension of DBSCAN in Online Clustering: An Approach Based on Three-Layer Granular Models. Appl. Sci. 2022, 12, 9402. [Google Scholar] [CrossRef]
- Unver, M.; Erginel, N. Clustering applications of IFDBSCAN algorithm with comparative analysis. J. Intell. Fuzzy Syst. 2020, 39, 6099–6108. [Google Scholar] [CrossRef]
- Ouyang, T.; Pedrycz, W.; Pizzi, N.J. Rule-Based Modeling With DBSCAN-Based Information Granules. IEEE Trans. Cybern. 2019, 51, 3653–3663. [Google Scholar] [CrossRef]
- Chen, Y.; Zhou, L.; Pei, S.; Yu, Z.; Chen, Y.; Liu, X.; Du, J.; Xiong, N. KNN-BLOCK DBSCAN: Fast Clustering for Large-Scale Data. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 3939–3953. [Google Scholar] [CrossRef]
- Chen, Y.; Zhou, L.; Bouguila, N.; Wang, C.; Chen, Y.; Du, J. BLOCK-DBSCAN: Fast clustering for large scale data. Pattern Recognit. 2021, 109, 107624. [Google Scholar] [CrossRef]
- Li, S.-S. An Improved DBSCAN Algorithm Based on the Neighbor Similarity and Fast Nearest Neighbor Query. IEEE Access 2020, 8, 47468–47476. [Google Scholar] [CrossRef]
- Li, C.; Liu, M.; Cai, J.; Yu, Y.; Wang, H. Topic Detection and Tracking Based on Windowed DBSCAN and Parallel KNN. IEEE Access 2021, 9, 3858–3870. [Google Scholar] [CrossRef]
- Hahsler, M.; Piekenbrock, M.; Doran, D. dbscan: Fast Density-Based Clustering with R. J. Stat. Softw. 2019, 91, 1–30. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Lu, S.; Hu, C.-b.; Xiang, D.; Liu, T.; Su, Y. Superpixel Generation for SAR Imagery Based on Fast DBSCAN Clustering With Edge Penalty. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 804–819. [Google Scholar] [CrossRef]
- Fu, H.; Li, H.; Dong, Y.; Xu, F.; Chen, F. Segmenting Individual Tree from TLS Point Clouds Using Improved DBSCAN. Forests 2022, 13, 566. [Google Scholar] [CrossRef]
- Sheng, D.; Deng, J.; Xiang, J. Automatic Smoke Detection Based on SLIC-DBSCAN Enhanced Convolutional Neural Network. IEEE Access 2021, 9, 63933–63942. [Google Scholar] [CrossRef]
- Sheridan, K.; Puranik, T.G.; Mangortey, E.; Pinon-Fischer, O.J.; Kirby, M.; Mavris, D.N. An Application of DBSCAN Clustering for Flight Anomaly Detection during the Approach Phase. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020. [Google Scholar]
- Deng, D. Application of DBSCAN Algorithm in Data Sampling. J. Phys. Conf. Ser. 2020, 1617, 042027. [Google Scholar] [CrossRef]
- Wibisono, S.R.; Anwar, M.T.; Supriyanto, A.; Amin, I.H.A. Multivariate weather anomaly detection using DBSCAN clustering algorithm. J. Phys. Conf. Ser. 2021, 1869, 012064. [Google Scholar] [CrossRef]
- Ji, Z.; Wang, C.-L. Accelerating DBSCAN Algorithm with AI Chips for Large Datasets. In Proceedings of the 50th International Conference on Parallel Processing, Lemont, IL, USA, 9–12 August 2021. Article No. 124. [Google Scholar]
- Zhu, Q.; Tang, X.; Elahi, A. Application of the novel harmony search optimization algorithm for DBSCAN clustering. Expert Syst. Appl. 2021, 178, 115054. [Google Scholar] [CrossRef]
- Mustakim; Rahmi, E.; Mundzir, M.R.; Rizaldi, S.T.; Okfalisa; Maita, I. Comparison of DBSCAN and PCA-DBSCAN Algorithm for Grouping Earthquake Area. In Proceedings of the 2021 International Congress of Advanced Technology and Engineering (ICOTEN), Virtual, 4–5 July 2021; pp. 1–5. [Google Scholar]
- Yang, Y.; Qian, C.; Li, H.; Gao, Y.; Wu, J.; Liu, C.-J. An efficient DBSCAN optimized by arithmetic optimization algorithm with opposition-based learning. Supercomputing 2022, 78, 19566–19604. [Google Scholar] [CrossRef]
- Shiba, K.; Chen, C.-C.; Sogabe, M.; Sakamoto, K.; Sogabe, T. Quantum-Inspired Classification Algorithm from DBSCAN–Deutsch–Jozsa Support Vectors and Ising Prediction Model. Appl. Sci. 2021, 11, 11386. [Google Scholar] [CrossRef]
- Xie, X.; Duan, L.-Z.; Qiu, T.; Li, J. Quantum algorithm for MMNG-based DBSCAN. Sci. Rep. 2021, 11, 6288. [Google Scholar] [CrossRef]
- Weng, S. h-DBSCAN: A simple fast DBSCAN algorithm for big data. In Proceedings of the Asian Conference on Machine Learning, Virtual, 17–19 November 2021. [Google Scholar]
- Jain, P.K.; Bajpai, M.; Pamula, R. A modified DBSCAN algorithm for anomaly detection in time-series data with seasonality. Int. Arab J. Inf. Technol. 2022, 19, 23–28. [Google Scholar] [CrossRef]
- Lee, H.-T.; Lee, J.-S.; Yang, H.; Cho, I.-S. An AIS Data-Driven Approach to Analyze the Pattern of Ship Trajectories in Ports Using the DBSCAN Algorithm. Appl. Sci. 2021, 11, 799. [Google Scholar] [CrossRef]
- Tang, X.; Liu, Y.; Chen, K. Air Traffic Trajectory Operation Mode Mining Based on Clustering. Appl. Sci. 2022, 12, 5944. [Google Scholar] [CrossRef]
- Yu, C.; Gong, B.; Song, M.; Zhao, E.; Chang, C.-I. Multiview Calibrated Prototype Learning for Few-shot Hyperspectral Image Classification. IEEE Trans. Geosci. Remote 2022, 60, 5544713. [Google Scholar] [CrossRef]
- Duan, Z.; Song, P.; Yang, C.; Deng, L.; Jiang, Y.; Deng, F.; Jiang, X.; Chen, Y.; Yang, G.; Ma, Y.; et al. The impact of hyperglycaemic crisis episodes on long-term outcomes for inpatients presenting with acute organ injury: A prospective, multicentre follow-up study. Front. Endocrinol. 2022, 13, 1057089. [Google Scholar] [CrossRef]
- Cai, J.; Ding, S.; Zhang, Q.; Liu, R.; Zeng, D.; Zhou, L. Broken ice circumferential crack estimation via image techniques. Ocean Eng. 2022, 259, 111735. [Google Scholar] [CrossRef]
- Ren, Z.; Zhen, X.; Jiang, Z.; Gao, Z.; Li, Y.; Shi, W. Underactuated control and analysis of single blade installation using a jackup installation vessel and active tugger line force control. Mar. Struct. 2023, 88, 103338. [Google Scholar] [CrossRef]
- Li, M.; Zhang, J.; Song, J.; Li, Z.; Lu, S. A clinical-oriented non severe depression diagnosis method based on cognitive behavior of emotional conflict. IEEE Trans. Comput. Soc. Syst. 2022, 10, 131–141. [Google Scholar] [CrossRef]
- Jin, T.; Zhu, Y.; Shu, Y.; Cao, J.; Yan, H.; Jiang, D. Uncertain optimal control problem with the first hitting time objective and application to a portfolio selection model. J. Intell. Fuzzy Syst. 2023, 44, 1585–1599. [Google Scholar] [CrossRef]
- Yu, Y.; Tang, K.; Liu, Y. A fine-tuning based approach for daily activity recognition between smart homes. Appl. Sci. 2023, 13, 5706. [Google Scholar] [CrossRef]
- Song, Y.; Zhao, G.; Zhang, B.; Chen, H.; Deng, W.Q.; Deng, Q. An enhanced distributed differential evolution algorithm for portfolio optimization problems. Eng. Appl. Artif. Intell. 2023, 121, 106004. [Google Scholar] [CrossRef]
- Jin, T.; Yang, X. Monotonicity theorem for the uncertain fractional differential equation and application to uncertain financial market. Math. Comput. Simul. 2021, 190, 203–221. [Google Scholar] [CrossRef]
- Xie, C.; Zhou, L.; Ding, S.; Liu, R.; Zheng, S. Experimental and numerical investigation on self-propulsion performance of polar merchant ship in brash ice channel. Ocean Eng. 2023, 269, 113424. [Google Scholar] [CrossRef]
- Huang, C.; Zhou, X.; Ran, X.; Wang, J.; Chen, H.; Deng, W. Adaptive cylinder vector particle swarm optimization with differential evolution for UAV path planning. Eng. Appl. Artif. Intell. 2023, 121, 105942. [Google Scholar] [CrossRef]
- Li, M.; Zhang, W.; Hu, B.; Kang, J.; Wang, Y.; Lu, S. Automatic assessment of depression and anxiety through encoding pupil-wave from HCI in VR scenes. ACM Trans. Multimed. Comput. Commun. Appl. 2022. [Google Scholar] [CrossRef]
- Chen, M.; Shao, H.; Dou, H.; Li, W.; Liu, B. Data augmentation and intelligent fault diagnosis of planetary gearbox using ILoFGAN under extremely limited sample. IEEE Trans. Reliab. 2022, 1–9. [Google Scholar] [CrossRef]
- Zhou, X.; Cai, X.; Zhang, H.; Zhang, Z.; Jin, T.; Chen, H.; Deng, W. Multi-strategy competitive-cooperative co-evolutionary algorithm and its application. Inf. Sci. 2023, 635, 328–344. [Google Scholar] [CrossRef]
- Sun, Q.; Zhang, M.; Zhou, L.; Garme, K.; Burman, M. A machine learning-based method for prediction of ship performance in ice: Part I. ice resistance. Mar. Struct. 2022, 83, 103181. [Google Scholar] [CrossRef]
- Chen, T.; Song, P.; He, M.; Rui, S.; Duan, X.; Ma, Y.; Armstrong, D.G.; Deng, W. Sphingosine-1-phosphate derived from PRP-Exos promotes angiogenesis in diabetic wound healing via the S1PR1/AKT/FN1 signalling pathway. Burn. Trauma 2023, 11, tkad003. [Google Scholar] [CrossRef]
- Chen, X.; Shao, H.; Xiao, Y.; Yan, S.; Cai, B.; Liu, B. Collaborative fault diagnosis of rotating machinery via dual adversarial guided unsupervised multi-domain adaptation network. Mech. Syst. Signal Process. 2023, 198, 110427. [Google Scholar] [CrossRef]
- Cai, Z.; Wang, J.; He, K. Adaptive Density-Based Spatial Clustering for Massive Data Analysis. IEEE Access 2020, 8, 23346–23358. [Google Scholar] [CrossRef]
- Sharma, A.; Sharma, A. KNN-DBSCAN: Using k-nearest neighbor information for parameter-free density-based clustering. In Proceedings of the 2017 International Conference on Intelligent Computing, Instrumentation and Control Technologies (ICICICT), Kerala, India, 6–7 July 2017; pp. 787–792. [Google Scholar]
- Zhang, W.; Tan, G.; Zhu, X. Application of spatial clustering of stops in scenic spot hot spot analysis. Comput. Eng. Appl. 2018, 54, 263–270. [Google Scholar]
- Gao, Q.; Wang, L.; Wang, R. Research on Least Squares Curve Fitting and Optimization Algorithm. Ind. Control Comput. 2021, 34, 100–101. [Google Scholar]
- Chen, X.; Xi, Q. Research and implementation of adaptive clustering algorithm based on DBSCAN. J. Huaiyin Normal Univ. (Nat. Sci. Ed.) 2021, 20, 228–234. [Google Scholar]
- Zhu, L.; Ma, B.; Zhao, X. Cluster validity analysis based on profile coefficient. Comput. Appl. 2010, 30 (Suppl. 2), 139–141. [Google Scholar]
- Feng, S.; Xiao, W. Research and improvement of DBSCAN clustering algorithm. China Univ. Min. Technol. 2008, 1, 105–111. [Google Scholar]
- Gionis, A.; Mannila, H.; Tsaparas, P. Clustering Aggregation (long version). ACM Trans. Knowl. Discov. Data 2007, 1, 1–30. [Google Scholar] [CrossRef] [Green Version]
- Zahn, C.T. Graph-Theoretical Methods for Detecting and Describing Gestalt Clusters. IEEE Trans. Comput. 1971, C-20, 68–86. [Google Scholar] [CrossRef] [Green Version]
- Steinbach, M.S.; Karypis, G.; Kumar, V. A Comparison of Document Clustering Techniques. In Proceedings of the KDD Workshop on Text Mining, Boston, MA, USA, 20 August 2000; pp. 525–526. [Google Scholar]
- Yang, X.; Zhu, Q.-P.; Huang, Y.; Xiao, J.; Wang, L.; Tong, F. Parameter-free Laplacian centrality peaks clustering. Pattern Recognit. Lett. 2017, 100, 167–173. [Google Scholar] [CrossRef]
- Yin, S.; Wang, T.; Xie, F. Cluster result evaluation method based on mutual information and profile coefficient. J. Weapon Equip. Eng. 2020, 41, 207–213. [Google Scholar]
- Qiu, B.; Tang, Y. Clustering algorithm for fast identification of density skeleton. Comput. Appl. 2017, 37, 3482–3486. [Google Scholar]













| Dataset | Number of Objects | Dimension | Clusters |
|---|---|---|---|
| Iris | 150 | 4 | 3 |
| Wine | 178 | 13 | 3 |
| Seeds | 210 | 7 | 3 |
| Ecoli | 336 | 7 | 8 |
| Glass | 214 | 9 | 6 |
| Thyroid | 215 | 5 | 3 |
| Pima | 768 | 8 | 2 |
| Banknote | 1372 | 4 | 2 |
| Dataset | Number of Objects | Dimension | Clusters |
|---|---|---|---|
| X-1 | 2048 | 16 | 2 |
| X-2 | 2048 | 64 | 16 |
| X-3 | 2050 | 128 | 16 |
| X-4 | 2050 | 256 | 16 |
| Time(s) | Aggregation | Compound | Jain | Flame | R15 |
|---|---|---|---|---|---|
| X-DBSCAN | 86.83 | 11.91 | 4.54 | 10.09 | 26.64 |
| MDA-DBSCAN | 52.98 | 10.59 | 3.68 | 9.83 | 22.73 |
| KANN-DBSCAN | 53.59 | 8.17 | 3.51 | 7.10 | 22.67 |
| AF-DBSCAN | 4.34 | 3.65 | 2.89 | 3.41 | 3.99 |
| DBSCAN | 5.84 | 3.72 | 2.99 | 3.68 | 5.23 |
| Datasets | Clusters | Clustering Algorithm | Cluster Count Result | Eps | MinPts | F-Score | ACC | AMI | ARI | Time |
|---|---|---|---|---|---|---|---|---|---|---|
| Aggregation | 7 | X-DBSCAN | 7 | 2.428 | 21 | 0.9963 | 0.9962 | 0.9943 | 0.9952 | 86.83 |
| MDA-DBSCAN | 7 | 2.101 | 15 | 0.9953 | 0.9949 | 0.9912 | 0.9940 | 52.98 | ||
| KANN-DBSCAN | 7 | 2.778 | 34 | 0.9858 | 0.9848 | 0.9799 | 0.9820 | 53.59 | ||
| AF-DBSCAN | 10 | 0.941 | 3 | 0.9412 | 0.9302 | 0.9218 | 0.9261 | 4.34 | ||
| DBSCAN | 5 | 1.518 | 4 | 0.8550 | 0.7906 | 0.8858 | 0.8074 | 5.84 | ||
| Compound | 6 | X-DBSCAN | 5 | 1.551 | 10 | 0.9354 | 0.9223 | 0.8916 | 0.9135 | 11.91 |
| MDA-DBSCAN | 6 | D1 = 1.506 | D1 = 9 | 0.9498 | 0.9298 | 0.9421 | 0.9668 | 10.59 | ||
| D2 = 4.990 | D2 = 7 | |||||||||
| KANN-DBSCAN | 5 | 1.467 | 13 | 0.9137 | 0.7644 | 0.8709 | 0.8836 | 8.17 | ||
| AF-DBSCAN | 5 | 0.752 | 4 | 0.8866 | 0.7243 | 0.8463 | 0.8457 | 3.65 | ||
| DBSCAN | 5 | 1.015 | 4 | 0.9106 | 0.7594 | 0.8684 | 0.8794 | 3.72 | ||
| Jain | 2 | X-DBSCAN | 2 | 1.913 | 11 | 0.9811 | 0.7775 | 0.8851 | 0.9522 | 10.09 |
| MDA-DBSCAN | 2 | D1 = 2.429 | D1 = 15 | 0.9988 | 0.9973 | 0.9871 | 0.9971 | 9.83 | ||
| D2 = 3.739 | D2 = 10 | |||||||||
| KANN-DBSCAN | 1 | 1.646 | 12 | 0.7265 | 0.7265 | 0.8958 | 0.9443 | 7.10 | ||
| AF-DBSCAN | 4 | 1.199 | 7 | 0.6149 | 0.3968 | 0.5139 | 0.3656 | 3.41 | ||
| DBSCAN | 6 | 2.03 | 4 | 0.7655 | 0.7655 | 0.7534 | 0.9053 | 3.68 | ||
| Flame | 2 | X-DBSCAN | 2 | 1.503 | 11 | 0.9944 | 0.9917 | 0.9704 | 0.9881 | 4.54 |
| MDA-DBSCAN | 2 | 1.488 | 9 | 0.9789 | 0.9875 | 0.9079 | 0.9551 | 3.68 | ||
| KANN-DBSCAN | 2 | 1.695 | 17 | 0.9483 | 0.9583 | 0.7995 | 0.8918 | 3.51 | ||
| AF-DBSCAN | 2 | 0.901 | 5 | 0.9203 | 0.9125 | 0.7553 | 0.8408 | 2.89 | ||
| DBSCAN | 1 | 1.237 | 4 | 0.6976 | 0.6375 | 0.0164 | 0.0128 | 2.99 | ||
| R15 | 15 | X-DBSCAN | 15 | 0.701 | 24 | 0.9983 | 0.9983 | 0.9985 | 0.9982 | 26.64 |
| MDA-DBSCAN | 15 | 0.575 | 17 | 0.9913 | 0.9917 | 0.9906 | 0.9907 | 22.73 | ||
| KANN-DBSCAN | 15 | 0.760 | 33 | 0.9801 | 0.9900 | 0.9933 | 0.9887 | 22.67 | ||
| AF-DBSCAN | 20 | 0.258 | 3 | 0.8421 | 0.8432 | 0.8839 | 0.8317 | 3.99 | ||
| DBSCAN | 14 | 0.345 | 4 | 0.8875 | 0.8933 | 0.9275 | 0.8794 | 5.23 |
| Time (s) | Iris | Wine | Seed | Ecoli | Glass | Thyroid | Pima | Banknote |
|---|---|---|---|---|---|---|---|---|
| X-DBSCAN | 2.87 | 3.43 | 3.89 | 7.22 | 4.41 | 5.03 | 71.41 | 415.22 |
| MDA-DBSCAN | 2.62 | 2.86 | 3.14 | 6.49 | 3.44 | 3.38 | 45.9 | 282.24 |
| KANN-DBSCAN | 2.55 | 2.97 | 3.22 | 6.71 | 3.36 | 3.56 | 43.15 | 378.10 |
| AF-DBSCAN | 2.22 | 2.39 | 2.88 | 3.51 | 2.19 | 2.19 | 2.66 | 3.99 |
| DBSCAN | 2.35 | 2.45 | 3.05 | 3.89 | 2.98 | 2.89 | 3.88 | 6.89 |
| Iris | Wine | Seed | Ecoli | |||||
| Clustering Algorithm | ACC | Time | ACC | Time | ACC | Time | ACC | Time |
| X-DBSCAN | 0.667 | 2.87 | 0.561 | 3.43 | 0.533 | 3.89 | 0.592 | 7.22 |
| MDA-DBSCAN | 0.320 | 2.62 | 0.354 | 2.86 | 0.509 | 3.14 | 0.408 | 6.49 |
| KANN-DBSCAN | 0.280 | 2.55 | 0.309 | 2.97 | 0.219 | 3.22 | 0.399 | 6.71 |
| AF-DBSCAN | 0.600 | 2.22 | 0.112 | 2.39 | 0.209 | 2.88 | 0.542 | 3.51 |
| DBSCAN | 0.607 | 2.35 | 0.416 | 2.45 | 0.405 | 3.05 | 0.426 | 3.89 |
| Glass | Thyroid | Pima | Banknote | |||||
| Clustering Algorithm | ACC | Time | ACC | Time | ACC | Time | ACC | Time |
| X-DBSCAN | 0.678 | 4.41 | 0.656 | 5.03 | 0.548 | 71.41 | 0.580 | 415.22 |
| MDA-DBSCAN | 0.505 | 3.44 | 0.595 | 3.38 | 0.527 | 45.90 | 0.024 | 282.24 |
| KANN-DBSCAN | 0.421 | 3.36 | 0.563 | 3.56 | 0.451 | 43.15 | 0.028 | 318.10 |
| AF-DBSCAN | 0.621 | 2.19 | 0.623 | 2.19 | 0.289 | 2.66 | 0.016 | 3.99 |
| DBSCAN | 0.481 | 2.98 | 0.648 | 2.89 | 0.639 | 3.88 | 0.546 | 6.89 |
| Datasets | Clustering Algorithm | Cluster Count Result | Eps | MinPts | F-Score | ACC | AMI | ARI | Time |
|---|---|---|---|---|---|---|---|---|---|
| X-1 | X-DBSCAN | 2 | 93.064 | 819 | 0.9996 | 0.9996 | 0.9998 | 0.9991 | 158.35 |
| X-2 | 16 | 53.129 | 51 | 0.9990 | 0.9990 | 0.9991 | 0.9990 | 174.38 | |
| X-3 | 16 | 82.042 | 51 | 1.0 | 1.0 | 1.0 | 1.0 | 182.26 | |
| X-4 | 16 | 46.417 | 51 | 0.9980 | 0.9980 | 0.9984 | 0.9979 | 182.68 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, L.; Hu, H.; Li, K.; Zheng, G.; Qu, Y.; Chen, H. Improvement of DBSCAN Algorithm Based on K-Dist Graph for Adaptive Determining Parameters. Electronics 2023, 12, 3213. https://doi.org/10.3390/electronics12153213
Yin L, Hu H, Li K, Zheng G, Qu Y, Chen H. Improvement of DBSCAN Algorithm Based on K-Dist Graph for Adaptive Determining Parameters. Electronics. 2023; 12(15):3213. https://doi.org/10.3390/electronics12153213
Chicago/Turabian StyleYin, Lifeng, Hongtao Hu, Kunpeng Li, Guanghai Zheng, Yingwei Qu, and Huayue Chen. 2023. "Improvement of DBSCAN Algorithm Based on K-Dist Graph for Adaptive Determining Parameters" Electronics 12, no. 15: 3213. https://doi.org/10.3390/electronics12153213
APA StyleYin, L., Hu, H., Li, K., Zheng, G., Qu, Y., & Chen, H. (2023). Improvement of DBSCAN Algorithm Based on K-Dist Graph for Adaptive Determining Parameters. Electronics, 12(15), 3213. https://doi.org/10.3390/electronics12153213






