Capacitance Estimation for Electrical Capacitance Tomography Sensors Using Digital Processing of Time-Domain Voltage Response to Single-Pulse Excitation
Abstract
:1. Introduction
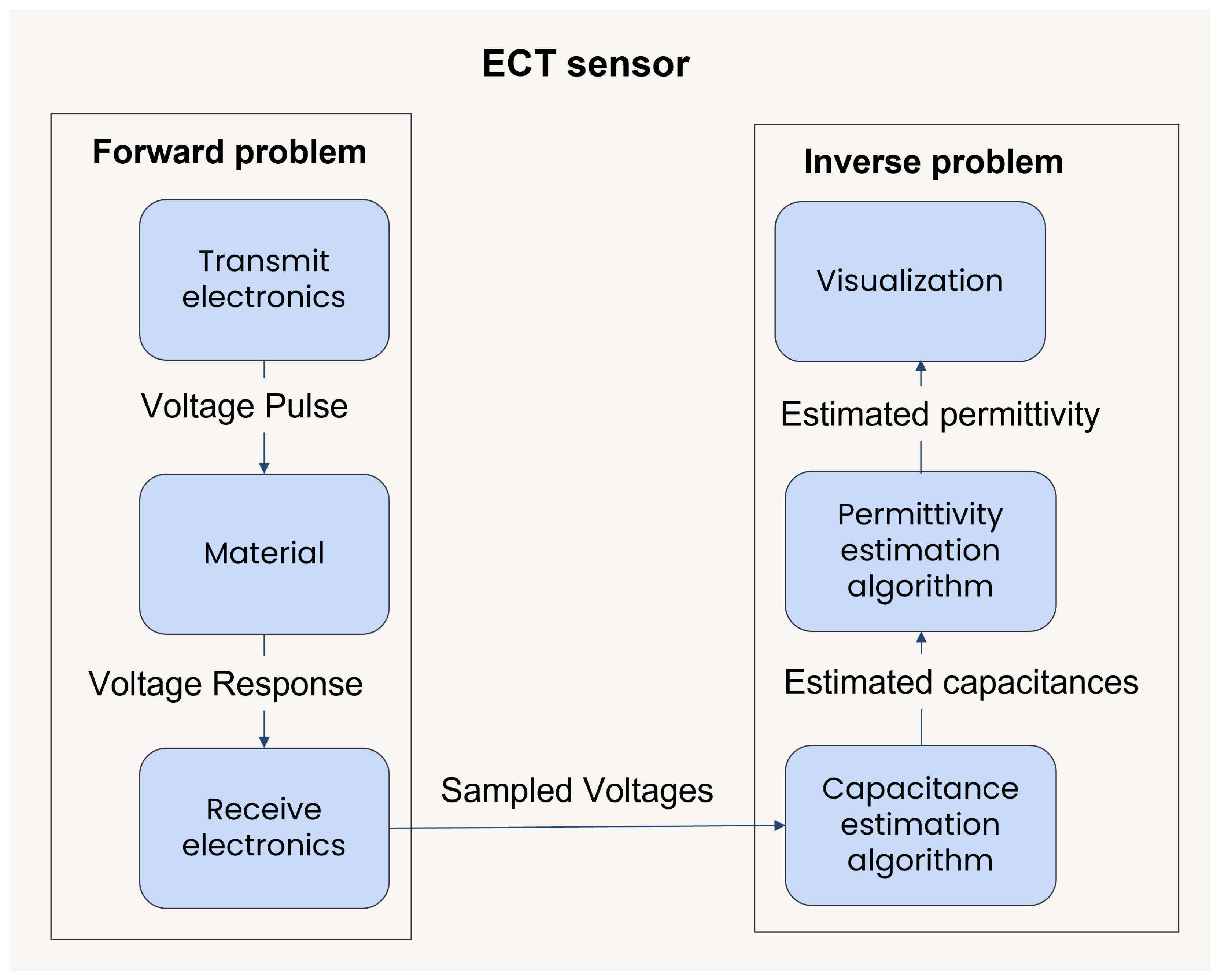
2. Materials and Methods
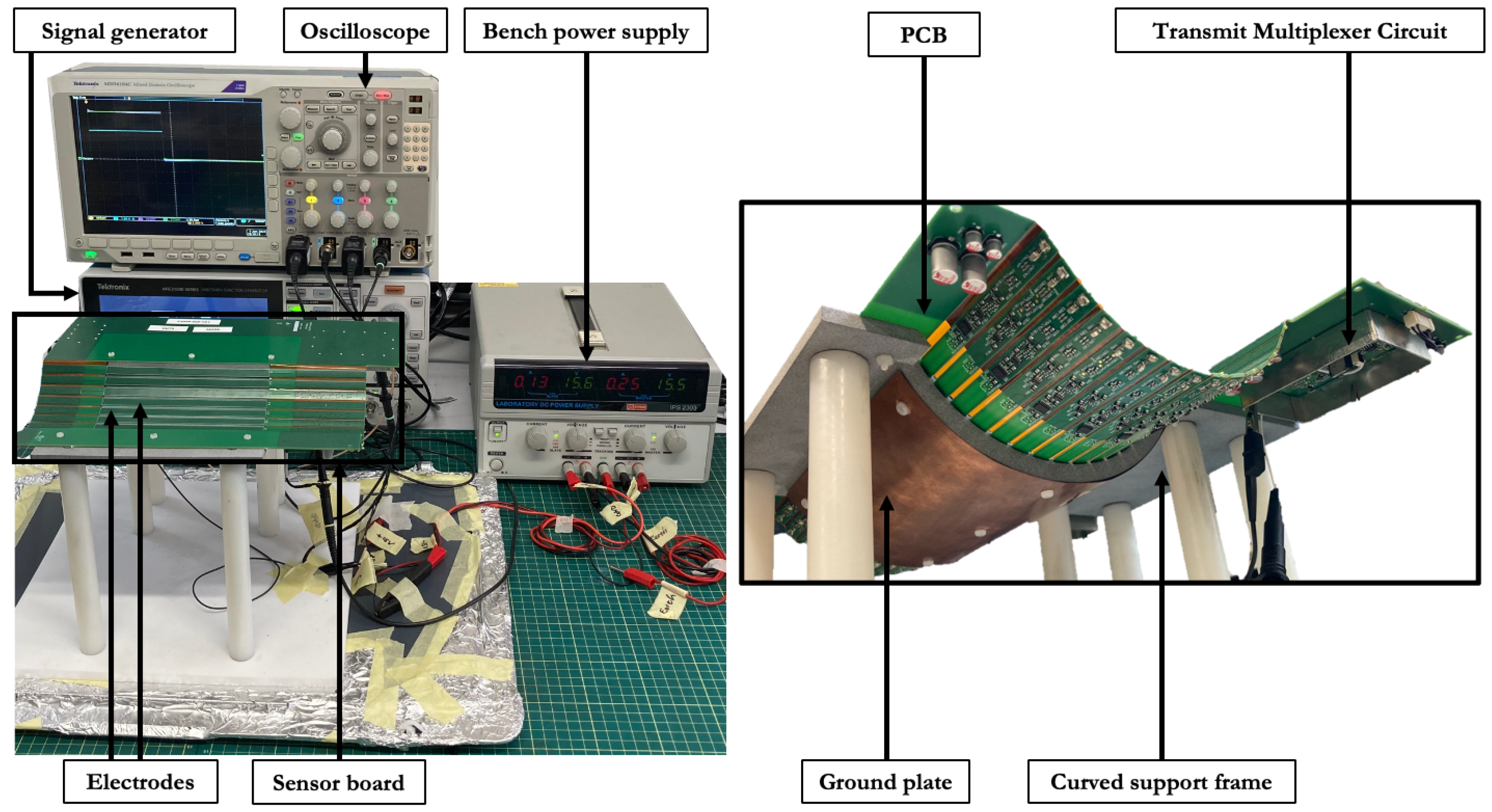
2.1. Prototype Sensor Board
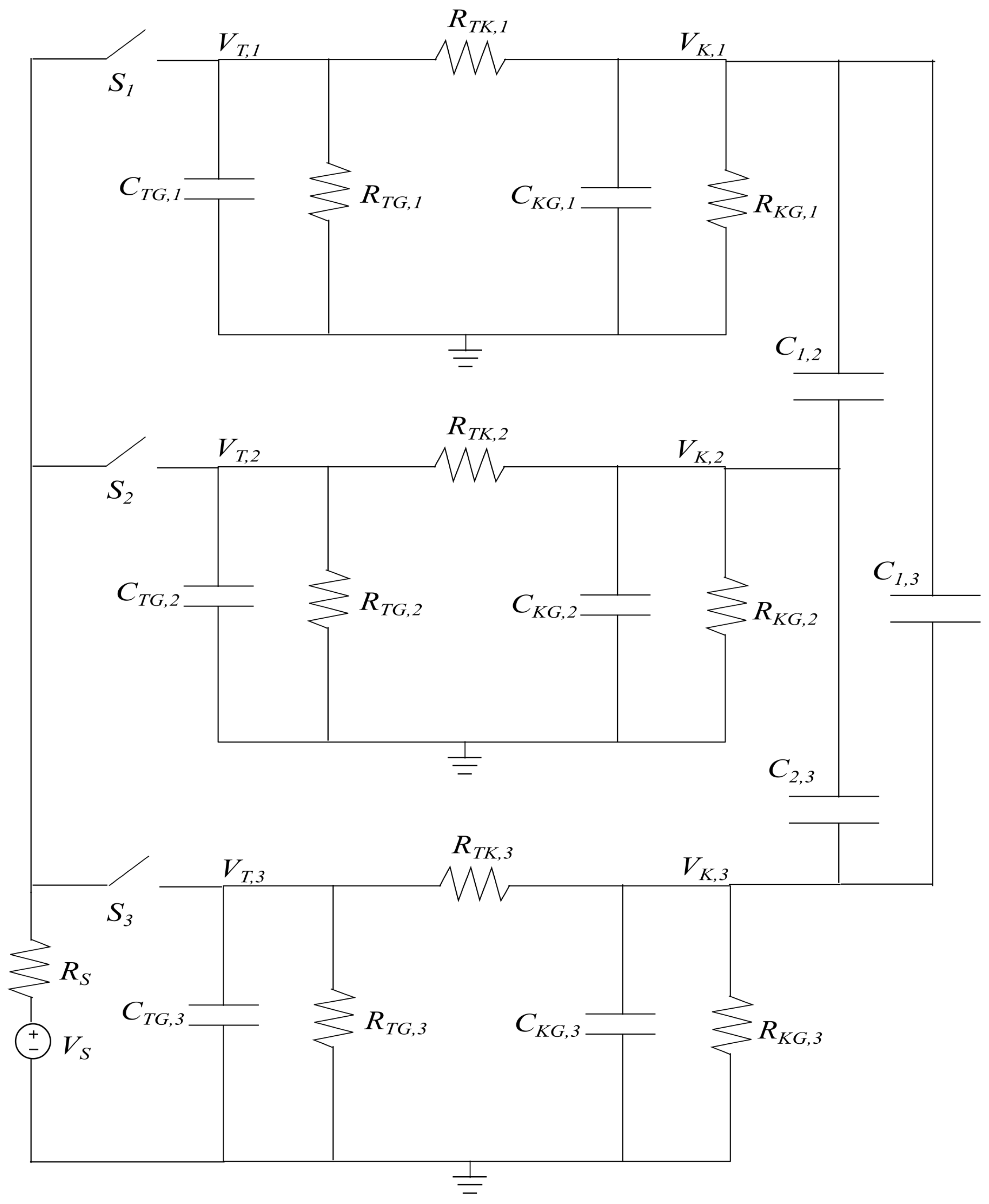
2.2. Equivalent Circuit Representation of the Sensor
2.3. Capacitance Estimation
2.4. Forward Model
3. Results and Discussion
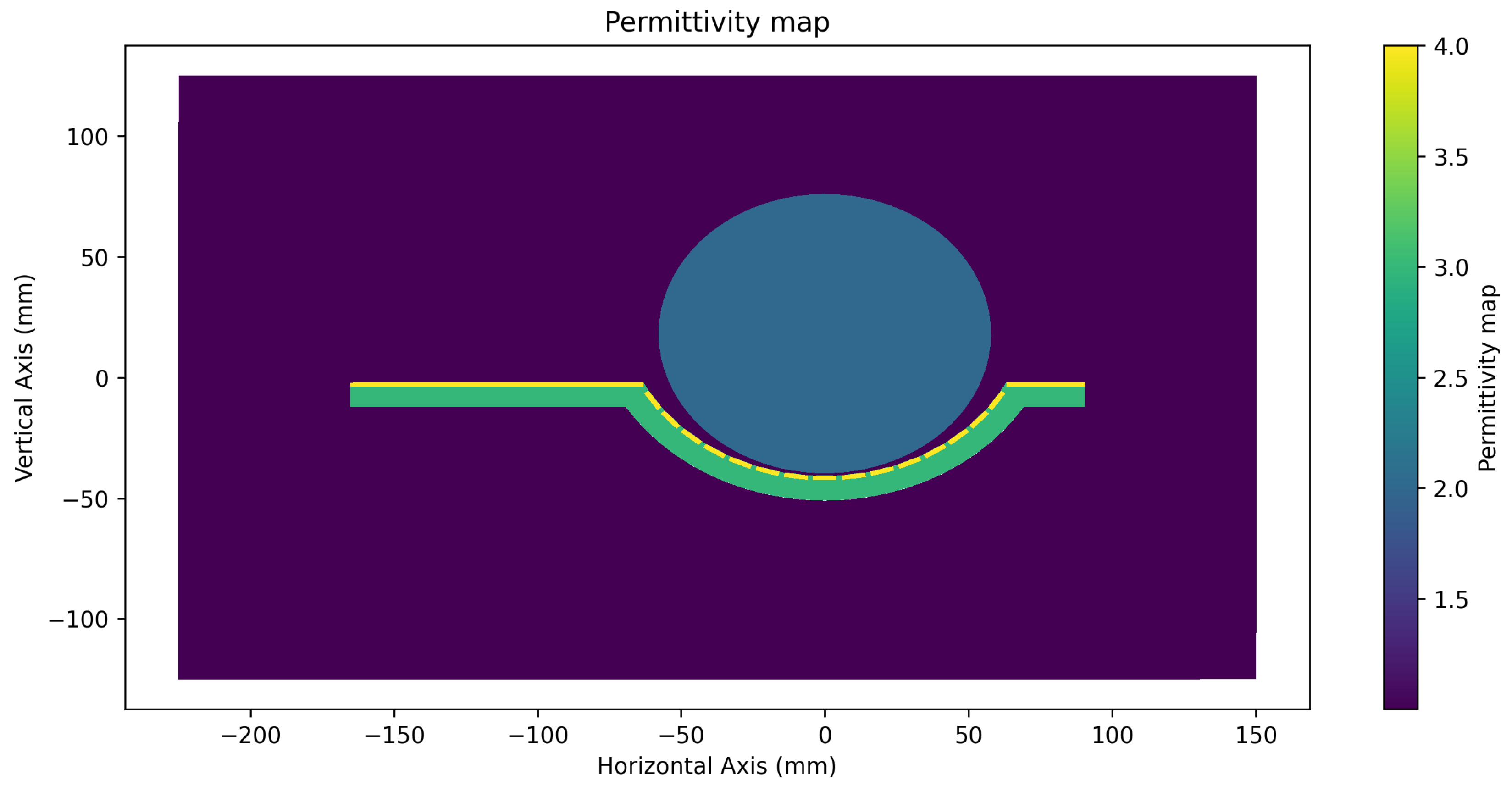
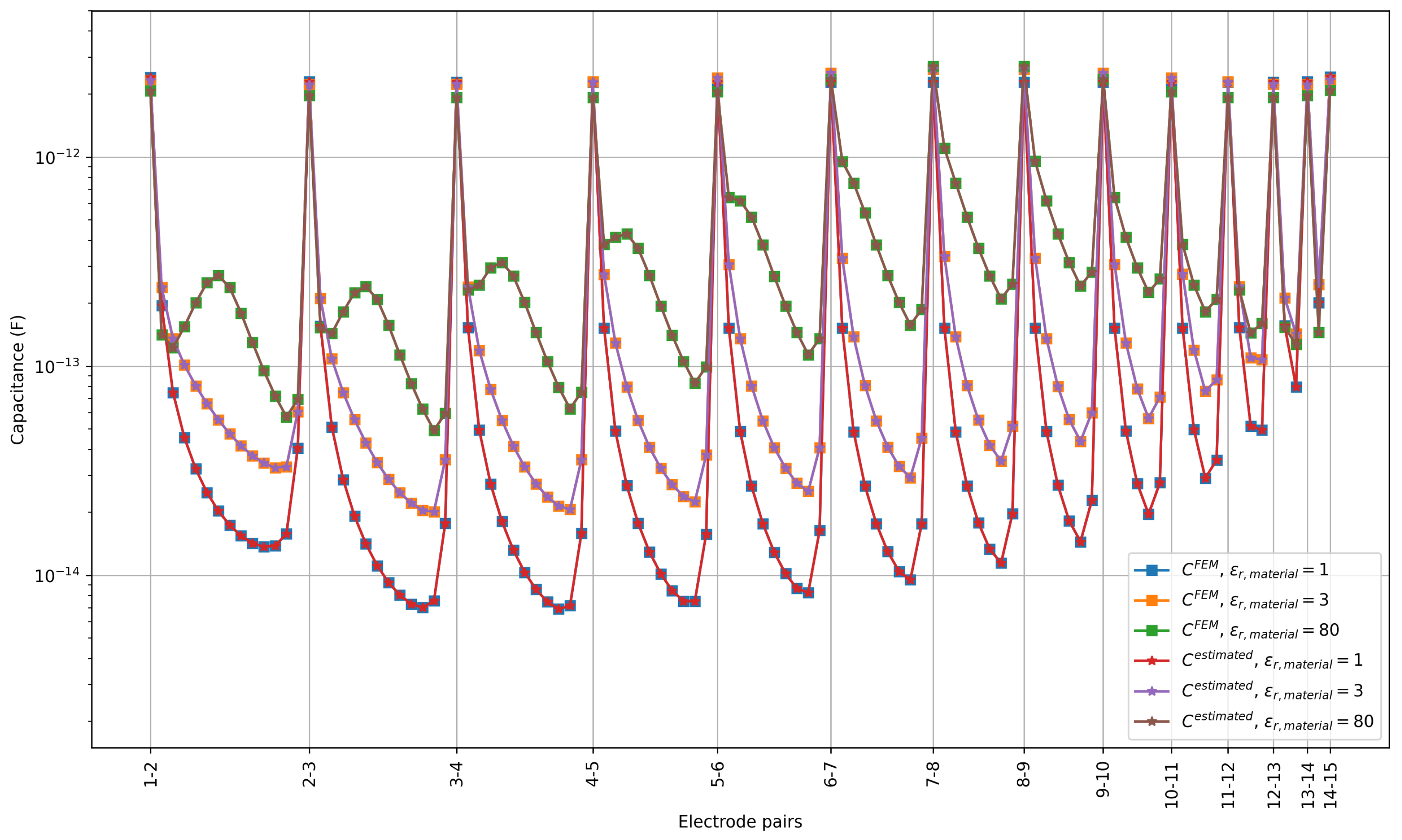
3.1. Forward Simulation
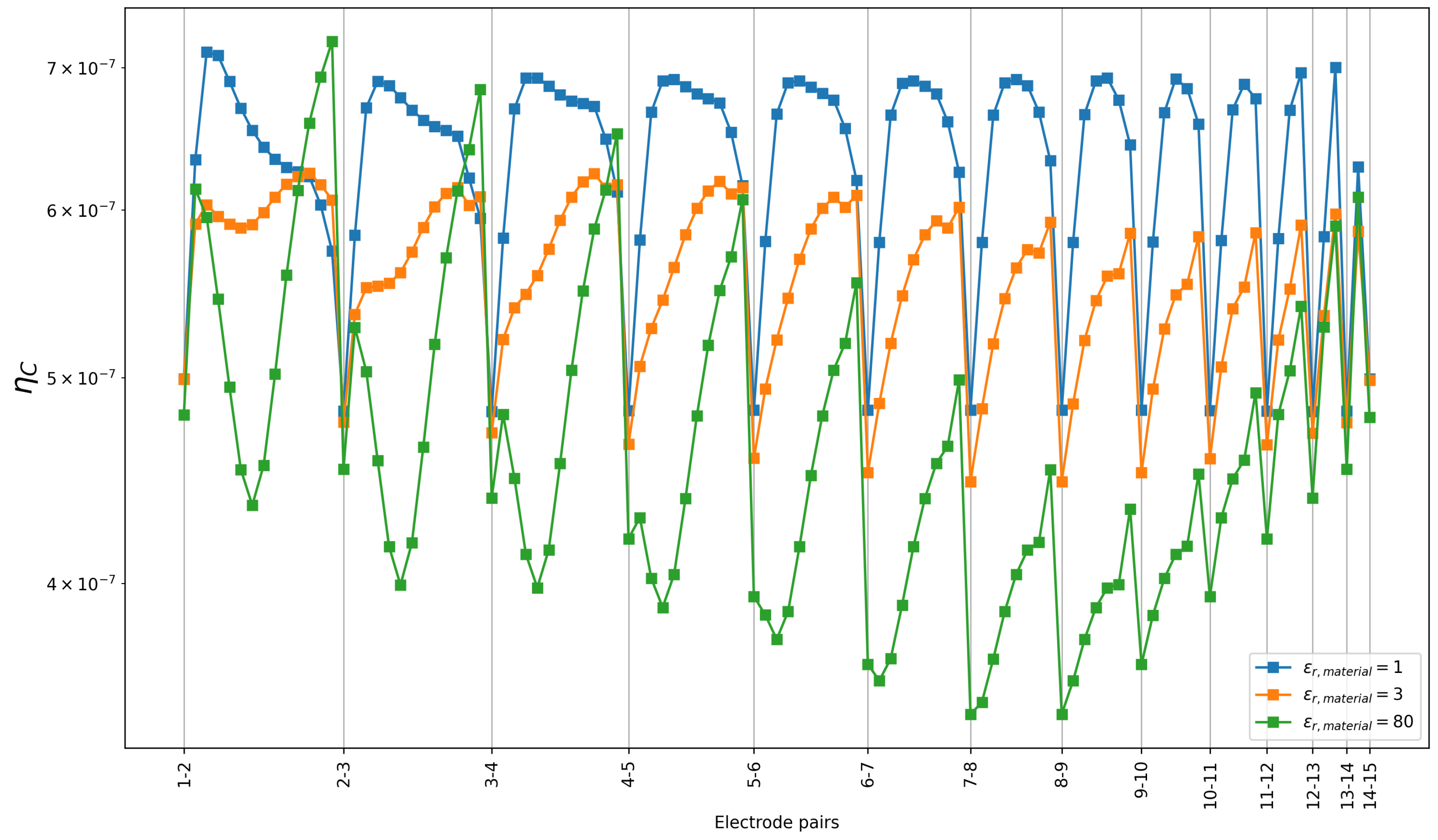
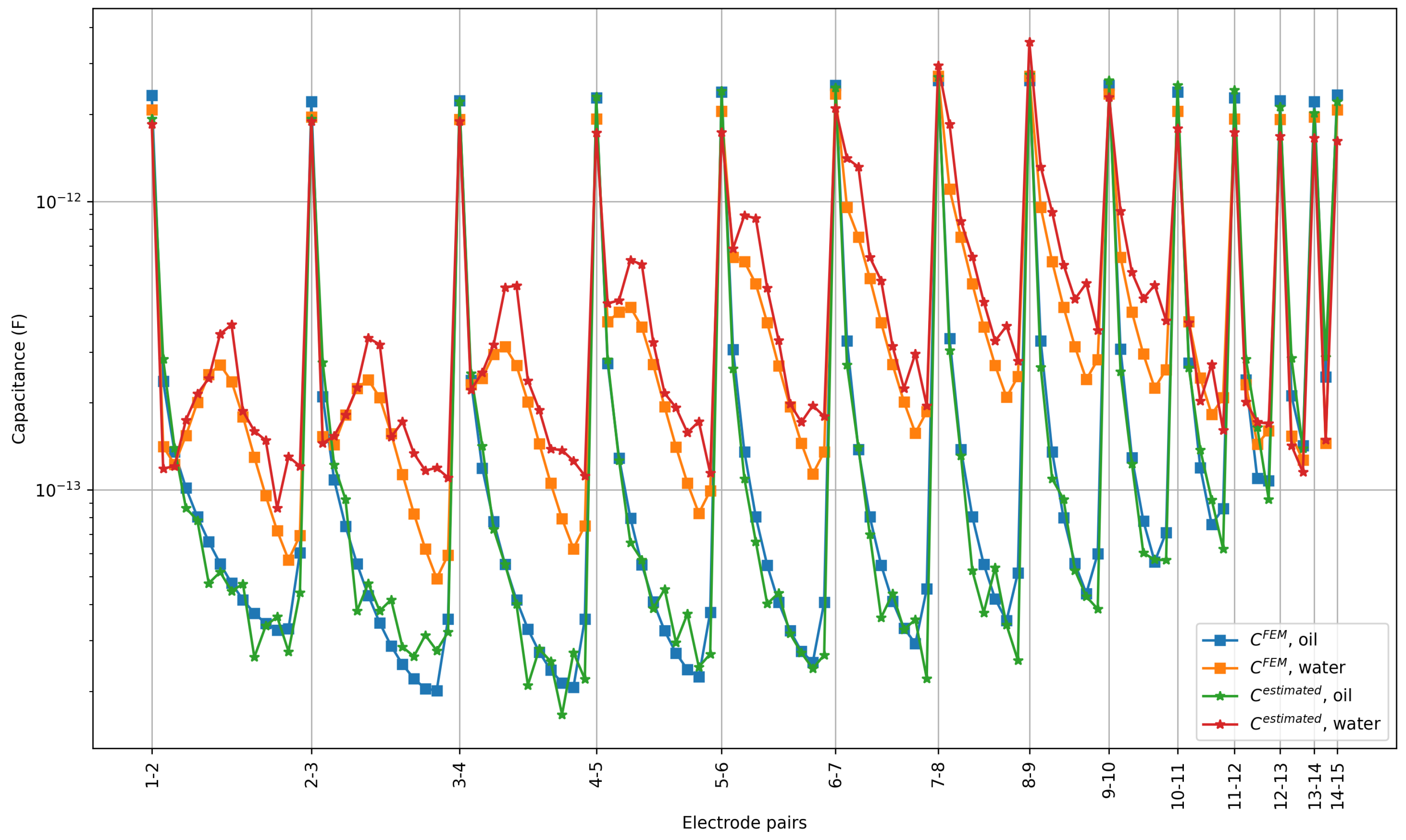
3.2. Estimated Capacitances Using the Algorithm
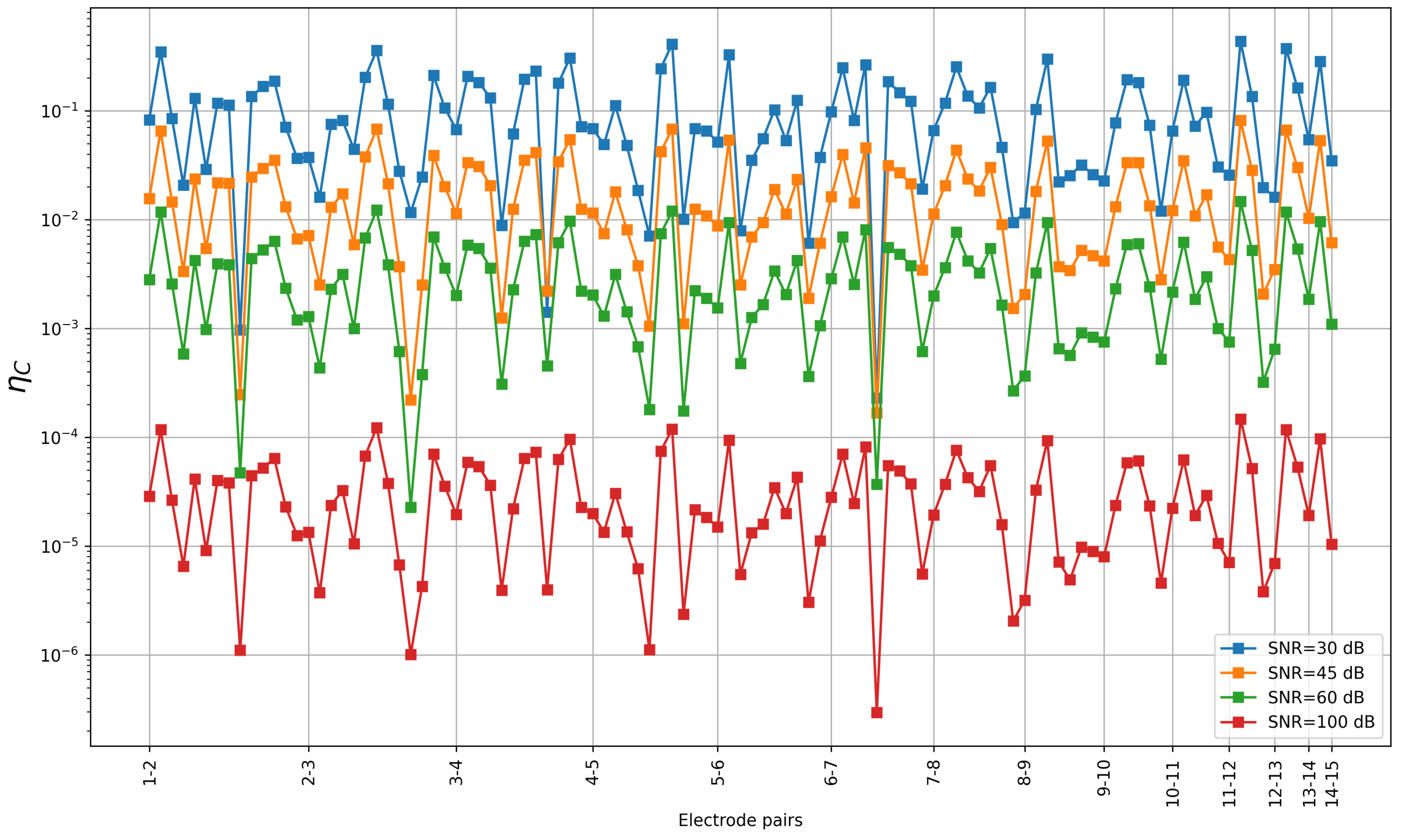
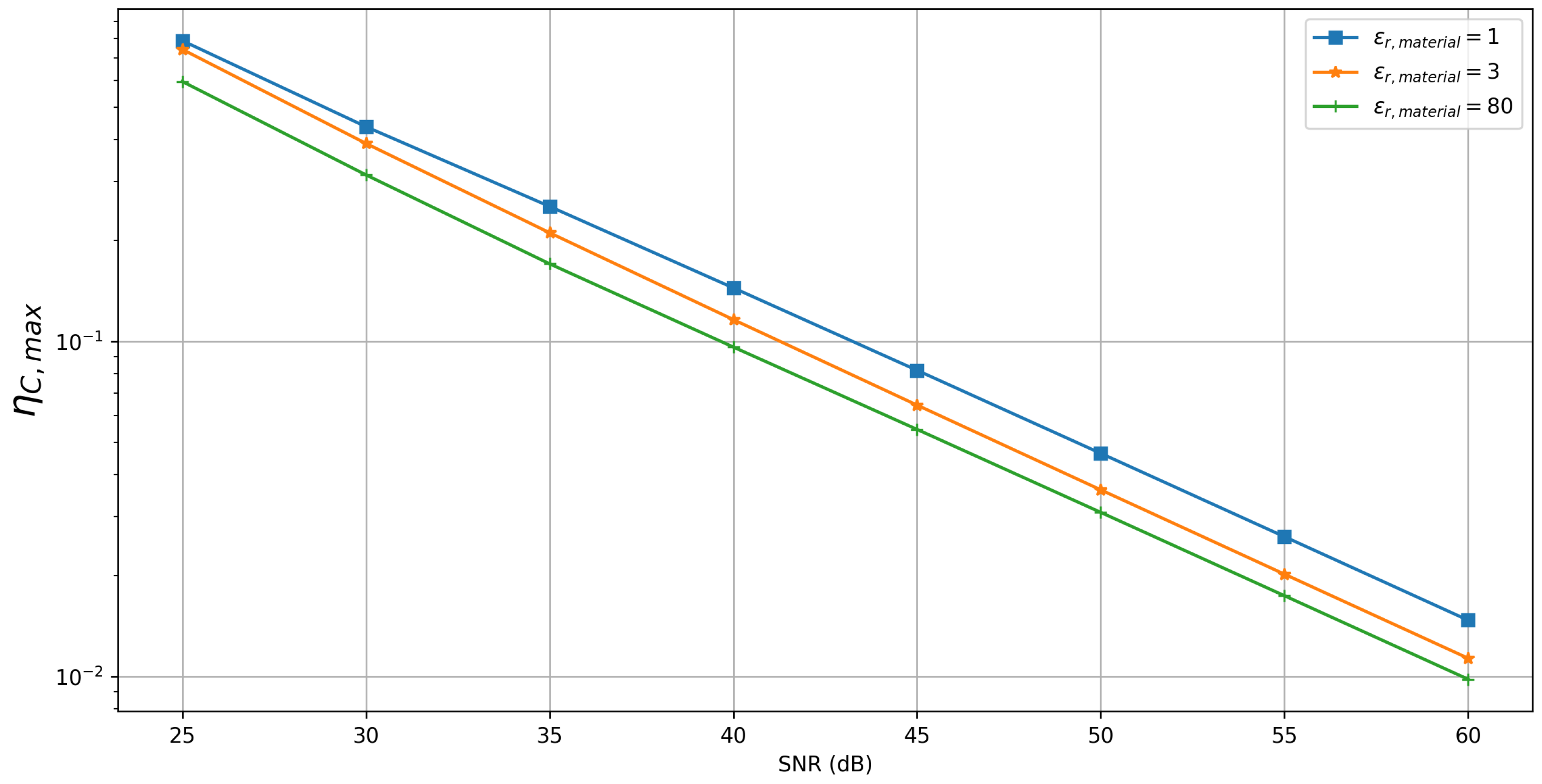
3.3. Sensitivity to Noise
3.4. Effect of Integration Time Window
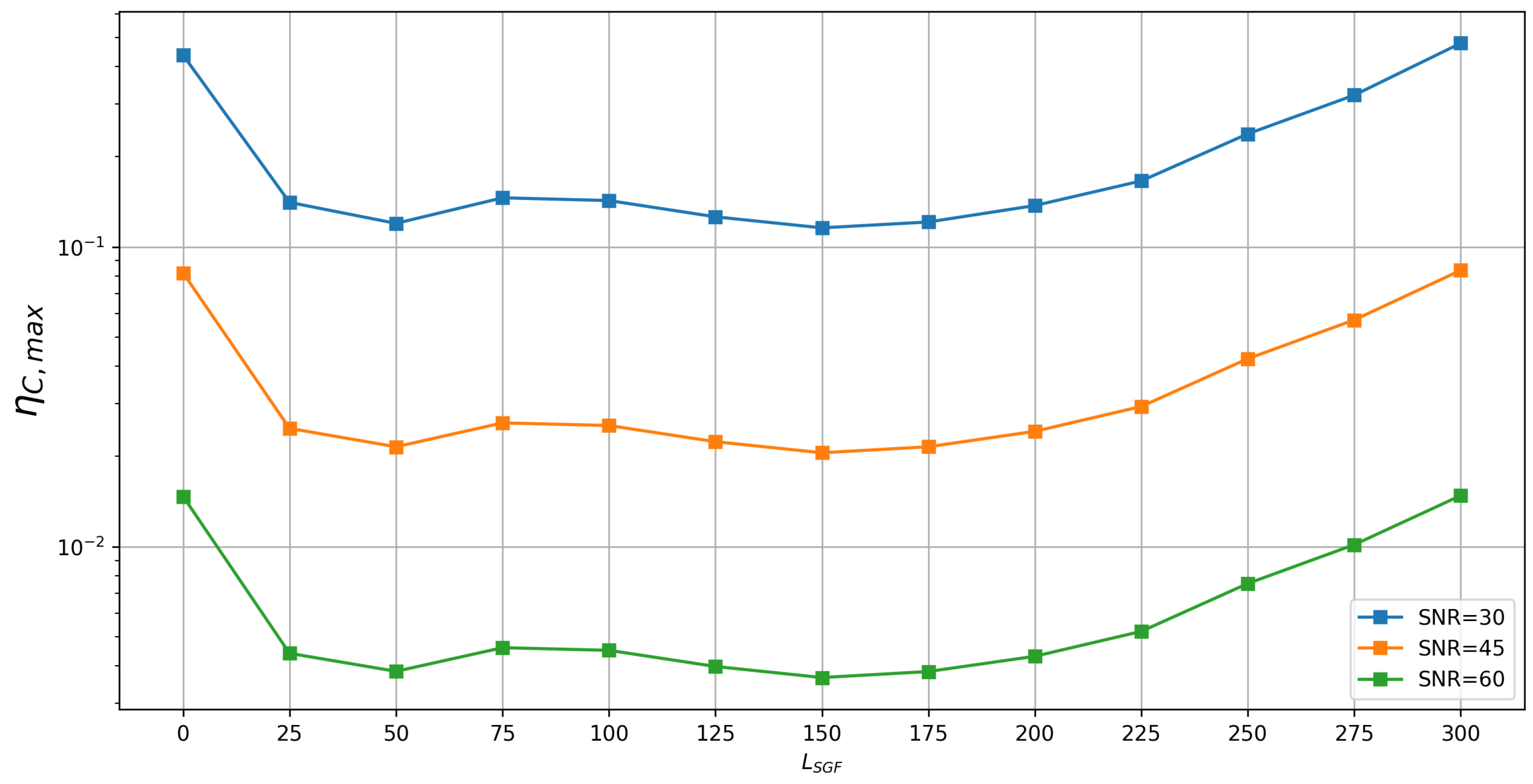
3.5. Effect of Denoising Filter
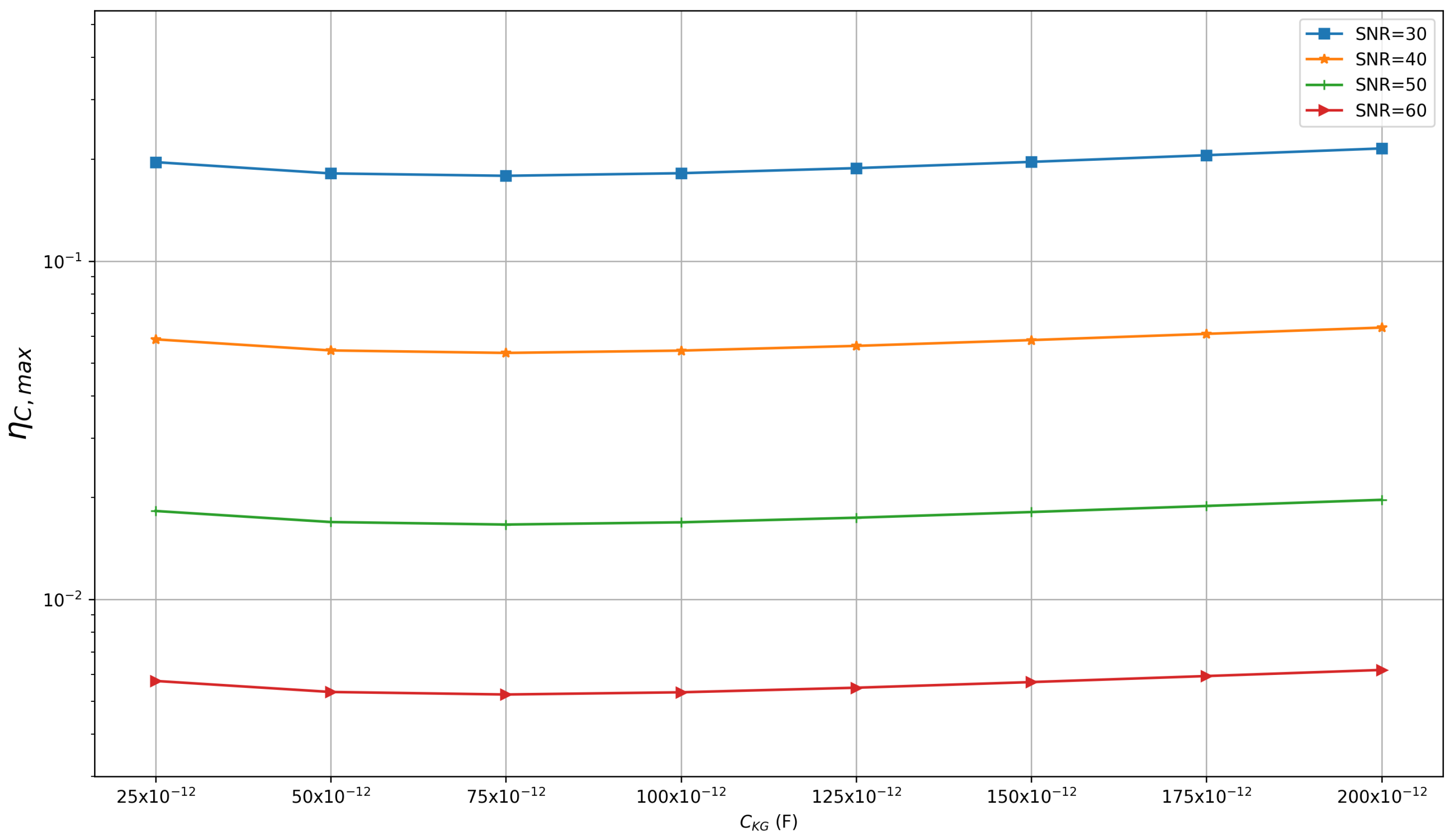
3.6. Effect of Stray Capacitances
3.7. Results with Measured Data
3.8. Comparison with Existing ECT Systems
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Huang, S.; Plaskowski, A.; Xie, C.; Beck, M. Tomographic imaging of two-component flow using capacitance sensors. J. Phys. E Sci. Instrum. 1989, 22, 173. [Google Scholar] [CrossRef]
- Marashdeh, Q.; Fan, L.S.; Du, B.; Warsito, W. Electrical capacitance tomography—A perspective. Ind. Eng. Chem. Res. 2008, 47, 3708–3719. [Google Scholar] [CrossRef]
- Rasel, R.K.; Chowdhury, S.M.; Marashdeh, Q.M.; Teixeira, F.L. Review of Selected Advances in Electrical Capacitance Volume Tomography for Multiphase Flow Monitoring. Energies 2022, 15, 5285. [Google Scholar] [CrossRef]
- Wang, H.; Yang, W. Application of electrical capacitance tomography in circulating fluidised beds—A review. Appl. Therm. Eng. 2020, 176, 115311. [Google Scholar]
- Yang, W.Q. Hardware design of electrical capacitance tomography systems. Meas. Sci. Technol. 1996, 7, 225. [Google Scholar]
- Yang, W. Design of electrical capacitance tomography sensors. Meas. Sci. Technol. 2010, 21, 042001. [Google Scholar] [CrossRef]
- Huang, S.M.; Stott, A.L.; Green, R.G.; Beck, M.S. Electronic transducers for industrial measurement of low value capacitances. J. Phys. E Sci. Instrum. 1988, 21, 242. [Google Scholar]
- Saied, I.; Meribout, M. Electronic hardware design of electrical capacitance tomography systems. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2016, 374, 20150331. [Google Scholar] [CrossRef]
- Huang, S.; Xie, C.; Beck, M.; Thorn, R.; Snowden, D. Design of sensor electronics for electrical capacitance tomography. IEE Proc. G Circuits Devices Syst. 1992, 139, 83–88. [Google Scholar] [CrossRef] [Green Version]
- Marashdeh, Q.; Warsito, W.; Fan, L.S.; Teixeira, F.L. A multimodal tomography system based on ECT sensors. IEEE Sens. J. 2007, 7, 426–433. [Google Scholar] [CrossRef]
- Hu, X.; Katsouros, M.; Yang, W.; Huang, S. Further analysis of charge/discharge capacitance measuring circuit used with tomography systems. Sens. Transducers J. 2007, 80, 1246–1256. [Google Scholar]
- Sun, S.; Cao, Z.; Huang, A.; Xu, L.; Yang, W. A high-speed digital electrical capacitance tomography system combining digital recursive demodulation and parallel capacitance measurement. IEEE Sens. J. 2017, 17, 6690–6698. [Google Scholar]
- Wang, B.; Ji, H.; Huang, Z.; Li, H. A high-speed data acquisition system for ECT based on the differential sampling method. IEEE Sens. J. 2005, 5, 308–312. [Google Scholar]
- Smolik, W.; Kryszyn, J.; Radzik, B.; Stosio, M.; Wróblewski, P.; Wanta, D.; Olszewski, T.; Szabatin, R. Single-shot high-voltage circuit for electrical capacitance tomography. Meas. Sci. Technol. 2016, 28, 025902. [Google Scholar] [CrossRef]
- Wanta, D.; Makowiecka, O.; Smolik, W.T.; Kryszyn, J.; Domański, G.; Midura, M.; Wróblewski, P. Numerical evaluation of complex capacitance measurement using pulse excitation in electrical capacitance tomography. Electronics 2022, 11, 1864. [Google Scholar] [CrossRef]
- Kryszyn, J.; Wanta, D.M.; Smolik, W.T. Gain adjustment for signal-to-noise ratio improvement in electrical capacitance tomography system EVT4. IEEE Sens. J. 2017, 17, 8107–8116. [Google Scholar]
- Jin, J.M. The Finite Element Method in Electromagnetics; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Yang, W.; Peng, L. Image reconstruction algorithms for electrical capacitance tomography. Meas. Sci. Technol. 2002, 14, R1. [Google Scholar] [CrossRef]
- Smolik, W.T.; Radomski, D. Performance evaluation of an iterative image reconstruction algorithm with sensitivity matrix updating based on real measurements for electrical capacitance tomography. Meas. Sci. Technol. 2009, 20, 115502. [Google Scholar] [CrossRef]
- Cui, Z.; Wang, Q.; Xue, Q.; Fan, W.; Zhang, L.; Cao, Z.; Sun, B.; Wang, H.; Yang, W. A review on image reconstruction algorithms for electrical capacitance/resistance tomography. Sens. Rev. 2016, 36, 429–445. [Google Scholar] [CrossRef]
- Westwood, T.J. PDE Based Models of Electric Field Sensors and Their Corresponding Inverse Problems. Ph.D. Thesis, University of Oxford, Oxford, UK, 2020. [Google Scholar]
- Anderson, E.; Bai, Z.; Bischof, C.; Blackford, S.; Demmel, J.; Dongarra, J.; Du Croz, J.; Greenbaum, A.; Hammarling, S.; McKenney, A.; et al. LAPACK Users’ Guide, 3rd ed.; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1999. [Google Scholar]
- Vogt, H.; Hendrix, M.; Nenzi, P.; Warning, D. Ngspice Users Manual Version 40 plus. 2023. Available online: https://ngspice.sourceforge.io/docs/ngspice-manual.pdf (accessed on 22 July 2023).
- Hecht, F. New development in FreeFem++. J. Numer. Math. 2012, 20, 251–266. [Google Scholar] [CrossRef] [Green Version]
- Jakoby, B.; Vellekoop, M.J. Physical sensors for water-in-oil emulsions. Sens. Actuators A Phys. 2004, 110, 28–32. [Google Scholar] [CrossRef]
- Press, W.H.; Teukolsky, S.A. Savitzky-Golay smoothing filters. Comput. Phys. 1990, 4, 669–672. [Google Scholar] [CrossRef]
- Yang, W. Calibration of capacitance tomography systems: A new method for setting system measurement range. Meas. Sci. Technol. 1996, 7, L863. [Google Scholar]
- Process Tomography Ltd. Electrical Capacitance Tomography System. Type TFLR 5000. Operating Manual Issue. 2009, Volume 1. Available online: http://www.tomography.com/pdf/Fundamentals%20of%20ECT.pdf (accessed on 22 July 2023).



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kalarickel Ramakrishnan, P.; Westwood, T.; Magalhães Gouveia, T.; Taani, M.; de Jager, K.; Murdoch, K.; Orlov, A.A.; Ozhgibesov, M.S.; Propodalina, T.V.; Wojtowicz, N. Capacitance Estimation for Electrical Capacitance Tomography Sensors Using Digital Processing of Time-Domain Voltage Response to Single-Pulse Excitation. Electronics 2023, 12, 3242. https://doi.org/10.3390/electronics12153242
Kalarickel Ramakrishnan P, Westwood T, Magalhães Gouveia T, Taani M, de Jager K, Murdoch K, Orlov AA, Ozhgibesov MS, Propodalina TV, Wojtowicz N. Capacitance Estimation for Electrical Capacitance Tomography Sensors Using Digital Processing of Time-Domain Voltage Response to Single-Pulse Excitation. Electronics. 2023; 12(15):3242. https://doi.org/10.3390/electronics12153242
Chicago/Turabian StyleKalarickel Ramakrishnan, Praveen, Timothy Westwood, Tomé Magalhães Gouveia, Mahdi Taani, Kylie de Jager, Kenny Murdoch, Andrey A. Orlov, Mikhail S. Ozhgibesov, Tatiana V. Propodalina, and Natalia Wojtowicz. 2023. "Capacitance Estimation for Electrical Capacitance Tomography Sensors Using Digital Processing of Time-Domain Voltage Response to Single-Pulse Excitation" Electronics 12, no. 15: 3242. https://doi.org/10.3390/electronics12153242
APA StyleKalarickel Ramakrishnan, P., Westwood, T., Magalhães Gouveia, T., Taani, M., de Jager, K., Murdoch, K., Orlov, A. A., Ozhgibesov, M. S., Propodalina, T. V., & Wojtowicz, N. (2023). Capacitance Estimation for Electrical Capacitance Tomography Sensors Using Digital Processing of Time-Domain Voltage Response to Single-Pulse Excitation. Electronics, 12(15), 3242. https://doi.org/10.3390/electronics12153242







