Pseudo Labels for Unsupervised Domain Adaptation: A Review
Abstract
1. Introduction
- We review in detail the background knowledge related to DA and pseudo-labeling methods and sort out the connections and differences between them.
- We have organized and analyzed the paper in detail in terms of both the pseudo-labeling generation method and the application of pseudo-labeling in unsupervised DA. To the best of our knowledge, it is the first attempt to summarize pseudo labels used in the community of domain adaptation.
- We conducted a comprehensive review of various pseudo-labeling methods within each category through experimental evaluations. This analysis enables readers to grasp the nuances of each technique and make informed decisions.
- We point out possible challenges and future directions for pseudo-labeling methods in DA applications.
2. Background
2.1. Unsupervised Domain Adaptation
2.2. Pseudo-Labeling
3. Pseudo-Labeling Generation Methods
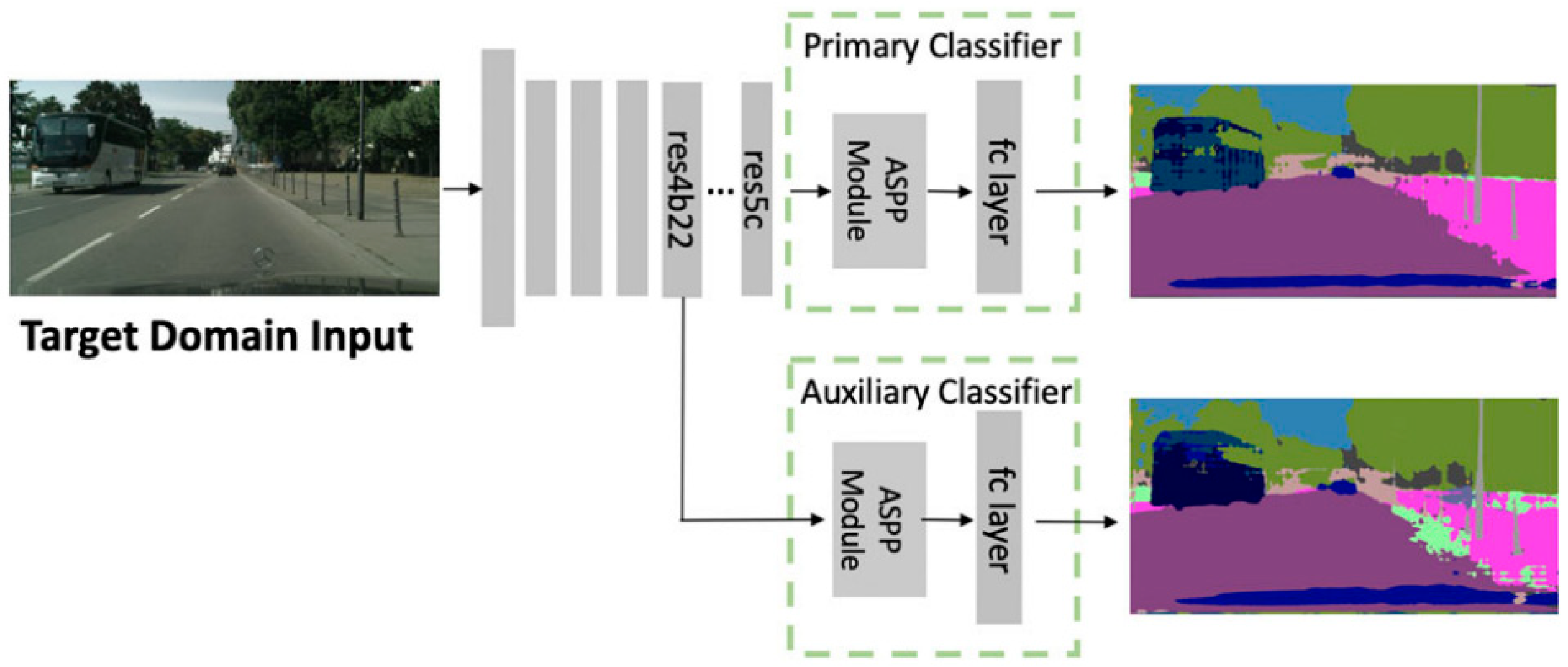
3.1. Single-Classifier-Based Generation Method
3.2. Multi-Classifier-Based Generation Methods
3.3. Category-Balancing Methods for Difficult Samples
4. Application of Pseudo-Labeling in Domain Adaptation
4.1. Application of Pseudo-Labeling in Improving Classifier Discrimination
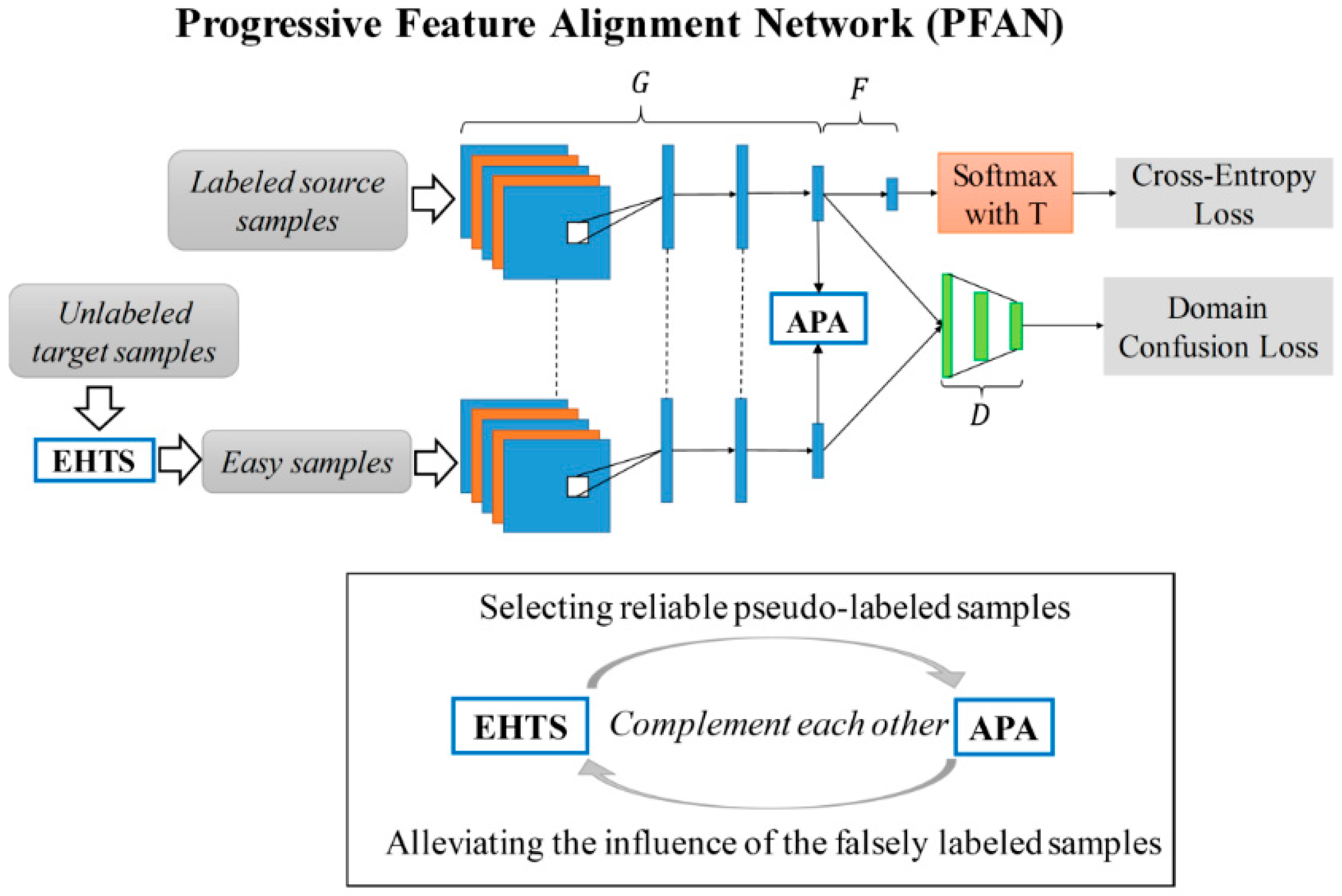
4.2. Application of Pseudo-Labeling in Category Feature Alignment
5. Experience Evaluation
6. Challenges and Future Directions
- (1)
- There is a lack of a common, universal indicator to evaluate the quality of pseudo-labels.
- (2)
- Cross-domain issues affect the quality of pseudo-labels.
- (3)
- The dataset is more homogeneous, while the real scenario is more complex.
- (4)
- Research has mainly focused on classification problems, and there is a lack of research on other DA problems.
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tan, C.; Sun, F.; Kong, T.; Zhang, W.; Yang, C.; Liu, C. A Survey on Deep Transfer Learning. arXiv 2018. [Google Scholar] [CrossRef]
- Mei, W.; Deng, W. Deep Visual Domain Adaptation: A Survey. Neurocomputing 2018, 312, 135–153. [Google Scholar] [CrossRef]
- Wilson, G.; Cook, D.J. A Survey of Unsupervised Deep Domain Adaptation. arXiv 2020. [Google Scholar] [CrossRef] [PubMed]
- Kouw, W.M.; Loog, M. A Review of Domain Adaptation without Target Labels. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 43, 766–785. [Google Scholar] [CrossRef]
- Fan, M.; Cai, Z.; Zhang, T.; Wang, B. A survey of deep domain adaptation based on label set classification. Multimedia Tools Appl. 2022, 81, 39545–39576. [Google Scholar] [CrossRef]
- Chen, W.; Hu, H. Generative attention adversarial classification network for unsupervised domain adaptation. Pattern Recognit. 2020, 107, 107440. [Google Scholar] [CrossRef]
- Ben-David, S.; Blitzer, J.; Crammer, K.; Kulesza, A.; Pereira, F.C.; Vaughan, J.W. A theory of learning from different domains. Mach. Learn. 2010, 79, 151–175. [Google Scholar] [CrossRef]
- Gretton, A.; Borgwardt, K.; Rasch, M.; Schölkopf, B.; Smola, A.J. A Kernel Two-Sample Test. J. Mach. Learn. Res. 2012, 13, 723–773. [Google Scholar]
- Ganin, Y.; Ustinova, E.; Ajakan, H.; Germain, P.; Larochelle, H.; Laviolette, F.; Marchand, M.; Lempitsky, V. Domain-Adversarial Training of Neural Networks. J. Mach. Learn. Res. 2015, 17, 2096-2030. [Google Scholar]
- Tzeng, E.; Hoffman, J.; Saenko, K.; Darrell, T. Adversarial Discriminative Domain Adaptation. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 2962–2971. [Google Scholar]
- Zhang, Y.; Jing, C.; Lin, H.; Chen, C.; Huang, Y.; Ding, X.; Zou, Y. Hard Class Rectification for Domain Adaptation. Knowl. Based Syst. 2020, 222, 107011. [Google Scholar] [CrossRef]
- Lee, D.-H. Pseudo-Label: The Simple and Efficient Semi-Supervised Learning Method for Deep Neural Networks. In Proceedings of the ICML 2013 Workshop: Challenges in Representation Learning (WREPL), Atlanta, GA, USA, 16–21 June 2013. [Google Scholar]
- Kong, L.; Hu, B.; Liu, X.; Lu, J.; You, J.; Liu, X. Constraining pseudo-label in self-training unsupervised domain adaptation with energy-based model. Int. J. Intell. Syst. 2022, 37, 8092–8112. [Google Scholar] [CrossRef]
- Zhou, Z.-H.; Li, M. Semi-supervised learning by disagreement. Knowl. Inf. Syst. 2010, 24, 415–439. [Google Scholar] [CrossRef]
- Zhu, X. Semi-Supervised Learning Literature Survey; Comput Sci, University of Wisconsin-Madison: Madison, WI, USA, 2008; p. 2. [Google Scholar]
- Grandvalet, Y.; Bengio, Y. Semi-supervised Learning by Entropy Minimization. In Proceedings of the Conférence Francophone sur L’apprentissage Automatique, Montpellier, LIF, France, 16–19 June 2004. [Google Scholar]
- Wang, Q.; Breckon, T. Unsupervised Domain Adaptation via Structured Prediction Based Selective Pseudo-Labeling. Proc. AAAI Conf. Artif. Intell. 2020, 34, 6243–6250. [Google Scholar] [CrossRef]
- Deng, Z.; Luo, Y.; Zhu, J. Cluster Alignment with a Teacher for Unsupervised Domain Adaptation. arXiv 2019. [Google Scholar] [CrossRef]
- Shin, I.; Woo, S.; Pan, F.; Kweon, I. Two-Phase Pseudo Label Densification for Self-Training Based Domain Adaptation; Springer International Publishing: Cham, Switzerland, 2020. [Google Scholar]
- Wang, F.; Han, Z.; Yin, Y. Source Free Robust Domain Adaptation Based on Pseudo Label Uncertainty Estimation. J. Softw. 2022, 33, 1183–1199. [Google Scholar] [CrossRef]
- Zhang, Y.; Deng, B.; Jia, K.; Zhang, L. Gradual Domain Adaptation via Self-Training of Auxiliary Models. arXiv 2021. [Google Scholar] [CrossRef]
- Qin, C.; Wang, L.; Zhang, Y.; Fu, Y. Generatively Inferential Co-Training for Unsupervised Domain Adaptation. In Proceedings of the IEEE/CVF International Conference on Computer Vision Workshops, Seoul, Republic of Korea, 27–28 October 2019; pp. 1055–1064. [Google Scholar] [CrossRef]
- Zhou, Z.-H.; Li, M. Tri-training: Exploiting unlabeled data using three classifiers. IEEE Trans. Knowl. Data Eng. 2005, 17, 1529–1541. [Google Scholar] [CrossRef]
- Saito, K.; Ushiku, Y.; Harada, T. Asymmetric Tri-training for Unsupervised Domain Adaptation. In Proceedings of the International Conference on Machine Learning, Sydney, Australia, 11–15 August 2017. [Google Scholar]
- Zhang, H.; Cisse, M.; Dauphin, Y.N.; Lopez-Paz, D. mixup: Beyond Empirical Risk Minimization. arXiv 2018. [Google Scholar] [CrossRef]
- Li, J.; Wang, G.; Chen, M.; Ding, Z.; Yang, H. Mixup Asymmetric Tri-Training for Heartbeat Classification under Domain Shift. IEEE Signal Process. Lett. 2021, 28, 718–722. [Google Scholar] [CrossRef]
- Venkat, N.; Kundu, J.; Singh, D.K.; Revanur, A.; VenkateshBabu, R. Your Classifier can Secretly Suffice Multi-Source Domain Adaptation. arXiv 2021. [Google Scholar] [CrossRef]
- Zheng, Z.; Yang, Y. Rectifying Pseudo Label Learning via Uncertainty Estimation for Domain Adaptive Semantic Segmentation. Int. J. Comput. Vis. 2020, 129, 1106–1120. [Google Scholar] [CrossRef]
- Zou, Y.; Yu, Z.; Kumar BV, K.V.; Wang, J. Domain Adaptation for Semantic Segmentation via Class-Balanced Self-Training. arXiv 2018. [Google Scholar] [CrossRef]
- Du, Z.; Li, J.; Su, H.; Zhu, L.; Lu, K. Cross-Domain Gradient Discrepancy Minimization for Unsupervised Domain Adaptation. arXiv 2021. [Google Scholar] [CrossRef]
- Saito, K.; Watanabe, K.; Ushiku, Y.; Harada, T. Maximum Classifier Discrepancy for Unsupervised Domain Adaptation. arXiv 2018. [Google Scholar] [CrossRef]
- Li, S.; Zhang, J.; Ma, W.; Liu, C.H.; Li, W. Dynamic Domain Adaptation for Efficient Inference. arXiv 2021. [Google Scholar] [CrossRef]
- Ge, Y.; Chen, D.; Li, H. Mutual Mean-Teaching: Pseudo Label Refinery for Unsupervised Domain Adaptation on Person Re-identification. arXiv 2020. [Google Scholar] [CrossRef]
- Chen, C.; Xie, W.; Xu, T.; Huang, W.; Rong, Y.; Ding, X.; Huang, Y.; Huang, J. Progressive Feature Alignment for Unsupervised Domain Adaptation. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 627–636. [Google Scholar]
- Kumar, M.P.; Packer, B.; Koller, D. Self-Paced Learning for Latent Variable Models. NIPS 2010, 1, 1189–1197. [Google Scholar]
- Liu, H.; Wang, J.; Long, M. Cycle Self-Training for Domain Adaptation. arXiv 2021. [Google Scholar] [CrossRef]
- Zhao, X.; Wang, S. (11 2019). Adversarial Learning and Interpolation Consistency for Unsupervised Domain Adaptation. IEEE Access 2019, 7, 170448–170456. [Google Scholar] [CrossRef]
- Hinton, G.E.; Vinyals, O.; Dean, J. Distilling the Knowledge in a Neural Network. arXiv 2015. [Google Scholar] [CrossRef]
- Zhang, W.; Ouyang, W.; Li, W.; Xu, D. Collaborative and Adversarial Network for Unsupervised Domain Adaptation. In Proceedings of the2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 3801–3809. [Google Scholar]
- Xie, S.; Zheng, Z.; Chen, L.; Chen, C. Learning Semantic Representations for Unsupervised Domain Adaptation. In Proceedings of the International Conference on Machine Learning, Stockholm Sweden, 10–15 July 2018. [Google Scholar]
- Wang, Q.; Bu, P.; Breckon, T. Unifying Unsupervised Domain Adaptation and Zero-Shot Visual Recognition. In Proceedings of the 2019 International Joint Conference on Neural Networks (IJCNN), Budapest, Hungary, 14–19 July 2019. [Google Scholar] [CrossRef]
- Kang, G.; Jiang, L.; Yang, Y.; Hauptmann, A. Contrastive Adaptation Network for Unsupervised Domain Adaptation. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 4888–4897. [Google Scholar]
- Chen, C.; Fu, Z.; Chen, Z.; Jin, S.; Cheng, Z.; Jin, X.; Hua, X. HoMM: Higher-order Moment Matching for Unsupervised Domain Adaptation. arXiv 2019. [Google Scholar] [CrossRef]
- Dong, J.; Fang, Z.; Liu, A.; Sun, G.; Liu, T. Confident Anchor-Induced Multi-Source Free Domain Adaptation. In Proceedings of the Neural Information Processing Systems, Virtual, 6–12 December 2021. [Google Scholar]
- Li, M.; Zhai, Y.; Luo, Y.; Ge, P.; Ren, C. Enhanced Transport Distance for Unsupervised Domain Adaptation. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 13933–13941. [Google Scholar]
- Yang, G.; Xia, H.; Ding, M.; Ding, Z. Bi-Directional Generation for Unsupervised Domain Adaptation. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020. [Google Scholar]
- Hu, L.; Kan, M.; Shan, S.; Chen, X. Duplex Generative Adversarial Network for Unsupervised Domain Adaptation. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 1498–1507. [Google Scholar]
- Russo, P.; Carlucci, F.M.; Tommasi, T.; Caputo, B. From Source to Target and Back: Symmetric Bi-Directional Adaptive GAN. 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 8099–8108. [Google Scholar]
- Goodfellow, I.J.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.C.; Bengio, Y. Generative Adversarial Networks. arXiv 2014. [Google Scholar] [CrossRef]
- Gui, J.; Sun, Z.; Wen, Y.; Tao, D.; Ye, J. A Review on Generative Adversarial Networks: Algorithms, Theory, and Applications. IEEE Trans. Knowl. Data Eng. 2020, 35, 3313–3332. [Google Scholar] [CrossRef]
- Radford, A.; Metz, L.; Chintala, S. Unsupervised Representation Learning with Deep Convolutional Generative Adversarial Networks. arXiv 2015. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Y.; Wang, Y.; Tian, Q. Domain-Invariant Adversarial Learning for Unsupervised Domain Adaption. arXiv 2018. [Google Scholar] [CrossRef]
- Chen, M.; Zhao, S.; Liu, H.; Cai, D. Adversarial-Learned Loss for Domain Adaptation. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020. [Google Scholar]
- Chadha, A.; Andreopoulos, Y. Improved Techniques for Adversarial Discriminative Domain Adaptation. IEEE Trans. Image Process. 2019, 29, 2622–2637. [Google Scholar] [CrossRef]
- Tanwani, A.K. DIRL: Domain-Invariant Representation Learning for Sim-to-Real Transfer. arXiv 2021. [Google Scholar] [CrossRef]
- Jiang, X.; Lao, Q.; Matwin, S.; Havaei, M. Implicit Class-Conditioned Domain Alignment for Unsupervised Domain Adaptation. arXiv 2020. [Google Scholar] [CrossRef]
- Yu, C.; Wang, J.; Chen, Y.; Huang, M. Transfer Learning with Dynamic Adversarial Adaptation Network. arXiv 2019. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, L. Self-adaptive Re-weighted Adversarial Domain Adaptation. arXiv 2020. [Google Scholar] [CrossRef]
- Xinhong, M.; Zhang, T.; Xu, C. GCAN: Graph Convolutional Adversarial Network for Unsupervised Domain Adaptation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 8258–8268. [Google Scholar] [CrossRef]
- Fang, X.; Bai, H.; Guo, Z.; Shen, B.; Hoi, S.; Xu, Z. DART: Domain-Adversarial Residual-Transfer networks for unsupervised cross-domain image classification. Neural Netw. 2020, 127, 182–192. [Google Scholar] [CrossRef] [PubMed]
- Cicek, S.; Soatto, S. Unsupervised Domain Adaptation via Regularized Conditional Alignment. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Long Beach, CA, USA, 15–20 June 2019; pp. 1416–1425. [Google Scholar]
- Gu, X.; Sun, J.; Xu, Z. Spherical Space Domain Adaptation with Robust Pseudo-Label Loss. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 9098–9107. [Google Scholar]
- Long, M.; Wang, J.; Ding, G.; Sun, J.; Yu, P.S. Transfer Feature Learning with Joint Distribution Adaptation. In Proceedings of the 2013 IEEE International Conference on Computer Vision, Sydney, Australia, 1–8 December 2013; pp. 2200–2207. [Google Scholar]
- Luo, Y.; Ren, C. Conditional Bures Metric for Domain Adaptation. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 13984–13993. [Google Scholar]
- Li, S.; Xie, M.; Gong, K.; Liu, C.H.; Wang, Y.; Li, W. Transferable Semantic Augmentation for Domain Adaptation. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 11511–11520. [Google Scholar]
- Tanwisuth, K.; Fan, X.; Zheng, H.; Zhang, S.; Zhang, H.; Chen, B.; Zhou, M. A Prototype-Oriented Framework for Unsupervised Domain Adaptation. Adv. Neural Inf. Process. Syst. 2021, 34, 17194–17208. [Google Scholar]
- Liang, J.; He, R.; Sun, Z.; Tan, T. Distant Supervised Centroid Shift: A Simple and Efficient Approach to Visual Domain Adaptation. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 2970–2979. [Google Scholar]
- Zhao, Y.; Wang, M.; Cai, L. Reducing the Covariate Shift by Mirror Samples in Cross Domain Alignment. In Proceedings of the 35th Conference on Neural Information Processing Systems, Online, 6–14 December 2021. [Google Scholar]
- Jabi, M.; Pedersoli, M.; Mitiche, A.; Ayed, I.B. Deep Clustering: On the Link Between Discriminative Models and K-Means. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 43, 1887–1896. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Jiang, K.; Zhang, X. Implicit Task-Driven Probability Discrepancy Measure for Unsupervised Domain Adaptation. Adv. Neural Inf. Process. Syst. 2021, 34, 25824–25838. [Google Scholar]
- Liang, J.; Hu, D.; Feng, J. Domain Adaptation with Auxiliary Target Domain-Oriented Classifier. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 16627–16637. [Google Scholar]
- Sharma, A.; Kalluri, T.; Chandraker, M. Instance Level Affinity-Based Transfer for Unsupervised Domain Adaptation. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 5357–5367. [Google Scholar]
- Xu, R.; Liu, P.; Wang, L.; Chen, C.; Wang, J.; He, K.; Zhang, X.; Ren, S.; Long, M.; Cao, Z.; et al. Reliable Weighted Optimal Transport for Unsupervised Domain Adaptation. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 4393–4402. [Google Scholar]
- Luo, Y.; Ren, C.; Ge, P.; Huang, K.; Yu, Y. Unsupervised Domain Adaptation via Discriminative Manifold Embedding and Alignment. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020. [Google Scholar]
- Hou, Y.; Zheng, L. Visualizing Adapted Knowledge in Domain Transfer. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 13819–13828. [Google Scholar]
- Zhu, P.; Wang, H.; Saligrama, V. Learning Classifiers for Target Domain with Limited or No Labels. In Proceedings of the International Conference on Machine Learning, Long Beach, CA, USA, 10–15 June 2019. [Google Scholar]
- Xu, M.; Zhang, J.; Ni, B.; Li, T.; Wang, C.; Tian, Q.; Zhang, W. Adversarial Domain Adaptation with Domain Mixup. In Proceedings of the AAAI Conference on Artificial Intelligence, Long Beach, CA, USA, 10–15 June 2019. [Google Scholar]
- Zhong, L.; Fang, Z.; Liu, F.; Lu, J.; Yuan, B.; Zhang, G. How does the Combined Risk Affect the Performance of Unsupervised Domain Adaptation Approaches? arXiv 2020. [Google Scholar] [CrossRef]
- Mignone, P.; Pio, G.; Ceci, M. Distributed Heterogeneous Transfer Learning for Link Prediction in the Positive Unlabeled Setting. In Proceedings of the 2022 IEEE International Conference on Big Data (Big Data), Osaka, Japan, 17–20 December 2022; pp. 5536–5541. [Google Scholar]
- He, Q.; Siu, S.W.; Si, Y. Attentive recurrent adversarial domain adaptation with Top-k pseudo-labeling for time series classification. Appl. Intell. 2022, 53, 13110–13129. [Google Scholar] [CrossRef]
- Yu, Z.; Li, J.; Du, Z.; Zhu, L.; Shen, H.T. A Comprehensive Survey on Source-free Domain Adaptation. arXiv 2023. [Google Scholar] [CrossRef]
- Long, M.; Zhu, H.; Wang, J.; Jordan, M.I. Deep Transfer Learning with Joint Adaptation Networks. In Proceedings of the International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016. [Google Scholar]









| Generation Methods | Method | A → W | D → W | W → D | A → D | D → A | W → A | Avg |
|---|---|---|---|---|---|---|---|---|
| Baselines | JAN [82] | 85.4 ± 0.4 | 96.7 ± 0.3 | 99.7 ± 0.1 | 85.1 ± 0.4 | 69.2 ± 0.4 | 70.7 ± 0.5 | 84.6 |
| SPL [17] | 92.7 | 98.7 | 99.8 | 93.0 | 76.4 | 76.8 | 89.6 | |
| Single-classifier | CAT [18] | 94.4 ± 0.1 | 98.0 ± 0.2 | 100.0 ± 0.0 | 90.8 ± 1.8 | 72.2 ± 0.6 | 70.2 ± 0.1 | 87.6 |
| PLUE-SFRDA [20] | 92.5 | 98.3 | 100.0 | 96.4 | 74.5 | 72.2 | 89.0 | |
| SImpAI [27] | 97.9 ± 0.2 | 97.9 ± 0.2 | 99.4 ± 0.2 | 99.4 ± 0.2 | 71.2 ± 0.4 | 71.2 ± 0.4 | 89.5 ± 0.3 | |
| Multi-classifier | MCS [67] | 97.2 | 97.2 | 99.4 | 99.4 | 61.3 | 61.3 | 86.0 |
| CAiDA [44] | 98.9 | 98.9 | 99.8 | 99.8 | 75.8 | 75.8 | 91.6 | |
| Difficult samples | HCRPL [11] | 95.9 ± 0.2 | 98.7 ± 0.1 | 100.0 ± 0.0 | 94.3 ± 0.2 | 75.0 ± 0.4 | 75.4 ± 0.4 | 89.9 |
| Application Scenario | A → W | D → W | W → D | A → D | D → A | W → A | Avg | |
|---|---|---|---|---|---|---|---|---|
| Baselines | JAN [80] | 85.4 ± 0.4 | 96.7 ± 0.3 | 99.7 ± 0.1 | 85.1 ± 0.4 | 69.2 ± 0.4 | 70.7 ± 0.5 | 84.6 |
| DIAL [52] | 91.7 ± 0.4 | 97.1 ± 0.3 | 99.8 ± 0.0 | 89.3 ± 0.4 | 71.7 ± 0.7 | 71.4 ± 0.2 | 86.8 | |
| MDD + Alignment [56] | 90.3 ± 0.2 | 98.7 ± 0.1 | 99.8 ± 0.0 | 92.1 ± 0.5 | 75.3 ± 0.2 | 74.9 ± 0.3 | 88.8 | |
| SRADA [58] | 95.2 | 98.6 | 100.0 | 91.7 | 74.5 | 73.7 | 89.0 | |
| DART [60] | 87.3 ± 0.1 | 98.4 ± 0.1 | 99.9 ± 0.1 | 91.6 ± 0.1 | 70.3 ± 0.1 | 69.7 ± 0.1 | 86.2 | |
| ALDA [53] | 95.6 ± 0.5 | 97.7 ± 0.1 | 100.0 | 94.0. ± 0.4 | 72.2 ± 0.4 | 72.5 ± 0.2 | 88.7 | |
| GAACN [6] | 90.2 | 98.4 | 100.0 | 90.4 | 67.4 | 67.7 | 85.6 | |
| RSDA-MSTN [62] | 96.1 ± 0.2 | 99.3 ± 0.2 | 100.0 ± 0 | 95.8 ± 0.3 | 77.4 ± 0.8 | 78.9 ± 0.3 | 91.1 | |
| TSA [65] | 94.8 | 99.1 | 100.0 | 92.6 | 74.9 | 74.4 | 89.3 | |
| Classifier discrimination | PCT [66] | 94.6 ± 0.5 | 98.7 ± 0.4 | 99.9 ± 0.1 | 93.8 ± 1.8 | 77.2 ± 0.5 | 76.0 ± 0.9 | 90.0 |
| MCS [67] | 97.2 | 97.2 | 99.4 | 99.4 | 61.3 | 61.3 | 86.0 | |
| Mirror [68] | 98.5 ± 0.3 | 99.3 ± 0.1 | 100.0 ± 0.0 | 96.2 ± 0.1 | 77.0 ± 0.1 | 78.9 ± 0.1 | 91.7 | |
| i-CDD [70] | 95.4 ± 0.4 | 98.5 ± 0.2 | 100.0 ± 0.0 | 96.3 ± 0.3 | 77.2 ± 0.3 | 78.3 ± 0.2 | 90.9 | |
| ATDOC [71] | 94.6 | 98.1 | 99.7 | 95.4 | 77.5 | 77.0 | 86.1 | |
| ILA-DA [72] | 95.7 | 99.2 | 100.0 | 93.3 | 72.1 | 75.4 | 89.3 | |
| RWOT [73] | 95.1 ± 0.2 | 94.5 ± 0.2 | 99.5 ± 0.2 | 100.0 ± 0.0 | 77.5 ± 0.1 | 77.9 ± 0.3 | 90.8 | |
| Fine-tuning [75] | 91.8 | 98.7 | 99.9 | 89.9 | 73.9 | 72.0 | 87.7 | |
| E-MixNet [78] | 93.0 ± 0.3 | 99.0 ± 0.1 | 100.0 ± 0.0 | 95.6 ± 0.2 | 78.9 ± 0.5 | 74.7 ± 0.7 | 90.2 | |
| iCAN [39] | 92.5 | 98.8 | 100.0 | 90.1 | 72.1 | 69.9 | 87.2 | |
| CAPLS [41] | 90.6 | 98.6 | 99.6 | 88.6 | 75.4 | 76.3 | 88.2 | |
| CAN [42] | 94.5 ± 0.3 | 99.1 ± 0.2 | 99.8 ± 0.2 | 95.0 ± 0.3 | 78.0 ± 0.3 | 77.0 ± 0.3 | 90.6 | |
| Category feature alignment | HoMM [43] | 91.7 ± 0.3 | 98.8 ± 0.0 | 100.0 ± 0.0 | 89.1 ± 0.3 | 71.2 ± 0.2 | 70.6 ± 0.3 | 86.9 |
| CAiDA [44] | 98.9 | 98.9 | 99.8 | 99.8 | 75.8 | 75.8 | 91.6 | |
| ETD [45] | 92.1 | 100.0 | 100.0 | 88.0 | 71.0 | 67.8 | 86.2 | |
| BDG [46] | 93.6 ± 0.4 | 99.0 ± 0.1 | 100.0 ± 0. | 93.6 ± 0.3 | 73.2 ± 0.2 | 72.0 ± 0.1 | 88.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Guo, L.; Ge, Y. Pseudo Labels for Unsupervised Domain Adaptation: A Review. Electronics 2023, 12, 3325. https://doi.org/10.3390/electronics12153325
Li Y, Guo L, Ge Y. Pseudo Labels for Unsupervised Domain Adaptation: A Review. Electronics. 2023; 12(15):3325. https://doi.org/10.3390/electronics12153325
Chicago/Turabian StyleLi, Yundong, Longxia Guo, and Yizheng Ge. 2023. "Pseudo Labels for Unsupervised Domain Adaptation: A Review" Electronics 12, no. 15: 3325. https://doi.org/10.3390/electronics12153325
APA StyleLi, Y., Guo, L., & Ge, Y. (2023). Pseudo Labels for Unsupervised Domain Adaptation: A Review. Electronics, 12(15), 3325. https://doi.org/10.3390/electronics12153325






