A Wideband Power Amplifier in 65 nm CMOS Covering 25.8 GHz–36.9 GHz by Staggering Tuned MCRs
Abstract
:1. Introduction
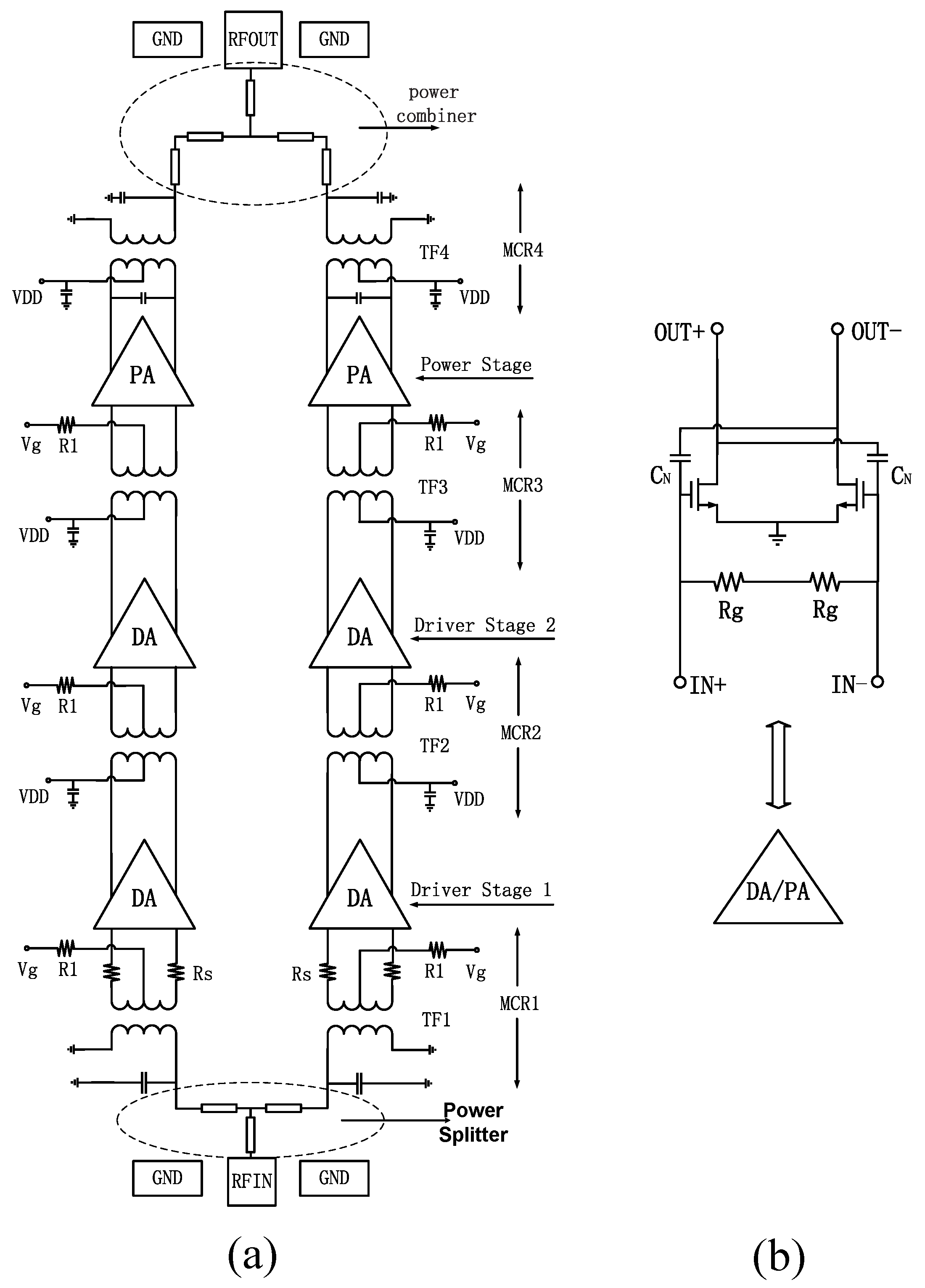
2. Analysis and Design
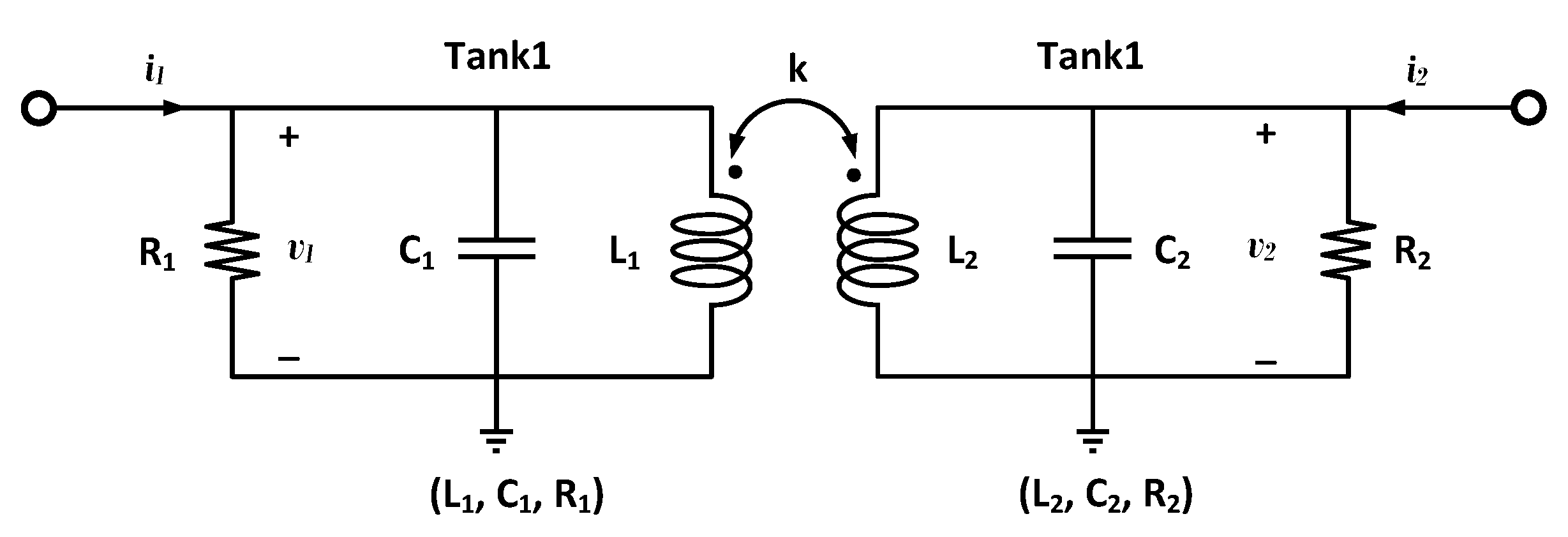
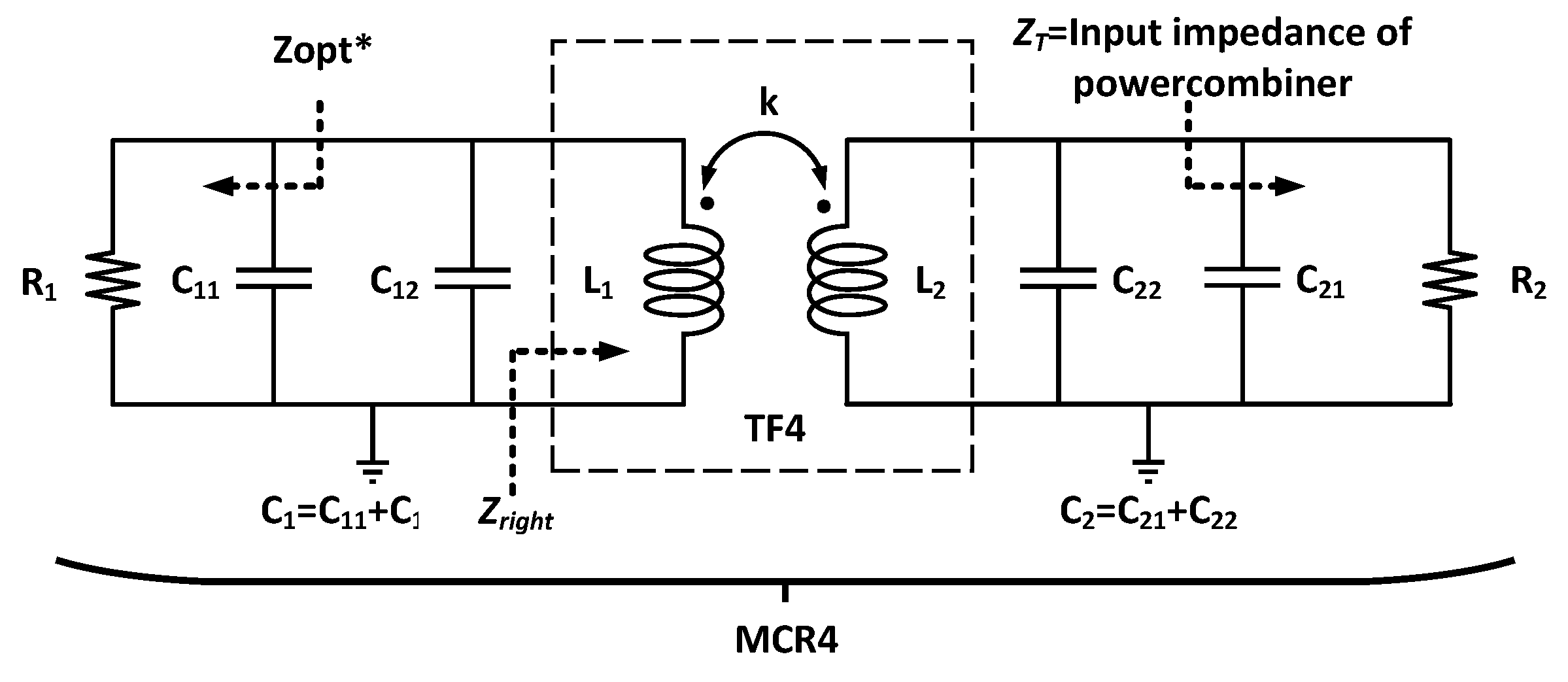
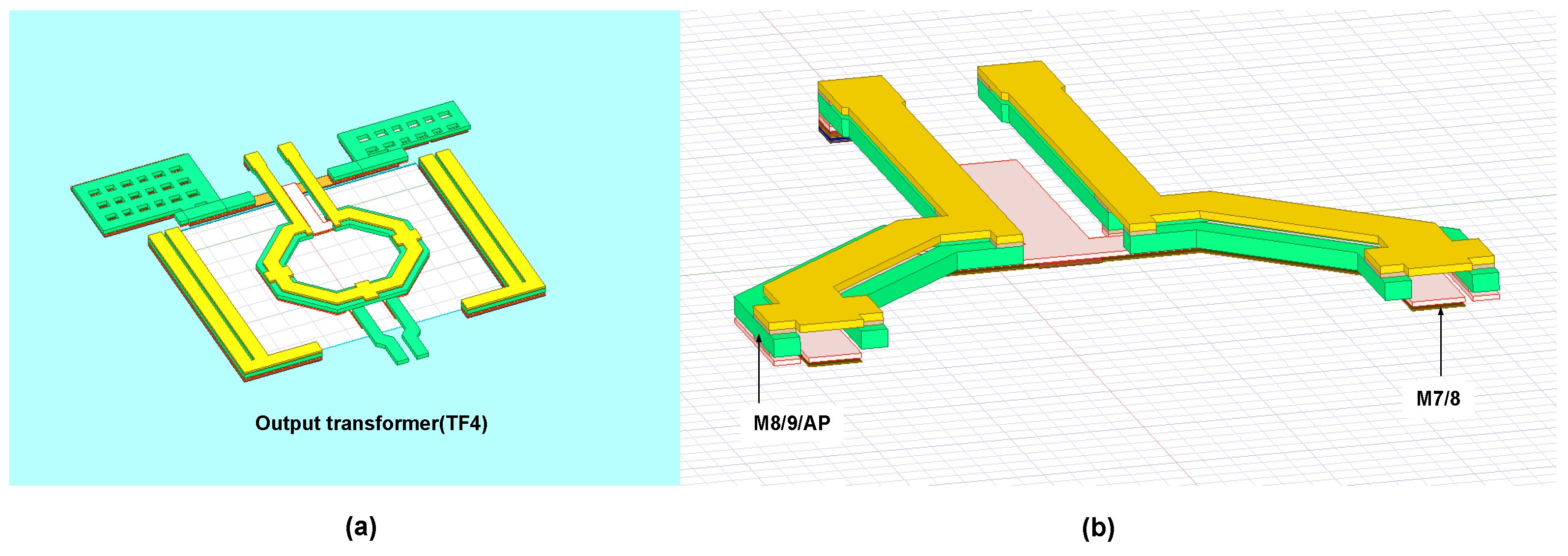
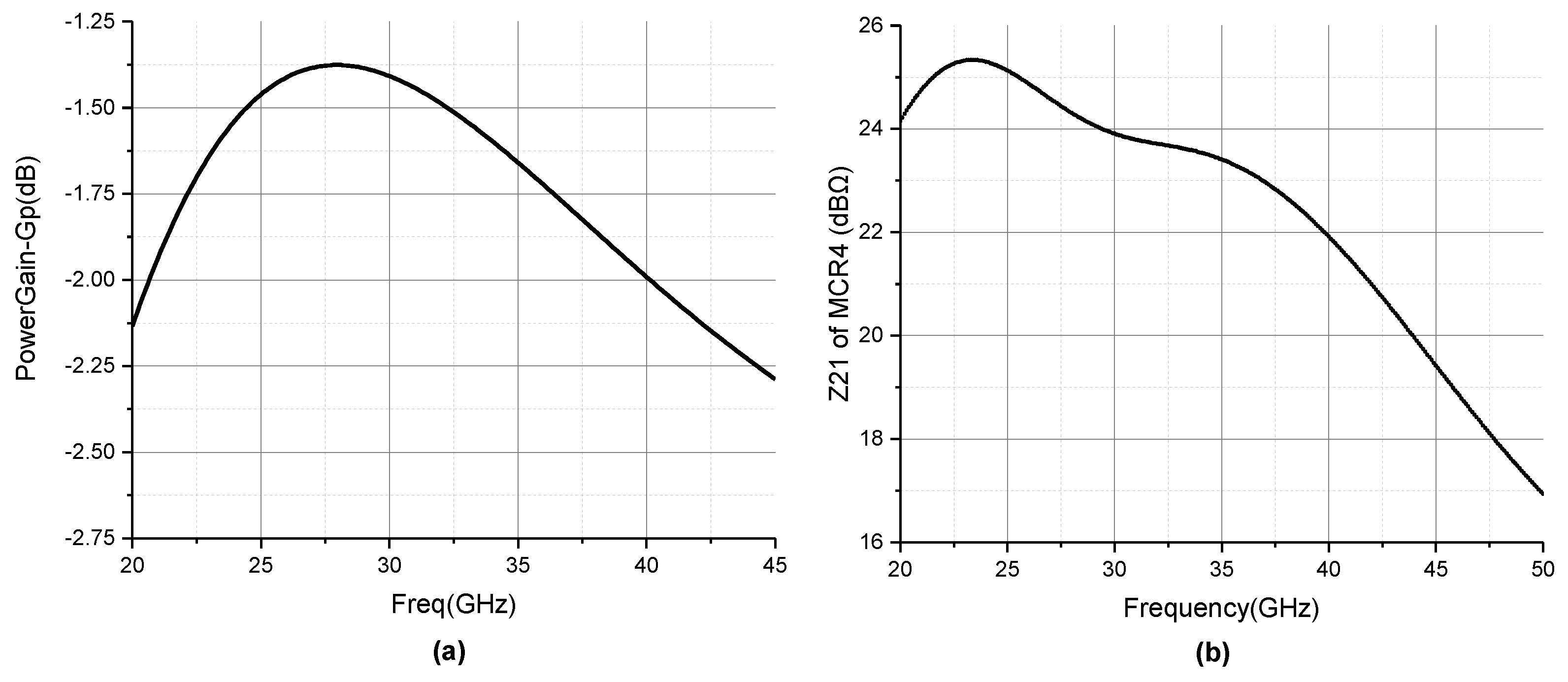
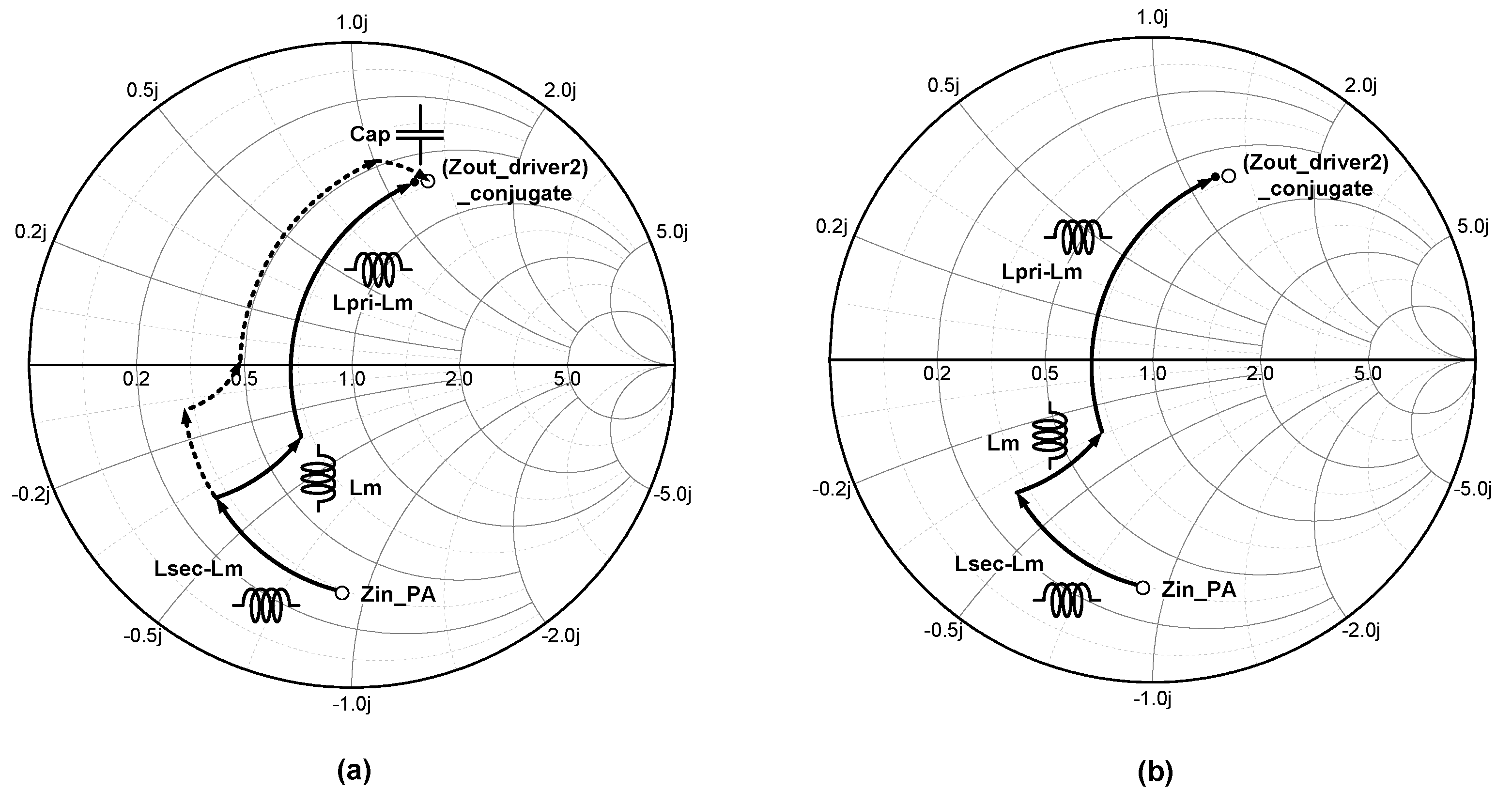
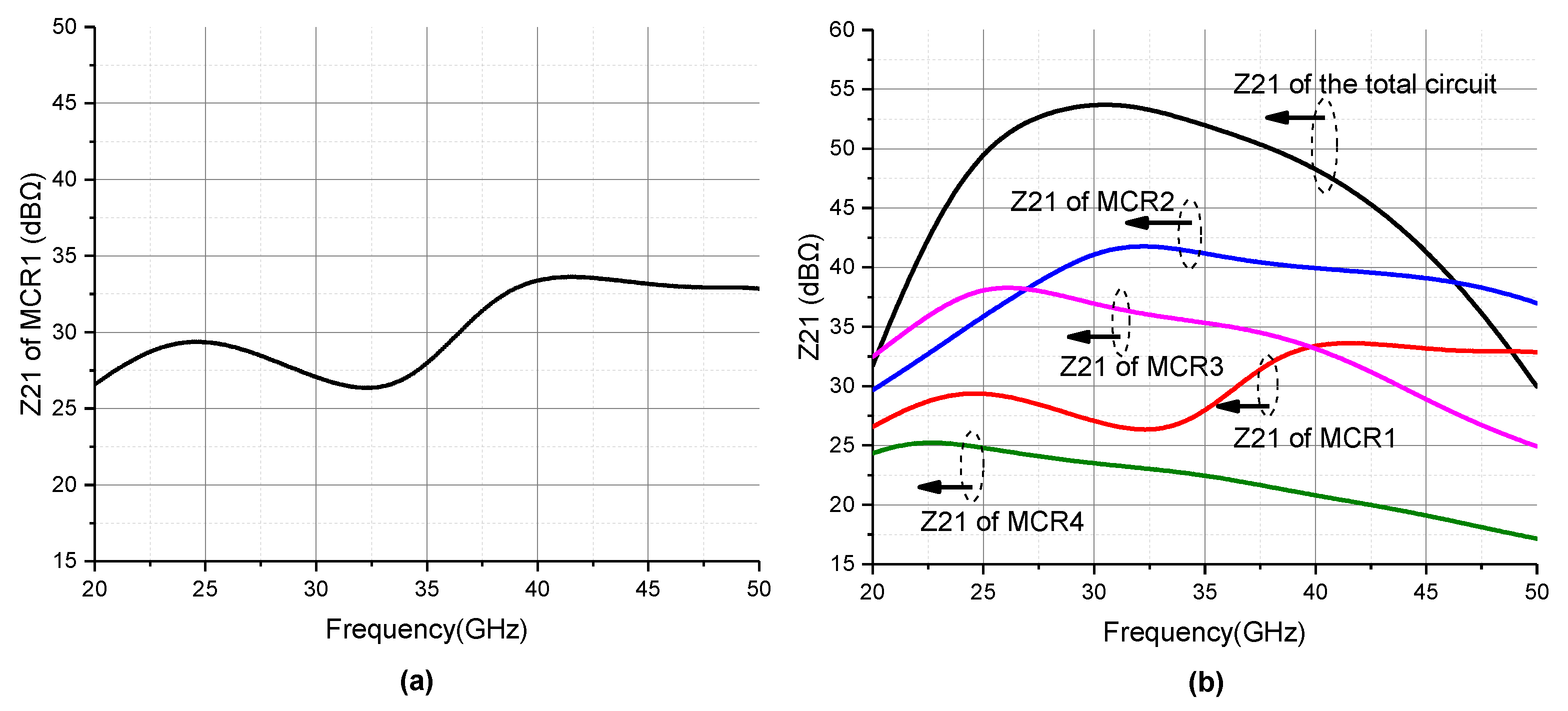
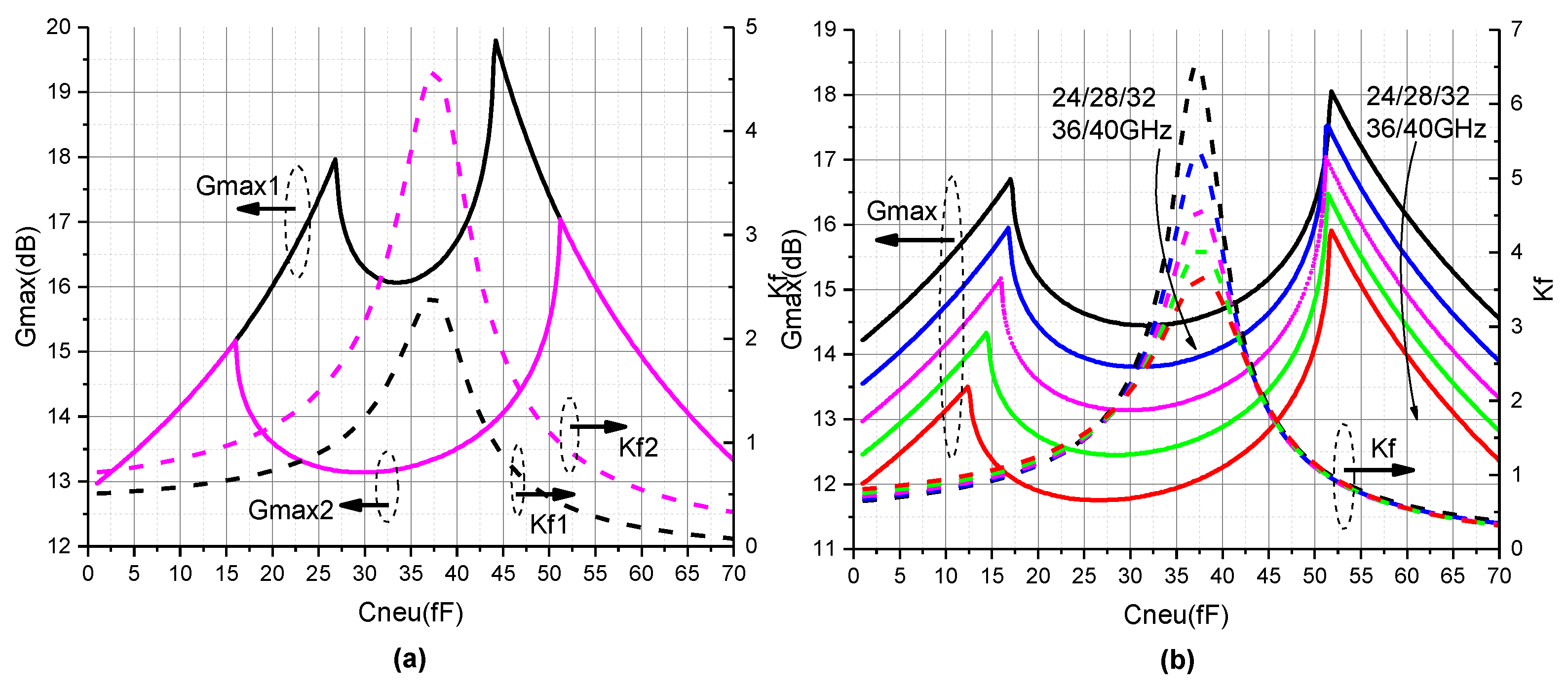
2.1. Wideband Output Matching Network Design
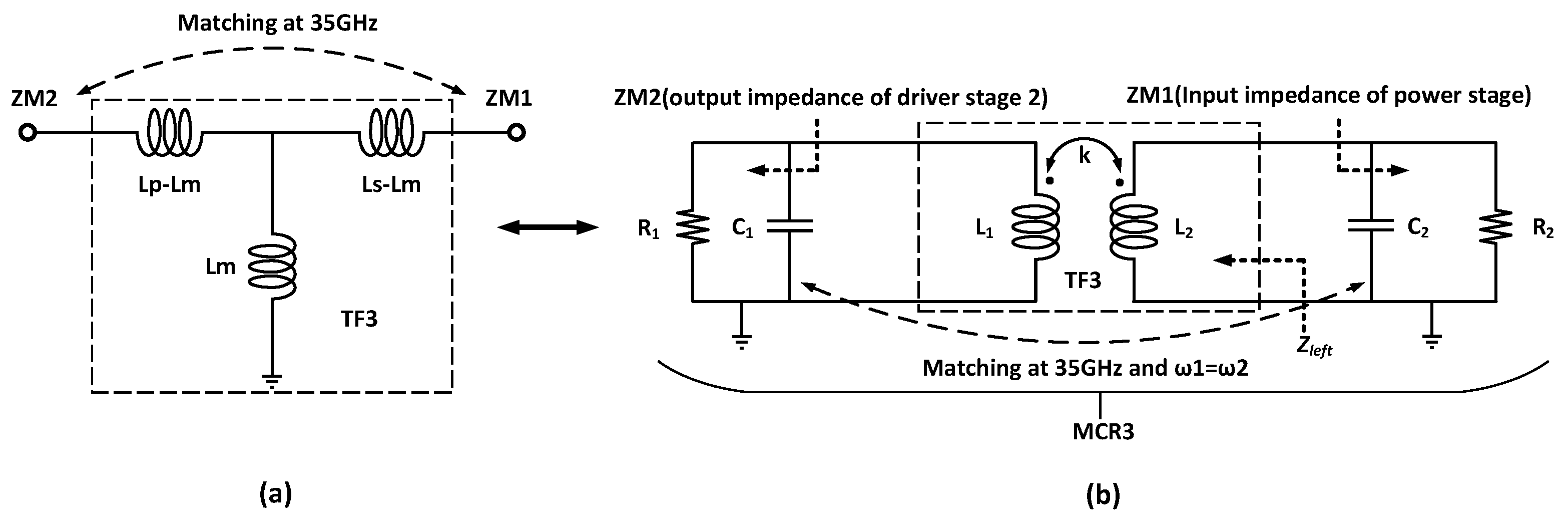
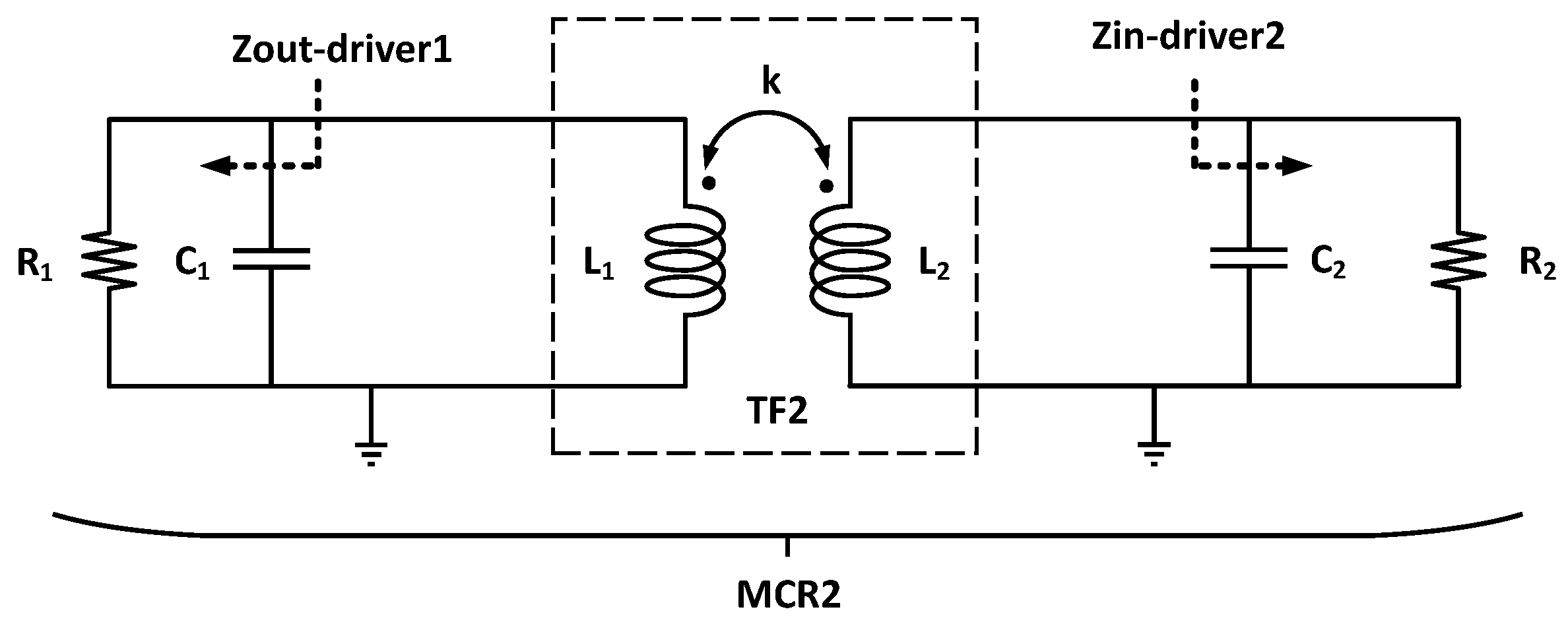
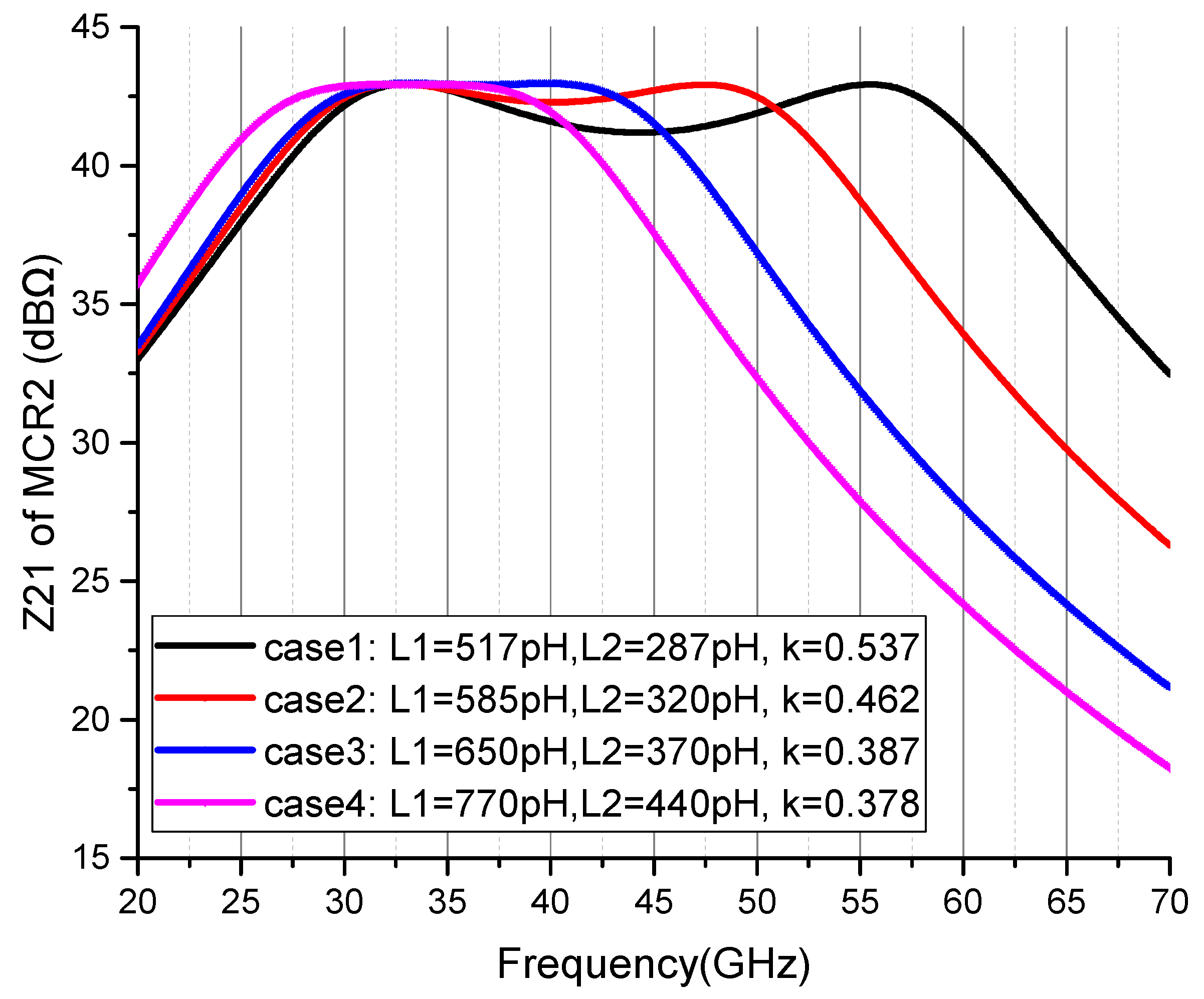
2.2. Interstage Matching Network Design
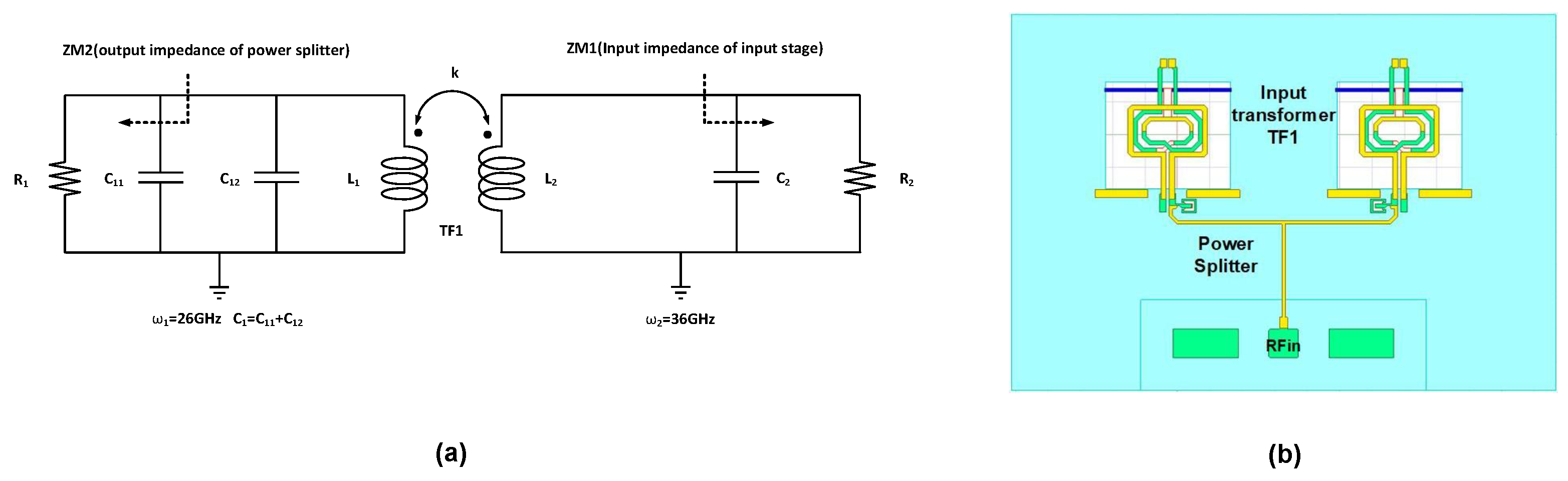
2.3. Input-Matching Network Design
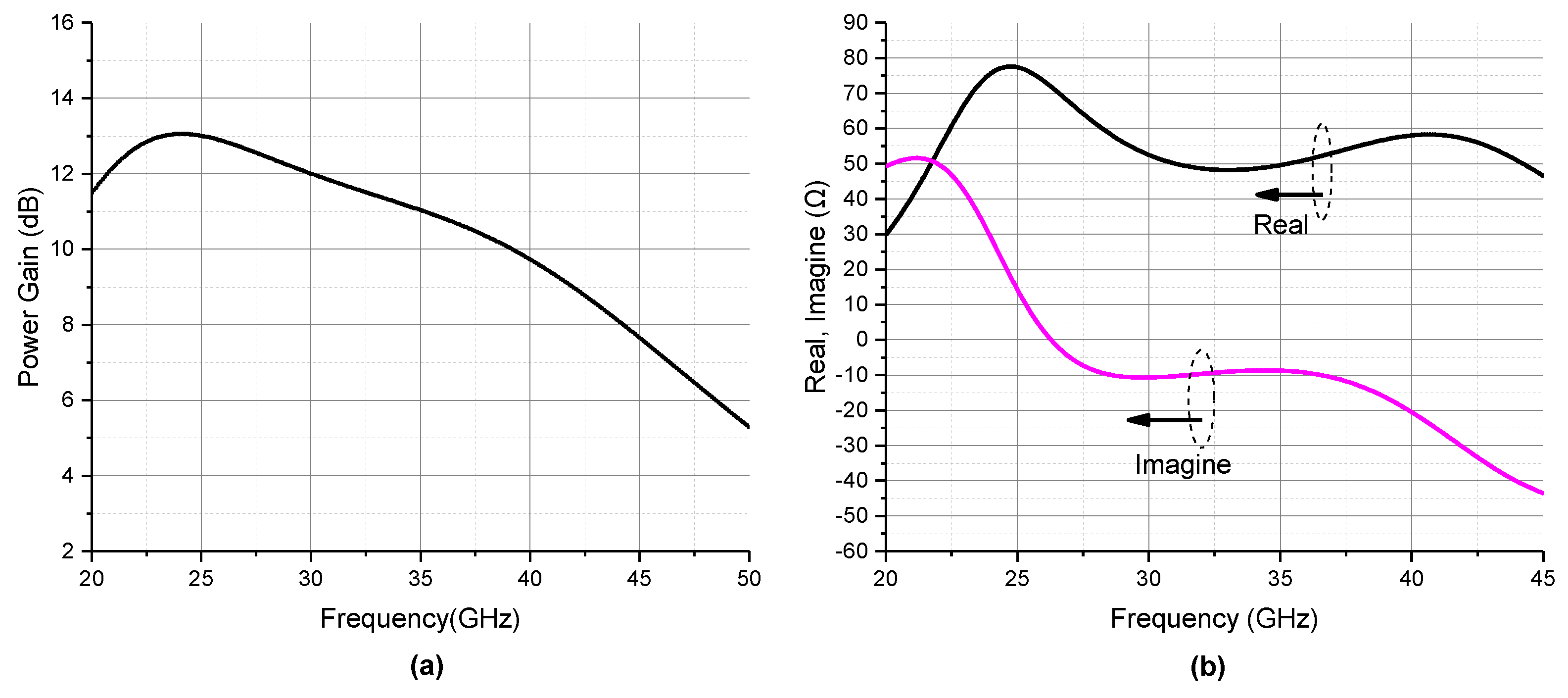
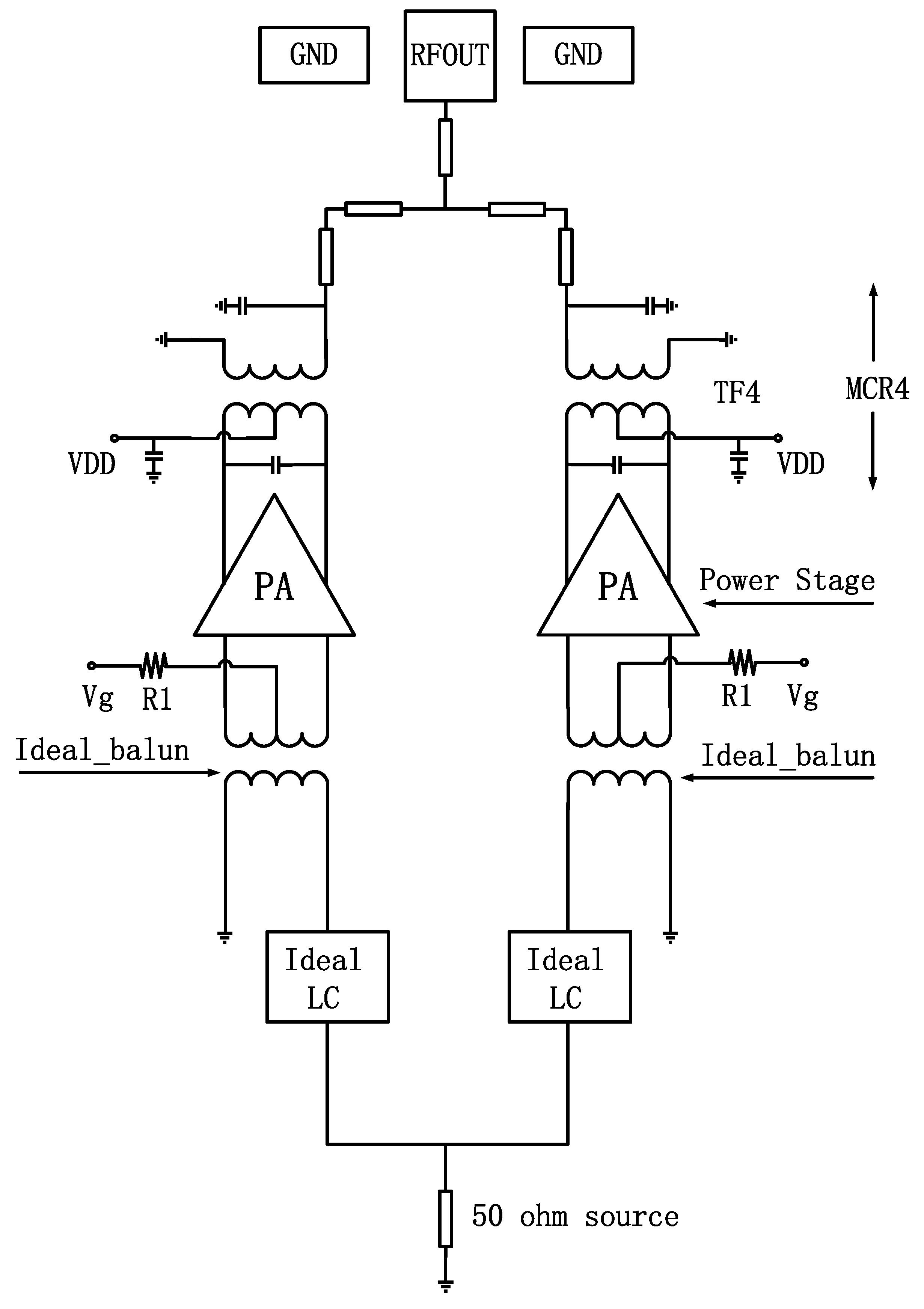
3. The PA Circuit Implementation
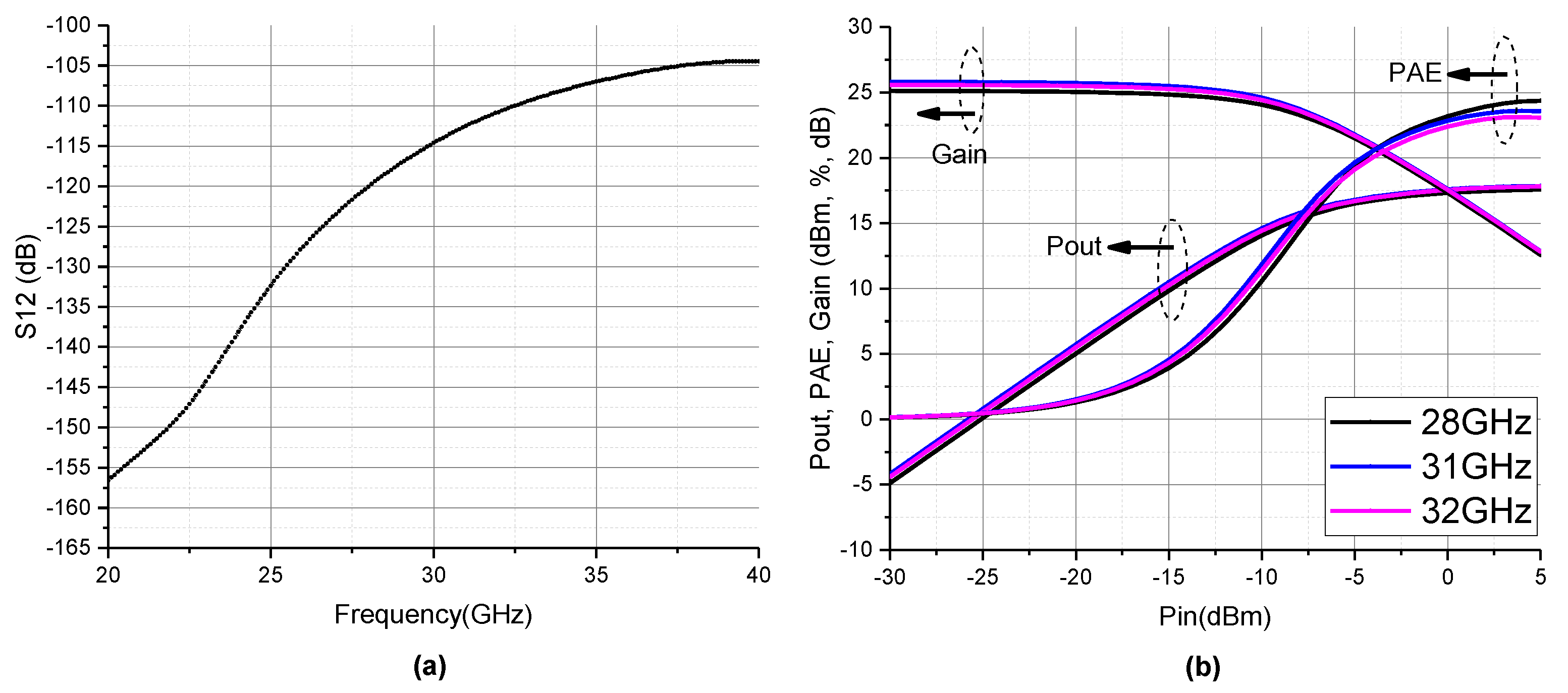
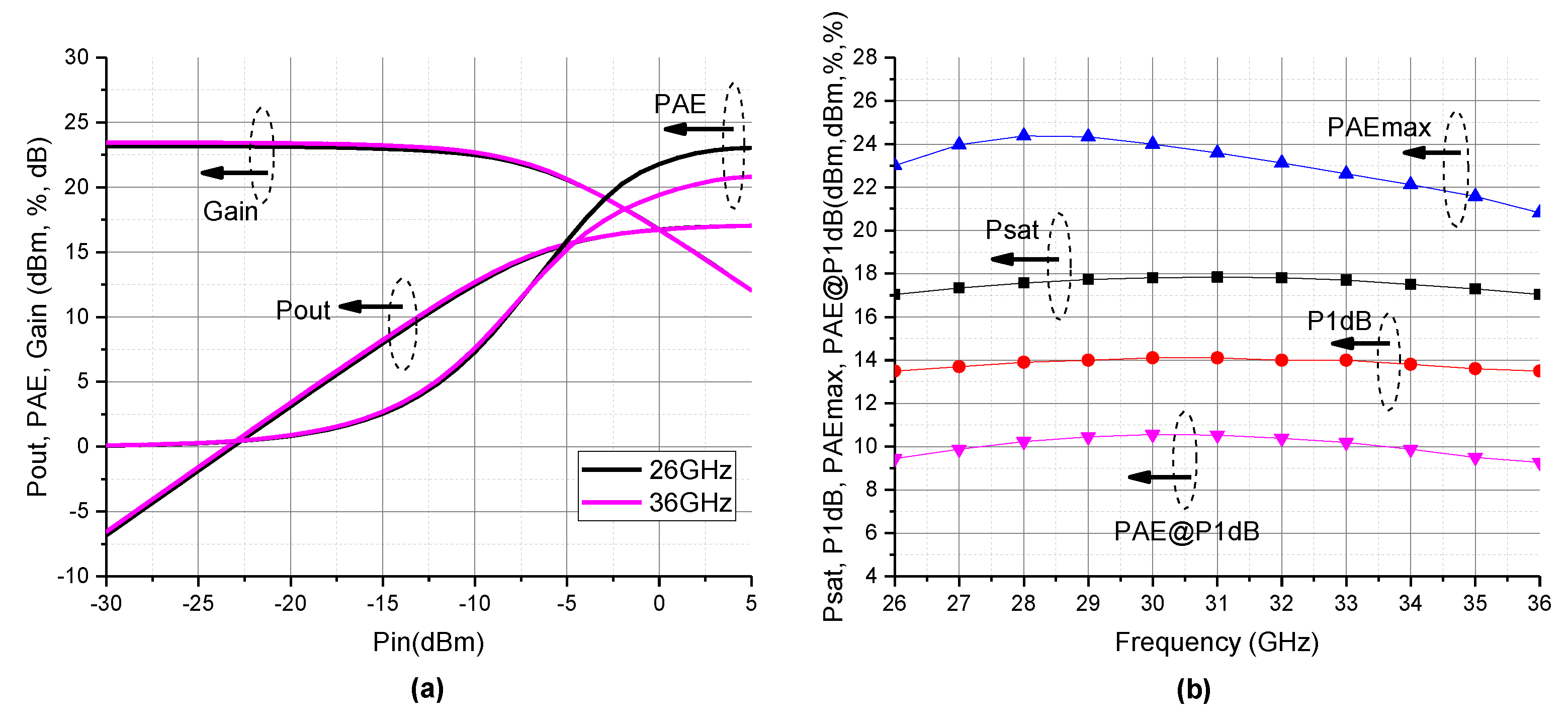
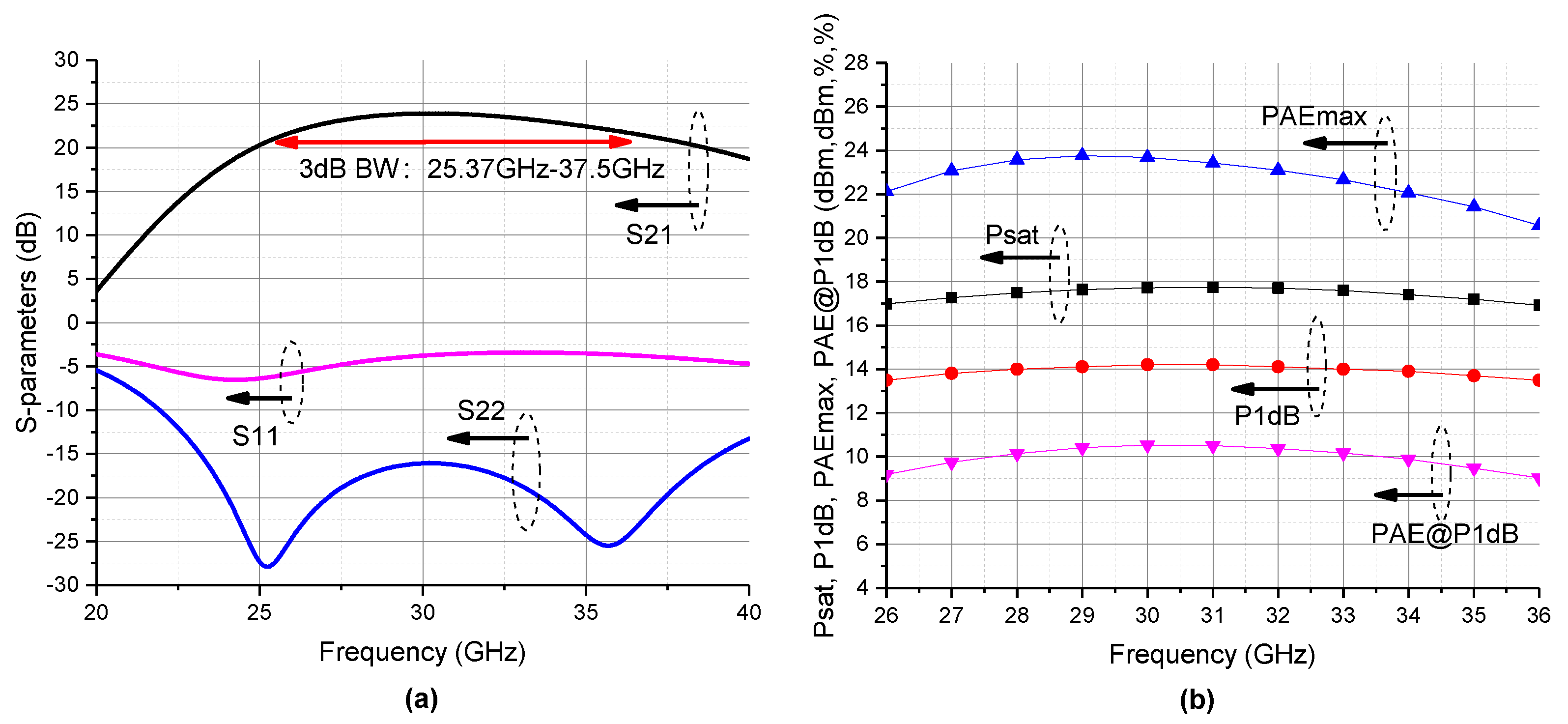
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhao, C.; Zhang, X.; Liu, H.; Yu, Y.; Wu, Y.; Kang, K. A SiGe Power Amplifier with Double Gain Peaks Based on the Control of Stationary Points of Impedance Transformation. IEEE Trans. Microw. Theory Tech. 2021, 69, 2279–2290. [Google Scholar] [CrossRef]
- Cheng, D.; Chen, X.; Chen, Q.; Li, L.; Sheng, B. Design of an Ultra-Compact 60-GHz Bi-Directional Amplifier in 65-nm CMOS. IEEE Microw. Wirel. Components Lett. 2022, 32, 343–346. [Google Scholar] [CrossRef]
- 3GPP 5G-NR Specifications. Available online: http://www.3gpp.org/DynaReport/38-series.htm> (accessed on 15 August 2019).
- Federal Communications Commission FCC 16–89. Available online: https://docs.fcc.gov/public/attachments/FCC-16-89A1.pdf (accessed on 15 August 2019).
- Wang, F.; Wang, H. A Broadband Linear Ultra-Compact mm-Wave Power Amplifier With Distributed-Balun Output Network: Analysis and Design. IEEE J. Solid State Circuits 2021, 56, 2308–2323. [Google Scholar] [CrossRef]
- Wang, F.; Wang, A.; Wang, H. A 22–37 GHz Broadband Compact Linear Mm-Wave Power Amplifier Supporting 64-/256-/512-QAM Modulations for 5G Communications. In Proceedings of the 2020 IEEE/MTT-S International Microwave Symposium (IMS), Los Angeles, CA, USA, 4–6 August 2020; pp. 1105–1108. [Google Scholar] [CrossRef]
- Wang, D.; Shen, Z.; Su, X.; Liu, Z.; Tan, Y.; Xu, C.; Liu, J.; Liao, H. A Gm-Compensated 46–101 GHz Broadband Power Amplifier for High-Resolution FMCW Radars. In Proceedings of the 2021 IEEE International Symposium on Circuits and Systems (ISCAS), Daegu, Republic of Korea, 22–28 May 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Mostajeran, A.; Naghavi, S.M.; Emadi, M.; Samala, S.; Ginsburg, B.P.; Aseeri, M.; Afshari, E. A High-Resolution 220-GHz Ultra-Wideband Fully Integrated ISAR Imaging System. IEEE Trans. Microw. Theory Tech. 2019, 67, 429–442. [Google Scholar] [CrossRef]
- Wu, H.F.; Cheng, Q.F.; Li, X.G.; Fu, H.P. Analysis and Design of an UltraBroadband Stacked Power Amplifier in CMOS Technology. IEEE Trans. Circuits Syst. II Express Briefs 2016, 63, 49–53. [Google Scholar] [CrossRef]
- Thayyil, M.V.; Li, S.; Joram, N.; Ellinger, F. A 4–32 GHz SiGe Multi-Octave Power Amplifier with 20 dBm Peak Power, 18.6 dB Peak Gain and 156. IEEE Microw. Wirel. Components Lett. 2019, 29, 745–748. [Google Scholar] [CrossRef]
- Lin, J.; Li, L.; Huang, J. A Design of Full Ka-Band Power Amplifier in 65 nm SOI CMOS. In Proceedings of the 2022 7th International Conference on Integrated Circuits and Microsystems (ICICM), Xi’an, China, 28–31 October 2022; pp. 295–298. [Google Scholar] [CrossRef]
- Arbabian, A.; Niknejad, A.M. Design of a CMOS Tapered Cascaded Multistage Distributed Amplifier. IEEE Trans. Microw. Theory Tech. 2009, 57, 938–947. [Google Scholar] [CrossRef]
- El-Aassar, O.; Rebeiz, G.M. A DC-to-108-GHz CMOS SOI Distributed Power Amplifier and Modulator Driver Leveraging Multi-Drive Complementary Stacked Cells. IEEE J. Solid State Circuits 2019, 54, 3437–3451. [Google Scholar] [CrossRef]
- Mosalam, H.; Allam, A.; Jia, H.; Abdel-Rahman, A.B.; Pokharel, R.K. High Efficiency and Small Group Delay Variations 0.18- μ m CMOS UWB Power Amplifier. IEEE Trans. Circuits Syst. II Express Briefs 2019, 66, 592–596. [Google Scholar] [CrossRef]
- Hadipour, K.; Ghilioni, A.; Mazzanti, A.; Bassi, M.; Svelto, F. A 40 GHz to 67 GHz bandwidth 23 dB gain 5.8 dB maximum NF mm-Wave LNA in 28 nm CMOS. In Proceedings of the 2015 IEEE Radio Frequency Integrated Circuits Symposium (RFIC), Phoenix, AZ, USA, 17–19 May 2015; pp. 327–330. [Google Scholar] [CrossRef]
- Jia, H.; Prawoto, C.C.; Chi, B.; Wang, Z.; Yue, C.P. A Full Ka-Band Power Amplifier with 32.965-nm CMOS. IEEE Trans. Circuits Syst. Regul. Pap. 2018, 65, 2657–2668. [Google Scholar] [CrossRef]
- Wan, C.; Zhang, H.; Zhao, Y.; Zeng, M.; Dong, J.; Li, L.; Wang, K. A Broadband SiGe HBT Cascode Power Amplifier Achieving Watt-Level Peak Output Power with 38.6. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 4734–4738. [Google Scholar] [CrossRef]
- Wei, D.; Wu, T.; Ma, S.; Chen, Y.; Ren, J. A 35-to-50 GHz CMOS Low-Noise Amplifier with 22.2 Bandwidth and 30.5-dB Maximum Gain for 5G New Radio. In Proceedings of the ESSCIRC 2021—IEEE 47th European Solid State Circuits Conference (ESSCIRC), Online, 6 September–30 November 2021; pp. 195–198. [Google Scholar] [CrossRef]
- Chou, C.F.; Hsiao, Y.H.; Wu, Y.C.; Lin, Y.H.; Wu, C.W.; Wang, H. Design of a V-Band 20-dBm Wideband Power Amplifier Using Transformer-Based Radial Power Combining in 90-nm CMOS. IEEE Trans. Microw. Theory Tech. 2016, 64, 4545–4560. [Google Scholar] [CrossRef]
- Xue, Y.; Shi, C.; Chen, G.; Chen, J.; Zhang, R. Two W-Band Wideband CMOS mmW PAs for Automotive Radar Transceivers. In Proceedings of the 2020 IEEE/MTT-S International Microwave Symposium (IMS), Los Angeles, CA, USA, 4–6 August 2020; pp. 1109–1112. [Google Scholar] [CrossRef]
- Zhang, R.; Xue, Y.; Jiang, C.; Shi, C.; Chen, G. Two High Power and Broadband Power Amplifiers using Transformer-based Resonating Peak Control Technique for E-Band Communication and Automotive Radars in 55-nm CMOS. In Proceedings of the 2020 International Conference on Microwave and Millimeter Wave Technology (ICMMT), Shanghai, China, 20–23 September 2020; pp. 1–3. [Google Scholar] [CrossRef]
- Gu, Q.J.; Xu, Z.; Chang, M.C.F. Two-Way Current-Combining W-Band Power Amplifier in 65-nm CMOS. IEEE Trans. Microw. Theory Tech. 2012, 60, 1365–1374. [Google Scholar] [CrossRef]
- Lee, J.; Hong, S. A 24–30 GHz 31.7% Fractional Bandwidth Power Amplifier with an Adaptive Capacitance Linearizer. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 1163–1167. [Google Scholar] [CrossRef]
- Hadipour, K.; Amschl, D.; Knauder, D.; Di Martino, S. A High GBW High Power Wideband Power Amplifier for Automotive Radar Application. In Proceedings of the 2021 16th European Microwave Integrated Circuits Conference (EuMIC), London, UK, 3–4 April 2022; pp. 76–79. [Google Scholar] [CrossRef]
- Cheung, T.; Long, J. A 21–26-GHz SiGe bipolar power amplifier MMIC. IEEE J. Solid State Circuits 2005, 40, 2583–2597. [Google Scholar] [CrossRef]
- Chowdhury, D.; Ye, L.; Alon, E.; Niknejad, A.M. An Efficient Mixed-Signal 2.4-GHz Polar Power Amplifier in 65-nm CMOS Technology. IEEE J. Solid State Circuits 2011, 46, 1796–1809. [Google Scholar] [CrossRef]
- Chowdhury, D.; Reynaert, P.; Niknejad, A.M. Design Considerations for 60 GHz Transformer-Coupled CMOS Power Amplifiers. IEEE J. Solid State Circuits 2009, 44, 2733–2744. [Google Scholar] [CrossRef]
- Liu, Y.; Mao, L.; Chi, B. 185–220 GHz wideband amplifier in 40 nm CMOS. Electron. Lett. 2018, 54, 802–804. [Google Scholar] [CrossRef]
- Zavarei, M.J.; Kim, K.; Song, H.J. A 26–40 GHz Wideband Power Amplifier with Transformer-Based High-Order Matching Networks in 28-nm CMOS FD-SOI. IEEE Microw. Wirel. Components Lett. 2022, 32, 1079–1082. [Google Scholar] [CrossRef]
- Yu, C.; Feng, J.; Zhao, D. A Ka-band 65-nm CMOS neutralized medium power amplifier for 5G phased-array applications. In Proceedings of the 2018 IEEE MTT-S International Wireless Symposium (IWS), Chengdu, China, 6–10 May 2018; pp. 1–3. [Google Scholar] [CrossRef]
- Li, C.H.; Kuo, C.N.; Kuo, M.C. A 1.2-V 5.2-mW 20–30-GHz Wideband Receiver Front-End in 0.18-μm CMOS. IEEE Trans. Microw. Theory Tech. 2012, 60, 3502–3512. [Google Scholar] [CrossRef]
- Mangraviti, G.; Parvais, B.; Vidojkovic, V.; Vaesen, K.; Szortyka, V.; Khalaf, K.; Soens, C.; Vandersteen, G.; Wambacq, P. A 52–66 GHz subharmonically injection-locked quadrature oscillator with 10 GHz locking range in 40 nm LP CMOS. In Proceedings of the 2012 IEEE Radio Frequency Integrated Circuits Symposium, Montreal, QC, Canada, 17–19 June 2012; pp. 309–312. [Google Scholar] [CrossRef]
- Jia, H.; Kuang, L.; Wang, Z.; Chi, B. A W-Band Injection-Locked Frequency Doubler Based on Top-Injected Coupled Resonator. IEEE Trans. Microw. Theory Tech. 2016, 64, 210–218. [Google Scholar] [CrossRef]
- Zhao, J.; Bassi, M.; Bevilacqua, A.; Ghilioni, A.; Mazzanti, A.; Svelto, F. A 40–67 GHz power amplifier with 13 dBm PSAT and 16CMOS LP. In Proceedings of the ESSCIRC 2014—40th European Solid State Circuits Conference (ESSCIRC), Venice, Italy, 22–26 September 2014; pp. 179–182. [Google Scholar] [CrossRef]
- Zhang, J.; Wu, T.; Nie, L.; Ma, S.; Chen, Y.; Ren, J. A 120–150 GHz Power Amplifier in 28-nm CMOS Achieving 21.9-dB Gain and 11.8-dBm Psat for Sub-THz Imaging System. IEEE Access 2021, 9, 74752–74762. [Google Scholar] [CrossRef]
- Son, H.S.; Jang, T.H.; Kim, S.H.; Jung, K.P.; Kim, J.H.; Park, C.S. Pole-Controlled Wideband 120 GHz CMOS Power Amplifier for Wireless Chip-to-Chip Communication in 40-nm CMOS Process. IEEE Trans. Circuits Syst. II Express Briefs 2019, 66, 1351–1355. [Google Scholar] [CrossRef]
- Deferm, N.L. Differential and common mode stability analysis of differential mm-wave CMOS amplifiers with capacitive neutralization. Analog. Integr. Circuits Signal Process. 2014, 80, 1–12. [Google Scholar] [CrossRef]
- Wan, C.; Zhang, H.; Li, L.; Wang, K. A 30-to-41 GHz SiGe Power Amplifier with Optimized Cascode Transistors Achieving 22.8 dBm output power and 27% PAE. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 1158–1162. [Google Scholar] [CrossRef]
- Shakib, S.; Elkholy, M.; Dunworth, J.; Aparin, V.; Entesari, K. 2.7 A wideband 28 GHz power amplifier supporting 8 × 100 MHz carrier aggregation for 5G in 40 nm CMOS. In Proceedings of the 2017 IEEE International Solid-State Circuits Conference (ISSCC), San Francisco, CA, USA, 5–9 February 2017; pp. 44–45. [Google Scholar] [CrossRef]











| TCAS-II 2021 [38] | TCAS-II 2021 [23] | MWCL 2022 [29] | ISSCC2017 [39] | This Work | |
|---|---|---|---|---|---|
| Technology | 130 nm SiGe | 28 nm CMOS | 28 nm FD-SOI | 40 nm CMOS | 65 nm CMOS |
| Frequency (GHz) | 35 | 24/26/28/30 | 30 | 27 | 31/32 |
| Peak gain (dB) | 25.3 | 21.2 | 19 | 22.4 | 25.87 dB@35.5 GHz |
| 3 dB S21 BW (GHz) | 11 | 21.8–30 | 26–39.8 | 26–32 | 25.8-36.9 |
| (dBm) | 22.8 | 19.7/20.3/20/20 | 17.1 | 15.1 | 17.84/17.81 |
| 1 dB BW (GHz) | 7 | N/A | 12 | N/A | 10 |
| (dBm) | 22.6 | 18.2/18.2/17.8/17.2 | 16.1 | 13.7 | 14.09/14.04 |
| 1 dB BW (GHz) | N/A | N/A | 13 | 7 | 10 |
| (%) | 27 | 34.5/33.1/30/30.3 | 25.3 | 33.7 | 24.37% |
| VDD (V) | 3.3 | 2.2 | N/A | 1.1 | 1.1 |
| Area () | 0.48 | 0.189 | 0.162 | 0.225 | 1.326 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Wang, X.; Liu, Y. A Wideband Power Amplifier in 65 nm CMOS Covering 25.8 GHz–36.9 GHz by Staggering Tuned MCRs. Electronics 2023, 12, 3566. https://doi.org/10.3390/electronics12173566
Wang Z, Wang X, Liu Y. A Wideband Power Amplifier in 65 nm CMOS Covering 25.8 GHz–36.9 GHz by Staggering Tuned MCRs. Electronics. 2023; 12(17):3566. https://doi.org/10.3390/electronics12173566
Chicago/Turabian StyleWang, Zhiqiang, Xiaosong Wang, and Yu Liu. 2023. "A Wideband Power Amplifier in 65 nm CMOS Covering 25.8 GHz–36.9 GHz by Staggering Tuned MCRs" Electronics 12, no. 17: 3566. https://doi.org/10.3390/electronics12173566
APA StyleWang, Z., Wang, X., & Liu, Y. (2023). A Wideband Power Amplifier in 65 nm CMOS Covering 25.8 GHz–36.9 GHz by Staggering Tuned MCRs. Electronics, 12(17), 3566. https://doi.org/10.3390/electronics12173566







