The Study of Crash-Tolerant, Multi-Agent Offensive and Defensive Games Using Deep Reinforcement Learning
Abstract
:1. Introduction
2. Scenario Description and Modeling
2.1. Scenario Description
2.2. Agent Modeling
3. Frozen Agent Method for MADDPG
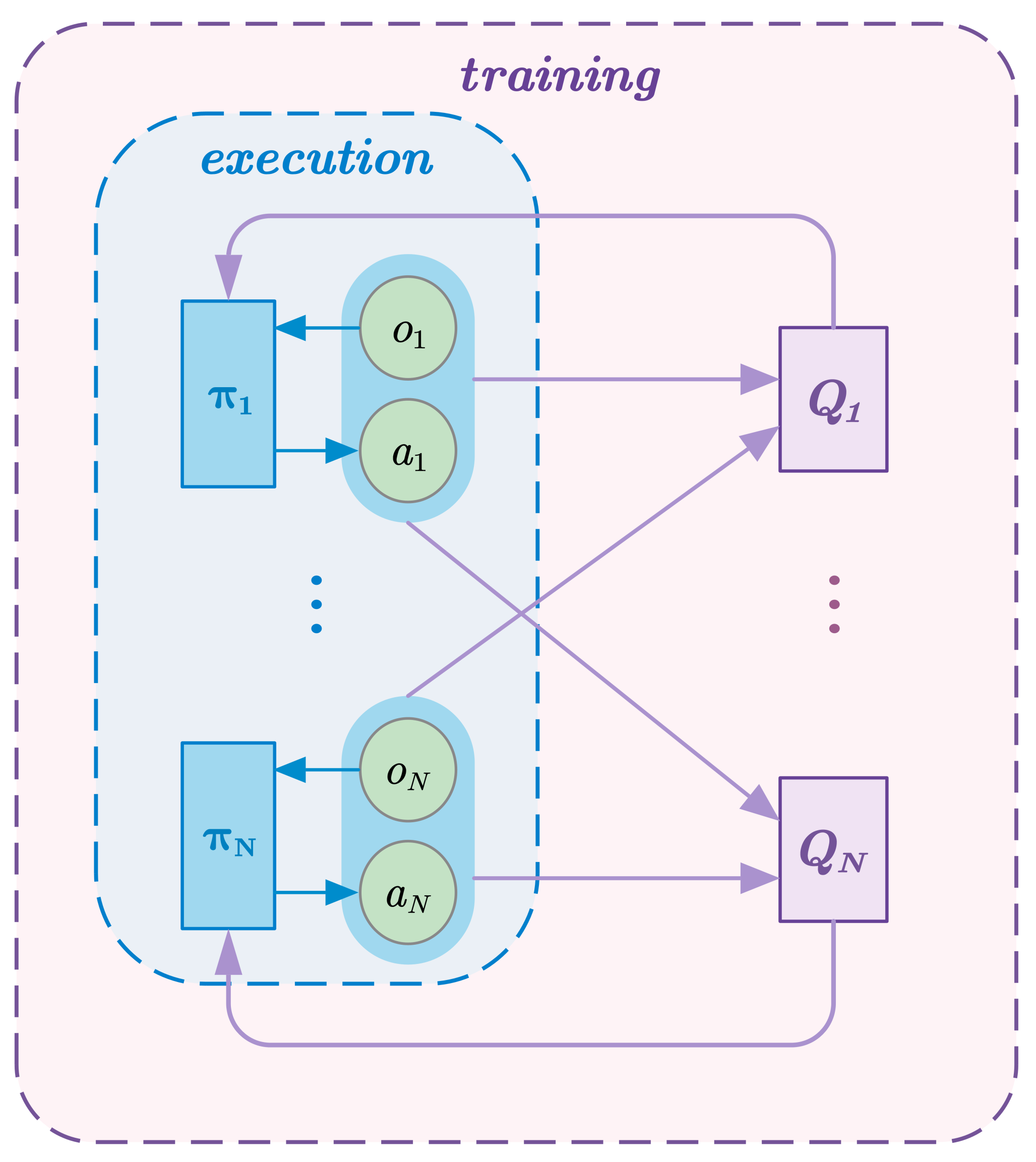
3.1. Problem Formulation
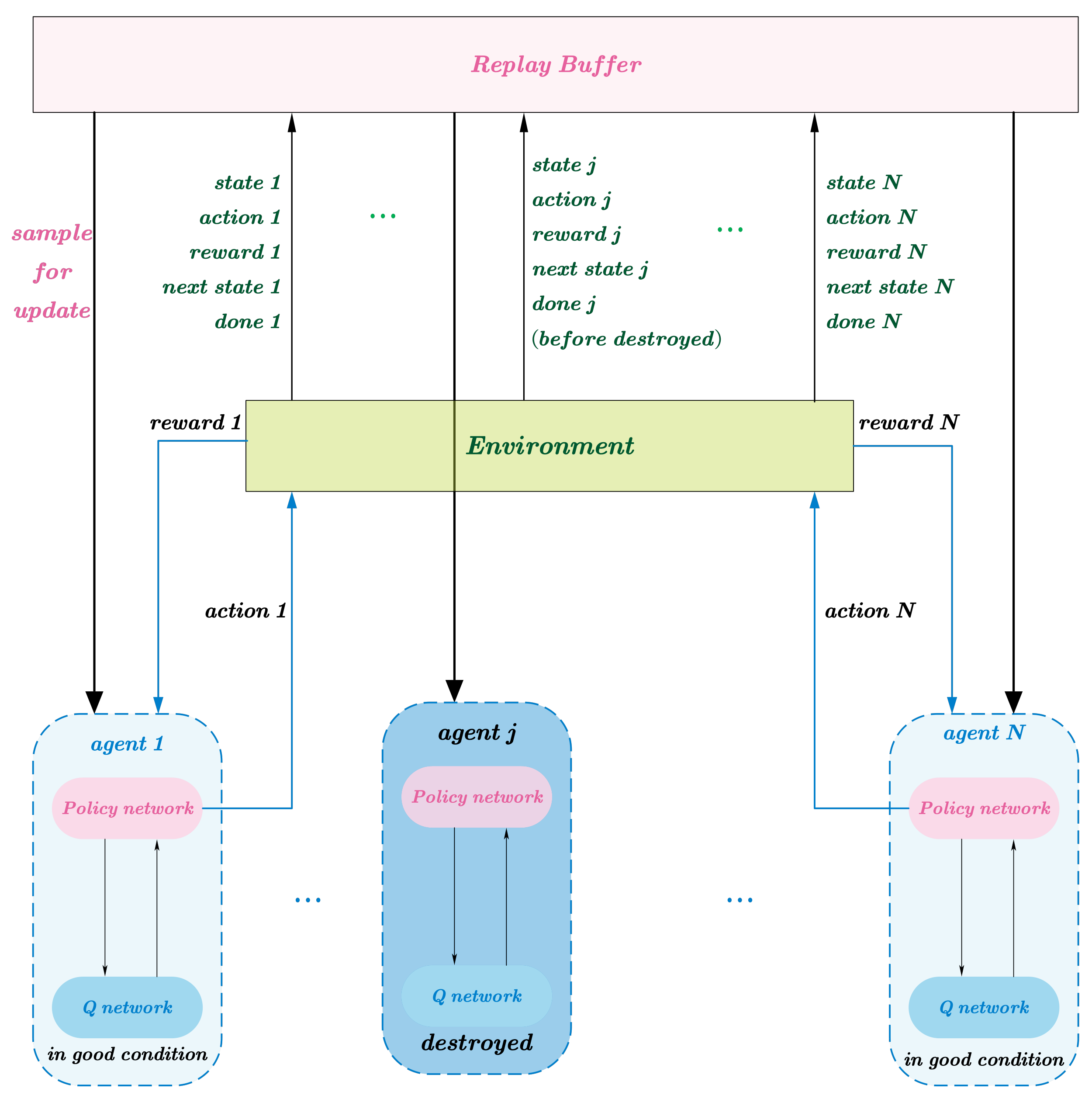
3.2. Frozen Agent Method
3.2.1. Details for FA-MADDPG
| Algorithm 1: Frozen-Agent Method for MADDPG. |
 |
3.2.2. Reward Function and Observation Settings
4. Training and Execution Results
4.1. Experiment Settings
4.2. Experiment Results and Analysis
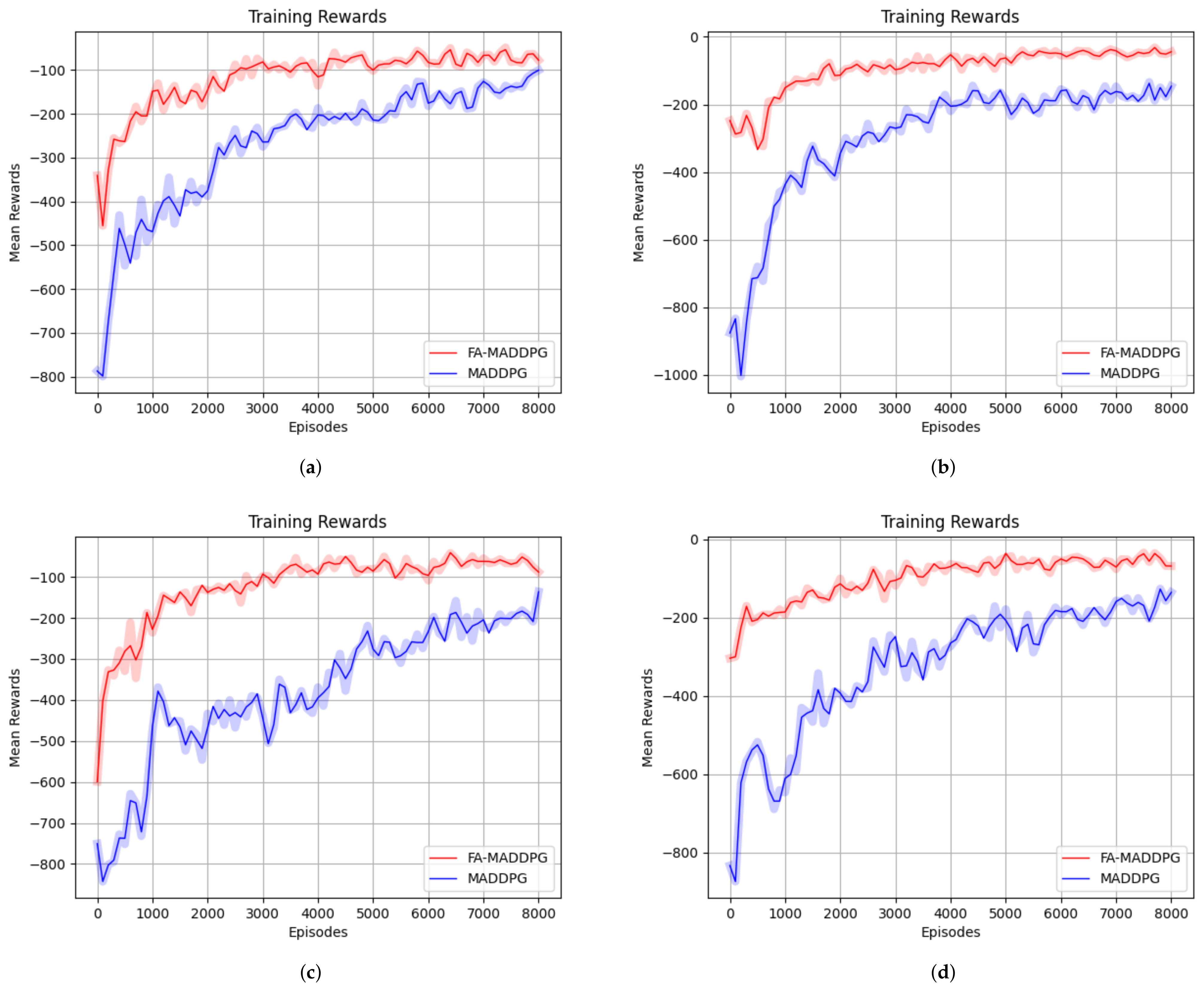
4.2.1. Reward Curves during Training
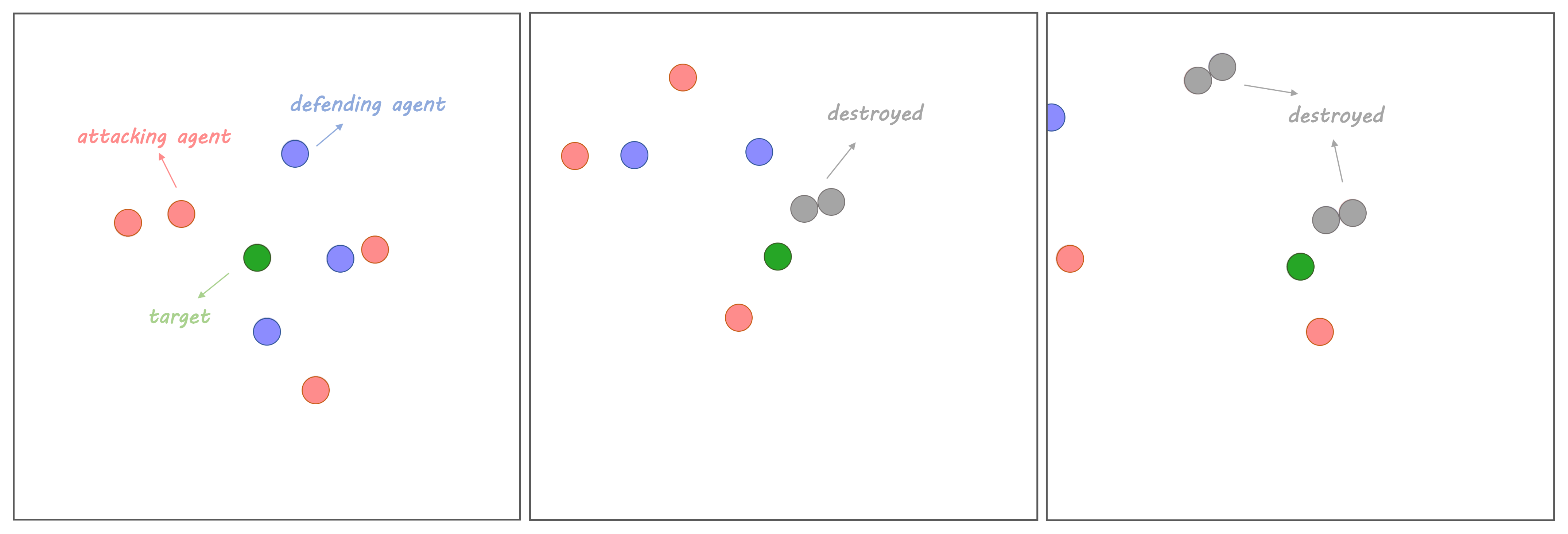
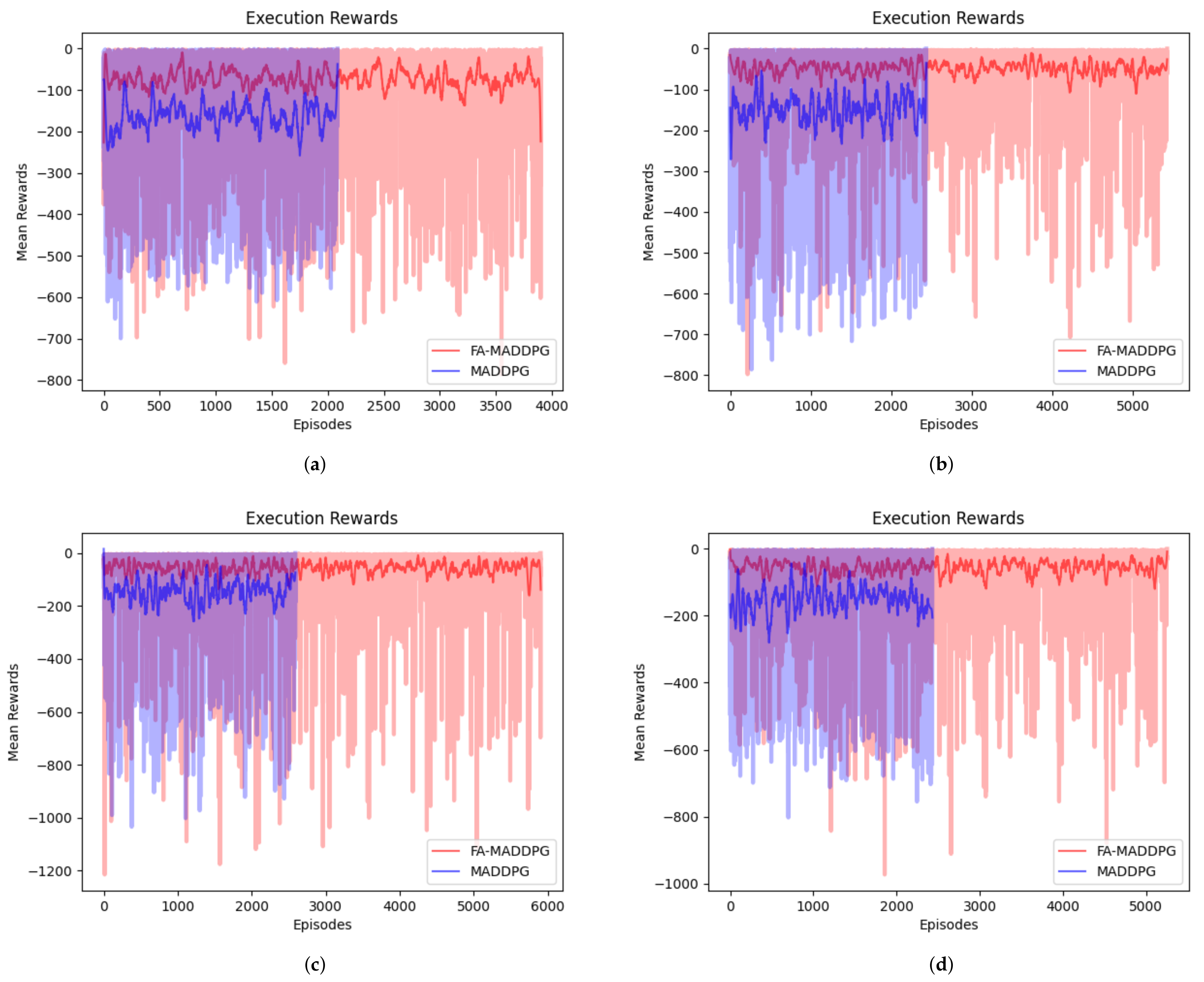
4.2.2. Execution Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, J.; Zha, W.; Peng, Z.; Gu, D. Multi-player pursuit–evasion games with one superior evader. Automatica 2016, 71, 24–32. [Google Scholar] [CrossRef] [Green Version]
- Margellos, K.; Lygeros, J. Hamilton–Jacobi Formulation for Reach–Avoid Differential Games. IEEE Trans. Autom. Control. 2011, 56, 1849–1861. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhang, W.; Ding, J.; Huang, H.; Stipanović, D.M.; Tomlin, C.J. Cooperative pursuit with Voronoi partitions. Automatica 2016, 72, 64–72. [Google Scholar] [CrossRef] [Green Version]
- Chen, M.; Zhou, Z.; Tomlin, C.J. Multiplayer reach-avoid games via pairwise outcomes. IEEE Trans. Autom. Control. 2016, 62, 1451–1457. [Google Scholar] [CrossRef]
- Zou, B.; Peng, X. A Bilateral Cooperative Strategy for Swarm Escort under the Attack of Aggressive Swarms. Electronics 2022, 11, 3643. [Google Scholar] [CrossRef]
- Zhang, S.; Ran, W.; Liu, G.; Li, Y.; Xu, Y. A Multi-Agent-Based Defense System Design for Multiple Unmanned Surface Vehicles. Electronics 2022, 11, 2797. [Google Scholar] [CrossRef]
- Yang, K.; Dong, W.; Cai, M.; Jia, S.; Liu, R. UCAV Air Combat Maneuver Decisions Based on a Proximal Policy Optimization Algorithm with Situation Reward Shaping. Electronics 2022, 11, 2602. [Google Scholar] [CrossRef]
- Zhao, X.; Yang, R.; Zhang, Y.; Yan, M.; Yue, L. Deep Reinforcement Learning for Intelligent Dual-UAV Reconnaissance Mission Planning. Electronics 2022, 11, 2031. [Google Scholar] [CrossRef]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial networks. Commun. ACM 2020, 63, 139–144. [Google Scholar] [CrossRef]
- Ibrahim, A.M.; Yau, K.-L.A.; Chong, Y.-W.; Wu, C. Applications of Multi-Agent Deep Reinforcement Learning: Models and Algorithms. Appl. Sci. 2021, 11, 10870. [Google Scholar] [CrossRef]
- Qi, H.; Huang, H.; Hu, Z.; Wen, X.; Lu, Z. On-Demand Channel Bonding in Heterogeneous WLANs: A Multi-Agent Deep Reinforcement Learning Approach. Sensors 2020, 20, 2789. [Google Scholar] [CrossRef]
- Jung, S.; Yun, W.J.; Kim, J.; Kim, J.-H. Coordinated Multi-Agent Deep Reinforcement Learning for Energy-Aware UAV-Based Big-Data Platforms. Electronics 2021, 10, 543. [Google Scholar] [CrossRef]
- Chen, C.; Ma, F.; Xu, X.; Chen, Y.; Wang, J. A Novel Ship Collision Avoidance Awareness Approach for Cooperating Ships Using Multi-Agent Deep Reinforcement Learning. J. Mar. Sci. Eng. 2021, 9, 1056. [Google Scholar] [CrossRef]
- Liang, L.; Deng, F.; Peng, Z.; Li, X.; Zha, W. A differential game for cooperative target defense. Automatica 2019, 102, 58–71. [Google Scholar] [CrossRef]
- Lowe, R.; Wu, Y.I.; Tamar, A.; Harb, J.; Pieter, A.; Mordatch, I. Multi-agent actor-critic for mixed cooperative-competitive environments. Adv. Neural Inf. Process. Syst. 2017, 30, 6382–6393. [Google Scholar]
- Wan, K.; Wu, D.; Zhai, Y.; Li, B.; Gao, X.; Hu, Z. An Improved Approach towards Multi-Agent Pursuit–Evasion Game Decision-Making Using Deep Reinforcement Learning. Entropy 2021, 23, 1433. [Google Scholar] [CrossRef] [PubMed]
- Xiang, L.; Xie, T. Research on UAV Swarm Confrontation Task Based on MADDPG Algorithm. In Proceedings of the 2020 5th International Conference on Mechanical, Control and Computer Engineering (ICMCCE), Harbin, China, 25–27 December 2020. [Google Scholar]
- Li, P.; Jia, S.; Cai, Z. Research on Multi-robot Path Planning Method Based on Improved MADDPG Algorithm. In Proceedings of the 2021 China Automation Congress (CAC), Beijing, China, 22–24 October 2021. [Google Scholar]
- Zhang, R.; Zong, Q.; Zhang, X.; Dou, L.; Tian, B. Game of Drones: Multi-UAV Pursuit-Evasion Game With Online Motion Planning by Deep Reinforcement Learning. IEEE Trans. Neural Netw. Learn. Syst. 2022. [Google Scholar] [CrossRef] [PubMed]
- Littman, M.L. Markov games as a framework for multi-agent reinforcement learning. In Machine Learning Proceedings 1994; Elsevier: Amsterdam, The Netherlands, 1994; pp. 157–163. [Google Scholar]
- Shao, K.; Zhu, Y.; Zhao, D. StarCraft Micromanagement With Reinforcement Learning and Curriculum Transfer Learning. IEEE Trans. Emerg. Top. Comput. Intell. 2019, 3, 73–84. [Google Scholar] [CrossRef]
- Peng, P.; Wen, Y.; Yang, Y.; Yuan, Q.; Tang, Z.; Long, H.; Wang, J. Multiagent bidirectionally-coordinated nets: Emergence of human-level coordination in learning to play starcraft combat games. arXiv 2017, arXiv:1703.10069. [Google Scholar]


| Parameter | Value |
|---|---|
| Policy network hidden layers | 2 |
| Policy network hidden units | 64 |
| Q network hidden layers | 2 |
| Q network hidden units | 64 |
| Activation function | ReLU |
| Scenario Number | Number of Defending Agents | Number of Attacking Agents |
|---|---|---|
| 1 | 3 | 3 |
| 2 | 3 | 4 |
| 3 | 3 | 5 |
| 4 | 4 | 3 |
| Scenario Number | Algorithm | Execution Episodes | Average Reward |
|---|---|---|---|
| 1 | FA-MADDPG | 3902 | −72.47 |
| MADDPG | 2088 | −163.27 | |
| 2 | FA-MADDPG | 5428 | −48.48 |
| MADDPG | 2435 | −148.8 | |
| 3 | FA-MADDPG | 5906 | −55.23 |
| MADDPG | 2591 | −145.15 | |
| 4 | FA-MADDPG | 5254 | −54.83 |
| MADDPG | 2432 | −151.25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Li, Z.; Zheng, X.; Yang, X.; Yu, X. The Study of Crash-Tolerant, Multi-Agent Offensive and Defensive Games Using Deep Reinforcement Learning. Electronics 2023, 12, 327. https://doi.org/10.3390/electronics12020327
Li X, Li Z, Zheng X, Yang X, Yu X. The Study of Crash-Tolerant, Multi-Agent Offensive and Defensive Games Using Deep Reinforcement Learning. Electronics. 2023; 12(2):327. https://doi.org/10.3390/electronics12020327
Chicago/Turabian StyleLi, Xilun, Zhan Li, Xiaolong Zheng, Xuebo Yang, and Xinghu Yu. 2023. "The Study of Crash-Tolerant, Multi-Agent Offensive and Defensive Games Using Deep Reinforcement Learning" Electronics 12, no. 2: 327. https://doi.org/10.3390/electronics12020327
APA StyleLi, X., Li, Z., Zheng, X., Yang, X., & Yu, X. (2023). The Study of Crash-Tolerant, Multi-Agent Offensive and Defensive Games Using Deep Reinforcement Learning. Electronics, 12(2), 327. https://doi.org/10.3390/electronics12020327






