Rethinking Liquid Crystal Tunable Phase Shifter Design with Inverted Microstrip Lines at 1–67 GHz by Dissipative Loss Analysis

Abstract

Growing 5G/6G phased-array beam-steering applications, for which liquid crystal (LC) is one of the enabling technology candidates, have sparked interest in the modulation of the phase (and amplitude) of microwave and millimeter-wave signals. In this communication, fresh insights into the systematic design analysis of a 1–67 GHz passive inverted microstrip line (IMSL) phase shifter filled with highly anisotropic LC as tunable dielectric media are obtained. Based on waveguide disturbance tests to characterize the dielectric properties of the non-tunable PCB and tunable LC used in the IMSL phase shift device filled with a GT3-24002 LC layer (125 µm thick) partially enclosing a 220 µm wide, 17 µm thick, 1.35 cm long copper core line, a 0–π differential phase shift in the 1–67 GHz range with less than 2 dB insertion loss is reported. Dissipative loss analysis shows that the dielectric absorption of the LC is 21.28% of the input signal power at 60 GHz. Further investigation is performed to quantify the impacts of dielectric substrate thicknesses (PCB and LC) on the wave-occupied volume ratio (and hence the phase tuning range), as well as on dissipative losses (including conductor loss and dielectric loss). Specifically, conductor loss is observed to follow a linear relationship with the reciprocal of the LC thickness.

1. Introduction

Passively tunable microwave elements such as phase shifters facilitate electrical beam steering by feeding phased antenna arrays. Typically, the phase shifting reconfigurability is achieved through semiconductor switches such as p-i-n diodes [1,2], varactors [3], varactor diodes [4], RF MEMS [5,6] (periodically loaded with capacitive switches that are electrically actuated), and ferroelectrics [7]. The achievable ~µs tuning speeds provide excellent temporal resolution in beam switching, whereas their digital switching in nature significantly affects the spatial resolution.

To address this shortcoming and target the beam direction at a higher spatial resolution, nematic liquid crystal (LC) can be introduced as a continuously tunable dielectric medium for continuous phase shift controlled by a low-amplitude bias voltage [8,9,10]. Arguably, LC-enabled RF tunable front-end devices and technologies are steadily evolving to provide essential functions for phased-array non-mechanical beam steering with continuous-tuning, low-insertion-loss, lighter, smaller, and less power-hungry advantages aimed at end-users in various industries. Although the true commercialization of LC-based phased array systems has yet to occur due to the difficulties listed in [9], each new generation of designs (device structure or material innovation) feeds the end-users’ demands slightly more and produces subsequent incremental contributions to information and communication technology services. For instance, the evolution of microwave LC material development (e.g., from 5CB, E7 to GT3-24002 and W1825) is evidenced by the simultaneous increased dielectric tunability and reduced dissipation factor, i.e., an improved figure-of-merit (FoM), as evidenced in [10,11,12].

However, when combining LC with specific guided structures (transmission line or waveguide), there is limited in-depth investigation on decomposing the device’s insertion loss into various materials’ dissipations, i.e., a lack of quantification of conductor loss and dielectric loss, which significantly limits the loss optimization opportunity from the device physics perspective. Resultantly, there is no knowledge of the feasibility of using LC as an electronically tunable medium to realize a passive 0–10 V continuously variable 0–π analog phase shifter with sufficiently low insertion loss (e.g., well below 2 dB specification) across a broad spectrum of 1–67 GHz, which motivates the ongoing research reported in this communication.

Regardless of the particular transmission line structure used to accommodate these tunable dielectric materials (i.e., LC) to realize an LC-based phase shifter (assuming a transmission type), the tuning principle and, therefore, the theoretical maximum tuning range occur when the wave occupancy volume ratio (WOVR) (defined by our previous work [13]) is assumed to be 100% in the tunable dielectric (i.e., LC) with respect to the overall dielectric volume space (including tunable and not tunable). By the standard electrically tuned bias method [12], the minimum permittivity of the device structure (${\mathsf{\epsilon }}_{\mathrm{eff} \left(\mathrm{ref}.\mathrm{bias}\right)}$) occurs in the reference perpendicular condition of the LC director when coupled to a microwave signal field. In contrast, the maximum dielectric constant of the device (${\mathsf{\epsilon }}_{\mathrm{eff} \left(\max .\mathrm{bias}\right)}$) occurs at the parallel state of the LC director [13]. Based on these well-established principles, Figure 1 below quantifies the maximum differential phase shift achievable with these academically recognized and commercially available nematic LC materials. Accordingly, the minimum effective line length (${\mathrm{L}}_{\mathrm{eff}}$) with LC to achieve a differential phase shift $\left(\Delta {\mathsf{\Phi }}_{21}\right)$ of 0–2π at frequency f is shown in Figure 2, based on the mathematical relationship [12,13] with the line length, frequency, and effective dielectric constant, as described in Equation (1), where ${\mathrm{c}}_0$ is the light velocity in a vacuum.

$${\mathrm{L}}_{\mathrm{eff}}=\frac{\Delta {\mathsf{\Phi }}_{21}}{2\mathsf{\pi }\mathrm{f}\left(\sqrt{{\mathsf{\epsilon }}_{\mathrm{eff} \left(\max .\mathrm{bias}\right)}}-\sqrt{{\mathsf{\epsilon }}_{\mathrm{eff} \left(\mathrm{ref}.\mathrm{bias}\right)} }\right)}{\mathrm{c}}_0,$$

(1)

It is well worth noting that not only does the employment of tunable dielectrics (i.e., LCs) matter, but understanding the limits and capabilities of PCB substrate materials (non-tunable) can also tip the balance, because the dielectric constant impacts the WOVR and hence the phase shift and insertion loss performance. The waveguide perturbation tests are thus performed for RT5880 and RO3003 (substrate materials both from Rogers Corporation) at different frequencies (10 GHz, 30 GHz, 50 GHz), with

Table 1. Dielectric response of RT5880 and RO3003 characterized at various frequency regimes (10 GHz, 30 GHz, and 50 GHz, respectively).

Substrate	Dielectric Constant			Dissipation Factor
	10 GHz	30 GHz	50 GHz	10 GHz	30 GHz	50 GHz
RT5880	2.200	2.197	2.195	0.0009	0.0010	0.0012
RO3003	3.000	2.997	2.993	0.0010	0.0014	0.0010

providing the constitutive parameters of the dielectric constants (${\mathsf{\epsilon }}_{\mathrm{r}}$) and dissipation factors (tan$\mathsf{\delta }$) defined as per Equation (2), where $\mathsf{\sigma }$ denotes the total effective conductivity caused by ionic conduction and displacement current.

$$\tan \mathsf{\delta }=\frac{\mathsf{\sigma }}{2\mathsf{\pi }\mathrm{f}{\mathsf{\epsilon }}_0{\mathsf{\epsilon }}_{\mathrm{r}}},$$

(2)

2. Materials and Methods

The phase shifter is constructed in an inverted microstrip line (IMSL) topology with metals and dielectrics (tunable and non-tunable) as arranged and denoted in Figure 3a. One of our recently fabricated and assembled LC-filled IMSL phase shifter device prototypes [14] is shown in Figure 3b, as an evolution from early developments [12,15] with a lack of in-depth understanding on various materials’ dissipative losses for device optimization.

In this communication, the designs and calculation models are performed using MATLAB and Ansys HFSS (full-wave simulations). By way of illustration, Figure 4 shows the wave port mode of the LC-filled IMSL phase shifter analyzed at 60 GHz.

The effective core line length (${\mathrm{L}}_{\mathrm{eff}}$) is designed to achieve 0–π shift at 60 GHz. A straight-line circuit (free from bending-related radiation and mismatching losses) is targeted using the highly anisotropic LC material (GT3-24002) with a layer thickness (${\mathrm{T}}_{\mathrm{LC}}$) of 125 µm. Low-loss PCB laminate RT5880 with a substrate thickness (${\mathrm{T}}_{\mathrm{PCB}}$) of 787 µm is applied with the copper (Cu) clad thickness (${\mathrm{T}}_{\mathrm{Cu}}$) of 17 µm and the Cu core line cross-sectional width (${\mathrm{W}}_{\mathrm{strip}}$) of 220 µm.

Accordingly, ${\mathrm{L}}_{\mathrm{eff}}$ is calculated from Equation (1), shown earlier in Section 1, for achieving 0–π shift, and 0–2π shift, respectively. The ${\mathrm{S}}_{21}$ results in phase (data processed in the format of differential phase shifts) are validated in Figure 5, with ${\mathrm{L}}_{\mathrm{eff}}$ of 1.35 cm for achieving the targeted 0–π shift capability, and 2.7 cm for the 0–2π shift functionality at 60 GHz. Figure 6 presents the ${\mathrm{S}}_{21}$ results in amplitude (dB), identifying the maximum insertion loss (at 0 V bias state) from 1.46 dB to 1.74 dB across ∆f/f = ±10% (i.e., 54 GHz to 67 GHz with the center frequency of 60 GHz) for the 0–π shift design, and from 2.74 dB to 3.33 dB for the 0–2π shift design, respectively. Note that for the ${\mathrm{S}}_{21}$ (amplitude in dB) in Figure 6, regarding the different line lengths, the relationship between ${\mathrm{S}}_{21}$ (dB) and the line length is nonlinear (as analyzed and discussed in our previous work [13,16]), as it is complicated by the different loss mechanisms (to be shown in Equations (6)–(11) in Section 3), resultantly causing the closed-form solution and simplified formula to fail to work accurately. This is why numerical simulation is introduced and, more specifically, this work proposes the use of the full-wave power dissipation analysis method to identify each loss fraction dissipated by each element of the device, the achievement of which will bridge the gap that experimental analysis cannot resolve (to separate diverse loss components from diverse materials constituting the device).

The ${\mathrm{S}}_{11}$ in amplitude (i.e., return loss) are also quantified for the corresponding 0 V and 10 V biasing states, as well as for the two designs of different lengths (${\mathrm{L}}_{\mathrm{eff}}$ of 1.35 cm for 0–π shift, and 2.7 cm for 0–2π shift at 60 GHz). As shown in Figure 7, the reflection losses are well below 20 dB for all the tuning states under analysis and across the spectrum of 1–67 GHz. This indicates decent impedance-matched performance with no concern regarding the dielectric-anisotropy-induced impedance spikes for this designed geometry. Furthermore, the 10 V biasing state exhibits a lower return loss than the 0 V driving ones (validated for both designs of 0–π shift and 0–2π shift).

One of the focuses and novelties of this communication is, as the title suggests, rethinking the LC IMSL phase shifter design via the proposed loss dissipation analysis (to be shown in Section 3) that decomposes each loss element with parameterized geometry sizes, the contribution of which cannot be achieved by traditional experimental measurements (e.g., it is not possible to characterize and separate each metal loss and each dielectric loss component by a vector network analyzer). Analytical and numerical simulations are thereby introduced in this work to bridge the gap and perform the loss component quantification to boost the understanding of which element dominates the insertion loss.

3. Full-Wave Power Dissipation Analysis and Results

The results are further analyzed by performing a full-wave power dissipation analysis using HFSS for all materials comprising the device. This assumes that an input power (${\mathrm{P}}_{\mathrm{in}}$) of 100% is injected, calculating the output power (${\mathrm{P}}_{\mathrm{out}}$, i.e., transmission), reflected power (${\mathrm{P}}_{\mathrm{reflected}}$, i.e., reflection), as well as the dissipated power in the materials (i.e., metal losses and dielectric losses).

Based on the assumption of ${\mathrm{P}}_{\mathrm{in}}$ = 100% and the obtained ${\mathrm{S}}_{21}$, the output power (${\mathrm{P}}_{\mathrm{out}}$, i.e., transmission) is derived by Equation (3) governing this two-port network, and hence is given in Equation (4).

$${\mathrm{S}}_{21}=10\times \log \frac{{\mathrm{P}}_{\mathrm{out}}}{{\mathrm{P}}_{\mathrm{in}}},$$

(3)

$${\mathrm{P}}_{\mathrm{out}}=\left({10}^{\frac{{\mathrm{S}}_{21}}{10}}\right)\times 100\%,$$

(4)

Similarly, the reflected power (${\mathrm{P}}_{\mathrm{reflected}}$, i.e., reflection) can be derived by Equation (5) and given in Equation (6) as below.

$${\mathrm{S}}_{11}=10\times \log \frac{{\mathrm{P}}_{\mathrm{reflected}}}{{\mathrm{P}}_{\mathrm{in}}},$$

(5)

$${\mathrm{P}}_{\mathrm{reflected}}=\left({10}^{\frac{{\mathrm{S}}_{11}}{10}}\right)\times 100\%,$$

(6)

For the dissipated power in metals (Cu core line and Al substrate as grounding plane), the principle of calculating these conductor losses follows Ohm’s Law by taking the integrals over the metal surface. By way of illustration, the IMSL core line’s metal loss per unit length can be expressed in the phasor form (${\mathrm{P}}_{{\mathrm{core}}_{{\mathrm{s}}_0}}$) given in Equation (7) by incorporating our previous derivation [13]. The peak phasor form of conductor loss for the grounding Al substrate can be given in a similar way.

$$\begin{array}{l}{\mathrm{P}}_{{\mathrm{core}}_{{\mathrm{s}}_0}}\left(\mathrm{per} \mathrm{unit} \mathrm{length}\right)={{\mathrm{I}}_{{\mathrm{s}}_0}}^2\mathrm{R}\\ =[{{\displaystyle \int }}_{\mathrm{x}=-{\mathrm{W}}_{\mathrm{strip}}/2}^{\mathrm{x}={\mathrm{W}}_{\mathrm{strip}}/2}{\mathsf{\sigma }\mathrm{E}}_{\mathrm{s}}{\left(\mathrm{x},\mathrm{y}=0\right)}_0\mathrm{dl}\\ {+{{\displaystyle \int }}_{\mathrm{x}=-{\mathrm{W}}_{\mathrm{strip}}/2}^{\mathrm{x}={\mathrm{W}}_{\mathrm{strip}}/2}{\mathsf{\sigma }\mathrm{E}}_{\mathrm{s}}{\left(\mathrm{x},\mathrm{y}=-{\mathrm{T}}_{\mathrm{strip}}\right)}_0\mathrm{dl}]}^2\times \frac{\sqrt{\mathsf{\pi }\mathrm{f}\mathsf{\sigma }\mathsf{\mu }}}{{\mathsf{\sigma }\mathrm{W}}_{\mathrm{strip}}}\\ +{[{{\displaystyle \int }}_{\mathrm{y}=-{\mathrm{T}}_{\mathrm{strip}}}^{\mathrm{y}=0}{\mathsf{\sigma }\mathrm{E}}_{\mathrm{s}}{\left(\mathrm{x}=0, \mathrm{y}\right)}_0\mathrm{dl}]}^2\times 2\frac{\sqrt{\mathsf{\pi }\mathrm{f}\mathsf{\sigma }\mathsf{\mu }}}{{\mathsf{\sigma }\mathrm{W}}_{\mathrm{strip}}} ,\end{array}$$

(7)

Loss dissipated in the volume of dielectrics (e.g., LC, RT5880 PCB substrate, and glue/spacer mixture in this work) can be derived analytically from a parallel capacitor model filled with lossy dielectrics [13]. Note that the cross-sectional size of the LC-filled cavity is far less than half the guided wavelength for 1–67 GHz under analysis; hence, a TEM nature is assumed (i.e., without higher-order waveguide modes) and the quasi-static approach based on circuit theory can be used. Accordingly, the peak phasor forms of the LC volumetric loss per unit length at the lossy 0 V biasing state are given by Equation (8).

$${\mathrm{P}}_{{\mathrm{LC}}_{{\mathrm{s}}_0}}\left(\mathrm{per} \mathrm{unit} \mathrm{length}\right)=2{\mathsf{\pi }\mathrm{f}\mathsf{\epsilon }}_0{\mathsf{\epsilon }}_{\mathrm{r}}^{\prime }{\tan \mathsf{\delta }}_{\mathrm{LC}}{{\displaystyle \int }}_{\mathrm{x}=-{\mathrm{W}}_{\mathrm{LC}}/2}^{\mathrm{x}={\mathrm{W}}_{\mathrm{LC}}/2}{{\displaystyle \int }}_{\mathrm{y}=-{\mathrm{T}}_{\mathrm{LC}}}^{\mathrm{y}=0}{\left|\overrightarrow{{\mathrm{E}}_{\mathrm{s}}{\left(\mathrm{x},\mathrm{y}\right)}_0}\right|}^2\mathrm{dxdy},$$

(8)

As charges are not uniformly distributed, the E field features a skin effect and proximity effect, which are significantly different from that at electrostatics. Thus, 3D full-wave simulations in HFSS are thereby performed to numerically quantify these effects and also to integrate the line length to produce the surface loss (for metals) and volumetric loss (for dielectrics). This is done by integrating the surface loss density (e.g., ${\mathrm{p}}_{\mathrm{core}}$ for the core line) over the metal surface (dS), and integrating the volume loss density (e.g., ${\mathrm{p}}_{\mathrm{LC}}$ for the LC) over the dielectric volume (dV), as specified in Equations (9) and (10), respectively. The mathematical manipulations are performed in the HFSS field calculator for the volumetric phasor field data generated from the finite element analysis.

$${\mathrm{P}}_{\mathrm{core} \mathrm{line}}=\iint {\mathrm{p}}_{\mathrm{core}} \mathrm{dS},$$

(9)

$${\mathrm{P}}_{\mathrm{LC}}=\iiint {\mathrm{p}}_{\mathrm{LC}} \mathrm{dV},$$

(10)

The remaining loss fraction that is not dissipated by the device itself can be indicated as radiation and hence is derived by Equation (11), with ${\mathrm{P}}_{\mathrm{conductors}}$ denoting the total losses of all metals, and ${\mathrm{P}}_{\mathrm{dielectrics}}$ representing the total losses from all dielectrics.

$${\mathrm{P}}_{\mathrm{radiated}}=100\% -{ \mathrm{P}}_{\mathrm{out}}-{ \mathrm{P}}_{\mathrm{reflected}}-{ \mathrm{P}}_{\mathrm{conductors}}-{ \mathrm{P}}_{\mathrm{dielectrics}},$$

(11)

The loss decomposition analysis results are presented in Figure 8, being specifically analyzed at 60 GHz for the 0 V biasing (lossy state of analysis interest). Obviously, the LC dielectric loss (21.28%) contributes the most significant part, followed by the core line metal loss of 5.19% (under the assumption of no surface roughness), and then the grounding Al metal loss (2.04%) and radiation loss of 1.39%. The material absorption losses in the glue/spacer mixture and RT5880 PCB substrate are infinitesimal (0.04% and 0.35%, respectively).

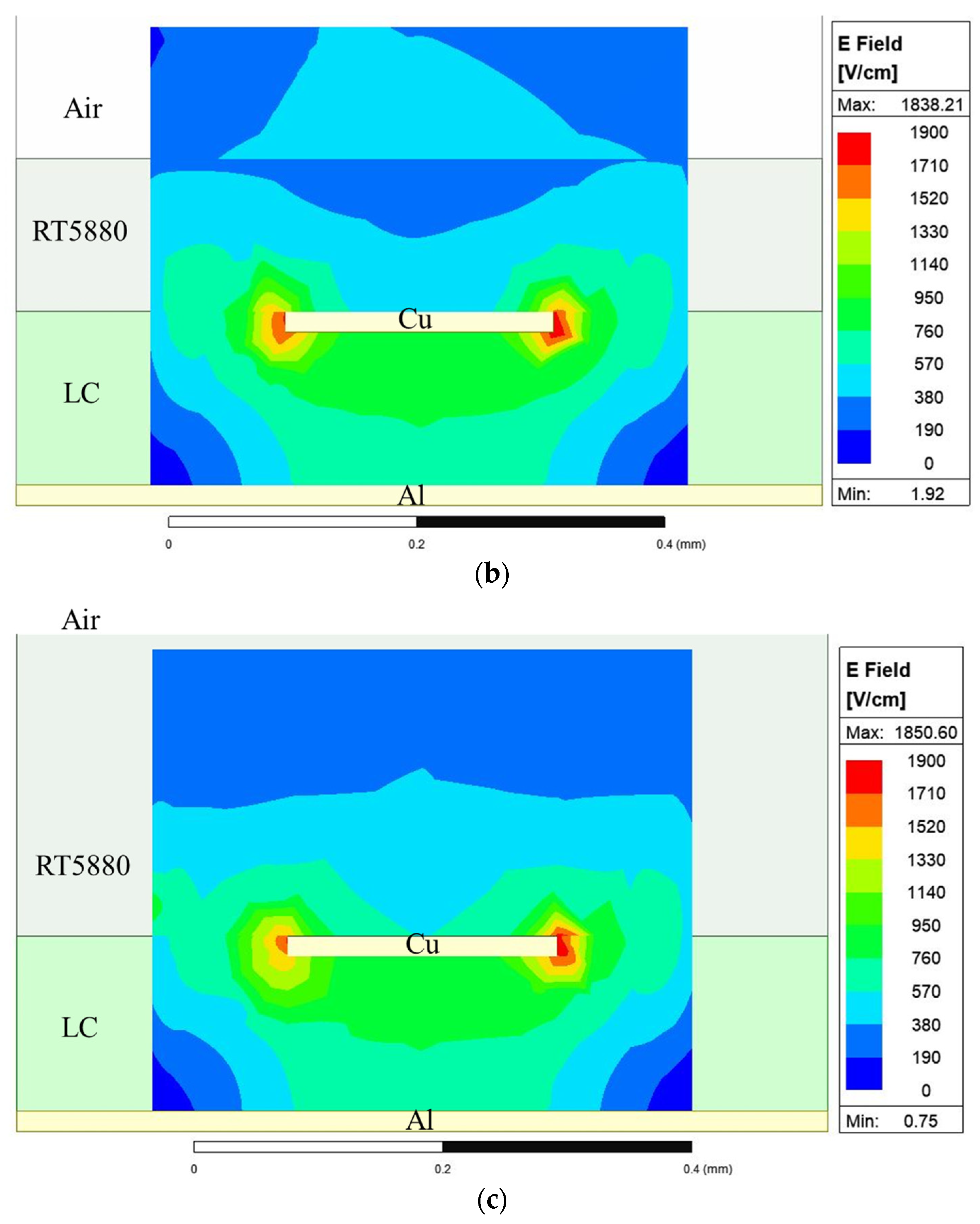
The effect of the PCB substrate thickness $({\mathrm{T}}_{\mathrm{PCB}})$ is well known to dominate the characteristics of a standard microstrip line, whereas it is of minor importance for an inverted microstrip line (IMSL). Instead, the liquid crystal layer thickness (${\mathrm{T}}_{\mathrm{LC}}$) is of paramount significance to the IMSL. This is due mainly to the wave-occupied volume ratio (WOVR), as illustrated differently in Figure 9a,b at 60 GHz.

Based on this understanding, the impacts of ${\mathrm{T}}_{\mathrm{PCB}}$ on the transmission line performance are quantified in Figure 10, Figure 11, Figure 12 and Figure 13 by comparing devices using ${\mathrm{T}}_{\mathrm{PCB}}$ = 0.787 mm and ${\mathrm{T}}_{\mathrm{PCB}}$ = 0.127 mm (RT5880 PCB), respectively. Note that for the change in ${\mathrm{T}}_{\mathrm{PCB}}$, the port size and air box sizes are rearranged accordingly to capture any radiation effect. The size arrangement of the assigned wave port for the calculation is a modeling-related representation problem concerning how to confine the signal (wave) as input (and output), which is different from (and out of scope for) the device’s physical governing equations as shown before. Here, the work follows the standard practice of assigning the wave port for the IMSL structure by balancing the computational efficiency and modeling accuracy (capturing all the possible modes in the dielectrics surrounding the electrodes). The other dimension sizes (${\mathrm{T}}_{\mathrm{LC}}$ = 0.125 mm and ${\mathrm{L}}_{\mathrm{eff}}$ = 1.35 cm) are kept equalized between both designs. As also visualized in Figure 9b,c, the WOVR of the ${\mathrm{T}}_{\mathrm{PCB}}$ = 0.127 mm design is higher than that of the ${\mathrm{T}}_{\mathrm{PCB}}$ = 0.787 mm design. This is supported by the results of the achievable differential phase shift in Figure 10, exhibiting a 5° difference at 60 GHz.

Regarding the forward transmission (${\mathrm{S}}_{21}$), the ${\mathrm{T}}_{\mathrm{PCB}}$ = 0.787 mm design exhibits a lower insertion loss (for both 0 V and 10 V biasing states) below 35 GHz. The 0.127 mm thick design exhibits a lower insertion loss (both 0 V and 10 V biasing states) above 45 GHz. Nevertheless, the difference is only 0.04 dB at 60 GHz between both designs.

In terms of the effective dielectric constant and hence the guided wavelength reported in Figure 13, it is verified that the effective dielectric constant of the ${\mathrm{T}}_{\mathrm{PCB}}$ = 0.787 mm design is larger than that of the ${\mathrm{T}}_{\mathrm{PCB}}$ = 0.127 mm one, the value of which at 10 V is larger than that at 0 V bias. Accordingly, the guided wavelength of the ${\mathrm{T}}_{\mathrm{PCB}}$ = 0.787 mm design is smaller than that of the ${\mathrm{T}}_{\mathrm{PCB}}$ = 0.127 mm one, the value of which at 10 V is smaller than that at 0 V bias. Consequently, the minimum guided wavelength is 2.57 mm for 67 GHz at 10 V bias.

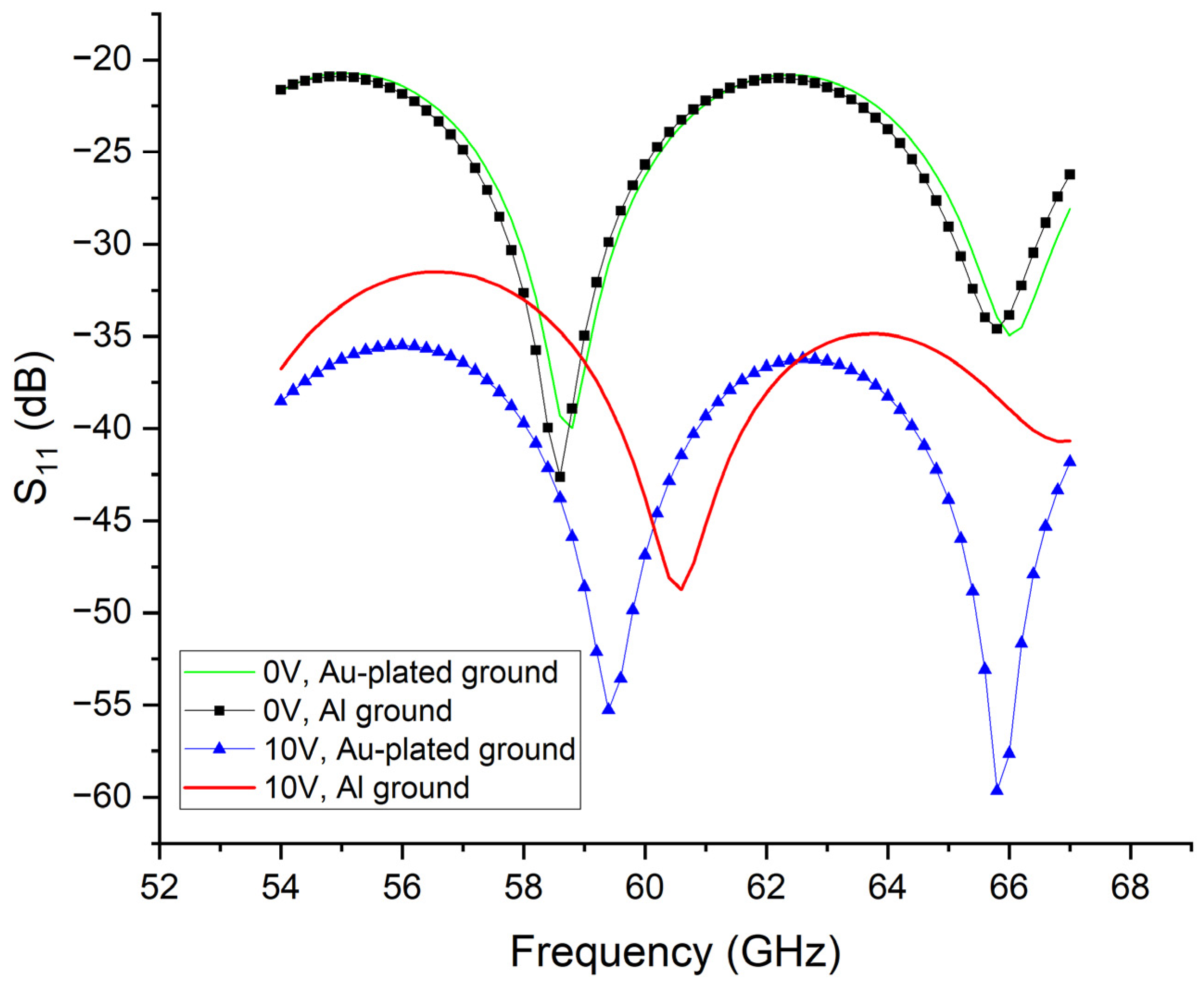
Further investigation is conducted on the impact of the grounding plane’s conductivity by comparing a gold (Au)-plated ground plane versus aluminum (Al) ground without plating. Figure 14, Figure 15, Figure 16 and Figure 17 present the phase shift, insertion loss, and return loss results. The gold-plated one reduces the insertion loss by 0.01 dB at 67 GHz (for both 0 V and 10 V biasing states).

The effect of the core line’s conductivity is also investigated and reported in Figure 17 and Figure 18. To be more specific, a 0.01 dB improvement in ${\mathrm{S}}_{21}$ is obtained by using a silver (Ag)-plated Cu core line compared to a Cu core line without Ag plating.

As shown in Figure 19, loss decomposition analysis (with the same calculating principle as Figure 8) is performed at 60 GHz for the cases of Figure 14, Figure 15, Figure 16, Figure 17 and Figure 18. With the design of a 125 μm thick LC dielectric layer, the circuit is dominated by dielectric loss. Therefore, reducing the surface roughness or using a more conductive electrode has a minor effect in mitigating the insertion loss.

Note that the dimension above gives the characteristic impedance ${\mathrm{Z}}_0$ = 54 Ω at 0 V bias. This is obtained under the quasi-TEM mode condition that applies to the LC IMSL, for which the characteristic impedance ${\mathrm{Z}}_0$ can be calculated computationally based on ${\mathrm{Z}}_0$ = $\frac{2{\mathrm{P}}_{\mathrm{avg}}}{{{\mathrm{I}}_0}^2}$, where ${\mathrm{P}}_{\mathrm{avg}}$ denotes the time-averaged power transmitted (which is obtained by integrating the Poynting vector across the IMSL’s cross-section), and ${\mathrm{I}}_0$ represents the longitudinal current.

To fine-tune the impedance to match 50 Ω, one can either reduce ${\mathrm{T}}_{\mathrm{LC}}$ or increase ${\mathrm{W}}_{\mathrm{strip}}$ (both can contribute a higher WOVR and hence higher tuning range and shorter line length to achieve π shift). We derive the design of IMSL with ${\mathrm{T}}_{\mathrm{LC}}$ = 125 μm (GT3-24002), ${\mathrm{T}}_{\mathrm{PCB}}$ = 0.787 mm (RT 5880), ${\mathrm{W}}_{\mathrm{strip}}$ = 0.248 mm (Cu core line), ${\mathrm{L}}_{\mathrm{LC}}$ = 13.5 mm (effective tunable line length to achieve 0–π phase shift).

4. Discussion

From our previous analytical analysis [13], the LC dielectric loss per unit volume P = $\mathsf{\sigma }{\left|\mathrm{E}\right|}^2=2{\mathsf{\pi }\mathrm{f}\mathsf{\epsilon }}_0{\mathsf{\epsilon }}^{\prime }\tan \mathsf{\delta }{\left|\mathrm{E}\right|}^2$, where E denotes the electric field intensity within the volume of analysis, f is the frequency of analysis, ${\mathsf{\epsilon }}^{\prime }$ is the relative permittivity of the dielectric volume of analysis. Reducing the LC layer thickness ${\mathrm{T}}_{\mathrm{LC}}$ in this work exhibits doubling effects. First, it means reducing the distance between the core line and the ground plane, thus increasing the local peaking of the electric field intensity E at the conductor surface (fixed area) and hence increasing the conductor loss (as per Ampere’s law [17] regarding the integration loop). Secondly, reducing ${\mathrm{T}}_{\mathrm{LC}}$ means reducing the LC volume but increasing E. Integrating the increased E over the reduced volume will jointly contribute to a reduced or increased dielectric volumetric loss, depending on which factor dominates the integral operation. It is reasonable to predict qualitatively that when reducing the LC thickness ${\mathrm{T}}_{\mathrm{LC}}$ to a certain value, the conductor loss will start to dominate. In this case, the surface roughness and conductivity of the conductors (mainly core line) will play an important role. The surface roughness will further increase the conductor loss as compared to the current study (without considering the surface roughness), which will exhibit a more dominant role of the conductor loss towards the insertion loss degradation. Note that the quantitative impact of the surface roughness on the insertion loss and other aspects of performance is a debatable topic, with a host of different models and experiments available in the literature [18,19,20,21,22], to which the interested readers can refer in order to explore this further.

Recall the results analysis performed for an all-optically-controlled LC-based microstrip [23]; for a ${\mathrm{T}}_{\mathrm{LC}}$ < 10 um cell, conductor loss dominates. Instead, increasing the LC cell thickness ${\mathrm{T}}_{\mathrm{LC}}$, the conductor losses reduce, as evidenced in Figure 20 below regarding the dissipative power analysis results of the Cu core line and the grounding transparent metal film, i.e., a conductive indium tin oxide (ITO) coating on an optically transparent polyethylene terephthalate (PET) substrate (denoted as transparent substrate in Figure 20). Interestingly, the conductor loss is found to vary linearly with 1/${\mathrm{T}}_{\mathrm{LC}}$, as quantified in Figure 21.

The intention and key contribution of this work (as a significant follow-up milestone based on our previous experimentally prototyped LC phase shifters) is not to produce a brand-new device topology to compete with other state-of-the-art phase shifters, but, instead, to contribute to solving and understanding the fundamental yet very important IMSL structure with LC via a new power dissipative analysis approach, which quantifies the conventionally unclear problem regarding each material loss element of the device with diverse geometry-coupled effects. Not limited to the IMSL topology, the proposed power dissipative analysis method can be generalized to other device structures (e.g., shielded coplanar waveguide [16], dielectric waveguide [24], dielectric image line [25], substrate integrated waveguide [26]) and enhance the state-of-the-art LC-based tunable microwave phase shifter design.

5. Concluding Remarks

This communication records the first results of a quantitative analysis of the feasibility of using liquid crystals as electronically tunable media to realize a passive 0–10 V continuously variable 0–π analog phase shifter with insertion loss well below 2 dB across a broad spectrum of 1–67 GHz. Full-wave power dissipation analysis is performed on a designed inverted microstrip line phase shifter filled with liquid crystal, achieving the above performance specifications. Results justify that the dielectric volumetric loss absorbed by the liquid crystals dominates the insertion loss by occupying 21.28% of the overall input signal power. Further investigation is performed to quantify the impacts of substrate thickness (${\mathrm{T}}_{\mathrm{PCB}}$ and ${\mathrm{T}}_{\mathrm{LC}}$) on the wave-occupied volume ratio (and hence the phase tuning range), as well as on the dissipative losses (including conductor loss and dielectric loss). Specifically, conductor loss is observed to follow a linear relationship with 1/${\mathrm{T}}_{\mathrm{LC}}$. The quantitative results obtained are envisioned to inform decision-making in optimizing the phase-shifting device geometry (with a focus on device physics) and engineering the LC molecules’ synthesis (from the perspective of material chemistry). This bridges the gaps in using LC IMSL phase shifters for achieving highly demanded beam-steering applications in reconfigurable front-end circuits for 5G [27] and beyond [28], as well as state-of-the-art radio astronomical instrumentation [23,29] for feeding the Square Kilometer Array (SKA) [30] from SKA-low to SKA-mid, towards SKA-high-frequency regimes with a unified phase shifter solution that can adapt to the reconfigurable needs, which will significantly save costs, reduce maintenance, and boost the ease of control and project rollout.