Sinogram Upsampling via Sub-Riemannian Diffusion with Adaptive Weighting
Abstract
:1. Introduction
- We formulate the sinogram upsampling problem as a sub-Riemannian diffusion process.
- We propose an adaptive weighting scheme to exploit the characteristics of sinogram upsampling problems with respect to projection angles.
- The experimental results verify that the proposed method is effective for upsampling a sinogram with respect to projection angles, compared to some model-based methods.
2. Related Works
2.1. Sinogram Inpainting
2.2. Image Processing via Sub-Riemannian Diffusion
3. Method
| Algorithm 1 Sinogram upsampling method |
|
3.1. Lifting
3.2. Sub-Riemannian Diffusion
3.2.1. Adaptive Weighting
3.2.2. Discretization
3.3. Projection
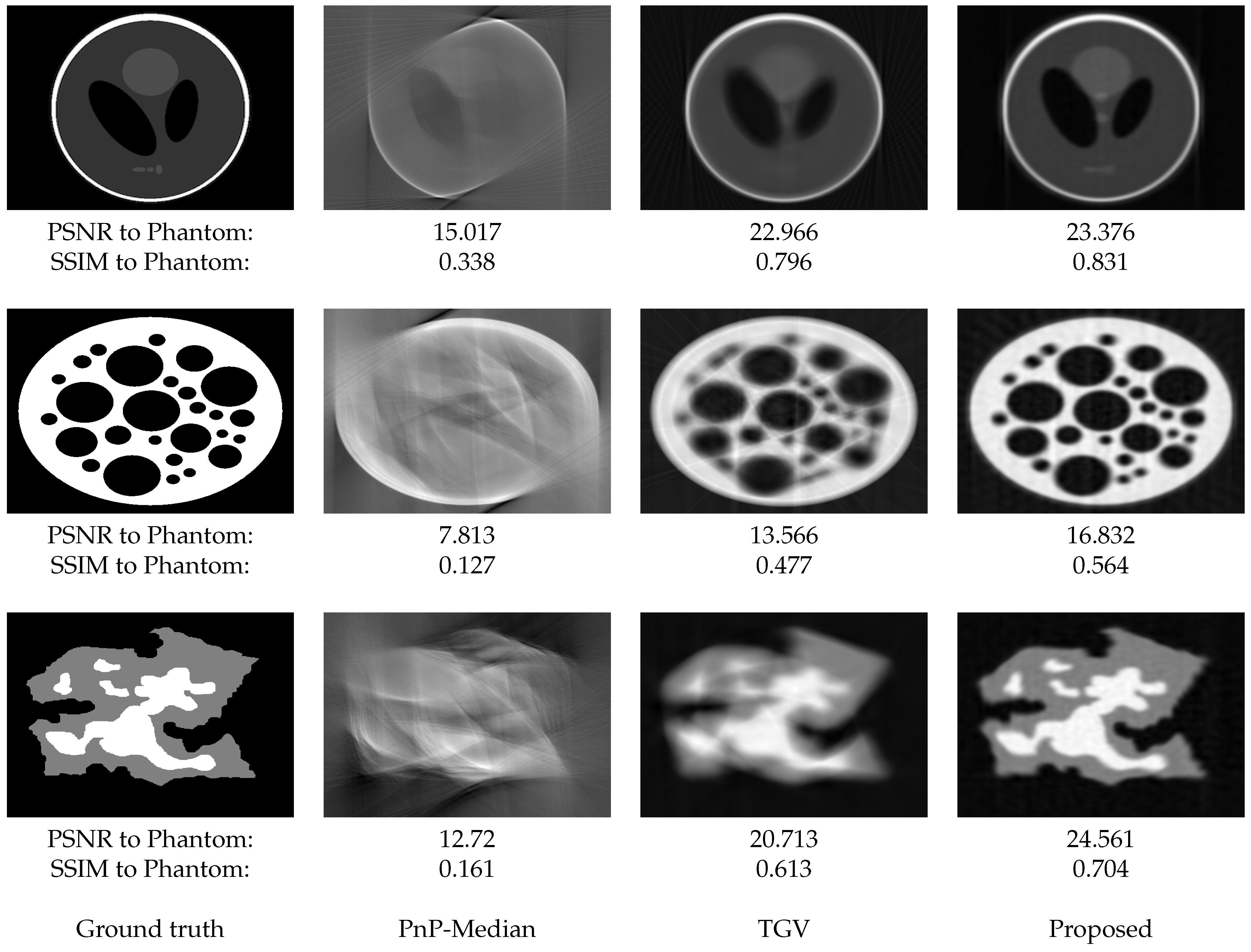
4. Results
4.1. Test Dataset
4.2. Comparison Methods
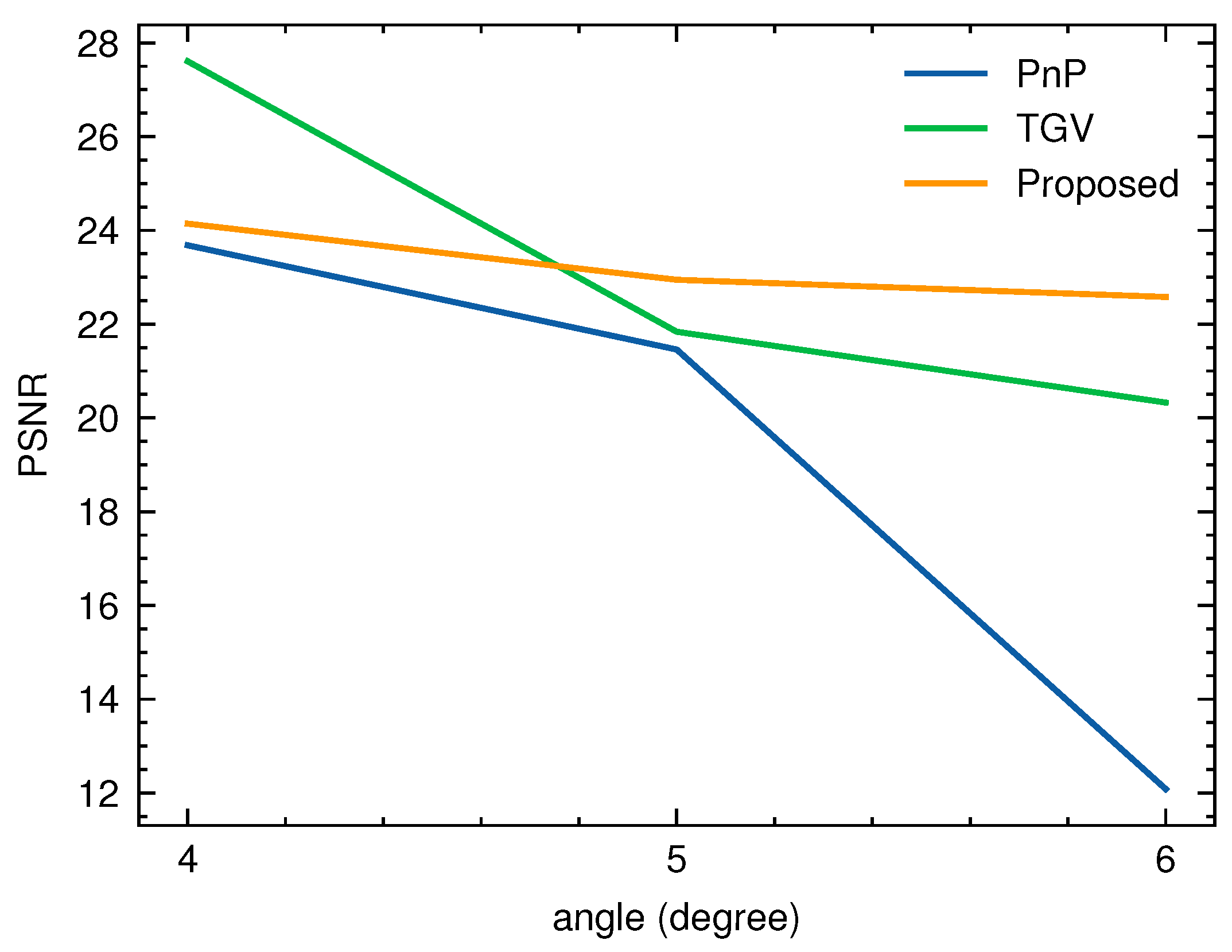
4.3. Experimental Results
5. Discussion and Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CT | Computed tomography |
| V1 | Primary visual cortex |
| PnP | Plug-and-Play |
| TGV | Total generalized variation |
References
- Buzug, T.M. Computed Tomography: From Photon Statistics to Modern Cone-Beam CT; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Huang, D.; Swanson, E.A.; Lin, C.P.; Schuman, J.S.; Stinson, W.G.; Chang, W.; Hee, M.R.; Flotte, T.; Gregory, K.; Puliafito, C.A. Optical Coherence Tomography. Science 1991, 254, 1178–1181. [Google Scholar] [CrossRef] [PubMed]
- Drexler, W.; Liu, M.; Kumar, A.; Kamali, T.; Unterhuber, A.; Leitgeb, R.A. Optical Coherence Tomography Today: Speed, Contrast, and Multimodality. J. Biomed. Opt. 2014, 19, 071412. [Google Scholar] [CrossRef] [PubMed]
- Cogliati, A.; Canavesi, C.; Hayes, A.; Tankam, P.; Duma, V.F.; Santhanam, A.; Thompson, K.P.; Rolland, J.P. MEMS-based Handheld Scanning Probe with Pre-Shaped Input Signals for Distortion-Free Images in Gabor-domain Optical Coherence Microscopy. Opt. Express 2016, 24, 13365–13374. [Google Scholar] [CrossRef] [PubMed]
- Măroiu, A.C.; Sinescu, C.; Duma, V.F.; Topală, F.; Jivănescu, A.; Popovici, P.M.; Tudor, A.; Romînu, M. Micro-CT and Microscopy Study of Internal and Marginal Gap to Tooth Surface of Crenelated versus Conventional Dental Indirect Veneers. Medicina 2021, 57, 772. [Google Scholar] [CrossRef] [PubMed]
- Hubel, D.H.; Wiesel, T.N. Receptive Fields of Single Neurones in the Cat’s Striate Cortex. J. Physiol. 1959, 148, 574–591. [Google Scholar] [CrossRef]
- Citti, G.; Sarti, A. A Cortical Based Model of Perceptual Completion in the Roto-Translation Space. J. Math. Imaging Vis. 2006, 24, 307–326. [Google Scholar] [CrossRef]
- Boscain, U.; Gauthier, J.; Prandi, D. Image Inpainting via a Control-Theoretical Model of Human Vision. In Proceedings of the 2018 IEEE 14th International Conference on Control and Automation (ICCA), Anchorage, AK, USA, 12–15 June 2018; pp. 963–968. [Google Scholar]
- Baspinar, E.; Sarti, A.; Citti, G. A Sub-Riemannian Model of the Visual Cortex with Frequency and Phase. J. Math. Neurosci. 2020, 10, 11. [Google Scholar] [CrossRef]
- Kostler, H.; Prummer, M.; Rude, U.; Hornegger, J. Adaptive Variational Sinogram Interpolation of Sparsely Sampled CT Data. In Proceedings of the 18th International Conference on Pattern Recognition (ICPR’06), Hong Kong, China, 20–24 August 2006; Volume 3, pp. 778–781. [Google Scholar]
- Benammar, A.; Allag, A.; Drai, R.; Yahi, M.; Boutkedjirt, T. Sinogram Interpolation Method for Limited-Angle Tomography. In Proceedings of the 2019 International Conference on Advanced Electrical Engineering (ICAEE), Algiers, Algeria, 19–21 November 2019; pp. 1–5. [Google Scholar]
- Lee, H.; Lee, J.; Cho, S. View-Interpolation of Sparsely Sampled Sinogram Using Convolutional Neural Network. Med. Imaging 2017, 10133, 1013328. [Google Scholar]
- Lee, H.; Lee, J.; Kim, H.; Cho, B.; Cho, S. Deep-Neural-Network-Based Sinogram Synthesis for Sparse-View CT Image Reconstruction. IEEE Trans. Radiat. Plasma Med. Sci. 2018, 3, 109–119. [Google Scholar] [CrossRef]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative Adversarial Nets. In Advances in Neural Information Processing Systems; The MIT Press: Cambridge, MA, USA, 2014; pp. 2672–2680. [Google Scholar]
- Anirudh, R.; Kim, H.; Thiagarajan, J.J.; Mohan, K.A.; Champley, K.; Bremer, T. Lose the Views: Limited Angle CT Reconstruction via Implicit Sinogram Completion. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 6343–6352. [Google Scholar]
- Pathak, D.; Krahenbuhl, P.; Donahue, J.; Darrell, T.; Efros, A.A. Context Encoders: Feature Learning by Inpainting. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 2536–2544. [Google Scholar]
- Yoo, S.; Yang, X.; Wolfman, M.; Gursoy, D.; Katsaggelos, A.K. Sinogram Image Completion for Limited Angle Tomography with Generative Adversarial Networks. In Proceedings of the 2019 IEEE International Conference on Image Processing (ICIP), Taipei, Taiwan, 22–25 September 2019; pp. 1252–1256. [Google Scholar]
- Valat, E.; Farrahi, K.; Blumensath, T. Sinogram Inpainting with Generative Adversarial Networks and Shape Priors. Tomography 2023, 9, 1137–1152. [Google Scholar] [CrossRef]
- Agrachev, A.; Barilari, D.; Boscain, U. A Comprehensive Introduction to Sub-Riemannian Geometry; Cambridge Studies in Advanced Mathematics; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar]
- Agrachev, A.; Barilari, D.; Boscain, U. Introduction to Geodesics in Sub-Riemannian Geometry. In EMS Series of Lectures in Mathematics, 1st ed.; Barilari, D., Boscain, U., Sigalotti, M., Eds.; EMS Press: Helsinki, Finland, 2016; pp. 1–83. [Google Scholar]
- Hoffman, W.C. The Visual Cortex Is a Contact Bundle. Appl. Math. Comput. 1989, 32, 137–167. [Google Scholar] [CrossRef]
- Petitot, J.; Tondut, Y. Vers une neurogéométrie. Fibrations corticales, structures de contact et contours subjectifs modaux. Math. Inform. Sci. Hum. 1999, 145, 5–101. [Google Scholar] [CrossRef]
- Baspinar, E. Multi-Frequency Image Completion via a Biologically-Inspired Sub-Riemannian Model with Frequency and Phase. J. Imaging 2021, 7, 271. [Google Scholar] [CrossRef] [PubMed]
- Sanguinetti, G.; Citti, G.; Sarti, A. Image Completion Using a Diffusion Driven Mean Curvature Flow in a Sub-Riemannian Space. In Proceedings of the Third International Conference on Computer Vision Theory and Applications, Funchal, Madeira, Portugal, 22–25 January 2008; pp. 46–53. [Google Scholar]
- Boscain, U.; Chertovskih, R.A.; Gauthier, J.P.; Remizov, A.O. Hypoelliptic Diffusion and Human Vision: A Semidiscrete New Twist. SIAM J. Imaging Sci. 2014, 7, 669–695. [Google Scholar] [CrossRef]
- Citti, G.; Franceschiello, B.; Sanguinetti, G.; Sarti, A. Sub-Riemannian Mean Curvature Flow for Image Processing. SIAM J. Imaging Sci. 2016, 9, 212–237. [Google Scholar] [CrossRef]
- Boscain, U.; Chertovskih, R.; Gauthier, J.P.; Prandi, D.; Remizov, A. Highly Corrupted Image Inpainting through Hypoelliptic Diffusion. J. Math. Imaging Vis. 2018, 60, 1231–1245. [Google Scholar] [CrossRef]
- Boscain, U.; Duplaix, J.; Gauthier, J.P.; Rossi, F. Anthropomorphic Image Reconstruction via Hypoelliptic Diffusion. SIAM J. Control Optim. 2012, 50, 1309–1336. [Google Scholar] [CrossRef]
- BertalmÃo, M. From Image Processing to Computational Neuroscience: A Neural Model Based on Histogram Equalization. Front. Comput. Neurosci. 2014, 8, 71. [Google Scholar] [CrossRef]
- Citti, G.; Sarti, A. Neurogeometry of Perception: Isotropic and Anisotropic Aspects. Axiomathes 2022, 32, 817–840. [Google Scholar] [CrossRef]
- Bertalmío, M.; Calatroni, L.; Franceschi, V.; Franceschiello, B.; Villa, A.G.; Prandi, D. Visual Illusions via Neural Dynamics: Wilson–Cowan-type Models and the Efficient Representation Principle. J. Neurophysiol. 2020, 123, 1606–1618. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.M. Introduction to Smooth Manifolds; Graduate Texts in Mathematics; Springer: New York, NY, USA, 2012; Volume 218. [Google Scholar]
- Unser, M. Splines: A Perfect Fit for Signal and Image Processing. IEEE Signal Process. Mag. 1999, 16, 22–38. [Google Scholar] [CrossRef]
- Duits, R.; Duits, M.; Van Almsick, M.; Ter Haar Romeny, B. Invertible Orientation Scores as an Application of Generalized Wavelet Theory. Pattern Recognit. Image Anal. 2007, 17, 42–75. [Google Scholar] [CrossRef]
- Favali, M.; Abbasi-Sureshjani, S.; Ter Haar Romeny, B.; Sarti, A. Analysis of Vessel Connectivities in Retinal Images by Cortically Inspired Spectral Clustering. J. Math. Imaging Vis. 2016, 56, 158–172. [Google Scholar] [CrossRef]
- Parikh, N.; Boyd, S. Proximal Algorithms. Found. Trends Optim. 2014, 1, 127–239. [Google Scholar] [CrossRef]
- Venkatakrishnan, S.V.; Bouman, C.A.; Wohlberg, B. Plug-and-Play Priors for Model Based Reconstruction. In Proceedings of the IEEE Global Conference on Signal and Information Processing, Austin, TX, USA, 3–5 December 2013. [Google Scholar]
- Geman, D.; Yang, C. Nonlinear Image Recovery with Half-Quadratic Regularization. IEEE Trans. Image Process. 1995, 4, 932–946. [Google Scholar] [CrossRef] [PubMed]
- Rudin, L.I.; Osher, S.; Fatemi, E. Nonlinear Total Variation Based Noise Removal Algorithms. Phys. D Nonlinear Phenom. 1992, 60, 259–268. [Google Scholar] [CrossRef]
- Bredies, K.; Kunisch, K.; Pock, T. Total Generalized Variation. SIAM J. Imaging Sci. 2010, 3, 492–526. [Google Scholar] [CrossRef]
- Boyd, S. Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers. Found. Trends® Mach. Learn. 2010, 3, 1–122. [Google Scholar] [CrossRef]
- Deepinv/Deepinv: PyTorch Library for Solving Imaging Inverse Problems Using Deep Learning. 2023. Available online: https://github.com/deepinv/deepinv (accessed on 15 August 2023.).
- Wang, Z.; Bovik, A.; Sheikh, H.; Simoncelli, E. Image Quality Assessment: From Error Visibility to Structural Similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef]
- Hämäläinen, K.; Harhanen, L.; Kallonen, A.; Kujanpää, A.; Niemi, E.; Siltanen, S. Tomographic X-ray data of a walnut. arXiv 2018, arXiv:1502.04064. [Google Scholar]
- Van der Walt, S.; Schönberger, J.L.; Nunez-Iglesias, J.; Boulogne, F.; Warner, J.D.; Yager, N.; Gouillart, E.; Yu, T. Scikit-Image: Image Processing in Python. PeerJ 2014, 2, e453. [Google Scholar] [CrossRef] [PubMed]

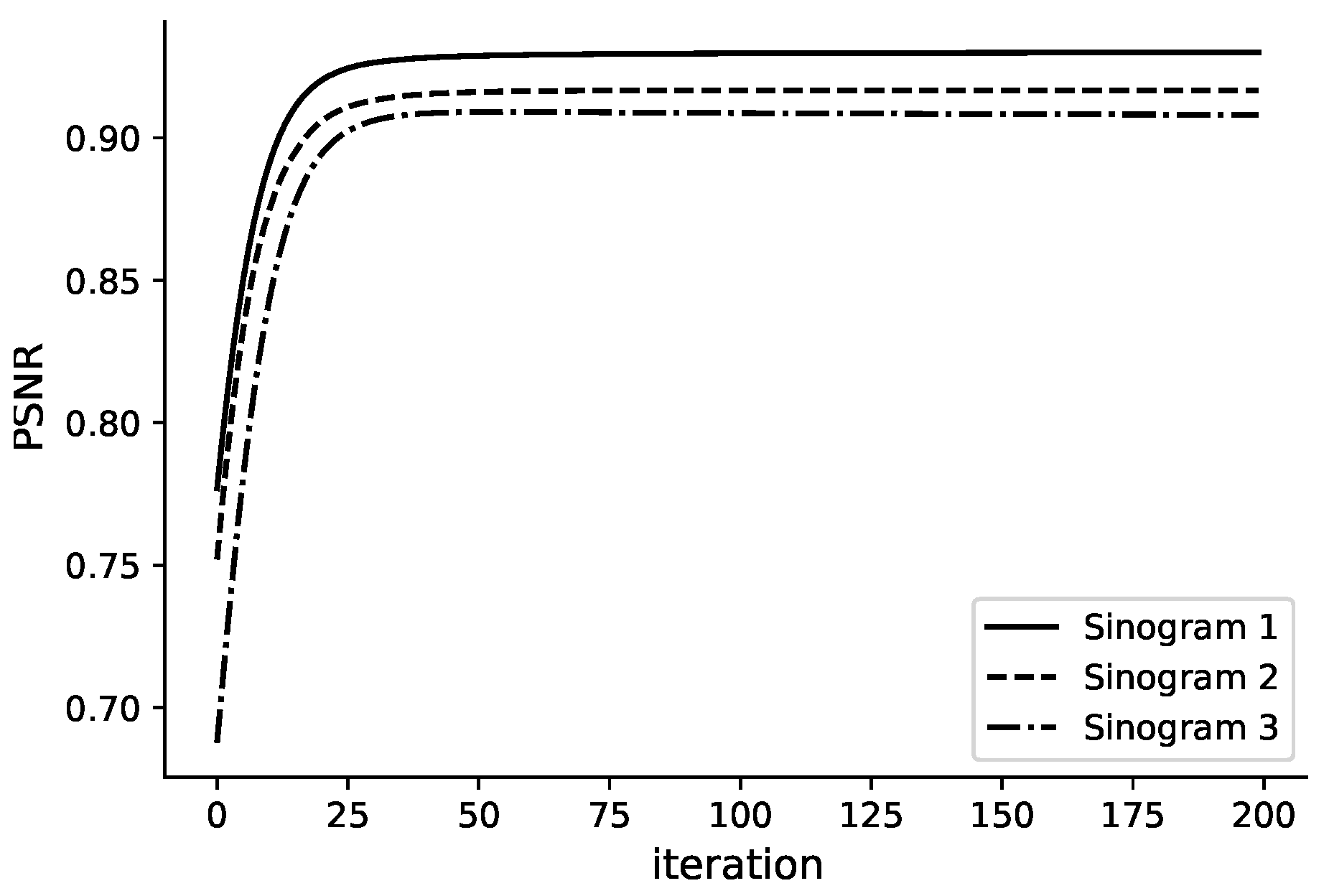





| Sinogram | Upsampled Angles | Metric | PnP-Median | TGV | Proposed |
|---|---|---|---|---|---|
| Sinogram 1 | 44 | PSNR | 32.588 | 39.615 | 33.591 |
| SSIM | 0.972 | 0.935 | 0.907 | ||
| Sinogram 2 | 44 | PSNR | 21.159 | 27.249 | 34.933 |
| SSIM | 0.913 | 0.899 | 0.917 | ||
| Sinogram 3 | 44 | PSNR | 36.573 | 38.818 | 42.215 |
| SSIM | 0.974 | 0.919 | 0.930 | ||
| Sinogram 1 | 88 | PSNR | 30.654 | 36.982 | 29.759 |
| SSIM | 0.944 | 0.927 | 0.909 | ||
| Sinogram 2 | 88 | PSNR | 19.833 | 27.006 | 30.424 |
| SSIM | 0.831 | 0.881 | 0.9123 | ||
| Sinogram 3 | 88 | PSNR | 31.8 | 36.275 | 40.914 |
| SSIM | 0.934 | 0.911 | 0.929 | ||
| Sinogram 1 | 132 | PSNR | 11.888 | 32.768 | 24.220 |
| SSIM | 0.784 | 0.911 | 0.901 | ||
| Sinogram 2 | 132 | PSNR | 12.249 | 25.336 | 26.586 |
| SSIM | 0.621 | 0.843 | 0.894 | ||
| Sinogram 3 | 132 | PSNR | 13.330 | 32.742 | 38.190 |
| SSIM | 0.708 | 0.891 | 0.923 |
| PnP-Median | TGV | Proposed | |
|---|---|---|---|
| Computational time (in seconds) | 0.26 | 27.82 | 3.11 = 1.3 + 1.7 + 0.11 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koo, J. Sinogram Upsampling via Sub-Riemannian Diffusion with Adaptive Weighting. Electronics 2023, 12, 4503. https://doi.org/10.3390/electronics12214503
Koo J. Sinogram Upsampling via Sub-Riemannian Diffusion with Adaptive Weighting. Electronics. 2023; 12(21):4503. https://doi.org/10.3390/electronics12214503
Chicago/Turabian StyleKoo, JaKeoung. 2023. "Sinogram Upsampling via Sub-Riemannian Diffusion with Adaptive Weighting" Electronics 12, no. 21: 4503. https://doi.org/10.3390/electronics12214503
APA StyleKoo, J. (2023). Sinogram Upsampling via Sub-Riemannian Diffusion with Adaptive Weighting. Electronics, 12(21), 4503. https://doi.org/10.3390/electronics12214503






