Attribute-Based Encryption Scheme with k-Out-of-n Oblivious Transfer

Abstract

Attribute-based encryption enables users to flexibly exchange and share files with others. In these schemes, users utilize their own attributes to acquire public-private key pairs from the key generation center. However, achieving this for users who wish to keep their attributes private poses a challenge. To address this contradiction, we propose an original scheme that combines ciphertext policy attribute-based encryption with a k-out-of-n oblivious transfer protocol. This scheme allows the distribution of corresponding public-private key pairs to users without the key generation center needing to obtain specific user attributes. Furthermore, it ensures the privacy of the key generation center. Security analysis demonstrates that the scheme is secure in the random oracle model. Our performance comparison and experimental results indicate that the scheme is both flexible and efficient.

1. Introduction

With the increasing application of cloud computing, a vast amount of data is stored in the cloud for processing. However, a significant portion of this data is sensitive and requires encryption to ensure its security. Traditional symmetric encryption methods, when applied to share encrypted files with multiple parties, necessitate the use of different symmetric keys for each encryption and decryption instance. This lack of flexibility in sharing and the complexity of key management pose challenges.

Attribute-based encryption (ABE) [1] emerges as a flexible solution that supports one-to-many encryption, providing an effective means to address the aforementioned challenges. The fundamental concept of ABE involves associating ciphertext and keys with attribute sets and access structures. ABE is generally categorized into Key Policy Attribute-Based Encryption (KP-ABE) [2] and Ciphertext Policy Attribute-Based Encryption (CP-ABE) [3]. KP-ABE involves the user’s key incorporating an access structure (access policy), and the ciphertext aligns with a series of attribute sets. The user can correctly decrypt the ciphertext only if the attribute set of the ciphertext satisfies the access structure (access policy) of the user key. This approach is suitable for static scenarios where users are the principal entities and only specific ciphertexts matching their access policies can be decrypted. On the other hand, CP-ABE associates the user’s key with a set of attributes, and the ciphertext contains an access structure (access policy). The user can correctly decrypt the ciphertext only if their attribute set aligns with the access structure (access policy) of the ciphertext. This design is more applicable to real-world scenarios where each user acquires keys from the Key Generation Center (KGC) based on their own attributes. Subsequently, the data owner encrypts the data with an access structure (access policy).

Therefore, CP-ABE is highly compatible with cloud computing. When implementing CP-ABE in cloud computing scenarios, users in possession of data can define an access structure (access policy) for the encrypted data. Only unique users whose attributes satisfy the access structure (access policy) can accurately decrypt the ciphertext. Consequently, there is no need for the user to replicate the encryption of the data when sharing it. This not only eliminates redundancy but also enhances flexibility for data owners in sharing data, thanks to the customizable access structure (access policy) settings.

While CP-ABE presents an algorithm based on public key cryptography capable of achieving precise access control functions, it encounters key escrow issues in practical applications. In traditional CP-ABE [4,5,6], users transmit their attribute sets to the KGC, which then generates the corresponding private key based on the user’s attributes. Subsequently, the user encrypts and shares files using this private key. It is evident in this process that KGC gains knowledge of the specific attributes of the user. In real-world usage scenarios, KGC acts as an honest but curious entity. The attributes involved are personal and private information for users who are understandably reluctant to disclose it. Consequently, users express concerns about the potential compromise of their privacy. To address this issue, some solutions currently implemented involve concealing the access structure [7,8,9]. However, this hidden access structure primarily addresses privacy protection against malicious access by unauthorized users. Another approach is the joint generation of private keys by multiple KGCs [10,11]. While this solution prevents attributes from being exclusively known by a single KGC, it does not entirely resolve the problem of user privacy exposure to any KGC. The pursuit of a robust solution to diminish the risk of privacy leakage in CP-ABE continues to be a formidable challenge.

Addressing the aforementioned concerns, we propose that the $k$-out-of-$n$ oblivious transfer protocol emerge as a potent solution. Fundamentally, the KGC maintains a set comprising $n$ attributes. Users are allowed to selectively choose $k$ attributes (where $k$ < $n$) that resonate with their individual sets from these $n$ attributes. Following this, users encrypt the chosen $k$ attributes and convey them to the KGC. Consequently, the KGC, leveraging these $k$ attributes, formulates the corresponding private key and allocates it to the users. A crucial aspect of this procedure is the KGC’s lack of awareness concerning the specific attributes chosen by the users, ensuring that the particulars used in the private key’s generation remain concealed. This method significantly bolsters user privacy safeguards in cloud computing contexts. Thus, the application of the $k$-out-of-$n$ oblivious transfer protocol is elucidated as a proficient approach, augmenting privacy safeguards while preserving the intrinsic functionality of attribute-based encryption.

2. Related Work

Originally, ABE was limited to executing threshold operations, and its policy expression lacked the necessary versatility. Subsequently, researchers proposed ABE mechanisms based on ciphertext policy and key policy. These advancements broadened the scope of attribute operations and facilitated the implementation of flexible access control policies.

In CP-ABE, the user’s key is identified by an attribute set, and the ciphertext is associated with the access structure. Before data is encrypted, the data owner is aware of the type of user permitted to access it. In the majority of CP-ABE scenarios, the access structure is made public. To protect the privacy of the data owner’s private attributes contained in the access structure, various research works on hiding access structures have been proposed. These works are primarily categorized into two groups: CP-ABE schemes that partially hide the access structure and CP-ABE schemes that fully hide the access structure. Kapadia [12] proposed a CP-ABE scheme capable of hiding the access policy. This method achieves policy hiding by re-encrypting the ciphertext for each user, introducing an online semi-trusted server. However, this method makes the server the bottleneck of the entire system in terms of efficiency and security.

To enhance the access structure’s flexibility in access control capabilities, Xu [13] utilized the tree access structure to implement a CP-ABE scheme capable of hiding the access policy. This scheme not only protects policies but also offers flexible access control capabilities. Zhang [14] introduced a CP-ABE scheme supporting partially hidden access structures (PHAS). Since attribute values are concealed in the ciphertext, users cannot directly judge the equivalence between their attributes and those in the access structure. They designed a DeJudge algorithm that uses linear algebra operations and LSSS monotonicity to help users calculate attributes, determining whether the set satisfies the access structure. However, a limitation is that the DeJudge algorithm imposes a significant computational burden on users. Chase [15] considered a distributed ABE scheme using the multi-authority model to address key escrow issues. They resolved challenges by involving multiple attribute authorities in the key generation process. However, the scheme’s performance is influenced by the number of attributes, and its access structure has limited expressiveness, supporting only AND gates, restricting data owners’ ability to formulate access policies. Zhao [16] designed a scheme combining multiple attribute authorities and a central authority structure. In this scheme, each attribute authority controls a distinct attribute set and sends the attribute private key to the user. To enhance performance, their scheme employs online/offline encryption to improve online computing efficiency. It is evident that existing approaches for hiding access policies often involve increased computing overhead or the incorporation of outsourced computing servers in the calculation process.

In addition to hiding the access structure, some ABE solutions achieve privacy protection through user key tracking. Liu [17] proposed a CP-ABE scheme equipped with black-box traceability. In this scheme, the user’s key accompanies all supersets of the attribute set, making it identifiable to multiple users for decryption. Subsequently, ABE with black-box traceability [18,19,20] has seen ongoing research on efficient tracking and revocation. Sethi [21] introduced a multi-authority CP-ABE scheme with white-box traceability, policy updates, and outsourced decryption. This scheme supports distributed authority management and accommodates monotonic access structures.

Preserving user privacy is of utmost importance, especially in sensitive application contexts like electronic health records and personal data sharing. In these situations, safeguarding the confidentiality of user attributes is imperative to mitigate the risks associated with unauthorized disclosures. In instances where the KGC acts as an honest-but-curious entity, existing methods fall short of achieving optimal outcomes—they are proficient at safeguarding against post-leakage tracking but ineffective at preempting the leakage of user privacy. Therefore, our primary focus is to investigate strategies that prevent the leakage of users’ privacy to the KGC during the key generation phase, particularly when the KGC operates as an honest-but-curious entity. This approach is also aimed at safeguarding the KGC from malicious users who might attempt to traverse the entire attribute set controlled by the KGC through continuous registration and access, thereby ensuring the privacy of both parties.

Through our research, we have discovered that the oblivious transfer protocol presents a promising approach to addressing this issue. Oblivious transfer (OT) is a vital cryptographic protocol fundamental in the realm of secure multi-party computations, serving as a cornerstone for enhancing privacy and security across various cryptographic endeavors. In an oblivious transfer, two primary entities are involved: a sender possessing certain information and a receiver who wishes to acquire a segment of this information. Unique in its operation, the protocol allows the receiver to select a specific piece of information from the sender without revealing the choice. This attribute ensures the sanctity of the receiver’s privacy, maintaining the confidentiality of the selected information segment. Below, we will introduce the development of oblivious transfer protocols.

Oblivious transfer is frequently employed as a crucial primitive in the design of security protocols. The OT primitive was proposed by Rabin [22]. In this scheme, the receiver can successfully decrypt the information sent by the sender with a probability of 1/2. After that, they even proposed a new 1-out-of-2 OT (${OT}_1^2$). In this scheme, the sender sends two encrypted messages to the receiver, and the receiver can only choose one of them to successfully decrypt. Brassard [23] designed a 1-out-of-$n$ OT (${OT}_1^n$) based on the former, and the receiver can choose one of the n messages from the sender to decrypt. Tzeng [24] improved the efficiency of the ${OT}_1^n$ by combining distributed ideas and secret sharing techniques. Moreover, $k$-out-$n$ OT (${OT}_k^n$) is a further extension of ${OT}_1^n$, where $k<n$. Naor proposed the ${OT}_k^n$ protocol [25] for the first time by using PRF. Under the premise of semi-honest receivers, the scheme mainly guarantees system security through onerous computation and communication expenses. In order to solve the above problems of high computational overhead and high communication costs, Chu [26] proposed a $k$-out-$n$ OT protocol, but it does not really solve the problem or minimize these costs. Tzeng [27] proposed a ${OT}_k^n$ protocol that uses two different ROMs under the Computational Diffie-Hellman Problem (CDH) assumption to keep the system secure in the presence of malicious receivers.

Compared to the solutions previously discussed, hidden access structures can mitigate attribute leakage due to unauthorized user access, but they fail to shield user privacy from the KGC. Additionally, schemes involving multiple authorization centers are susceptible to collusion attacks, providing only partial attribute concealment from the KGC without completely obscuring individual attributes. In the context of key tracking solutions, their effectiveness is predominantly in post-event accountability, falling short of proactive user privacy protection. In contrast, our proposed method leverages the oblivious transfer protocol, safeguarding user attributes during the key generation phase. This approach ensures that an honest-but-curious KGC remains unaware of the specific attributes associated with a user’s private key during the key distribution process. The evolution of OT has inspired us, leading us to consider the utilization of ${OT}_k^n$ for generating private keys in ABE. In simple terms, the KGC possesses $n$ attributes. When a user requests a private key from the KGC, the user selects $k$ attributes from the KGC. Consequently, the KGC remains unaware of the specific $k$ attributes selected by the user, thereby achieving privacy protection for the user.

3. Preliminaries

3.1. $k$-Out-of-$n$ Oblivious Transfer

The $k$-out-of-$n$ oblivious transfer [25] is defined as follows: In this protocol, the sender and the receiver are generally involved. The sender is in charge of $n$ messages $\{m_0{, m}_1, {\cdots , m}_n\}$, and the receiver has a set of $k$ numbers $\{r_1, r_2, \cdots {, r}_k\}\subset \left\{0, 1, \cdots , n-1\right\}$. When the oblivious transfer protocol is completed, the receiver only holds $k$ messages $\left\{m_{r_1}, m_{r_2}, \cdots , m_{r_k}\right\}$ without knowing anything about $m_{\xi }$, where $\xi \in \left\{0, 1,\cdots ,n-1\right\}$and $\xi \notin \left\{r_1, r_2, \cdots {, r}_k\right\}$, while the sender knows nothing about the message chosen by the receiver $\left\{r_1, r_2, \cdots {, r}_k\right\}$.

3.2. Bilinear Pairings

Bilinear mapping means a map is defined as follows: ${\mathbb{G}}_0$ and ${\mathbb{G}}_1$ be two multiplicative cyclic groups of prime order $p$. Let $g$ be a generator of ${\mathbb{G}}_0$ and e be a bilinear map, e: ${\mathbb{G}}_0\times {\mathbb{G}}_0\to {\mathbb{G}}_1$. The bilinear map e has the following properties:

(a)

Bilinearity: For all $g_1,g_2\in {\mathbb{G}}_0$ and $u,v \in {\mathbb{Z}}_p$ has $e\left(g_1^u,g_2^v\right)={e\left(g_1,g_2\right)}^{uv}$.

(b)

Non-degeneracy: Given a generator $g$ of the group ${\mathbb{G}}_0$, $e\left(g,g\right)\ne 1$.

3.3. Access Structure

Use a tree $\mathbb{T}$ to represent the access structure. All non-leaf nodes in the tree are represented as a threshold gate, determined by its child node and a threshold value. Define ${num}_x$ as the number of children of a node $x$ and $V_x$ as threshold value of the node $x$, where $0<V_x\le {num}_x$. $V_x=1$it is an AND gate, case $V_x={num}_x$. Let $ATT=\left\{{att}_1, {att}_2, \cdots , {att}_n\right\}$ be an attribute set; all leaf nodes $x$ are represented as an attribute ${att}_i\in ATT$ and its threshold value $V_x=1$. We denote $par\left(x\right)$ to represent the parent of the node $x$. We can define a function $att\left(x\right)$, where a node $x$ is a leaf node associated with an attribute. Furthermore, we define the order between the children of each node in the $\mathbb{T}$ by labeling the children of each node starting from 1. The function $index\left(x\right)$ replies to the amount associated with the node $x$, and the value of $index\left(x\right)$ is particularly assigned to the node in $\mathbb{T}$ for a specified key.

4. Our Construction

In this area, we give the details of how to construct our scheme. We begin by explaining the system model and introducing its main algorithms and functions. Afterwards, we provide a description of our attribute-based encryption scheme with ${OT}_k^n$ protocol. Finally, we will discuss the security analysis and experimentation of this scheme.

4.1. Notions

The notions utilized in this paper are enumerated in Table 1.

Table 1. Notions and definitions for our scheme.

Notions	Definition
λ	a security parameter
$MPK$	the system’s public parameters
$MSK$	the master private parameters
$M$	a message
$\mathbb{T}$	the tree access structure
$\mathbb{A}$	the set of leaf nodes
$V_x$	the threshold value of the node
$f_x$	a polynomial equation
$CT$	$\mathrm{a} \mathrm{ciphertext} \mathrm{with} \mathrm{access} \mathrm{structure} \mathbb{T}$
$S$	a user’s attributes
$PK$	a user’s public key
$SK$	a user’s private key
$\mathbb{G}$	$\mathrm{a} \mathrm{cyclic} \mathrm{additive} \mathrm{group} \mathrm{of} \mathrm{prime} \mathrm{order} \mathcal{l}$
${\mathbb{G}}_T$	a multiplicative group
e: $\mathbb{G}\times \mathbb{G}\to {\mathbb{G}}_T$	the bilinear map
$g$	$\mathrm{a} \mathrm{generator} \mathrm{of} \mathbb{G}$
$ATT$	the whole attribute set
${att}_i$	$\mathrm{the} i$$\mathrm{th} \mathrm{attribute} \mathrm{of} ATT$
$n$	the number of whole attributes in the system
$k$	the number of users’ attributes

4.2. System Model

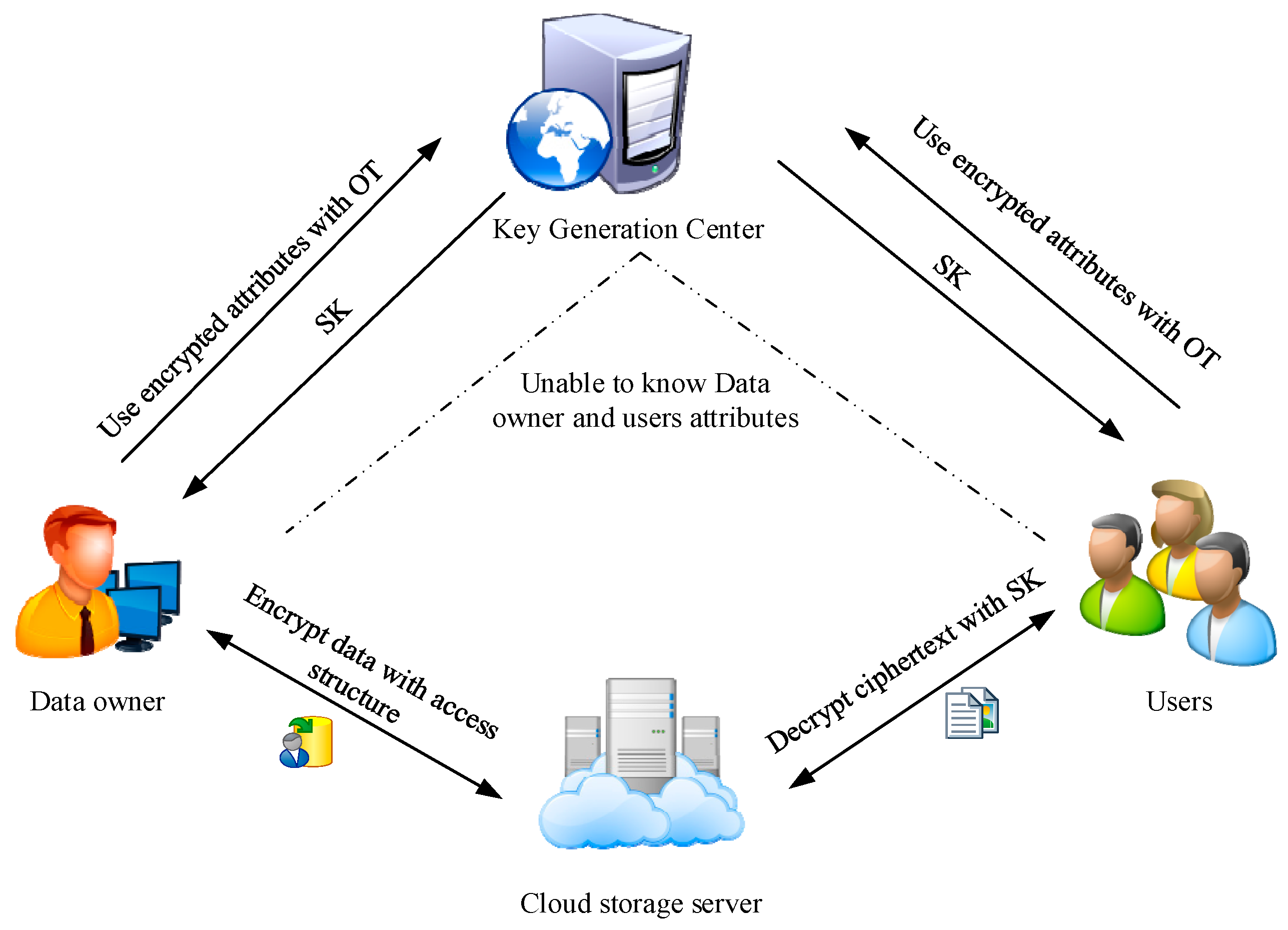
This paper proposes an attribute-based encryption with an oblivious transfer protocol, which mainly includes four parts: KGC, cloud storage server, data owner, and user. This scheme alleviates the problem of attribute privacy protection between the KGC and the user through the ${OT}_k^n$ protocol. The system model of CP-ABE with ${OT}_k^n$ is shown in Figure 1. The scheme proposed in this paper includes the following four stages:

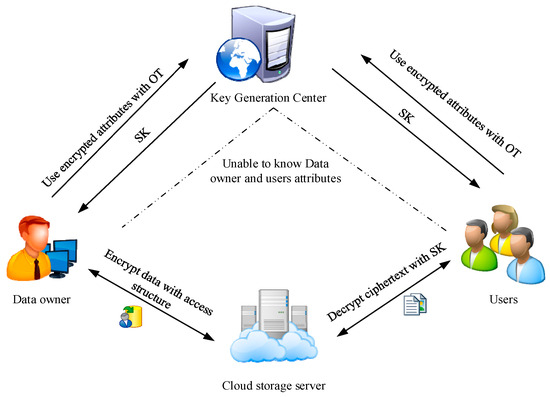
Figure 1. System model of CP-ABE with k-out-of-n oblivious transfer.

Setup ($1^{\lambda }$)$\to$($MPK, MSK$): The Setup algorithm is run by KGC. Input the security parameter λ, and the algorithm outputs the system public parameter $MPK$ and master private key $MSK$. KGC publicizes $MPK$ and keeps $MSK$ secret.

Encrypt ($MPK,M,\mathbb{T}$)$\to CT$: The encryption algorithm is run by the data owner. Input a system public parameter $MPK$, a message $M$, and the tree access structure $\mathbb{T}$, and the algorithm outputs ciphertext $CT$.

KeyGen ($MPK,S$)$\to SK$: The KeyGen algorithm is run by KGC and the user. Input a system public parameter $MPK$ and the user’s attributes $S,$ and the algorithm outputs the user’s private key $SK$.

Decrypt ($CT,SK$)$\to M$: The decryption algorithm is run by the user. Input ciphertext $CT$ and the user’s private key $SK$, and the algorithm outputs the message $M$.

4.3. Proposed Scheme

Setup ($1^{\lambda }$)$\to$($MPK, MSK$): The setup algorithm is run by KGC. Let $\mathbb{G}$ be a cyclic additive group of prime order $\mathcal{l}$, and let $g$ be a generator of $\mathbb{G}$. In addition, let $e$: $\mathbb{G}\times \mathbb{G}\to {\mathbb{G}}_T$ denote the bilinear map, and let ${\mathbb{G}}_T=e\left(g,g\right)$ be a multiplicative group. Taking as input a security parameter $\lambda$ and an attribute set $ATT=\left\{{att}_1, {att}_2, \cdots , {att}_n\right\}$ and supposing the attribute ${att}_1$ is mapped to index$i$ for all $i=1, 2, \cdots , n$. We will employ the hash functions H: ${\{0, 1\}}^{*}\to {\{0, 1\}}^l, H_1: {\{0, 1\}}^{*}\times \mathbb{G}\to {\mathbb{Z}}_q/\mathcal{l}, H_2: {\{0, 1\}}^{*}\to \mathbb{G}, H_3:\mathbb{G}\to {\{0, 1\}}^l$ that we would model as a random oracle. The construction is as follows:

(1)

Choose a random $s\in {\mathbb{Z}}_q$ and calculate $P_{pub}=g^s$. Pick two random exponents $a,b\in {\mathbb{Z}}_q$, and compute $P=g^b$.

(2)

The public parameters are published as $\left(MPK,MSK\right)$, where $MPK=\left(\mathbb{G},{\mathbb{G}}_T,l,g,P_{pub},P,{e(g,g)}^a,H,H_1,H_2,H_3\right)$ and $MSK=\left(s,b,g^a\right)$.

Encrypt ($MPK,M,\mathbb{T}$)$\to CT$: The algorithm of encryption is run by the data owner. Our encryption is based on the Bethencourt approach [2]. It uses the tree access structure $\mathbb{T}$ to encrypt the message $M$. The details are as follows:

(1)

Choose a polynomial $f_x$ for each node or leaf $x$ in the tree $\mathbb{T}$. For each node $x$ in the $\mathbb{T}$, set the degree $D_x$ of the polynomial $f_x$ to be one less than the threshold value $V_x$ of that node, that is, $D_x=V_x-1$. We use a top-down approach to pick these polynomials, and it begins with the root node $R$. First, the algorithm randomly chooses a $b\in {\mathbb{Z}}_q$ and initializes $f_R\left(0\right)=c$. Then, it chooses $D_R$ other points of the polynomial $f_R$ randomly to define it entirely. For another node $x$, it sets $f_x\left(0\right)=f_{Par\left(x\right)}\left(index\left(x\right)\right)$ and chooses $D_R$ other points randomly to entirely define $f_x$.

(2)

On input the set of leaf nodes $\mathbb{A}\subseteq \mathbb{T}$, then compute $\forall i\in \mathbb{A}:$ $C_{1,i}=g^{f_i\left(0\right)}$, $C_{2,i}={H_2\left(att\left(i\right)\right)}^{f_i\left(0\right)}$, $C_3=P^c$. Inputting a message $M$, compute $C=M{e\left(g,g\right)}^{ac}$.

The data owner outputs ciphertext $CT=\left(\mathbb{T},C,C_{1,i},C_{2,i},C_3\right)$.

KeyGen($MPK,S$)$\to SK$. The algorithm for key generation is run by the user and KGC. Users give the attribute $S\subseteq ATT$ to KGC, and KGC outputs the key associated with that $S$. To prevent KGC from learning the key consistent with a set of attributes $S$, we combine the idea of k-out-of-n oblivious transfer protocol. The details are as follows:

(1)

KGC uses its ${ID}_{kgc}$ to compute $OT.{PK}_{kgc}=H_2\left({ID}_{kgc}\right)$, $OT.{SK}_{kgc}{=sH}_2\left({ID}_{kgc}\right)$. Then, on input user $ID$, compute $OT.{PK}_{ID}=H_2\left(ID\right)$, $OT.{SK}_{ID}{=sH}_2\left(ID\right)$ reply for the user.

(2)

The user sets ${\gamma }_j$ to denote the number of these attributes $S$ according to $ATT=\left\{{att}_1, {att}_2, \cdots , {att}_n\right\}$, and randomly chooses $\alpha ,\beta \in {\mathbb{Z}}_q$. Then computes $K=\alpha \beta OT.{PK}_{ID}, K_j={H\left({\gamma }_j\right)}^{\beta }OT.{SK}_{ID}$, where $j=1, 2, \cdots , k$ and ${\gamma }_j\in \{1, 2, \cdots , n\}$. Afterwards, the user randomly chooses $\eta \in {\mathbb{Z}}_q$ and computes ${\rho }_{id}=H_3\left(ID,K,K_1, K_2, \cdots , K_k\right)$. Then the user computes a signature ${\sigma }_{id}=(U_{id},V_{id})$, where $U_{id}=\eta OT.{PK}_{ID}, V_{id}=\left(\eta +h_{id}\right)OT.{SK}_{ID}$, and $h_{id}=H_1({\rho }_{id},U_{id})$. Finally, user output $M_{id}=\{ID,K,K_1, K_2, \cdots , K_k,{\sigma }_{id}\}$.

(3)

When KGC receives the $M_{id}$, it first computes ${\varpi }_{id}=H_3\left({ID}_r,K,K_1, K_2, \cdots , K_k\right)$, verifying $\left(P,V_{id}\right)=e(P_{pub},U_{id}+{\varpi }_{id}OT.{PK}_{ID})$. If it is false, output $\perp$; otherwise, randomly chooses $\phi \in {\mathbb{Z}}_q$ and computes ${\mathsf{A}}_1=\phi K_1,{\mathsf{A}}_2=\phi K_2, \cdots , {\mathsf{A}}_k=\phi K_k$.

(4)

Afterwards, KGC randomly chooses a $r\in {\mathbb{Z}}_p$, and then randomly chooses $r_n\in {\mathbb{Z}}_p$ for each attribute $ATT=\left\{{att}_1, {att}_2, \cdots , {att}_n\right\}$. Then it computes the key message as $M_{key}=\left({SK}_1,M.{SK}_{2,n}\right)$, where ${SK}_1=g^{(a+r)/b}$, $M.{SK}_{2,n}={e(H\left({\psi }_n\right)K,OT.{SK}_{kgc})}^{\phi }\oplus (D_{1,n},D_{2,n})$. Moreover, $D_{1,j}={g^r{·H}_2\left(n\right)}^{r_n}$, $D_{2,j}=g^{r_n}$, and ${\psi }_n$ is a number from $1$ to $n$ in order.

(5)

KGC randomly chooses $\xi \in {\mathbb{Z}}_p$ and computes ${\rho }_{kgc}=H_3\left(A_1, A_2, \cdots , A_k,M_{key}\right)$ and outputs signature ${\sigma }_{kgc}=(U_{kgc},V_{kgc})$, where $U_{kgc}=\xi ·OT.{PK}_{kgc}, V_{kgc}=\left(\xi +h_{kgc}\right)OT.{SK}_{kgc}$ and $h_{kgc}=H_1({\rho }_{kgc},U_{kgc})$. Finally, KGC outputs $M_{kgc}=\{{ID}_{kgc},A_1, A_2, \cdots , A_k,M_{key},{\sigma }_{kgc}\}$.

(6)

When the user receives the $M_{kgc}$, it first computes ${\varpi }_{kgc}=H_3\left({ID}_{kgc},A_1, A_2, \cdots , A_k,M_{key}\right)$, verifying $e\left(P,V_{kgc}\right)=e(P_{pub},U_{kgc}+{\varpi }_{kgc}OT.{PK}_{kgc})$. If it is false, output $\perp$; otherwise, compute ${SK}_{2,t}=M.{SK}_{2,n}\oplus {e\left(A_t,OT.{PK}_{kgc}\right)}^{\alpha },t\in \left\{1, 2, \cdots , k\right\}$. Finally, the user obtains $SK=\left({SK}_1,{SK}_{2,t}\right)$.

Decrypt ($CT,SK$)$\to M$: The decryption procedure is run by the user. We define the following recursive algorithm:

(1)

If the node $x$ is a leaf node, we can let $w=att\left(x\right)$ and define it as follows: If $w\in ATT=\left\{{att}_1, {att}_2, \cdots , {att}_n\right\}$, the user executes the recursive algorithm $Dec\left(CT,SK,x\right)=\frac{e(D_{1,j},C_{1,i})}{e(D_{2,j},C_{2,i})}$, otherwise $Dec\left(CT,SK,x\right)$ output $\perp .$

(2)

If the node $x$ is a non-leaf node, for all nodes $\omega$ that are children of $x$, it calls $Dec\left(CT, SK,\omega \right)$ and stores the output as $F_{\omega }$. Let ${ATT}_x$ be an arbitrary $k_x$-sized set of child nodes $\omega$ such that $F_{\omega }\ne$ $\perp$. If no such set exists, then the node was not satisfied, and the function returned $\perp$. Otherwise, the user computes:

$$\begin{array}{c}{F}_{\omega }={\displaystyle \prod _{\omega \in {ATT}_x}}{F_{\omega }}^{{∆}_{i,{{{ATT}^{\prime }}_x}^{\left(0\right)}}}\\ ={\displaystyle \prod _{\omega \in {ATT}_x}}{\left({e(g,g)}^{r·f_{\omega }\left(0\right)}\right)}^{{∆}_{i,{{{ATT}^{\prime }}_x}^{\left(0\right)}}}\\ ={\displaystyle \prod _{\omega \in {ATT}_x}}{\left({e(g,g)}^{r·f_x\left(i\right)}\right)}^{{∆}_{i,{{{ATT}^{\prime }}_x}^{\left(0\right)}}}\\ ={e(g,g)}^{r·f_x\left(0\right)},where{ATT}_x^{\prime }=\left\{index\left(\omega \right):\omega \in {ATT}_x\right\},i=\mathrm{index}(\omega )\end{array}$$

(3)

If the tree is satisfied by $ATT=\left\{{att}_1, {att}_2, \cdots , {att}_n\right\}$, user set $A=Dec\left(CT,SK,r\right)={e\left(g,g\right)}^{r{f}_R\left(0\right)}={e\left(g,g\right)}^{rc}$, and computes $C/\left(e\left(C_3,{SK}_1\right)/A\right)$. If it is false, output $\perp$; otherwise, output $M$ as the decryption of the ciphertext.

Figure 2 is a schematic diagram of the algorithm steps and data flow of our solution.

Figure 2. Our scheme flow chart.

5. Security Analysis

In this area, we analyze the security of this protocol and prove that the protocol can achieve KGC’s privacy and the user’s privacy protection.

Security Assumptions. For our attribute-based encryption scheme with the ${OT}_k^n$ protocol against malicious users, we will use two hardness problem assumptions: one is the Decisional Diffie-Hellman (DDH) problem, and the other is the Chosen-Target Computational Diffie-Hellman (CT-CDH) problem.

Assumption 1.

Decisional Diffie-Hellman assumption. Let $p=2q+1$, where $p and q$ are two primes, and let ${\mathbb{G}}_p$  be the subgroup of ${\mathbb{Z}}_q$ with order $p$. The following two distribution ensembles are computationally indistinguishable:

$Y_1={\left\{(g,g^a,g^b,g^{ab})\right\}}_{{\mathbb{G}}_p}$, where $g$ is a generator of ${\mathbb{G}}_p$ and randomly chooses $a,b \in {\mathbb{Z}}_q$.

$Y_2={\left\{(g,g^a,g^b,g^c)\right\}}_{{\mathbb{G}}_p}$, where $g$ is a generator of ${\mathbb{G}}_p$ and randomly chooses $a,b,c\in {\mathbb{Z}}_q$.

Assumption 2.

Chosen-Target Computational Diffie-Hellman assumption. Let ${\mathbb{G}}_p$ be a group of prime order $q$, $g$ be a generator of ${\mathbb{G}}_p$, and randomly choose $x\in {\mathbb{Z}}_q$. Let $H_1:{\left\{0, 1\right\}}^{*}\to {\mathbb{G}}_p$ be a cryptographic hash function. The adversary $A$ is given input $\left(q,g,g^x,H_1\right)$ and two oracles: the target oracle $T_G\left(·\right)$ that returns a random element $w_i\in {\mathbb{G}}_p$ at the $i$-th query and the helper oracle $H_G\left(·\right)$ that returns ${\left(·\right)}^{*}$. Let $q_T$ and $q_H$ be the number of queries $A$ made to the target oracle and helper oracle, respectively. The probability that $A$ outputs $k$ pairs $(\left(v_1,j_1\right),\left(v_2,j_2\right), \cdots , \left(v_k,j_k\right))$, where $v_i={\left(w_{j_i}\right)}^x$ for $i\in \left\{1, 2, \cdots , k\right\}$, $q_H\le k\le q_T$, is negligible.

Theorem 1.

The proposed protocol can realize the protection of users’ privacy.

Proof. 

During the key distribution process, the user selected the number of some attributes ${\gamma }_j\in \left\{1, 2, \cdots , n\right\}$ from the all attribute collection $ATT=\left\{{att}_1, {att}_2, \cdots , {att}_n\right\}$. First, the user hashed and randomized ${\gamma }_j$ by $H$ and $\beta$, and output $K_j={H\left({\gamma }_j\right)}^{\beta }OT.{SK}_{ID}$. We maintain that the choice ${\gamma }_j$ can only be known by the user themselves and not by anyone else. Due to the computational difficulty of the DDH problem, even if the adversary has the ability to obtain the user’s private key $OT.{SK}_{ID}$, they would still be unable to obtain ${H\left({\gamma }_j\right) }^{\beta }$ from $K_j$. In other words, it is impossible for adversary $A$ to determine ${\gamma }_j$ as they are unable to compute ${H\left({\gamma }_j\right) }^{\beta }$ and therefore cannot obtain any information about it. Let $\mathcal{A}=\left\{({\gamma }_j,\beta )\in {\mathbb{Z}}_q\ast {\mathbb{Z}}_n |{ H\left({\gamma }_j\right) }^{\beta }OT.{SK}_{ID}=K_j\right\}$; that is to say, all the possible pairs $(\beta ,{\gamma }_j)$ satisfying the equation ${ H\left({\gamma }_j\right) }^{\beta }OT.{SK}_{ID}=K_j$ together constitute $\mathcal{A}$. Given a value $K_j$ and a fixed value of $OT.{SK}_{ID}$, there exists only one unique value of ${ H\left({\gamma }_j\right) }^{\beta }$ that satisfies the equation. From the definition of a hash function, we know that if a specific value of ${ H\left({\gamma }_j\right) }^{\beta }$ is given, then it is possible to uniquely determine the corresponding value of ${\gamma }_j$ and $\beta$. There is a one-to-one correspondence between ${\gamma }_j$ and $\beta$. Given this fact, we can observe that there are $n\left(\beta ,{\gamma }_j\right)$ pairs in $\mathcal{A}$, with the dimension of ${\gamma }_j$ being $n$. Specifically, $\mathrm{P}\mathrm{r}\left[{\gamma }_j|K_j\right]=\mathrm{P}\mathrm{r}\left[{\gamma }_j\right]=1/n$; this means that, upon seeing a particular $K_j$, there is no way to reveal the user’s choice ${\gamma }_j$ other than guesswork. Therefore, the proposed protocol has the ability to protect users’ privacy. □

Theorem 2.

The proposed protocol can realize the protection of KGC’s privacy.

Proof. 

We can prove that under Arguments 1 and 2, it is computationally impossible for the malicious user $U^{\mathrm{*}}$ to obtain the $(k+1)$th message. Specifically, for argument (1), $U^{\mathrm{*}}$ should pursue the scheme steps to generate the values of $K$ and $k{K}_{j}s$; on the contrary, $U^{\mathrm{*}}$ fails to get the $k$ selected messages that it intended. In arguments (2), we will prove that $U^{\mathrm{*}}$ cannot obtain the $\left(k+1\right)$th messages other than his choice, because when he tries to obtain the $\left(k+1\right)$th messages, he is actually solving the difficult problem of the CT-CDH problem. □

Argument 1.

$U^{*}$must comply with the scheme to calculate the values of  $K\left(=\alpha \beta {·OT.PK}_{ID}^{*}\right)$ and $K_j\left(={H\left({\gamma }_j\right)}^{\beta }{·OT.SK}_{ID}^{*}\right)$, for $j=1$ to $k$; if not, $U^{*}$ cannot receive the $k$ messages that it has chosen.

Next, we will discuss in detail three cases: (a) $U^{\mathrm{*}}$ fakes $K$ but makes $K_j$ honest; (b) $U^{\mathrm{*}}$ counterfeits $K_j$ but honestly generates $K$; and (c) $U^{\mathrm{*}}$ forges the values of $K$ and $K_j$.

(a) $U^{\mathrm{*}}$ fakes $K$ but makes $K_j$ honestly. Suppose $U^{\mathrm{*}}$ is dishonest in calculating $K$, but honestly calculating $K_j$ as given in the scheme. Let us suppose the $U^{\mathrm{*}}$ computes $K_j={H\left({\gamma }_j\right)}^{\beta }{·OT.SK}_{ID}^{*}$ and chooses an $X\in \mathbb{G}$ at random to replace $K$. Then, the KGC will compute ${\mathsf{A}}_k=\phi K_k, M.{SK}_{2,n}={e(H\left({\psi }_n\right)X,OT.{SK}_{kgc})}^{\phi }⨁(D_{1,n},D_{2,n})$ and return them to $U^{\mathrm{*}}$. In consequence, $U^{\mathrm{*}}$ is unable to decrypt $M.{SK}_{2,n}$ to receive the $k$ messages since $e{\left(A_t,OT.{PK}_{kgc}\right)}^{\alpha }$ is certainly not equal to ${e(H\left({\psi }_n\right)X,OT.{SK}_{kgc})}^{\phi }$. For obtaining the $k$ messages, the $U^{\mathrm{*}}$ can only compute ${e(H\left(i\right)X,OT.{SK}_{kgc})}^{\phi }$ equal to ${\left(A_t,OT.{PK}_{kgc}\right)}^{\alpha }$ by obtaining KGC’s private key $OT.{SK}_{kgc}$ and one-time secrecy $\phi$. However, this is computationally infeasible because extracting $\phi$ from ${\mathsf{A}}_k$is a DDH problem.

(b) $U^{\mathrm{*}}$ fakes ${sK}_j$ but forms $K$ honestly. Suppose $U^{\mathrm{*}}$ is dishonest in calculating ${sK}_j$, and honestly generates $K$ as given in the scheme. Let us suppose, the $U^{\mathrm{*}}$ computes $K=\alpha \beta ·{OT.PK}_{ID}^{*}$, and chooses $X_j\in \mathbb{G}$ at random to replace $K$. Then, the KGC will compute ${\mathsf{A}}_k=\phi K_k$, $M.{SK}_{2,n}={e\left(H\left(i\right)K,OT.{SK}_{kgc}\right)}^{\phi }⨁\left(D_{1,n},D_{2,n}\right)$, for $i=1 \mathrm{t}\mathrm{o} n$, and return them to $U^{\mathrm{*}}$. In consequence, $U^{\mathrm{*}}$ unable decrypt $M.{SK}_{2,n}$ since $e{\left(A_t,OT.{PK}_{kgc}\right)}^{\alpha }$= $e{\left(\phi X_j,OT.{PK}_{kgc}\right)}^{\alpha }$ is certainly not equal to ${e\left(H\left(i\right)K,OT.{SK}_{kgc}\right)}^{\phi }$. For obtaining the $k$ messages, the $U^{\mathrm{*}}$ can only compute ${e\left(H\left(i\right)K,OT.{SK}_{kgc}\right)}^{\phi }\left(={e\left(H\left(i\right)\alpha \beta {OT.PK}_{ID}^{*},OT.{SK}_{kgc}\right)}^{\phi }\right)$ equal to ${\left(A_t,OT.{PK}_{kgc}\right)}^{\alpha }$ by obtaining KGC’s private key $OT.{SK}_{kgc}$ and one-time secrecy $\phi$. However, this is computationally infeasible because extracting $\phi$ from ${\mathsf{A}}_k$is a DDH problem.

(c) $U^{\mathrm{*}}$ fakes both the values of $K$ and $K_j$. Let us suppose the $U^{\mathrm{*}}$ chooses $X\in \mathbb{G}$ at random to replace $K$ and fakes $K_j$ as $H\left({\gamma }_j\right)X$. Under the assumption, the value of ${\mathsf{A}}_k=\phi K_k=\phi H\left({\gamma }_j\right)X$ is calculated by the sender as well as the ciphertexts $M.{SK}_{2,n}=$ ${e\left(H\left({\gamma }_j\right)X,OT.{SK}_{kgc}\right)}^{\phi }⨁\left(D_{1,n},D_{2,n}\right)$ for $j=1 \mathrm{t}\mathrm{o} \mathrm{k}$. Although $U^{\mathrm{*}}$ is aware of the value of $\phi H\left({\gamma }_j\right)X$ (because it is exactly equal to the ${\mathsf{A}}_k$obtained from KGC), it still cannot calculate $e\left(\phi H\left({\gamma }_j\right)X,OT.{SK}_{kgc}\right)$in the absence of knowledge of $OT.{SK}_{kgc}$. According to the above description, we know that when $K$ is $X$ and $K_k$ is $H\left({\gamma }_j\right)X$, $U^{\mathrm{*}}$ cannot get $M.{SK}_{2,n}$. In addition, $U^{\mathrm{*}}$ probably sets $K_k$ as $H\left({\gamma }_j\right)Y$, where $Y\left(\ne X\right)$ is a random value in $\mathbb{G}$. In conclusion, under the violation of calculating the values of $K$ and $K_k$, $U^{\mathrm{*}}$ was unable to acquire the$k$ chosen messages.

Argument 2.

If $U^{*}$ accompanies the scheme truthfully to get $k$ messages, though it wants to process the $(k+1)\mathrm{t}\mathrm{h}$ message, afterwards it would confront the tough CT-CDH problem with the assumption of a random oracle.

The $U^{\mathrm{*}}$ intends to get messages means $U^{\mathrm{*}}$ would possess the awareness of ${e\left(H\left(i\right)K,OT.{SK}_{kgc}\right)}^{\phi }\left(={e\left(A_t,OT.{PK}_{kgc}\right)}^{\alpha }\right)$, in fact, according to argument (1), an honest user $U$ should have knowledge of $k$ values, where ${e\left(H\left(i\right)K,OT.{SK}_{kgc}\right)}^{\phi }$, for $i=1 \mathrm{t}\mathrm{o} n$, whereas ${e\left(H\left(i\right)K,OT.{SK}_{kgc}\right)}^{\phi }={e\left(A_t,OT.{PK}_{kgc}\right)}^{\alpha }$, for $t={\gamma }_j$ and j $=1 \mathrm{t}\mathrm{o} k$. Let suppose $y^{\left(i\right)}\in {\mathbb{G}}_T$ and ${e\left(H\left(i\right)K,OT.{SK}_{kgc}\right)}^{\phi }=y^{\left(i\right)}$. In consonance with argument (1), for acquiring the $k$ selected message, $U^{\mathrm{*}}$ is unable to modify the structures of $K\left(=\alpha \beta {·OT.PK}_{ID}^{\mathrm{*}}\right)$ and $K_k={H\left({\gamma }_j\right)}^{\beta }{·OT.SK}_{ID}^{\mathrm{*}}$. In these conditions $y^{\left(i\right)}$ can only be decomposed into $y^{\left(i\right)}={e\left(H\left(i\right)\alpha \beta {·OT.PK}_{ID}^{\mathrm{*}},OT.{SK}_{kgc}\right)}^{\phi }$ = ${e\left(\alpha \beta H\left(i\right){·OT.SK}_{ID}^{\mathrm{*}},OT.{PK}_{kgc}\right)}^{\phi }$ since $OT.{SK}_{kgc}=s·OT.{PK}_{kgc}$ and ${OT.SK}_{ID}^{\mathrm{*}}=s{·OT.PK}_{ID}^{\mathrm{*}}$. Furthermore, under the assumption of random oracle and the fact that $U^{\mathrm{*}}$ is able to learn the $\alpha ,\beta ,{OT.SK}_{ID}^{\mathrm{*}}$ and $OT.{PK}_{kgc}$, $y^{\left(i\right)}$ could be expressed as ${\left(g_i\right)}^{\phi }$, where $g_i$ = $e\left(\alpha \beta H\left(i\right){·OT.SK}_{ID}^{\mathrm{*}},OT.{PK}_{kgc}\right)$ and $\phi \in {\mathbb{G}}_T$ is a random element. Thereafter, the malicious $U^{\mathrm{*}}$ actually encounters the determination of the $\left(k+1\right)\mathrm{t}\mathrm{h}$ pair $\left({\gamma }_{k+1},{\left(g_{{\gamma }_{k+1}}\right)}^{\phi }\right)$ with the awareness of $k$ pairs of $\left({\gamma }_1,{\left(g_{{\gamma }_1}\right)}^{\phi }\right),\left({\gamma }_2,{\left(g_{{\gamma }_2}\right)}^{\phi }\right), \cdots , \left({\gamma }_k,{\left(g_{{\gamma }_k}\right)}^{\phi }\right)$, where ${\left(g_{{\gamma }_j}\right)}^{\phi }={e\left(A_t,OT.{PK}_{kgc}\right)}^{\alpha }$, but without the awareness of KGC’s secrecy $\phi$ (because it is DDH difficult problem for calculating $\phi$ from $A_t(=\phi K_k$). Consequently, the user was unable to get the $\left(k+1\right)$th message.

In accordance with Arguments 1 and 2, we have proven Theorem 2 that our scheme is able to realize the protection of KGC’s privacy.

6. Experiment and Evaluation

In this part, we will verify the effectiveness of this scheme with respect to theoretical examination and experimental verification.

Theoretical examination: To be fair, we only consider the adopt tree structure CP-ABE scheme. Table 2 shows the comparison of the properties between the schemes. From Table 2, we can know that our solution is aimed at protecting the user’s attribute privacy from being known by KGC under the condition that KGC is honest and curious. At the same time, our solution does not require multiple authorization centers or additional outsourced calculations. In Table 3 and Table 4, we conduct theoretical analysis from two aspects of computing overhead and storage overhead for the preferred scheme and our scheme. The storage overhead is mainly for the amount of PK, SK, and CT, and the computing overhead is basically for the time cost of KeyGen, encryption, and decryption. The PK refers to the size of the user’s public key. The SK means the size of the user’s private key. The CT means the size of the ciphertext. Expand in detail; suppose the access structure $\mathbb{T}$ contains $k$-level nodes. Let |${\mathbb{T}}_R$| and |${\mathbb{T}}_i$| express the complete amount of the leaf nodes in $\mathbb{T}$ as well as in the subtree rooted at level node $V_x$ in $\mathbb{T}$ individually. The $\left|\mathbb{G}\right|$ and ${|\mathbb{G}}_T|$ mean the length of one element in $\mathbb{G}$, ${\mathbb{G}}_T$; the |$S$| means the groups of attributes; and the $n$ means the number of attributes. The $E_G,E_T$ means an exponentiation operation time expense in $\mathbb{G}$, ${\mathbb{G}}_T$; the $P$ means a pairing computation time expense.

Table 2. Properties comparison.

Scheme	Type of Hiding	Multiple Authority	KGC Model	User Attributes Protection
Efficient CP-ABE [28]	Partially hidden	N	honest	N
Multiauthority CP-ABE [29]	Partially hidden	Y	honest	N
Privacy-preserving and efficient CP-ABE [30]	Fully hidden	N	honest and curious	N
Our Scheme	Fully hidden	N	honest and curious	Y

Table 3. Storage overhead comparison of different schemes.

Scheme	PK	SK	CT
Efficient CP-ABE [28]	6$\left|\mathbb{G}\right|+{|\mathbb{G}}_T|$	$(2\left|S\right|+1)\left|\mathbb{G}\right|$	$\left(2\left|{\mathbb{T}}_R\right|+n\right)\left|\mathbb{G}\right|+{|\mathbb{G}}_T|$
Multiauthority CP-ABE [29]	$7\left|\mathbb{G}\right|+{|\mathbb{G}}_T|$	$(n+\left|S\right|)\left|\mathbb{G}\right|$	($2n+2\left|{\mathbb{T}}_R\right|$) $\left|\mathbb{G}\right|+{2|\mathbb{G}}_T|$
Privacy-preserving and efficient CP-ABE [30]	$7\left|\mathbb{G}\right|+{2|\mathbb{G}}_T|$	$(\left|S\right|+1)\left|\mathbb{G}\right|$	$\left(2n+1+2\left|{\mathbb{T}}_R\right|\right)\left|\mathbb{G}\right|$ + ${|\mathbb{G}}_T|$
Our Scheme	$8\left|\mathbb{G}\right|+{2|\mathbb{G}}_T|$	$\left(2n+\left|S\right|+1\right)\left|\mathbb{G}\right|+{n|\mathbb{G}}_T|$	$\left(2n+\left|{\mathbb{T}}_R\right|+1\right)\left|\mathbb{G}\right|+{|\mathbb{G}}_T|$

Table 4. Computation efficiency comparison of different schemes.

Scheme	KeyGen	Encryption	Decryption
Efficient CP-ABE [28]	$\left(3n+2\right)E_G$	$(n+2|{\mathbb{T}}_R\left|\right)E_G$+$E_T$	($n+2\left|{\mathbb{T}}_R\right|$) $P+\left|{\mathbb{T}}_R\right|E_T$
Multiauthority CP-ABE [29]	$(n+2) E_G$	$\left(4n+2+2\left|{\mathbb{T}}_R\right|\right)E_G+2P+2E_T$	$\left(4n+2\right)P+$ 2 $\left|{\mathbb{T}}_R\right|E_T$
Privacy-preserving and efficient CP-ABE [30]	$(2n+1) E_G$	$\left(2n+\left|{\mathbb{T}}_R\right|+1\right)E_G$  $+{ E}_{T}2P$	$\left(2n +\left|{\mathbb{T}}_R\right|+1\right)P$  $+n{E}_T$
Our Scheme	$\left(2n+1\right)E_G+nP$  $+{ nE}_T$	$\left(2n+\left|{\mathbb{T}}_R\right|+1\right)E_G$  $+E_T+P$	$\left(2n +\left|{\mathbb{T}}_R\right|\right)P$  ${+(2n+\left|{\mathbb{T}}_R\right|)E}_T$

Experimental verification: In order to verify the results of our above theoretical analysis, based on the PBC library [31], we simulated and implemented the schemes in [28,29,30] and our system, respectively. Specifically, we experimented on our MacBook Air, whose CPU has an Intel Core i5 (1.1 GHz), 8 GB of RAM, and runs Ventura 13.3. For the purpose of the 80-bit security level target, our scheme adopted the super-singular curve $y^2=x^3+x$ over a 512-bit finite field to design a 160-bit elliptic curve group to simulate running these schemes. In these figures, the units of computation cost are milliseconds, while the total of the execution times of all algorithms is considered the total execution time. The experimental verification is conducted using the PBC library to implement the cryptographic computation code. The experimental process mainly entails implementing the cryptographic formulas and computations involved in the discussed schemes through the C program. Figure 3 below depicts the actual computation time derived from running the code on our computer. We precisely conducted the experimental verification of our scheme and the selected comparative schemes on the same platform and library.

Figure 3. Cryptography computation runtime overhead.

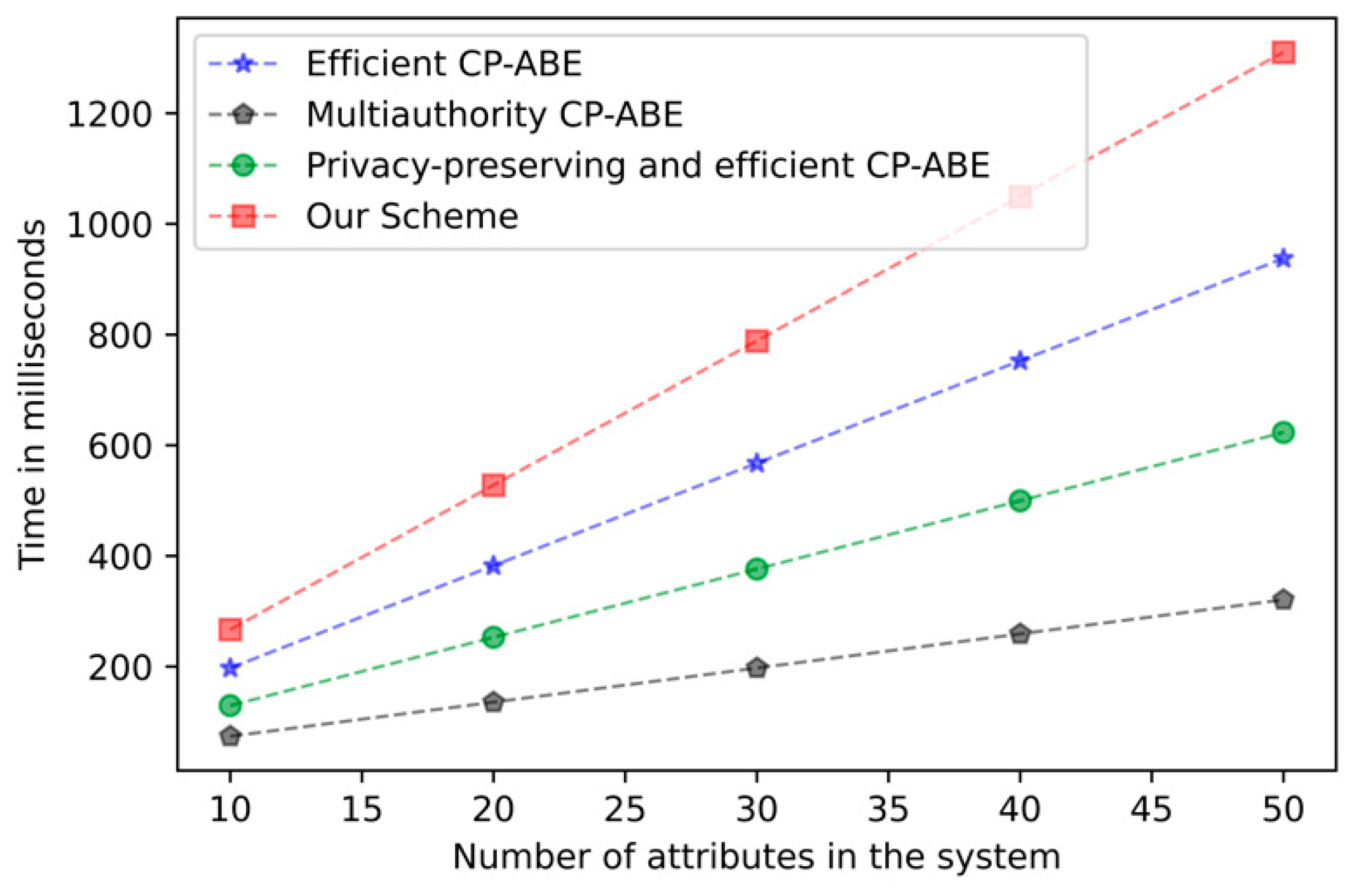
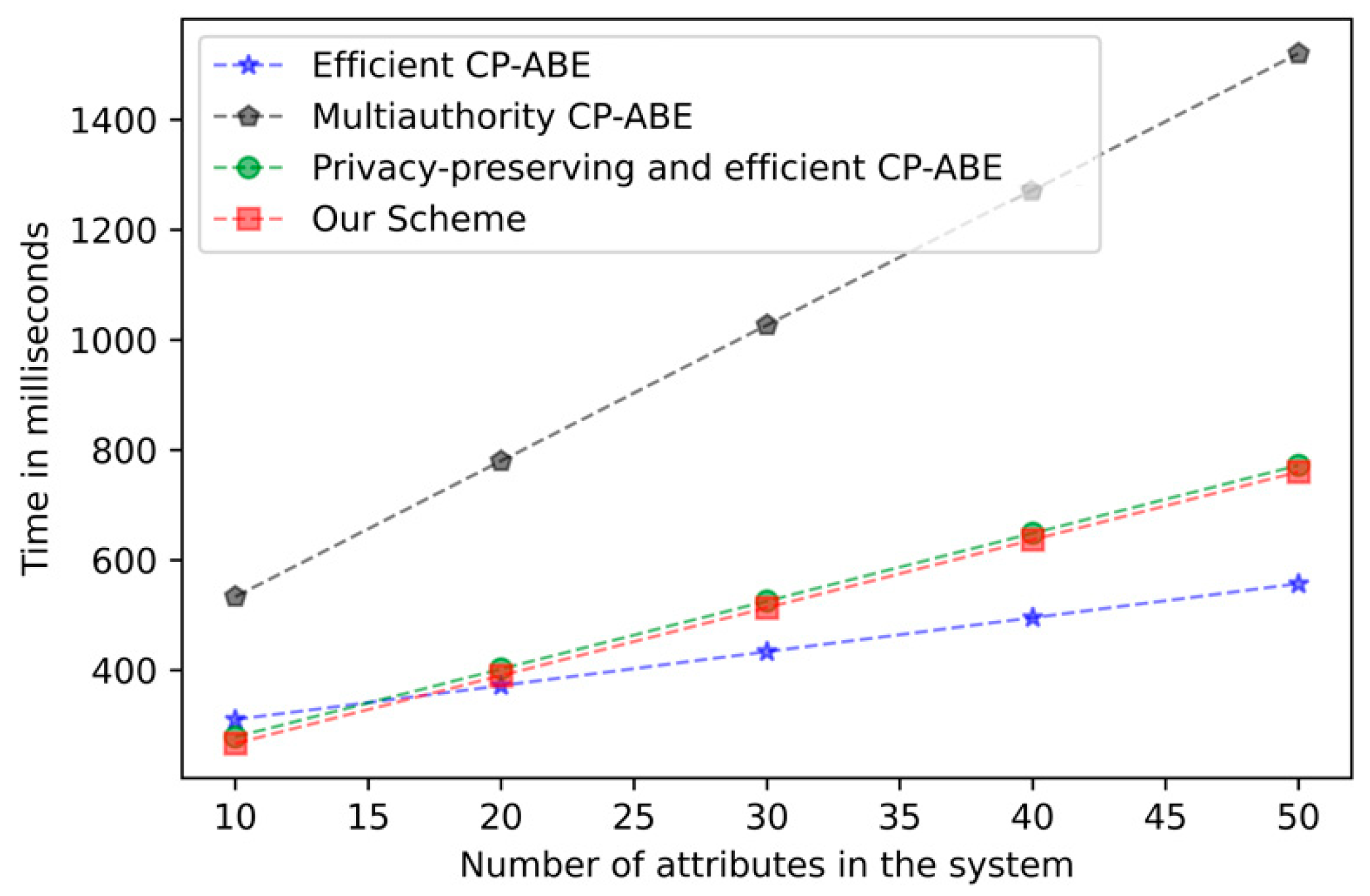
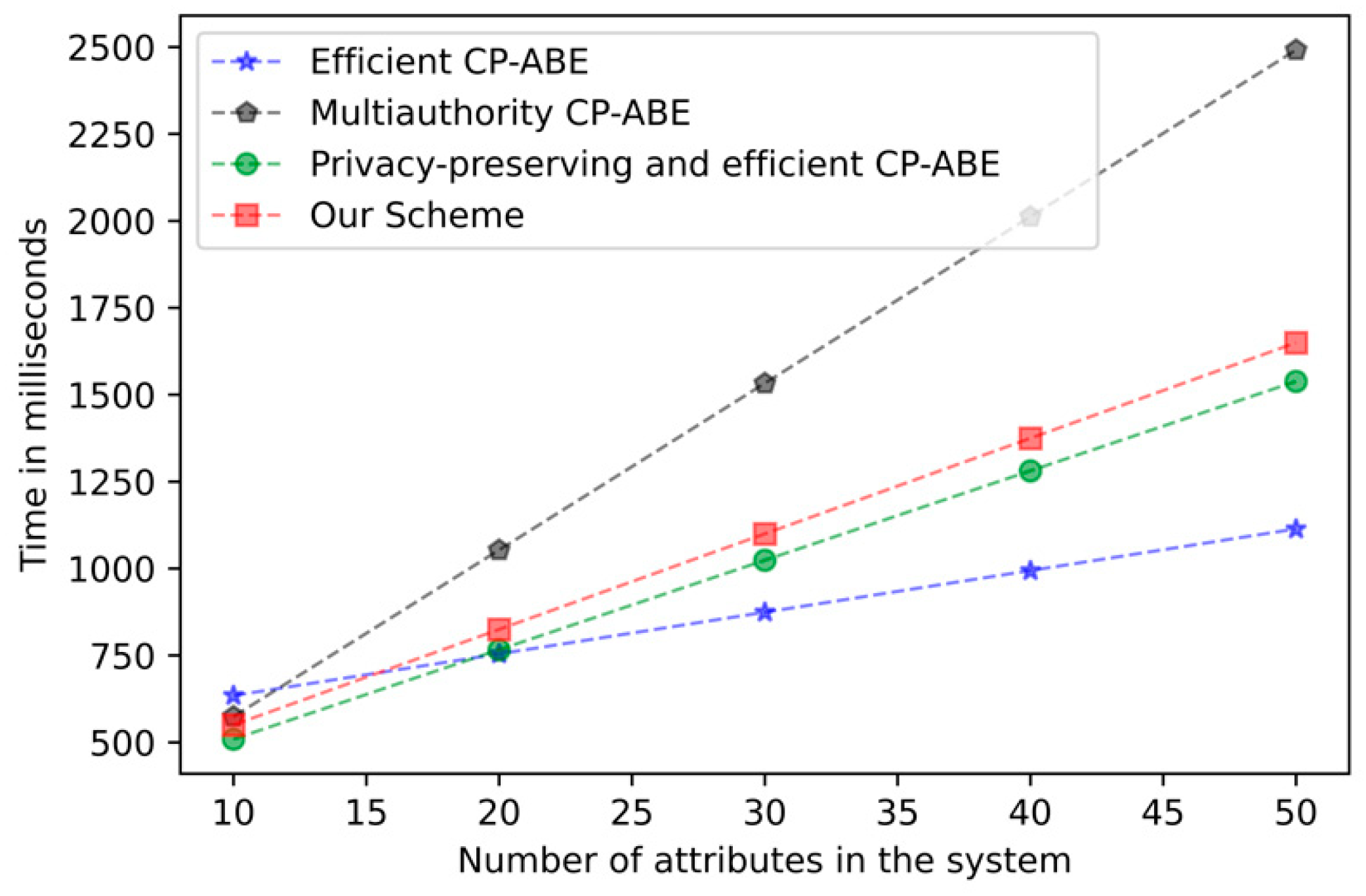
Figure 4 mainly presents the trend of computing time for key generation as the attribute increases. Due to the oblivious transfer protocol, our scheme has additional overhead in the key generation stage, but the added overhead is still acceptable. Figure 5 shows the computation time required for encryption as the attribute increases. In the encryption stage, our overhead is basically the same as other tree structures in the CP-ABE scheme. Figure 6 demonstrates the relationship between the computation time of decrypting overhead and the number of attributes. As with other schemes, the computational overhead in the decryption stage increases with the number of attributes. It has been proven by experiments that the addition of the k-out-of-n oblivious transfer protocol will not significantly affect the performance of the scheme under the condition of protecting user privacy.

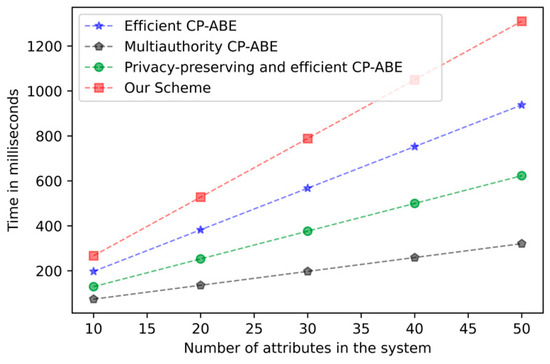
Figure 4. Key generation computation time comparison.

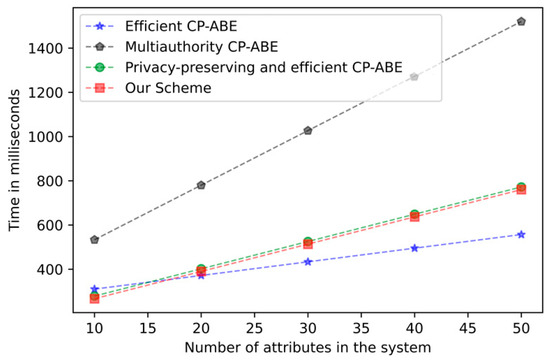
Figure 5. Encryption computation time comparison.

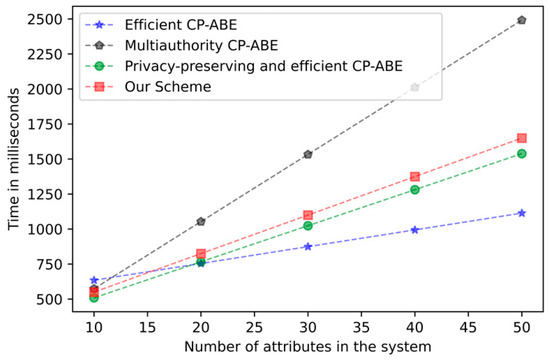
Figure 6. Decryption computation time comparison.

7. Conclusions

Attribute-based encryption offers an ideal solution for flexible data sharing, yet the credibility of the KGC within the attribute encryption scheme is pivotal for user confidence. In this paper, we introduce an innovative scheme that combines a ${OT}_k^n$ protocol with a CP-ABE scheme. During the computation of the user’s public-private key pair, the KGC employs the ${OT}_k^n$ protocol to hide the user’s essential attributes, preventing the leakage of user privacy. Distinguished from other solutions, our approach primarily addresses the challenge of safeguarding user attribute privacy, assuming that the KGC operates as an honest curiosity model. This allows the KGC to generate private keys for users without knowledge of the specific attributes associated with each user. In the security analysis of this scheme, we specifically examined two situations: (1) the protection of the user’s privacy; and (2) the protection of KGC’s privacy. By utilizing the DDH and CT-CDH assumptions, we demonstrated that the scheme effectively safeguards user privacy from disclosure. Furthermore, we conducted a performance comparison of this scheme with other CP-ABE schemes of the same type. After incorporating the ${OT}_k^n$ protocol, the computation time overhead for key generation, encryption, and decryption within the scheme did not experience a significant increase. Therefore, we are confident that this concept can provide substantial support for the wider adoption of attribute encryption in the future. While our current scheme is suitable for tree access structures, we recognize the flexibility and diversity of access control structures in attribute encryption. Our future research aims to develop a general method to utilize the oblivious transfer protocol with any access structure.