Electrical Performance Compensation of Reflector Antenna Based on Sub-Reflector Array
Abstract
:1. Introduction
1.1. Background
1.2. Research Status at Home and Abroad
2. Sub-Reflector Array Optimization
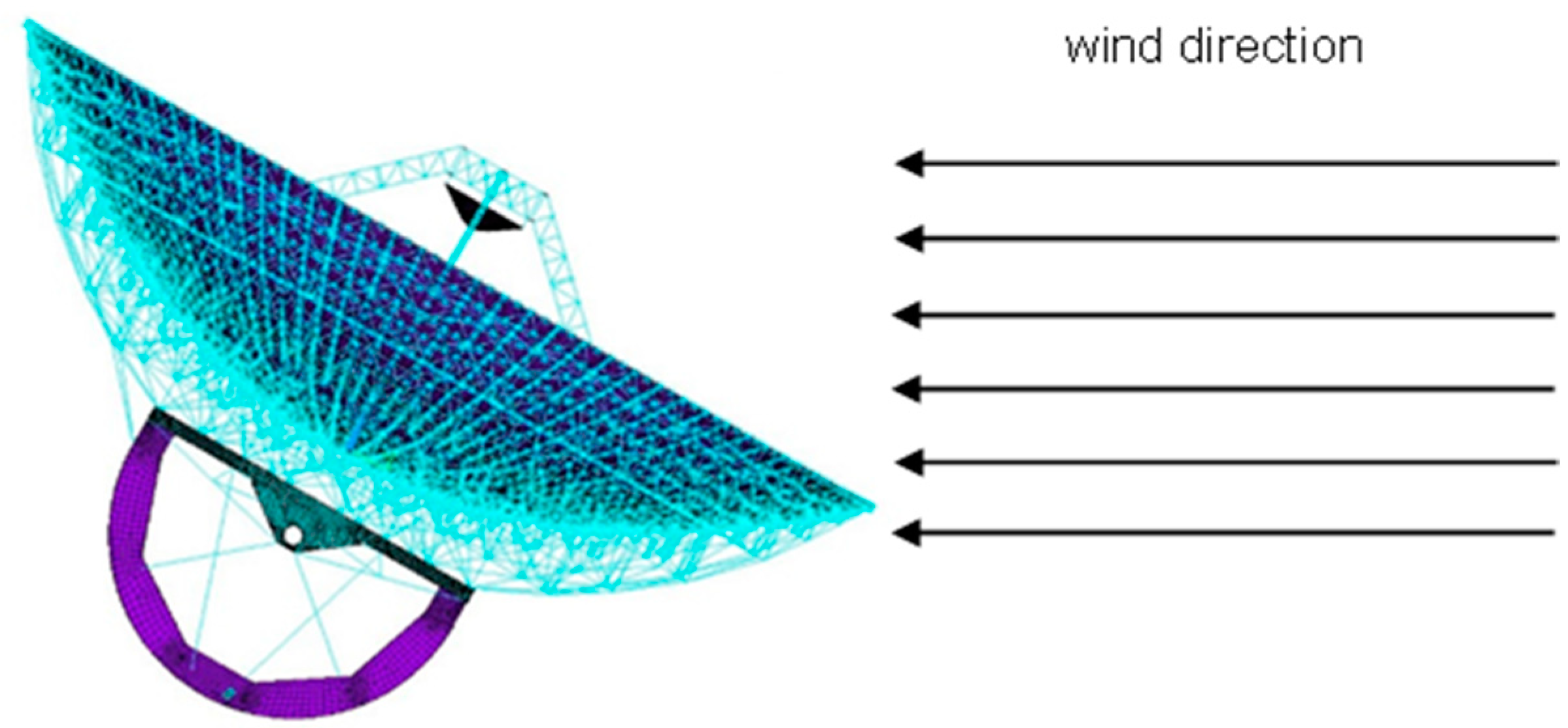
2.1. Influence of Environmental Load on Antenna’s Aperture Field
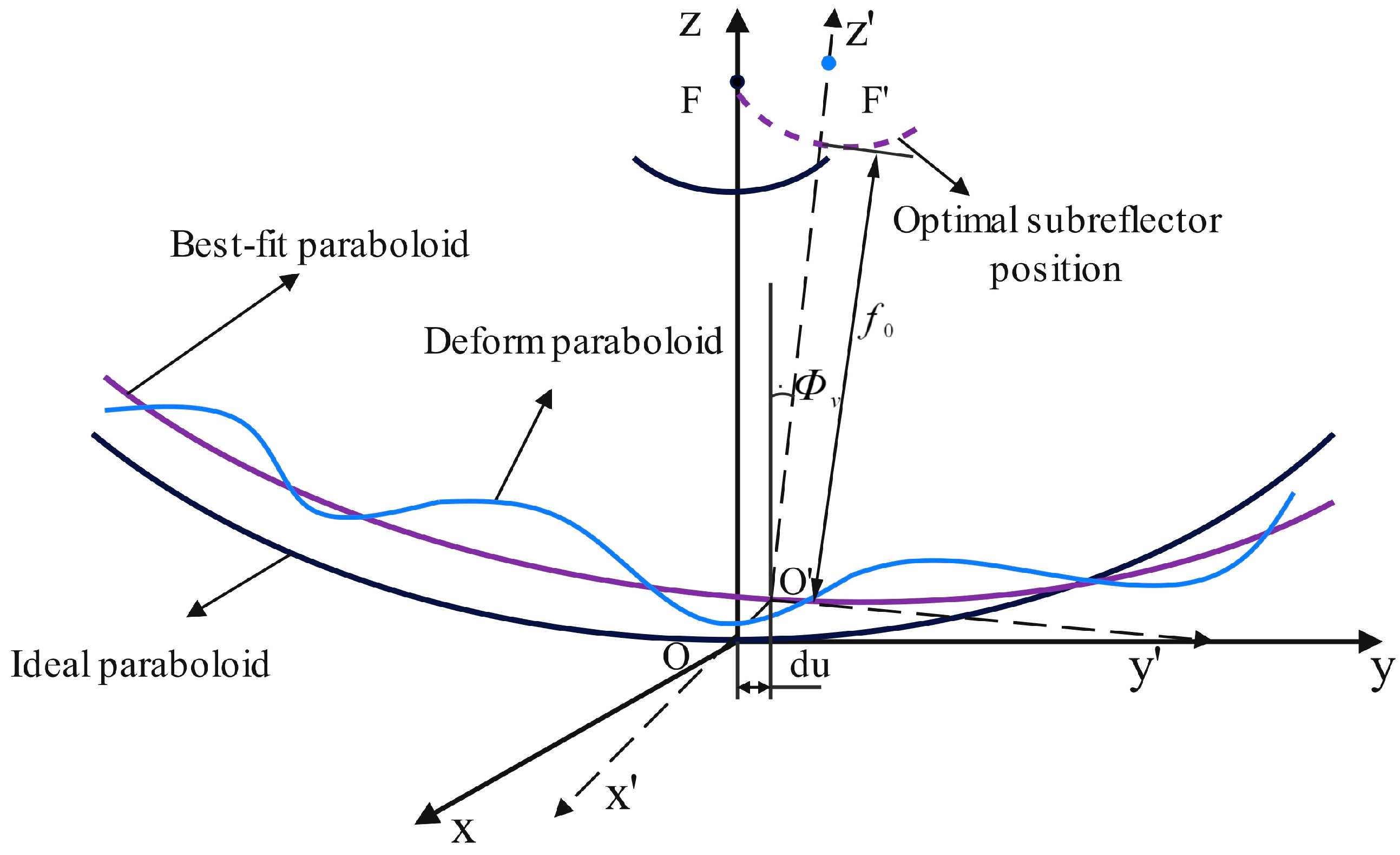
2.2. Determining the Error Compensation Interval
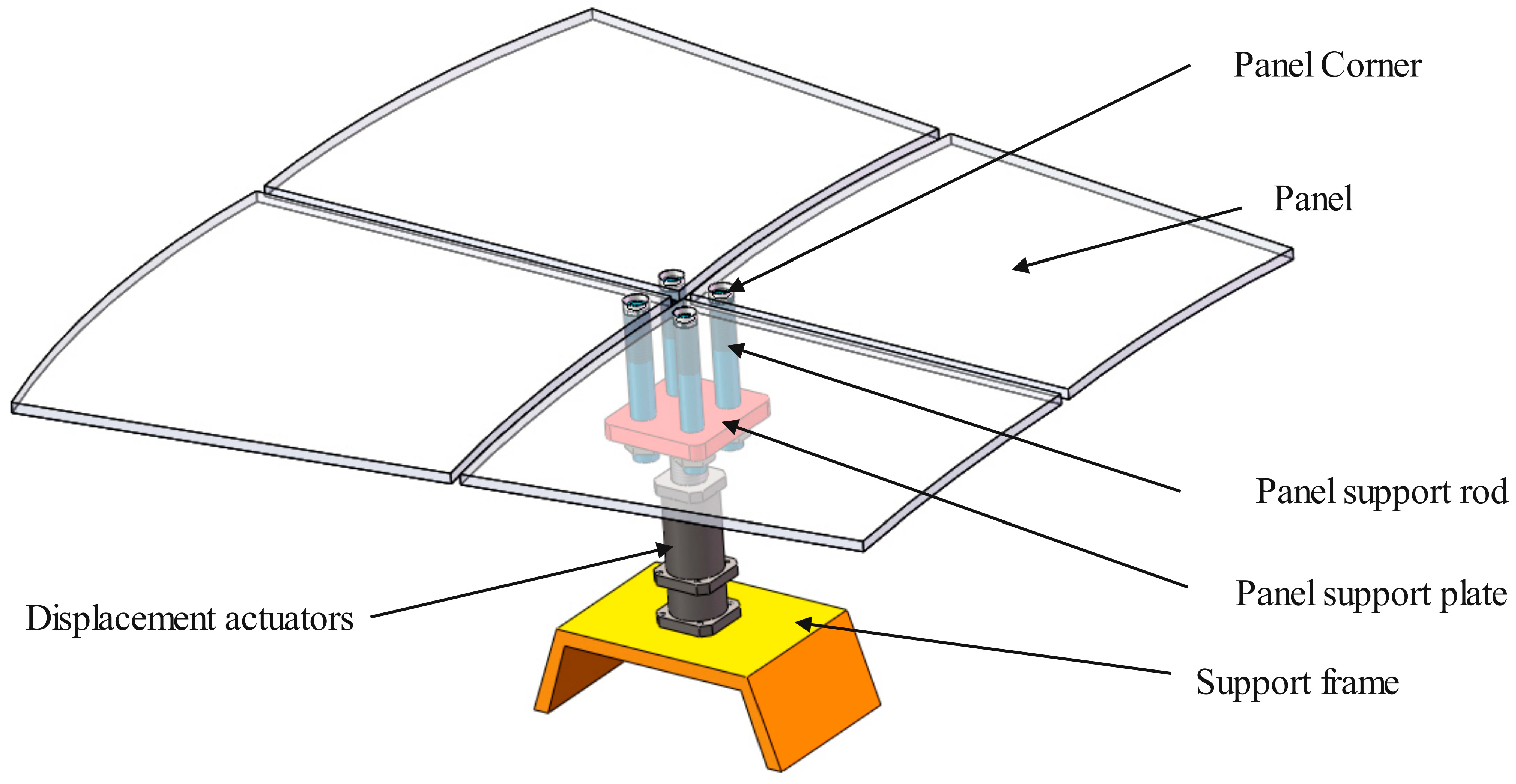
2.3. Optimization of Sub-Reflector Array
3. Electrical Performance Method of Sub-Reflector Array
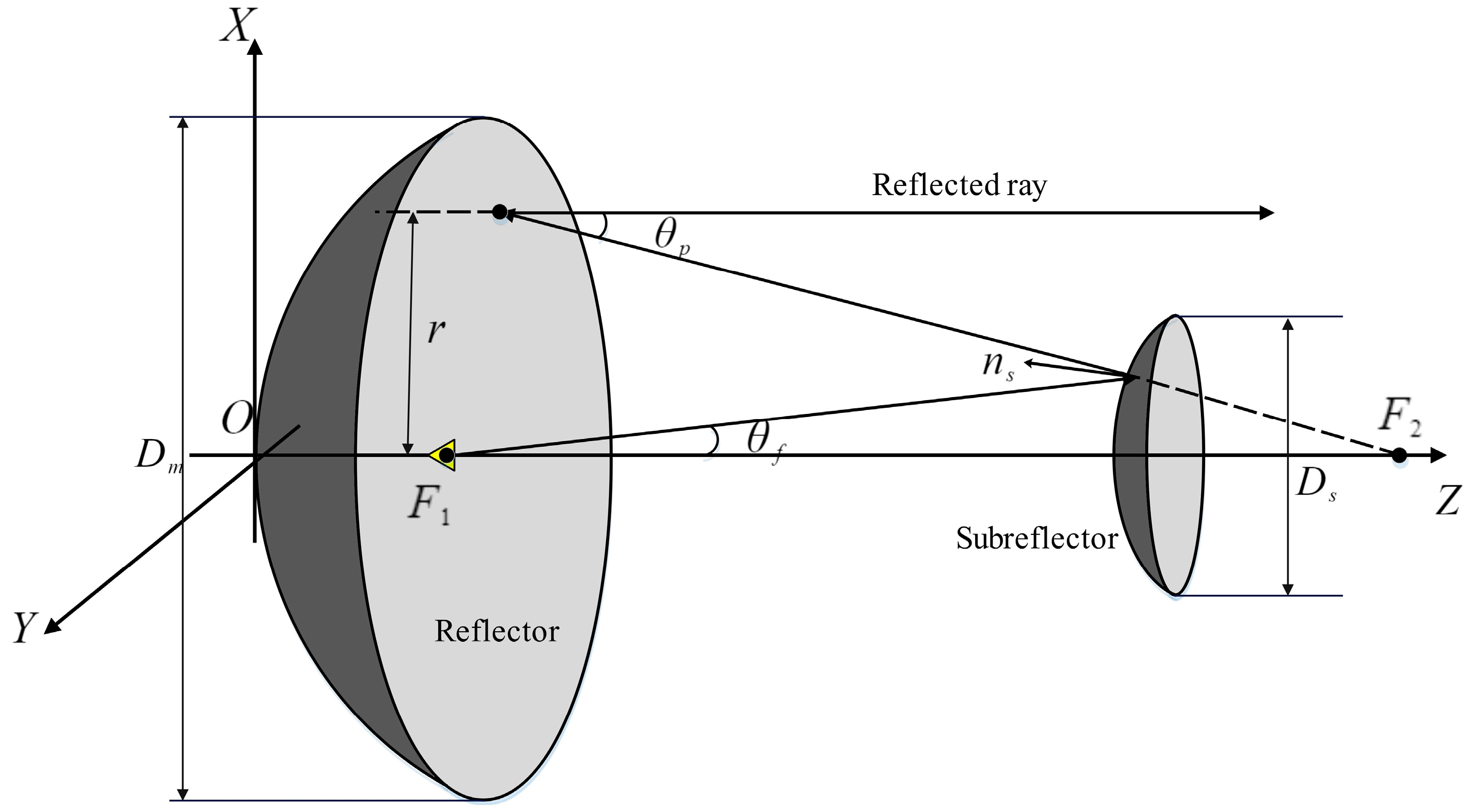
3.1. Electromechanical Coupling Model of Dual-Reflector Antenna
3.2. Calculation of Compensation
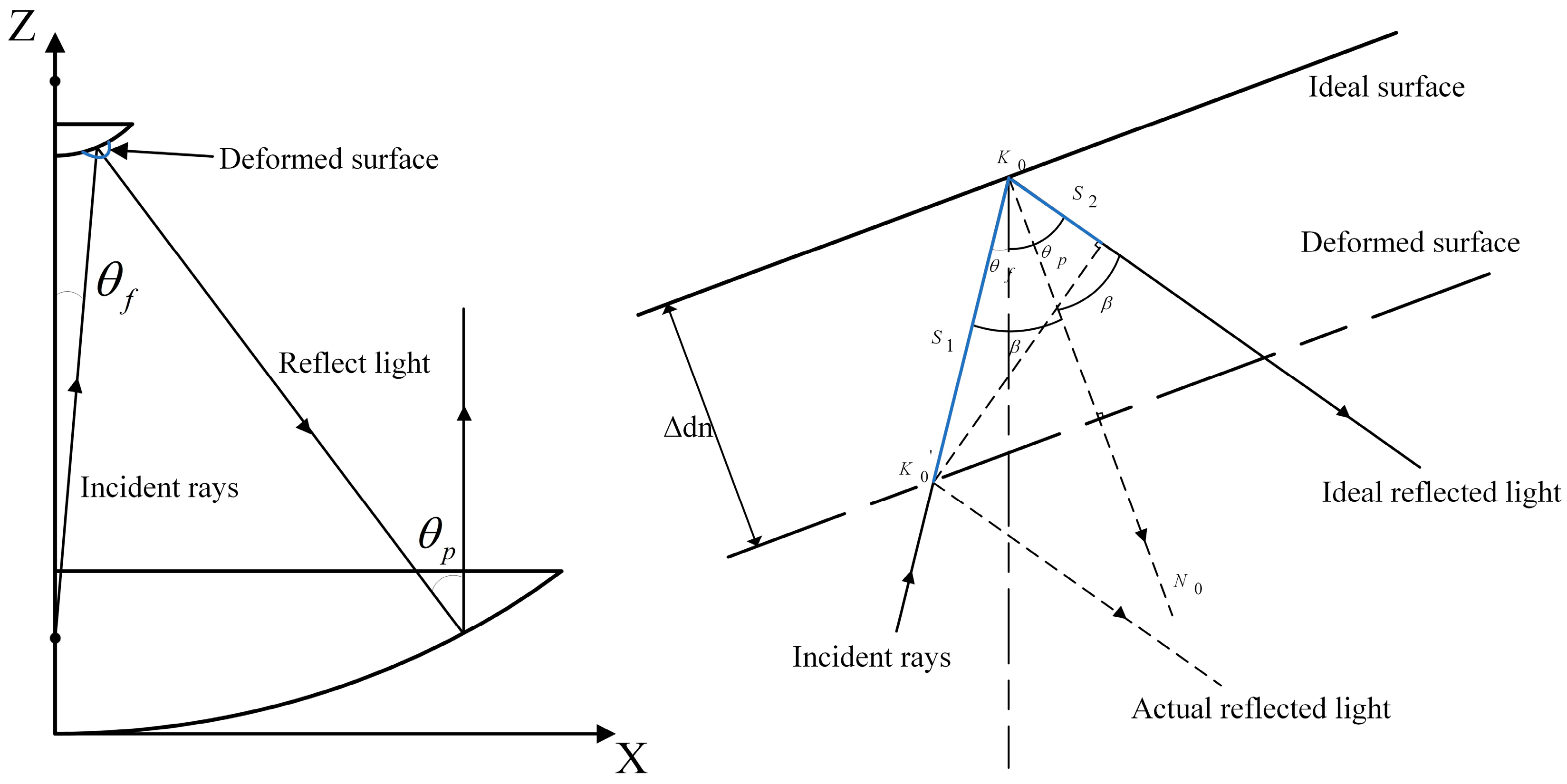
3.2.1. Sub-Reflector Form and Posture Adjustment
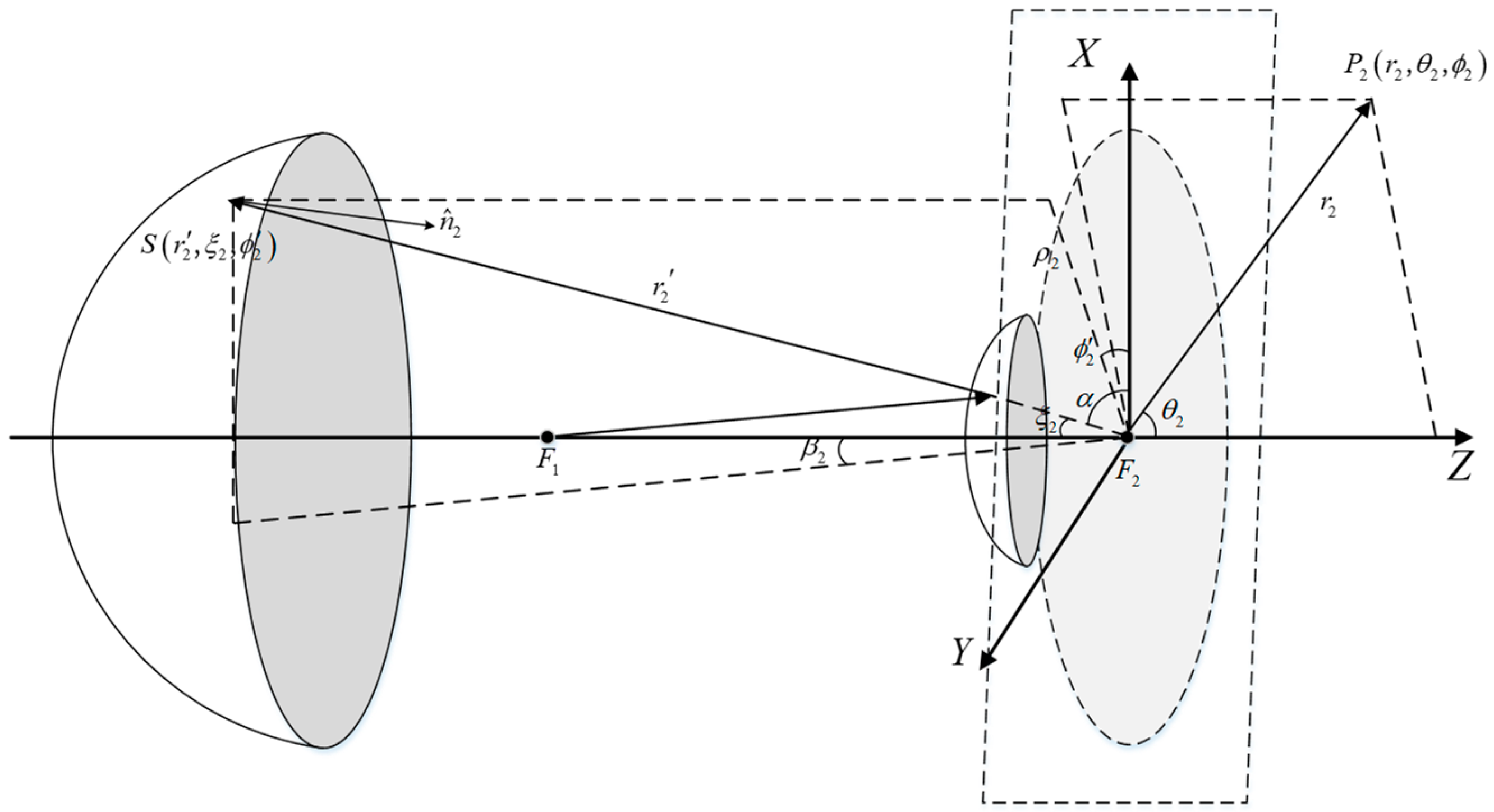
3.2.2. Sub-Reflector Shape Adjustment
4. Example Analysis
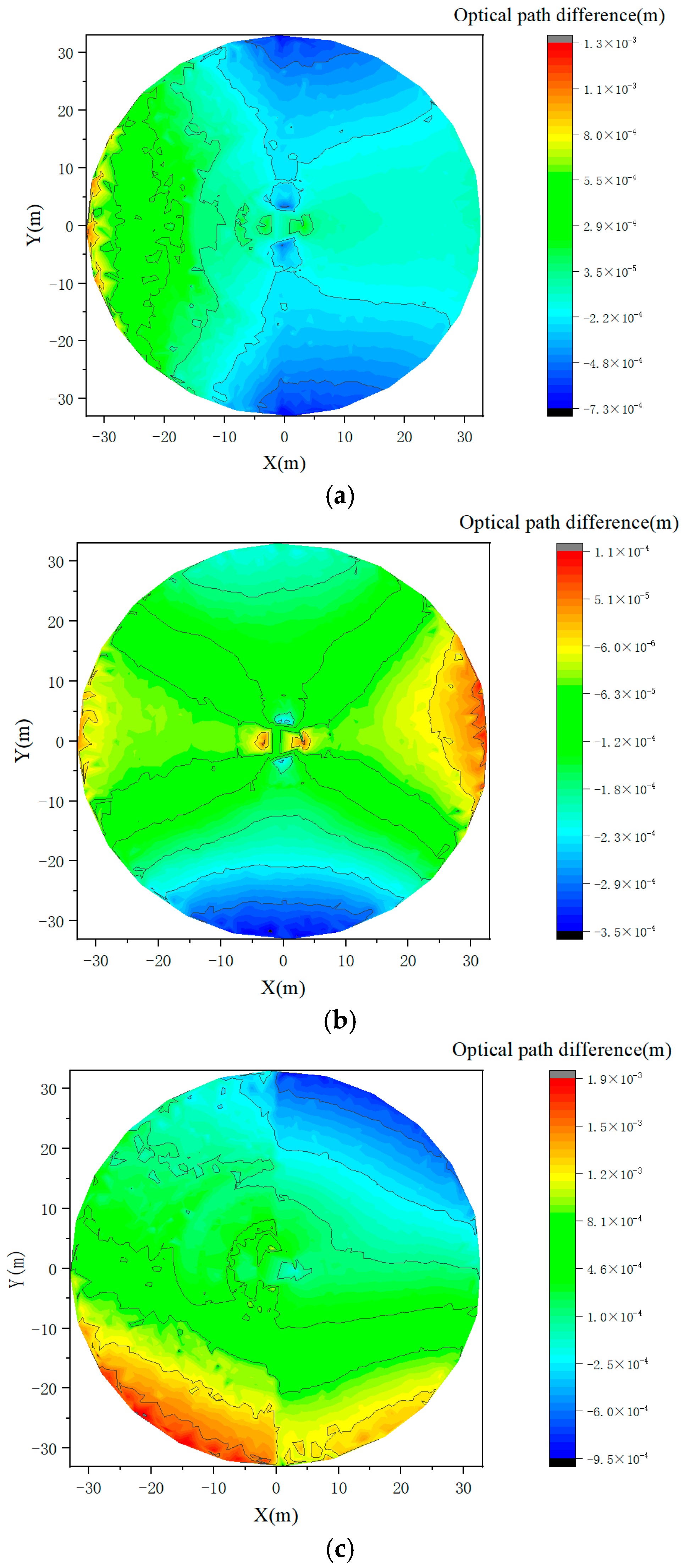
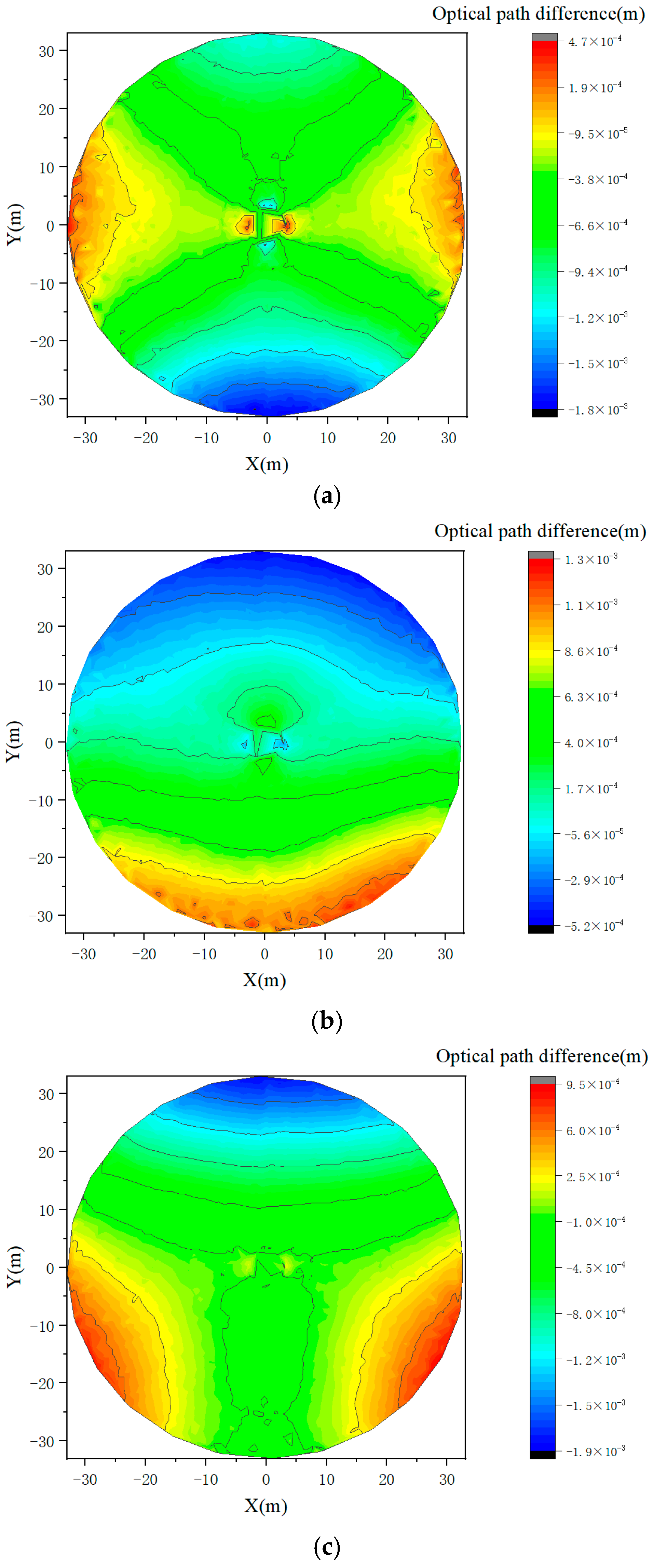
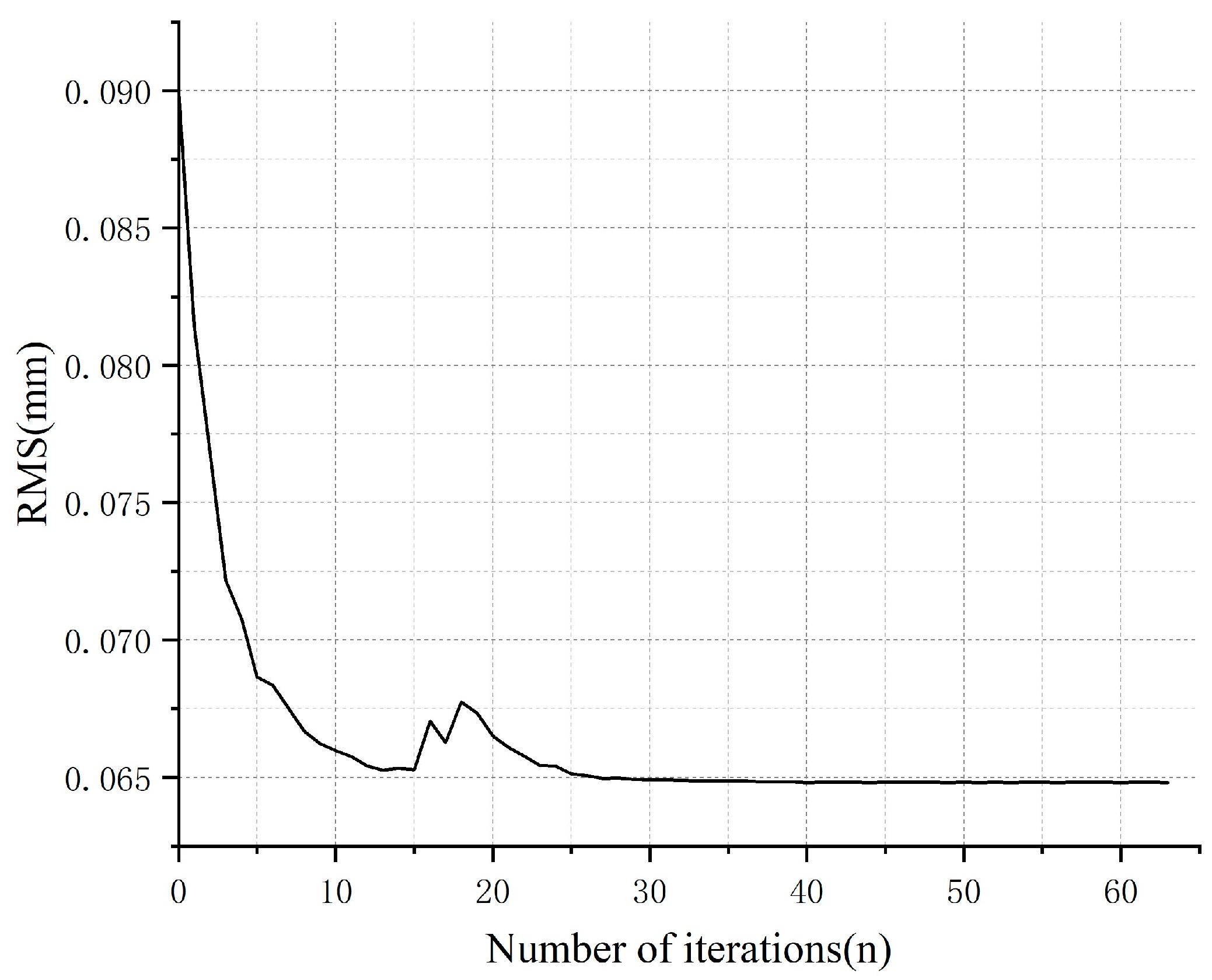
4.1. Optimization Result of Sub-Reflector Array
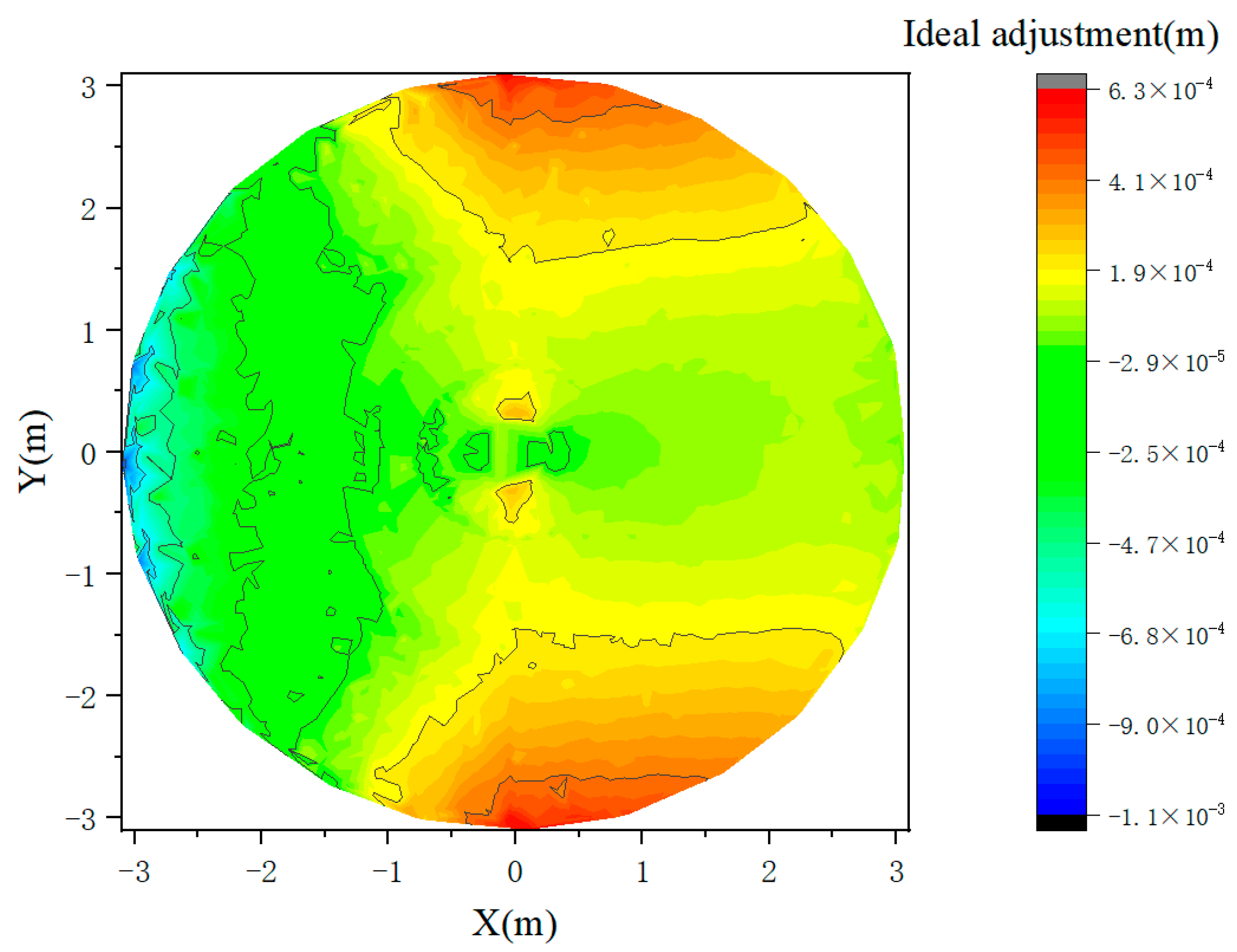
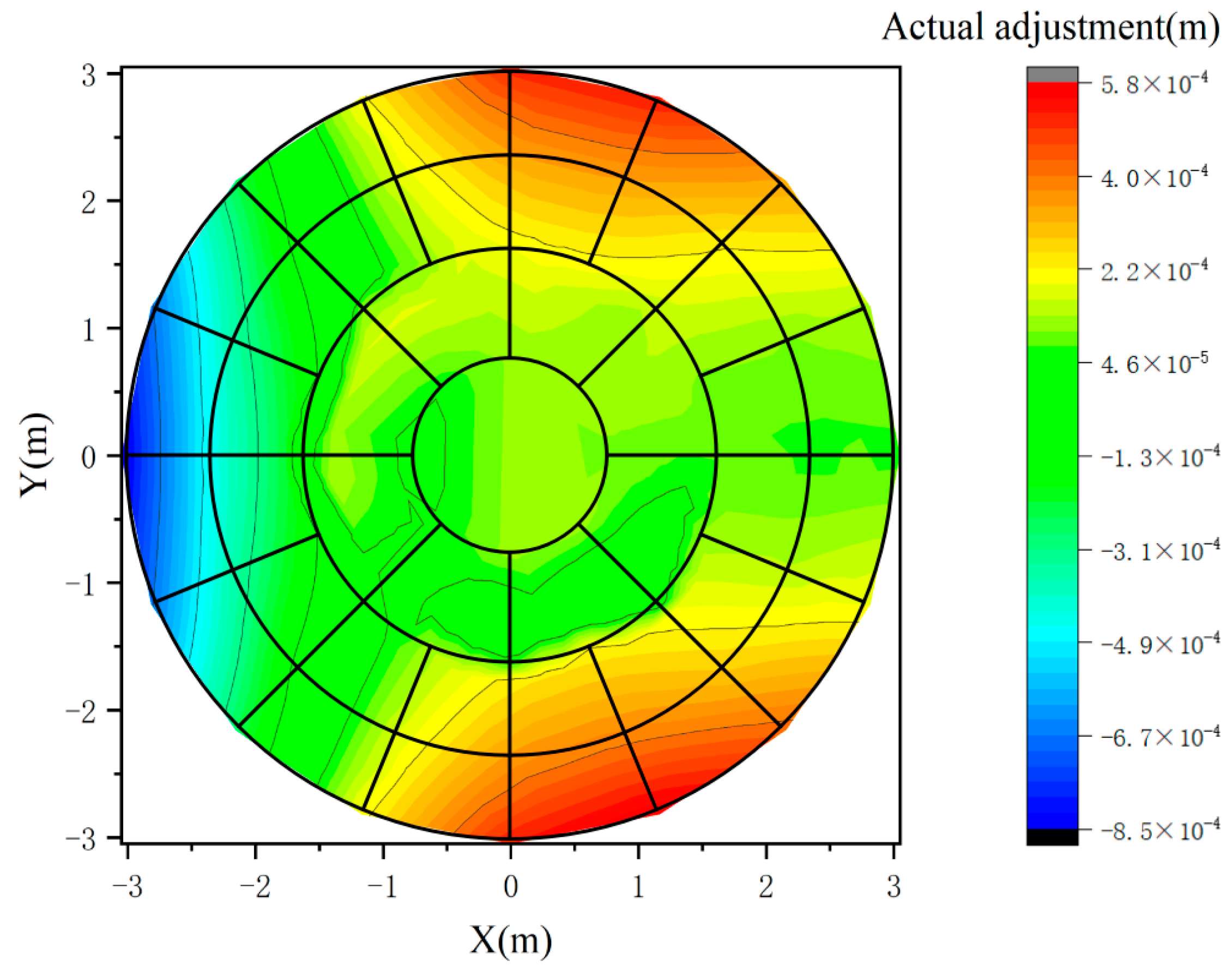
4.2. Adjustment of Sub-Reflector Array
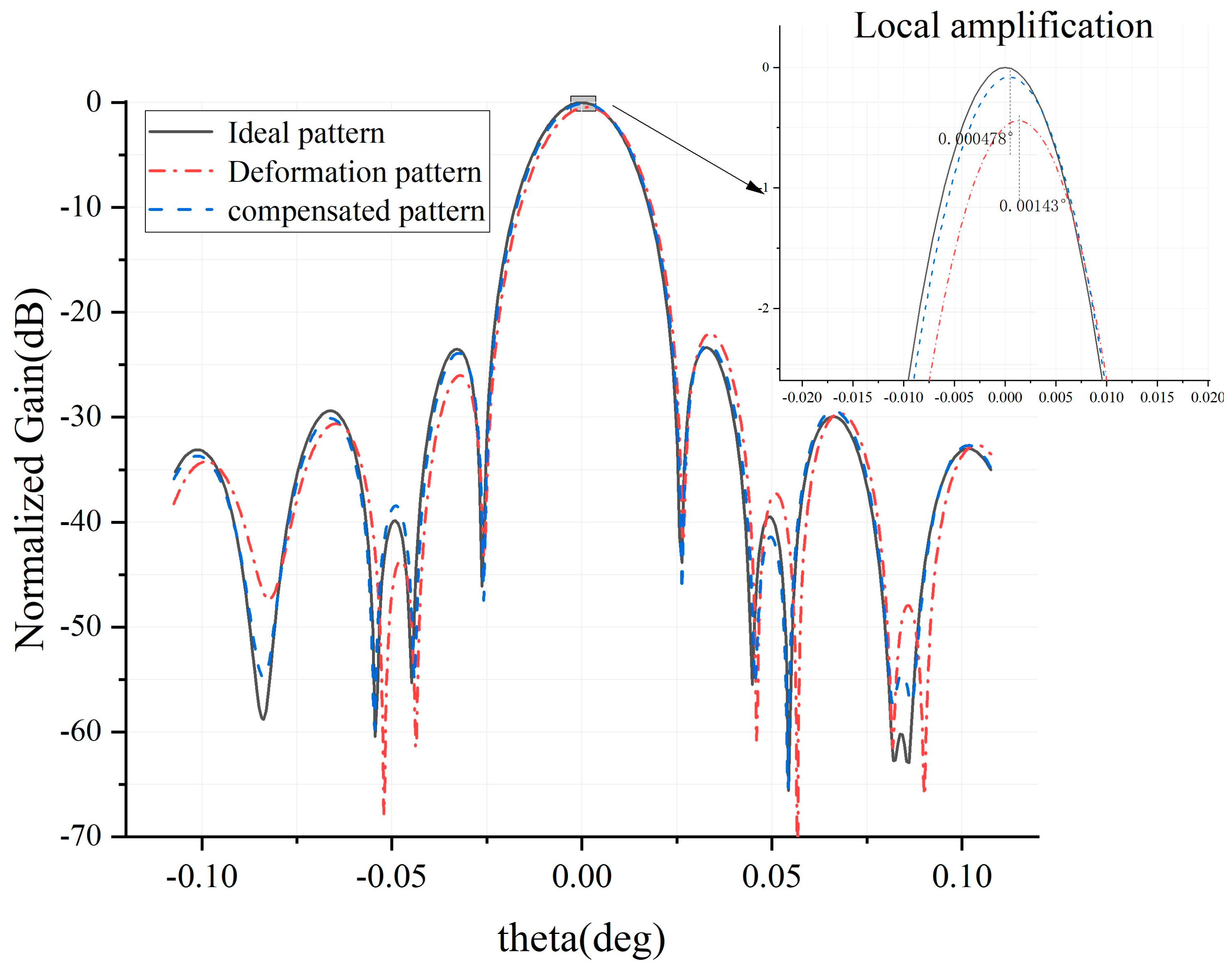
4.3. Sub-Reflector Position Adjustment Amount
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, C.S.; Xiao, L.; Wang, W.; Xu, Q.; Xiang, B.B.; Zhong, J.F.; Jiang, L.; Bao, H.; Wang, N. An adjustment method for active reflector of large high-frequency antennas considering gain and boresight. Res. Astron. Astrophys. 2017, 17, 41–52. [Google Scholar] [CrossRef]
- Li, P.; Duan, B.Y.; Wang, W.; Zheng, F. Electromechanical Coupling Analysis of Ground Reflector Antennas under Solar Radiation. IEEE Antennas Propag. Mag. 2012, 54, 40–57. [Google Scholar] [CrossRef]
- Wang, C.S.; Wang, W.; Song, L.W. Microwave Antenna Multi Field Coupling Theory and Technology; Science Press: Beijing, China, 2015. (In Chinese) [Google Scholar]
- Lacasse, R.J. Green Bank Telescope active surface system. In Green: Proceedings of Astronomical Telescopes and Instrumentation; International Society for Optics and Photonics: Bellingham, WA, USA, 1998. [Google Scholar]
- Gawronski, W. Control and Pointing Challenges of Large Antennas and Telescopes. IEEE Trans. Control Syst. Technol. 2007, 15, 276–289. [Google Scholar] [CrossRef]
- Zhang, J.; Huang, J.; Zhou, J.; Wang, C.; Zhu, Y. A Compensator for Large Antennas Based on Pointing Error Estimation under a Wind Load. IEEE Trans. Control Syst. Technol. 2017, 25, 1912–1920. [Google Scholar] [CrossRef]
- Zhang, J.; Huang, J.; Wang, S.; Wang, C. An Active Pointing Compensator for Large Beam Waveguide Antenna Under Wind Disturbance. IEEE/ASME Trans. Mechatron. 2015, 21, 860–871. [Google Scholar] [CrossRef]
- Leng, G.J.; Wang, W.; Duan, B.Y.; Li, X.P. Sub-reflector real-time compensation for main reflector deformation of shaped Cassegrain antenna. Syst. Eng. Electron. Technol. 2011, 33, 996–1000. (In Chinese) [Google Scholar]
- Ban, Y.; Wang, C.; Feng, S.; Duan, B.; Wang, W. Iteration Path-Length Error Correction Approach to Sub-reflector Shaping for Distortion Compensation of Large Reflector Antenna. IEEE Trans. Antennas Propag. 2019, 67, 2729–2734. [Google Scholar] [CrossRef]
- Huang, J.; Encinar, J.A. Reflectarray Antennas; IEEE Press: New York, NY, USA, 2008. [Google Scholar]
- Xu, S.; Rahmat-Samii, Y.; Imbriale, W.A. Subreflectarrays for Reflector Surface Distortion Compensation. IEEE Trans. Antennas Propag. 2009, 57, 364–372. [Google Scholar] [CrossRef]
- Xiang, B.; Zheng, T.; Wang, W.; Lian, P.; Kazezkhan, G.; Zhou, J.; Li, K. Active Adjustment of the Subreflector Shape for the Large Dual-Reflector Antenna. Micromachines 2023, 14, 1893. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Huang, J.; Qiu, L.; Song, R. Analysis of Reflector Vibration-Induced Pointing Errors for Large Antennas Subject to Wind Disturbance: Evaluating the pointing error caused by reflector deformation. IEEE Antennas Propag. Mag. 2015, 57, 46–61. [Google Scholar] [CrossRef]
- Ye, S.; Duan, B. A Unified Approach of Structural Optimization on Geometrical Configuration and Member Sizing of Antenna Structure. Comput. Struct. Mech. Appl. 1986, 3, 57–65. (In Chinese) [Google Scholar]
- Chen, J.; Li, L.; Long, S. Solving the Bending Problem of Arbitrary Quadrilateral Plates by Generalized Kantorovich Method. Eng. Mech. 1991, 8, 59–72. (In Chinese) [Google Scholar]
- Wei, W. Antenna Principle; National Defense Industry Press: Arlington, VA, USA, 1985. [Google Scholar]
- Xu, H.; Heng, Y.; Shang, Y.; Xia, L. A Fast Computing Method for Dual Reflector Antennas. Guid. Fuze 2018, 2, 42–45. [Google Scholar]
- Lian, P.; Wang, C.; Xue, S.; Xu, Q.; Wang, N.; Xiang, B.; Shi, Y.; Jia, Y. Panel Adjustment and Error Analysis for a Large Active Main Reflector Antenna by Using the Panel Adjustment Matrix. IEEE Trans. Antennas Propag. 2021, 69, 6351–6363. [Google Scholar] [CrossRef]
- Liu, G.; Zheng, Y. Antenna Design of Shanghai 65 m Radio Telescope; The 54th Research Institute of China Electronics Technology Corporation: Shijiazhuang, China, 2009. [Google Scholar]






| Number of Rings (N) | R1 (m) | R2 (m) | R3 (m) | R4 (m) |
|---|---|---|---|---|
| 3 | 0.772 | 1.644 | 2.386 | 3.05 |
| Actuator Number | Adjustment Amount (mm) | Actuator Number | Adjustment Amount (mm) |
|---|---|---|---|
| 1 | 0.161 | 47 | 0.101 |
| 2 | 0.081 | 48 | 0.081 |
| 3 | 0.102 | 49 | 0.149 |
| 4 | 0.114 | 50 | 0.127 |
| 5 | 0.102 | 51 | 0.106 |
| 6 | 0.108 | 52 | 0.084 |
| 7 | 0.113 | 53 | 0.158 |
| 8 | 0.118 | 54 | 0.134 |
| 9 | 0.101 | 55 | 0.111 |
| 10 | 0.109 | 56 | 0.087 |
| Compensation Method | Root mean square error (RMS) (mm) |
| Main Face Compensation | 0.24 |
| Flexible Sub-Face Compensation | 0.1438 |
| Block Sub-Face Compensation | 0.0508 |
| Freedom | du | dv | dw | df |
| Variation (m) | 4.37 × 10−5 | 1.76 × 10−6 | 1.67 × 10−4 | 1.07 × 10−5 |
| Freedom | φu | φv | ||
| Variation (°) | 6.86 × 10−5 | 1.70 × 10−3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Kong, X.; Zhang, C.; Gao, Y.; He, Q. Electrical Performance Compensation of Reflector Antenna Based on Sub-Reflector Array. Electronics 2023, 12, 4771. https://doi.org/10.3390/electronics12234771
Zhang J, Kong X, Zhang C, Gao Y, He Q. Electrical Performance Compensation of Reflector Antenna Based on Sub-Reflector Array. Electronics. 2023; 12(23):4771. https://doi.org/10.3390/electronics12234771
Chicago/Turabian StyleZhang, Jie, Xiangpeng Kong, Chuyun Zhang, Yifan Gao, and Qiang He. 2023. "Electrical Performance Compensation of Reflector Antenna Based on Sub-Reflector Array" Electronics 12, no. 23: 4771. https://doi.org/10.3390/electronics12234771
APA StyleZhang, J., Kong, X., Zhang, C., Gao, Y., & He, Q. (2023). Electrical Performance Compensation of Reflector Antenna Based on Sub-Reflector Array. Electronics, 12(23), 4771. https://doi.org/10.3390/electronics12234771






