A Methodology for Efficient Antenna Deployment in Distributed Massive Multiple-Input Multiple-Output Systems
Abstract
1. Introduction
- A methodology for efficient antenna deployment in D-mMIMO systems is presented. The method is site-specific and relies on the combination of RT for channel characterization with a metaheuristic optimization-based approach.
- Starting with a maximum number of potential active antennas, the method proposed makes it possible to optimize, i.e., reduce, the set of antennas necessary in the D-mMIMO system to meet certain channel requirements.
- The fitness function to be minimized takes into account the differences in the CDFs along the full frequency band for both spectral efficiency and fairness; therefore, the optimization considers the wideband nature of time-division duplex orthogonal frequency-division multiplexing (TDD-OFDM) schemes.
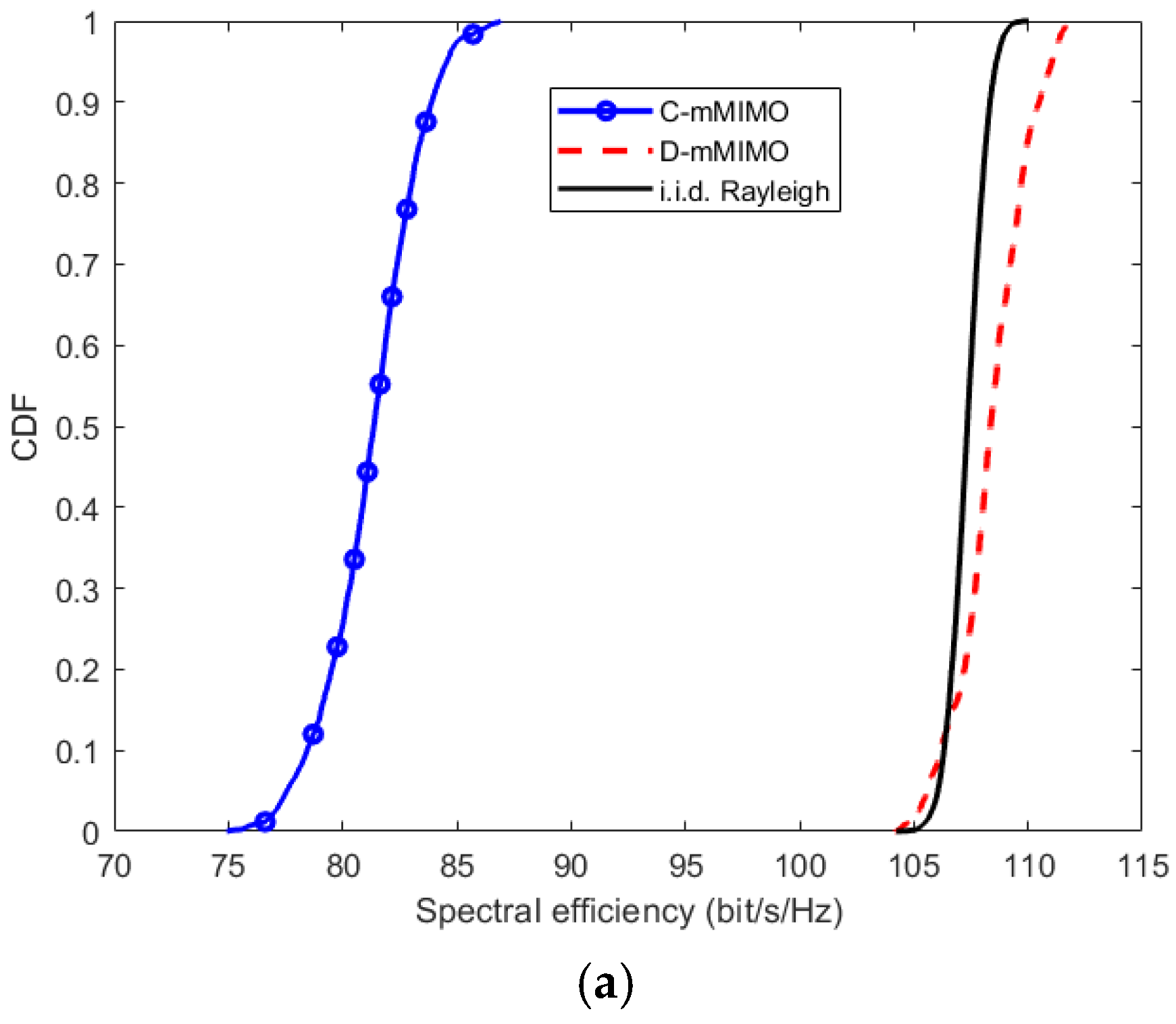
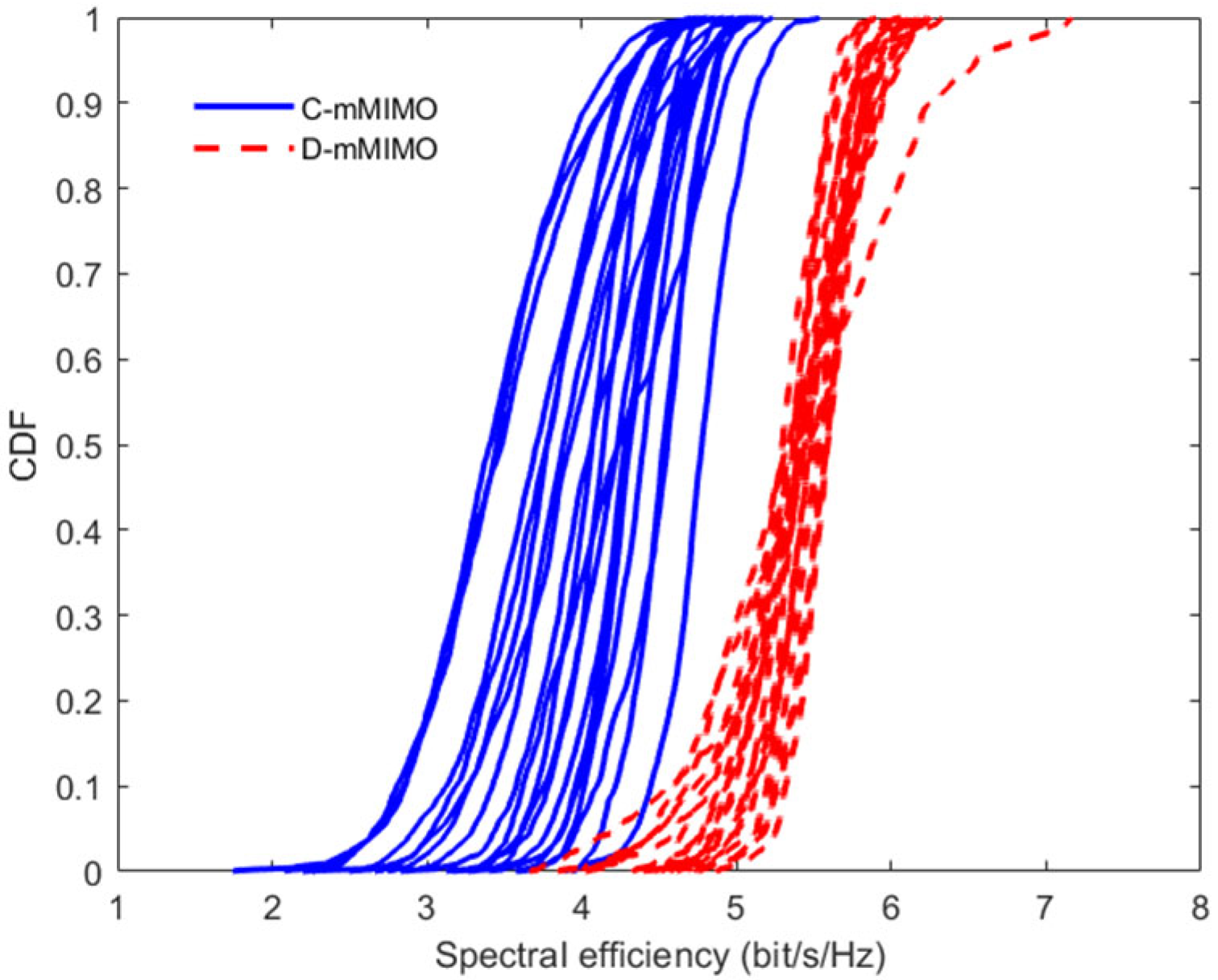
- The methodology leads to a significant reduction in the antennas needed in the distributed system compared to the concentrated one.
- It is a flexible approach in which any other QoS indicators can be considered, making it possible to modulate the search by modifying the fitness function if desired.
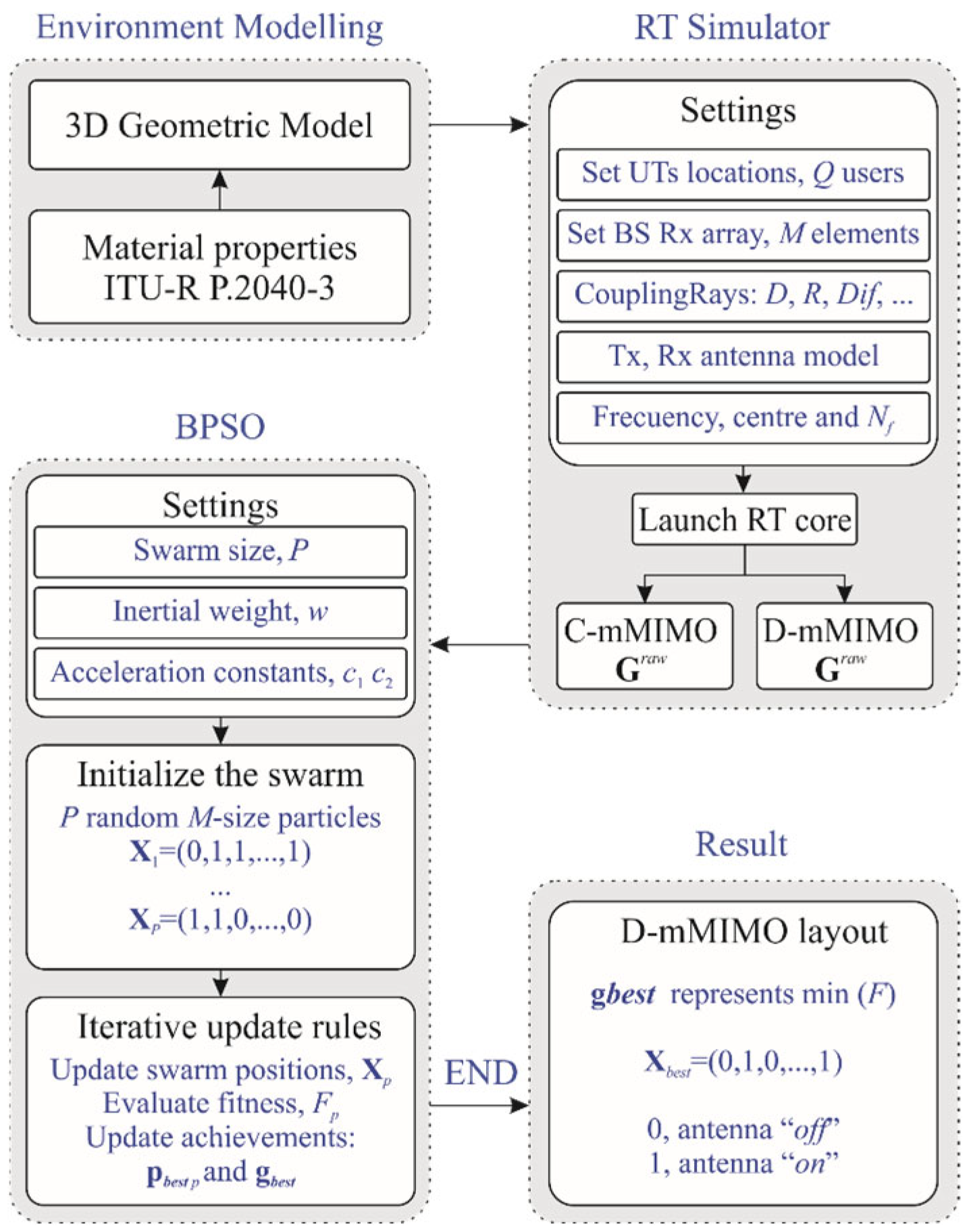
2. Methodology
2.1. Up-Link Massive MIMO Model
2.2. Channel Matrix Using Ray Tracing
2.3. D-mMIMO Optimization Aproach
3. Results and Discussion
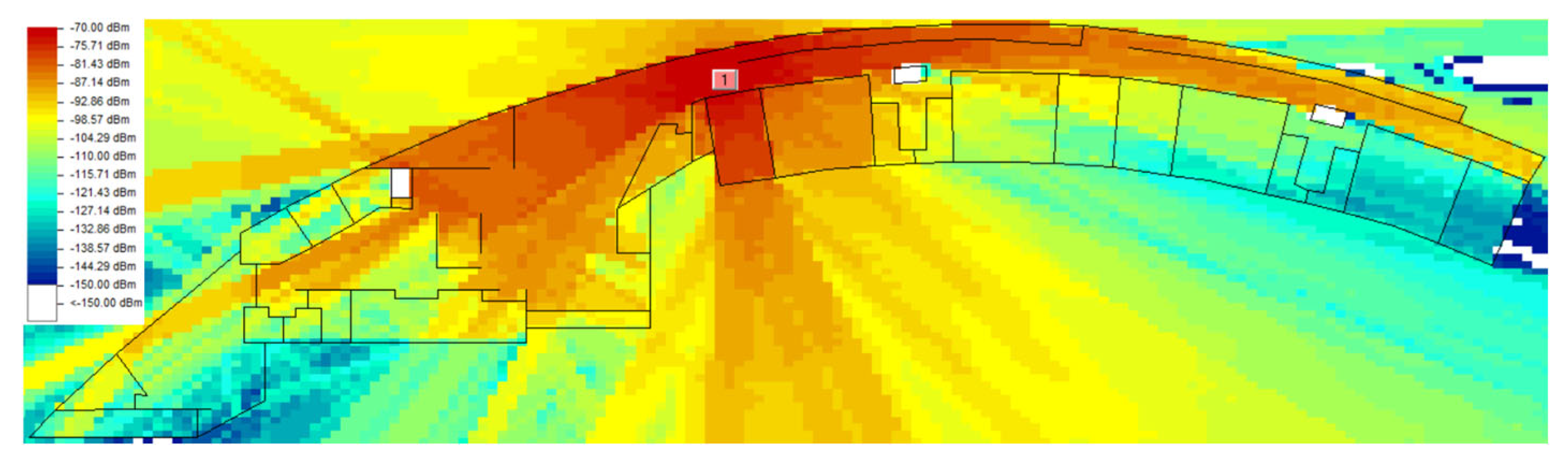
3.1. Environment and Settings
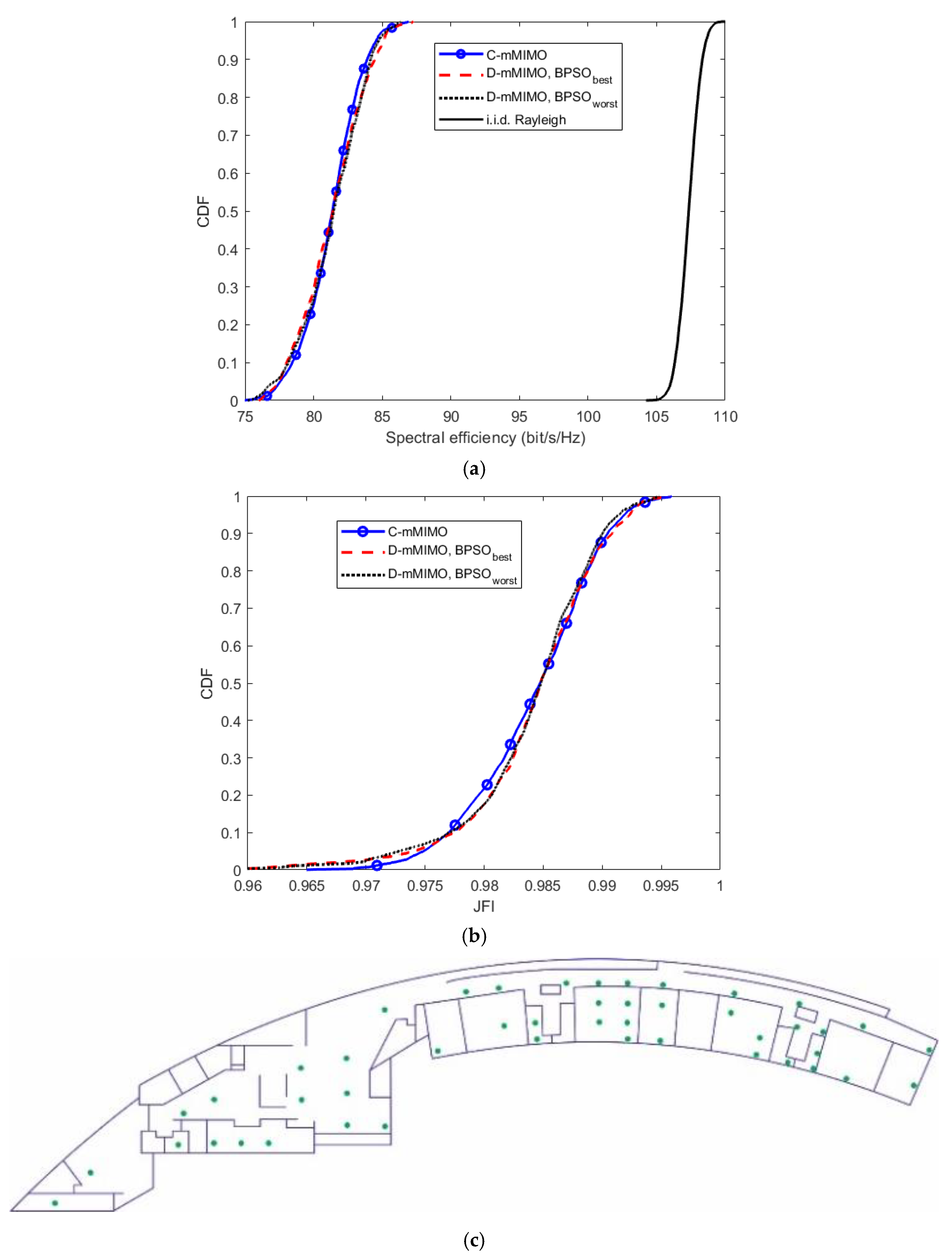
3.2. D-mMIMO Results: Analysis and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| 3D | Three-dimensional |
| 5G | Fifth generation |
| 6G | Sixth generation |
| BPSO | Binary PSO |
| BS | Base station |
| CAD | Computer-aided design |
| CDF | Cumulative distribution function |
| C-mMIMO | Concentrated massive multiple-input multiple-output |
| D-mMIMO | Distributed massive multiple-input multiple-output |
| EE | Energy efficiency |
| GA | Genetic algorithm |
| GO/UTD | Geometrical optics/uniform theory of diffraction |
| JFI | Jain’s fairness index |
| MIMO | Multiple-input multiple-output |
| mMIMO | Massive multiple-input multiple-output |
| PSO | Particle swarm optimization |
| QoS | Quality of service |
| RT | Ray tracing |
| Rx | Receiver |
| SE | Spectral efficiency |
| SINR | Signal-to-interference-plus-noise ratio |
| SNR | Signal-to-noise ratio |
| TDD-OFDM | Time-division duplex orthogonal frequency-division multiplexing |
| Tx | Transmitter |
| UTs | User terminals |
| ZF | Zero-forcing |
References
- Larsson, E.; Edfors, O.; Tufvesson, F.; Marzetta, T. Massive MIMO for next generation wireless systems. IEEE Commun. Mag. 2014, 52, 186–195. [Google Scholar] [CrossRef]
- Björnson, E.; Sanguinetti, L.; Wymeersch, H.; Hoydis, J.; Marzetta, T.L. Massive MIMO is a reality—What is next?: Five promising research directions for antenna arrays. Digit. Signal Process. 2019, 94, 3–20. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, J.; Du, H.; Sha, W.E.I.; Ai, B.; Niyato, D.; Debbah, M. Extremely large-scale MIMO: Fundamentals, challenges, solutions, and future directions. IEEE Wirel. Commun. 2024, 31, 117–124. [Google Scholar] [CrossRef]
- Ngo, H.Q.; Interdonato, G.; Larsson, E.G.; Caire, G.; Andrews, J.G. Ultradense cell-free massive MIMO for 6G: Technical overview and open questions. Proc. IEEE 2024, 112, 805–831. [Google Scholar] [CrossRef]
- Zhou, S.; Zhao, M.; Xu, X.; Wang, J.; Yao, Y. Distributed wireless communication system: A new architecture for future public wireless access. IEEE Commun. Mag. 2003, 41, 108–113. [Google Scholar] [CrossRef]
- Ngo, H.Q.; Ashikhmin, A.; Yang, H.; Larsson, E.G.; Marzetta, T.L. Cell-Free Massive MIMO Versus Small Cells. IEEE Trans. Wirel. Commun. 2017, 16, 1834–1850. [Google Scholar] [CrossRef]
- Interdonato, G.; Björnson, E.; Quoc, H.; Frenger, P.; Larsson, E.G. Ubiquitous cell-free Massive MIMO communications. J. Wirel. Commun. Netw. 2019, 197, 197. [Google Scholar] [CrossRef]
- Dai, H. Distributed Versus Co-Located MIMO Systems with Correlated Fading and Shadowing. In Proceedings of the IEEE International Conference on Acoustics Speed and Signal Processing, Toulouse, France, 14–19 May 2006; pp. 561–564. [Google Scholar] [CrossRef]
- Dai, L. A Comparative Study on Uplink Sum Capacity with Co-Located and Distributed Antennas. IEEE J. Sel. Areas Commun. 2011, 29, 1200–1213. [Google Scholar] [CrossRef]
- Almelah, H.B.; Hamdi, K.A. Spectral Efficiency of Distributed Large-Scale MIMO Systems with ZF Receivers. IEEE Trans. Veh. Technol. 2017, 66, 4834–4844. [Google Scholar] [CrossRef]
- Clark, M.V.; Willis, T.M.; Greenstein, L.J.; Rustako, A.J.; Erceg, V.; Roman, R.S. Distributed versus centralized antenna arrays in broadband wireless networks. In Proceedings of the IEEE VTS 53rd Vehicular Technology Conference, Rhodes, Greece, 6–9 May 2001; Volume 1, pp. 33–37. [Google Scholar] [CrossRef]
- Kumagai, S.; Kobayashi, T.; Oyama, T.; Akiyama, C.; Tsutsui, M.; Jitsukawa, D.; Seyama, T.; Dateki, T.; Seki, H.; Minowa, M.; et al. Experimental trials of 5G ultra high-density distributed antenna systems. In Proceedings of the IEEE 90th Vehicular Technology Conference, Honolulu, HI, USA, 22–25 September 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Chen, C.; Guevara, A.P.; Pollin, S. Scaling up distributed massive MIMO: Why and how. In Proceedings of the 51st Asilomar Conference on Signals, Systems, and Computers, Pacific Grove, CA, USA, 29 October–1 November 2017; pp. 271–276. [Google Scholar] [CrossRef]
- Okuyama, T.; Suyama, S.; Mashino, J.; Okumura, Y.; Shiizaki, K.; Akiyama, C. Antenna Deployment of 5G Ultra High-Density Distributed Massive MIMO by Low-SHF-Band Indoor and Outdoor Experiments. In Proceedings of the IEEE 86th Vehicular Technology Conference, Toronto, ON, Canada, 24–27 September 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Chen, C.-M.; Wang, Q.; Gaber, A.; Guevara, A.P.; Pollin, S. User Scheduling and Antenna Topology in Dense Massive MIMO Networks: An Experimental Study. IEEE Trans. Wirel. Commun. 2020, 19, 6210–6223. [Google Scholar] [CrossRef]
- Pérez, J.R.; Fernández, Ó.; Valle, L.; Bedoui, A.; Et-tolba, M.; Torres, R.P. Experimental analysis of concentrated versus distributed massive MIMO in an indoor cell at 3.5 GHz. Electronics 2021, 10, 1646. [Google Scholar] [CrossRef]
- Pérez, J.R.; Valle, L.; Fernández, O.; Torres, R.P.; Rubio, L.; Rodrigo-Peñarrocha, V.M.; Reig, J. A comparison between concentrated and distributed massive MIMO channels at 26 GHz in a large indoor environment using ray-tracing. IEEE Access 2022, 10, 65623–65635. [Google Scholar] [CrossRef]
- Fernández, O.; Valle, L.; Domingo, M.; Torres, R.P. Flexible Rays. IEEE Veh. Technol. Mag. 2008, 3, 18–27. [Google Scholar] [CrossRef]
- Moreno, J.; Domingo, M.; Valle, L.; Pérez, J.R.; Torres, R.P.; Basterrechea, J. Design of Indoor WLANs: Combination of a ray-tracing tool with the BPSO method. IEEE Antennas Propag. Mag. 2015, 57, 22–33. [Google Scholar] [CrossRef]
- Tsai, C.-W.; Cho, H.-H.; Shih, T.K.; Pan, J.-S.; Rodrigues, J.J.P.C. Metaheuristics for the deployment of 5G. IEEE Wirel. Commun. 2015, 22, 40–46. [Google Scholar] [CrossRef]
- Sapkota, B.; Ghimire, R.; Pujara, P.; Ghimire, S.; Shrestha, U.; Ghimire, R.; Dawadi, B.R.; Joshi, S.R. 5G network deployment planning using metaheuristic approaches. Telecom 2024, 5, 588–608. [Google Scholar] [CrossRef]
- Alruwaili, M.; Kim, J.; Oluoch, J. Optimizing 5G power allocation with device-to-device communication: A Gale-Shapley algorithm approach. IEEE Access 2024, 12, 30781–30795. [Google Scholar] [CrossRef]
- Luna, F.; Luque-Baena, R.M.; Martínez, J.; Valenzuela-Valdés, J.F.; Padilla, P. Addressing the 5G cell switch-off problem with a multi-objective cellular genetic algorithm. In Proceedings of the IEEE 5G World Forum (5GWF), Silicon Valley, CA, USA, 9–11 July 2018; pp. 422–426. [Google Scholar] [CrossRef]
- Wang, R.; Jiang, Y. Distributed optimization of Uplink Cell-Free Massive MIMO Networks. In Proceedings of the IEEE 96th Vehicular Technology Conference (VTC2022-Fall), London, UK, 26–29 September 2022; pp. 1–5. [Google Scholar] [CrossRef]
- Gao, Y.; Vinck, H.; Kaiser, T. Massive MIMO antenna selection: Switching architectures, capacity bounds, and optimal antenna selection algorithms. IEEE Trans. Signal Process. 2018, 66, 1346–1360. [Google Scholar] [CrossRef]
- Ouyang, C.; Ou, Z.; Zhang, L.; Yang, H. Optimal Transmit Antenna Selection Algorithm in Massive MIMOME Channels. In Proceedings of the IEEE Wireless Communications and Networking Conference (WCNC), Marrakesh, Morocco, 15–18 April 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Benmimoune, M.; Driouch, E.; Ajib, W.; Massicotte, D. Novel transmit antenna selection strategy for massive MIMO downlink channel. Wirel. Netw. 2017, 3, 2473–2484. [Google Scholar] [CrossRef]
- Souza, J.H.I.; Amiri, A.; Abrão, T.; Carvalho, E.; Popovski, P. Quasi-distributed antenna selection for spectral efficiency maximization in subarray switching XL-MIMO systems. IEEE Trans. on Veh. Technol. 2021, 70, 6713–6725. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R.C. A discrete binary version of the particle swarm algorithm. In Proceedings of the IEEE International Conference on Systems, Man, and Cybernetics, Computational Cybernetics and Simulation, Orlando, FL, USA, 12–15 October 1997; pp. 4104–4108. [Google Scholar] [CrossRef]
- Khanesar, M.A.; Teshnehlab, M.; Shoorehdeli, M.A. A novel binary particle swarm optimization. In Proceedings of the Mediterranean Conference on Control & Automation, Athens, Greece, 27–29 June 2007; pp. 1–6. [Google Scholar] [CrossRef]
- Gao, X.; Edfors, O.; Rusek, F.; Tufvesson, F. Massive MIMO Performance Evaluation Based on Measured Propagation Data. IEEE Trans. Wirel. Commun. 2015, 14, 3899–3911. [Google Scholar] [CrossRef]
- Pérez, J.R.; Torres, R.P.; Domingo, M.; Valle, L.; Basterrechea, J. Analysis of massive MIMO performance in an indoor picocell with high number of users. IEEE Access 2020, 8, 107025–107034. [Google Scholar] [CrossRef]
- Jain, R.K.; Chiu, D.-M.W.; Hawe, W.R. A Quantitative Measure of Fairness and Discrimination; Eastern Research Laboratory, Digital Equipment Corporation: Hudson, MA, USA, 1984. [Google Scholar]
- Kennedy, J.; Eberhart, R.C. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar] [CrossRef]
- ITU. Effects of Building Materials and Structures on Radiowave Propagation Above About 100 MHz; ITU Radiowave Propagation Series Recommendation ITU-R P.2040-3, Release 3; International Telecommunication Union: Geneva, Switzerland, 2023. [Google Scholar]
- Kennedy, J.; Eberhart, R.C.; Shi, Y. Swarm Intelligence; Morgan Kaufmann: San Francisco, CA, USA, 2001; pp. 289–296. [Google Scholar]




| Material | εr | σ (S/m) | Use |
|---|---|---|---|
| Brick | 3.91 | 0.0401 | Walls |
| Concrete | 5.24 | 0.5908 | Floor, ceiling |
| Glass | 6.31 | 0.2828 | Front walls |
| Perfect conductor | 1 | 1 × 107 | Lifts |
| P | w | c1 | c2 | Vmax | w1 |
|---|---|---|---|---|---|
| 25 | 0.5 | 1.0 | 1.0 | 4.0 | 0.002 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pérez, J.R.; Torres, R.P.; Valle, L.; Rubio, L.; Rodrigo-Peñarrocha, V.M.; Reig, J. A Methodology for Efficient Antenna Deployment in Distributed Massive Multiple-Input Multiple-Output Systems. Electronics 2025, 14, 1233. https://doi.org/10.3390/electronics14061233
Pérez JR, Torres RP, Valle L, Rubio L, Rodrigo-Peñarrocha VM, Reig J. A Methodology for Efficient Antenna Deployment in Distributed Massive Multiple-Input Multiple-Output Systems. Electronics. 2025; 14(6):1233. https://doi.org/10.3390/electronics14061233
Chicago/Turabian StylePérez, Jesús R., Rafael P. Torres, Luis Valle, Lorenzo Rubio, Vicent M. Rodrigo-Peñarrocha, and Juan Reig. 2025. "A Methodology for Efficient Antenna Deployment in Distributed Massive Multiple-Input Multiple-Output Systems" Electronics 14, no. 6: 1233. https://doi.org/10.3390/electronics14061233
APA StylePérez, J. R., Torres, R. P., Valle, L., Rubio, L., Rodrigo-Peñarrocha, V. M., & Reig, J. (2025). A Methodology for Efficient Antenna Deployment in Distributed Massive Multiple-Input Multiple-Output Systems. Electronics, 14(6), 1233. https://doi.org/10.3390/electronics14061233









