Distributed, Dynamic and Recursive Planning for Holonic Multi-Agent Systems: A Behavioural Model-Based Approach

Abstract

In this work, we propose a new distributed, dynamic, and recursive planning approach able to consider the hierarchical nature of the holonic agent and the unpredictable evolution of its behaviour. For each new version of the holonic agent, introduced because of the agent members obtaining new roles to achieve new goals and adapt to the changing environment, the approach generates a new plan that can solve the new planning problem associated with this new version against which the plans, executed by the holonic agent, become obsolete. To do this, the approach starts by generating sub-plans capable of solving the planning subproblems associated with the groups of the holonic agent at its different levels. It then recursively links the sub-plans, according to their hierarchical and behavioural dependency, to obtain a global plan. To generate the sub-plans, the approach exploits the behavioural model of the holonic agent’s groups, thereby minimising the computation rate imposed by other multi-agent planning methods. In our work, we have used a concrete case to show and illustrate the usefulness of our approach.

1. Introduction

In artificial intelligence, planning [1] is a discipline that consists of choosing, according to a given criterion, which actions should be carried out among a set of actions, and in what order they should be applied to achieve a specific goal. In its traditional version [2], planning has experienced considerable growth due to the richness of modelling languages and the efficiency of plan generation systems [3,4,5,6,7]. However, traditional planification suffered from a weakness caused by the fact that it is based on two strong assumptions, namely (i) the availability of perfect knowledge, at all times, of the state and the actions’ effects; and (ii) the certainty that modifications of the system’s state of the system come only from the execution of the actions of the plan. To compensate for this limitation, the field of uncertainty [8] was proposed, suggesting the integration of actions with probabilistic effects and additive utility functions into the goals. This leads to a family of approaches for planification [9,10,11,12] based on decision theory and using representation languages that are traditionally known in artificial intelligence: logic [13], constraints [14], or Bayesian networks [15], to cite a few. The use of these representation languages has increased complexity in plan generation algorithms, whose resolution has become a challenge for the artificial intelligence community.

In the field of multi-agent systems (MAS), multi-agent planning (MAP) [16,17] has been presented as a methodology to integrate the planning capabilities of intelligent agents so that a group of agents can develop a plan of action to achieve a set of common or individual goals by combining their knowledge, information, and capabilities [18,19,20,21,22]. MAP is intrinsically based on the distribution of the generation and/or execution of the action plans over a set of agents. These agents can be (i) individualistic if they have personal goals that they can achieve on their own. In this case, each agent generates its own plan locally and then coordinates it in a distributed manner. Therefore, the plan generation, coordination process, and execution are performed in a distributed manner. Alternatively, they can be (ii) cooperative if they have common goals and complement each other in achieving them. In this case, the plans are generated centrally and then distributed to the agents. Therefore, only the execution of the plan is distributed. In both cases, the agents must be able to produce plans that enable the achievement of either the individual goals or the subgoals required for the overall goal.

Justified by the distributed nature of the MAS’s problems and reasoning, MAP focuses on aspects related to distributed control. These include activities such as decomposition and allocation of tasks to agents and utilisation of resources [23,24]; reducing communication costs and restrictions among agents [25,26]; or incorporating group decision making for distributed plan management in collaborative settings. Through the use of the advantages of MAS, MAP has improved the field of planning. In fact, it has made it possible to go beyond the use of traditional representation languages and it has also greatly expanded the field of automated planning methods. In the literature, several planning and coordinating techniques have been proposed, such as techniques to merge the local plans of the agents [27,28,29], heuristic techniques for agents to solve their sub-plans [30], mechanisms to coordinate concurrent interacting actions [31,32], or distributed constraint optimisation techniques to coordinate conflicts among agents [33,34]. Although these techniques have provided important answers to various problems related to MAP, most of these methods require high computation rates imposed on the planning agent in the case of centralised planning or on all the agents when coordinating their plans in the case of distributed planning. In addition to this, they do not consider the specificities of holonic multi-agent systems (HMAS) [35]. In MAS, the vision of holons is someway closer to the one that MAS researchers have of recursive or composed agents. A holon constitutes a way to gather local and global, individual, and collective points of view. A holon is a self-similar structure composed of holons as substructures, and a hierarchical structure composed of holons is called a holarchy. A holon can be seen, depending on the level of observation, either as an autonomous whole entity or as an organisation of holons (this is often called the Janus effect, in reference to the two faces of a holon [36]. This duality enables the holonic agent to have individual behaviours, as for regular atomic agents, or collective behaviours built up from the behaviours of the holonic agents that are composing this top holonic agent. This makes them intrinsically recursive and capable of naturally describing complex systems of a hierarchical nature [35]. According to [37], holonic agents to adapt their behaviours to external or internal events or changes. If the holonic agent is not composed of sub-agents, then the adaption mechanism is like those that are used in nonhierarchical multi-agent systems or adaptive multi-agent systems. If the holonic agent is composed of sub-agents, then the super-holonic agent must implement a decision-making policy through the definition of rules and groups that are dedicated to this purpose inside the super-holonic agent. These groups are called holonic groups by [38,39]. These groups implement the way in which the other groups in the super-holonic agent are evolving, as well as these associated goals. These groups are assumed to be dedicated to a specific application case.

When planning HMAS, two problems arise:

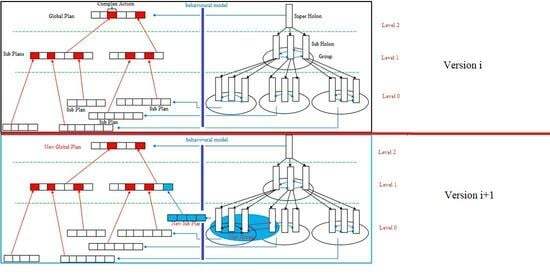
• The behaviour and structure of the holonic agent change over time to achieve new goals and adapt to the changing environment. This adaptation is ensured by the fact that each agent in the holonic agent can obtain new roles and new capabilities and introduce new interactions with other members during its lifetime [35]. On this basis, the plans generated to enable the holonic agent to achieve its first goals, defined in its first version, become insufficient for the new goals that have been introduced. Therefore, there is a need to generate new plans that enable the holonic agent to achieve these new goals.
• The global objective of the holonic agent, for which we want to generate plans, is decomposed hierarchically and recursively into a set of sub-objectives. Each sub-goal is supported by a group of roles played by the members (or sub-agents) of the holonic agent to achieve it. In this case, the planning problem in HMAS is composed of subproblems linked together recursively. Indeed, the generation of plans amounts to generating, in the first step, the sub-plans that allow the members of the holonic agent to reach the sub-objectives. The global plan will then be generated recursively by linking the sub-plans and considering the dependency that exists between them.

To solve these problems, a new distributed, dynamic, and recursive planning approach is proposed in this paper to consider the hierarchical nature of holonic agents as well as the unpredictable evolution of their behaviour. The approach consists of generating for each group, based on its behavioural model, sub-plans capable of solving the sub-problem associated with it, and then establishing links between these sub-plans based on their hierarchical and behavioural dependency in order to obtain global plans capable of solving global planning problems. Generating sub-plans from group behaviour models overcomes the drawbacks of other MAP methods by minimising their computation rate. Indeed, unlike these methods, which attempt to determine from the zero how to solve a given problem, the behavioural model used in our approach can serve as a support containing all the possible behaviours capable of solving the desired problem.

The rest of this work is organised as follows. In Section 2, we provide a brief overview of the main related work. In Section 3, the basic concepts of HMAS. In Section 4, we describe the proposed distributed, dynamic, and recursive planning approach for holonic multi-agent systems. Section 5 presents a concrete case study on which the approach has been applied to show the feasibility and interests of the approach. Some conclusions and future directions of the work are presented in Section 6.

2. Related Works

For MAP, various works have been proposed in the literature. These are synthesised in the following:

• Torreño, A. et al. [40] introduced a general-purpose MAP architecture intended to address issues with any level of coupling when there is insufficient information. Agents in the MAP-proposed paradigm share only the knowledge that is necessary and that directly impacts other agents, preserving a distributed understanding of the task. Through the use of an iterative refinement planning process and single-agent planning technology, agents are able to complete MAP tasks.
• Daniel Borrajo and Susana Fernández [41] proposed a distributed approach and a centralised approach for MAP. In the first approach, agents receive prior agents’ plans, goals, and states to iteratively solve problems. They create new plans using the plans of earlier agents and they then distribute the new plans and some obscured private data to subsequent agents. The second approach has agents that create an obfuscated version of their problems in order to preserve their privacy, and then they present it to another agent that handles centralised planning.
• Jan Tožička et al. [42] proved the theoretical limits of strong privacy-preserving planning based on the most common MAP paradigms, such as distributed state space search. They also proposed a more refined definition of strong privacy, where some aspects of the problem are known as priori, and only the details remain strongly private.
• Jan Tožička et al. [43] developed a MAP framework for solving classical planning tasks for cooperative agents with private information. The objective is to minimise planning time, maximise the quality of the plans, and maximise the level of privacy between agents. The main motivation for these systems is to be able to use any current state-of-the-art planner as a basic solution to the problem (planner-independent).
• In Dehimi et al. [44], we proposed a new distributed dynamic planning approach based on constraint satisfaction that can consider the satisfaction of the constraints in all new versions of generated plans. As part of the proposed approach, each agent generates a new plan every time an agent’s set of planned actions changes due to unforeseen changes in the environment. For this, the approach ensures the correct placement of all new actions brought about by modifications in the new plan, maintaining the satisfaction of the constraints. The method employs a genetic algorithm, where the fitness function is established following the requirements that must be met.
• Leonardo Henrique et al. [45], developed a domain-independent statistical framework to assess recovery solutions in dynamic situations. The number of agents, goals, actions, failure probability, and the extent of agent connection were all varied in the authors’ simulation studies to validate the suggested methodology. Plan length and planning time are two indicators of evaluation. The findings demonstrate that replanning produces plans with fewer steps than fixing and that repairing planning time is lower with at least 94% certainty. The authors examined plan recovery solutions in dynamic multi-agent environments and showed that while repairing produces better results quickly, replanning produces superior plans since the length of the final plan is directly connected with the likelihood of failure.

These works have significantly contributed to the field by suggesting novel MAP strategies; however, they suffer from two problems: (i) they do not consider the hierarchical characteristics of HMAS. These works are mainly designed for agents that are defined as atomic entities, whereas holonic agents are defined as agents composed of agents. (ii) Most of these methods require high calculation rates, which makes them difficult to apply to complex cases. This can be seen in both centralised and distributed MAP methods. Consequently, in this paper, a new distributed, dynamic, and recursive planning approach is proposed that considers the hierarchical nature of holonic agents as well as the unpredictable evolution of their behaviour. The proposed approach is based on the behavioural model of groups of holonic agents, making it possible to overcome the difficulties encountered when applying other MAP methods.

3. Basic Concepts of Holonic Multi-Agent Systems

The holonic agent is a self-similar entity composed of holons as substructures [36] where the compound holon is qualified as a super-holon and the holons that compose a super-holon are called subholons or holons members. Each composite holon is characterised by its roles, capabilities, and knowledge [38]. Capacity is the abstract description of a skill. It includes the description of means that enable the achievement of a task (action). It constitutes an interface between the agent and the role, where to obtain a role, the agent must have all the capabilities required by the tasks (actions) of this role. An agent originally possesses a set of basic capabilities that can evolve dynamically. In fact, in addition to its basic capabilities, a super-holon can possess new capabilities, realised through a service provided by its lower-level members [46]. This is because a group of agents can provide a service (or a capability implementation) resulting from collaboration between the different members of the group [38]. The fact that a super-holon possesses a new capability implies that it can play a new role that was not available to it at the beginning. Therefore, capacity also constitutes an interface between two adjacent levels of abstraction in the holonic agent. It allows us to explain the hierarchical and behavioural dependence between members of the latter in its different levels.

Role describes an expected behaviour in a specific organisation, according to the CRIO organisational metamodel [38]. Each role is associated with a set of actions through the required capacities that an agent must possess to play this role. These actions can be either (i) simple actions in the case where their implementation is included directly in the behaviour of the role or (ii) complex actions in the case where their implementation is based on a service (or capacity implementation) published by a lower-level group. An agent will play several roles simultaneously or successively during its execution. It tends to satisfy the objectives that have been assigned to the roles it plays, and to exhibit the behaviour of these roles as a contract with the other agents that are playing roles in the same group (or instance of organisation). An agent can dynamically change its roles according to its needs and objectives. This means that the behaviour and overall structure of the holonic agent may change over time, enabling it to satisfy new objectives and adapt to changes in the environment.

Communication between agents is constrained by the definition of interactions between the roles they are playing at a given moment. Indeed, two agents can only communicate if each one plays a role in a common group, which specifies how they are organised and how they interact within it to satisfy the group objectives (functional needs) assigned to them. Each of these needs to be satisfied by the group behaviour emerging from the interactions of all or some of the roles played by the agents in the group. According to the ASPECS methodology and its associated metamodel, there are two types of groups [39]:

• Production groups are instances of organisations that describe how members interact and coordinate to meet the objectives and tasks assigned to their super-holon. The definition of these organisations depends on the problem being addressed.
• The holonic group is an instance of the holonic organisation that specifies how the members are organised to manage the super-holon in terms of the distribution of authority and power. It consists of five roles, qualified as holonic roles, namely Head (in charge of the administration of the super-holon), Representative (acts as an interface between the inside and the outside of the super-holon), Part (in charge of the execution of the tasks assigned to them by the Heads), MultiPart (in charge of the identification of members shared between several super-holons), and Stand-Alone (represents the status attributed to the nonmember holons to manage the recruitment of new members within a super-holon).

In the following section, a novel approach for MAP with HMAS is proposed and detailed.

4. Multi-Agent Planning for Holonic Multi-Agent Systems

The proposed approach consists of dynamically generating, for each evolution of the holonic agent, the set of action plans to be executed by the members of the holonic agent to solve the planning problem associated with the latter and enable it to achieve its objectives. For the generation of these plans, the proposed approach adopts a recursive technique (Figure 1). Indeed, it starts by generating the sub-plans associated with the planning subproblems of each group of the holonic agent. These sub-plans are linked in a second stage according to the hierarchical and behavioural dependency that exist between them to obtain the global plan. The generation of sub-plans for each evolution introduced at time t is based on the behavioural model of the holonic agent’s groups at that time. These models are presented in the form of sequence and activity diagrams generated for each group during the modelling phase planned for the development of the holonic agent.

The proposed approach starts with a version V₀ for which, in the first step, sub-plans are generated for solving the planning subproblems associated with the groups in the different levels. In the second step, the sub-plans are recursively linked, according to hierarchical and behavioural dependencies, to obtain a global plan related to the solving of the planning problem Π₀. This two-step approach is applied again for each new version of the holonic agent V_t, introduced because of the members obtaining new roles to achieve new objectives and to adapt themselves to the change of the environment. The result of this set of iterations generates a new global plan that is capable of solving the new planning problem Π_t, associated with the new version V_t, against which the plans that the holonic agent was executing become obsolete.

The two stages of the proposed approach are detailed in the following and are illustrated in Figure 2:

• Generation of sub-plans: This phase consists of generating, for each group G_ikt (group k of level i at time t), the sub-plans of actions SP_ikt (sub-plans generated for the group k of level i at time t) to be executed at time t, by the members who play roles in this group, in order to solve the planning sub-problem Π_ikt (sub-problem associated with the group k of level i at time t) associated with this group and to enable it to achieve its objectives (the sub-objectives associated with this group). The generation of the sub-plans of each group G_ik is carried out by the member who plays the Head holonic role in this group AHead_ikt (the agent who plays the Head role in group k of level i at time t). For this purpose, each member AHead_ikt, responsible for generating the plans of the G_ikt group, uses the sequence diagram and the activity diagram of this group to determine the possible behaviour scenarios that allow it to wait for the subgoals of its group and to solve the planning sub-problem Π_ikt associated with the latter. Indeed, it uses the sequence diagram of this group to determine the interaction scenarios that need to be executed between the members who play roles in this group to achieve the subgoals of the group. It also uses the activity diagram of this group to determine the role actions that need to be performed by the members playing roles in this group by responding to these interactions. The order of these actions represents a sub-plan that can solve the planning sub-problem Π_ikt associated with the G_ikt group.
• Generation of the global plan: This phase consists of linking, according to the hierarchical and behavioural dependence which exists between the roles of the groups of the different levels, the sub-plans SP_ikt obtained for each group in the first phase. This is performed in order to obtain a global action plan GP_t (global plans of the holonic agent at time t). Its execution allows the holonic agent to solve the planning problem Π_t associated with it and to achieve the global goal. Generation of the global plan is ensured by the member who plays the holonic role Head in the top-level group AHead_nt (the agent who plays the role Head in the top-level group n at time t). To do this, it recursively replaces the complex actions of each SPikt sub-plan, generated in the first phase, with the SP_i−1kt of the lower-level groups (I − 1) that were at the origin of the publication of the services that implement the capabilities required by these complex actions.

To automate the two phases of our approach, each member AHead_ikt, responsible for generating the sub-plans of the group G_ikt, transforms the sequence diagram and the activity diagram of its group into a graph Graph_ikt (the graph of group k of level i at time t). In this graph, each path represents a possible interaction scenario, presented in the sequence diagram, whose execution allows the members, who play roles in the group, to wait for one of the subgoals associated with this group.

Each node in this graph contains the actions presented in the activity diagram to a member following the activation of a given interaction. It can be either (i) a simple node in the case where it contains simple actions (their implementation is included directly in the behaviour of the role played by the member receiving the interaction) or (ii) a complex node in the case where it contains complex actions (their implementation is extracted in the form of capabilities implemented through a service published thanks to a set of interactions between members of another lower-level group). In this case, the node represents a graph in relation to the lower level.

In the following, a formal definition of the planning problem Π_t of each version t of the holonic agent is presented, as well as a formal definition of the graph Graph_ikt. The two phases of our approach are also detailed.

4.1. The Formal Definition of Πt

The planning problem for version t is defined as follows:

Π_t = {Π_ikt, N₀, N_f}/_{0≤I≤n,s1≤k≤m}, where Π_ikt represents the sub-planning problem k associated with group k of level i at time t.

✓

Π_ikt = {G_ikt, H_ikt, N_0ik, N_fik}, in which the definitions are as follows:

-

G_ikt represents the group k of level i at time t.

G_ikt = {R_ikj}/_1≤j≤a, where R_ikj represents the role j of the group k of level i.

R_ikj = {α_ikjl}/_1≤l≤b, where α_ikjl represents the action l of role j of group k of level i. It can take two values:

• Sα_ikjl in case it represents a simple action implemented directly in the R_ikj.
• Cα_ikjl in the case where it represents a complex action extracted as an ability implemented by a lower-level group. In this case, Cα_{ikjl =} Π_i−1mt represents the planning problem associated with the group m of levels i − 1 at time t that implements the capacity of the action Cα_ikjl.

-

H_ikt represents the set of member holons that play roles in group k of level i at time t.

-

N_0ik represents the initial state of the sub-planning problem Π_ikt.

-

N_fik is the set of final states of the sub-planning problem Π_ikt.

✓

N₀ represents the initial state of the global planning problem Π_t.

✓

N_f is the set of final states of the global planning problem Π_t.

4.2. The Formal Definition of Graph_ikt

According to our approach, each graph Graph_ikt of the group G_ikt (the group k of level I at time t) associated with the planning sub-problem Π_ikt is defined as follows:

Graph_ikt = {P_j}/_0≤j≤c, in which the definitions are as follows:

▪

P_j represents a path j in the graph associated with the scenario S_j. Each path P_j is defined as follows:

P_j = {n₀, SN, CN, n_jf}, in which the definitions are as follows:

▪

n₀ is the initial node representing the initial state of the planning sub-problem Π_ikt (the precondition of scenario S_j corresponding to P_j).

▪

n_jf is the final node of the path j representing one of the final states of the planning sub-problem Π_ikt (the postconditions of the scenario S_j corresponding to P_j).

▪

SN is the set of simple nodes that contain simple actions (implemented directly in the agent’s role) of the path P_j where each node n_q belongs to SN is defined as follows: n_q = <Agent_T, Activityn_q>, in which the definitions are as follows:

• Agent_T is the receiver of the interaction represented by node n_q.
• Activityn_q represents the set of simple actions nα_ikql to be executed, because of the interaction represented by node n_q, by the receiving agent.

▪

CN is the set of nodes that contain complex actions (extracted as capabilities implemented by a lower-level group) of the path P_j, where each node n_q belongs to CN is defined as follows: n_q = <Agent_T, Graph_i−1mt>, in which the definitions are as follows:

• Agent_T is the receiver of the interaction represented by node n_q.
• Graph_i-1mt represents the lower-level graphs that implement the complex actions Cα_ikjl of node n_q.

4.3. Dynamic Generation of Plans

Initially, for the planning problem Π₀ at time t₀, each agent AHead_ikt of the group G_ik0 (the group k of level i at time t₀) generates the set of subaction plans SP_ik0 to be executed by the members of this group to solve the planning sub-problem Π_ik0 associated with it. To do this, each agent AHead_ik0 must first generate the graph Graph_ik0 associated with its group. It then applies the following sub-plan generation algorithm to the generated graph. For the first version of the holonic agent, the algorithm is executed with t = 0, whereas from the second version of the holonic agent onwards, Algorithm 1 is executed with t = new t (the instant of the change in behaviour).

Algorithm 1: Sub-plans_Generation

To calculate the sub-plans SP_ik0 of the group G_ik0, the algorithm must traverse the entire path P_j (the possible behavioural scenarios) of the graph Graph_ikt, where, from the simple nodes, it acquires the activities stored in these nodes, while from the complex nodes, it acquires only the identifier of the lower-level group it represents. The final state of each SP_jik0 generated in this phase is initially equal to the final state n_jf (the postcondition) of the path P_j from which it was generated.

After the generation of the sub-plans, the agent AgentH_nk0 applies, to the obtained sub-plans SP_ik0, another algorithm to generate the global plans GP₀. This algorithm consists of replacing the identifier of each lower-level group by its sub-plans that are generated following the application of the sub-plans generation algorithm on the graph associated with this group.

At the end of the execution of Algorithm 2, we obtain all possible global plans that can be executed by the holonic agent can execute at time t = 0. The final state of each global plan obtained is equal to the union of the final states n_jf of all the sub-plans SP_jik0 involved in generating this plan. According to these final states, the holonic agent executes the plan whose final state is equal to or close to the final state N_f of the global planning problem Π_t.

Algorithm 2: Gplans_Generation.

During the execution of the global plan GP₀ generated for the V0 version of the holonic agent, if the latter finds itself, at a given time t, in front of a new planning problem Π_t with new objectives, it must generate another global plan GP_t. It starts with the generation of the sub-plans. For this, each Head agent AagentH_ikt of the G_ikt group, concerned by the change, must generate another set of sub-plans SP_ikt. In effect, it generates the graph for its group on which it reapplies the sub-plan generation algorithm. These new sub-plans will be linked using the global plan generation algorithm.

In the following section, the proposed approach is applied in a case study in the field of transport planning.

5. Case Study

To validate our approach, we apply it to a concrete case study: “Transport planning system”. In the following, the system chosen for the application of our approach is presented, then the two stages are presented on two successive versions of the chosen system, namely the generation of sub-plans and the generation of global plans.

5.1. Presentation of the Transport Planning System

The transport planning system chosen for the application of our approach aims at providing transport to local cities LVi and to the distance cities DVi. The chosen system is functionally decomposed into several groups, each of which is responsible for achieving a specific objective. Among these groups, we find the following:

• G4 “Local Transport” (LT) is responsible for processing local requests: (a) receiving local transport requests from “Distribution Orientation”, (b) performing local transport tasks, and (c) generating a local transport report.
• G5 “Transport Orientation” (TO) is responsible for receiving and directing requests: (a) receiving transport requests from different cities, (b) checking requests, (c) locating requests, (d) classifying requests, (e) sending the transport request to (LT) and/or (DT), and (f) receiving execution reports from (LT) and/or (DT).
• G8 “Distance Transport” (DT) is responsible for processing distance requests: (a) receiving distance transport requests from “Distribution Orientation”, (b) executing distance transport tasks, and (e) generating the distance transport report.

The behaviour of each group is broken down into a set of interacting roles. For example, let us take the Local transport group, in which we have four roles:

• LT Interface: in charge of receiving local requests.
• Taxi: in charge of executing requests that require a taxi.
• Bus: in charge of executing requests that require a bus.
• Tram: in charge of executing requests that require a tram.

The roles of each group will subsequently be instantiated by agents (members of the holonic agent). Based on the roles they play at a given time t, the members of the holonic agent must find action plans that are capable of solving the transport requests received by the system at time t (the Πt planning problem).

As in the first version (V₀) of our system, the roles needed for transport to distance cities DVi (the G8 roles) are not instantiated. The holonic structure of the “Transport Planning System” in its initial version (V₀) is presented in Figure 3. In this figure, the members who play the Head holonic role in each group are shown in green (the member responsible for the generation of the sub-plans in its group) and the member who plays the Head holonic role in the higher-level group is shown in blue (the member responsible for the generation of the plan by linking the sub-plans).

At level 2 of the holarchy, we find two super-holons, H1 and H2, which play the roles of Transport Orientation (TO) and Local Transport (LO), respectively, in the group G1: “Transport planning system”. At level 1, the holons H3, H4, and H5 are members of the H1 holon. They play the roles of TO interface, Verifier, and Analyser, respectively, in group G5: Transport Orientation. The holons H6, H7, H8, and H9 are members of the H2 holon. They play the roles of LT interface, Taxi, Bus, and Tramway, respectively, in group G4: “Local Transport”. At level 0, the holons H10, H11, and H12 are members of the holon H3. They play the roles of Analyser Interface, Locator, and Classifier respectively in Group G7: “Analyzer”.

5.2. Application of Our Approach to the V₀ Version of the Holonic Agent

For its V₀ version, the holonic agent must generate, in the first step, sub-plans capable of solving the planning subproblems associated with its groups at its different levels. In a second step, the holonic agent must recursively link, according to hierarchical and behavioural dependency, the sub-plans to obtain a global plan able to solve the planning problem Π₀.

5.2.1. Generation of Sub-Plans for V₀

The generation of the sub-plans is carried out by the member who plays the head holonic role of each group. It consists of two phases:

• Generation of the graph of each group: In this phase, the member who plays the head holonic role in each group transforms the sequence diagram and the activity diagram of its group into a graph. As part of the process of creating this graph, an intermediate step is taken in which the sequence diagram and the activity diagram are first converted into an XML file. This will make it easier to create and populate the various graph nodes. The following figures (Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14 and Figure 15) show (i) the sequence and activity diagrams of each group. These diagrams are extensions of UML for modelling HMAS defined in the ASPECS methodology [38]. (ii) The graphs obtained from the transformation of these diagrams. In these graphs, the nodes shown in red represent a graph that concerns the lower level.
• Generation of the sub-plans of each group: In this phase, the member who plays the Head holonic role in each group applies the algorithm for generating the sub-plans presented in the previous section to the graph of the latter.

  Table 1. The sub-plans of G1, G4, G5, and G7 of V₀.

  Sub-plansG1	Plan 1: H1[R1.G5, R1.A2: failed request].
  	Plan 2: H1[R1.G5], H2[R2.G4], H1[R1.A9: service terminated].
  Sub-plansG4	Plan 1: H6[R6.A13: Send transport request], H7[R7.A10: move LV1, R7.A11: stop LV1, R7.A12: get down travellers LV1].
  	Plan 2: H6[R6.A13: Send transport request], H7[R7.A10: move LV1, R7.A11: stop LV1, R7.A12: get down travellers LV1], H8[R8.A10: move LV3, R8. A11: stop LV3, R8.A12: get down travellers LV3].
  	Plan 3: H6[R6.A13: Send transport request], H7[R7.A10: move LV1, R7.A11: stop LV1, R7.A12: get down travellers LV1], H8[R8.A10: move LV3, R8. A11: stop LV3, R8.A12: get down travellers LV3],H9[R9.A10: move LV5, R9.A11: stop LV5, R9.A12: get down travellers LV5].
  	Plan 4: H6[R6.A13: Send transport request], H7[R7.A10: move LV1, R7.A11: stop LV1, R7.A12: get down travellers LV1], H9[R9.A10: move LV4, R9.A11: stop LV4, R9.A12: get down travellers LV4].
  	Plan 5: H6[R6.A13: Send transport request], H7[R7.A10: move LV1, R7.A11: stop LV1, R7.A12: get down travellers LV1], H9[R9.A10: move LV4, R9.A11: stop LV4, R9.A12: get down travellers LV4],H7[R7.A10: move LV6, R7.A11: stop LV6, R7.A12: get down travellers LV6].
  	Plan 6: H6[R6.A13: Send transport request], H7[R7.A10: move LV1, R7.A11: stop LV1, R7.A12: get down travellers LV1], H9[R9.A10: move LV4, R9.A11: stop LV4, R9.A12: get down travellers LV4], H8[R8.A10: move LV2, R8.A11: stop LV2, R8.A12: get down travellers LV2].
  	Plan 7: H6[R6.A13: Send transport request], H8[R8.A10: move LV2, R8.A11: stop LV2, R8.A12: get down travellers LV2].
  	Plan 8: H6[R6.A13: Send transport request], H8[R8.A10: move LV2, R8.A11: stop LV2, R8.A12: get down travellers LV2], H9[R9.A10: move LV7, R9.A11: stop LV7, R9.A12: get down travellers LV7].
  	Plan 9: H6[R6.A13: Send transport request], H8[R8.A10: move LV2, R8.A11: stop LV2, R8.A12: get down travellers LV2], H9[R9.A10: move LV7, R9.A11: stop LV7, R9.A12: get down travellers LV7],H8[R8.A10: move LV3, R8.A11: stop LV3, R8.A12: get down travellers LV3].
  	Plan 10: H6[R6.A13: Send transport request], H8[R8.A10: move LV2, R8.A11: stop LV2, R8.A12: get down travellers LV2], H9[R9.A10: move LV7, R9.A11: stop LV7, R9.A12: get down travellers LV7], H7[R7.A10: move LV1, R7.A11: stop LV1, R7.A12: get down travellers LV1].
  	Plan 11: H6[R6.A13: Send transport request], H9[R9.A10: move LV8, R9.A11: stop LV8, R9.A12: get down travellers LV8].
  Sub-plansG5	Plan 1: H4[R4.A3: availability], H3[R3.A2: failed service].
  	Plan 2: H4[R4.A3: availability], H3[R3.A4: validate information city], H5[R5.G7], H3[R3.A8: response request].
  Sub-plansG7	Plan 1: H11[R11.A5: determinate name city], H12[R12.A6: locate the city], H10[R10.A7: classify city].

  represents the sub-plans obtained for each group. Each sub-plan represents a sequence of actions, each of which is defined by its identifier, the role in which it is included, and the holon that plays this role.

5.2.2. Generation of Global Plans for V₀

The generation of the global plan is carried out by the member that plays the Head holonic role in the top-level group AHead_nt (the agent who plays the Head role in the top-level group n at time t). It consists of linking the sub-plans, associated with the groups, using the algorithm for generating global plans presented in the previous chapter.

Table 2. The Global Plans of V₀.

Global Plans of V0
Global Plan1: H1[R1. [H4 [R4.A3: availability], H3 [R3.A2: failed service]], H1[R1.A1: failed request].
Global Plan2: H1[R1. [H4 [R4.A3: availability], H3[R3.A4: validation information city], H5[R5. [H11[R11.A5: determinate name city], H12 [R12.A6: locate the city], H10[R10.A7: classify city]]], H3[R3.A8: response request]]], H2[R2. [H6[R6.A13: Send transport request], H7[R7.A10: move LV1, R7.A11: stop LV1, R7.A12: get down travellersLV1]]], H1[ R1.A9: service terminated].
Global Plan3: H1[R1. [H4 [R4.A3: availability], H3[R3.A4: validation information city], H5[R5.[H11[R11.A5: determinate name city], H12 [R12.A6: locate the city], H10[R10.A7: classify city]]], H3[R3.A8: response request]]], H2[R2. [H6[R6.A13: Send transport request], H7[R7.A10: move LV1, R7.A11: stop LV1, R7.A12: get down travellersLV1], H8[R8.A10: move LV3, R8.A11: stop LV3, R8.A12: get down travellersLV3]]], H1[ R1.A9: service terminated]
Global Plan4: H1[R1. [H4 [R4.A3: availability], H3[R3.A4: validation information city], H5[R5.[H11[R11.A5: determinate name city], H12 [R12.A6: locate the city], H10[R10.A7: classify city]]], H3[R3.A8: response request]]], H2[R2. [H6[R6.A13: Send transport request], H7[R7.A10: move LV1, R7.A11: stop LV1, R7.A12: get down travellersLV1], H8[R8.A10: move LV3, R8.A11:stop LV3, R8.A12: get down travellersLV3], H9[R9.A10: move LV5, R9.A11: stop LV5, R9.A12: get down travellersLV5]]], H1[R1.A9: service terminated].
Global Plan5: H1[R1. [H4 [R4.A3: availability], H3[R3.A4: validation information city], H5[R5. [H11 R11.A5: determinate name city], H12 [R12.A6: locate the city], H10 [R10.A7: classify city]]], H3[R3.A8: response request]]], H2[R2. [H6[R6.A13: Send transport request], H7[R7.A10: move LV1, R7.A11: stop LV1, R7.A12: get down travellersLV1], H9[R9.A10: move LV4, R9.A11: stop LV4, R9.A12: get down travellersLV4]]], H1[R1.A9: service terminated].
Global Plan6: H1[R1. [H4 [R4.A3: availability], H3[R3.A4: validation information city], H5[R5. [H11 [R11.A5: determinate name city], H12 [R12.A6: locate the city], H10[R10.A7: classify city]]], H3[R3.A8: response request]]], H2[R2. [H6[R6.A13: Send transport request], H7[R7.A10: move LV1, R7.A11: stop LV1, R7.A12: get down travellersLV1], H9[R9.A10: move LV4, R9.A11: stop LV4, R9.A12: get down travellersLV4], H7[R7.A10: move LV6, R7.A11: stop LV6, R7.A12: get down travellersLV6]]], H1[R1.A9: service terminated].
Global Plan7: H1[R1. [H4 [R4.A3: availability], H3[R3.A4: validation information city], H5[R5. [H11[R11.A5: determinate name city], H12 [R12.A6: locate the city], H10[R10.A7: classify city]]], H3[R3.A8: response request]]], H2[R2. [H6[R6.A13: Send transport request], H7[R7.A10: move LV1, R7.A11: stop LV1, R7.A12: get down travellersLV1], H9[R9.A10: move LV4, R9.A11: stop LV4, R9.A12: get down travellersLV4], H8[A10: move LV2, A11: stop LV2, A12: get down travellersLV2]]], H1[R1.A9: service terminated].
Global Plan8: H1[R1. [H4 [R4.A3: availability], H3[R3.A4: validation information city], H5[R5. [H11[R11.A5: determinate name city], H12 [R12.A6: locate the city], H10[R10.A7: classify city]]], H3[R3.A8: response request]]], H2[R2. [H6[R6.A13: Send transport request], H8[R8.A10: move LV2, R8.A11: stop LV2, R8.A12: get down travellersLV2]]], H1[R1.A9: service terminated].
Global Plan9: H1[R1. [H4 [R4.A3: availability], H3[R3.A4: validation information city], H5[R5. [H11[R11.A5: determinate name city], H12 [R12.A6: locate the city], H10[R10.A7: classify city]]], H3[R3.A8: response request]]], H2[R2. [H6[R6.A13: Send transport request], H8[R8.A10: move LV2, R8.A11: stop LV2, R8.A12: get down travellersLV2], H9[R9.A10: move LV7, R9.A11: stop LV7, R9.A12: get down travellersLV7]]], H1[R1.A9: service terminated].
Global Plan10: H1[R1. [H4 [R4.A3: availability], H3 [R3.A4: validation information city], H5[R5. [H11 [R11.A5: determinate name city], H12 [R12.A6: locate the city], H10[R10.A7: classify city]]], H3[R3.A8: response request]]], H2[R2. [H6[R6.A13: Send transport request], H8[R8.A10: move LV2, R8.A11: stop LV2, R8.A12: get down travellersLV2], H9[R9.A10: move LV7, R9.A11: stop LV7, R9.A12: get down travellersLV7], H8[R8.A10: move LV3, R8.A11: stop LV3, R8.A12: get down travellersLV3]]], H1[R1. A9: service terminated].
Global Plan11: H1[R1. [H4 [R4.A3: availability], H3 [R3.A4: validation information city], H5[R5. [H11 [R11.A5: determinate name city], H12 [R12.A6: locate the city], H10[R10.A7: classify city]]], H3[R3.A8: response request]]], H2[R2. [H6[R6.A13: Send transport request], H8[R8.A10: move LV2, R8.A11: stop LV2, R8.A12: get down travellersLV2], H9[R9.A10: move LV7, R9.A11: stop LV7, R9.A12: get down travellersLV7], H7[R7.A10: move LV1, R7.A11: stop LV1, R7.A12: get down travellersLV1]]], H1[R1.A9: service terminated].
Global Plan12: H1[R1. [H4 [R4.A3: availability], H3 [R3.A4: validation information city], H5[R5. [H11 [R11.A5: determinate name city], H12 [R12.A6: locate the city], H10[R10.A7: classify city]]], H3[R3.A8: response request]]], H2[R2. [H6[R6.A13: Send transport request], H9[A10: move LV8, A11: stop LV8, A12: get down travellers LV8]]], H1[R1.A9: service terminated].

represents the global plans obtained for the V₀ version of the holonic agent.

5.3. Application of Our Approach to the New V₁ Version of the Holonic Agent

The plans generated for the V₀ version are limited to solving transportation requests to local cities. In version V₁, the members of the holonic agent have been given new roles. Indeed, agent H6 of level 1 obtained the role “DT interface”, agent H7 of level 1 obtained the role “Tram”, agent H8 of level 1 obtained the role “Taxi”, agent H9 of level 1 obtained the role “Bus”, and agent H2 of level 2 obtained the role “Distance Transport”. This is expressed by the fact that the level 2 agent H2 tried to play the role “Distance Distribution” in order to be able to respond to the requests for transport to remote cities that it starts to receive. Not having the capacity to play this role, the H2 agent had to perform a dynamic capacity acquisition. It instantiated the Distance Transport organisation as a group (G8) and distributed the roles to its members H6, H7, H8 and H9 according to their capacity. The holonic structure of the system in its version (V₁) is presented in the following figure (Figure 16). In this figure, the members who have obtained new roles are coloured pink.

The acquisition of these new roles by the members of the holonic agent makes the behaviour and the global structure of the latter develop and gives it the possibility to satisfy new objectives (the possibility of solving transport requests to distant cities). This confronts the holonic agent with new planning problems Π₁ in relation to which the plans it was executing become obsolete as they are limited to solving transportation requests to local cities.

The holonic agent is therefore forced to generate new plans, in which it must integrate the new roles obtained so that it can solve the new planning problems and achieve the new objectives. To do this, the holonic agent must first generate sub-plans capable of solving the new planning subproblems associated with the groups affected by the changes. In the second step, the holonic agent must recursively link the sub-plans, according to the hierarchical and behavioural dependency, to obtain a global plan able to solve the new planning problem Π₁.

5.3.1. Generation of Sub-Plans for V₁

• Generation of the graph of each group affected by the change: the following figures (Figure 17, Figure 18, Figure 19, Figure 20, Figure 21 and Figure 22) show the sequence diagram and activity diagram of the groups involved in the change and the graph obtained from the transformation of these diagrams.
• Generation of sub-plans for each group affected by the change: the following table (

  Table 3. The sub-plans of G1 and G8 of V₁.

  Sub-plansG1	Plan 1: H1[R1. G5, R1.A2: failed request].
  	Plan 2: H1[R1.G5], H2[R2.G4], H1[R1.A9: service terminated].
  	Plan 3: H1[R1.G5], H2[R2.G8], H1[R1.A9: service terminated].
  Sub-plansG8	Plan 1: H6[R6.A13: send transport request],.H8[R8.A10:move DV1,R8.A11:stop DV1,R8.A12: get down travellers DV1].
  	Plan 2: H6[R6.A13: send transport request],H8[R8.A10:move DV1, R8.A11:stop DV1, R8.A12: get down travellers DV1], H9[R9.A10:move DV3, R9.A11:stop DV3, R9.A12: get down travellers DV3].
  	Plan 3: H6[R6.A13: send transport request],H8[R8.A10:move DV1, R8.A11:stop DV1, R8.A12: get down travellers DV1], H9[R9.A10:move DV3, R9.A11:stop DV3, R9.A12:get down travellers DV3], H7[R7.A10:move DV4, R7.A11:stop DV4, R7.A12:get down travellers DV4].
  	Plan 4: H6[R6.A13: send transport request], H9 [R9.A10:move DV2, R9.A11:stop DV2, R9.A12:get down travellers DV2].
  	Plan 5: H6[R6.A13: send transport request],H9 [R9.A10:move DV2, R9.A11:stop DV2, R9.A12:get down travellers DV2], H8[R8.A10:move DV1, R8.A11:stop DV1, R8.A12:get down travellers DV1].
  	Plan 6: H6[R6.A13: send transport request],H9 [R9.A10:move DV2, R9.A11:stop DV2, R9.A12:get down travellers DV2], H8[R8.A10:move DV1, R8.A11:stop DV1, R8.A12:get down travellers DV1], H7[R7.A10:move DV5, R7.A11:stop DV5, R7.A12:get down travellers DV5].

  ) represents the sub-plans obtained for the groups affected by the changes (G1 and G8).

5.3.2. Generation of Global Plans for V₁

The following table (

Table 4. The global plans of V₁.

Global Plans of V1
Global Plan13: H1[R1. [H4 [R4.A3: availability], H3[R3.A4: validation information city], H5[R5. [H11[R11.A5: determinate name city], H12[R12.A6: locate the city], H10 [R10.A7: classify city]]], H3[A8: response request]]], H2[R2. [H6 [R6.A13: send transport request], H8[R8.A10: move DV1, R8.A11: stop DV1, R8.A12: get down travellersDV1]]], H1[R1.A9: service terminated].
Global Plan14: H1[R1. [H4 [R4.A3: availability], H3[R3.A4: validation information city], H5[R5. [H11[R11.A5: determinate name city], H12[R12.A6: locate the city], H10[R10.A7: classify city]]], H3[A8: response request]]], H2[R2. [H6 [R6.A13: send transport request], H8[R8.A10: move DV1, R8.A11: stop DV1, R8.A12: get down travellersDV1], H9[R9.A10: move DV3, A11: stop DV3, A12: get down travellersDV3]]], H1[ R1.A9: service terminated].
Global Plan15: H1[R1. [H4 [R4.A3: availability], H3[R3.A4: validation information city], H5[R5. [H11[R11.A5: determinate name city], H12[R12.A6: locate the city], H10[R10.A7: classify city]]], H3[A8: response request]]], H2[R2. [H6 [R6.A13: send transport request], H8[R8.A10: move DV1, R8.A11: stop DV1, R8.A12: get down travellersDV1], H9[R9.A10: move DV3, A11: stop DV3, A12: get down travellersDV3], H7[R7.A10: move DV4, R7.A11: stop DV4, R7.A12: get down travellersDV4]]], H1[R1.A9: service terminated].
Global Plan16: H1[R1. [H4 [R4.A3: availability], H3[R3.A4: validation information city], H5[R5. [H11[R11.A5: determinate name city], H12[R12.A6: locate the city], H10[R10.A7: classify city]]], H3[A8: response request]]], H2[R2. [H6 [R6.A13: send transport request], H9[R9.A10: move DV2, R9.A11: stop DV2, R9.A12: get down travellersDV2]]], H1[R1.A9: service terminated].
Global Plan17: H1[R1. [H4 [R4.A3: availability], H3[R3.A4: validation information city], H5[R5.[H11[R11.A5: determinate name city], H12[R12.A6: locate the city], H10[R10.A7: classify city][], H3[A8: response request]]], H2[[R2.H6 [R6.A13: send transport request], H9[R9.A10: move DV2, R9.A11: stop DV2, R9.A12: get down travellersDV2], H8[R8.A10: move DV1, R8.A11: stop DV1, R8.A12: get down travellersDV1]]], H1[R1.A9: service terminated].
Global Plan18: H1[R1. [H4 [R4.A3: availability], H3[R3.A4: validation information city], H5[R5. [H11[R11.A5: determinate name city], H12 [R12.A6: locate the city], H10[R10.A7: classify city]]], H3[A8: response request]]], H2[R2. [H6 [R6.A13: send transport request], H9[R9.A10: move DV2, R9.A11: stop DV2, R9.A12: get down travellersDV2], H8[R8.A10: move DV1, R8.A11: stop DV1, R8.A12: get down travellersDV1], H7[A10: move DV5, A11: stop DV5, A12: get down travellersDV5]]], H1[R1.A9: service terminated].

) shows the new global plans obtained for the V1 version of the holonic agent.

5.4. Developed Tool

The results shown in the previous sections are automatically obtained using a software tool that we have developed on the SARL platform (SARL agent programming language and framework: http://www.sarl.io, accessed on 25 March 2022) [47]. The following figures (Figure 23 and Figure 24) show, respectively, the generated sub-plans for the groups of version V₀ and the generated global plans after having linked the sub-plans. In Figure 23, the groups represented in red are those that have completed the generation of their sub-plans.

Figure 25 and Figure 26 show the execution of a global plan chosen by the holonic agent to solve a given query. Here, the traceability of the execution shows that the holonic agent has followed exactly the chosen plan it generated. In Figure 25 and Figure 26 the red point is used to check traceability.

The following figure (Figure 27) shows the sub-plans for the groups in version V₁ affected by the changes (G1 and G8), as well as the global plans for this version. In these figures, the groups shown in yellow represent the groups that have finished generating their sub-plans.

Figure 28 and Figure 29 represent the execution of a global plan by the holonic agent to resolve a given query. Like in version V₀, the traceability of the execution shows that the holonic agent has followed exactly the chosen plan that it generated. In Figure 28 and Figure 29 the yellow point is used to check traceability.

5.5. Discussion and Limitations

Applying our approach to the chosen case study allowed us to illustrate the need for recursively and dynamically generating plans. In fact, using this example has also allowed us to demonstrate the benefits of our approach, including the following:

• The dynamic generation of plans for each newly developed version Vt of the holonic agent allows the implication of the new behaviours (acquired following the acquisition of new roles, new capacities, and the introduction of new interactions between the members of the holonic agent) in the new plans of the holonic agent. This allows it to solve the new planning problem Π_t associated with its new version Vt for which the plans of the present version have become obsolete. As a result, the method may be very useful for open and complex multi-agent systems.
• The technique adopted for the generation of the plans, which consists of generating sub-plans for each group of the holonic agent and linking them to obtain the global plan, makes it possible to (i) simplify the planning problem following its decomposition into subproblems and (ii) minimise the generation time of the global plans following the possibility of generating the sub-plans in parallel. Consequently, the size of the system does not affect the calculation of the time required to generate the plans.
• The use of the sequence and activity diagrams of each group for the generation of its sub-plans has made it possible (i) to automate the generation of these sub-plans and consequently the generation of the global plan. As a result, the method can be easily adapted for multi-agent software that uses models in the analysis and design phases. (ii) To generate all possible sub-plans for each sub-objective (and consequently the generation of all possible global plans), giving the holonic agent the possibility to choose the most suitable plan with its constraints and conditions when executing the plans. (iii) To introduce, for each version of the holonic agent, a strong link between the real behaviour of each group (presented by the group’s sub-plans) and its behavioural model (presented by the group’s sequence and activity diagrams). This indirectly ensures an emergence control of the global behaviour of each version of the holonic agent.

As for limitations, our approach is very sensitive to the accuracy and reliability of the behavioural models of the groups that make up the holonic agent. Indeed, a simple modelling error in the sequence or activity diagram of a given group affects the reliability of all the global plans in which its sub-plans are involved. In addition, our approach is hampered by the difficulty of detecting any changes in the environment that may need to change the goals of the HMAS and the associated plans. More specifically, the question is as follows: is it relevant to link each holonic agent (at any level of the holarchy) to the environment, and if so, how? If all the holonic agents are not linked to the environment, it means that the goal and plan changes must be triggered by the super-holonic agents only. This top-down approach may cause problems related to the support of emergent phenomena that are usually studied in adaptive multi-agent systems [48].

6. Conclusions

MAP has enriched the field of task planning by exploiting the advantages of the multi-agent paradigm. Indeed, it has made it possible to go beyond the use of classical representation languages, and it has also greatly expanded the field of automated planning methods. Although the approaches proposed for MAP have provided important answers to various problems related to distributed planning, they do not consider the specificities of holonic multi-agent systems (HMAS). Indeed, these approaches are mainly designed for agents that are defined as atomic entities, whereas holonic agents are defined as agents composed of agents. This leaves several unresolved problems in HMAS planning that are related, on the one hand, to the hierarchical nature of the holonic agent, whose global objective, for which we want to generate plans, is decomposed hierarchically and recursively into a set of sub-objectives associated with the groups of the holonic agent in its different levels. On the other hand, the unpredictable evolution of the behaviour of the holonic agent, with its ability to dynamically obtain new roles in order to satisfy new objectives and to adapt to changes in the environment, presents it with new planning problems in relation to which the plans it was executing become obsolete.

In this work, we have presented a new, distributed, dynamic, and recursive planning approach able to take into account the specificities of the holonic agent. It consists of dynamically generating, for each new version developed of the holonic agent (introduced following the obtaining of new roles by the members of the holonic agent in order to wait for new objectives and to adapt with the change of the environment), the set of action plans to be executed by the members of the holonic agent in order to solve the planning problem associated with the latter and to allow it to reach its objectives. The generation of plans for each developed version of the holonic agent is based on the behaviours it has at the time of development. For the generation of these plans, the approach starts, in the first step, with the generation of sub-plans capable of solving the planning subproblems associated with the groups of the holonic agent in its different levels. In the second step, the approach recursively links the sub-plans according to the hierarchical and behavioural dependency to obtain a global plan.

The proposed approach, supported by the tool we have developed, has been validated in a specific case study: “Transport planning system”. In the short and medium term, we plan to (i) integrate our approach into the internal architecture of the holonic agent to support the planning process in the latter, (ii) validate the scalability of the proposed approach on a real, large-scale application, and (iii) make a systematic comparison with other planning approaches for complex systems.