Li-Ion Battery Immersed Heat Pipe Cooling Technology for Electric Vehicles
Abstract
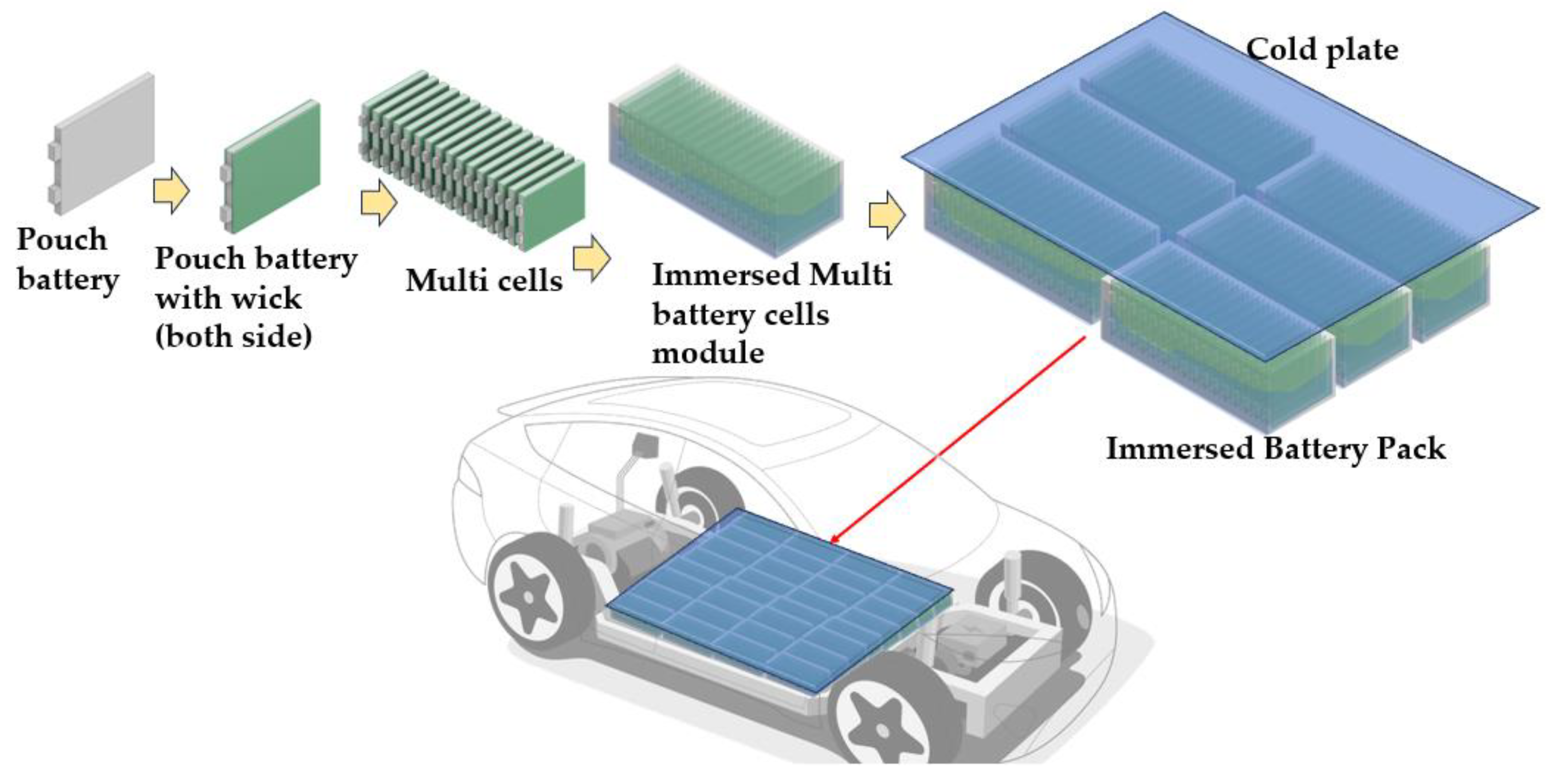
:1. Introduction
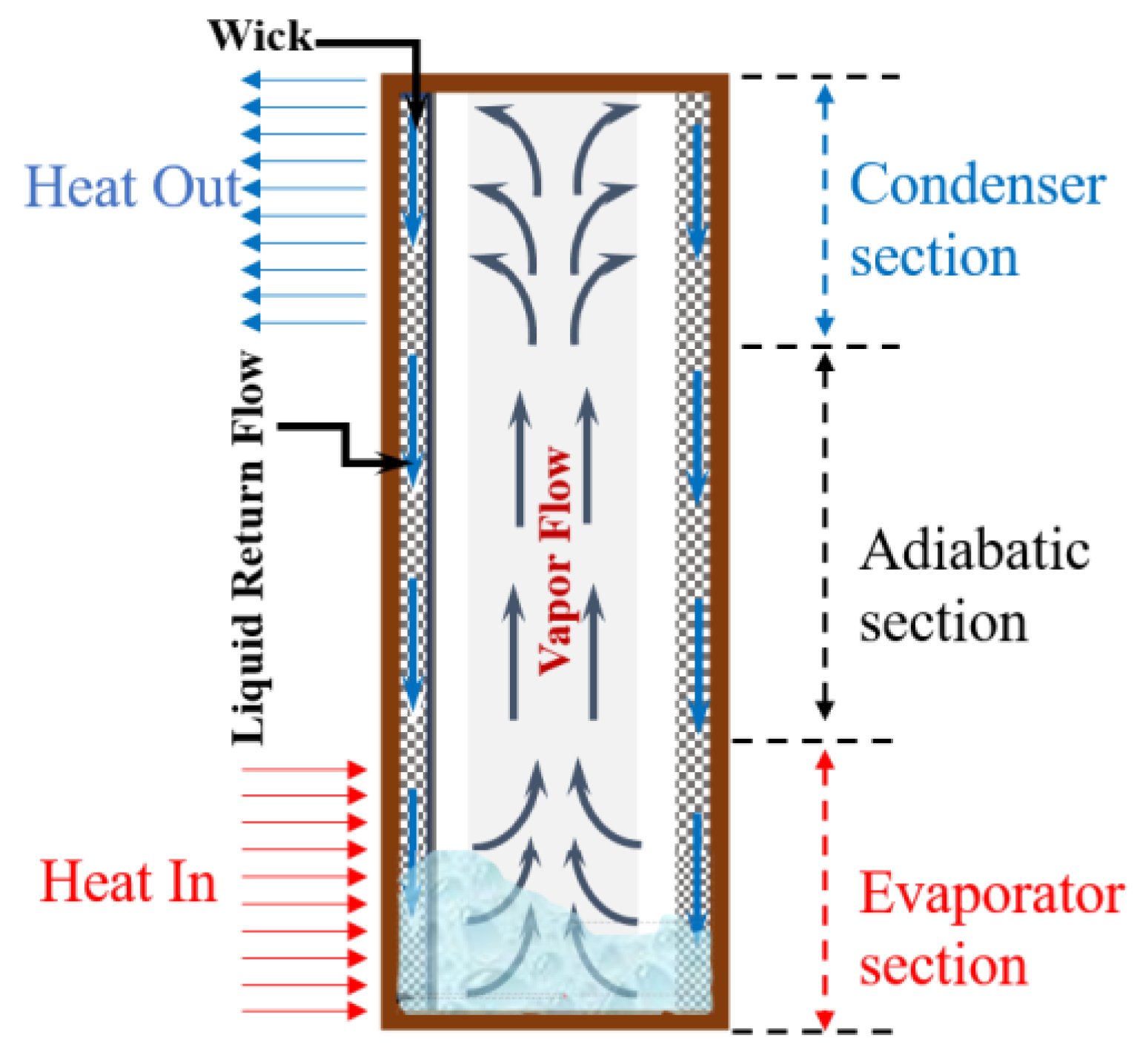
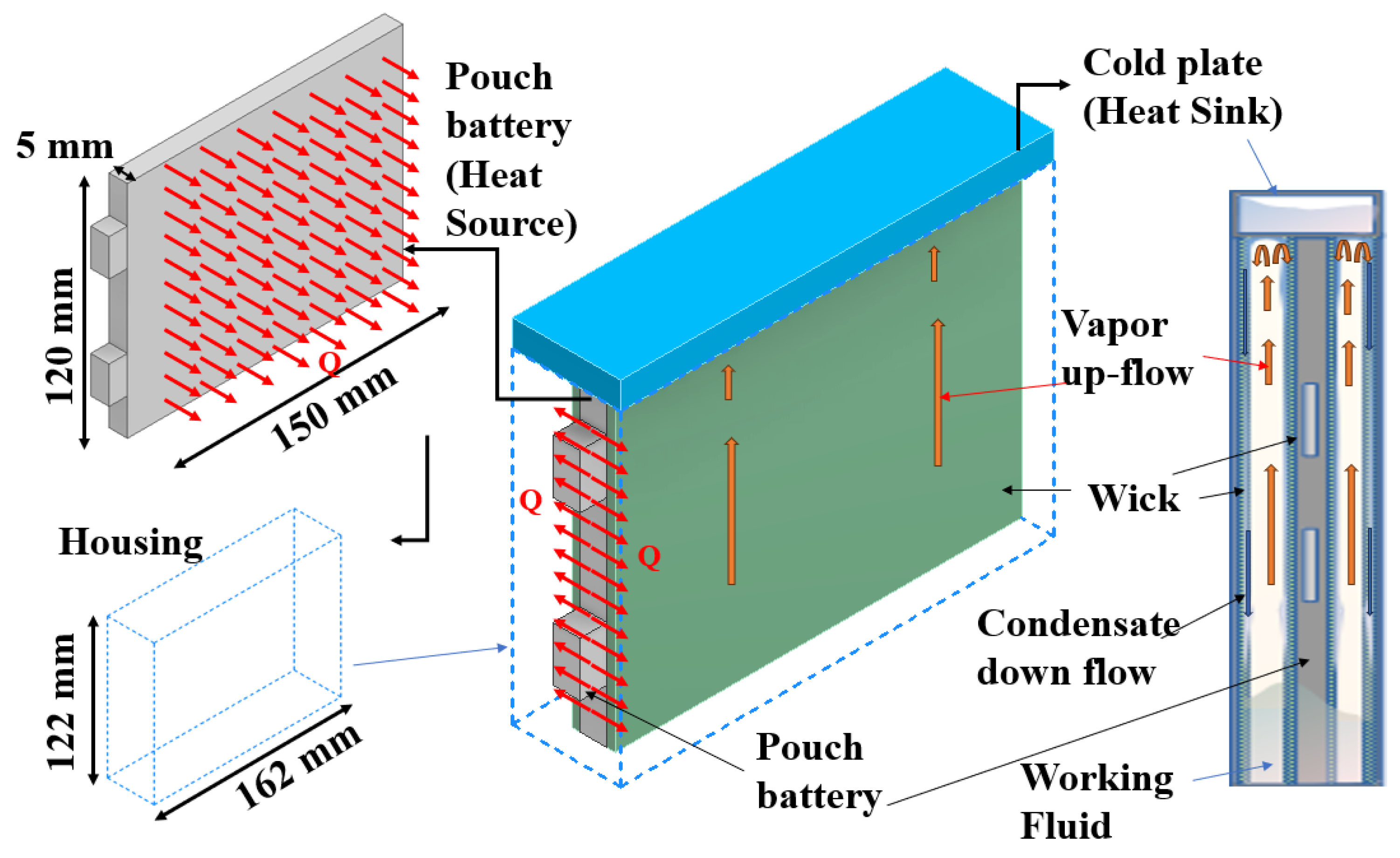
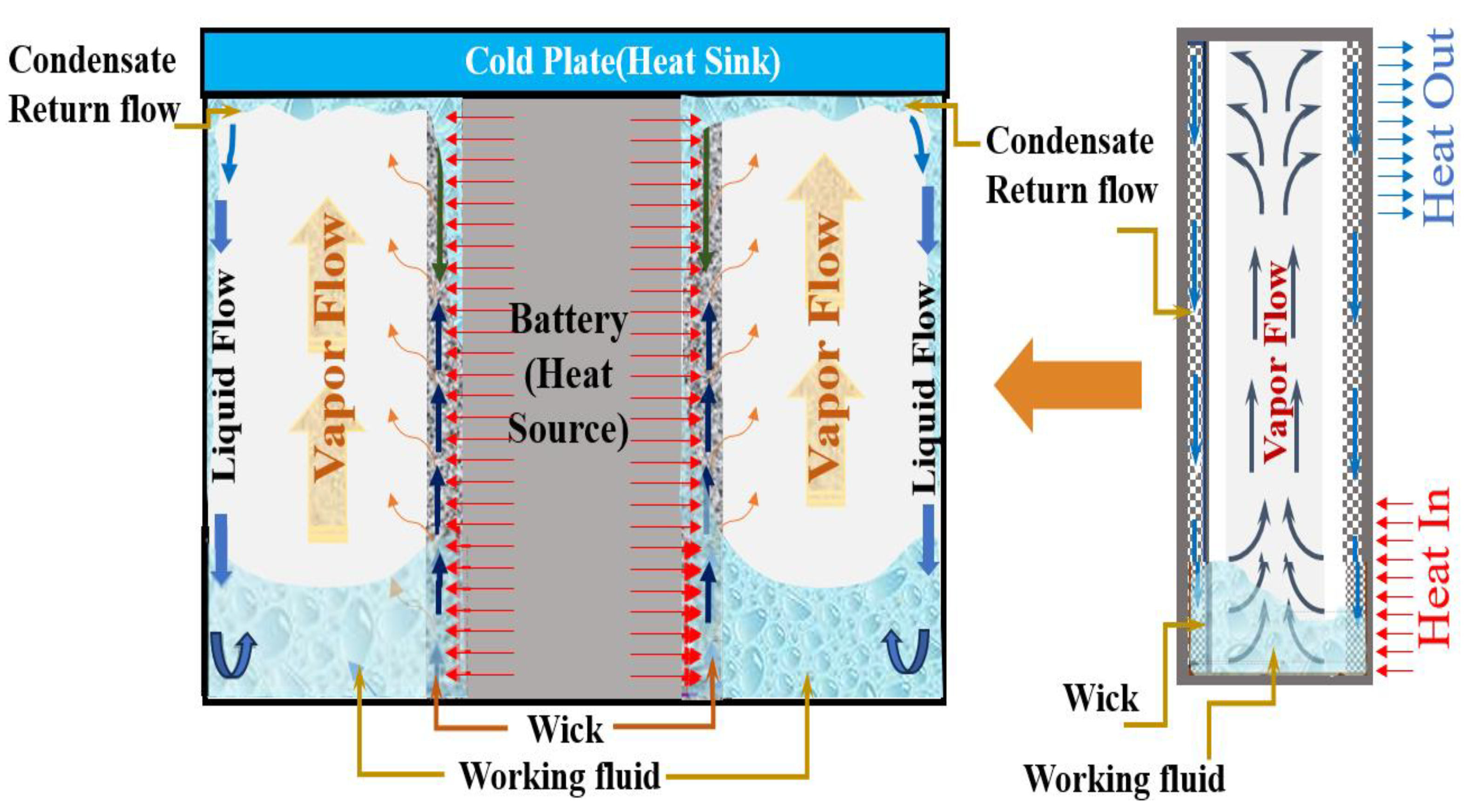
2. Description of the Research Model and Theoretical Background
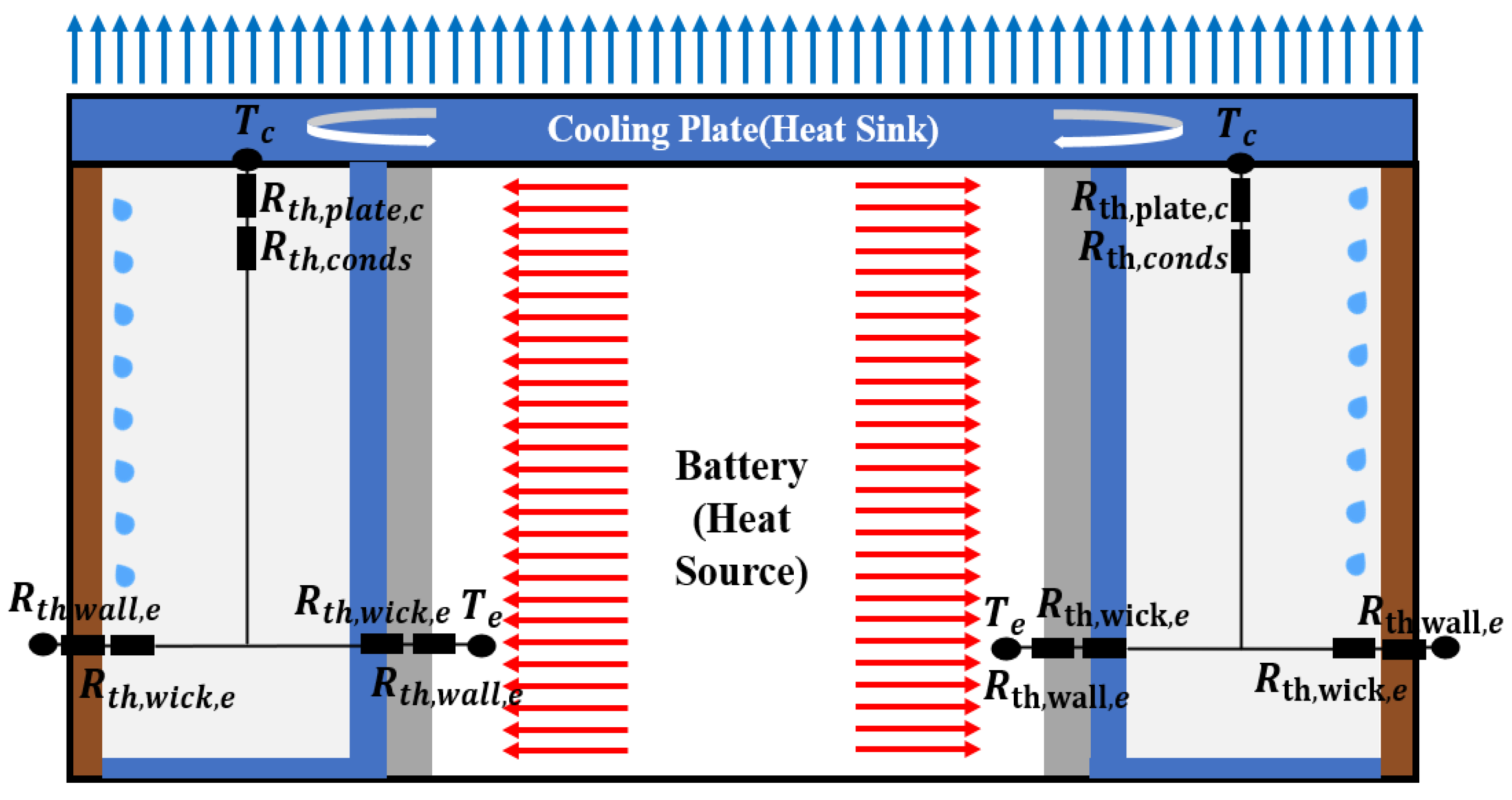
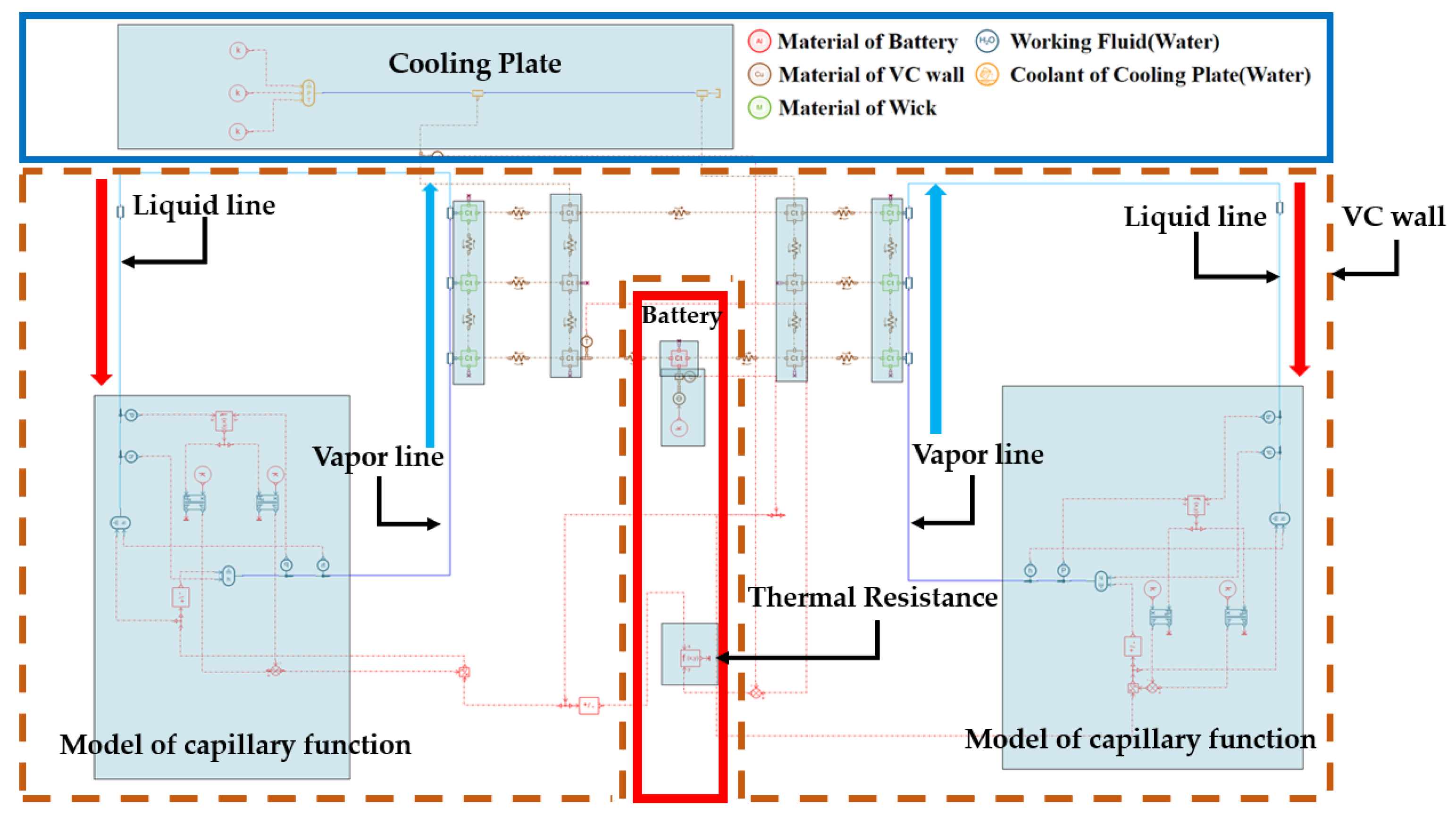
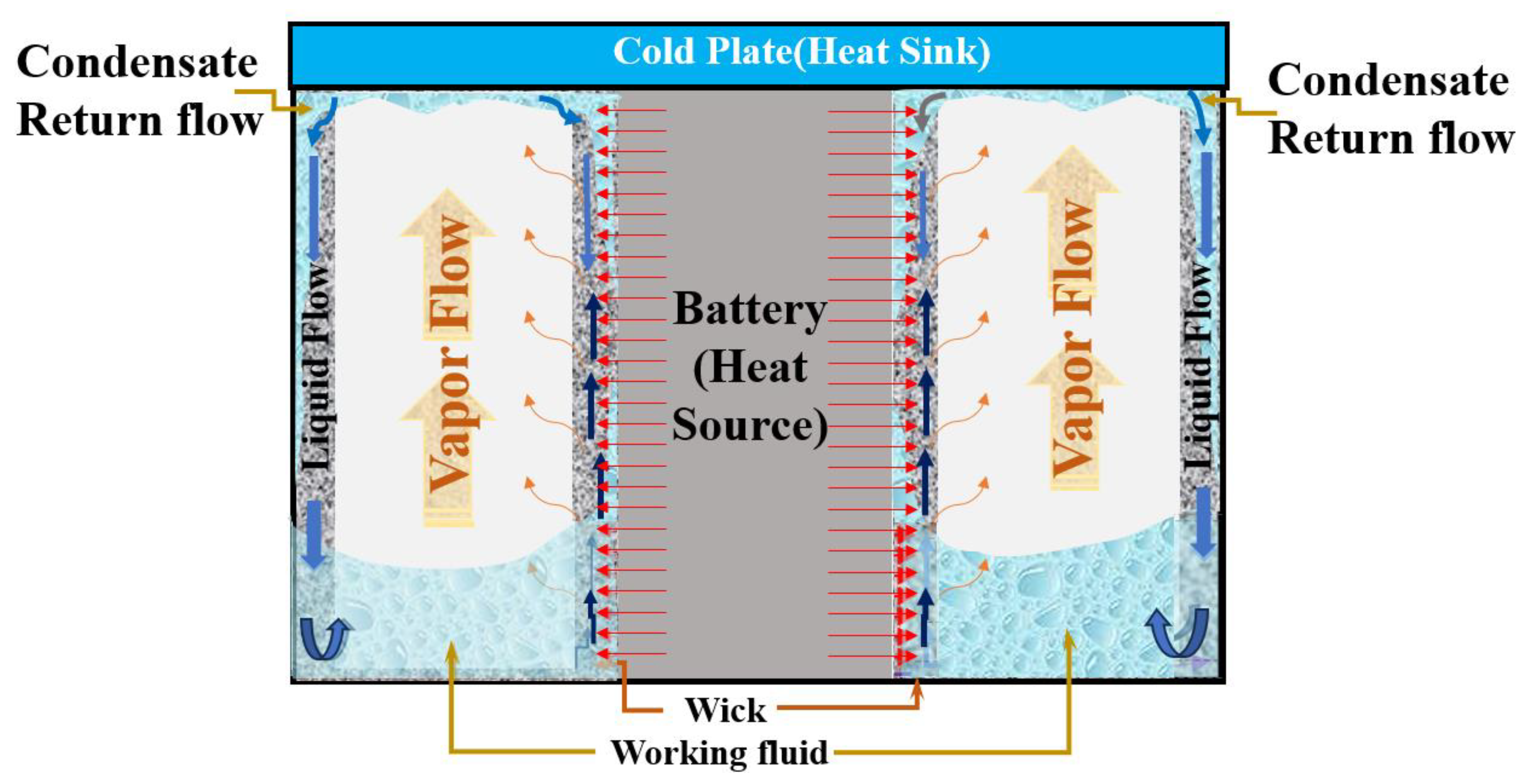
2.1. Description of the Modeling
2.2. Initial and Boundary Conditions of the Modeling
2.3. Theoretical Background of the Modeling
- Complete Wick Immersion: We assumed full immersion of the wick structure within the working medium, ensuring that every part of the wick made contact with the fluid.
- Darcy’s Flow: We classified the flow within the wick as Darcy’s flow, simplifying the modeling process by applying well-established fluid flow principles.
- Effective Thermal Conductivity: Given that the flow in the wick is characterized as Darcy’s flow and is fully immersed, we applied the concept of effective thermal conductivity to the wick structure to account for heat transfer more accurately.
- Post-Condensation Liquid Film: After the condensation process, we considered the formation of a liquid film exclusively along the inner wall of the system and the wick.
2.3.1. Effective Thermal Conductivity Model
2.3.2. Thermal Resistance Network
2.3.3. Porosity, Filling Ratio, Liquid Flim Thickness, Vaporcore Thickness
2.3.4. Merit Number
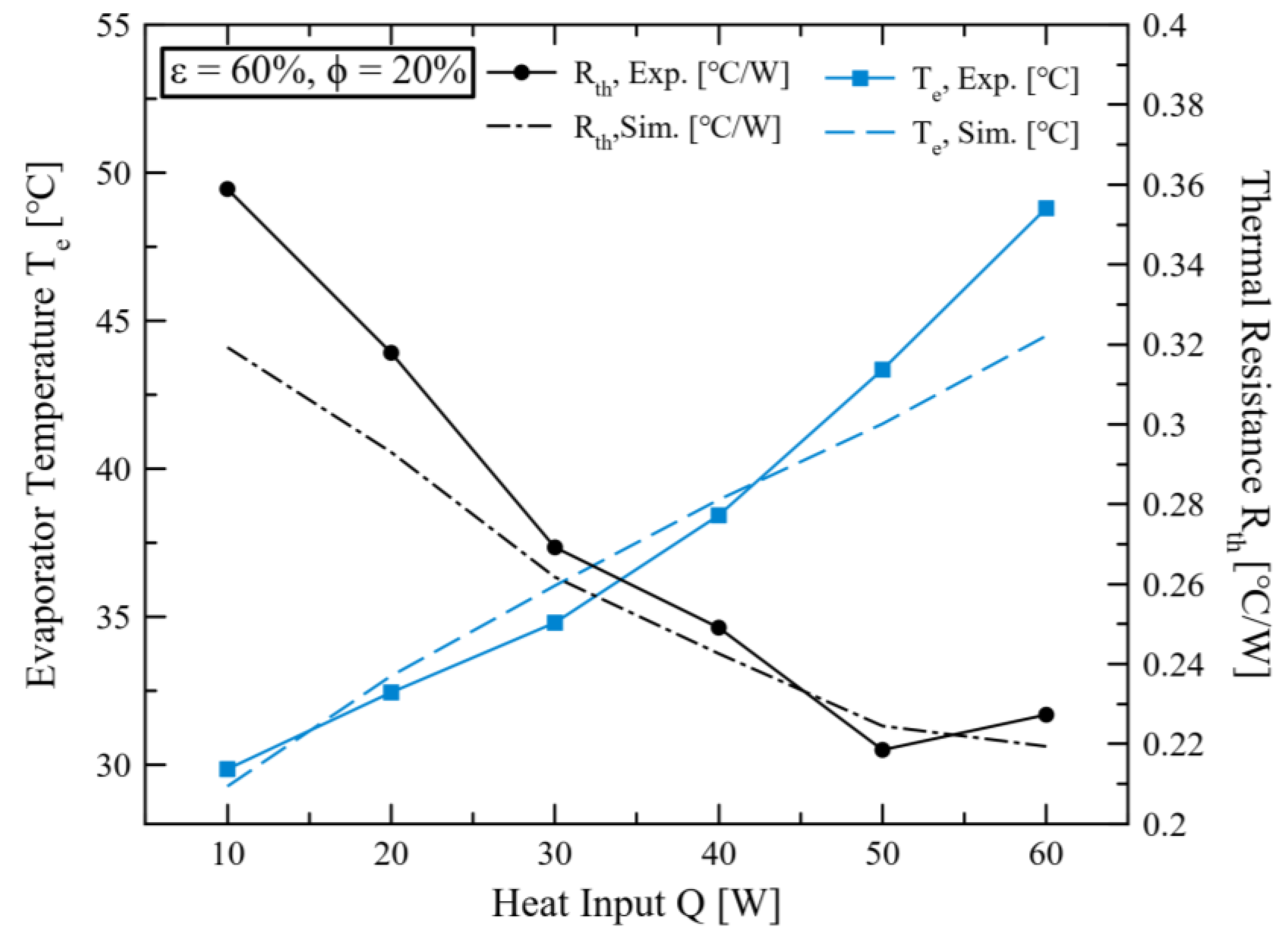
2.4. Validation Modeling in This Study
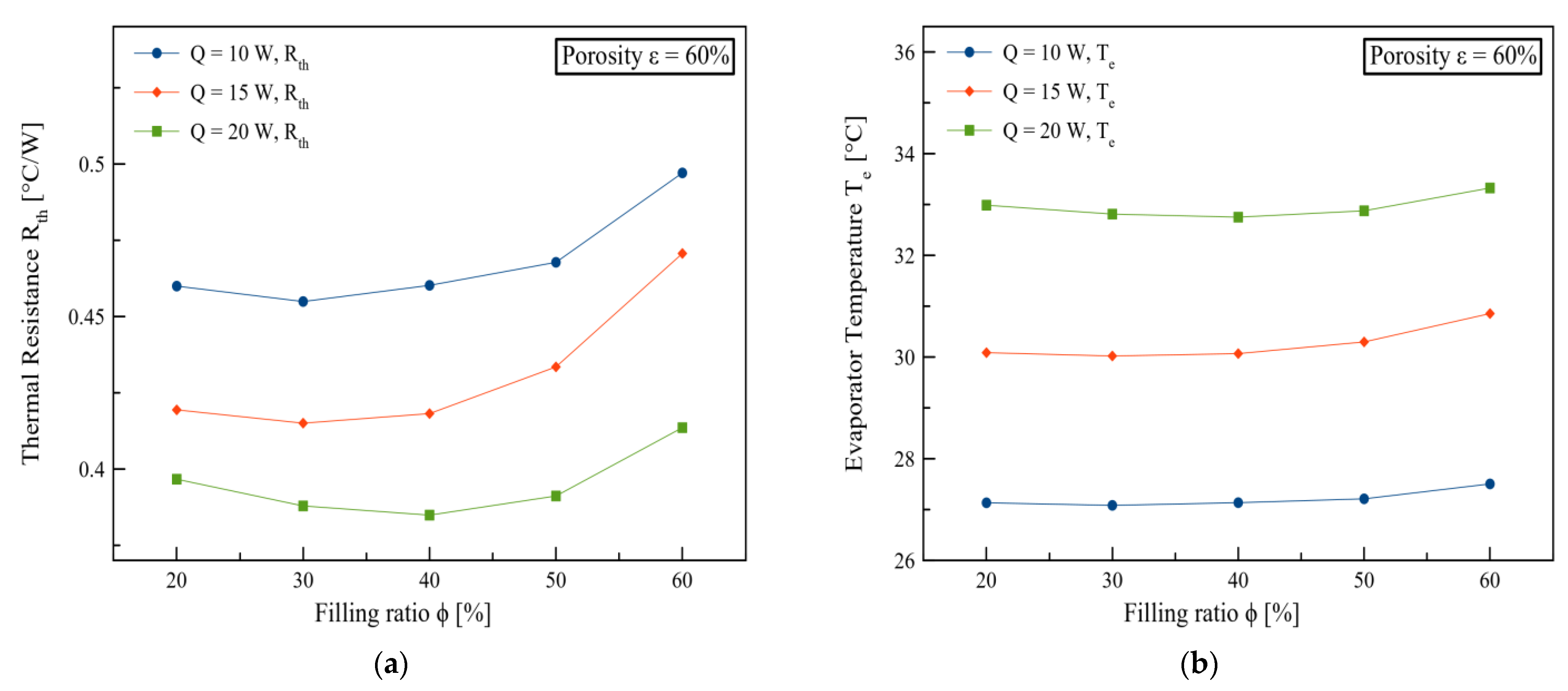
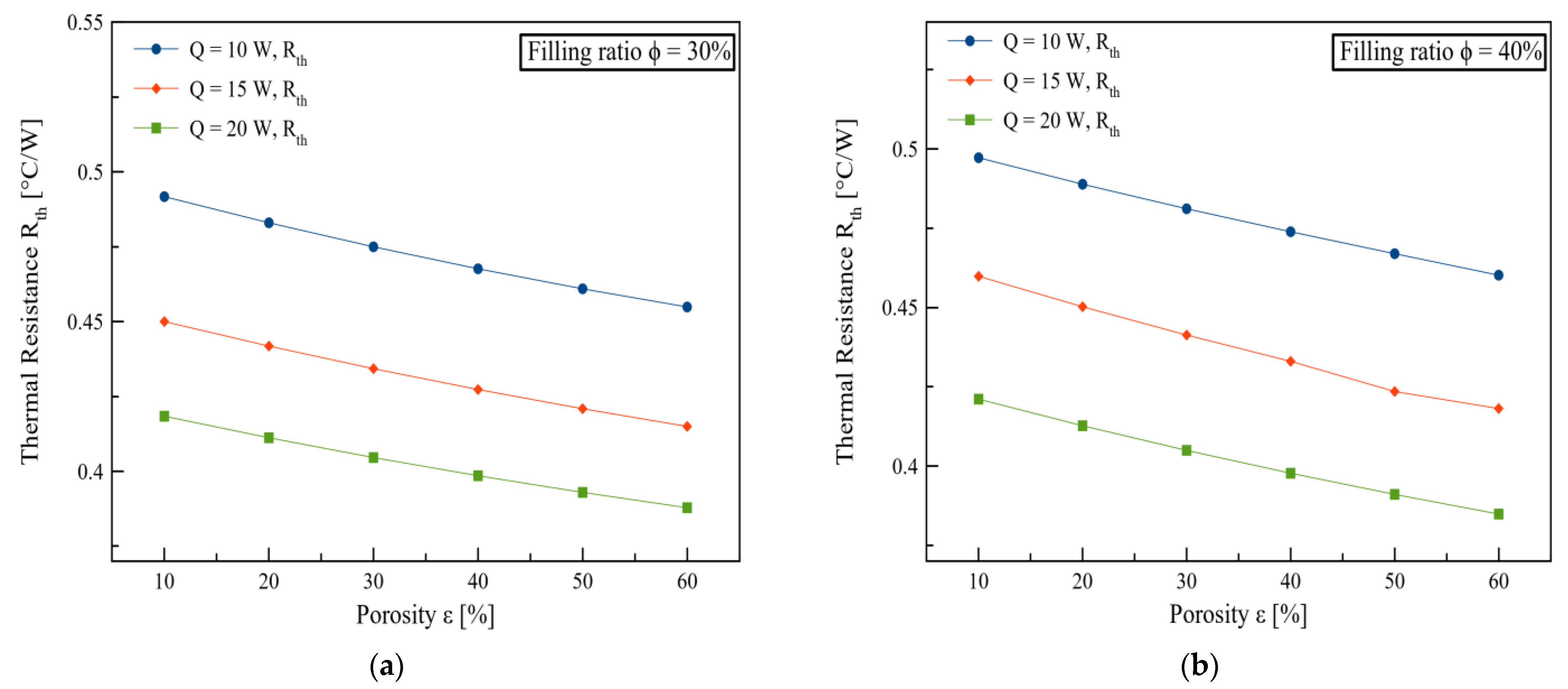
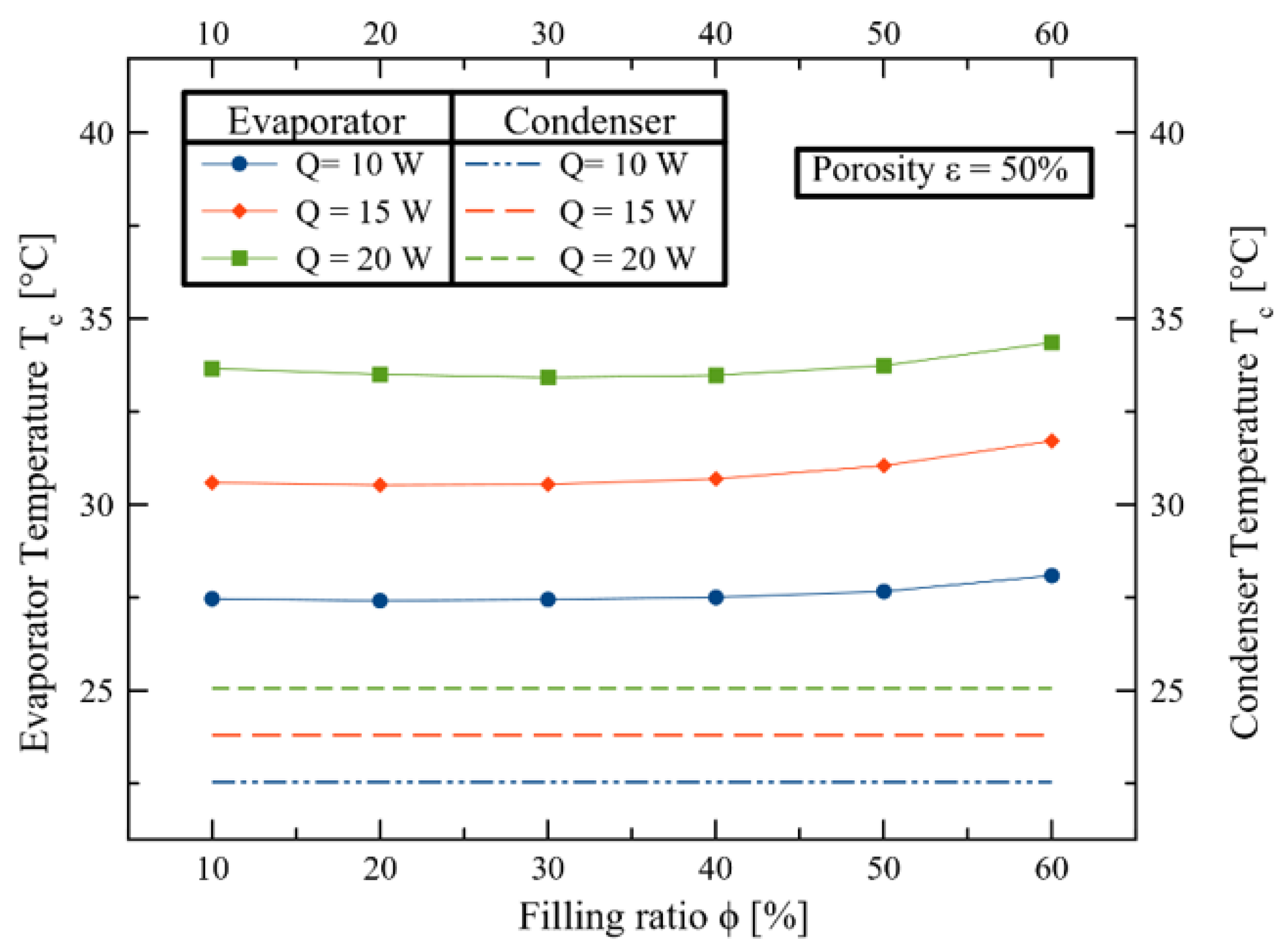
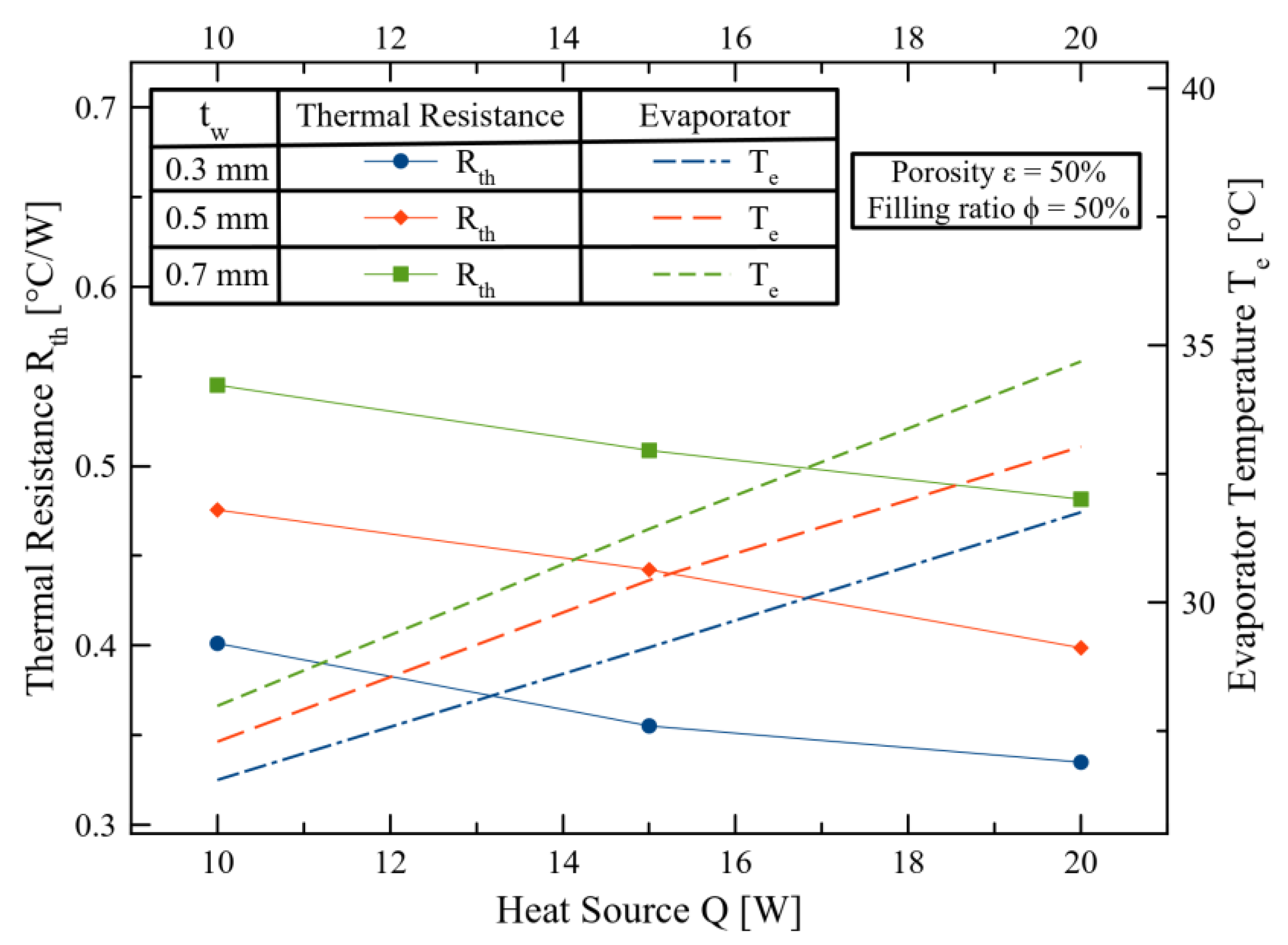
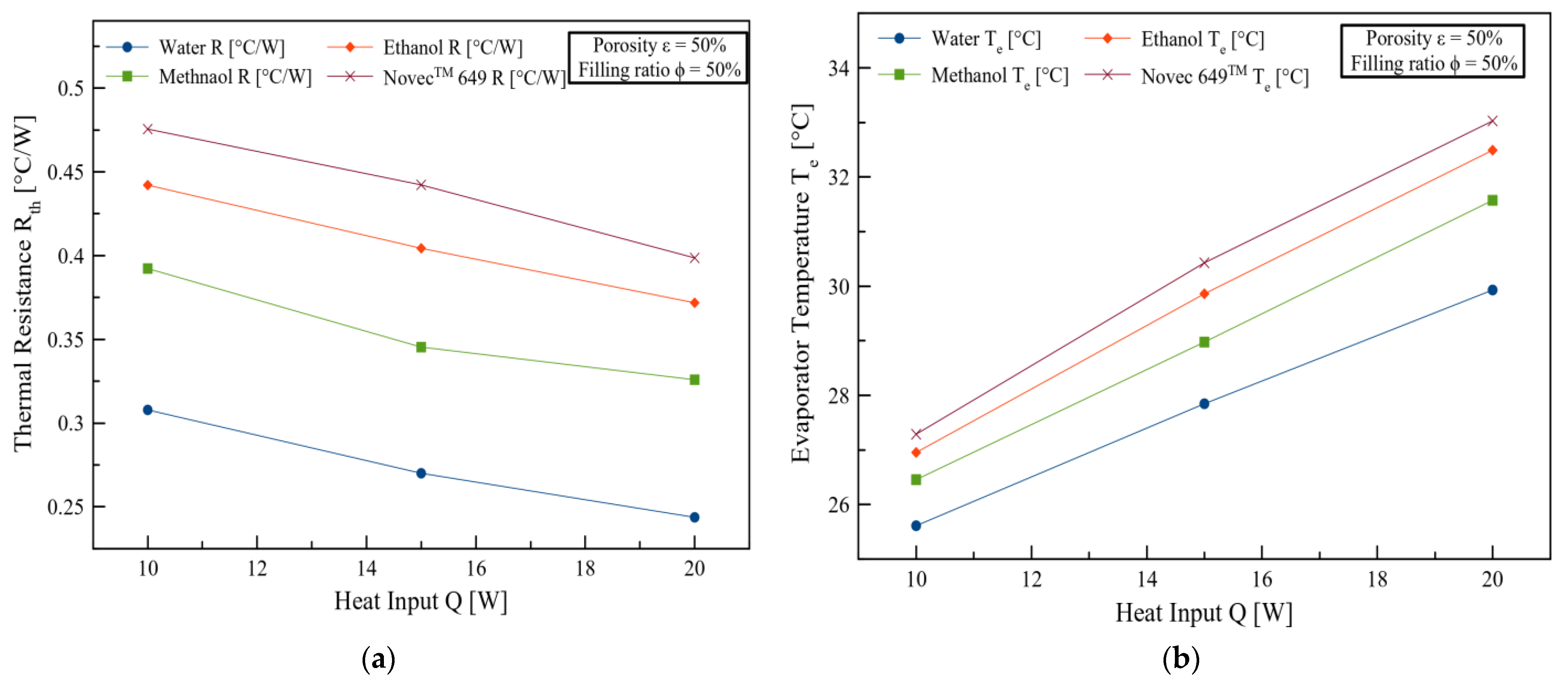
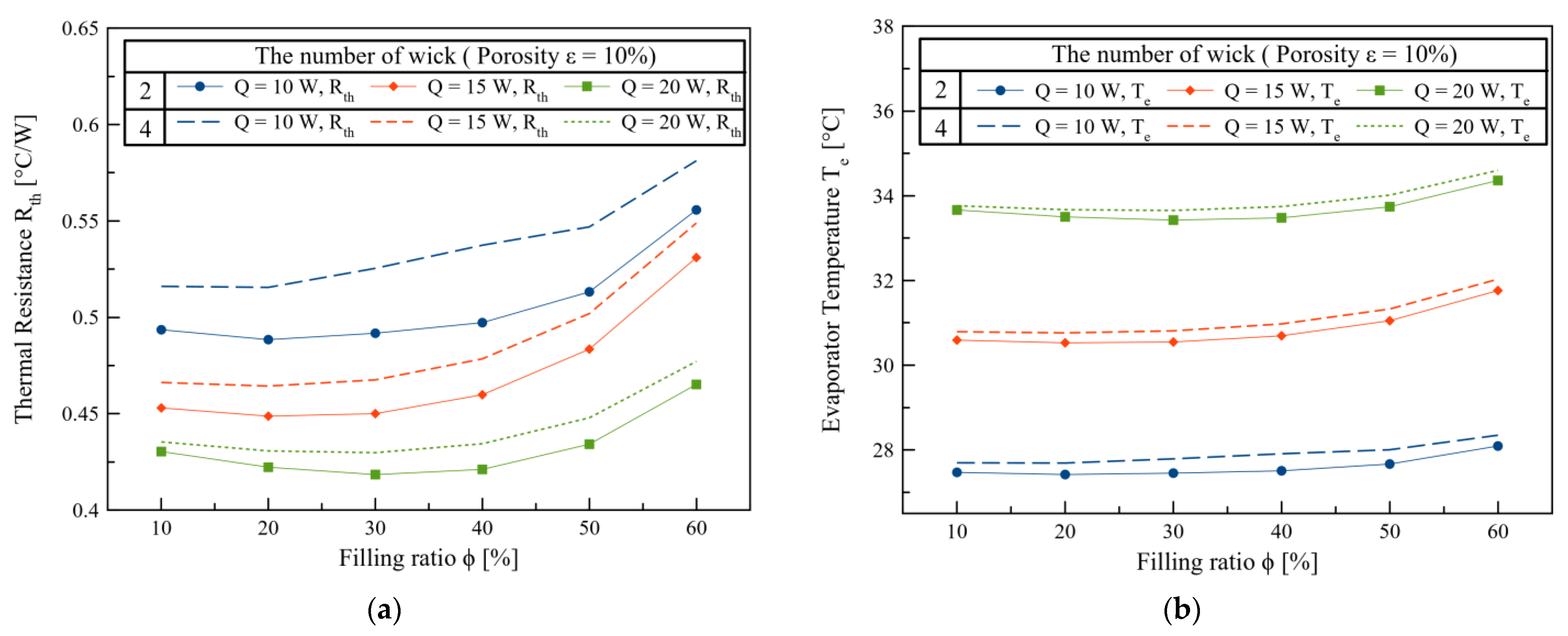
3. Results and Discussions
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| A | |
| Hydraulic diameter, m | |
| f | Fiction coefficient |
| F | Correction factor |
| Gr | Grashof number, dimensionless |
| H | |
| h | Height, m |
| Lc | Characteristic length, m |
| l | Length, m |
| Total mass of the working fluid, kg | |
| Nu | Nusselt number, dimensionless |
| Pr | Prandtl number, dimensionless |
| Q | Heat transfer rate, W |
| Re | Reynolds number, dimensionless |
| t | Thickness, m |
| T | |
| V | |
| w | Liquid film thickness + Vapor core thickness, m |
| x | Quality |
| Greek | |
| Porosity, dimensionless | |
| Subscripts | |
| all | Total |
| c | Condenser, |
| cr | critical |
| cv | Convective |
| e | Evaporator |
| Effectiveness | |
| f | Fluid |
| l | Liquid |
| LO | Liquid only |
| NcB | Nucleate Boiling |
| plate | Cooling plate |
| TP | Two-phase flow |
| red | Reducing |
| v | Vapor |
| w | Wick |
| wall | Battery wall |
| surface | Surface |
| Surrounding air |
References
- Etacheri, V.; Marom, R.; Elazari, R.; Salitra, G.; Aurbach, D. Challenges in the Development of Advanced Li-Ion Batteries: A Review. Energy Environ. Sci. 2011, 4, 3243. [Google Scholar] [CrossRef]
- Xie, F.; Xu, J.; Liao, Q.; Zhang, Q.; Liu, B.; Shao, L.; Cai, J.; Shi, X.; Sun, Z.; Wong, C. Progress in niobium-based oxides as anode for fast-charging Li-ion batteries. Energy Rev. 2023, 2, 100027. [Google Scholar] [CrossRef]
- Shah, K.; Chalise, D.; Jain, A. Experimental and Theoretical Analysis of a Method to Predict Thermal Runaway in Li-Ion Cells. J. Power Sources 2016, 330, 167–174. [Google Scholar] [CrossRef]
- Wang, Q.; Ping, P.; Zhao, X.; Chu, G.; Sun, J.; Chen, C. Thermal Runaway Caused Fire and Explosion of Lithium Ion Battery. J. Power Sources 2012, 208, 210–224. [Google Scholar] [CrossRef]
- Lisbona, D.; Snee, T. A Review of Hazards Associated with Primary Lithium and Lithium-Ion Batteries. Process Saf. Environ. Prot. 2011, 89, 434–442. [Google Scholar] [CrossRef]
- Ling, Z.; Zhang, Z.; Shi, G.; Fang, X.; Wang, L.; Gao, X.; Fang, Y.; Xu, T.; Wang, S.; Liu, X. Review on Thermal Management Systems Using Phase Change Materials for Electronic Components, Li-Ion Batteries and Photovoltaic Modules. Renew. Sustain. Energy Rev. 2014, 31, 427–438. [Google Scholar] [CrossRef]
- Xie, Y.; He, X.; Hu, X.; Li, W.; Zhang, Y.; Liu, B.; Sun, Y. An Improved Resistance-Based Thermal Model for a Pouch Lithium-Ion Battery Considering Heat Generation of Posts. Appl. Therm. Eng. 2020, 164, 114455. [Google Scholar] [CrossRef]
- Li, Y.; Chen, M.; Bai, F.; Song, W.; Feng, Z. Thermal Equilibrium Characteristic of Large-Size Lithium-Ion Pouch Battery: Resting Time between Charge and Discharge. Energy Procedia 2019, 158, 2623–2630. [Google Scholar] [CrossRef]
- Pesaran, A. Battery Thermal Management in EVs and HEVs: Issues and Solutions. Battery Man 2001, 43, 34–49. [Google Scholar]
- Khan, M.R.; Swierczynski, M.J.; Kær, S.K. Towards an Ultimate Battery Thermal Management System: A Review. Batteries 2017, 3, 9. [Google Scholar] [CrossRef]
- Kim, J.; Oh, J.; Lee, H. Review on Battery Thermal Management System for Electric Vehicles. Appl. Therm. Eng. 2019, 149, 192–212. [Google Scholar] [CrossRef]
- Zhao, G.; Wang, X.; Negnevitsky, M.; Zhang, H. A Review of Air-Cooling Battery Thermal Management Systems for Electric and Hybrid Electric Vehicles. J. Power Sources 2021, 501, 230001. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, Y.; Zhang, J.; Liu, Z. Shortcut Computation for the Thermal Management of a Large Air-Cooled Battery Pack. Appl. Therm. Eng. 2014, 66, 445–452. [Google Scholar] [CrossRef]
- Chen, K.; Wu, W.; Yuan, F.; Chen, L.; Wang, S. Cooling Efficiency Improvement of Air-Cooled Battery Thermal Management System through Designing the Flow Pattern. Energy 2019, 167, 781–790. [Google Scholar] [CrossRef]
- Kim, G.-H.; Pesaran, A. Battery Thermal Management Design Modeling. World Electr. Veh. J. 2007, 1, 126–133. [Google Scholar] [CrossRef]
- Xu, X.M.; He, R. Research on the Heat Dissipation Performance of Battery Pack Based on Forced Air Cooling. J. Power Sources 2013, 240, 33–41. [Google Scholar] [CrossRef]
- Sun, H.; Dixon, R. Development of Cooling Strategy for an Air Cooled Lithium-Ion Battery Pack. J. Power Sources 2014, 272, 404–414. [Google Scholar] [CrossRef]
- Na, X.; Kang, H.; Wang, T.; Wang, Y. Reverse Layered Air Flow for Li-Ion Battery Thermal Management. Appl. Therm. Eng. 2018, 143, 257–262. [Google Scholar] [CrossRef]
- Lu, Z.; Meng, X.Z.; Wei, L.C.; Hu, W.Y.; Zhang, L.Y.; Jin, L.W. Thermal Management of Densely-Packed EV Battery with Forced Air Cooling Strategies. Energy Procedia 2016, 88, 682–688. [Google Scholar] [CrossRef]
- Egab, K.; Oudah, S.K. Thermal Management Analysis of Li-Ion Battery-Based on Cooling System Using Dimples with Air Fins and Perforated Fins. Int. J. Therm. Sci. 2022, 171, 107200. [Google Scholar] [CrossRef]
- Shahjalal, M.; Shams, T.; Islam, M.E.; Alam, W.; Modak, M.; Hossain, S.B.; Ramadesigan, V.; Ahmed, M.R.; Ahmed, H.; Iqbal, A. A Review of Thermal Management for Li-Ion Batteries: Prospects, Challenges, and Issues. J. Energy Storage 2021, 39, 102518. [Google Scholar] [CrossRef]
- An, Z.; Shah, K.; Jia, L.; Ma, Y. A Parametric Study for Optimization of Minichannel Based Battery Thermal Management System. Appl. Therm. Eng. 2019, 154, 593–601. [Google Scholar] [CrossRef]
- Wu, W.; Wang, S.; Wu, W.; Chen, K.; Hong, S.; Lai, Y. A Critical Review of Battery Thermal Performance and Liquid Based Battery Thermal Management. Energy Convers. Manag. 2019, 182, 262–281. [Google Scholar] [CrossRef]
- Lu, M.; Zhang, X.; Ji, J.; Xu, X.; Zhang, Y. Research Progress on Power Battery Cooling Technology for Electric Vehicles. J. Energy Storage 2020, 27, 101155. [Google Scholar] [CrossRef]
- Saw, L.H.; Tay, A.A.O.; Zhang, L.W. Thermal Management of Lithium-Ion Battery Pack with Liquid Cooling. In Proceedings of the 2015 31st Thermal Measurement, Modeling & Management Symposium (SEMI-THERM), San Jose, CA, USA, 15–19 March 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 298–302. [Google Scholar]
- Shang, Z.; Qi, H.; Liu, X.; Ouyang, C.; Wang, Y. Structural Optimization of Lithium-Ion Battery for Improving Thermal Performance Based on a Liquid Cooling System. Int. J. Heat Mass Transf. 2019, 130, 33–41. [Google Scholar] [CrossRef]
- Qian, Z.; Li, Y.; Rao, Z. Thermal Performance of Lithium-Ion Battery Thermal Management System by Using Mini-Channel Cooling. Energy Convers. Manag. 2016, 126, 622–631. [Google Scholar] [CrossRef]
- Sheng, L.; Su, L.; Zhang, H.; Li, K.; Fang, Y.; Ye, W.; Fang, Y. Numerical Investigation on a Lithium-Ion Battery Thermal Management Utilizing a Serpentine-Channel Liquid Cooling Plate Exchanger. Int. J. Heat Mass Transf. 2019, 141, 658–668. [Google Scholar] [CrossRef]
- Behi, H.; Behi, M.; Karimi, D.; Jaguemont, J.; Ghanbarpour, M.; Behnia, M.; Berecibar, M.; Van Mierlo, J. Heat Pipe Air-Cooled Thermal Management System for Lithium-Ion Batteries: High Power Applications. Appl. Therm. Eng. 2021, 183, 116240. [Google Scholar] [CrossRef]
- Al Hallaj, S.; Selman, J.R. A Novel Thermal Management System for Electric Vehicle Batteries Using Phase-Change Material. J. Electrochem. Soc. 2000, 147, 3231. [Google Scholar] [CrossRef]
- Huang, Y.-H.; Cheng, W.-L.; Zhao, R. Thermal Management of Li-Ion Battery Pack with the Application of Flexible Form-Stable Composite Phase Change Materials. Energy Convers. Manag. 2019, 182, 9–20. [Google Scholar] [CrossRef]
- Verma, A.; Shashidhara, S.; Rakshit, D. A Comparative Study on Battery Thermal Management Using Phase Change Material (PCM). Therm. Sci. Eng. Prog. 2019, 11, 74–83. [Google Scholar] [CrossRef]
- Deng, Y.; Feng, C.; Jiaqiang, E.; Zhu, H.; Chen, J.; Wen, M.; Yin, H. Effects of Different Coolants and Cooling Strategies on the Cooling Performance of the Power Lithium Ion Battery System: A Review. Appl. Therm. Eng. 2018, 142, 10–29. [Google Scholar] [CrossRef]
- Lv, Y.; Yang, X.; Li, X.; Zhang, G.; Wang, Z.; Yang, C. Experimental Study on a Novel Battery Thermal Management Technology Based on Low Density Polyethylene-Enhanced Composite Phase Change Materials Coupled with Low Fins. Appl. Energy 2016, 178, 376–382. [Google Scholar] [CrossRef]
- Alipanah, M.; Li, X. Numerical Studies of Lithium-Ion Battery Thermal Management Systems Using Phase Change Materials and Metal Foams. Int. J. Heat Mass Transf. 2016, 102, 1159–1168. [Google Scholar] [CrossRef]
- Hussain, A.; Tso, C.Y.; Chao, C.Y. Experimental Investigation of a Passive Thermal Management System for High-Powered Lithium Ion Batteries Using Nickel Foam-Paraffin Composite. Energy 2016, 115, 209–218. [Google Scholar] [CrossRef]
- Hémery, C.-V.; Pra, F.; Robin, J.-F.; Marty, P. Experimental Performances of a Battery Thermal Management System Using a Phase Change Material. J. Power Sources 2014, 270, 349–358. [Google Scholar] [CrossRef]
- Fathabadi, H. High Thermal Performance Lithium-Ion Battery Pack Including Hybrid Active–Passive Thermal Management System for Using in Hybrid/Electric Vehicles. Energy 2014, 70, 529–538. [Google Scholar] [CrossRef]
- Zhang, X.; Li, Z.; Luo, L.; Fan, Y.; Du, Z. A Review on Thermal Management of Lithium-Ion Batteries for Electric Vehicles. Energy 2022, 238, 121652. [Google Scholar] [CrossRef]
- Siddique, A.R.M.; Mahmud, S.; Van Heyst, B. A Comprehensive Review on a Passive (Phase Change Materials) and an Active (Thermoelectric Cooler) Battery Thermal Management System and Their Limitations. J. Power Sources 2018, 401, 224–237. [Google Scholar] [CrossRef]
- Feng, L.; Zhou, S.; Li, Y.; Wang, Y.; Zhao, Q.; Luo, C.; Wang, G.; Yan, K. Experimental Investigation of Thermal and Strain Management for Lithium-Ion Battery Pack in Heat Pipe Cooling. J. Energy Storage 2018, 16, 84–92. [Google Scholar] [CrossRef]
- Smith, J.; Singh, R.; Hinterberger, M.; Mochizuki, M. Battery Thermal Management System for Electric Vehicle Using Heat Pipes. Int. J. Therm. Sci. 2018, 134, 517–529. [Google Scholar] [CrossRef]
- Greco, A.; Cao, D.; Jiang, X.; Yang, H. A Theoretical and Computational Study of Lithium-Ion Battery Thermal Management for Electric Vehicles Using Heat Pipes. J. Power Sources 2014, 257, 344–355. [Google Scholar] [CrossRef]
- Yuan, W.; Yan, Z.; Tan, Z.; Chen, W.; Tang, Y. Heat-Pipe-Based Thermal Management and Temperature Characteristics of Li-Ion Batteries. Can. J. Chem. Eng. 2016, 94, 1901–1908. [Google Scholar] [CrossRef]
- Roe, C.; Feng, X.; White, G.; Li, R.; Wang, H.; Rui, X.; Li, C.; Zhang, F.; Null, V.; Parkes, M. Immersion Cooling for Lithium-Ion Batteries—A Review. J. Power Sources 2022, 525, 231094. [Google Scholar] [CrossRef]
- Lander, L.; Kallitsis, E.; Hales, A.; Edge, J.S.; Korre, A.; Offer, G. Cost and Carbon Footprint Reduction of Electric Vehicle Lithium-Ion Batteries through Efficient Thermal Management. Appl. Energy 2021, 289, 116737. [Google Scholar] [CrossRef]
- Patil, M.S.; Seo, J.-H.; Lee, M.-Y. A Novel Dielectric Fluid Immersion Cooling Technology for Li-Ion Battery Thermal Management. Energy Convers. Manag. 2021, 229, 113715. [Google Scholar] [CrossRef]
- Nelson, P.; Dees, D.; Amine, K.; Henriksen, G. Modeling Thermal Management of Lithium-Ion PNGV Batteries. J. Power Sources 2002, 110, 349–356. [Google Scholar] [CrossRef]
- Patil, M.S.; Seo, J.H.; Bang, Y.M.; Kim, D.W.; Ekanayake, G.; Singh, G.; Kim, H.M.; Choi, Y.H.; Lee, M.Y. A Novel Design for Lithium Ion Battery Cooling Using Mineral Oil. In Proceedings of the 3rd International Mega-Conference on Green and Smart Technology (GST 2016), Jeju Island, Republic of Korea, 21–23 December 2016; pp. 21–23. [Google Scholar]
- Zhou, H.; Dai, C.; Liu, Y.; Fu, X.; Du, Y. Experimental investigation of battery thermal management and safety with heat pipe andimmersion phase change liquid. J. Power Sources 2020, 473, 228545. [Google Scholar] [CrossRef]
- Dubey, P.; Pulugundla, G.; Srouji, A.K. Direct comparison of immersion and cold-plate based cooling for automotive Li-ion battery modules. Energies 2021, 14, 1259. [Google Scholar] [CrossRef]
- Li, Y.; Zhou, Z.; Hu, L.; Bai, M.; Gao, L.; Li, Y.; Liu, X.; Li, Y.; Song, Y. Experimental studies of liquid immersion cooling for 18650 lithium-ion battery under different discharging conditions. Case Stud. Therm. Eng. 2022, 34, 102034. [Google Scholar] [CrossRef]
- Jithin, K.V.; Rajesh, P.K. Numerical analysis of single-phase liquid immersion cooling for lithium-ion battery thermal management using different dielectric fluids. Int. J. Heat Mass Transf. 2022, 188, 122608. [Google Scholar] [CrossRef]
- Giammichele, L.; D’Alessandro, V.; Falone, M.; Ricci, R. Experimental study of a direct immersion liquid cooling of a Li-ion battery for electric vehicles applications. Int. J. Heat Technol. 2022, 40, 1–8. [Google Scholar] [CrossRef]
- Williams, N.P.; O’Shaughnessy, S.M. Immersion Cooling of Lithium-ion Batteries for Electric Vehicles. In Proceedings of the 2022 28th International Workshop on Thermal Investigations of ICs and Systems (THERMINIC), Dublin, Ireland, 28–30 September 2022; pp. 1–4. [Google Scholar]
- Han, J.W.; Garud, K.S.; Hwang, S.G.; Lee, M.Y. Experimental Study on Dielectric Fluid Immersion Cooling for Thermal Management of Lithium-Ion Battery. Symmetry 2022, 14, 2126. [Google Scholar] [CrossRef]
- Luo, M.; Cao, J.; Liu, N.; Zhang, Z.; Fang, X. Experimental and Simulative Investigations on a Water Immersion Cooling System for Cylindrical Battery Cells. Front. Energy Res. 2022, 10, 803882. [Google Scholar] [CrossRef]
- Wang, Y.F.; Li, B.; Hu, Y.; Mao, Z.; Song, B.; Tian, W.; Sunden, B. Experimental study on immersion phase change cooling of lithium-ion batteries based on R1233ZD (E)/ethanol mixed refrigerant. Appl. Therm. Eng. 2023, 220, 119649. [Google Scholar] [CrossRef]
- Satyanarayana, G.; Sudhakar, D.R.; Goud, V.M.; Ramesh, J.; Pathanjali, G.A. Experimental investigation and comparative analysis of immersion cooling of lithium-ion batteries using mineral and therminol oil. Appl. Therm. Eng. 2023, 225, 120187. [Google Scholar] [CrossRef]
- Li, Y.; Bai, M.; Zhou, Z.; Wu, W.-T.; Lv, J.; Gao, L.; Huang, H.; Li, Y.; Li, Y.; Song, Y. Experimental investigations of liquid immersion cooling for 18650 lithium-ion battery pack under fast charging conditions. Appl. Therm. Eng. 2023, 227, 120287. [Google Scholar] [CrossRef]
- Wang, Z.; Zhao, R.; Wang, S.; Huang, D. Heat transfer characteristics and influencing factors of immersion coupled direct cooling for battery thermal management. J. Energy Storage 2023, 62, 106821. [Google Scholar] [CrossRef]
- Celen, A. Experimental Investigation on Single-Phase Immersion Cooling of a Lithium-Ion Pouch-Type Battery under Various Operating Conditions. Appl. Sci. 2023, 13, 2775. [Google Scholar] [CrossRef]
- Choi, H.; Lee, H.; Kim, J.; Lee, H. Hybrid single-phase immersion cooling structure for battery thermal management under fast-charging conditions. Energy Convers. Manag. 2023, 287, 117053. [Google Scholar] [CrossRef]
- Shah, J.M.; Eiland, R.; Siddarth, A.; Agonafer, D. Effects of Mineral Oil Immersion Cooling on IT Equipment Reliability and Reliability Enhancements to Data Center Operations. In Proceedings of the 2016 15th IEEE Intersociety Conference on Thermal and Thermomechanical Phenomena in Electronic Systems (ITherm), Las Vegas, NV, USA, 31 May–3 June 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 316–325. [Google Scholar]
- Vincent, M.; Ghaffari, O.; Nabavi Larimi, Y.; Grenier, F.; Jasmin, S.; Fréchette, L.; Sylvestre, J. Experimental Investigation of the Thermal Resistance of Advanced Novel Two-Phase Thermosyphon Heatsinks. Available at SSRN 4457244. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=4457244 (accessed on 25 June 2023).
- 3M NovecTM 649 Engineered Fluid Datasheet. Available online: http://www.lookpolymers.com/polymer_3M-Novec-649-Engineered-Fluid.php (accessed on 8 August 2023).
- Table 3-Thermal Properties of the Manufactured Nonwoven. Available online: https://www.researchgate.net/figure/Thermal-properties-of-the-manufactured-nonwoven_tbl3_322982943 (accessed on 27 June 2023).
- Kaviany, M. Principles of Heat Transfer in Porous Media; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar]
- SIEMENS. Integration Algorithms and Library User Guides Used in Simcenter Amesim; SIEMENS: Munich, Germany, 2020; Available online: https://plm.sw.siemens.com/en-US/simcenter/systems-simulation/amesim/ (accessed on 26 June 2023).
- Patil, K.; Molla, S.K.; Schulze, T. Hybrid Vehicle Model Development Using ASM-AMESim-Simscape Co-Simulation for Real-Time HIL Applications. In Proceedings of the SAE 2012 World Congress & Exhibition, Detroit, MI, USA, 24–26 April 2012. [Google Scholar]
- Zhao, Q.; Duan, J.J.; Wang, C. Modeling and Simulation of Vehicle Hydraulic ABS Based on AMEsim. Adv. Mater. Res. 2012, 590, 441–445. [Google Scholar] [CrossRef]
- El-Nasr, A.A.; El-Haggar, S.M. Effective Thermal Conductivity of Heat Pipes. Heat Mass Transf. 1996, 32, 97–101. [Google Scholar] [CrossRef]
- Kapekov, A. Development of an Innovative Cooling Concept for Turbofan Engines. 2018. Available online: http://kth.diva-portal.org/smash/record.jsf?pid=diva2:1295797 (accessed on 3 March 2023).
- Peterson, G.P. An Introduction to Heat Pipes; John Wiley& Sons. Inc.: New York, NY, USA, 1994. [Google Scholar]
- Chan, C.W.; Siqueiros, E.; Ling-Chin, J.; Royapoor, M.; Roskilly, A.P. Heat Utilisation Technologies: A Critical Review of Heat Pipes. Renew. Sustain. Energy Rev. 2015, 50, 615–627. [Google Scholar] [CrossRef]
- Wallin, P. Heat Pipe, Selection of Working Fluid. Heat and Mass Trasfer Project Report. 2012. pp. 1–7. Available online: https://www.ht.energy.lth.se/fileadmin/ht/Kurser/MVK160/2012/Per_Wallin.pdf (accessed on 25 March 2023).
- Anand, A.R.; Vedamurthy, A.J.; Chikkala, S.R.; Kumar, S.; Kumar, D.; Gupta, P.P. Analytical and Experimental Investigations on Axially Grooved Aluminum-Ethane Heat Pipe. Heat Transf. Eng. 2008, 29, 410–416. [Google Scholar] [CrossRef]
- Reay, D.; McGlen, R.; Kew, P. Heat Pipes: Theory, Design and Applications; Butterworth-Heinemann: Oxford, UK, 2013. [Google Scholar]
- Gou, J.; Liu, W. Feasibility Study on a Novel 3D Vapor Chamber Used for Li-Ion Battery Thermal Management System of Electric Vehicle. Appl. Therm. Eng. 2019, 152, 362–369. [Google Scholar] [CrossRef]
- Li, H.; Liu, Z.; Chen, B.; Liu, W.; Li, C.; Yang, J. Development of Biporous Wicks for Flat-Plate Loop Heat Pipe. Exp. Therm. Fluid Sci. 2012, 37, 91–97. [Google Scholar] [CrossRef]
- Li, J.; Lu, N.; Sun, Y. Research Progress and Prospect of Heat Pipe Capillary Wicks. Front. Heat Mass Transf. (FHMT) 2022, 18. [Google Scholar] [CrossRef]
- Brautsch, A.; Kew, P.A. Examination and Visualisation of Heat Transfer Processes during Evaporation in Capillary Porous Structures. Appl. Therm. Eng. 2002, 22, 815–824. [Google Scholar] [CrossRef]
- Li, C.; Peterson, G.P.; Wang, Y. Evaporation/Boiling in Thin Capillary Wicks (l)—Wick Thickness Effects. 2006. Available online: https://www.researchgate.net/publication/245362585_EvaporationBoiling_in_Thin_Capillary_Wicks_l-Wick_Thickness_Effects (accessed on 5 March 2023).
- Chang, F.L.; Hung, Y.M. The Coupled Effects of Working Fluid and Solid Wall on Thermal Performance of Micro Heat Pipes. Int. J. Heat Mass Transf. 2014, 73, 76–87. [Google Scholar] [CrossRef]
- Henderson-Sellers, B. A New Formula for Latent Heat of Vaporization of Water as a Function of Temperature. Q. J. R. Meteorol. Soc. 1984, 110, 1186–1190. [Google Scholar] [CrossRef]
- Kestin, J.; Sokolov, M.; Wakeham, W.A. Viscosity of Liquid Water in the Range −8 °C to 150 °C. J. Phys. Chem. Ref. Data 1978, 7, 941–948. [Google Scholar] [CrossRef]
- Vargaftik, N.B.; Volkov, B.N.; Voljak, L.D. International Tables of the Surface Tension of Water. J. Phys. Chem. Ref. Data 1983, 12, 817–820. [Google Scholar] [CrossRef]
- Larrañaga, A.; Gómez, M.A.; Patiño, D.; Porteiro, J. Experimental Study on the Stability and Transient Behavior of a Closed-Loop Two-Phase Thermosyphon (CLTPT) Charged with NOVEC 649. Energies 2021, 14, 7920. Available online: https://www.mdpi.com/1996-1073/14/23/7920 (accessed on 1 August 2023). [CrossRef]
- Chupka, G.M.; Christensen, E.; Fouts, L.; Alleman, T.L.; Ratcliff, M.A.; McCormick, R.L. Heat of Vaporization Measurements for Ethanol Blends Up To 50 Volume Percent in Several Hydrocarbon Blendstocks and Implications for Knock in SI Engines. SAE Int. J. Fuels Lubr. 2015, 8, 251–263. [Google Scholar] [CrossRef]
- Gonçalves, F.A.M.M.; Trindade, A.R.; Costa, C.S.M.F.; Bernardo, J.C.S.; Johnson, I.; Fonseca, I.M.A.; Ferreira, A.G.M. PVT, Viscosity, and Surface Tension of Ethanol: New Measurements and Literature Data Evaluation. J. Chem. Thermodyn. 2010, 42, 1039–1049. [Google Scholar] [CrossRef]
- Dunn, P.D.; Reay, D.A. The Heat Pipe. Phys. Technol. 1973, 4, 187–201. [Google Scholar] [CrossRef]



| Thermal Conductivity, K | Specific Heat | ||
|---|---|---|---|
| Non-woven | 0.038 | 400 | 1200 |
| NovecTM 649 | 0.059 | 1600 | 1103 |
| Category | Conditions |
|---|---|
| Material of battery | Aluminum |
| Material of wick | Non-woven |
| Working fluid | NovecTM 649, Water, Ethanol, Methanol |
| Coolant of cooling plate | Water |
| Initial temperature of battery (°C) | 35 |
| Temperature of cooling plate coolant (°C) | 20 |
| Mass flow rate of coolant (L/min) | 2.4 |
| Thickness of wick (mm) | 0.3, 0.5, 0.7 |
| Porosity (%) | 10~60 |
| Filling ratio (%) | 10~60 |
| Heat input (W) | 10, 15, 20 |
| Library Component | Component Name | Description |
|---|---|---|
 | Thermal capacity | It computes the temperature dynamics of a solid mass with respect to incoming heat flux. |
 | Conductive exchange | Generic conduction. |
 | Temperature sensor | It is a tool to measure the temperature of the evaporation part and the condensation part of this research model. |
 | Conversion of signal to a heat flow | Conversion of signal to a heat flow. |
 | Power/Energy/Activity sensor | This sensor is used to compute the power or energy at ports of one system’s component. |
 | Thermal plug | It can stop the heat flow rate at a port. |
 | Thermal properties | Thermal properties. |
 | Thermodynamic state transformer | It can choose between nine predefined choices to define the thermodynamic state at input and at output. |
 | Fluid property sensor | Generic sensor with additional thermodynamic state variable. |
 | Two-phase flow pipe volume | Pipe with heat exchange with 2 thermal ports (R-C), related to various two-phase flow models. |
 | Modulated source | A modulated source of mass flow rate and enthalpy flow rate. |
 | Fluid property(two-phase) | Fluid property (two-phase). |
 | Modulated source | A modulated source of mass flow rate, temperature rate, and pressure rate. |
 | Thermal-hydraulic pipe volume | Pipe with heat exchange with thermal port (C-R), related to various thermal-hydraulic models. |
 | Thermal-hydraulic fluid property | Thermal-hydraulic fluid property. |
 | Constant signal | outputs a signal with a constant specified value. |
 | Mathematical function | It applies a user supplied function to two signals input at ports X and Y, and the result is the output on another port. |
 | Reverse the sign of input | A signal conversion submodel that reverses the sign of the input signal. |
 | Division function | Division function. |
| Category | Condition |
|---|---|
| Material of battery | Aluminum |
| Material of wick | No. 200 Sintered Copper |
| Working fluid | Water |
| Coolant of cooling plate | Water |
| Initial temperature of battery (°C) | 35 |
| Temperature of cooling plate coolant (°C) | 25 |
| Mass flow rate of coolant (L/min) | 3 |
| Thickness of wick (mm) | 0.5 |
| Porosity (%) | 60 |
| Filling ratio (%) | 10, 20 |
| Heat input (W) | 10~60 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oh, I.-T.; Lee, J.-S.; Han, J.-S.; Lee, S.-W.; Kim, S.-J.; Rhi, S.-H. Li-Ion Battery Immersed Heat Pipe Cooling Technology for Electric Vehicles. Electronics 2023, 12, 4931. https://doi.org/10.3390/electronics12244931
Oh I-T, Lee J-S, Han J-S, Lee S-W, Kim S-J, Rhi S-H. Li-Ion Battery Immersed Heat Pipe Cooling Technology for Electric Vehicles. Electronics. 2023; 12(24):4931. https://doi.org/10.3390/electronics12244931
Chicago/Turabian StyleOh, In-Taek, Ji-Su Lee, Jin-Se Han, Seong-Woo Lee, Su-Jong Kim, and Seok-Ho Rhi. 2023. "Li-Ion Battery Immersed Heat Pipe Cooling Technology for Electric Vehicles" Electronics 12, no. 24: 4931. https://doi.org/10.3390/electronics12244931
APA StyleOh, I.-T., Lee, J.-S., Han, J.-S., Lee, S.-W., Kim, S.-J., & Rhi, S.-H. (2023). Li-Ion Battery Immersed Heat Pipe Cooling Technology for Electric Vehicles. Electronics, 12(24), 4931. https://doi.org/10.3390/electronics12244931







