Magnetic Field Testing Technique of System-Generated Electromagnetic Pulse Based on Magnetoresistance Effects
Abstract
:1. Introduction
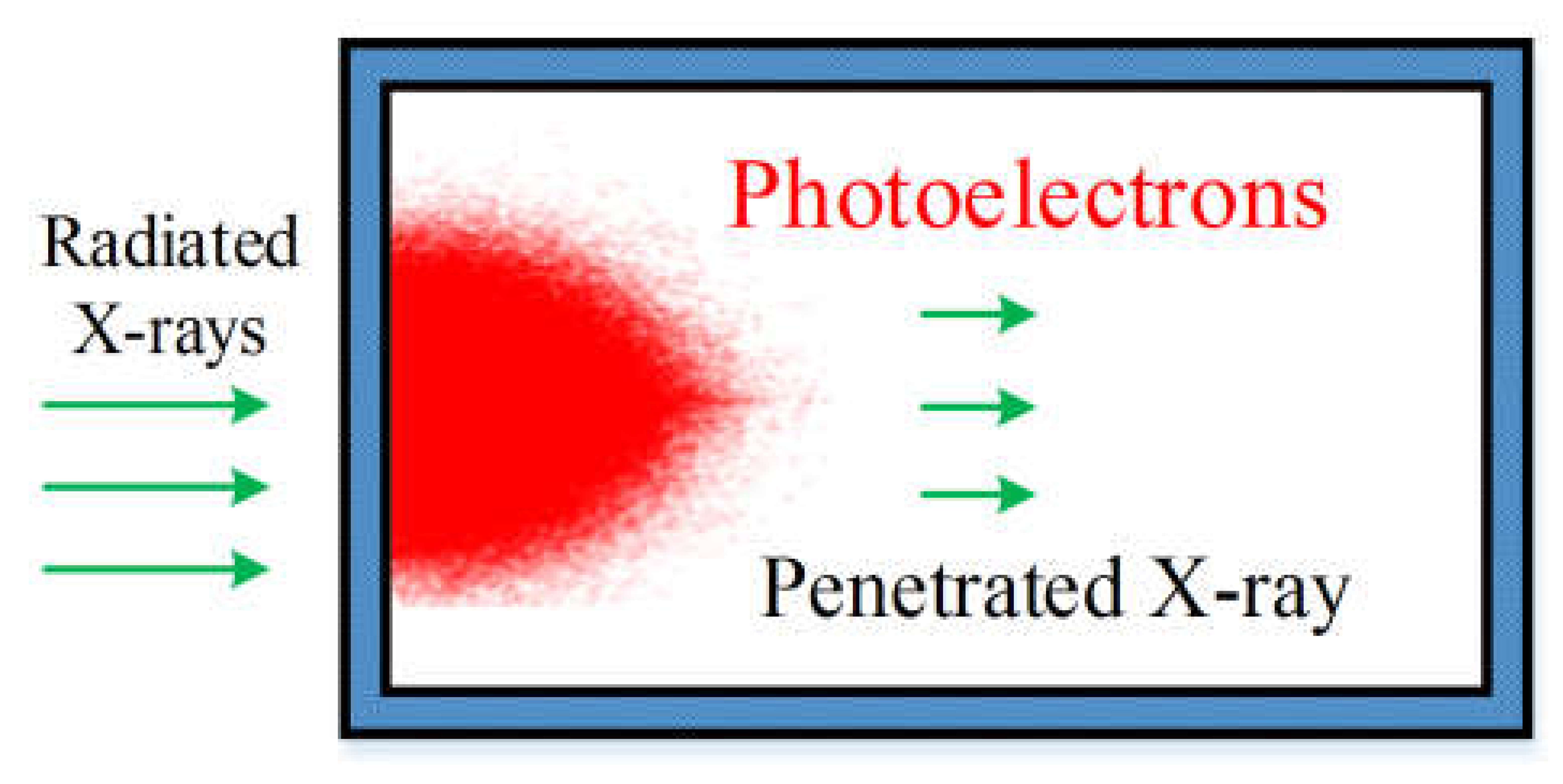
2. Theoretical Analysis of SGEMP
3. Design and Calibration of Magnetoresistance Detectors
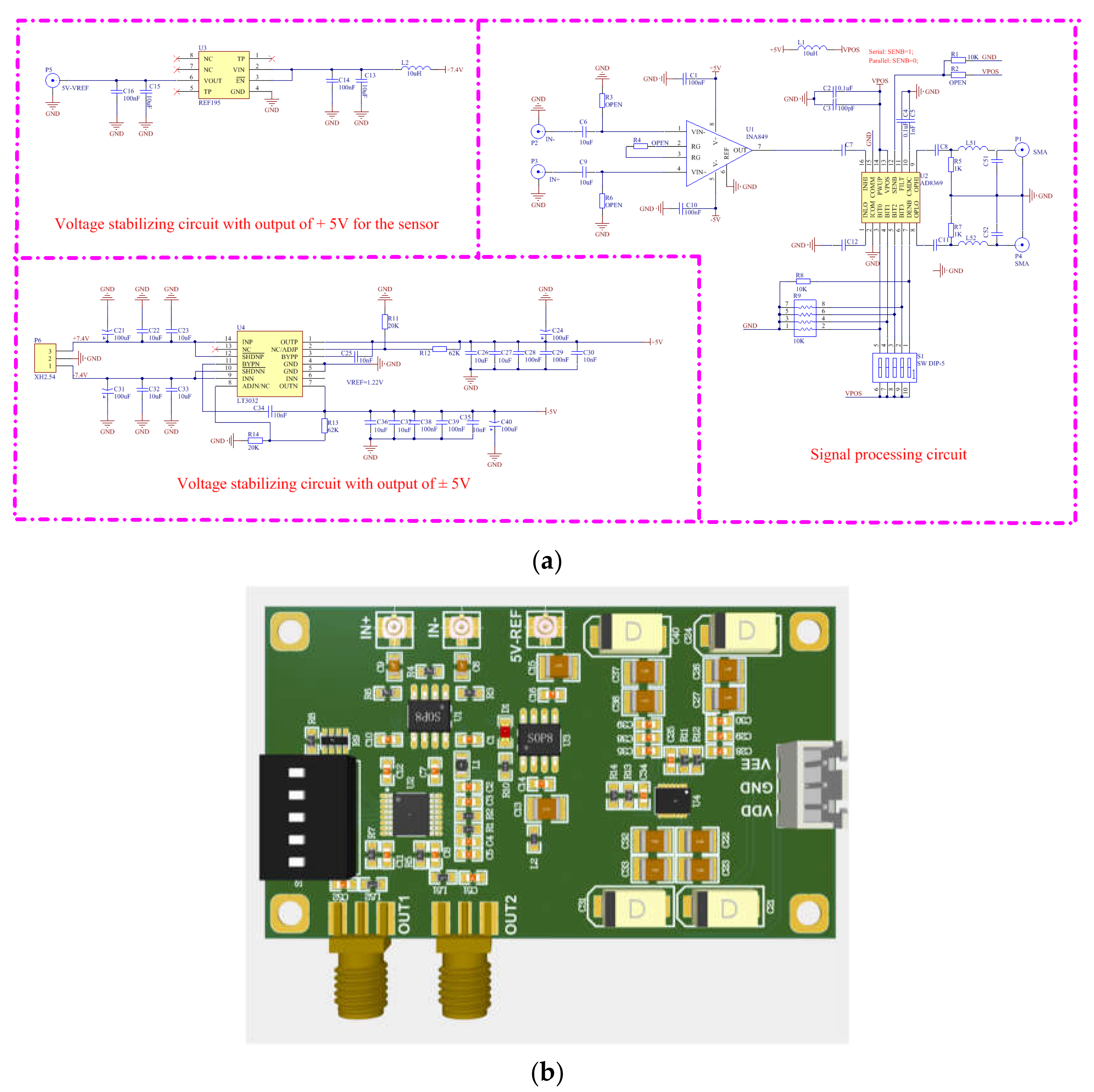
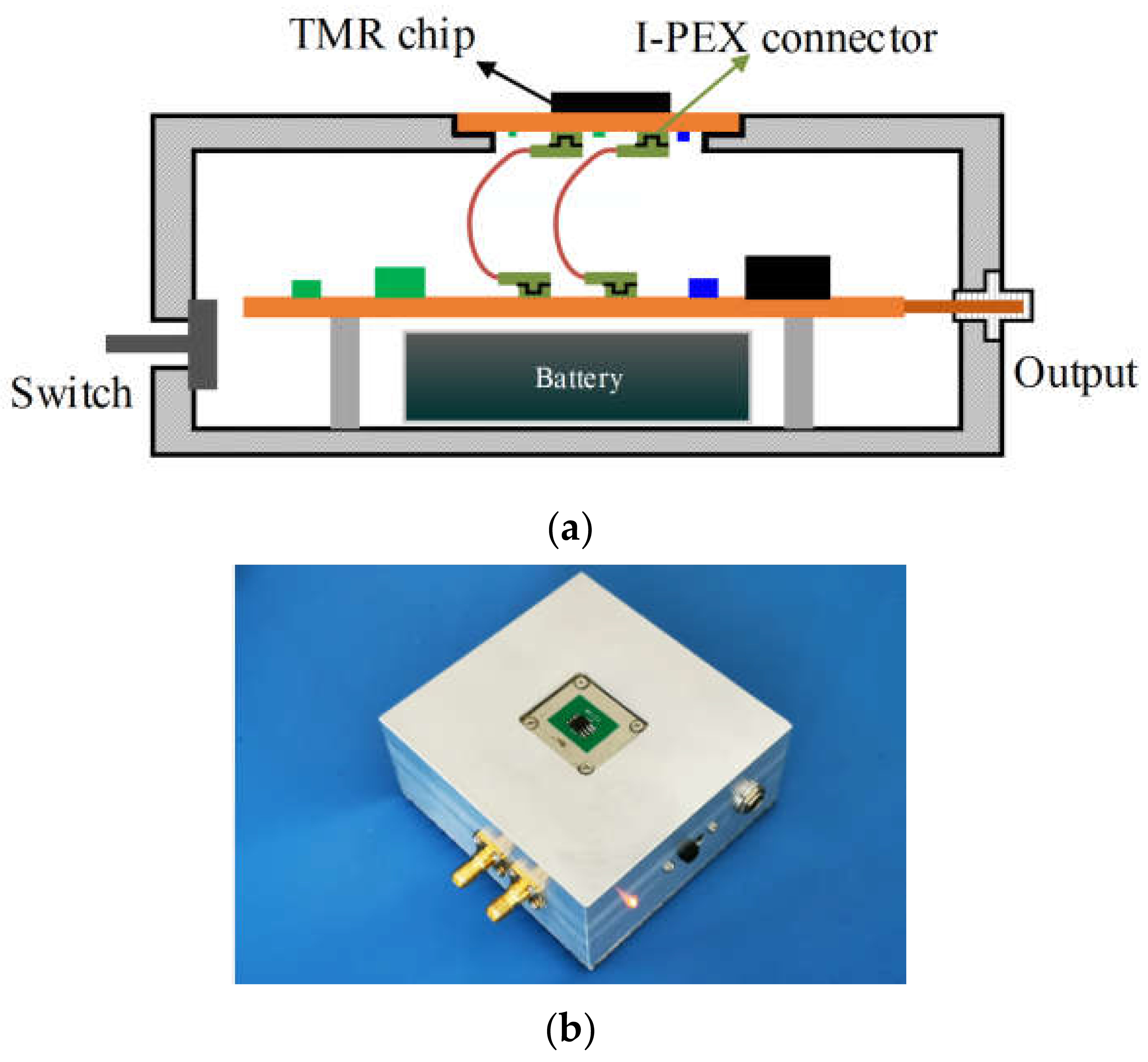
3.1. Design of Detectors
3.2. Calibration of Detectors
4. Measurement and Analysis of SGEMP
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rich, W.F.; Stringer, T.A. System-generated electromagnetic pulse and spacecraft charging effects: A review of the technology as applied to system hardening problems. IEEE Trans. Nucl. Sci. 1980, 27, 1523–1528. [Google Scholar] [CrossRef]
- Longmire, C.L. On the electromagnetic pulse produced by nuclear explosions. IEEE Trans. Antennas Propag. 1978, 26, 3–13. [Google Scholar] [CrossRef]
- Higgins, D.F.; Longmire, C.L.; O’Dell, A.A. A Method for Estimating the X-ray Produced Electromagnetic Pulse Observed in the Source Region of a High-Altitude Nuclear Burst; Mission Res. Corp: Santa Barbara, CA, USA, 1973. [Google Scholar]
- Woods, A.J.; Delmer, T.N. The arbitrary body of revolution code (ABORC) for SGEMP/IEMP. In Topical Report, September 1975–June 1976. United States; IRT Corp.: San Diego, CA, USA, 1976. [Google Scholar]
- Cui, M.; Zhiqian, X.; Yunsheng, J.; Wanguo, Z.; Zhao, D. Numerical simulation of the SGEMP inside a target chamber of a laser inertial confinement facility. IEEE Trans. Nucl. Sci. 2017, 64, 2618–2625. [Google Scholar] [CrossRef]
- Chen, J.; Wang, J.; Chen, Z.; Ren, Z.; Qiao, H. Study of SGEMP Field-Coupling inside and outside reentrant cavity. IEEE Trans. Electromagn. Compat. 2022, 64, 1182–1189. [Google Scholar] [CrossRef]
- Cheng, Y.; Zhou, H.; Li, B.; Chen, M.; Wu, W.; Qiao, D. Simulation of system-generated electromagnetic pulse caused byemitted photoelectron in cavity. High Power Laser Part. Beams 2004, 16, 1029–1032. [Google Scholar]
- Zhou, Y.; Cheng, Y.; Zhu, Z.; Ma, L.; Chen, P.; Wang, W.; Wang, X. Simulation study of air Effects on SGEMP based on Swarm Mode. IEEE Trans. Nulear Sci. 2022, 69, 26–34. [Google Scholar] [CrossRef]
- Zhang, H.; Zhou, Q.; Zhou, H. Effect of secondary electron emission on SGEMP. Acta Phys. Sin. 2021, 70, 195–203. [Google Scholar]
- Zhou, K.; Wang, Y.; Deng, J. Development and test of measurement system for cable system generated electromagnetic pulse effects. High Power Laser Part. Beams 2014, 26, 175–179. [Google Scholar]
- Lenz, J.; Edelstein, A.S. Magnetic sensors and their applications. IEEE Sens. J. 2006, 6, 631–649. [Google Scholar] [CrossRef]
- Li, J.; Wu, W.; Guo, J.; Liu, Y.; Zhao, M.; Ma, L.; Cheng, Y. Verification of numerical simulation model for SGEMP generated in Flash-Ⅱ accelerator environment. Mod. Appl. Phys. 2016, 7, 26–30. [Google Scholar]
- Chen, J.; Wang, J.; Tao, Y.; Chen, Z.; Wang, Y.; Niu, S. Simulation of SGEMP using particle–in-cell method based on conformal technique. IEEE Trans. Nucl. Sci 2019, 66, 820–826. [Google Scholar] [CrossRef]
- Wu, W.; Zhao, M.; Li, J.; Zhou, H. Study on the parameters of cavity system-generate electromagnetic pulse (SGEMP) calculation model base on Maxwell-Valsov equation. In Proceedings of the IEEE 3rd International Conference on Automation, Electronics and Electrical Engineering, Shenyang, China, 20–22 November 2020; pp. 484–487. [Google Scholar]
- Karst, J.P.; Groh, C. Calculable field generation using TEM cells applied to the calibration of a novel E-Field probe. IEEE Trans. Electromagn. Compat. 2002, 44, 59–71. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Wu, W.; Li, J.; Zhao, M.; Wei, F.; Ren, S.; Huang, T. Magnetic Field Testing Technique of System-Generated Electromagnetic Pulse Based on Magnetoresistance Effects. Electronics 2023, 12, 492. https://doi.org/10.3390/electronics12030492
Liu Y, Wu W, Li J, Zhao M, Wei F, Ren S, Huang T. Magnetic Field Testing Technique of System-Generated Electromagnetic Pulse Based on Magnetoresistance Effects. Electronics. 2023; 12(3):492. https://doi.org/10.3390/electronics12030492
Chicago/Turabian StyleLiu, Yifei, Wei Wu, Jinxi Li, Mo Zhao, Feng Wei, Shuqing Ren, and Tao Huang. 2023. "Magnetic Field Testing Technique of System-Generated Electromagnetic Pulse Based on Magnetoresistance Effects" Electronics 12, no. 3: 492. https://doi.org/10.3390/electronics12030492
APA StyleLiu, Y., Wu, W., Li, J., Zhao, M., Wei, F., Ren, S., & Huang, T. (2023). Magnetic Field Testing Technique of System-Generated Electromagnetic Pulse Based on Magnetoresistance Effects. Electronics, 12(3), 492. https://doi.org/10.3390/electronics12030492







