Design of High-Order Resonator HTS Diplexer with Very Different FBW
Abstract
:1. Introduction
2. Synthesis of Diplexer Coupling Matrix
2.1. Synthesis of Filter Coupling Matrix
2.2. Synthesis of Diplexer Coupling Matrix
- 1
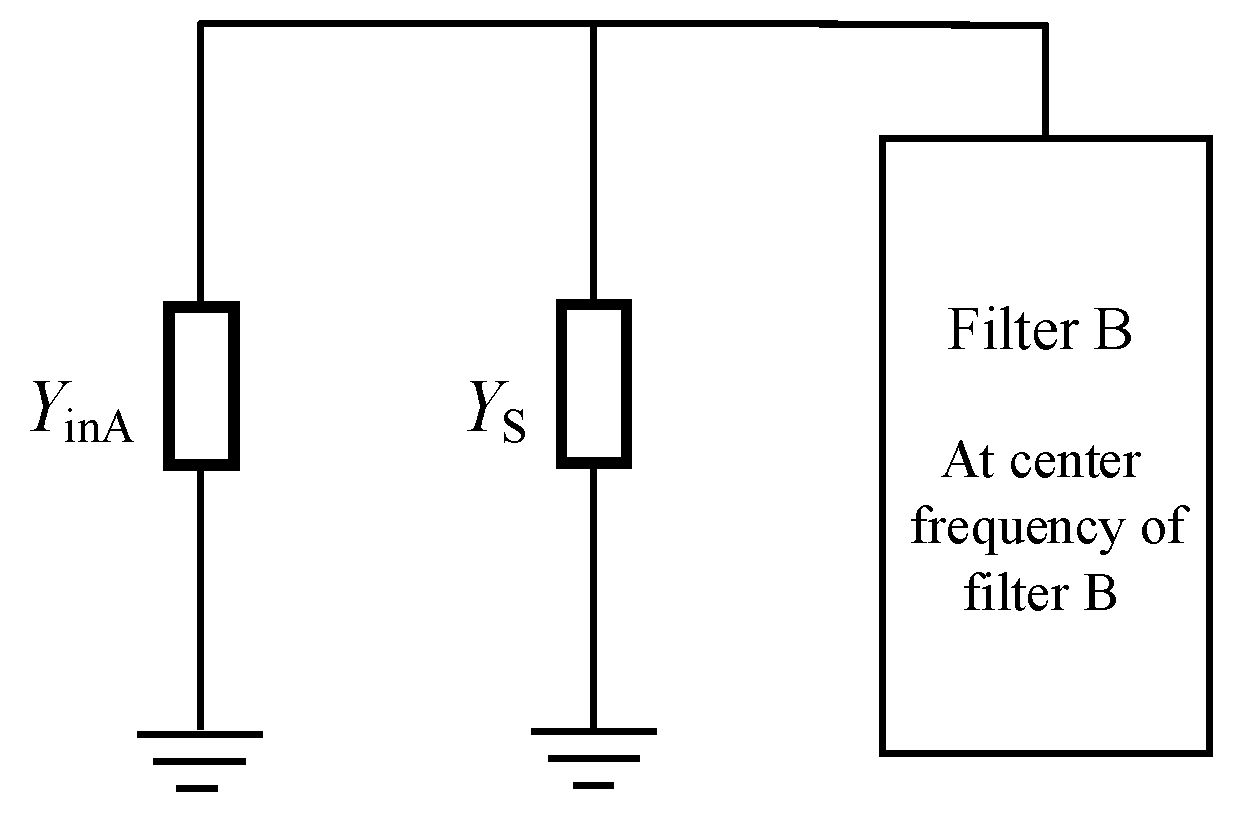
- Assuming that the center frequencies of filters A and B are f1 and f2, respectively, take the initial source impedance Y1(0) = Y2(0) = YS = 50 Ω of filters A and B, with the allowable error and > 0. In this design, set = = 0.001, and k = 1.
- 2
- Set the source admittance of filter A as Y1 (k − 1), and recalculate the coupling matrix M1 (k) of filter A. Set the source impedance of filter B to Y2 (k − 1), and recalculate the coupling matrix M2 (k) of filter B. Stop iteration when the formula (6) is established.
- 3
- When the source impedance is Y1 (k − 1) and the coupling matrix is M1 (k), calculate the input admittance YinA (k) of filter A at f2; then, the source impedance of filter B becomes Y2 (k) =Ys + Y1 (k). When the source impedance is Y2 (k − 1), and the coupling matrix is M2 (k), calculate the input admittance YinB(k) of filter B at f1; then, the source impedance of filter B becomes Y1 (k)= Ys + YinB (k).
- 4
- Let k = k + 1, and return to Step 2.
3. Verification of Proposed Configuration
3.1. Analysis of the SIR Resonator
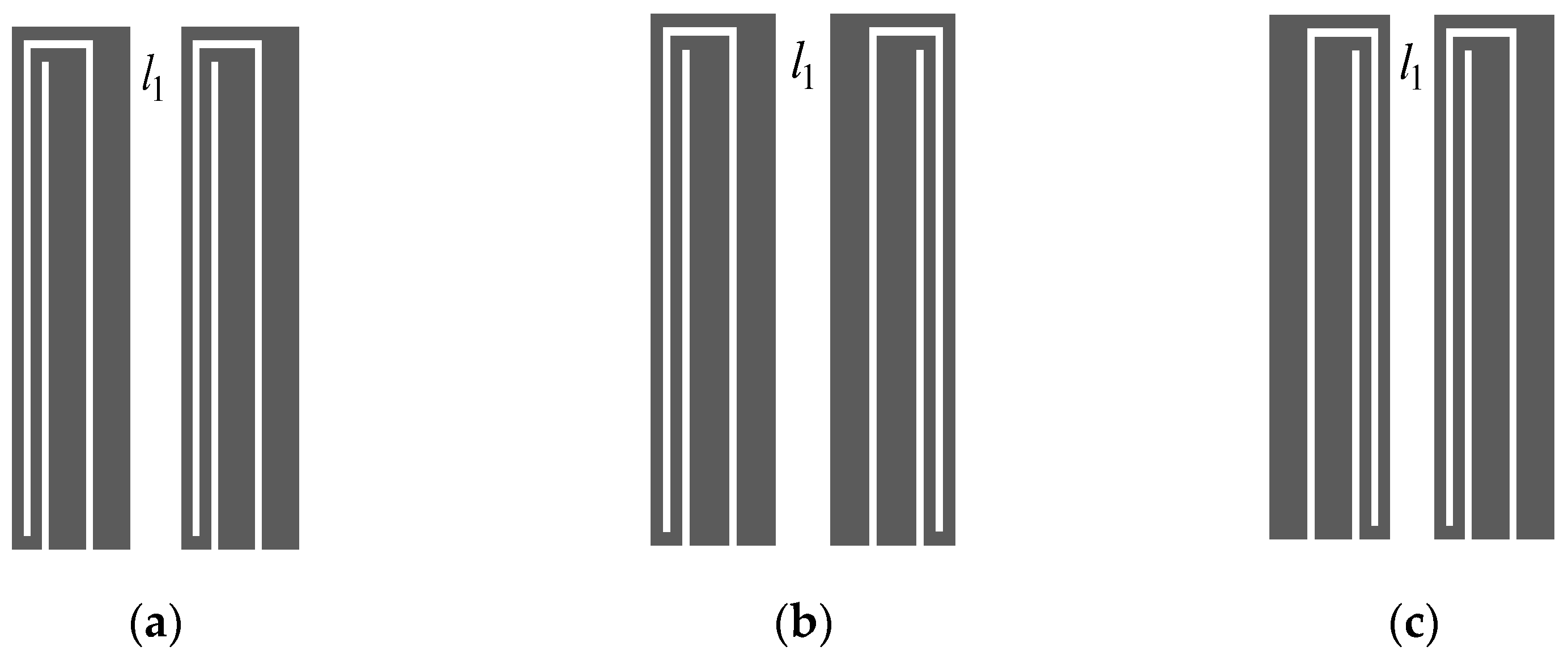
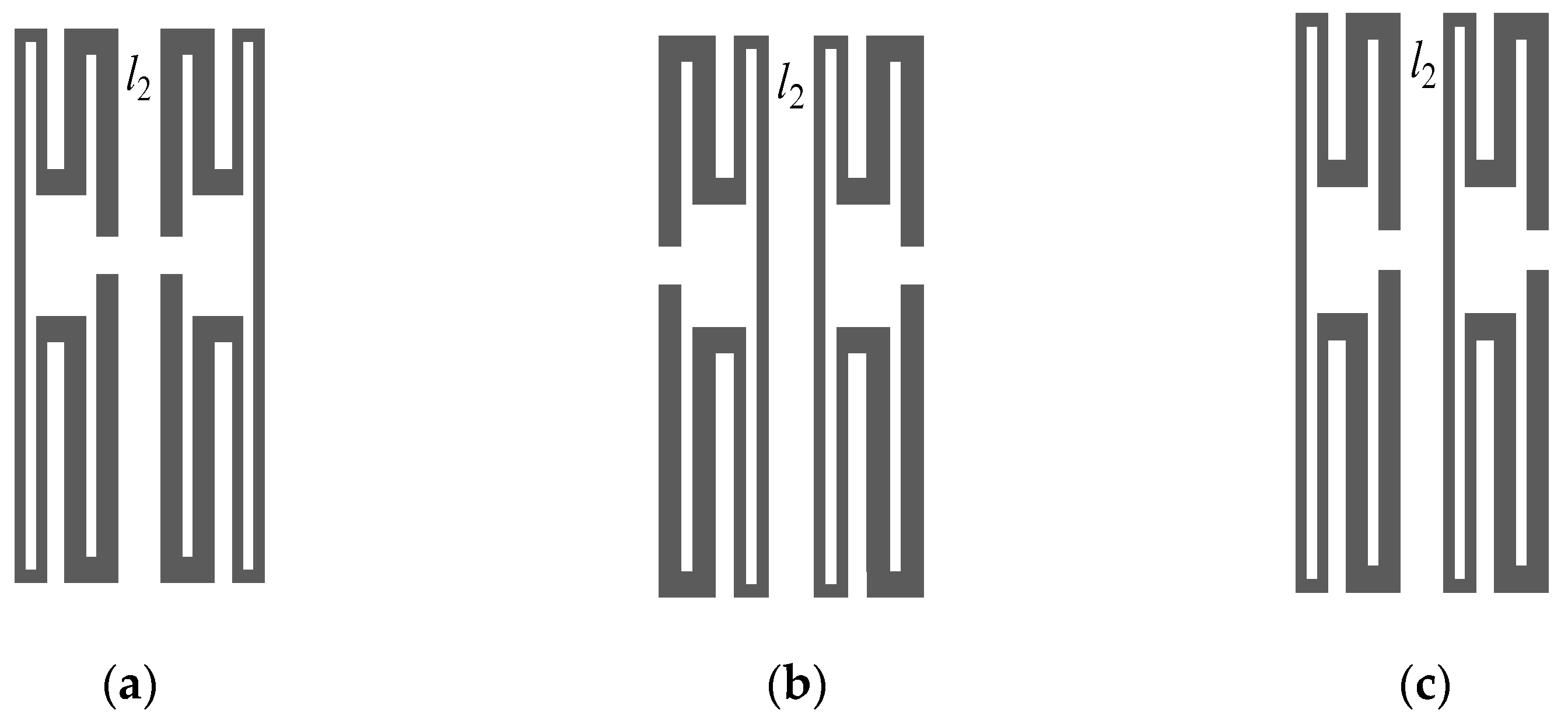
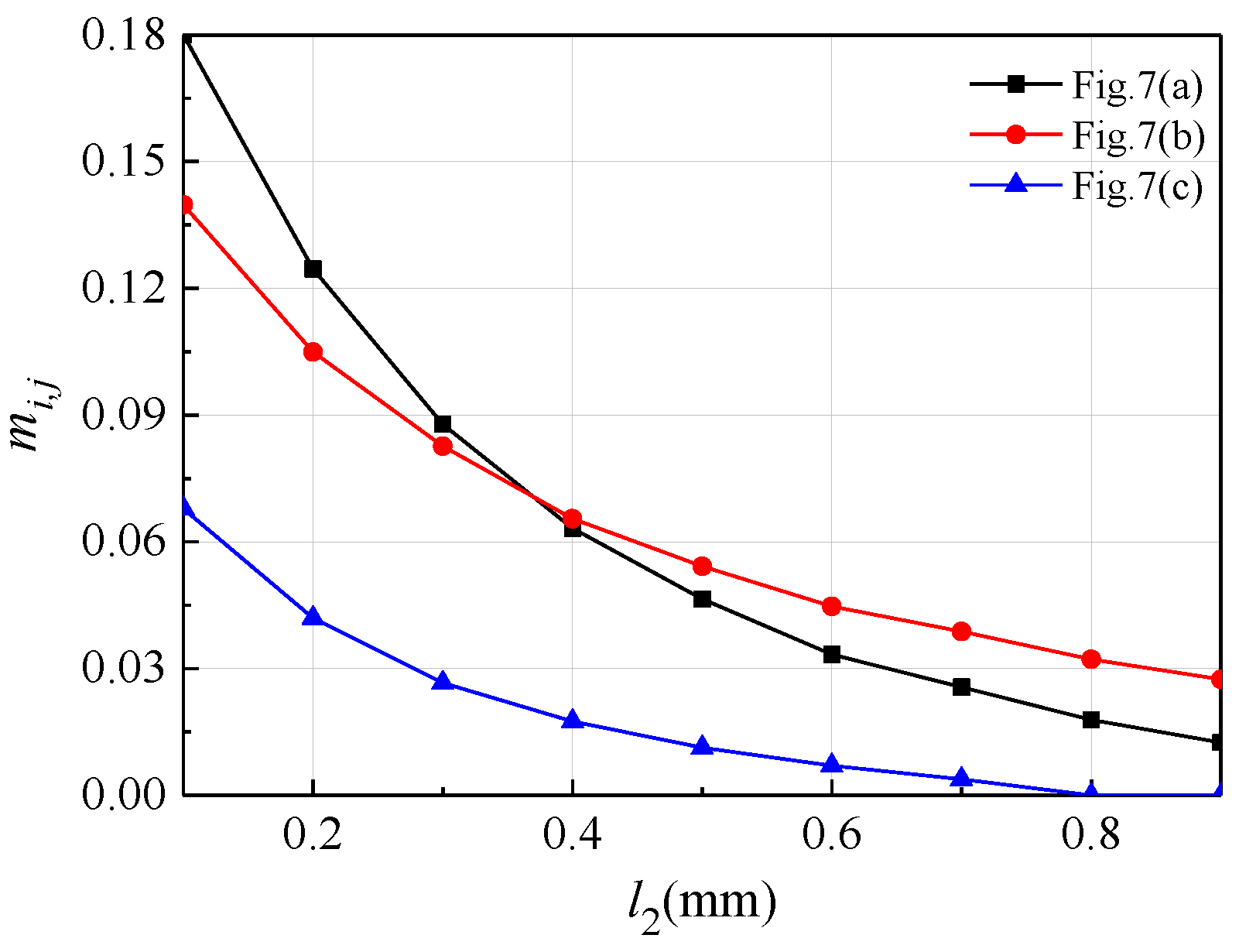
3.2. Analysis of the Internal Coupling Structure
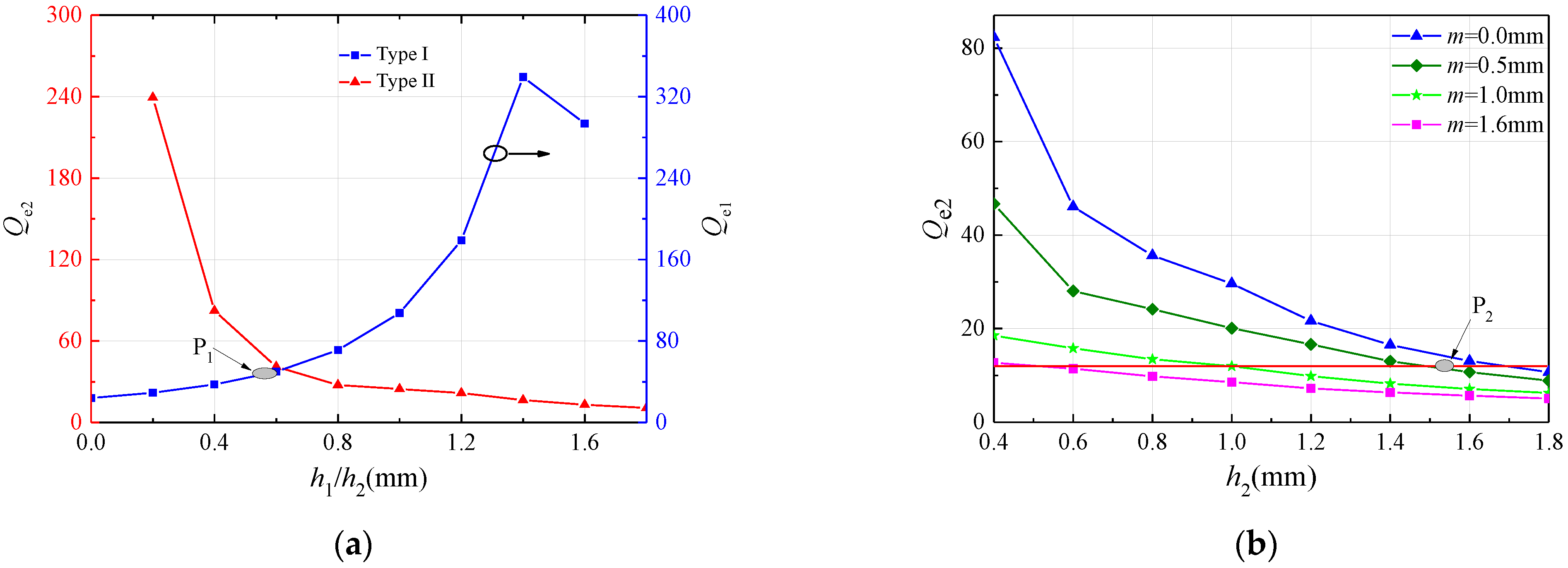
3.3. Analysis of the External Coupling Structure
3.4. Design of the T-Junction
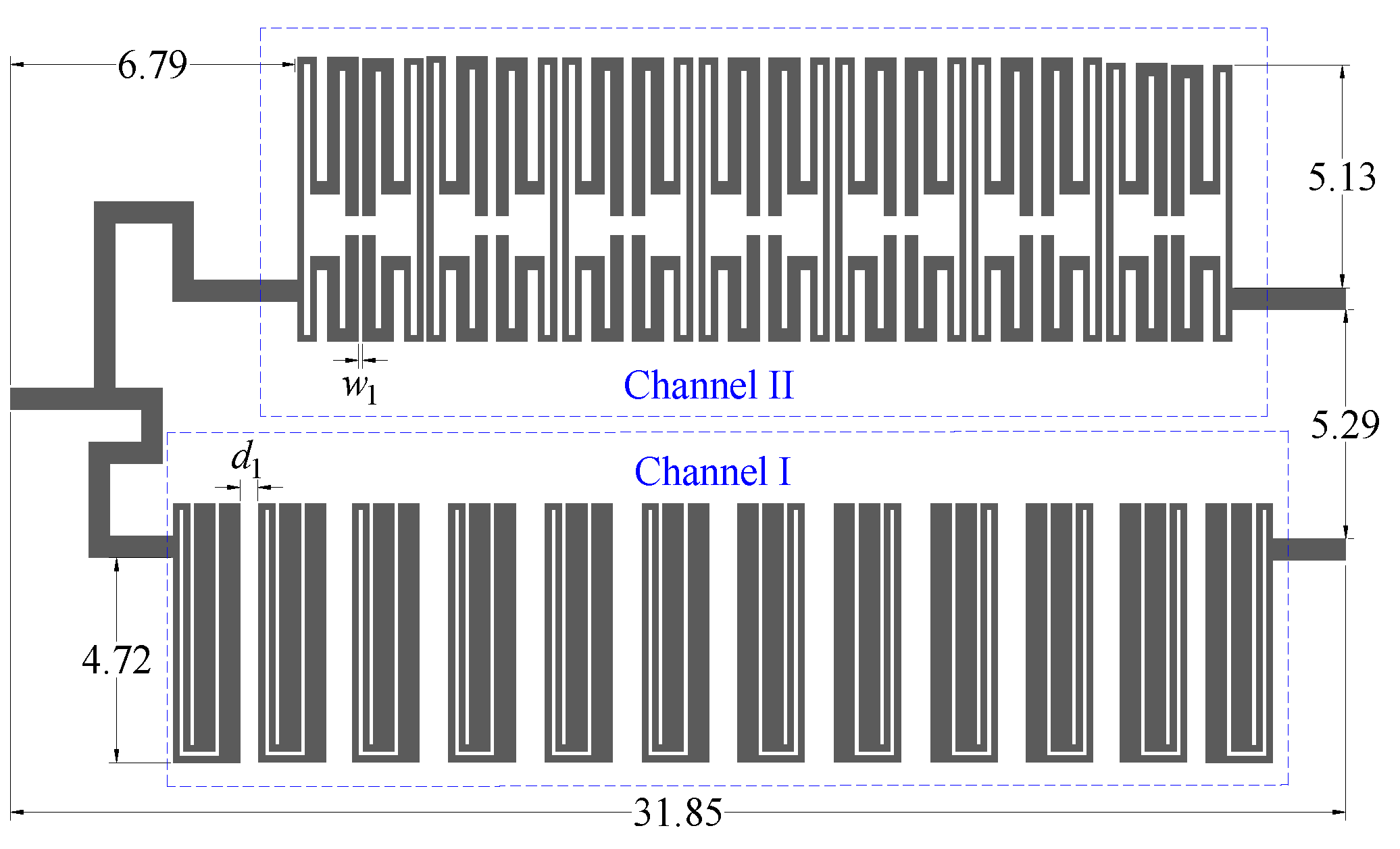
3.5. Design of Circuit Layout
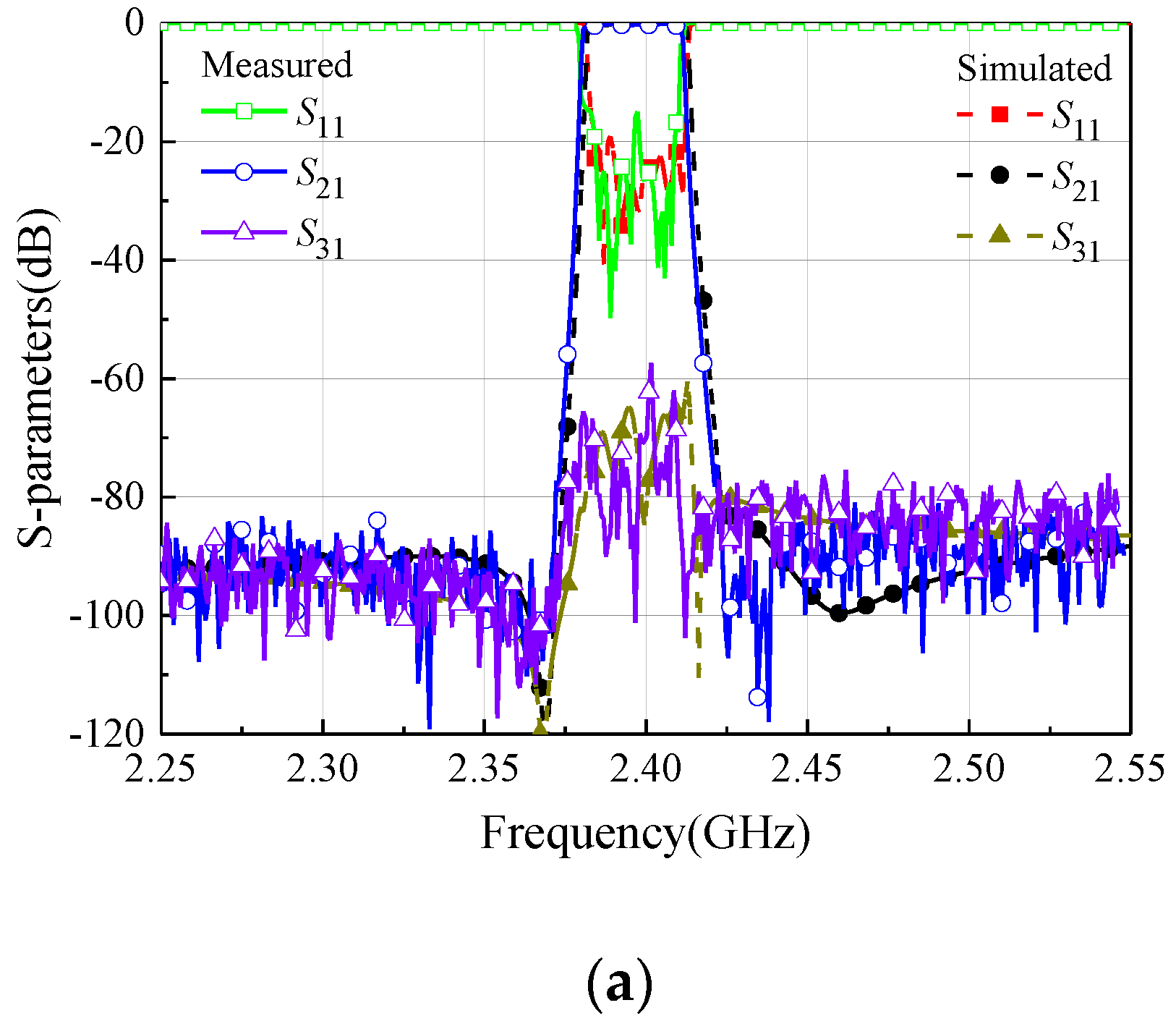
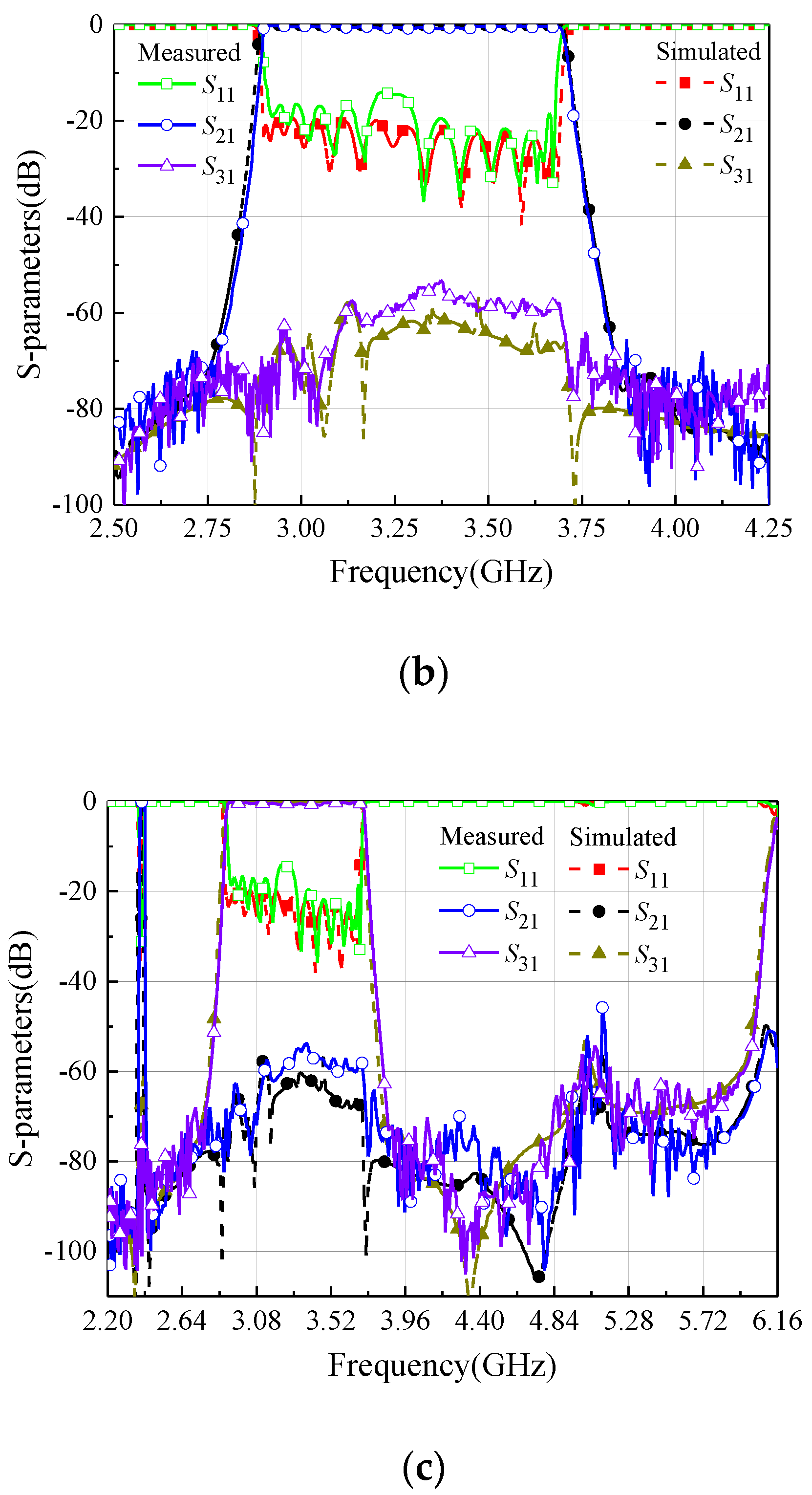
4. Design of HIS Diplexer
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hendry, D.R.; Abbosh, A.M. Compact high-isolation base-station duplexer using triple-mode ceramic cavities. IEEE Trans. Ind. Electron. 2018, 65, 8092–8100. [Google Scholar] [CrossRef]
- Xie, Y.; Chen, F.C.; Chu, Q.X. Tunable Cavity Filter and Diplexer Using In-Line Dual-Post Resonators. IEEE Trans. Microw. Theory Tech. 2022, 70, 3188–3199. [Google Scholar] [CrossRef]
- Wu, Y.; Wu, H.; Wang, W.; Yang, Y.; Lai, Z.; Yang, Q. A Compact Low-Loss High-Selectivity Excellent-Isolation FBAR Duplexer Integrated Chip for LTE Band-3 Industrial Applications. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 4563–4567. [Google Scholar] [CrossRef]
- Tian, H.; Chen, Z.; Chang, L.; Wang, R.; Wang, S.; Liu, H.; Du, C.; Zhou, D.; Ma, Z. Differentially Fed Duplex Filtering Dielectric Resonator Antenna With High Isolation and CM Suppression. IEEE Trans. Circuits Syst. II Express Briefs 2021, 69, 979–983. [Google Scholar] [CrossRef]
- van Liempd, B.; Visweswaran, A.; Ariumi, S.; Hitomi, S.; Wambacq, P.; Craninckx, J. Adaptive RF front-ends using electrical-balance duplexers and tuned SAW resonators. IEEE Trans. Microw. Theory Tech. 2017, 65, 4621–4628. [Google Scholar] [CrossRef]
- Psychogiou, D.; Gómez-García, R.; Peroulis, D. Tune-all RF planar duplexers with intrinsically switched channels. IEEE Microw. Wirel. Compon. Lett. 2017, 27, 350–352. [Google Scholar] [CrossRef]
- Park, J.; Jin, S.; Moon, K.; Kim, B. Wide-band duplexer based on electrical balance of hybrid transformer having two notches. Electron. Lett. 2016, 52, 1151–1153. [Google Scholar] [CrossRef]
- Li, C. Recent progress of superconducting electronics in China. Acta Phys. Sin. 2021, 70, 184–209. [Google Scholar] [CrossRef]
- Wang, L.T.; He, M.; Xiong, Y.; Zhang, W.; Chen, H.-H.; Ji, L. Design of high selectivity narrowband eight-order high-temperature superconducting sextaplexer. Supercond. Sci. Technol. 2020, 33, 115016. [Google Scholar] [CrossRef]
- Kuroda, A.; Saito, A.; Ohshima, S. Design and Fabrication of Compact HTS Duplexers Using a CQ Structure With a High Qu Resonator. IEEE Trans. Appl. Supercond. 2014, 25, 1–4. [Google Scholar] [CrossRef]
- Xu, Z.; Jingping, L.; Shaolin, Y.; Lan, F.; Bo, Z.; Xinjie, Z. Miniaturized high-temperature superconducting multiplexer with cascaded quadruplet structure. Supercond. Sci. Technol. 2015, 28, 065016. [Google Scholar] [CrossRef]
- Cameron, R.J.; Harish, A.; Radcliffe, C.J. Synthesis of advanced microwave filters without diagonal cross-couplings. IEEE Trans. Microw. Theory Tech. 2002, 50, 2862–2872. [Google Scholar] [CrossRef]
- Guan, X.; Gui, P.; Ren, B.; Zhang, X. Compact quad-channel high-temperature superconducting diplexer based on stub-loaded square ring resonator. Int. J. RF Microw. Comput.-Aided Eng. 2019, 29, e21725. [Google Scholar] [CrossRef]
- Yue, H.; Tang, H.; Wang, L.; Gong, L.; Li, C.; Wei, B.; Xie, Q.; Duan, J. Design of miniature high-temperature superconducting quadruplexer with wide stopband suppression. Phys. C Supercond. Its Appl. 2020, 579, 1353735. [Google Scholar] [CrossRef]
- Zhou, L.G.; Zhang, W.; Wong, P.K.J.; Bai, X.D.; Long, Z.H.; Zhang, T.L. Synthesis and design of asymmetric cul-de-sac structure HTS filter with transmission zero introduced in Pairs. Supercond. Sci. Technol. 2022, 35, 115004. [Google Scholar] [CrossRef]
- Zhou, L.; Li, H.; Long, Z.; Wu, H.; Zhang, T.; Qiao, M. Novel configuration of a HTS filter with adjustable transmission zeros based on a modified cascaded quartet structure. Supercond. Sci. Technol. 2018, 31, 085008. [Google Scholar] [CrossRef]
- Teng, Z.; Zhong, L.; Chen, G.; Zhou, T.; Gong, L.; He, M.; Zhang, X. Design of extensible superconducting multiplexer with modular structure to overcome the limit of wafer size. Phys. C Supercond. Its Appl. 2020, 578, 1353736. [Google Scholar] [CrossRef]
- Zhou, L.; Long, Z.; Wu, H.; Han, Y.; Li, H.; Zhang, T. Design of special asymmetric cul-de-sac unit configuration high temperature superconductor filter with multi-pair of transmission zeros. Supercond. Sci. Technol. 2020, 33, 085006. [Google Scholar] [CrossRef]

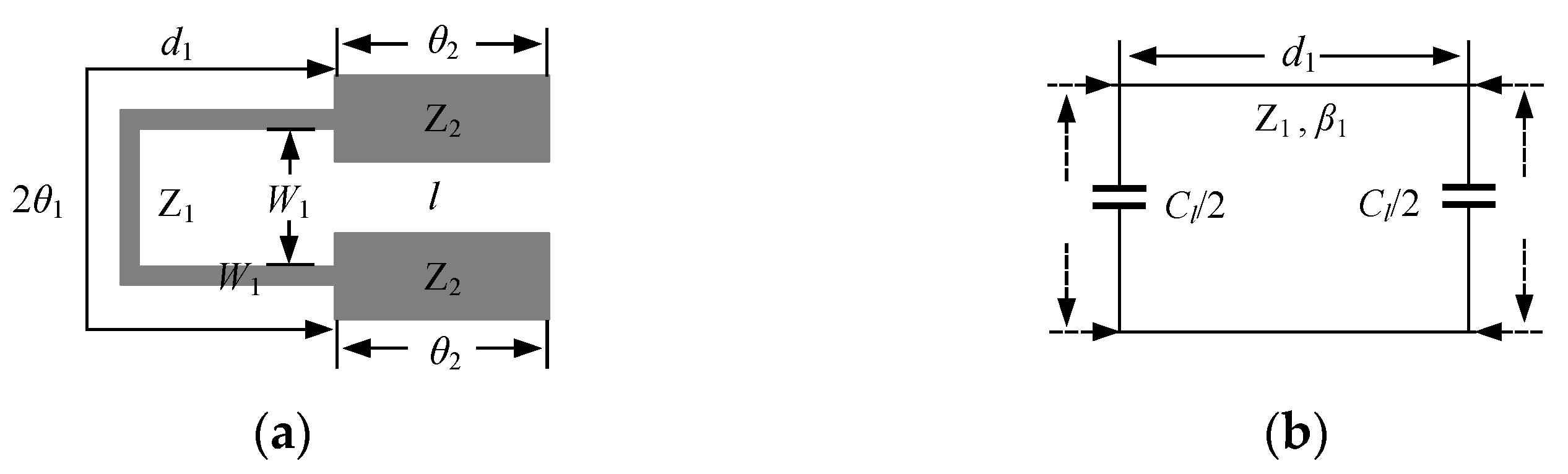

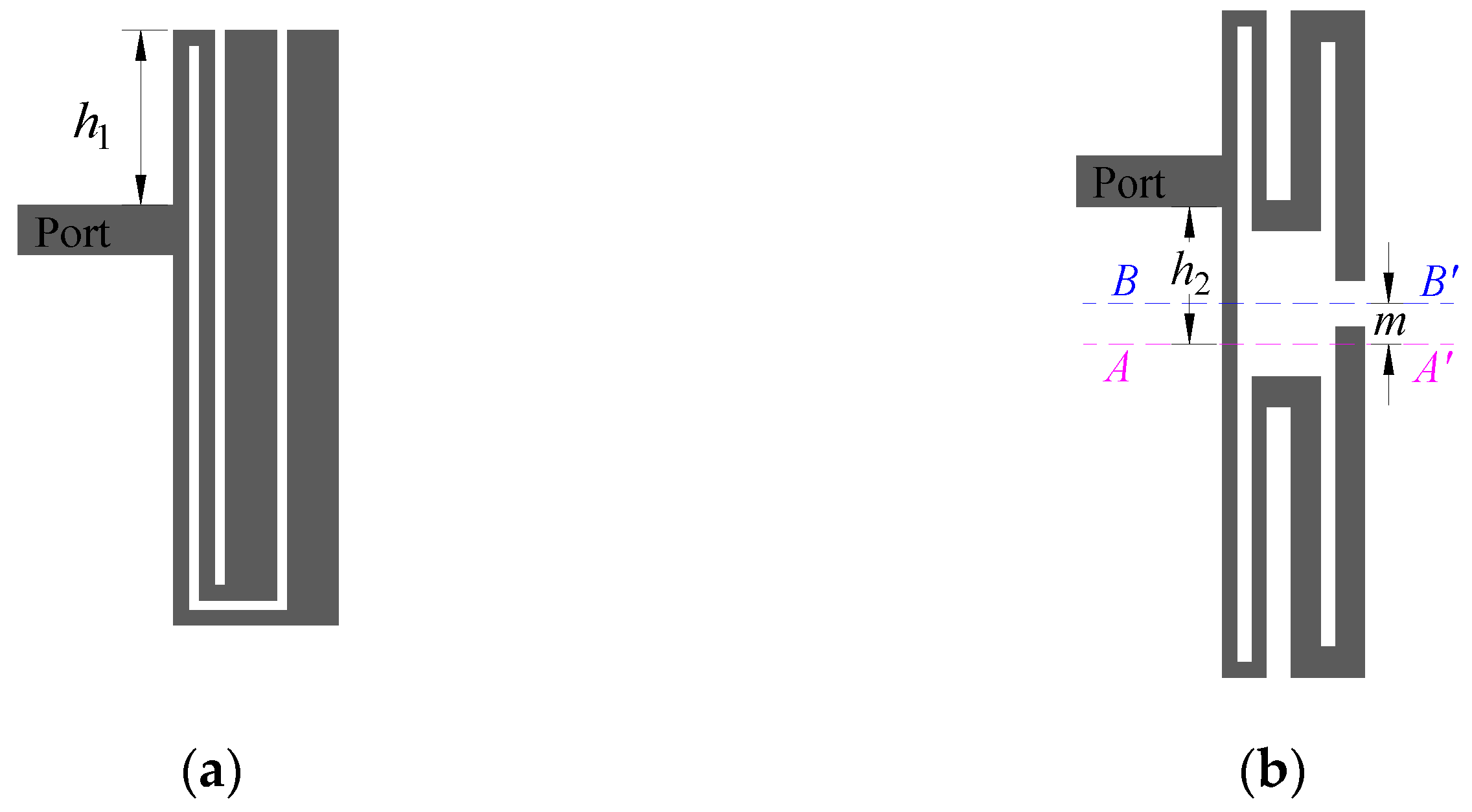
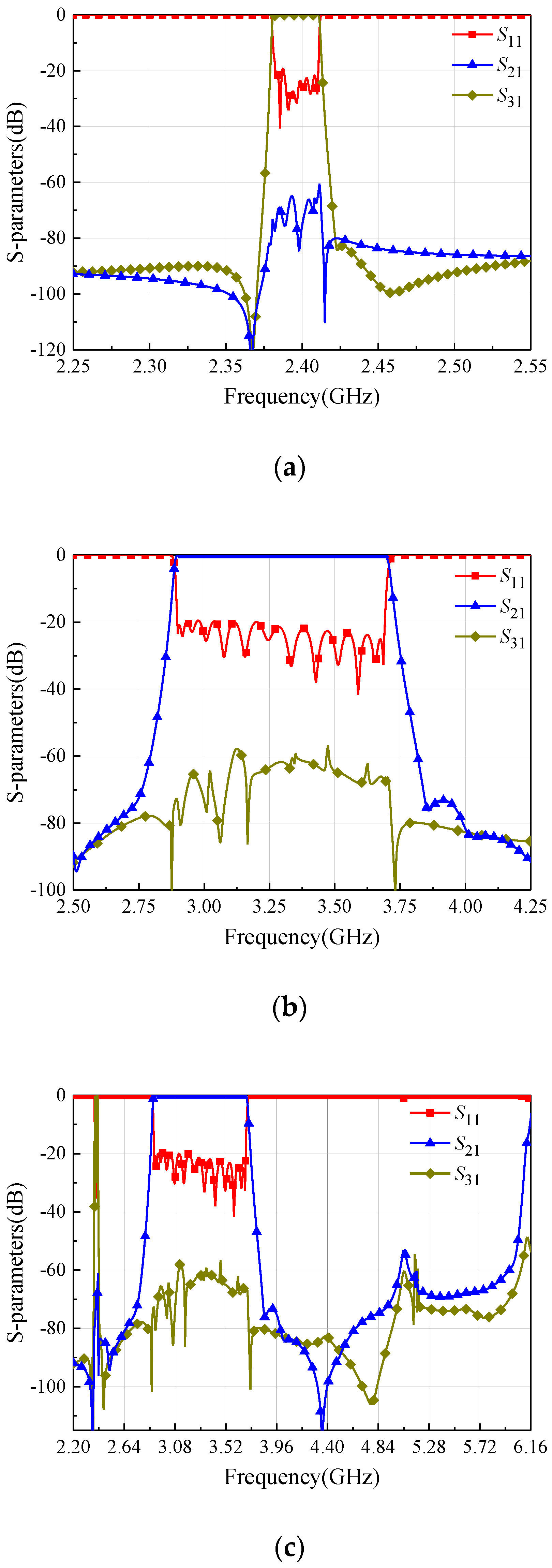

| Filter A | Filter B | |
|---|---|---|
| Passband bandwidth (MHz) | 2380~2410 | 2900~3700 |
| Insert loss (dB) | ≤0.2 | ≤0.2 |
| Fractional bandwidths (%) | 1.25 | 24.24 |
| Out-of-band suppression (dB) | ≥80 | ≥70 |
| Order of filter | 12 | 14 |
| Return loss (dB) | ≤−20 | ≤−20 |
| Parasitic passband (GHz) | ≥5.2 GHz | ≥6.6 GHz |
| Ratio of f1/f0 | ≥2.2 | ≥2 |
| Filter | Coupling Coefficient | |||||
|---|---|---|---|---|---|---|
| A | m1,2 | m2,3 | m3,4 | m4,5 | m5,6 | m6,7 |
| 0.0164 | 0.0091 | 0.0074 | 0.0070 | 0.0069 | 0.0068 | |
| m7,8 | m8,9 | m9,10 | m10,11 | m11,12 | Q | |
| 0.0069 | 0.0070 | 0.0074 | 0.0091 | 0.0164 | 46.95 | |
| B | m1,2 | m2,3 | m3,4 | m4,5 | m5,6 | m6,7 |
| 0.1971 | 0.1405 | 0.1305 | 0.1272 | 0.1260 | 0.1256 | |
| m7,8 | m8,9 | m9,10 | m10,11 | m11,12 | Q | |
| 0.1260 | 0.1272 | 0.1305 | 0.1405 | 0.1971 | 13.47 | |
| Channel | Coupling Coefficient | |||||
|---|---|---|---|---|---|---|
| I | m1,2 | m2,3 | m3,4 | m4,5 | m5,6 | m6,7 |
| 0.0149 | 0.0092 | 0.0079 | 0.0075 | 0.0073 | 0.0071 | |
| m7,8 | m8,9 | m9,10 | m10,11 | m11,12 | Q | |
| 0.0071 | 0.0073 | 0.0077 | 0.0089 | 0.0154 | 46.19 | |
| II | m1,2 | m2,3 | m3,4 | m4,5 | m5,6 | m6,7 |
| 0.2001 | 0.1404 | 0.1322 | 0.1286 | 0.1275 | 0.1268 | |
| m7,8 | m8,9 | m9,10 | m10,11 | m11,12 | Q | |
| 0.1270 | 0.1285 | 0.1314 | 0.1404 | 0.1955 | 12.24 | |
| Specifications | Simulated | Measured |
|---|---|---|
| Channel I (MHz) | 2379~2411 | 2378~2410 |
| Channel II (MHz) | 2898~3701 | 2900~3702 |
| Out-of-band rejection (dB) | 82/80 | 80/80 |
| Insertion loss (dB) | 0.08/0.09 | 0.11/0.12 |
| Return loss (dB) | −21/−21 | −16/−15 |
| Band-edge steepness (dB/MHz) | 9.9/2.2 | 9.7/2.3 |
| Isolation (dB) | 62/60 | 59/57 |
| Parasitic passband (GHz) | 2.2/2.0 | 2.2/2.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, L.; Zhou, W.; Sun, Y.; Han, Y.; Jiang, J.; Zhang, D. Design of High-Order Resonator HTS Diplexer with Very Different FBW. Electronics 2023, 12, 691. https://doi.org/10.3390/electronics12030691
Zhou L, Zhou W, Sun Y, Han Y, Jiang J, Zhang D. Design of High-Order Resonator HTS Diplexer with Very Different FBW. Electronics. 2023; 12(3):691. https://doi.org/10.3390/electronics12030691
Chicago/Turabian StyleZhou, Liguo, Weikang Zhou, Yuehang Sun, Yu Han, Jiang Jiang, and Dongwei Zhang. 2023. "Design of High-Order Resonator HTS Diplexer with Very Different FBW" Electronics 12, no. 3: 691. https://doi.org/10.3390/electronics12030691
APA StyleZhou, L., Zhou, W., Sun, Y., Han, Y., Jiang, J., & Zhang, D. (2023). Design of High-Order Resonator HTS Diplexer with Very Different FBW. Electronics, 12(3), 691. https://doi.org/10.3390/electronics12030691





