Review of Methodologies and Metrics for Assessing the Quality of Random Number Generators
Abstract
:1. Introduction
- Dieharder [5]: This is a suite of statistical tests designed to evaluate the quality of RNGs. It includes a wide range of tests that measure different aspects of the output, including uniformity, independence, and unpredictability.
- PractRand [6]: This is another suite of statistical tests that are designed to evaluate the quality of RNGs. It includes a range of tests that measure different aspects of the output, including uniformity, independence, and unpredictability.
- ENT [7]: ENT (short for “Entropy”) is a command-line tool that can be used to test the quality of Pseudo-Random Number Generators (PRNGs). ENT can be used to evaluate the quality of a PRNG by comparing its output to the output of a True Random Number Generator (TRNG).
- RaBiGeTe [8]: RaBiGeTe (short for “Random Bit Generators Tester”) is a tool for evaluating the quality of PRNGs. It runs a series of statistical tests on their output. The tests are designed to detect biases or patterns in the output of the PRNG that may indicate poor quality.
- In Section 2, we present and describe the taxonomy and the classification methods for RNGs;
- In Section 3, we analyse and schematise the entropy validation procedure according to the most important standardisation agency and provide a simplified workflow to ease the setup of such procedures;
- In Section 4, the same is carried out for randomness evaluation procedures;
- In Section 5, we conclude our work.
2. RBG: Classification, Construction, and Functionality Classes
2.1. NIST Classification and Construction
2.1.1. SP800-90A [12]
- An instantiate function, which involves the acquisition of randomness to initialise the DRBG and its internal state.
- A generate function, which produces the output bitstream and updates the internal state of the DRBG.
- Health testing to determine whether the DRBG operates properly.
2.1.2. SP 800-90B [9]
2.1.3. SP 800-90C [13]
2.2. BSI Classification and Construction
2.2.1. DRG.2, DRG.3, and DRG.4
2.2.2. PTG.2 and PTG.3
2.2.3. NTG.1
3. Procedures for Entropy Assessment
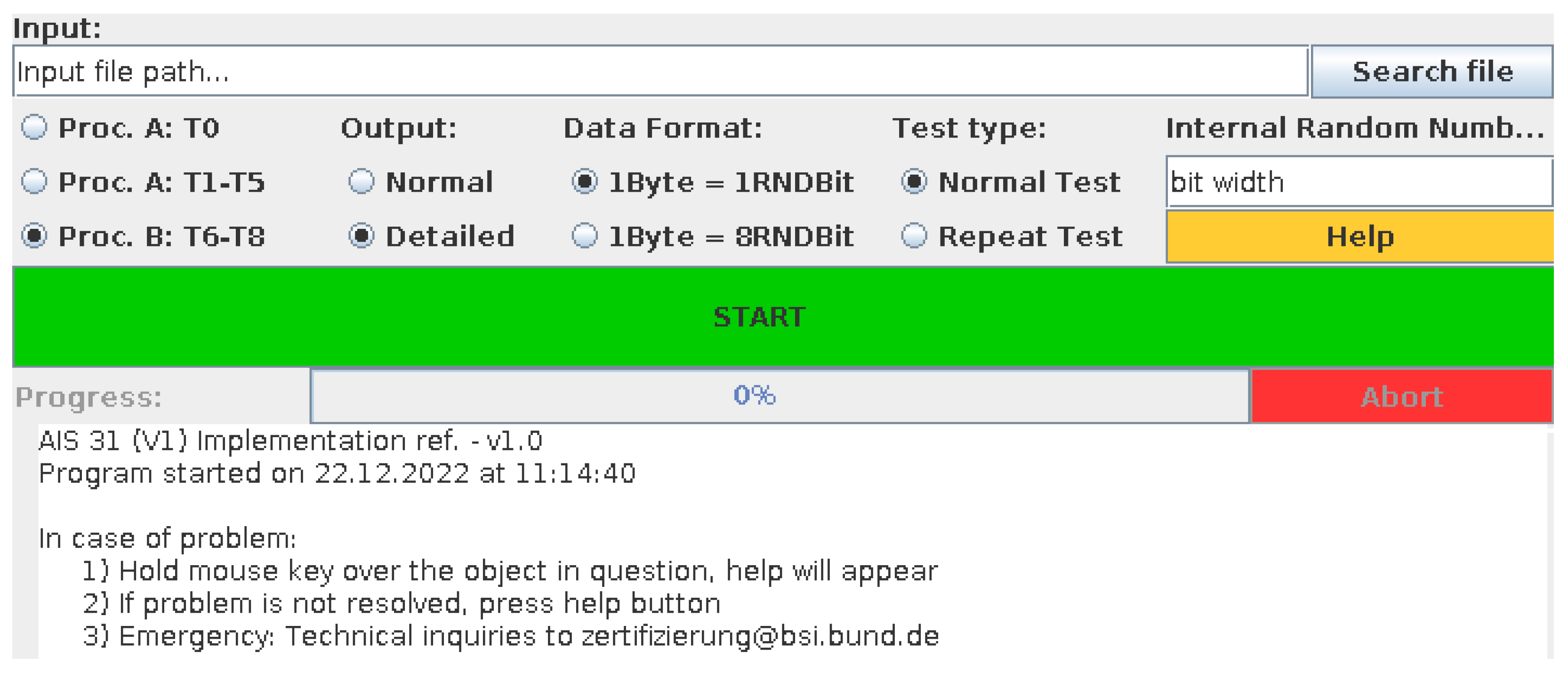
- procedure B of the BSI suite, i.e., the battery of tests T6 to T8;
- the NIST EA suite.
3.1. Entropy Assessment with Procedure B of the BSI Suite
| Listing 1. Output of procedure B of BSI suite. |
 |
3.2. Entropy Assessment with the NIST EA Suite
- an analogue source of noise (i.e., the analogue entropy source);
- a block for the digitisation of the analogue source of noise;
- an optional conditioning block (for post-processing of the digitised source of noise);
- an optional (parallel) unit for online health tests.
- EA Independent and Identically Distributed (IID) (ea_iid executable);
- EA non-IID (ea_non_iid executable);
- EA Restart (ea_restart executable);
- EA Conditioning (ea_conditioning executable),
- first entropy () estimation by using the ea_iid executable (or ea_non_iid);
- second entropy () estimation by using the ea_restart executable to update ;
- third entropy () estimation by using the ea_conditioning executable to update .
| Listing 2. Output of the ea_iid test of the NIST EA suite. The elements H_original and H_bitstring correspond, respectively, to the values of Horiginal and Hbitstring in the text. |
 |
| Listing 3. Output ea_restart test of the NIST EA suite. The elements H_I, H_r, and H_c correspond, respectively, to the values of HI, Hr, and Hc in the text. |
 |
3.3. Shannon Entropy
4. Procedure for Randomness Assessment
- the p-value, which is defined as the probability that a perfect random number generator would have produced a sequence that is less random than the tested sequence;
- the significance (or confidence) level, which is denoted by .
4.1. Randomness Assessment with Procedure A of the BSI Suite
- execution of test T0;
- execution of the group of tests T1–T5.
| Listing 4. Output of procedure A (test T0) of the BSI suite. |
 |
| Listing 5. Output of procedure A (tests T1–T5) of the BSI suite. |
 |
4.2. Randomness Assessment with the (Fast) NIST STS Suite
- The p-value of each sequence is calculated, and the sequences for which p-value are discarded;
- The PR value is calculated as the ratio between the number of sequences that passed the test (p-value ) and the total number of tested sequences (k);
- The p-values of sequences that passed the test are distributed in the range by splitting it into 10 equal sub-intervals named C1, C2, C3, and so on, up to C10, respectively, for ranges , , , …, up to , and the uniformity of the p-values’ distribution is calculated by exploiting the chi-square (other notations of this function are chi-squared or ) function. This measure of uniformity corresponds to the PoP value.
- The PR value lies in the confidence interval defined as ;
- PoP .
- the input file containing the samples;
- the number of sequences (k);
- the bit length of input sequences (n);
- the block length (M) for the Block Frequency Test;
- the block length (m) for the NonOverlapping Template Test;
- the block length (m) for the Overlapping Template Test;
- the block length (m) for the Approximate Entropy Test;
- the block length (m) for the Serial Test;
- the block length (M) for the Linear Complexity Test.
- (for );
- ;
- M (Block Frequency Test) ;
- m (NonOverlapping Template Test) ;
- m (Overlapping Template Test) ;
- m (Approximate Entropy Test) ;
- m (Serial Test) ;
- M (Linear Complexity Test) .
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Simion, E. Entropy and Randomness: From Analogic to Quantum World. IEEE Access 2020, 8, 74553–74561. [Google Scholar] [CrossRef]
- Lin, Y.; Wang, F.; Liu, B. Random number generators for large-scale parallel Monte Carlo simulations on FPGA. J. Comput. Phys. 2018, 360, 93–103. [Google Scholar] [CrossRef]
- Ergun, S. Security analysis of a chaos-based random number generator for applications in cryptography. In Proceedings of the 2015 15th International Symposium on Communications and Information Technologies (ISCIT), Nara, Japan, 7–9 October 2015; pp. 319–322. [Google Scholar] [CrossRef]
- Ryabko, B. Time-adaptive statistical test for random number generators. Entropy 2020, 22, 630. [Google Scholar] [CrossRef] [PubMed]
- Marsaglia, G. The Marsaglia Random Number CDROM Including the Diehard Battery of Tests of Randomness. 2008. Available online: http://www.stat.fsu.edu/pub/diehard/ (accessed on 2 January 2023).
- Sleem, L.; Couturier, R. TestU01 and Practrand: Tools for a randomness evaluation for famous multimedia ciphers. Multimed. Tools Appl. 2020, 79, 24075–24088. [Google Scholar] [CrossRef]
- Walker, J. ENT—A Pseudorandom Number Sequence Test Program. Available online: https://www.fourmilab.ch/random/ (accessed on 30 November 2022).
- Random Bit Generator Tester (RaBiGeTe)—Random Bit Generators Tester. Available online: http://cristianopi.altervista.org/RaBiGeTe_MT/ (accessed on 30 November 2022).
- NIST. Recommendation for the Entropy Sources Used for Random Bit Generation; SP 800-90B; NIST: Gaithersburg, MD, USA, 2018. [Google Scholar]
- BSI. Implementation of Test Procedure A and Test Procedure B for Application Notes and Interpretation of the Scheme (AIS) 20/31 Standard. Available online: https://www.bsi.bund.de/SharedDocs/Downloads/DE/BSI/Zertifizierung/Interpretationen/AIS_31_testsuit_zip.zip (accessed on 30 November 2022).
- NIST. A Statistical Test Suite for Random and Pseudorandom Number Generators for Cryptographic Applications; SP 800-22; NIST: Gaithersburg, MD, USA, 2010. [Google Scholar]
- NIST. Recommendation for Random Number Generation Using Deterministic Random Bit Generators; SP 800-90A Rev. 1; NIST: Gaithersburg, MD, USA, 2015. [Google Scholar]
- NIST. Recommendation for Random Bit Generator (RBG) Constructions; SP 800-90C (Draft); NIST: Gaithersburg, MD, USA, 2016. [Google Scholar]
- BSI. A Proposal for Functionality Classes for Random Number Generators. Available online: https://www.bsi.bund.de/SharedDocs/Downloads/EN/BSI/Certification/Interpretations/AIS_31_Functionality_classes_for_random_number_generators_e.pdf?__blob=publicationFile&v=4 (accessed on 30 November 2022).
- Nannipieri, P.; Di Matteo, S.; Baldanzi, L.; Crocetti, L.; Belli, J.; Fanucci, L.; Saponara, S. True Random Number Generator Based on Fibonacci-Galois Ring Oscillators for FPGA. Appl. Sci. 2021, 11, 3330. [Google Scholar] [CrossRef]
- Crocetti, L.; Di Matteo, S.; Nannipieri, P.; Fanucci, L.; Saponara, S. Design and Test of an Integrated Random Number Generator with All-Digital Entropy Source. Entropy 2022, 24, 139. [Google Scholar] [CrossRef] [PubMed]
- Killmann, W.; Schindler, W. A proposal for: Functionality Classes for Random Number Generators, Version 2.0. In Mathematical-Technical Reference of AIS 20/31; T-Systems GEI GmbH: Bonn, Germany, 2011. [Google Scholar]
- NIST. SP 800-90B Entropy Assessment Software, Version 1.0. 2019. Available online: https://github.com/usnistgov/SP800-90B_EntropyAssessment (accessed on 30 November 2022).
- Baldanzi, L.; Crocetti, L.; Falaschi, F.; Belli, J.; Fanucci, L.; Saponara, S. Digital Random Number Generator Hardware Accelerator Intellectual Property (IP)-Core for Security Applications. In Applications in Electronics Pervading Industry, Environment and Society. ApplePies 2019; Lecture Notes in Electrical Engineering (LNEE); Springer: Berlin/Heidelberg, Germany, 2020; Volume 627, pp. 117–123. [Google Scholar] [CrossRef]
- Baldanzi, L.; Crocetti, L.; Falaschi, F.; Bertolucci, M.; Belli, J.; Fanucci, L.; Saponara, S. Cryptographically Secure Pseudo-Random Number Generator IP-Core Based on Secure Hash Algorithm (SHA)2 Algorithm. Sensors 2020, 20, 1869. [Google Scholar] [CrossRef] [PubMed]
- Nannipieri, P.; Bertolucci, M.; Baldanzi, L.; Crocetti, L.; Di Matteo, S.; Falaschi, F.; Fanucci, L.; Saponara, S. SHA2 and SHA-3 accelerator design in a 7 nm technology within the European Processor Initiative. Microprocess. Microsystems 2021, 87, 103444. [Google Scholar] [CrossRef]
- Sýs, M.; Riha, Z.; Matyas, V.; Marton, K.; Suciu, A. On the Interpretation of Results from the NIST Statistical Test Suite. Rom. J. Inf. Sci. Technol. (ROMJIST) 2015, 18, 18–32. [Google Scholar]
- Sỳs, M.; Říha, Z. NIST STS Optimised v6.0.1. 2020. Available online: https://github.com/sysox/NIST-STS-optimised/files/4052762/Fast_NIST_STS_v6.0.1.zip (accessed on 30 November 2022).
- NIST. SP 800-22 STS Software, Version 2.1.1. 2010. Available online: https://csrc.nist.gov/CSRC/media/Projects/Random-Bit-Generation/documents/sts-2_1_2.zip (accessed on 30 November 2022).
- BSI. Functionality Classes and Evaluation Methodology for Physical Random Number Generators, Version 1; AIS 31; BSI: Herndon, VA, USA, 2001. [Google Scholar]








| General Term | RBGs | ||
|---|---|---|---|
| Deterministic or non-deterministic | DRBGs | Entropy source | |
| Noise sources | – | Physical | Non-physical |
| RBG.1 | |||
| Constructions | RBG.2 | ||
| RBG.3 | |||
| General Term | RNGs | ||
|---|---|---|---|
| Deterministic or non-deterministic | DRNGs | TRNGs | |
| Noise sources | – | PTRNGs | NPTRNGs |
| Functionality classes | DRG.2 DRG.3 DRG.4 | PTG.2 PTG.3 | NTG.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Crocetti, L.; Nannipieri, P.; Di Matteo, S.; Fanucci, L.; Saponara, S. Review of Methodologies and Metrics for Assessing the Quality of Random Number Generators. Electronics 2023, 12, 723. https://doi.org/10.3390/electronics12030723
Crocetti L, Nannipieri P, Di Matteo S, Fanucci L, Saponara S. Review of Methodologies and Metrics for Assessing the Quality of Random Number Generators. Electronics. 2023; 12(3):723. https://doi.org/10.3390/electronics12030723
Chicago/Turabian StyleCrocetti, Luca, Pietro Nannipieri, Stefano Di Matteo, Luca Fanucci, and Sergio Saponara. 2023. "Review of Methodologies and Metrics for Assessing the Quality of Random Number Generators" Electronics 12, no. 3: 723. https://doi.org/10.3390/electronics12030723









