A Novel Monogenic Sobel Directional Pattern (MSDP) and Enhanced Bat Algorithm-Based Optimization (BAO) with Pearson Mutation (PM) for Facial Emotion Recognition
Abstract
:1. Introduction
- A novel feature-extraction technique based on fractional Sobel edge detection is proposed as MSDP that is rotation, scale, and blur-resistant;
- A novel Pearson Mutation (PM) operator-based Bat algorithm-based optimization (BAO) is used for obtaining best parameters of MSDP;
- A novel Pearson Kernel-based Supervised Principal Component Analysis (PKSPCA) for dimension reduction is proposed for reducing the dimension of features.
2. Related Works
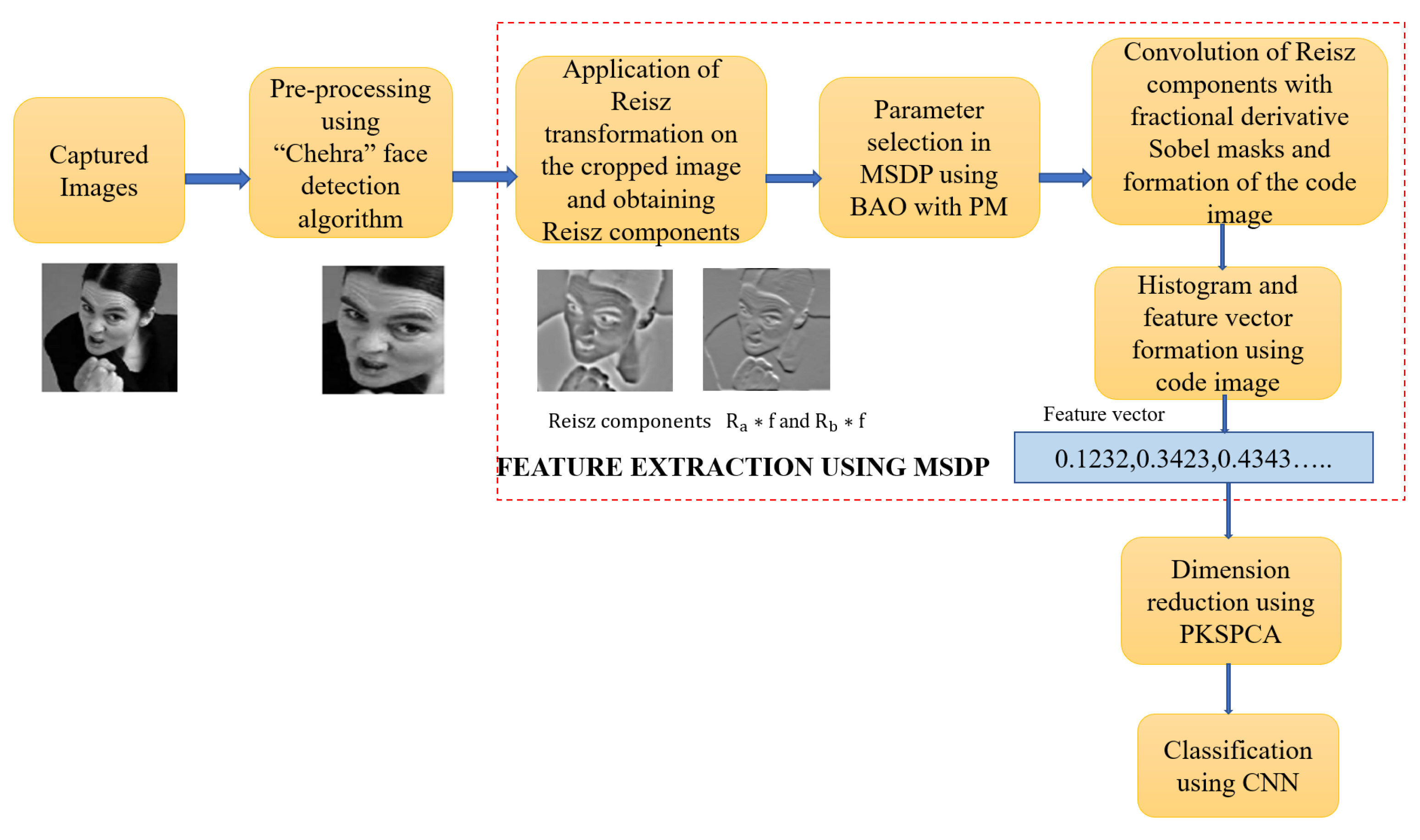
3. Methodology of the Proposed Work
3.1. Face Detection Using Chehra
3.2. Proposed Feature Descriptor MSDP
Creation of Multiscale, Noise Insensitive, Rotation Invariant Edge, and Texture Features as MSDP
3.3. Bat Algorithm-Based Optimization of Parameters with Pearson Mutation
| Algorithm 1 Bat algorithm-based optimization of parameters with Pearson Mutation. |
| Procedure BAO_PM (α, λ) Input: A range of values for α and λ of MSDP Output: Optimized values of α and λ Parameters: α—Set of values of α λ—Set of values of frequencies new_α—Optimized value for α of MSDP new_λ—Optimized value for λ αi—ith value of α λj—jth value of λ CNN acc—Accuracy obtained with CNN using αi and λj CNN acc is considered as the fitness parameter and objective function of this algorithm |
| 1. Set the values of α and λ; |
| 2. Evaluate the preliminary population; |
| 3. While the finish condition is not attained; |
| 4. Create new solutions by altering αi and λj; |
| 5. |
| 6. ; |
| 7. ; |
| 8. Update αi and λj using Pearson Mutation; |
| 9. Obtain CNN acc; |
| 10. If CNN acc > best_accuracy; |
| 11. Set new_α = αi; |
| 12. Set new_λ = λj; |
| 13. Set best_accuracy = CNN acc; |
| 14. Rank the best_accuracy as globally best accuracy; |
| 15. Update αi and λj; |
| 16. End; |
| 17. End While; |
| 18. Store new_α and new_λ; |
| 19. Assign the values of α and λ as new_α and new_λ; |
| 20. Return new optimized values of α and λ; |
| 21. End Procedure. |
3.4. Feature Vector Construction from the Histogram of Grids
3.5. The Proposed Pearson Kernel-Based Supervised Principal Component Analysis (PKSPCA)
3.6. Classification
4. The Analysis and Validation of Results Obtained Using the Proposed Method
4.1. Datasets
4.2. Experimental Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Calculation of Optimal Number of Eigen Vectors and Principal Components for PKSPCA
| Number of Principal Components (p) | 5 | 15 | 25 | 35 | 45 | 55 |
|---|---|---|---|---|---|---|
| Accuracy in% | 89.4 | 90.2 | 95.4 | 97.6 | 97.6 | 97.6 |
| Number of Eigen Vectors (d) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Accuracy in % | 86.4 | 90.2 | 92.2 | 94.4 | 94.8 | 94.9 | 97.6 | 97.6 | 97.6 | 97.7 |
References
- Mehta, D.; Siddiqui, M.F.H.; Javaid, A.Y. Facial Emotion Recognition: A Survey and Real-World User Experiences in Mixed Reality. Sensors 2018, 18, 416. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.; Gong, J. Facial expression recognition based on improved LeNet-5 CNN. In Proceedings of the 2019 Chinese Control and Decision Conference (CCDC), Nanchang, China, 3–5 June 2019; pp. 5655–5660. [Google Scholar]
- Alphonse, A.S.; Dharma, D. Novel directional patterns and a Generalized Supervised Dimension Reduction System (GSDRS) for facial emotion recognition. Multimed. Tools Appl. 2018, 77, 9455–9488. [Google Scholar] [CrossRef]
- Garcia Freitas, P.; Da Eira, L.P.; Santos, S.S.; Farias, M.C. On the application LBP texture descriptors and its variants for no-reference image quality assessment. J. Imaging 2018, 4, 114. [Google Scholar] [CrossRef]
- Chikkerur, S.; Cartwright, A.N.; Govindaraju, V. Fingerprint enhancement using STFT analysis. Pattern Recognit. 2007, 40, 198–211. [Google Scholar] [CrossRef]
- Huang, X.; Zhao, G.; Zheng, W.; Pietikainen, M. Spatiotemporal local monogenic binary patterns for facial expression recognition. IEEE Signal Process Lett. 2012, 19, 243–246. [Google Scholar] [CrossRef]
- Chen, J.; Huang, C.; Du, Y.; Lin, C. Combining fractional-order edge detection and chaos synchronisation classifier for fingerprint identification. IET Image Process 2014, 8, 354–362. [Google Scholar] [CrossRef]
- Chi, C.; Gao, F. Palm Print Edge Extraction Using Fractional Differential Algorithm. J. Appl. Math. 2014, 2014, 896938. [Google Scholar] [CrossRef]
- Dong, F.; Chen, Y. A Fractional-order derivative based variational framework for image denoising. Inverse Probl. Imaging 2016, 10, 27–50. [Google Scholar] [CrossRef]
- Ismail, S.M.; Said, L.A.; Madian, A.H.; Radwan, A.G. Fractional-order edge detection masks for diabetic retinopathy diagnosis as a case study. Computers 2021, 10, 30. [Google Scholar] [CrossRef]
- Cajo, R.; Mac, T.T.; Plaza, D.; Copot, C.; De Keyser, R.; Ionescu, C. A survey on fractional order control techniques for unmanned aerial and ground vehicles. IEEE Access 2019, 7, 66864–66878. [Google Scholar] [CrossRef]
- Ojansivu, V.; Rahtu, E.; Heikkila, J. Rotation invariant local phase quantization for blur insensitive texture analysis. In Proceedings of the 2008 19th International Conference on Pattern Recognition, Tampa, FL, USA, 8–11 December 2008; pp. 1–4. [Google Scholar]
- Hamester, D.; Barros, P.; Wermter, S. Face expression recognition with a 2- channel convolutional neural network. In Neural Networks (IJCNN), Proceedings of the 2015 International Joint Conference on Killarney, Ireland, 12–17 July 2015; IEEE: New York City, NY, USA, 2015; pp. 1–8. [Google Scholar]
- Huang, G.B.; Zhou, H.; Ding, X.; Zhang, R. Extreme learning machine for regression and multiclass classification. Part B IEEE Trans. Syst. Man Cybern. 2012, 42, 513–529. [Google Scholar] [CrossRef]
- Huang, G.B.; Zhu, Q.Y.; Siew, C.K. Extreme learning machine: A new learning scheme of feedforward neural networks. Neural Netw. 2004, 2, 985–990. [Google Scholar]
- Reddy, G.T.; Khare, N. Hybrid firefly-bat optimized fuzzy artificial neural network-based classifier for diabetes diagnosis. Int. J. Intell. Eng. Syst. 2017, 10, 18–27. [Google Scholar] [CrossRef]
- Vincent, O.R.; Folorunso, O. A descriptive algorithm for sobel image edge detection. In Proceedings of the Informing Science & IT Education Conference (InSITE), Macon, GA, USA, 12–15 June 2009; Volume 40, pp. 97–107. [Google Scholar]
- Reddy, G.T.; Khare, N. An efficient system for heart disease prediction using hybrid OFBAT with rule-based fuzzy logic model. J. Circuits Syst. Comput. 2017, 26, 1750061. [Google Scholar] [CrossRef]
- Asthana, A.; Zafeiriou, S.; Cheng, S.; Pantic, M. Incremental face alignment in the wild. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Washington, DC, USA, 23–28 June 2014; pp. 1859–1866. [Google Scholar]
- Yang, X.S.; He, X. Bat algorithm: Literature review and applications. Int. J. BioInspired Comput. 2013, 5, 141–149. [Google Scholar] [CrossRef]
- Üstün, B.; Melssen, W.J.; Buydens, L.M. Facilitating the application of Support Vector Regression by using a universal Pearson VII function based Kernel. Chemom. Intell. Lab. Syst. 2006, 81, 29–40. [Google Scholar] [CrossRef]
- Jia, B.; Huang, B.; Gao, H.; Li, W. Dimension reduction in radio maps based on the supervised kernel principal component analysis. Soft Comput. 2018, 22, 7697–7703. [Google Scholar] [CrossRef]
- Lucey, P.; Cohn, J.F.; Kanade, T.; Saragih, J.; Ambadar, Z.; Matthews, I. The extended cohn-kanade dataset (ck+): A complete dataset for action unit and emotion-specified expression. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), San Francisco, CA, USA, 13–18 June 2010; pp. 94–101. [Google Scholar]
- Lyons, M.; Akamatsu, S.; Kamachi, M.; Gyoba, J. Coding facial expressions with gabor wavelets. In Proceedings of the Third IEEE International Conference on Automatic Face and Gesture Recognition, Nara, Japan, 14–16 April 1998; pp. 200–205. [Google Scholar]
- Zhao, G.; Huang, X.; Taini, M.; Li, S.Z.; Pietikäinen, M. Facial expression recognition from near-infrared videos. Image Vis. Comput. 2010, 29, 607–619. [Google Scholar] [CrossRef]
- Ojala, T.; Pietikainen, M.; Maenpaa, T. Multiresolution gray-scale and rotation invariant texture classification with local binary patterns. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 971–987. [Google Scholar] [CrossRef]
- Pantic, M.; Valstar, M.; Rademaker, R.; Maat, L. Web-based database for facial expression analysis. In Proceedings of the Multimedia and Expo, IEEE International Conference, Amsterdam, The Netherlands, 6 July 2005; p. 5. [Google Scholar]
- Valstar, M.; Pantic, M. Induced disgust, happiness and surprise:an addition to the MMI facial expression database. In Proceedings of the 3rd International Workshop on EMOTION (Satellite of LREC): Corpora for Research on Emotion and Affect, London, UK, 23 May 2010. [Google Scholar]
- Pu, Y.-F. Fractional differential analysis for texture of digital image. J. Algorithms Comput. Technol. 2007, 1, 357–380. [Google Scholar]
- Aifanti, N.; Papachristou, C.; Delopoulos, A. The MUG facial expression database. In Proceedings of the 11th International Workshop on Image Analysis for Multimedia Interactive Services (WIAMIS), Desenzano, Italy, 12–14 April 2010. [Google Scholar]
- Dhall, A.; Goecke, R.; Joshi, J.; Sikka, K.; Gedeon, T. Emotion recognition in the wild challenge 2014: Baseline, data and protocol, ACM ICMI. In Proceedings of the 16th International Conference on Multimodal Interaction, Istanbul, Turkey, 12–16 November 2014. [Google Scholar]
- Dhall, A.; Goecke, R.; Lucey, S.; Gedeon, T. Collecting Large, Richly Annotated Facial Expression Databases from Movies. IEEE MultiMedia 2012, 19, 34–41. [Google Scholar] [CrossRef]
- Jabid, T.; Kabir, M.H.; Chae, O. Local directional pattern (LDP) for face recognition. In Proceedings of the 2010 Digest of Technical Papers International Conference on Consumer Electronics (ICCE), Las Vegas, NV, USA, 9–13 January 2010; pp. 329–330. [Google Scholar]
- Alphonse, A.S.; Dharma, D. A novel Monogenic Directional Pattern (MDP) and pseudo-Voigt kernel for facilitating the identification of facial emotions. J. Vis. Commun. Image Represent. 2017, 49, 459–470. [Google Scholar] [CrossRef]
- Fogel, I.; Sagi, D. Gabor filters as texture discriminator. Biol. Cybern. 1989, 61, 103–113. [Google Scholar] [CrossRef]
- Arya, R.; Vimina, E.R. Local triangular coded pattern: A texture descriptor for image classification. IETE J. Res. 2021, 1–2. [Google Scholar] [CrossRef]
- Qazi, H.A.; Jahangir, U.; Yousuf, B.M.; Noor, A. Human action recognition using SIFT and HOG method. In Proceedings of the 2017 International Conference on Information and Communication Technologies (ICICT), Karachi, Pakistan, 30–31 December 2017; pp. 6–10. [Google Scholar]
- Ahonen, T.; Rahtu, E.; Ojansivu, V.; Heikkila, J. Recognition of blurred faces using local phase quantization. In Proceedings of the 2008 19th International Conference on Pattern Recognition, Tampa, FL, USA, 8–11 December 2008; pp. 1–4. [Google Scholar]
- Zhang, B.; Shan, S.; Chen, X.; Gao, W. Histogram of gabor phase patterns (hgpp): A novel object representation approach for face recognition. IEEE Trans. Image Process 2006, 16, 57–68. [Google Scholar] [CrossRef]
- Zhang, W.; Shan, S.; Gao, W.; Chen, X.; Zhang, H. Local gabor binary pattern histogram sequence (lgbphs): A novel non-statistical model for face representation and recognition. In Proceedings of the Tenth IEEE International Conference on Computer Vision (ICCV’05) Volume 1, Beijing, China, 17–21 October 2005. [Google Scholar]
- Felzenszwalb, P.F.; Huttenlocher, D.P. Pictorial structures for object recognition. Int. J. Comput. Vis. 2005, 61, 55–79. [Google Scholar] [CrossRef]
- Lu, J.; Zhou, X.; Tan, Y.P.; Shang, Y.; Zhou, J. Neighborhood repulsed metric learning for kinship verification. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 36, 331–345. [Google Scholar]
- Hu, J.; Lu, J.; Liu, L.; Zhou, J. Multi-view geometric mean metric learning for kinship verification. In Proceedings of the 2019 IEEE International Conference on Image Processing (ICIP), Taipei, Taiwan, 22–25 September 2019; pp. 1178–1182. [Google Scholar]
- Guillaumin, M.; Mensink, T.; Verbeek, J.; Schmid, C. Tagprop: Discriminative metric learning in nearest neighbor models for image auto-annotation. In Proceedings of the 2009 IEEE 12th International Conference on Computer Vision, Kyoto, Japan, 29 September–2 October 2009; pp. 309–316. [Google Scholar]
- Huang, S.; Lin, J.; Huangfu, L. Class-prototype discriminative network for generalized zero-shot learning. IEEE Signal Process Lett. 2020, 27, 301–305. [Google Scholar] [CrossRef]
- Mahpod, S.; Keller, Y. Kinship verification using multiview hybrid distance learning. Comput. Vis. Image Underst. 2018, 167, 28–36. [Google Scholar] [CrossRef]
- Matsukawa, T.; Suzuki, E. Kernelized cross-view quadratic discriminant analysis for person re-identification. In Proceedings of the 2019 16th International Conference on Machine Vision Applications (MVA), Tokyo, Japan, 27–31 May 2019; pp. 1–5. [Google Scholar]
- Bessaoudi, M.; Ouamane, A.; Belahcene, M.; Chouchane, A.; Boutellaa, E.; Bourennane, S. Multilinear side-information based discriminant analysis for face and kinship verification in the wild. Neurocomputing 2019, 329, 267–278. [Google Scholar] [CrossRef]
- Shankar, P.B.; Vani, Y.D. Conceptual Glance of Genetic Algorithms in the Detection of Heart Diseases. In Proceedings of the 2021 International Conference on Advances in Electrical, Computing, Communication and Sustainable Technologies (ICAECT), Bhilai, India, 19–20 February 2021; pp. 1–4. [Google Scholar]
- Liu, P.; Han, S.; Meng, Z.; Tong, Y. Facial expression recognition via a boosted deep belief network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 1805–1812. [Google Scholar]
- Turan, C.; Lam, K.M.; He, X. Soft Locality Preserving Map (SLPM) for Facial Expression Recognition. arXiv 2018, arXiv:1801.03754. [Google Scholar]
- Wang, W.; Sun, Q.; Chen, T. A Fine-Grained Facial Expression Database for End-to-End Multi-Pose Facial Expression Recognition. arXiv 2019, arXiv:1907.10838. [Google Scholar]
- Yang, H.; Ciftci, U.; Yin, L. Facial expression recognition by de-expression residue learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 23–28 June 2018; pp. 2168–2177. [Google Scholar]
- Zhang, Z.; Luo, P.; Chen, C.L.; Tang, X. From facial expression recognition to interpersonal relation prediction. Int. J. Comput. Vis. 2018, 126, 1–20. [Google Scholar] [CrossRef]
- Zhao, R.; Liu, T.; Xiao, J.; Lun, D.P.; Lam, K.M. Deep multi-task learning for facial expression recognition and synthesis based on selective feature sharing. In Proceedings of the 2020 25th International Conference on Pattern Recognition (ICPR), Milan, Italy, 10–15 January 2021; pp. 4412–4419. [Google Scholar]
- Zheng, H.; Wang, R.; Ji, W.; Zong, M.; Wong, W.K.; Lai, Z.; Lv, H. Discriminative deep multi-task learning for facial expression recognition. Inf. Sci. 2020, 533, 60–71. [Google Scholar] [CrossRef]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An image is worth 16x16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Cui, Y.; Ma, Y.; Li, W.; Bian, N.; Li, G.; Cao, D. Multi-EmoNet: A Novel Multi-Task Neural Network for Driver Emotion Recognition. IFAC-PapersOnLine 2020, 53, 650–655. [Google Scholar] [CrossRef]
- Gera, D.; Balasubramanian, S. Landmark guidance independent spatio-channel attention and complementary context information based facial expression recognition. Pattern Recognit. Lett. 2021, 145, 58–66. [Google Scholar] [CrossRef]














| Resolution | Accuracy of MSDP for JAFFE (%) |
|---|---|
| 250 × 250 | 99.1 |
| 200 × 200 | 98.9 |
| 132 × 132 | 98.8 |
| 120 × 120 | 98.7 |
| 100 × 100 | 98.2 |
| Em (Emotions) | Anger (Ang) | Disgust (Dis) | Fear (Fear) | Happy (Hap) | Neutral (Neu) | Sad (Sad) | Surprise (Surp) |
|---|---|---|---|---|---|---|---|
| Ang | 99.67 | 0.33 | |||||
| Dis | 99.8 | 0.2 | |||||
| Fear | 93.44 | 1.0 | 3.53 | 2.03 | |||
| Hap | 0.5 | 96.8 | 2.2 | 0.5 | |||
| Neu | 98.2 | 1.8 | |||||
| Sad | 3.67 | 96.33 | |||||
| Surp | 0.8 | 99.2 |
| Em | Ang | Dis | Hap | Fear | Neu | Sad | Surp |
|---|---|---|---|---|---|---|---|
| Ang | 98 | 0.5 | 1.5 | ||||
| Dis | 99.3 | 0.10 | 0.60 | ||||
| Hap | 0.3 | 99.2 | 0.5 | ||||
| Fear | 99.74 | 0.26 | |||||
| Neu | 0.4 | 99 | 0.6 | ||||
| Sad | 100 | ||||||
| Surp | 0.46 | 99.54 |
| Em | Ang | Dis | Fear | Hap | Neu | Sad | Surp |
|---|---|---|---|---|---|---|---|
| Ang | 95.17 | 0.83 | 3.3 | 0.43 | 0.27 | ||
| Dis | 0.31 | 95.56 | 0.23 | 0.24 | 3.66 | ||
| Fear | 1.6 | 97.44 | 0 | 0.51 | 0.34 | 0.11 | |
| Hap | 0.17 | 0.51 | 99.08 | 0.24 | |||
| Neu | 0.23 | 99.77 | |||||
| Sad | 0.61 | 0.38 | 0.18 | 98.82 | |||
| Surp | 1.77 | 2.23 | 96.00 |
| Em | Ang | Dis | Fear | Hap | Neu | Sad | Surp |
|---|---|---|---|---|---|---|---|
| Ang | 63.7 | 1.3 | 4.3 | 4.7 | 14 | 7 | 5 |
| Dis | 6 | 64.4 | 0.6 | 7 | 4.9 | 9.1 | 8 |
| Fear | 14 | 81 | 2.5 | 2 | 0.5 | 0 | |
| Hap | 2 | 21.0 | 0.9 | 54.8 | 0 | 19 | 3 |
| Neu | 2 | 10.4 | 20 | 43 | 15.6 | 9 | |
| Sad | 16.4 | 4.3 | 16.4 | 14.2 | 40.7 | 8 | |
| Surp | 5.1 | 2.7 | 14 | 0.9 | 0 | 77.3 |
| Em | Ang | Dis | Fear | Hap | Neu | Sad | Surp |
|---|---|---|---|---|---|---|---|
| Ang | 97.67 | 2.33 | |||||
| Dis | 91.67 | 5 | 3.33 | ||||
| Fear | 13 | 0 | 77.94 | 6 | 11.03 | 3.03 | |
| Hap | 0.3 | 99 | 0.7 | ||||
| Neu | 0.1 | 9.8 | 88.1 | 1.1 | 0.9 | ||
| Sad | 2.6 | 8 | 0.4 | 5.67 | 83.0 | 0.33 | |
| Surp | 0.61 | 2.39 | 97.0 |
| Em | Ang | Dis | Fear | Hap | Neu | Sad | Surp |
|---|---|---|---|---|---|---|---|
| Ang | 94.87 | 0 | 1.4 | 0.33 | 0.4 | 3 | |
| Dis | 92.87 | 4 | 3.13 | ||||
| Fear | 12 | 82.74 | 0.8 | 1.03 | 3.03 | ||
| Hap | 1.3 | 98 | 0.7 | ||||
| Neu | 1.1 | 15 | 8.8 | 74.1 | 0.1 | 0.9 | |
| Sad | 0.6 | 7 | 0.4 | 6.57 | 85.2 | 0.33 | |
| Surp | 0.61 | 3.39 | 0.7 | 95.3 |
| Accuracy (%) | ||||||
|---|---|---|---|---|---|---|
| JAFFE | CK+ | MUG | SFEW | MMI | Oulu-CASIA | |
| LDP | 97.5 | 97.7 | 96.2 | 34.2 | 83.3 | 88.1 |
| LBP | 96.1 | 96.4 | 93.4 | 36.3 | 84.6 | 86.4 |
| Gabor | 98.3 | 96.1 | 94.2 | 35.9 | 84.1 | 88.2 |
| LDTP | 98.5 | 96.3 | 95.4 | 34.2 | 82.3 | 88.2 |
| LDN | 98.0 | 96.2 | 96.1 | 34.0 | 81.5 | 89.0 |
| LPQ | 96.1 | 96.2 | 97.2 | 34.0 | 82.0 | 88.0 |
| SIFT | 98.2 | 97.4 | 93.4 | 36.1 | 82.2 | 86.1 |
| HOG | 99.2 | 98.4 | 96.3 | 36.2 | 82.3 | 88.3 |
| RI-LPQ | 88.0 | 88.4 | 87.3 | 52.9 | 76.3 | 87.4 |
| HGPP | 88.0 | 84.2 | 84.1 | 28.9 | 78.4 | 86.4 |
| MRDNP | 97.0 | 97.0 | 95.1 | 35.3 | 82.3 | 87.0 |
| MDP | 97.0 | 97.0 | 95.2 | 35.4 | 82.3 | 87.1 |
| Proposed | 97.6 | 99.2 | 97.4 | 60.7 | 89.0 | 90.6 |
| Technique | Dataset | Classification Accuracy (%) |
|---|---|---|
| Hamester et al. [13] | JAFFE | 95.8 |
| Liu et al. [50] | JAFFE | 91.8 |
| Turan et al. [51] | JAFFE | 91.8 |
| Wang et al. [52] | JAFFE | 95.8 |
| Proposed | JAFFE | 97.6 |
| Yang et al. [53] | CK+ | 97.3 |
| Zhang et al. [54] | CK+ | 98.9 |
| Zhao et al. [55] | CK+ | 97.8 |
| Zheng et al. [56] | CK+ | 97.6 |
| Dosovitskiy et al. [57] | CK+ | 96.8 |
| Cui et al. [58] | CK+ | 99.1 |
| Proposed | CK+ | 99.2 |
| Yang et al. [53] | MUG | 95.4 |
| Zhang et al. [54] | MUG | 96.3 |
| Proposed | MUG | 97.4 |
| Zhang et al. [54] | SFEW | 38.9 |
| Turan et al. [51] | SFEW | 39.5 |
| Gera et al. [59] | SFEW | 58.9 |
| Proposed | SFEW | 60.7 |
| Yang et al. [53] | Oulu-CASIA | 88.0 |
| Zhang et al. [54] | Oulu-CASIA | 86.9 |
| Proposed | Oulu-CASIA | 90.6 |
| Yang et al. [53] | MMI | 87.4 |
| Zhang et al. [54] | MMI | 88.7 |
| Zhao et al. [55] | MMI | 75.3 |
| Zheng et al. [56] | MMI | 67.7 |
| Proposed | MMI | 89.0 |
| Technique | Dataset |
|---|---|
| (Cg, Cp, Cw) | (0.3, 0.6, 0.8) |
| Nr | 40 |
| Ng | 25 or consider the generation in which accuracy is high |
| Nsol | 32 |
| Epoch | 10 |
| Activation function | ReLU |
| Classifier | Softmax |
| Optimizer | Stochastic Gradient Descent |
| Loss function calculation | Cross entropy |
| Dataset | Accuracy (%) |
|---|---|
| JAFFE | 50.1 |
| CK+ | 89.2 |
| SFEW | 50.2 |
| MMI | 68.5 |
| MUG | 70.2 |
| OULU-CASIA | 67.6 |
| Linear | , | 0.999–1.000 |
| Polynomial (d = 2) | , | 0.989–0.999 |
| Polynomial2 (d = 3) | , | 0.988–0.999 |
| Polynomial3 (d = 4) | , | 0.988–0.999 |
| Radial Basis Function (σ = 0.5) | , | 0.999–1.000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alphonse, A.S.; Abinaya, S.; Arikumar, K.S. A Novel Monogenic Sobel Directional Pattern (MSDP) and Enhanced Bat Algorithm-Based Optimization (BAO) with Pearson Mutation (PM) for Facial Emotion Recognition. Electronics 2023, 12, 836. https://doi.org/10.3390/electronics12040836
Alphonse AS, Abinaya S, Arikumar KS. A Novel Monogenic Sobel Directional Pattern (MSDP) and Enhanced Bat Algorithm-Based Optimization (BAO) with Pearson Mutation (PM) for Facial Emotion Recognition. Electronics. 2023; 12(4):836. https://doi.org/10.3390/electronics12040836
Chicago/Turabian StyleAlphonse, A. Sherly, S. Abinaya, and K. S. Arikumar. 2023. "A Novel Monogenic Sobel Directional Pattern (MSDP) and Enhanced Bat Algorithm-Based Optimization (BAO) with Pearson Mutation (PM) for Facial Emotion Recognition" Electronics 12, no. 4: 836. https://doi.org/10.3390/electronics12040836
APA StyleAlphonse, A. S., Abinaya, S., & Arikumar, K. S. (2023). A Novel Monogenic Sobel Directional Pattern (MSDP) and Enhanced Bat Algorithm-Based Optimization (BAO) with Pearson Mutation (PM) for Facial Emotion Recognition. Electronics, 12(4), 836. https://doi.org/10.3390/electronics12040836






