Social Recommendation Algorithm Based on Self-Supervised Hypergraph Attention

Abstract

Social network information has been widely applied to traditional recommendations that have received significant attention in recent years. Most existing social recommendation models tend to use pairwise relationships to explore potential user preferences, but overlook the complexity of real-life interactions between users and the fact that user relationships may be higher order. These approaches also ignore the dynamic nature of friend influence, which leads the models to treat different friend influences equally in different ways. To address this, we propose a social recommendation algorithm that incorporates graph embedding and higher-order mutual information maximization based on the consideration of social consistency. Specifically, we use the graph attention model to build higher-order information among users for deeper mining of their behavioral patterns on the one hand; while on the other hand, it models user embedding based on the principle of social consistency to finally achieve finer-grained inference of user interests. In addition, to alleviate the problem of losing its own hierarchical information after fusing different levels of hypergraphs, we use self-supervised learning to construct auxiliary branches that fully enhance the rich information in the hypergraph. Experimental results conducted on two publicly available datasets show that the proposed model outperforms state-of-the-art methods.

1. Introduction

Recommendation systems have had great success in various applications that predict how likely a user is to be interested in a particular item. Nevertheless, the data collection is often labor-intensive, which leads to a high risk of cold-start problems in recommendation [1,2]. Aiming to alleviate this problem, researchers have added various auxiliary information to recommender systems to improve their accuracy. This auxiliary information plays a significant role as side information of the user-item interaction, thus accurately mining the user’s interests, for instance, tourism recommendation [3], food recommendation [4], etc. In this regard, fusing users’ social information with user-project interaction data effectively improves recommendation performance. Consequently, in recent years, social recommendation algorithms use social information as auxiliary information, which is then used to outline a more complete user profile. This leads to personalized recommendations for users’ interests, which has attracted the attention of an increasing number of researchers.

Generally, the social recommendation model uses the direct social relationships formed among users (such as friends, concerns and worries, user relevance, etc.) as auxiliary information to improve recommendation performance. On the basis of the matrix decomposition collaborative filtering method with the user-item interaction matrix as input, researchers tried to fuse the information of the user’s social relationship matrix in different ways [5,6] to build a socialized recommendation model. Then users and items were mapped into low-dimensional space, and embedded representations of users and items were obtained for subsequent prediction and recommendation. At present, many fruitful works have been developed by researchers in the field of social recommendation, thus effectively mining the influence of social friends on user preferences. Guo et al. [7] explore how to use the graph neural network (GNN) model to solve the problems of online data management and blurred preference feedback boundaries in social recommendation. Paolo et al. [8] proposed the use of trust metrics among users to improve the performance of recommendations, which can be used to replace the trust weights of similarity weights. Jamali et al. [9] presented a random wandering model that combines a trust relationship-based approach to model user social relationships with a collaborative filtering approach. Jamali et al. [10] introduced a social network recommendation approach based on matrix decomposition techniques. Chen et al. [11] suggested using an attention-based memory module fusing the aspect- and friend-level of users. Tao et al. [12] explored the social recommendation problem in depth and introduced knowledge distillation techniques in the model training.

The above works have achieved good research results, but the following problems are still a challenge:

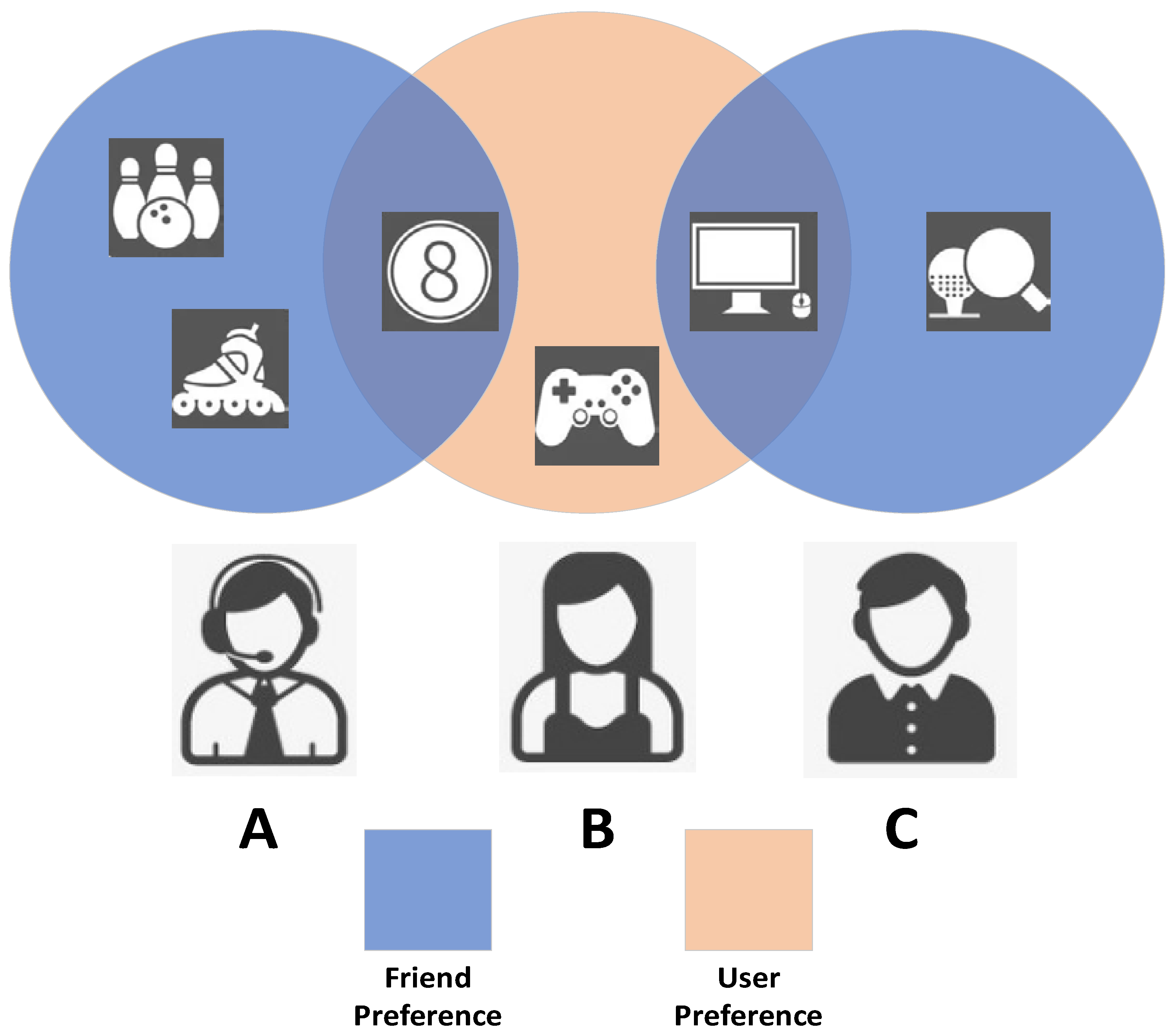
• Most research work in social recommendation assumes that all of the user’s friends have the same influence on them or that they all have similar interests to them. This assumption is too far from the actual real-life situation due to the different types of friends. In real life, different friends have different influences on a user’s decision-making [13]. As shown in Figure 1, user B has two friends; B and A both like to play volleyball and have the same preference for singing as C. B takes A’s suggestion more into account when doing outdoor activities and C’s suggestion more into account when doing indoor activities. Singing and playing volleyball, however, have different degrees of influence on the users. Chen et al. [14] proposed to fuse social influence between users with two attention networks for modeling complex dynamic and general static preferences of users in social recommendations. However, only the importance of friends is considered and the impact on users in different aspects is neglected.
• GNN-based social recommendation models have shown outstanding performance [15,16,17]. Nevertheless, these models widely exploit only simple pairwise user relationships and overlook the complex higher-order relationships between users. Inspired by hypergraph learning [18], Yu et al. [19] used social information for constructing hypergraphs to model higher-order interactions through multi-channel hypergraph convolution. Problems in constructing multiple levels of hypergraph for fusion, however, cannot take into account the independence of different levels of hypergraph modeling itself.

To address the above problems, inspired by the social inconsistency modeling proposed by Yang et al. [20] In this paper, we develop a novel self-supervised social recommendation model called Hypid Graph Attention Hypergraph model (henceforth HGATH). Specifically, we use a hypergraph attention network to mine the implicit higher-order information in the original user embedding. The hypergraph is constructed by unifying the user–friend–items that form triangular relationships, and a multi-channel hypergraph convolutional attention model mines the hidden information between users. We aim to construct hypergraph models of different aspects of user attributes based on different channels representing different types of high-level relationships of users, which leads to the study’s richer user representations with higher-order implicit information. Simultaneously, we propose a combination of sampling as well as relational attention mechanisms that highlight the different effects of different types of friends on the performance of the final recommendation results based on the idea of social inconsistency. In addition, inspired by self-supervised learning, in this paper, we exploit the ranked nature of the hypergraph structure to hierarchically maximize the mutual information among users, user-centric sub-hypergraphs, and global hypergraphs to achieve performance improvement. The experiment results show that HGATH has superior performance with respect to mean absolute error (MAE), and root mean square error (RMSE) compared to current state-of-the-art methods.

The contributions are as follows.

• By modeling different levels of hypergraphs to enrich user feature expressions, and introducing hypergraphs to dig deeper into the higher-order information among users, we conclude with a description of the transcendent pairwise relationships among users through hypergraph modeling.
• Based on the consideration of social consistency, a new attention framework is proposed to highlight the influence of different friends on the final recommendation results. This framework also deeply highlights the important influence of friends who make important suggestions in a certain aspect on the final recommendation results, which better simulates the real recommendation scenario.
• We propose to integrate the self-supervised learning strategy seamlessly with hypergraph model training to enhance the model’s performance.
• Experiments on two publicly available datasets show that the proposed model HGATH outperforms state-of-the-art social recommendation models.

2. Related Works

In this section, we give a brief review of two lines of research related to our work: recommendation algorithms based on attention mechanisms and social recommendation algorithms based on GNNs.

2.1. Social Recommendation Based on Attention Mechanism

Social recommendation has been studied in recent years with the formation and development of social networks in various online services that use consumers’ social information as auxiliary information to alleviate the problem of sparse interaction data in traditional recommendation systems to improve recommendation performance. Related sociological theories have also demonstrated that a user’s preferences are similar to or easily influenced by those around him/her. Social recommendation based on matrix decomposition is one of the most commonly used methods because matrix decomposition methods have the advantages of accurate recommendation effect, good scalability, and low implementation complexity. The basic idea of these methods is to incorporate users’ social relationship information grounded in collaborative filtering recommendation methods which are based on matrix decomposition, aimed at the mining of better potential feature vectors.

As the publication of the literature shows [21], researchers have started to consider the use of attention mechanisms to improve existing relevant social recommendation algorithms that have fruitful results [19,20,21,22]. Pei et al. [22] proposed a new interactive attention-gated recursive network for social recommendations to accurately capture their joint impact on user-item interactions and to better model the dynamics of user and item changes. In particular, the attention mechanism is innovatively applied to learn the attention scores of user and item histories, and thus explore the dynamic dependencies between users and items. Zhang et al. [23] proposed a new meta-path-based social recommendation model to strengthen the model performance by using meta-paths to simulate the user-item-society relationship, where a combination of attention mechanism and multigraph representation model was used to achieve the representation fusion of multigraph models. Yu et al. [24] proposed a multi-channel hypergraph network, which deeply explores the higher-order associations between users-items through hypergraph modeling, while employing an attention mechanism to efficiently aggregate embeddings modeled from multiple channels. Zhang et al. [25] proposed an inductive context personalization (ICP) framework based on context learning, in which a neural aggregator based on an attention network is introduced to fuse the heterogeneous content of entities for optimizing the sorting scheme by expressing the paired relationship between entities.

2.2. Social Recommendation Based on Graph Neural Networks

Deep learning has been successful in artificial intelligence and machine learning by bringing great progress to society; it is characterized by stacking multiple layers of neural networks, which then have better learning representation capabilities. Many scholars have applied deep learning techniques to the field of recommendation and have achieved good results [26,27].

Since GNNs establish a deep learning framework for graph structure, they can utilize both graph structure information and node feature information, and construct more complex and deeper neural networks for representation learning when compared with network representation learning methods, thus becoming a popular research topic in recent years. To simplify the problem and facilitate modeling, most of the early GNNs were based on simple graph structures, i.e., static, homogeneous pairwise graph structures. GraphRec [28] constructed the user, item, and social network as a graph model integrating node information and topology, then captured the interaction information between the graph models using a principled strategy based on the consideration of user social relationship heterogeneity. DiffNet [29] and the follow-up work of the same team DiffNet++ [30] model the diffusion of users’ social influence and potential interest based on the diffusion model and its theory. They constructed heterogeneous graphs of social and interest networks, digging deeper into higher-order social and interest networks, then aggregated the embeddings of the heterogeneous graphs based on a new attention mechanism to precisely learn the representations of nodes in the graph. Wu et al. [29] argued that it is the user’s friends who are dynamic and multiple aspects influence the user’s preferences. Therefore, they constructed two graph-embedding models to model the user and item domains, and then further aggregated the graph-embedding models based on the reinforcement learning and attention frameworks by adaptively adjusting the weighting influence of multifaceted graph embeddings. Song et al. [31] developed a new GNN social recommendation model that addresses the problems of ignoring potential personal interests hidden in user-item interactions and high computational costs in the social recommendation which is based on the influence of partially important social relationships, and uses diffusion theory to make the computation more efficient.

In the real world, the relationships between things are often not in pairs, but between two or more entities that together form an interactive relationship [32]. Using simple graphs to represent such non-pairwise relationships would result in information loss [33]. Hypergraphs extend the definition of simple graphs. In the hypergraph, a hyperedge can contain any number of nodes, so it can store non-pairwise relationships directly. Hypergraphs have more flexible edge definitions than simple graphs, and thus are more powerful for representing complex relationships.

The hypergraph neural network (HGNN) [34] was the first work to design hypergraph convolution operations from a spectral perspective to deal with complex data correlations in representation learning. Tan et al. [35] pioneered the study of user alignment in social networks using a hypergraph structure, which differs from the traditional approach in which a hypergraph approach is used to model higher-order relationships. Ji et al. [36] developed a jump hypergraph convolutional collaborative filtering solution based on a two-channel learning strategy, which exploits the hypergraph structure to deeply explore the higher-order relationships between users and items, while using a two-channel strategy to flexibly characterize users and items. In addition, hybrid matrix factorization (HMF) [37] combines matrix decomposition techniques and hypergraph networks in the field of social recommendation; this exploits the hypergraph structure to model contextual relationships while comprehensively exploring the role of contextual information in the recommendation process based on the matrix decomposition model. Location based social networks (LBSN2Vec) [35] focus on the relationship between user mobility and social relationships, and thus propose specialized hypergraph embedding methods for inferring user preferences, which combine hypergraphs and random wandering strategies for learning node representations of hypergraphs based on sampling in terms of user check-ins and social relationships. Comparison between HGATH and the competing methods are given in

Table 1. Comparison between HGATH and other related works.

Approaches	Details	Gaps
Attention network-based modeling	The combination of attention mechanisms with different neural network models has yielded fruitful results in social recommendation models, including gated neural network approaches [22], meta-paths [23], and especially joint work with hypergraphs [24] and the application of multilayer attention networks in so cial recommendation models [25].	User representation modeling
Simple graph-based modeling	Different graph neural network models have achieved fruitful results in social recommendation models, including the graph convolution approach [28], graph diffusion approach [29,30,31], etc.	User representation modeling based on different diffusion ideas
Hypergraph-based modeling	The application of hypergraphs in social recommendation models has yielded fruitful results, for example, in the literature [34,35,36], especially work on the combination of hypergraphs and matrix decomposition techniques [37] and the combination of hypergraphs and random roaming strategies in social recommendation models [38].	High-order relations between users and complex relations between users and items

.

Our work is different from the previous approaches. First, we construct different levels of hypergraphs based on the actual situation of realistic scenarios, thus obtaining a richer representation of user features. Second, based on the starting point of social consistency, we propose a framework that integrates sampling and attention mechanisms to accurately model the importance of users’ different friends.

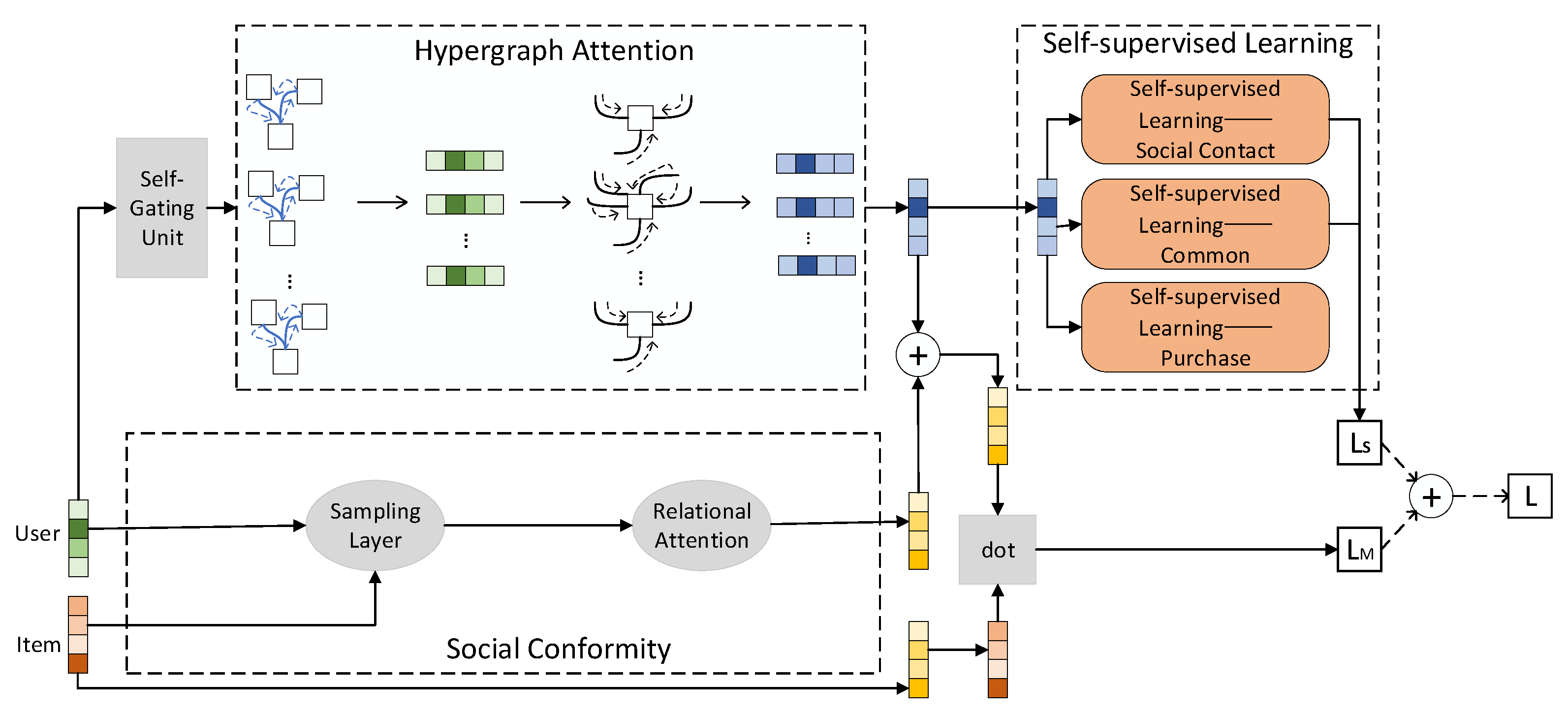
3. Self-Supervised Hypergraph Attention Recommendation Model

In this section, the proposed self-supervised hypergraph attention model HGATH is introduced in detail, and the overall structure of the model is illustrated in Figure 2 below. HGATH model has three submodules. The first is the social consistency module, which aims to extract friends who have higher consistency with users. The second submodule is the hypergraph attention module, which is designed to model higher-level connections between users. The third is a self-supervised learning module, which alleviates the problem of data sparsity in social recommendation. Specifically, first in the social consistency module, we transform the input user data $U=\left\{u_1,u_2,\dots ,u_m\right\}$ and item data $\mathcal{T}=\left\{t_1,t_2,\dots ,t_n\right\}$ into user and item embeddings, respectively, afterwards. Then, we unite the two obtained embeddings together to generate a query embedding to select consistent neighbors. Next, we perform the selection using a neighbor sampling strategy, in which the sampling probability is based on the consistency score between the query embedding and the neighbor embedding. After sampling, the neighbors with consistent relationships are given higher weights for aggregation using relational attention, and finally the consistency-processed user embeddings $U_c$ and item embeddings $T_c$ are obtained. In this way, the influence of different friends on the user is highlighted, while the importance of friends who give essential advice in a certain area to the user is also strongly highlighted. Meanwhile, in the hypergraph attention module, according to $U=\left\{u_1,u_2,\dots ,u_m\right\}$, we use the semantic hypergraphs constructed for different aspects and the graph attention network to learn the higher-order relations of user information, thus presenting key user semantic information. Finally, we use hypergraph encoded user information combined with user embeddings modeled utilizing a consistency policy to obtain more comprehensive user representations $U_T$. Then, the obtained accurate user embedding is fed into the self-supervised learning module. For self-supervised tasks, further enhanced user representation is achieved by hierarchically maximizing the information based on the interaction between different aspects of the user representation. Comprehensive user representations, which were considered to contain multiple types of higher-order relational information, were obtained based on a self-supervised task. Finally, the recommendation list was obtained by an inner product operation with the precise item embeddings obtained in the social consistency module.

To facilitate the understanding of the forthcoming text and formulae we introduce the nomenclature of symbols used in this paper in

Table 2. The nomenclature of mathematical symbols used in this paper.

Symbol	Description
$U=\left\{u_1,u_2,\dots ,u_m\right\}$	User data.
$\mathcal{T}=\left\{t_1,t_2,\dots ,t_n\right\}$	Item data.
$U_T$, $e_u$	User embedding.
$T_c$, $e_t$	Item embedding.
$q_{u,t}$	Query embedding.
$e_u,e_t\in {ℝ}^d$	Embedding of the nodes $u$ and $t$.
$\psi$	ReLU activation function.
$W^{(l)}\in {ℝ}^{2d\times d}$	Encoding function.
$h_v^{(0)}$	Initial embedding of node $v$.
$o^{(l)}(i;b)$	Node embedding of node i at layer $l$.
${\alpha }_i^{(l)}$	Importance of the i-th neighbor sampled.
Q	Sum of the neighbors sampled.
$r_i$	Relationship of edge $\left(v,i\right)$.
${\mathrm{e}}_{r_i}\in {ℝ}^d$	Relational embedding of relation $r_i$.
$w_a\in {ℝ}^{2d}$	Trainable parameter.
$a_i$	Attention weight.
$h_u^{(L)}$	Embeddings of $u$.
$h_t^{(L)}$	Embeddings of $t$.
$E_u^{(0)}$	Original user embedding.
$E_t^{(0)}$	Original item embedding.
$W_g^c\in {ℝ}^{d\times d}$	Training weight parameter.
$b_g^c\in {ℝ}^d$	Bias parameter.
$c$	Different hypergraph channels.
$\sigma$	Sigmoid function.
$W_f$	Trainable weight matrix.
$x_k^{l-1}$	Feature information of node $k$ in the lth layer of the neural network.
$a_1^T$	Weight parameter.
$u_k$	Correlation of node $K$ on the hyperedge ${\mathrm{e}}_j$.
$a_{jk}$	Different weights when super-edge aggregation.
$h_i^l$	Updated feature information of node $v_i$.
$W_h$	Weight matrix.
$b_{ij}$	Attention coefficient of node $v_i$ on the hyperedge $e_j$.
$a_2^T$	Weight parameter.
$v_j$	Correlation of super-edges at node $i$.
$H_t$	User embedding vector after averaging.
$E_t^{(l)}$	Potential feature vector of the user.
$A_c$	Adjacency matrix.
$a_u^c$	Row vector of $A_c$.
$sum\left(a_u^c\right)$	Number of the sub-hypergraph.
${\eta }_{ou{t}_2}:{ℝ}^{m\times d}\to {ℝ}^d$	Readout function.
$f_D(\cdot ):{ℝ}^d\times {ℝ}^d\mapsto ℝ$	Discriminant function.
${ℰ}_{rating}$	Rating error (RMSE) between ${ℰ}_{rating}$ and the true value $(u,t)$ for all ${\widehat{R}}_{u,t}$ pairs in $R_{u,t}$.
${\widehat{y}}_i$	Predicted value.
$y_i$	True value.

.

3.1. Social Consistency

Wu et al. [29] utilize embedding technology for the first step of item and user formalization. Inspired by the work [29], $U=\left\{u_1,u_2,\dots ,u_m\right\}$ and $\mathcal{T}=\left\{t_1,t_2,\dots ,t_n\right\}$ are first transformed into user embeddings $e_u$ and item embeddings $e_t$,

$${\mathrm{q}}_{u,t}=\sigma \left({\mathrm{W}}_q^{\top }\left({\mathrm{e}}_u\oplus {\mathrm{e}}_t\right)\right)$$

(1)

where $q_{u,t}$ is the query embedding and $e_u,e_t\in {ℝ}^d$ is the embedding of the nodes $u$ and $t$. This part is designed with a query layer that dynamically samples the neighbors according to different items. The embedding obtained after node aggregation is as follows:

$$h_v^{(l)}=\psi \left(W^{(l)\top }\left(h_v^{(l-1)}\oplus {\mathrm{AGG}}^{(l)}\left\{h_i^{(l-1)}\mid i\in {\mathcal{N}}_v\right\}\right)\right)$$

(2)

where $\psi$ is the ReLU activation function, $W^{(l)}\in {ℝ}^{2d\times d}$ is the encoding function, and $h_v^{(0)}$ is the initial embedding of node $v$. Moreover, it is recommended to emphasize more consistent rather than inconsistent neighbors when aggregating them. Therefore, the consistency score across all neighbors is as follows:

$$p^{(l)}(i;b)=o^{(l)}(i;b)/\sum _{j\in {\mathcal{N}}_v}{o}^{(l)}(j;b)$$

(3)

where $o^{(l)}(i;b)$ denotes the node embedding of node I at layer $l$.

Thus, we utilize relational attention to learn the importance of these sampled nodes. Relational attention attributes a significant factor to each sampled node $i$. Then the AGG function in (2) can be reformulated as follows:

$${\mathrm{AGG}}^{(l)}=\sum _{i=1}^Q{\alpha }_i^{(l)}\cdot {\mathrm{h}}_i^{(l-1)}$$

(4)

where ${\alpha }_i^{(l)}$ denotes the importance of the i-th neighbor sampled and Q denotes the sum of the neighbors sampled. Assuming that the relationship of edge $\left(v,i\right)$ is $r_i$, the attention formula for ${\alpha }_i$ is obtained as:

$${\alpha }_i^{(l)}=\frac{\exp \left(w_a^{\top }\left(h_i^{(l-1)}\oplus e_{r_i}\right)\right)}{{\displaystyle \sum _{j=1}^Q}\exp \left(w_a^{\top }\left(h_j^{(l-1)}\oplus e_{r_j}\right)\right)}$$

(5)

where ${\mathrm{e}}_{r_i}\in {ℝ}^d$ denotes the relational embedding of relation $r_i$, $w_a\in {ℝ}^{2d}$ is the trainable parameter, and $a_i$ is the attention weight.

Following L-layer propagation, the embeddings of $u$ and $t$ can be obtained, denoted as $h_u^{(L)}$ and $h_t^{(L)}$, respectively.

3.2. Hypergraph Attention Network

The hypergraph was first used to construct user-item and social networks. In this paper, similar to the literature [19], we also designed a multi-channel hypergraph network to represent users in many aspects. Inspired by the literature [39], we also used a gate network to process the user embedding and separate it into different channels; the original user embedding $E_u^{(0)}$ is defined as follows. Meanwhile, we generated the original item embedding $E_t^{(0)}$ based on the same principle.

$$E_u^{(0)}=f_{gate}^c\left(e_u\right)=e_u\odot \sigma \left(e_u{W}_g^c+b_g^c\right)$$

(6)

$$E_t^{(0)}=f_{gate}^c\left(e_t\right)=e_t\odot \sigma \left(e_t{W}_g^c+b_g^c\right)$$

(7)

In (6), $W_g^c\in {ℝ}^{d\times d}$ and $b_g^c\in {ℝ}^d$ denote the training weight parameter and bias parameter, respectively, $c$ refers to different hypergraph channels, and $e_u$ and $e_t$ are the initial user embedding and item embedding, respectively.

We used two different attention mechanisms through two aggregation processes to get the final representation.

We first learned the hyperedge representation of node based on the attention mechanism in combination with hypergraph attention (HyperGAT) [40] for characterized node feature.

$$f_j^l=\sigma \left(\sum _{v_k\in e_j}{a}_{jk}{W}_f{x}_k^{l-1}\right)$$

(8)

$$X^{(0)}=g\left(E_u^{(0)}\oplus E_t^{(0)}\right)$$

(9)

$$a_{jk}=\frac{\exp \left(a_1^T{u}_k\right)}{{\displaystyle \sum _{v_p\in e_j}}\exp \left(a_1^T{u}_p\right)}$$

(10)

$$u_k=LeakyReLU\left(W_1{x}_k^{l-1}\right)$$

(11)

where $\sigma$ is the Sigmoid function, $W_f$ is a trainable weight matrix, and $x_k^{l-1}$ denotes the feature information of node $k$ in the lth layer of the neural network. Equation (9) show the fusion of user information and item information. $a_1^T$ is the weight parameter and $u_k$ denotes the correlation of node $K$ on the hyperedge ${\mathrm{e}}_j$. $a_{jk}$ highlights the effect of different weights when there is super-edge aggregation.

Next, all hyperedges are denoted as $\{f_j^l\mid \forall e_j\in E_i\}$. We used the high-order relationship of users based on hyperedge modeling to learn the representation of nodes

$$h_i^l=\sigma \left(\sum _{e_j\in E_i}{b}_{ij}{W}_h{f}_j^l\right)$$

(12)

where $h_i^l$ is the updated feature information of node $v_i$, $W_h$ represents the weight matrix, and $b_{ij}$ indicates the attention coefficient of node $v_i$ on the hyperedge $e_j$, as follows:

$$b_{ij}=\frac{\exp \left(a_2^T{v}_j\right)}{{\displaystyle \sum _{e_p\in E_i}}\exp \left(a_2^T{v}_p\right)}$$

(13)

$$v_j=LeakyReLU\left(\left[W_2{f}_j^l\parallel W_f{h}_i^{l-1}\right]\right)$$

(14)

where, $a_2^T$ is the weight parameter, $v_j$ denotes the correlation of super-edges at node $i$.

The final-user representation of the hypergraph is as follows:

$$H_t=\frac{1}{L+1}\sum _{l=0}^L{E}_t^{(l)}$$

(15)

where $H_t$ denotes the user embedding vector after averaging and $E_t^{(l)}$ refers to the potential feature vector of the user.

3.3. Self-Supervised Learning

Inspired by the literature [16], self-supervised learning was added to the training of the model in order to improve the performance. The three semantic hypergraphs capture higher-order information using the adjacency matrix $A_c$. Each row in $A_c$ represents a subgraph of the corresponding hypergraph with the user represented by the index of that row at its center. Thus a hierarchical structure can be derived based on the relationship between hypergraphs and sub-hypergraphs: user nodes—user-centered sub-hypergraphs—hypergraphs, and from this structure self-supervised signals are created. We designed a new function ${\eta }_{ou{t}_1}:{ℝ}^{m\times d}\to {ℝ}^d$, as follows:

$$z_u^c={\eta }_{ou{t}_1}\left(P_c,a_u^c\right)=\frac{P_c{a}_u^c}{sum\left(a_u^c\right)}$$

(16)

where $P_c=f_{gate}^c(P)$ is to control P. We set $a_u^c$ to represent the row vector of $A_c$ the subgraph. $sum\left(a_u^c\right)$ denotes the number of the sub-hypergraph. Similarly, another readout function ${\eta }_{ou{t}_2}:{ℝ}^{m\times d}\to {ℝ}^d$ is defined, which is actually an average set that summarizes the obtained sub-hypergraph embedding:

$$h^c={\eta }_{ou{t}_2}\left(Z_c\right)={\mathrm{AveragePooling}(\mathrm{Z}}_c)$$

(17)

In accordance with deep graph infomax (DGI), we used info noise contrastive estimation (InfoNCE) as the learning objective using hierarchical mutual information maximization. As a result, the objective function of the self-supervised task is defined as follows.

$$\begin{array}{c}{ℒ}_s=-{\displaystyle \sum _{c\in \{s,j,p\}}}\{{\displaystyle \sum _{u\in U}}\log \sigma \left(f_D\left(p_u^c,z_u^c\right)-f_D\left(p_u^c,{\tilde{z}}_u^c\right)\right)\\ +{\displaystyle \sum _{u\in U}}\log \sigma \left(f_D\left(z_u^c,h^c\right)-f_D\left({\tilde{z}}_u^c,h^c\right)\right)\}\end{array}$$

(18)

where $f_D(\cdot ):{ℝ}^d\times {ℝ}^d\mapsto ℝ$ is a discriminant function. We break $Z_c$ by shuffling between rows and columns to create negative examples of ${\tilde{Z}}_c$.

3.4. Model Optimization

For the user representation $h_t^{(L)}$, the score is obtained by summing and averaging the $H_t$ and calculating the inner product with the item representation $h_t^{(L)}$

$${\widehat{R}}_{u,t}=Avg(h_u^{(L)}+H_t)\cdot h_t^{(L)}$$

(19)

where $Avg\left(\right)$ is the mean function and ${\widehat{R}}_{u,t}$ is the scoring score. The primary loss function for the recommendation task is referred to as the root mean square error (RMSE) between ${ℰ}_{rating}$ and the true value $(u,t)$ for all ${\widehat{R}}_{u,t}$ pairs in $R_{u,t}$:

$${ℒ}_m=\sqrt{\frac{\underset{{\displaystyle {\sum }_{(u,t)\in {ℰ}_{\mathrm{rating}}}{\left(R_{u,t}-{\widehat{R}}_{u,t}\right)}^2}}{}}{\left|{ℰ}_{\mathrm{rating}}\right|}}$$

(20)

Thus, the total loss consists of two parts: one is the loss of recommended tasks and the other is the loss of self-supervised learning tasks, as follows:

$$ℒ={ℒ}_m+\mathsf{\beta }{ℒ}_s$$

(21)

where β adjusts two loss functions.

4. Experiment Comparison and Analysis

4.1. Dataset

We conducted experiments on two public datasets, Epinions [13] and Ciao [41]. Epinions is an online social network that provides an item evaluation and review service to allow other users to add to their own trust list, indicating the approval of this user’s ratings and reviews. The dataset contains a list of ratings given to items by users, as well as the social relationships between users and trusted users. The Ciao dataset is similar to Epinions with the exception of the point in time when the trust relationship was established, but it captures the text content of each comment and information about the comment from other users. To preprocess the data, we delete users with non-social connections because they are not present in the social referrals, while linking neighboring items that share more than 50%. The datasets’ statistical parameters are summarized in

Table 3. Statistical information of the datasets.

Dataset	Ciao	Epinions
#of Users	6776	15,210
#of Items	101,415	233,929
#of Interactions	271,573	644,715
Interaction Density	0.0395%	0.0181%

.

4.2. Evaluation Criteria

To evaluate the performance of the algorithms used, we selected two evaluation metrics frequently used in recommendations—mean absolute error (MAE) and root mean square error (RMSE) [42], both of which are often used for performance analysis [43]. The formulas for their calculation are:

$$MAE=\frac{1}{n}{\displaystyle \sum _{i=1}^n\left|{\widehat{y}}_i-y_i\right|}$$

(22)

$$RMSE=\sqrt{\frac{1}{n}{\displaystyle \sum _{i=1}^n{({\widehat{y}}_i-y_i)}^2}}$$

(23)

where ${\widehat{y}}_i$ is the predicted value and $y_i$ is the true value.

4.3. Experimental Setting

We verified the efficiency of this model from the following aspects.

• We considered a comparison with mainstream advanced algorithms to verify the efficiency and advancement of the algorithm proposed in this module.
• We compared this model with graph neural networks to verify the effectiveness of the employed hypergraph attention.
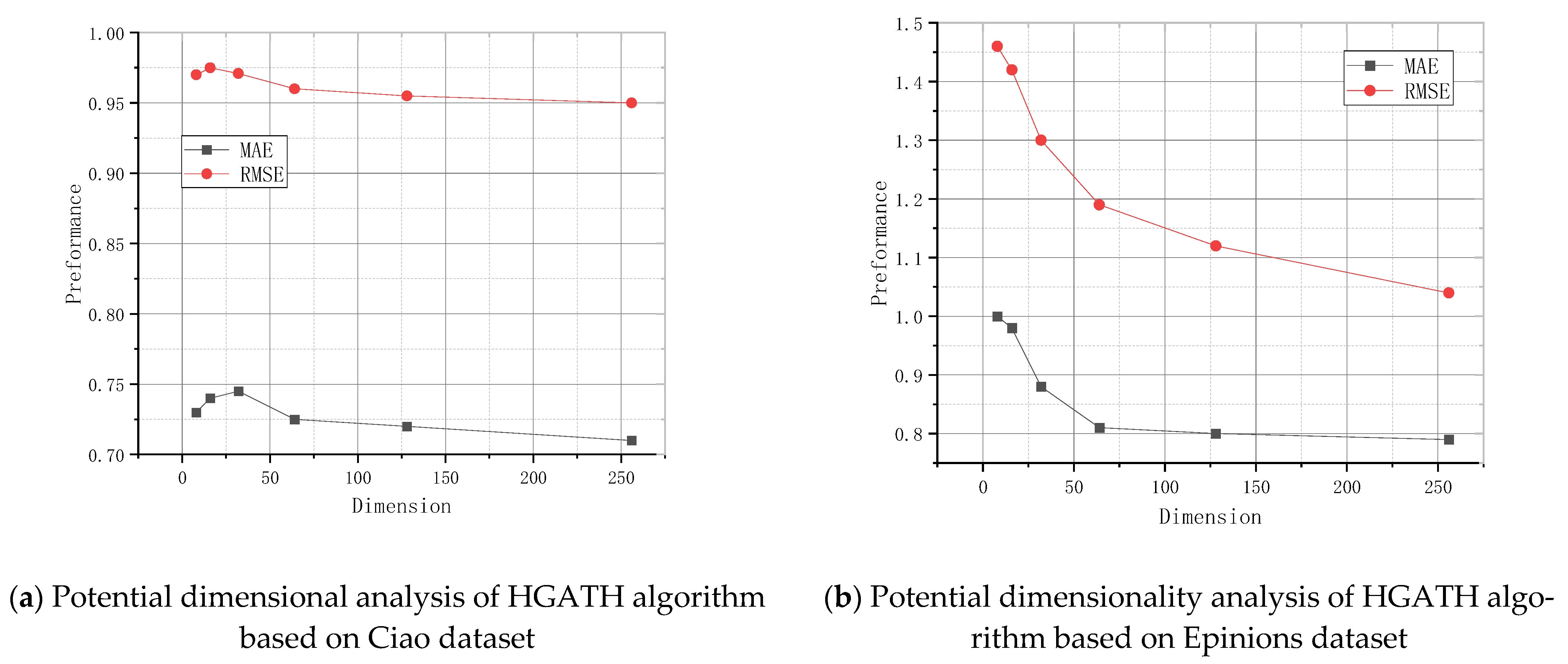
• We considered potential dimensionality factor analysis to test the effective dimensionality in various cases based on differing potential dimensionality factors to verify the robustness of the algorithm proposed in this module.

First, seven social recommendation algorithms proposed in recent years were selected for comparison.

• SoRec [44] combined social information with matrix decomposition.
• SocialMF [10] proposed a new social recommendation model, which is based on the matrix decomposition model and integrates the user’s trust propagation mechanism to model social networks.
• SoReg [44] proposed a recommendation algorithm based on social relations, which constrained the learning of users’ potential feature vectors in the traditional matrix decomposition by social relations in a way of social regularization, so as to make the potential feature vectors of two users with social relations as similar as possible.
• The collaborative user network embedding (CUNE) [45] proposed to dig deep into the implicit social relationship of users based on user feedback to identify the implicit important friends of users, and eventually realized the ranking of user preferences based on the Matrix Factorization (MF) ranking model.
• Graph Convolution Matrix Completion with Spectral Nonlinear (GCMC + SN) [46] proposed a bipartite interactive graph-based graph autoencoder framework for differentiable message passing based on graph structure data.
• Graph Recommendation (GraphRec) [28] developed a new graph neural network framework for social recommendation, which is the first time that a graph neural network was combined with a principled method to model users and projects and the complex interaction between them.
• ConsisRec [15] used a sampling strategy to mine complex relationships among neighbors based on the principle of social consistency, thus modeling neighbors, and uses an attention mechanism to highlight the influence weights of different important users.

Second, we compared graph convolution, graph attention, and hypergraph convolution with hypergraph attention to verify the effectiveness of the hypergraph attention used in this paper. Finally, this model tested the impact of this algorithm under different latent dimensions and verified the robustness of the algorithm exhibited by the latent dimensions employed in this paper.

The dataset was randomly divided into training, validation, and test sets according to 60%, 20%, and 20% probability. The validation set was used to adjust the hyperparameters, and the predicted data from the training set was compared with the test set to obtain the final results. Meanwhile, we searched for percentages between 0.2, 0.4, 0.6, 0.8, and 1.0. For the embedding size, we adjusted between 8, 16, 32, 64, 128, and 256. The learning rate was adjusted between 0.0005, 0.001, 0.005, 0.01, 0.05, and 0.1 for batch sizes ranging from 32, 64, 128, and 256.

4.4. Experimental Analysis

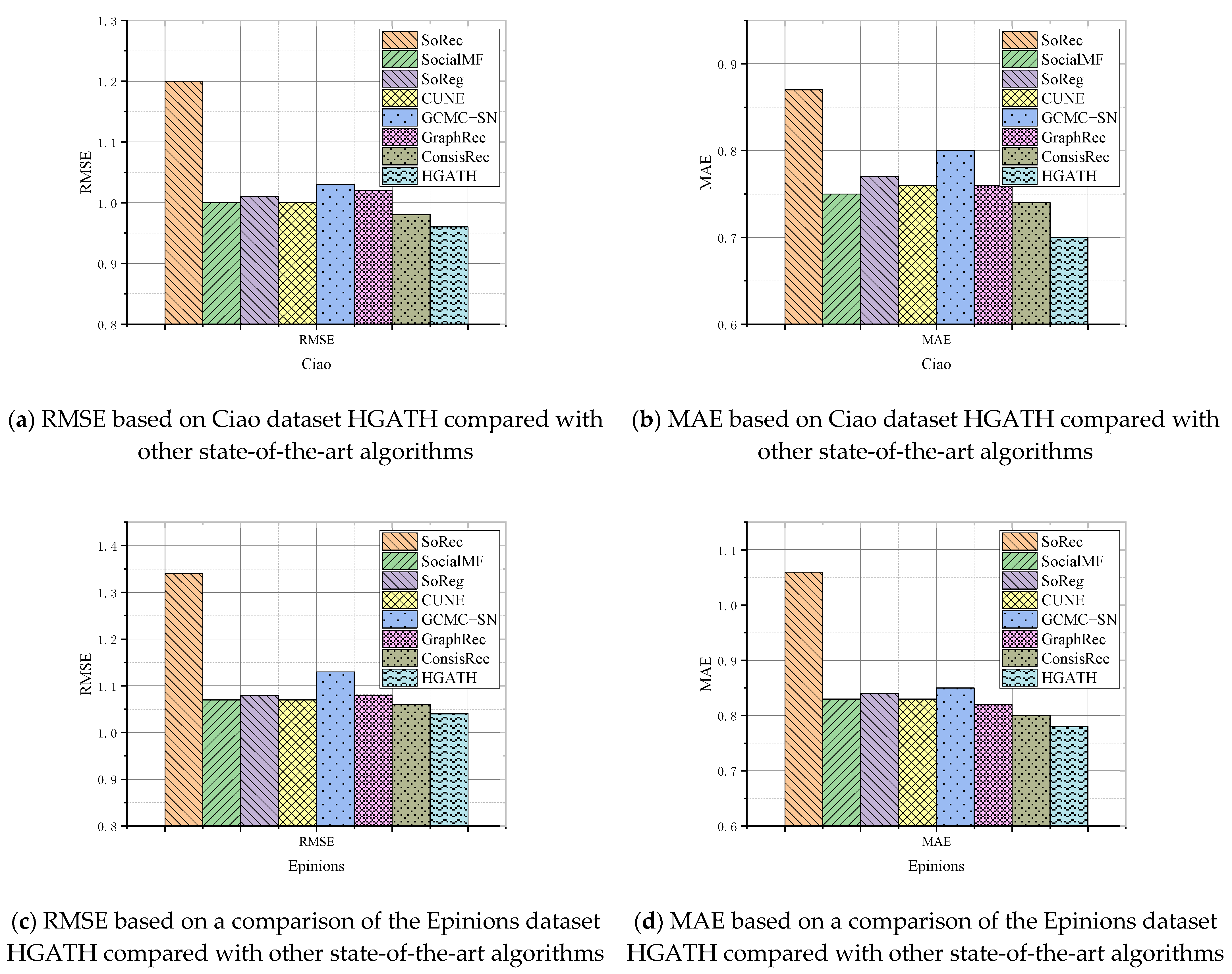
4.4.1. Performance Comparison

The experimental results of all compared algorithms on the two datasets are shown in Figure 3 above. We observed the following conclusions:

(a)

On both datasets, CUNE, ConsisRec, and HGATH algorithms work better than SoRec, SocialMF, and SoReg, which shows the superior function of considering the consistency of social relationships shown on the model.

(b)

Among the social recommendation-based algorithms, HGATH outperforms the CUNE and ConsisRec algorithms, which indicates that for social recommendation, it is not enough to extract valid social relationships from users’ social relationships. Obviously, the higher-order relationships among users must be considered. Meanwhile, compared with the simple graph structure that can only connect two nodes, the inset attention focuses on more complex relationships and mines richer user interaction information.

(c)

HGATH is more effective than GCMC + SN and GraphRec, which means that higher-order information interactions can maximize the inheritance of different aspects of hypergraph information.

(d)

On all the evaluation metrics, all comparison algorithms perform better on the Ciao dataset than the Epinions dataset; this is because the Epinions dataset is sparser than the Ciao dataset.

We adopted Recall@K and Normalized Discounted Cumulative Gain@K (NDCG@K) to evaluate the performance of all methods, where K = 5.10. These two metrics have been widely used in previous recommendation studies to validate the accuracy. For each dataset, we used 80% as a training set to learn the parameters, 10% as a validation set to tune the hyperparameters, and 10% as a test set. We also followed similar experimental settings in the literature [39].

The performance of different methods on the Epinion and Ciao datasets are considered in

Table 4. Comparisons of different methods on the Epinion dataset.

	SoRec	SocialMF	SoReg	CUNE	GCMC + SN	GraphRec	ConsisRec	HGATH
Recal@5	0.217	0.215	0.221	0.233	0.241	0.249	0.255	0.261
Recal@10	0.259	0.263	0.257	0.271	0.282	0.287	0.297	0.323
NDCG@5	0.183	0.187	0.178	0.192	0.211	0.209	0.212	0.224
NDCG@10	0.198	0.207	0.211	0.228	0.241	0.238	0.249	0.267

and

Table 5. Comparisons of different methods on the Ciao dataset.

	SoRec	SocialMF	SoReg	CUNE	GCMC + SN	GraphRec	ConsisRec	HGATH
Recall@5	0.229	0.235	0.234	0.244	0.257	0.261	0.271	0.271
Recall@10	0.274	0.277	0.275	0.291	0.322	0.318	0.326	0.347
NDCG@5	0.186	0.191	0.188	0.201	0.222	0.226	0.237	0.243
NDCG@10	0.208	0.211	0.215	0.233	0.251	0.256	0.266	0.275

, respectively.

In this section, we verify whether HGATH outperforms the baselines. We obtained the following observations.

• HGATH beats all baselines, which shows the effectiveness of the proposed method in this paper.
• The graph model-based recommendation algorithms (e.g., GCMC + SN, GraphRec) outperform the social recommendation algorithms that do not employ graph learning methods (e.g., SoRec, SocialMF, SoReg, CUNE), which validates the powerful learning capability of graph models in recommendation scenarios.
• The performance difference between SoRec, SocialMF, and SoReg is not significant, which also validates that all three models are essentially MF-based recommendation models. The same reasoning applies to GCMC + SN and GraphRec.
• The performance of each model based on the Epinion dataset is generally slightly lower than that of the Ciao dataset, which is consistent with the fact that the Ciao dataset is not as sparse as the Epinion one.

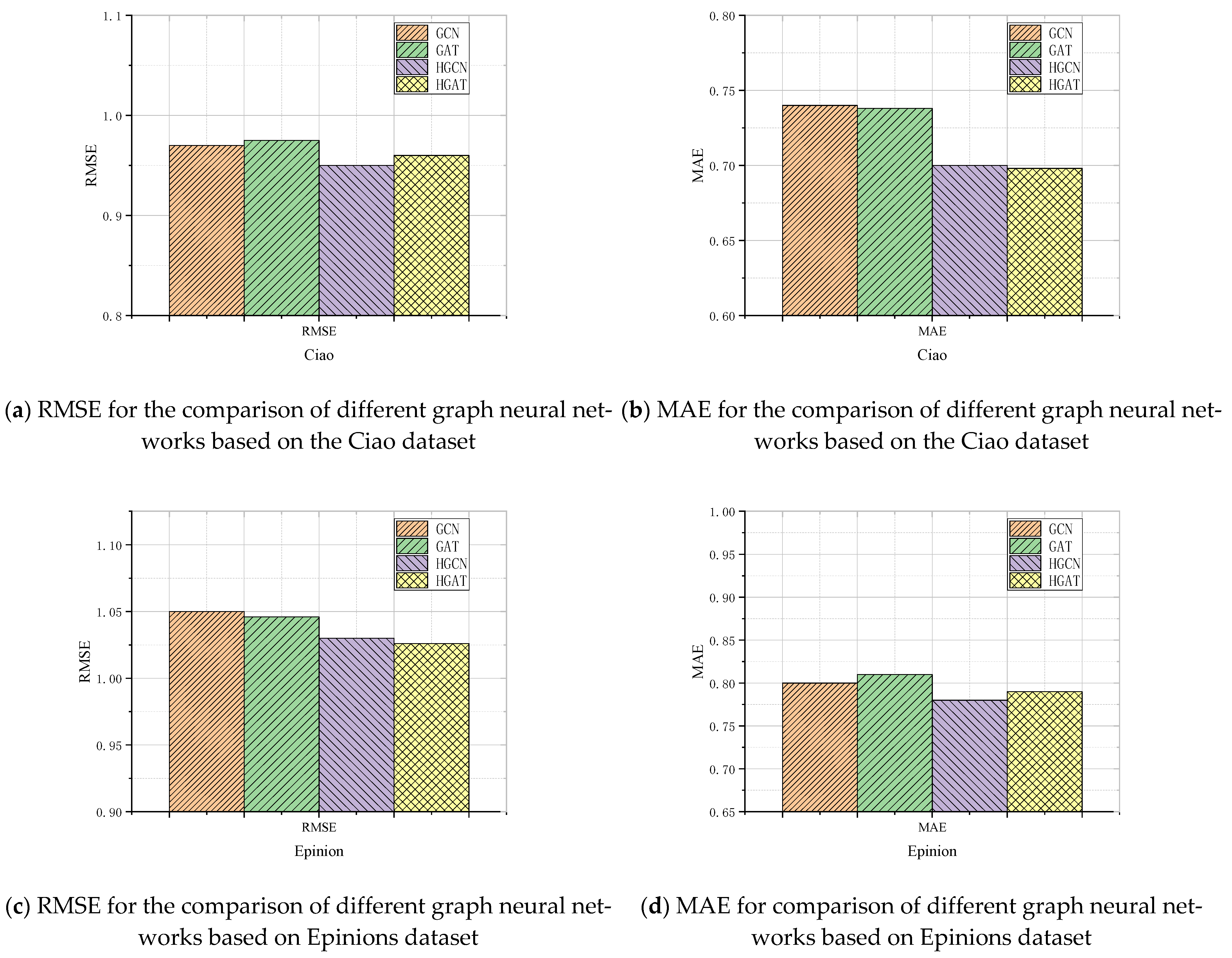
4.4.2. Comparative Analysis of Graph Neural Networks

To validate the presence or absence of graph neural network structure and the different effects brought by different graph neural network structures on the algorithm, this paper presents experiments and comparative analysis of graph convolution, graph attention, hypergraph convolution, and hypergraph attention. The experimental results are shown in the following Figure 4. The graph convolution network (GCN), graph attention (GAT), hypergraph convolution (HGCN), and hypergraph attention (HGAT) are presented in Figure 4.

First, HGATH shows better performance in the two datasets. Moreover, the structure created using the hypergraph is obviously better than the simple graph structure, which proves the effectiveness of the hypergraph structure constructed in this paper for higher-order information extraction. Second, the difference between hypergraph convolution and hypergraph attention for two different metrics is not very obvious in the different datasets, which shows that although they are different hypergraph structures, they have their strengths and weaknesses in dealing with data with sparsity.

4.4.3. Potential Dimensional Analysis

The variation of potential dimensions also has a certain degree of influence on the experimental results, which are compared and analyzed to observe the adaptability of different potential dimensions to the algorithm. The experimental results are shown in Figure 5 below.

As shown by the experimental results, the effect becomes more pronounced when the dimensionality is larger, whereas the relative increase in the potential dimensionality increases memory usage and computing time. It is therefore obvious that the improvement of the algorithm levels off when the potential dimension increases to a certain level. Thus, the potential dimension 256 used in this paper is the optimal choice after comprehensive consideration.

5. Discussion

In this section, we summarize the results of the experiments and presents the discussion of the contributions made by our work as below:

• In contrast to other social recommendation work that uses simple graph models to learn user representations, we used hypergraphs to learn user representations. The hypergraphs were used to learn the representation of the user based on multiple aspects of the user. As a complex graph, the hypergraph has the property of linking multiple nodes within one edge, which makes it naturally advantageous for the representation of complex data relationships between nodes. By taking advantage of the supergraph’s superior learning ability to fully learn the user’s representations, the complex relationships between users are well described, while higher-order relationships are accurately modeled. The results in Figure 3 and Figure 4 verify the effectiveness and efficiency of the method in this paper.
• Users are influenced differently by different friends when making decisions. Instead of using the vanilla attention mechanism to distinguish the importance of friends, we designed a hierarchical iterative aggregation to learn the relational attention network of user representations. First, the user’s friend features are dynamically sampled in a single layer based on item features, and then a dynamic aggregation operation is performed based on a relational attention mechanism to learn the user’s representation. Next, each layer takes the previous layer’s user’s embedding as input, which finally outputs the user’s iterative updated embedding. The whole process simulates how the potential embeddings of the users evolve with the dynamic influence of the project until the precise user embeddings are finally generated. In the process of simulated evolution, the attention network proposed in this paper accurately manifests the social consistency principle.
• In order to further contextualize the effect of data sparsity while fully inheriting the rich user representation learned from the hypergraph, we innovatively incorporated self-supervised learning into the training of the recommendation model proposed in this paper. By considering the hypergraphs reflecting different aspects of user representations as different views in the self-supervised contrastive learning considered, the mutual information of these views was maximized to achieve rich user representations in the recommendation task for better performance.
• Self-supervised learning is a fresh direction in the future recommendation field. However, graph learning-based recommendation models in self-supervised learning tasks mostly arbitrarily employ operations such as item cropping and masking to improve the variability among views in the self-supervised comparative learning process. Such operations also bring about the problem of creating more sparse training data. In the future, we will further investigate how to perform robust self-supervised learning while preserving the original data.

6. Conclusions

Considering social information as auxiliary information provides a big help to the recommendation system. Hence, we view social consistency as the first basis for considering social relationships in real scenarios and used hypergraph attention to model higher-order relationships among users when extracting special higher-order user information features. Simultaneously, higher-order mutual information maximization was used to alleviate the problem of higher-order information loss caused by fusing different aspects of hypergraph information. The experiments on two real datasets verify that the proposed algorithm outperformed the state-of-the social recommendation algorithms. Further, in the future, we will consider how to simulate the changing interaction information in realistic scenarios based on dynamic graph models about the impact of friends on users.