A Novel Electrolytic-Free Quasi-Z-Source Ćuk LED Driver for Automotive Application

Abstract

This paper proposes a novel electrolytic-free quasi-Z-Source Ćuk LED driver for automotive applications. Compared to the traditional Ćuk converter, the first merit of the novel converter is higher gain, which makes it apt to switch between multiple applications. Secondly, the proposed converter combines the inherent characteristics of LED load to operate in a wide range in Continuous Conduction Mode (CCM), so the inductors can assist in energy storage, and only small capacitance is required. Thirdly, inductors can be integrated and use only one core, and capacitors are electrolytic-free, which will benefit integration and long life. All merits are important to automotive application. Detailed analysis and design steps are presented. Then, with the help of the simulation software Saber, several key parts of the converter are simulated. Finally, a prototype controlled by the micro control unit stm32f103c8t6 is built, and the feasibility is verified by the experiment results.

1. Introduction

LEDs are increasingly preferred in automotive lighting applications for their long lifetime, mechanical robustness, and energy saving [1,2]. Batteries (12/24 V) are commonly used as the input of LED drivers in automotive applications, and different battery voltage systems are available sometimes. Therefore, LED drivers capable of operating in a wide input range are needed [3,4,5]. In addition, different automotive applications, such as headlights, brake lights, and turn signals, require different levels of lighting brightness, so different numbers of LEDs in series are required. Moreover, the same application may require a different number of LEDs in series (such as headlamps for high beam and low beam).

Switched-mode dc–dc converters with both step-up and step-down capability can address the above challenges. A four-switch buck–boost converter [3] is presented, whose structure can be exchanged between the buck, boost, and buck–boost to provide a desired voltage gain, but the converter efficiency drops in the buck–boost operation due to the cascaded structure. Ćuk-converter-based automotive LED drivers have also been reported [6,7,8]. The Ćuk converter of [6] has reduced efficiency due to hard-switching at a 500 kHz switching frequency. High-frequency Ćuk converters that achieve zero-voltage switching are presented in [7,8], but they have two or more active switches to drive, with higher complexity and more components. The latest literature is mostly based on resonant converters [4,5,9,10,11,12,13]. These solutions have higher efficiency and a compact size, but similar to [7,8], they usually have more switches to drive and complex structure, and variable-frequency control usually necessitates the use of large EMI filters.

Life incompatibility between electrolytic capacitors and other components of LED drivers has gradually become one of the main concerns in recent years. There are two main solutions to this problem: through new topology or control schemes [14,15,16]. The authors of [17] used an inductor to assist energy storage, but the inductance is quite large because the inductor works at a low frequency.

Many new topologies have been proposed based on a quasi-Z-source network to achieve high-voltage gain [18,19,20,21]. Combining a quasi-Z-source network with the Ćuk converter, and integrating the three inductors, a novel high-gain quasi-Z-source Ćuk converter is proposed in this paper. It is suitable for a wide range of input and output, and requires small space. Because of the combination of characteristics with LED load, the converter works in CCM in a wide range, with small capacitance and long life.

This paper is organized as follows. Section 2 gives the circuit configuration and operating principle. Parameter design and control strategy are briefly described in Section 3. Then, in Section 4, the experimental results of a prototype are presented. Finally, the conclusions of this work are detailed in Section 5.

2. Circuit Configuration and Operating Principle

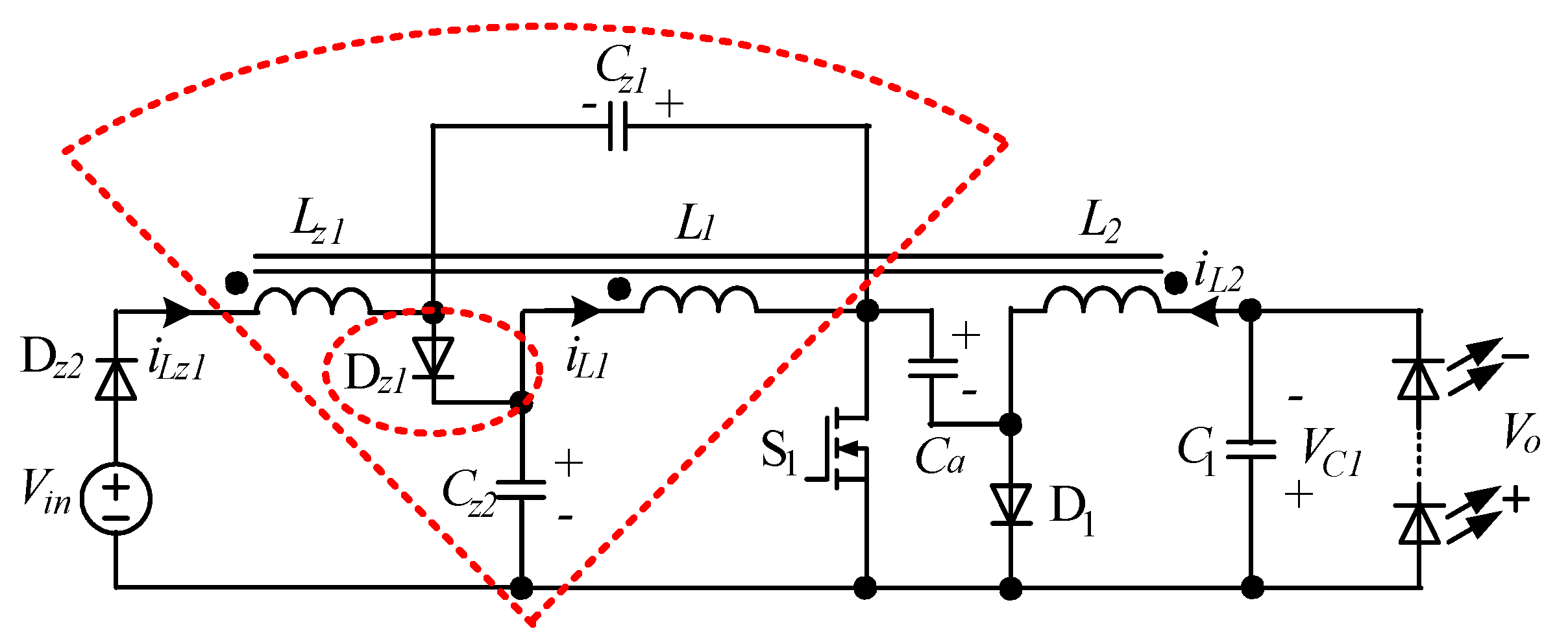
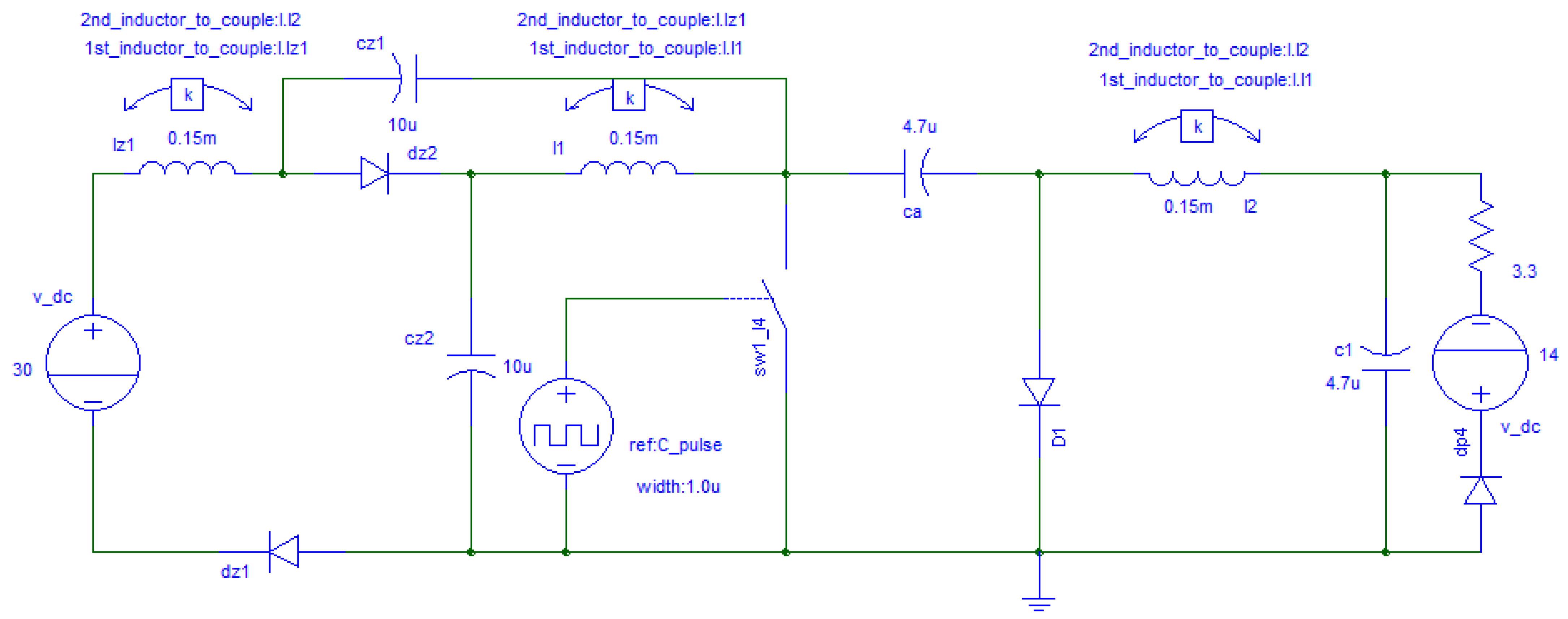
2.1. Circuit Configuration

The topology of the proposed quasi-Z-source Ćuk converter is shown in Figure 1 below, where L_z1, L₁, L₂ represent the three windings of the mutual inductors integrated on a magnetic core with the same number of turns. Compared with the traditional Ćuk converter, an inductor is replaced by the quasi-Z-source network, which is composed of L₁, L_z1, capacitors C_z1, C_z2, and diode D_z1 surrounded by the sector dotted line. D_z2 is added to suppress the low-frequency oscillation between L₁, L_z1, C_z1, C_z2 and input V_in under light load. The signs and arrows in Figure 1 indicate the positive direction of capacitor voltage and inductor current, respectively.

Figure 2 shows the equivalent circuit of the quasi-Z source Ćuk Converter in four work modes in steady state. The steady-state analysis of the integrated inductor in CCM can be firstly carried out as three independent inductors, as the inductor voltage and current change in the same direction, and the coupling of inductors only causes an increase in the equivalent inductance.

The proposed converter contains three work modes as in Figure 2a–c in CCM, while it contains one more mode in Discontinuous Conduction Mode (DCM), which can be Figure 2d or Figure 2e according to the load. The arrows in Figure 2 indicate the actual direction of the loop current, and the positive and negative signs also indicate the actual direction of the element voltage. The work details are as follows:

Mode 1[t₀–t₁]: The switch S₁ is turned on at t₀, and D_z1 is reverse-biased for V_cz2 > V_cz1. D₁ is also off by withstanding V_ca. There are three current loops in this mode, and all the inductors are charged, while all the capacitors are discharging. The input voltage V_in and C_z1 are connected in series to charge L_z1; C_z2 charges L₁, and C_a supplies power to L₂ and the load.

Mode 2[t₁–t₂]: Mode 2 begins when S₁ is turned off. It should be noted that except C_a, all the other inductors/capacitors interchange between storing and releasing energy in this mode. The operation of the converter can be divided into three parts. V_in and L_z1 are connected in series to charge C_z2, L₁ charges C_z1, and C_a together with L₂ supplies power to C_z1, C_z2, and the load.

Mode 3[t₂–t₃]: C_a also changes to be charged in this mode, and D₁ is turned on. Therefore, all the inductors are discharging, while all the capacitors are charged. Part of i_L1 and i_Lz1 are in series with V_in to charge C_a, and the remaining current of L₁ and L_z1 is utilized to charge C_z1 and C_z2 separately. At the same time, L₂ freewheels through D₁ and charges the load.

Figure 3 presents the current and voltage waveforms on the integrated three inductors, and the current waveform of C_a, where t_s is the switching cycle, and d₁, d₂, and d₃ are the duty ratios corresponding to the duration of modes 1, 2, and 3, respectively. It is easy to understand that the voltage waveforms on the integrated three inductors are the same with the same number of turns, but the current waveforms of i_L1 and i_Lz1 are different from i_L2.

If the load is light enough, the converter will enter into DCM, and the converter has a fourth mode in a switching cycle as in Figure 2d,e, where the switch and diodes are always off.

Mode 4-1[t₃–t_s]: i_Lz1 cannot be reversed due to D_z2 in light discontinuous mode, so it remains zero. The slew rate of i_Lz1 is zero, and the voltage on L_z1 is also zero, resulting in zero voltage on other windings of the mutual inductor at the same time. There is only one current loop: C_a charges C₁ and C_z2, and i_L1 and i_L2 basically stay constant at this stage.

Mode 4-2[t₃–t_s]: Since the output current is very small and the output voltage is also higher in deep discontinuous mode, i_L2 drops faster than i_L1 and i_Lz1 to negative at the end of mode 3, while i_L1 and i_Lz1 remain positive. The only thing that happens is that C_z1, C_z2, and C₁ charge C_a with a constant current in this interval.

The theoretical waveforms of the proposed converter in DCM are presented in Figure 4 below. If the converter is just at the boundary of CCM and DCM, that is in Boundary Current Mode (BCM), i_Lz1 is zero at the end of the cycle. Note that there is no time that all winding currents are zero in this DCM, but the total magnetic flux of the core is zero during mode 4. Although the mutual inductor is designed to have the same name end when the voltage is applied, the reverse current always appears in DCM, which may actually reduce the equivalent inductance.

The major feature is that the charging and discharging of the capacitors are always in series with the inductors, resulting in a smooth variation of the capacitor voltage. Therefore, the inductances and capacitances can be relatively small, which is good for integration and heat dissipation.

2.2. General Analysis

In the following analysis, the switch and diodes are assumed to be ideal. The voltage on L_z1, L₁, L₂ in CCM are given by Equations (1) and (2) below according to mode 1–3. Note that the equations of inductor voltage for mode 2 and 3 are the same:

$$\{\begin{array}{c}{V}_{in}+V_{cz1}=V_{Lz1}\\ V_{cz2}=V_{L1}\\ V_{ca}=V_{L2}+V_o\end{array}$$

(1)

$$\{\begin{array}{c}{V}_{in}+V_{Lz1}=V_{cz2}\\ V_{L1}=V_{cz1}\\ V_{cz2}+V_{L1}=V_{ca}\\ V_{L2}=V_o\end{array}$$

(2)

Since the voltages on L_z1, L₁, L₂ are the same, the relationship between the capacitor voltages can be inferred from Equations (1) and (2):

$$\{\begin{array}{c}{V}_{cz2}=V_{in}+V_{cz1}\\ V_{ca}=V_{cz1}+V_{cz2}\end{array}$$

(3)

Then the following relationship can be obtained from the volt-second balance of L_z1, L₁, and L₂:

$$\begin{array}{c}{L}_{z1}\\ L_1\\ L_2\end{array}\{\begin{array}{c}{d}_1\left(V_{in}+V_{cz1}\right)=\left(d_2+d_3\right)\left(V_{cz2}-V_{in}\right)\\ d_1{V}_{cz2}=\left(d_2+d_3\right)V_{cz1}\\ d_1\left(V_{ca}-V_o\right)=\left(d_2+d_3\right)V_o\end{array}$$

(4)

Substituting Equation (3) into Equation (4), from the volt-second balance relationship of L₁ and L₂ we can get V_cz1 = V_o. Then, plugging it into the volt-second balance equation of L_z1 in Equation (4), and eliminating V_cz1 and V_cz2, yields the important relationship among input, output voltage, and duty ratio:

$$d_1\left(V_{in}+V_o\right)=\left(d_2+d_3\right)\left(\frac{d_2+d_3}{d_1}{V}_o-V_{in}\right)$$

(5)

There is no mode 4 in CCM, so the relationship of duties becomes: d₂ + d₃ = 1 − d₁. Substituting this into Equation (5), the expression for the output voltage in CCM is given by:

$$V_o=V_{in}\frac{d_1}{\left(1-2d_1\right)}$$

(6)

This relationship looks similar to the basic converters, where the output voltage is not directly related to the output current in CCM. Further analysis needs to introduce the current equation corresponding to the capacitor’s charge balance:

$$\begin{array}{c}{C}_{z1}\\ C_{z2}\\ C_a\end{array}\{\begin{array}{c}{d}_1{I}_{Lz1}=d_2\left(I_{L1}+I_{L2}\right)+d_3\alpha I_{L1}\\ d_1{I}_{L1}=d_2\left(I_{Lz1}+I_{L2}\right)+d_3\beta I_{Lz1}\\ \left(d_1+d_2\right)I_{L2}=d_3\left(1-\alpha \right)I_{L1}\end{array}$$

(7)

where α and β are the scale factors when i_L1 and i_lz1 are divided into two parts in mode 3, respectively. Since L₁ and L_z1 charge C_a in series in mode 3, the current is equal, i.e.,

$$\left(1-\alpha \right)I_{L1}=\left(1-\beta \right)I_{Lz1}$$

(8)

Regarding the circuit containing D_z1 enclosed by the dashed ellipse in Figure 1 as a node, Kirchhoff’s current law can be applied. Because of charge balance, the average current of C_z1 and C_z2 in a whole cycle is zero, so a new current relationship is achieved:

$$I_{L1}=I_{Lz1}$$

(9)

Synthesizing Equations (8) and (9), we know α = β. After substituting it back into Equation (7), we find that C_z1 and C_z2 are charged and discharged in the same way, and their charge balance equations are the same. According to mode 3, C_z1 and C_z2 are both charged by the current αI_L1, and C_a is charged by the current (1 − α)I_L1. The three capacitors form a voltage loop, so the voltage increment of these capacitors should be equal, that is:

$$\Delta V_{ca}=\left(1-\alpha \right)I_{L1}/C_a=\Delta V_{cz1}+\Delta V_{cz2}=\alpha I_{L1}/C_{z1}+\alpha I_{L1}/C_{z2}$$

(10)

Eliminate I_L1 from Equation (10) and simplify the expression to obtain:

$$\alpha =1/\left(1+C_a/C_{z1}+C_a/C_{z2}\right)$$

(11)

Thus, α is determined by the capacitance ratio. From Figure 2d or Figure 2e in mode 4, we know that:

$$V_{ca}=V_o+V_{cz2}$$

(12)

Comparing Equations (12) and (3), we can infer that V_cz1 = V_o, and V_ca = V_in + 2V_o.

The output voltage gain of the traditional Ćuk converter is d₁/(1 − d₁) in CCM. Figure 5 below shows the gain comparison between the traditional and the proposed Ćuk converter, whose gain is based on Equation (6). It can be seen that the output voltage of the quasi-Z-source converter is much larger than that of the traditional Ćuk converter in CCM.

3. Parameter Design and Control Strategy

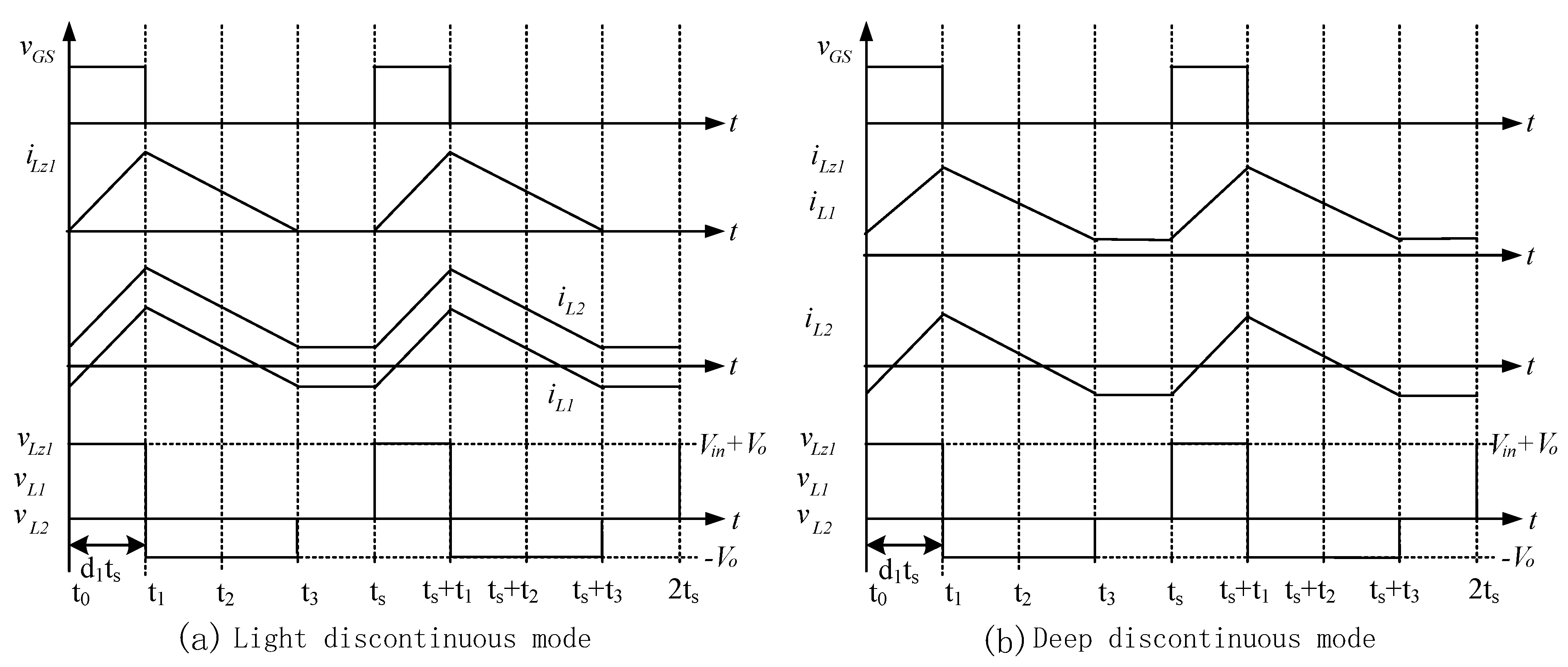
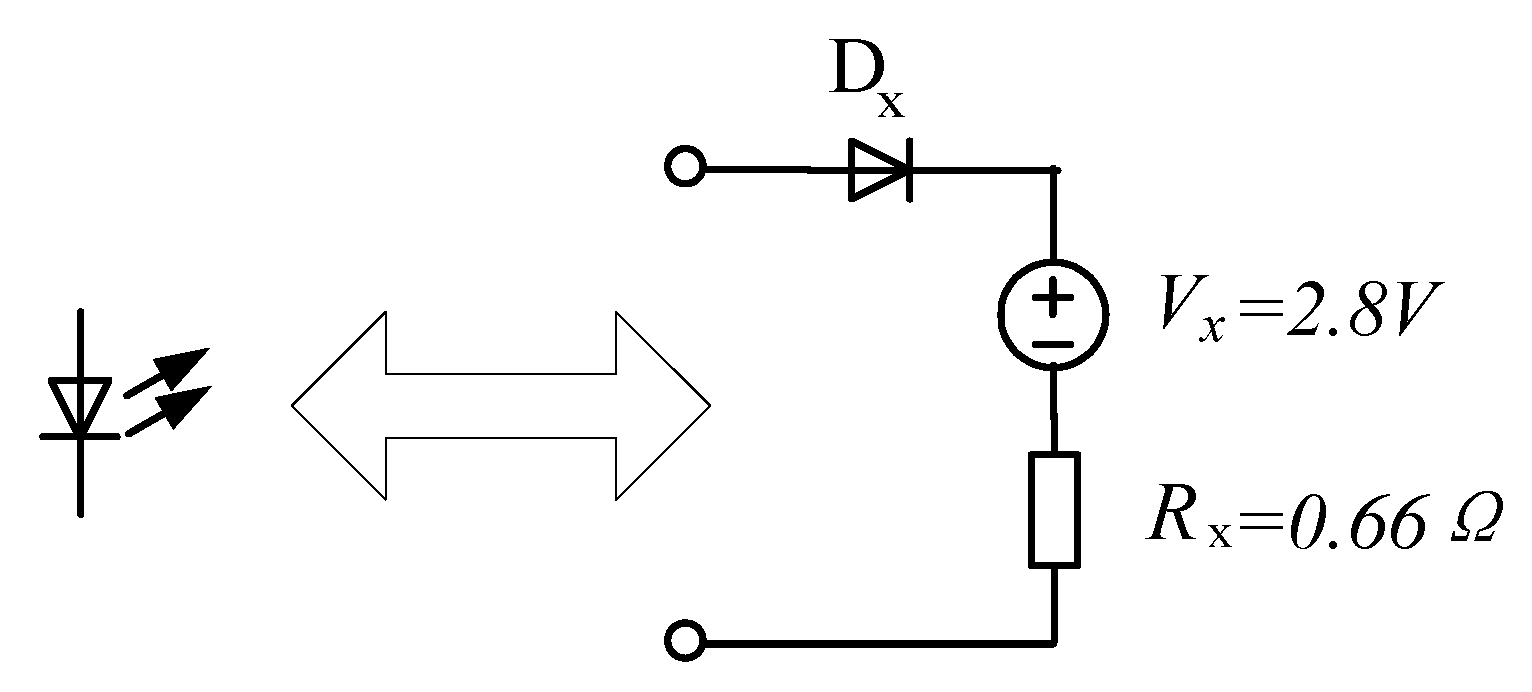
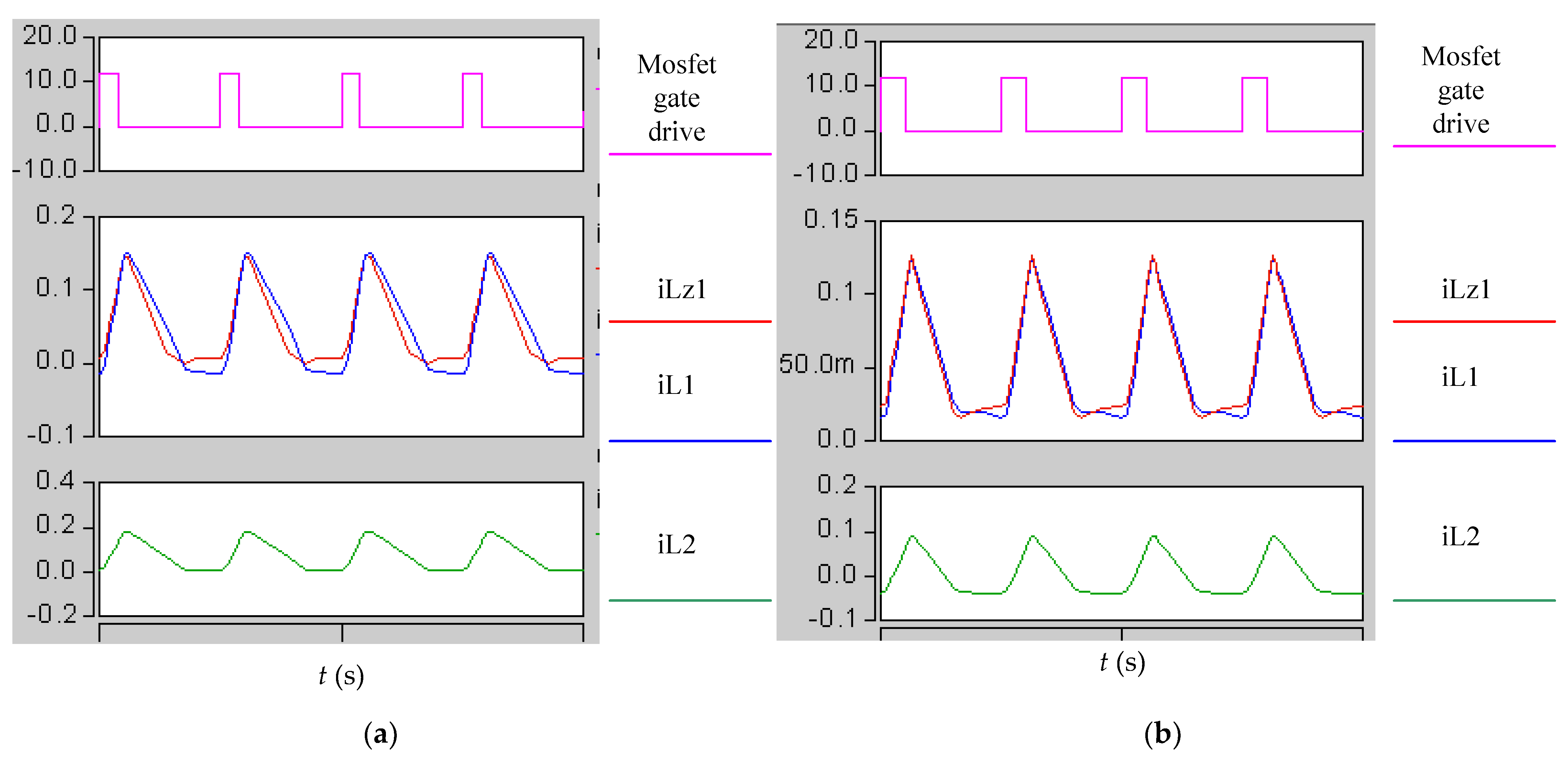
3.1. Boundary Analysis

The inductor can help to store energy only in CCM mode. Furthermore, the reverse flow of current occurs in DCM lead to lower efficiency. Therefore, the converter should be designed to operate in CCM, and the boundary current from CCM to the light DCM with a decrease in load current should be estimated, since i_Lz1 is zero at the end of the cycle in BCM, and the waveform of i_Lz1 in one cycle is triangular. According to the triangle area formula, the peak value is twice the average value. Therefore, it can be obtained from the analysis of mode 1 based on Faraday’s law of electromagnetic induction:

$$\left(V_{in}+V_{cz1}\right)d_1{t}_s/L_{z1}=\Delta i_{Lz1}=2I_{Lz1}$$

(13)

It is necessary to model the LED load to calculate the boundary load current. A single LED is modeled as a series connection of an ideal diode, a voltage source, and a resistor, similar as in [12]. The model circuit and its parameters used in the following analysis are shown in the Figure 6 below. The linearized model can be obtained by making a tangent at the rated current on the nonlinear voltage and current curve of power LED Luxeon LXM3-PW81 [22] used in the experiment, and the corresponding parameters can be achieved. Note that temperature factor is ignored here.

According to this LED model, the output voltage can be obtained from I_o:

V_o = N_led * V_x + R_x * N_led * I_o

(14)

where N_led represents the number of LEDs in the load.

Given V_in, L_z1, and LED load, I_o is initialized to be zero, V_o can be achieved through Equation (13). Three steps are taken to obtain the BCM load current, which is utilized to design the integrated inductor in the next subsection.

• d₁ can be obtained from Equation (6), and the boundary current I_Lz1 can be inferred from Equation (13).
• From the balance of input and output power, we know that:

$$V_{in}{I}_{Lz1}=V_o{I}_o$$

(15)

3.

Then Io can be obtained.

4.

A new Vo is calculated through Equation (14). The iteration stops when the error of Vo obtained by the two adjacent iterations is small enough, or we return to step 1.

When the error is set to 0.0001, less than 5 iterations are needed for a certain LED load.

3.2. Integrated Inductor Design

The design of the integrated inductor is decided by the CCM range of the load. The load current curve of BCM under different input voltages and different self-inductance of L_z1 is shown in Figure 7 based on the numerical iteration algorithm in the previous subsection. It can be seen that the boundary load current increases significantly with the increase in input voltage, and slightly increases with the decrease in the LED load. A self-inductance of 150 μH is selected to guarantee the converter to work in CCM in a wide range.

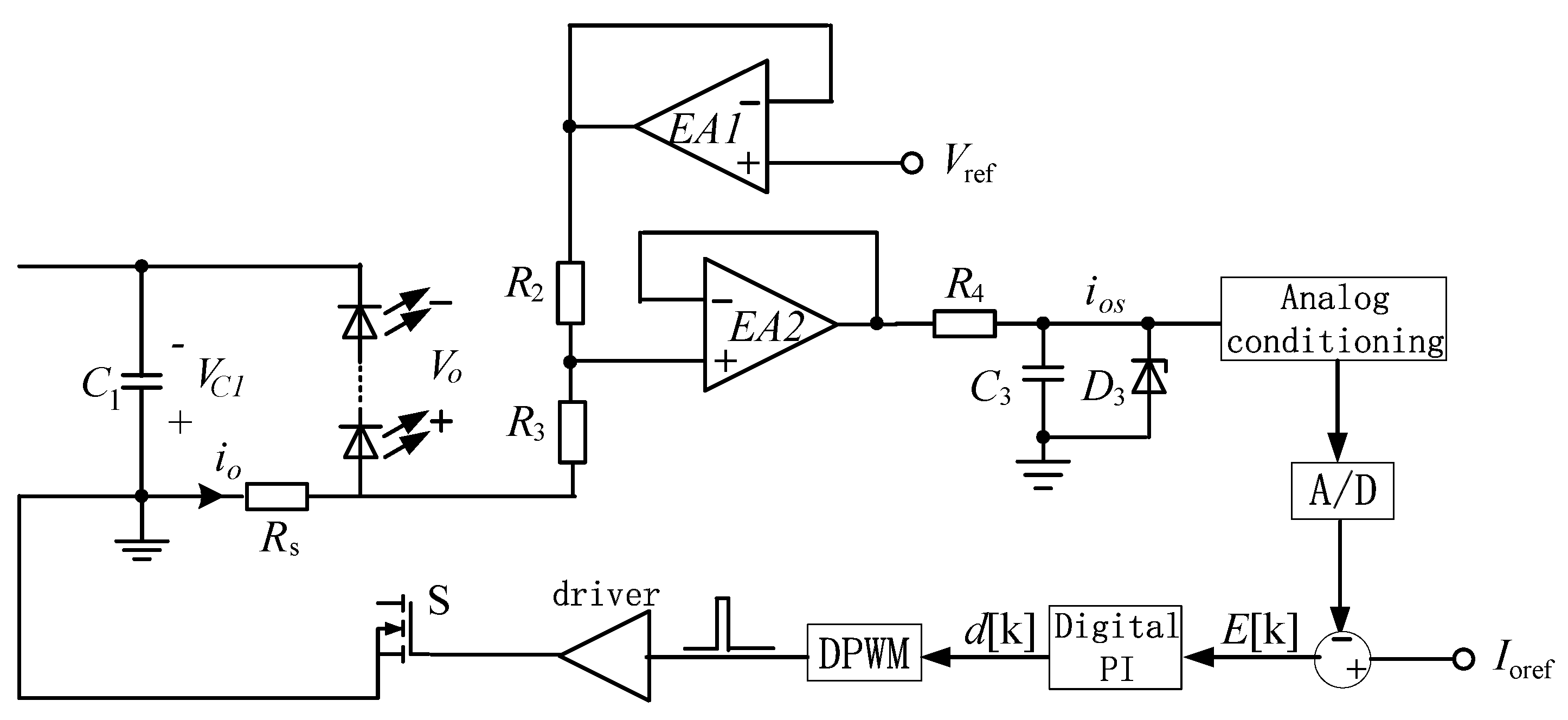
3.3. Circuit Control

Figure 8 shows the control block diagram of the proposed converter. To avoid excessive current during startup, soft startup is set in the program. At the beginning of startup, a slightly large duty is set for the converter for open-loop operation. The incremental current closed-loop PI duty cycle control is activated when the output current reaches within a certain range. Note that the output voltage of the proposed Ćuk converter is negative, so the potential of the sampling current on R_s is negative. A level-raising circuit is added to make it positive, and then the subsequent signal conditioning circuit and PI block are used to perform closed-loop control.

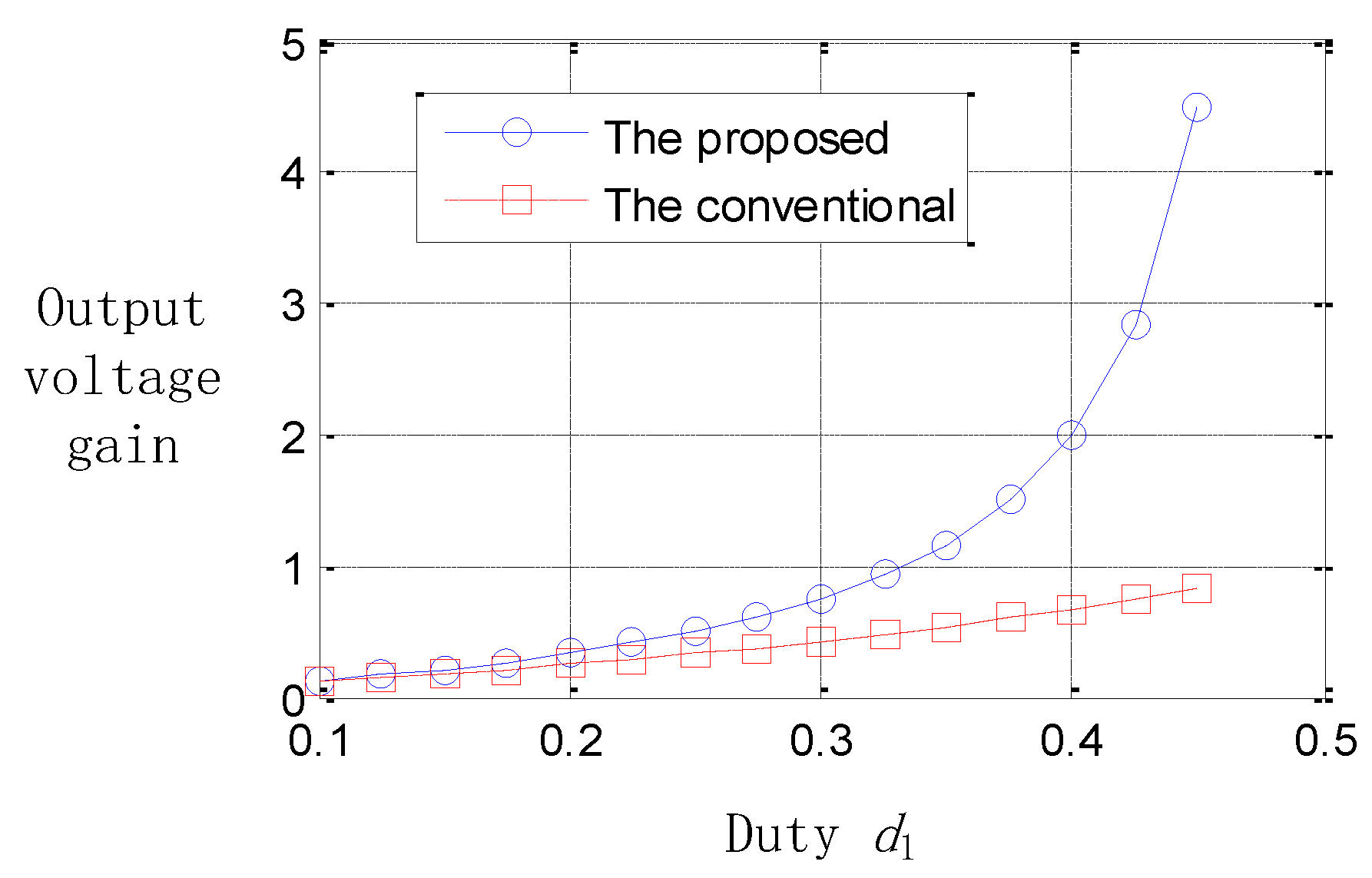
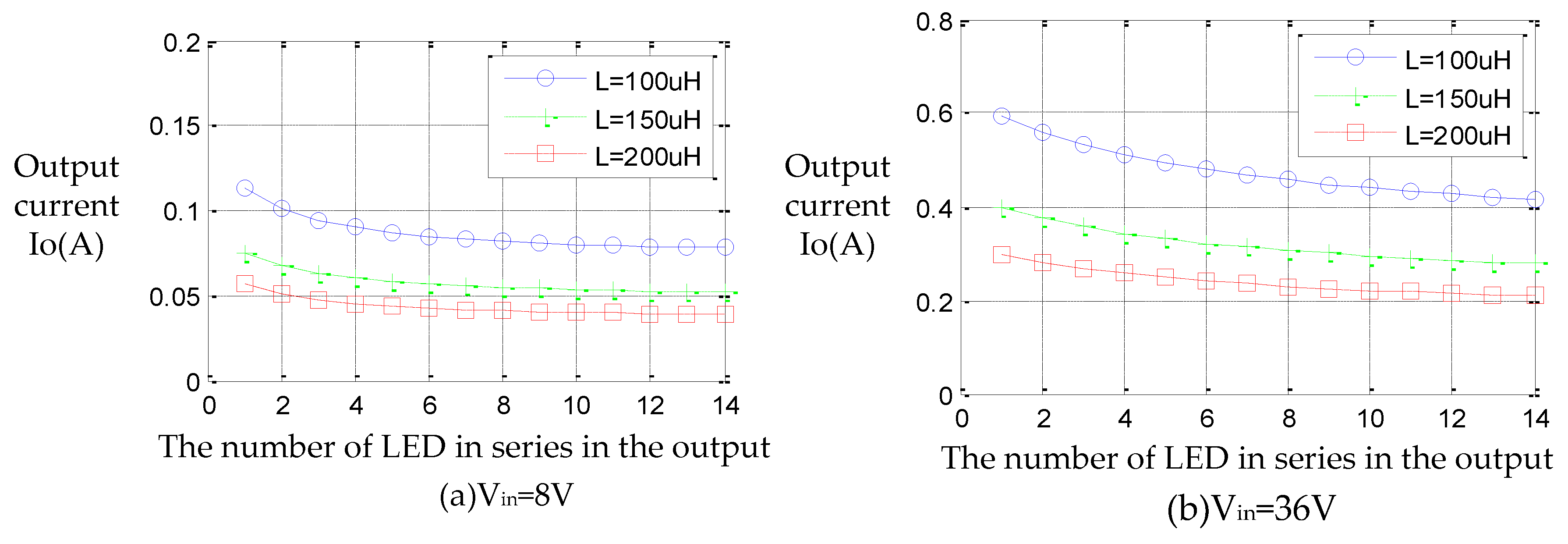
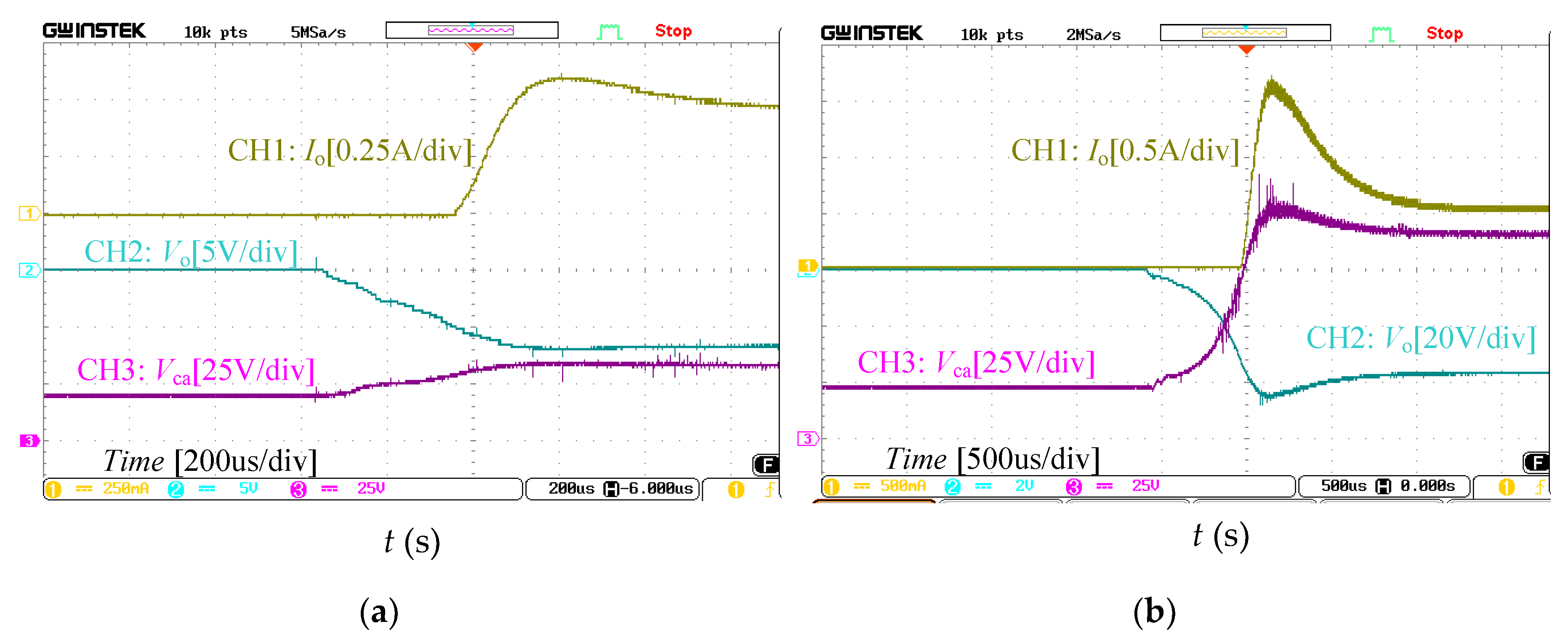
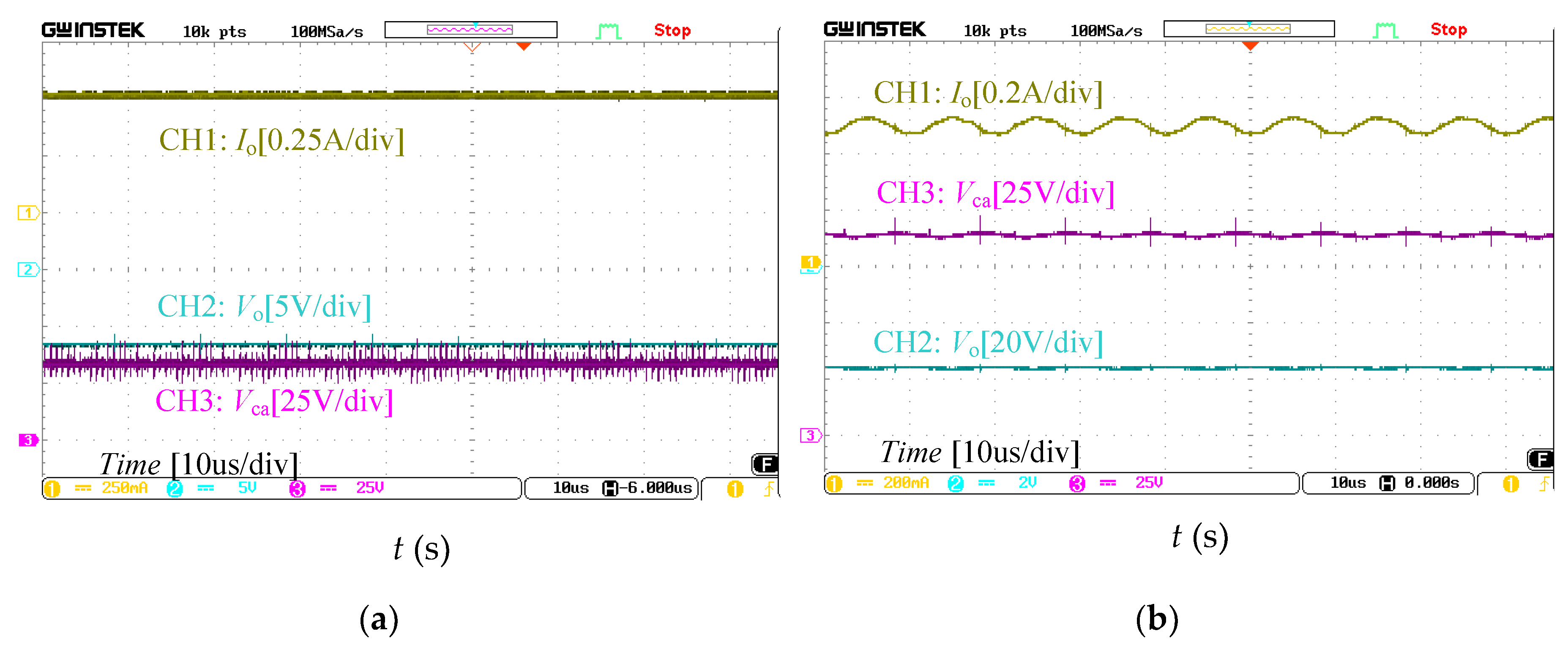
4. Simulation and Experimental Verification

The key of this converter simulation is the modeling of the multi-winding coupling inductor, which has been discussed in many studies recently [23,24]. Saber is a simulation software that can help. For the simulation model of mutual inductors, the coupling coefficient between windings should be defined in pairs, so three inductors and three coupling coefficients should be defined for three winding coupled inductors, as shown in Figure 9 below. In order to obtain a more accurate coupling coefficient, the windings of the fabricated coupling inductor are connected in series to measure mutual inductance in pairs. After obtaining the self-inductance of each winding, the simulation model is established.

The simulation waveform in Figure 10 presents the operation waveforms of two DCM modes under different load current. In Figure 10a, iLz1 remains zero in the fourth mode, while iL1 is negative and iL2 is positive. In Figure 10b, both iLz1 and iL1 remain positive, while iL2 is negative for a period of time. The verification of the operation waveform of DCM mode provides the basis for the design of the integrated inductor, and also validates the theoretical analysis in the previous section.

To verify the validity of the proposed LED driver, a prototype, shown in Figure 11, has been built and tested. The key components used in the prototype are listed in

Table 1. Key parameters of the protype.

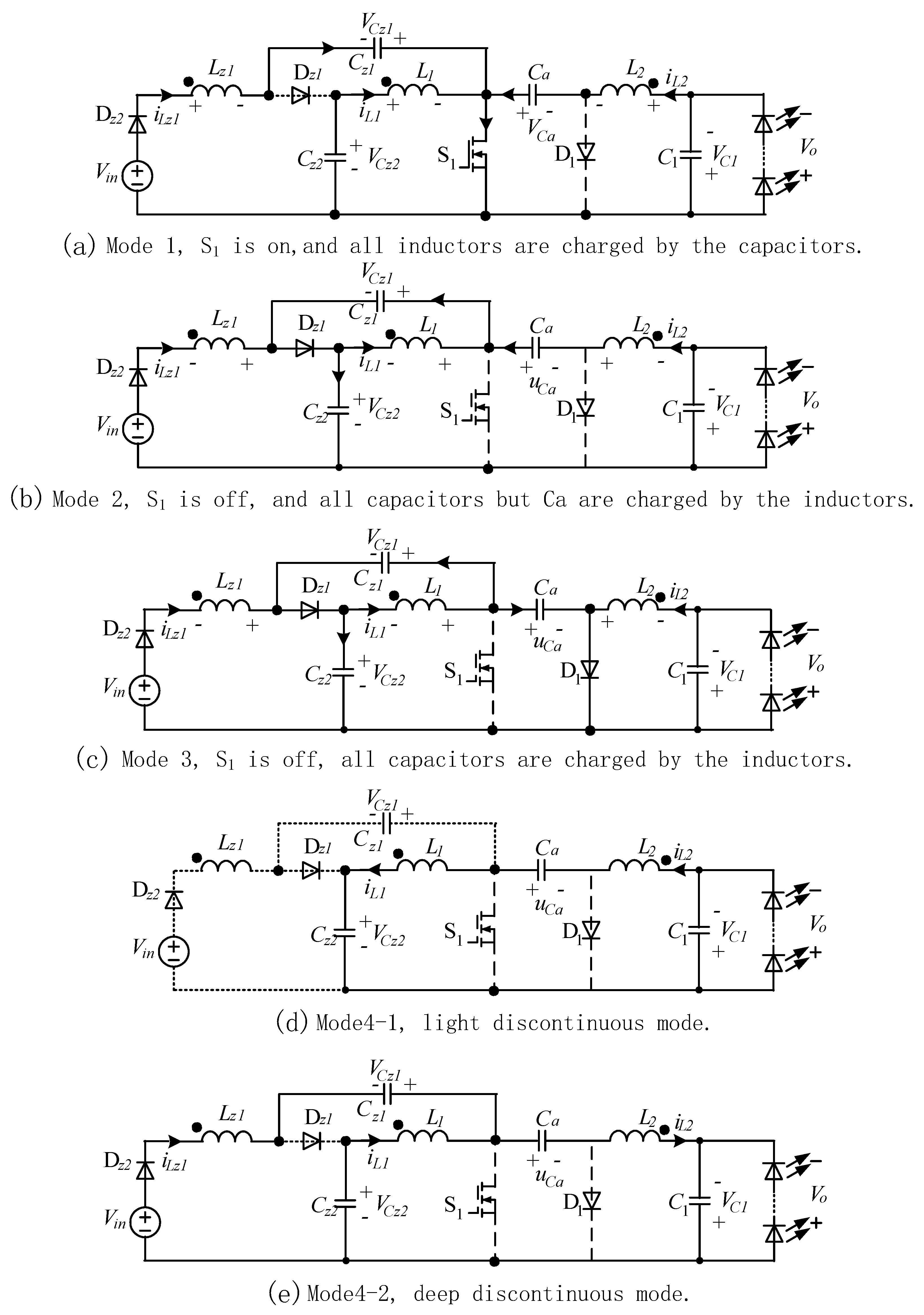
Parameter	Value	Parameter	Value
Input voltage Vin	8 V–36 V	Capacitor Cz1, Cz2	10 μF
Number of LED in series	2–12	Capacitor Ca, C1	4.7 μF
Rated load current	0.5 A	Switching frequency fs	100 KHz
Self-inductance of L1, Lz1, L2	150 μH	N-MOSFET S1	FQPF28N15/16.7 A, 150 V
D1, Dz1, Dz2	SR5150/5 A, 150 V

, and the control is realized by a micro control unit (stm32f103c8t6). The load consists of one LED string, according to the number of LEDs, and the output voltage ranges from 6 V to 36 V.

Figure 12 shows the startup waveform of I_o, V_o, and V_ca under a load of 2 LEDs and 12 LEDs in series with rated 0.5 A current, respectively. Before startup, V_ca is equal to V_in; when S₁ obtains the effective drive, V_ca and V_o change immediately. Note that the output voltage is negative. It can be seen from the experimental waveform that the dynamic characteristics of the converter are relatively fast under different loads.

Figure 13 displays the steady-state waveform of I_o, V_o, and V_ca under the load of 2 LEDs and 12 LEDs with rated 0.5 A current, respectively. It is indicated that the output is quite stable, and the output ripple current is less than 10% under the rated load.

Figure 14 shows the efficiency of the converter when the input voltage range is 8–36 V, where the corresponding number of load LEDs in series N_led is 2,6,10,12, and the rated output current is 0.5 A. It can be seen that the system efficiency increases gradually with the increase in input voltage and load. As the input voltage increases, the input current decreases, and the switch turn-off voltage rises. However, the decrease in the input current seems to have a greater impact on the efficiency.

5. Conclusions

In this paper, a novel quasi-Z-source Ćuk converter topology is proposed, and its work mode is analyzed in detail. Compared with the traditional Ćuk converter, its output voltage gain is greatly improved, which makes it more apt for wide input and load changes. Furthermore, the proposed converter combines the inherent characteristics of LED load to operate in a wide range in CCM, so the inductor can assist in energy storage, and electrolytic-free is available when small capacitance is required. In addition, inductors can be integrated and use only one core. Therefore, the converter requires less space. Finally, the feasibility of the proposed new topology is verified by experiments.