PCB Rogowski Coils for Capacitors Current Measurement in System Stability Enhancement
Abstract
1. Introduction
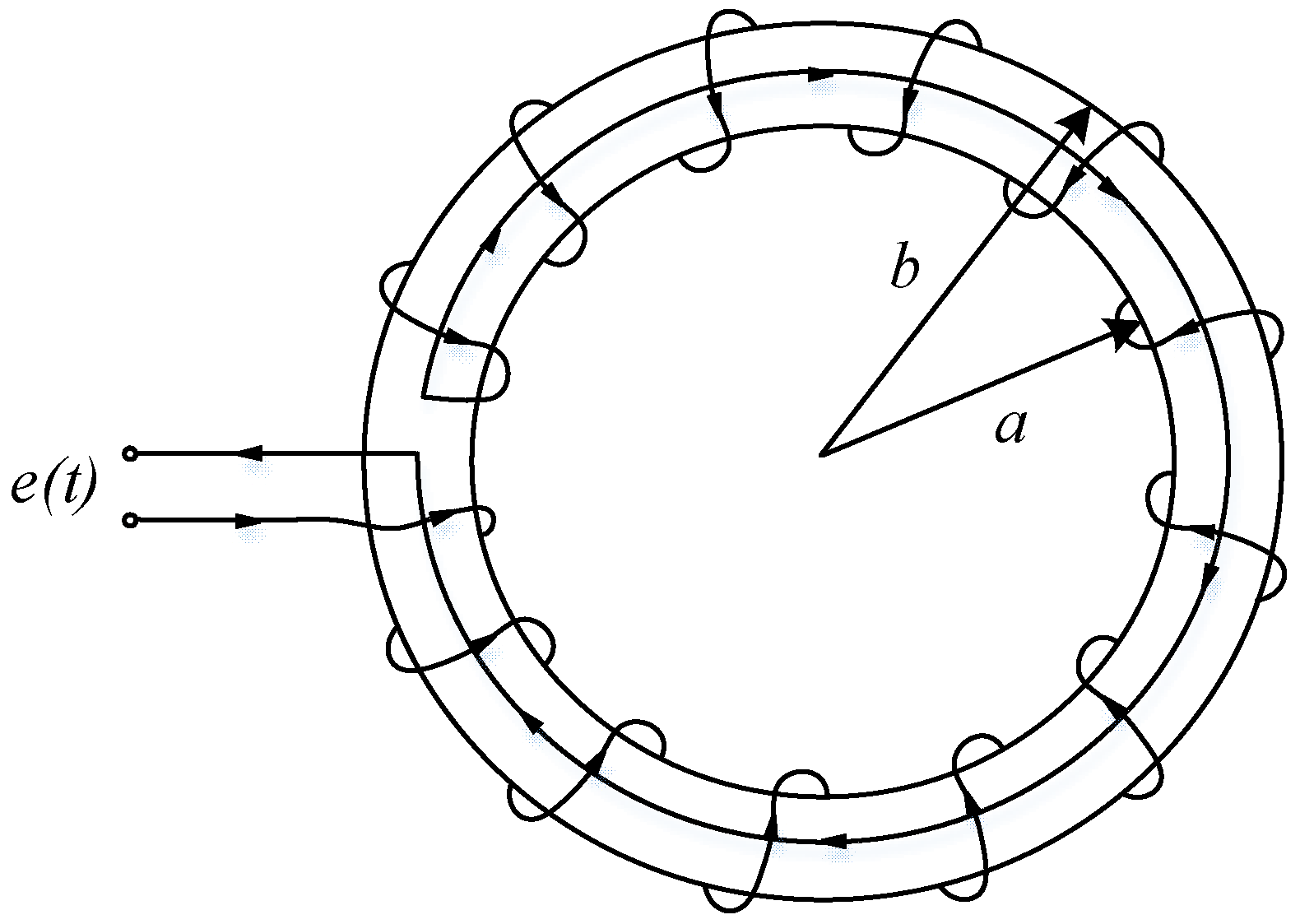
2. Working Principle of PCB Rogowski Coil
3. Coil Structure
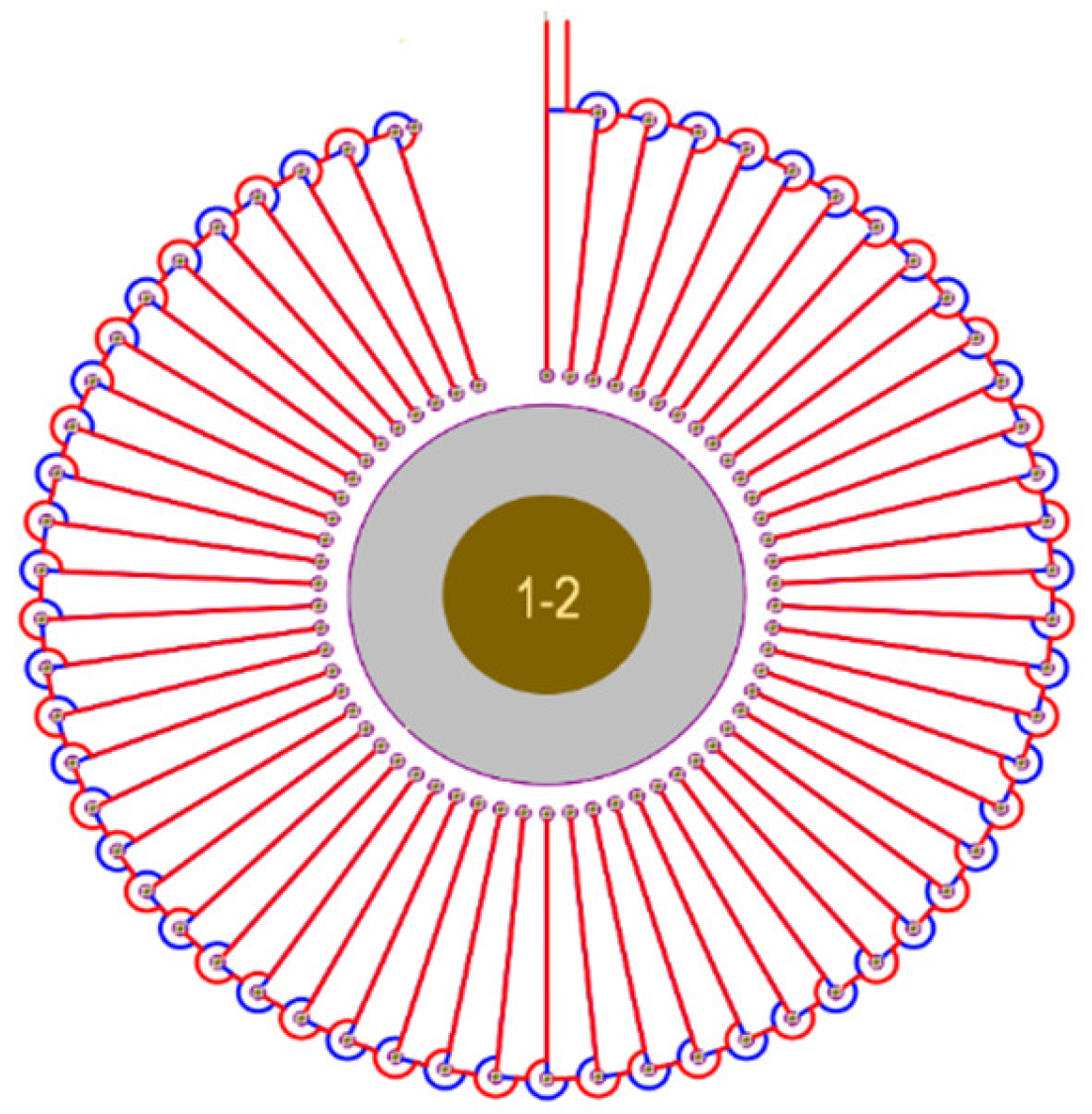
3.1. Four Types of Double-Layer Coils
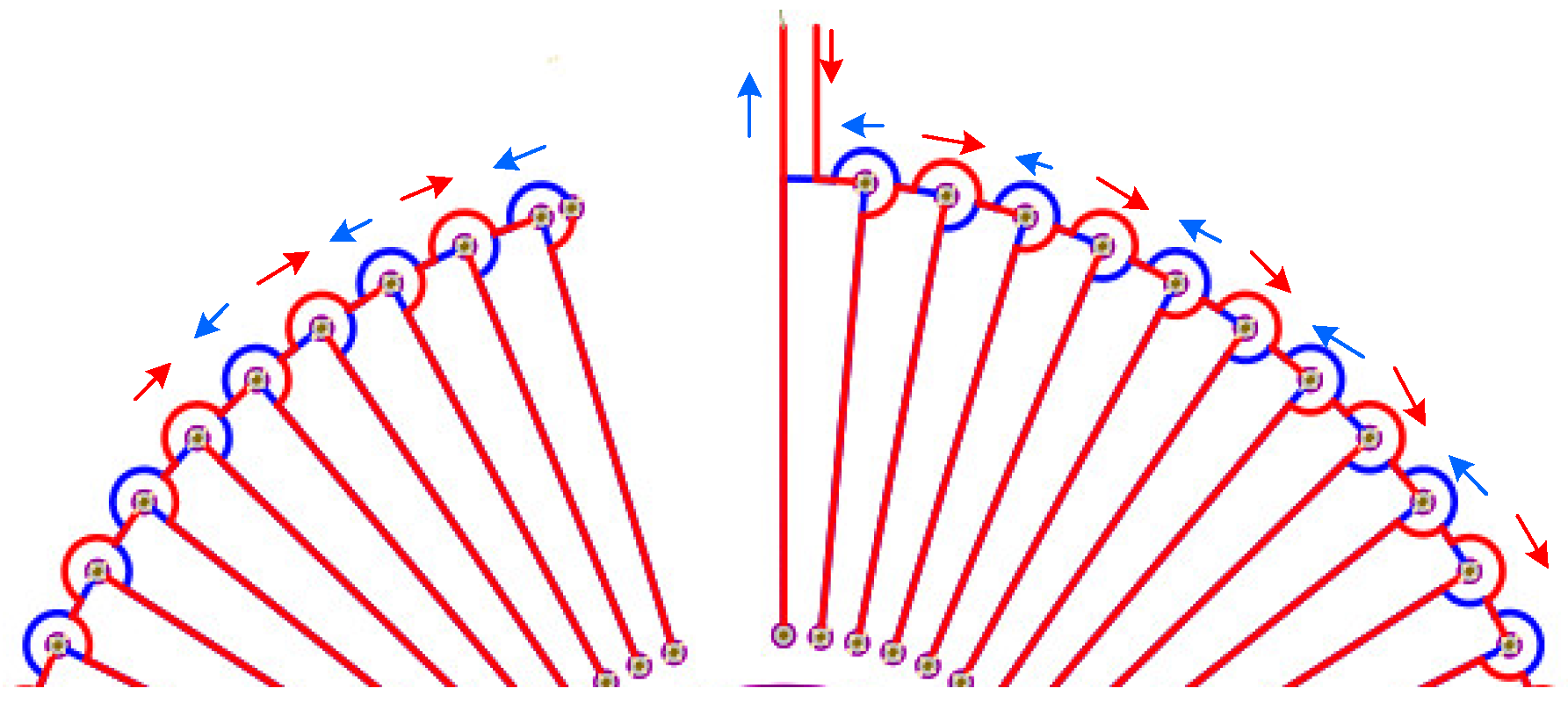
3.2. Differential Winding Coils
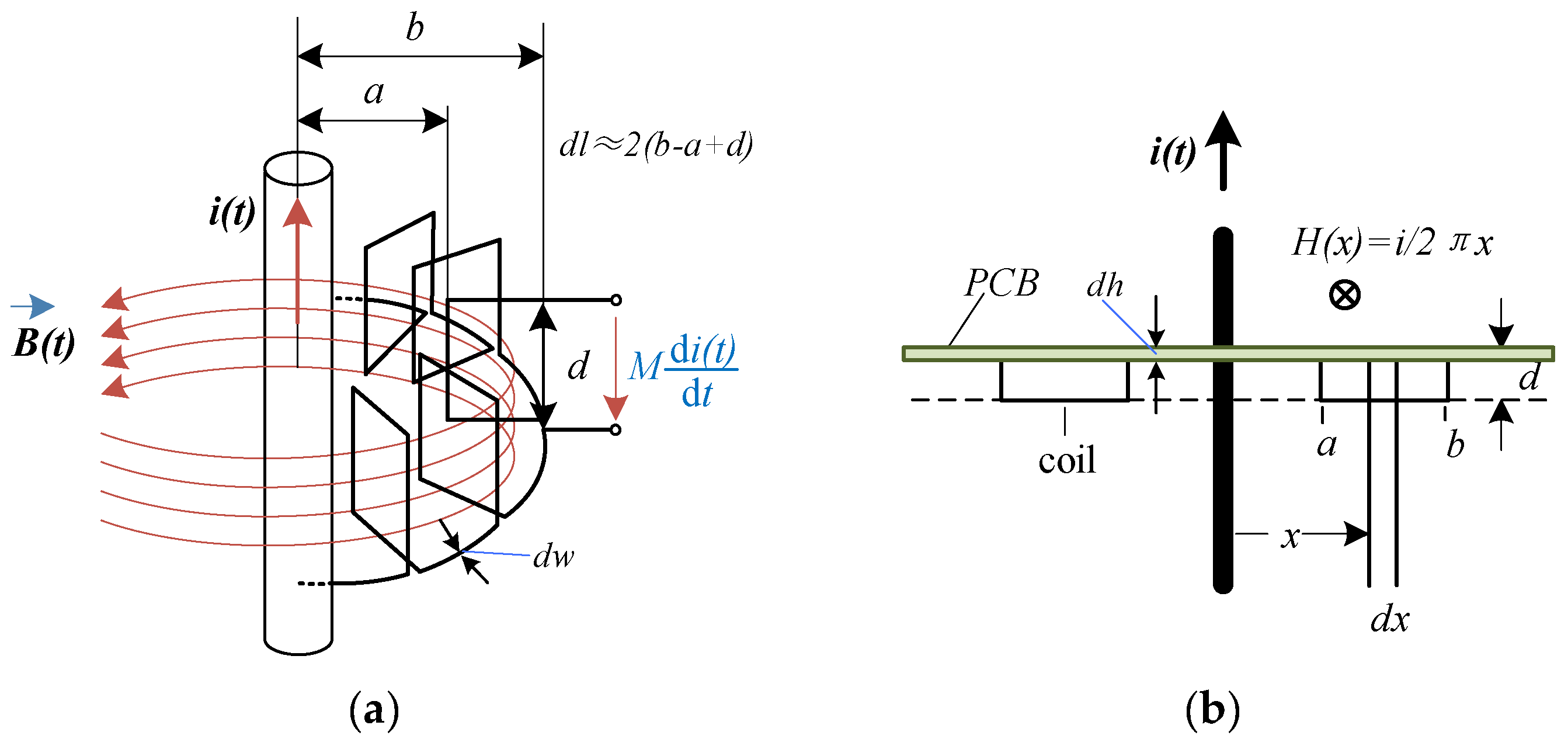
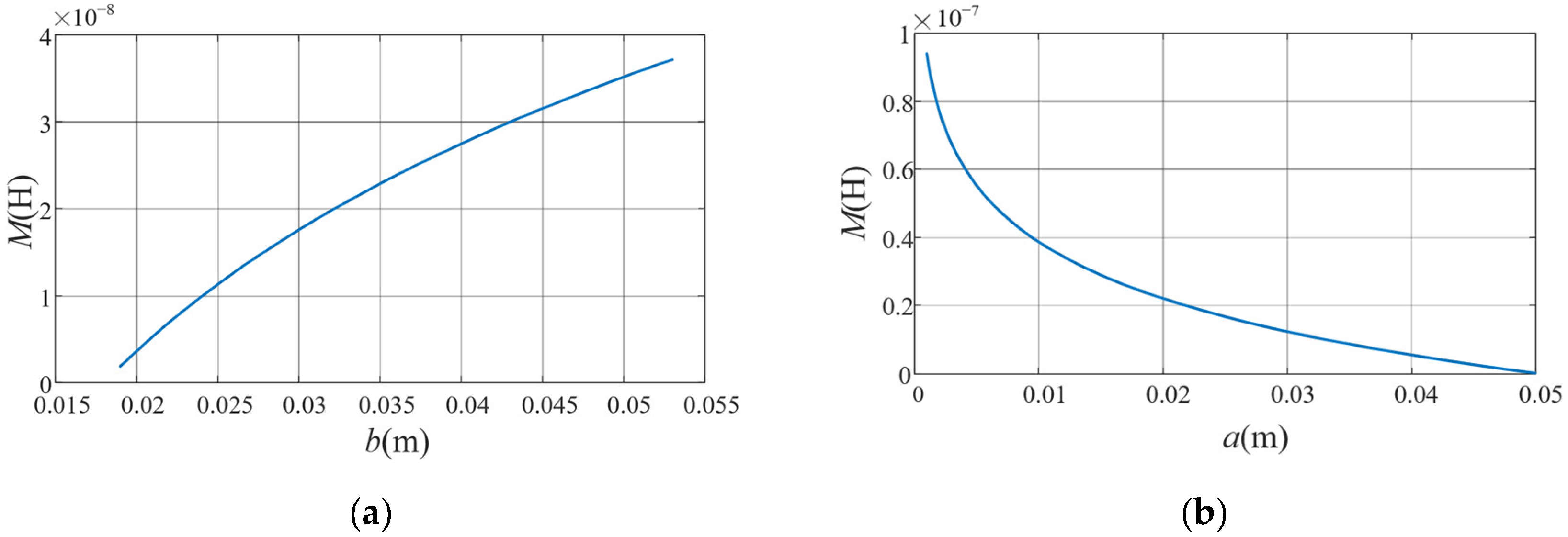
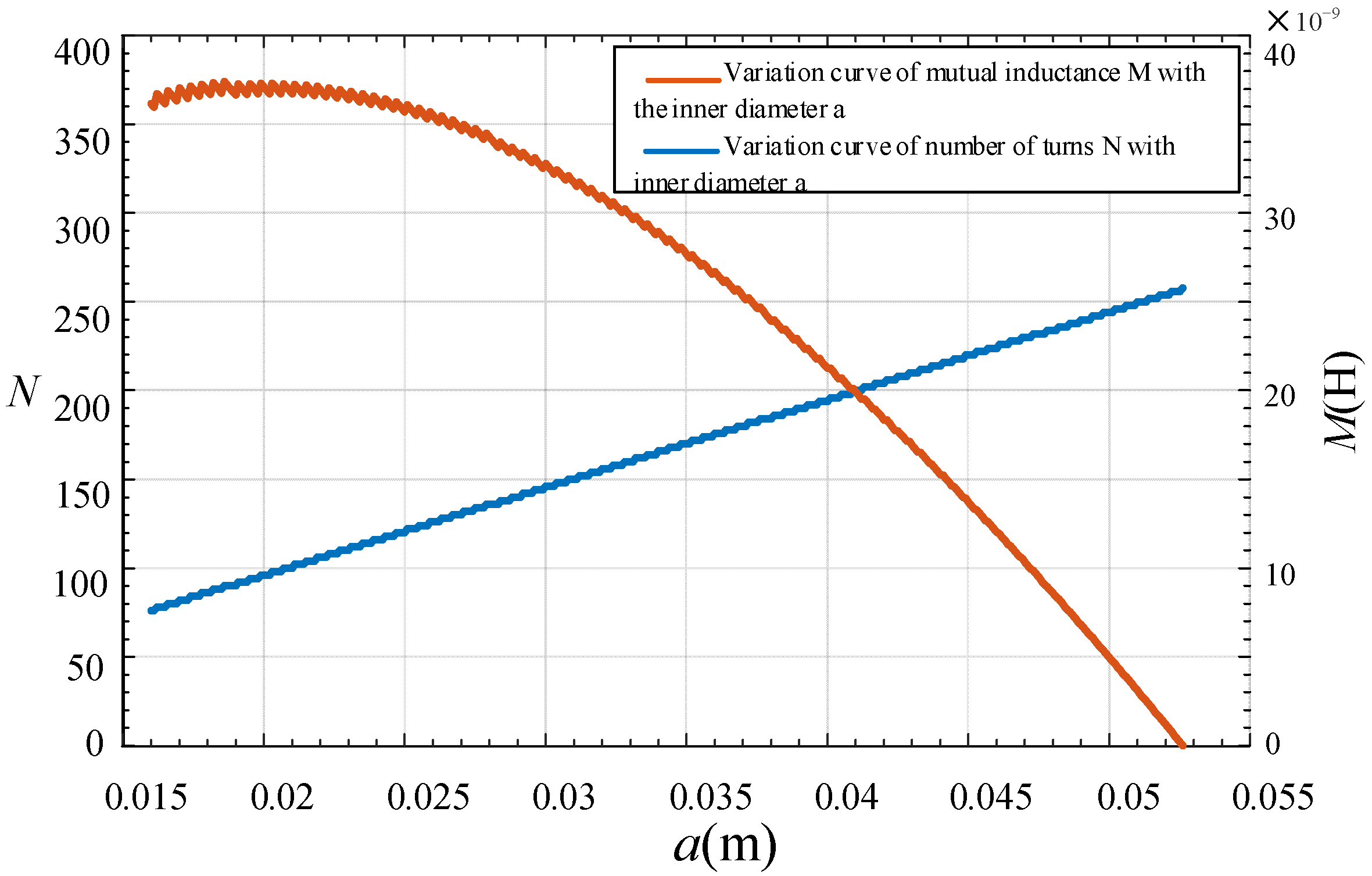
3.3. Influence of Structural Parameters
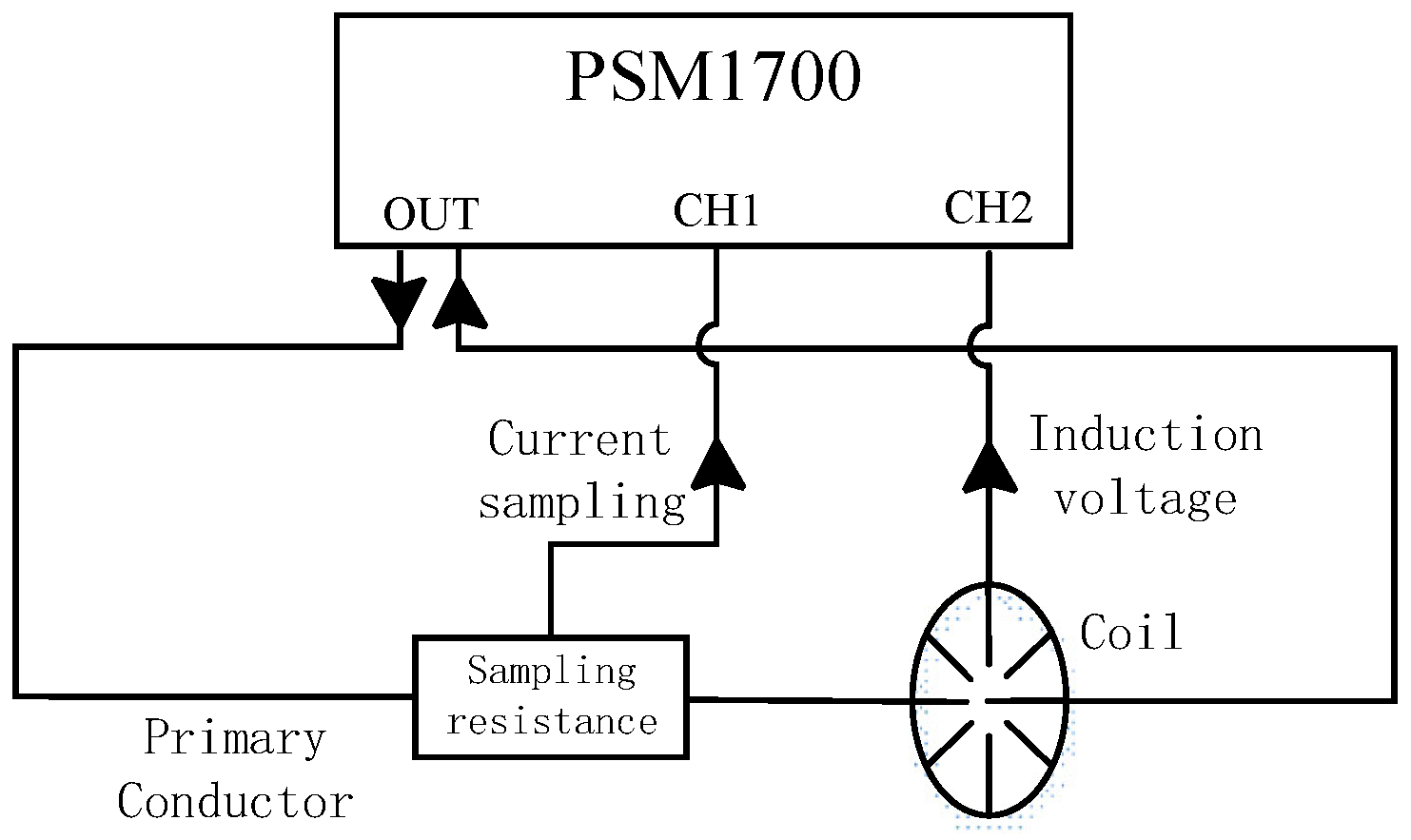
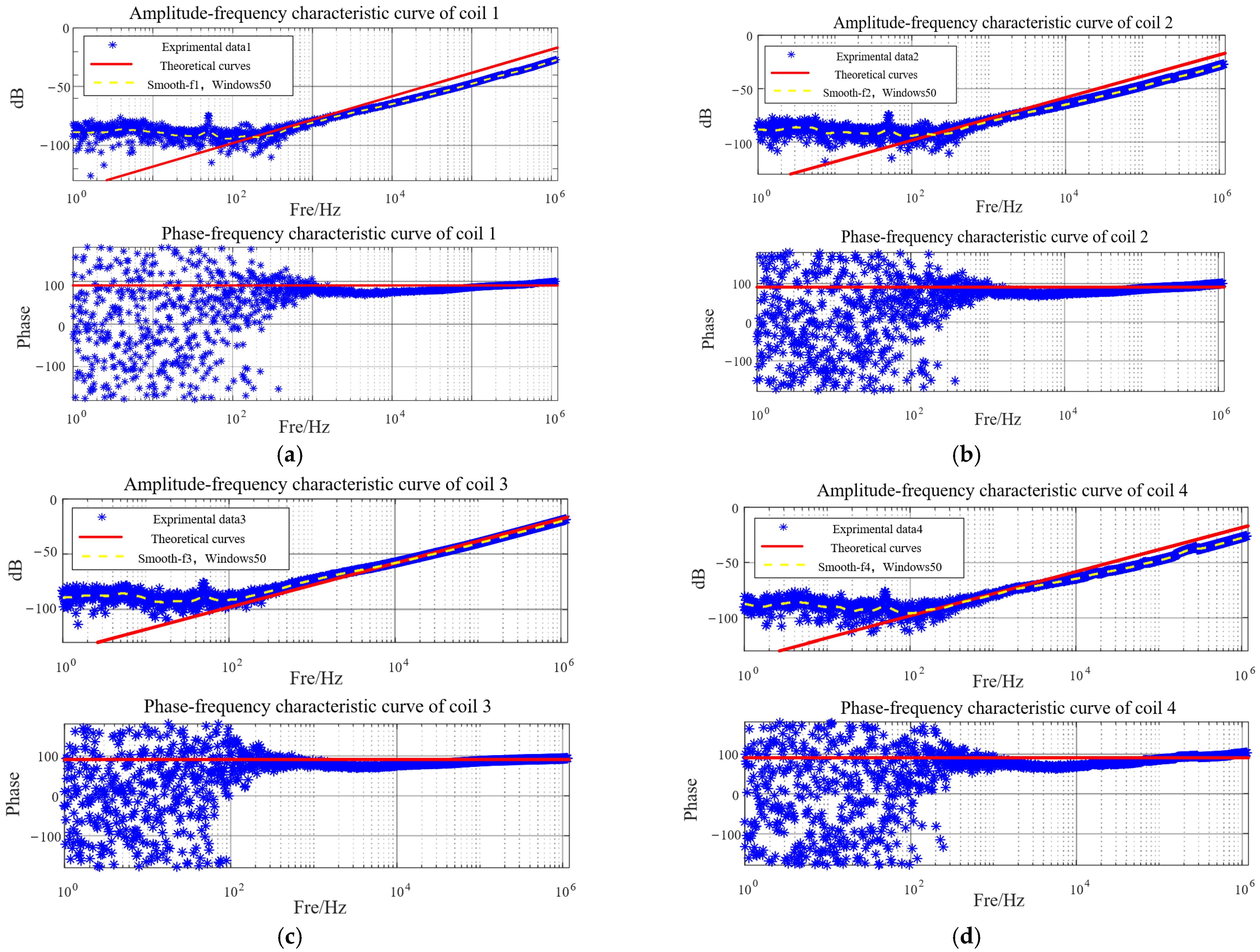
4. Experiment Verification
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Blaabjerg, F.; Pedersen, J.K.; Jaeger, U.; Thoegersen, P. Single current sensor technique in the DC link of three-phase PWM-VS inverters. IEEE Trans. Ind. Appl. 1997, 33, 1241–1253. [Google Scholar] [CrossRef]
- Ziegler, S.; Woodward, R.C.; Iu, H.; Borle, L.J. Current sensing techniques: A review. Sensors 2009, 9, 354–376. [Google Scholar] [CrossRef]
- Aiello, O.; Fiori, F. A new current sensor based on MagFET highly immune to EMI. In Proceedings of the 2009 International Conference on Electromagnetics in Advanced Applications, Turin, Italy, 14–18 September 2009; pp. 784–787. [Google Scholar]
- Sun, K.; Wei, Q.; Huang, L.; Matsuse, K. An Overmodulation Method for PWM-Inverter-Fed IPMSM Drive with Single Current Sensor. IEEE Trans. Ind. Electron. 2010, 57, 3395–3404. [Google Scholar] [CrossRef]
- Aiello, O.; Grovetti, P.; Fiori, F. Investigation on the susceptibility of hall-effect current sensors to EMI. In Proceedings of the EMC Europe 2011, York, UK, 26–30 September 2011; pp. 368–372. [Google Scholar]
- Ouyang, Y.; He, J.; Hu, J.; Wang, S.X. A current sensor based on the giant magnetoresistance effect: Design and potential smart grid applications. Sensors 2012, 12, 15520–15541. [Google Scholar] [CrossRef] [PubMed]
- Aiello, O.; Fiori, F. A New MagFET-Based integrated current sensor highly immune to EMI. Microelectron. Reliab. 2013, 53, 573–581. [Google Scholar] [CrossRef]
- Aiello, O.; Fiori, F. A new mirroring circuit for power MOS current sensing highly immune to EMI. Sensors 2013, 13, 1856–1871. [Google Scholar] [CrossRef]
- Aiello, O. Hall-effect current sensors susceptibility to emi: Experimental study. Electronics 2019, 8, 1310. [Google Scholar] [CrossRef]
- Lim, H.J. Current Detection Technique Using DC-Shunt and FET Voltage Drop of Three Phase Inverter; Kookmin University: Seoul, Republic of Korea, 2020. [Google Scholar]
- Jena, M.R.; Mohanty, K.B. Maximum efficiency controller for IPMSM using single DC link current sensor. In Proceedings of the 2020 IEEE International Symposium on Sustainable Energy, Signal Processing and Cyber Security (iSSSC), Gunupur Odisha, India, 16–17 December 2020. [Google Scholar]
- Tong, Q.; Chen, C.; Zhang, Q.; Zou, X. A Sensorless Predictive Current Controlled Boost Converter by Using an EKF with Load Variation Effect Elimination Function. Sensors 2015, 15, 9986–10003. [Google Scholar] [CrossRef]
- Hwang, J.-Y.; Park, J.-H.; Choi, J.-H.; Uhm, J.-I.; Lee, G.-H.; Lim, H.-S. A Precise Current Detection Method Using a Single Shunt and FET Rds(on) of a Low-Voltage Three-Phase Inverter. Electronics 2022, 11, 9. [Google Scholar] [CrossRef]
- Min, R.; Chen, C.; Zhang, X.; Zou, X.; Tong, Q.; Zhang, Q. An Optimal Current Observer for Predictive Current Controlled Buck DC-DC Converters. Sensors 2014, 14, 8851–8868. [Google Scholar] [CrossRef]
- Asada, T.; van Wyk, J.D.; Xiao, C.; Odendaal, W.G.; Zhao, L. An overview of integratable current sensor technologies. In Proceedings of the 38th IAS Annual Meeting on Conference Record of the Industry Applications Conference, Salt Lake City, UT, USA, 12–16 October 2003; pp. 1251–1258. [Google Scholar]
- Lu, C.; Ren, H.; Lei, S.; Wang, X.; Yuan, G. Principle and application of TMR anti-DC current sensor. Electr. Meas. Instrum. 2022, 59, 126–132. [Google Scholar]
- Zhang, H.; Li, Y.; Liu, J. Design of magnetic ring for open-close Hall sensor for calibration. Electr. Meas. Instrum. 2022, 59, 171–175. [Google Scholar]
- Cooper, J. On the high-frequency response of a Rogowski coil. J. Nucl. Energy Part C Plasma Phys. Accel. Thermonucl. Res. 1963, 5, 285. [Google Scholar] [CrossRef]
- Ramboz, J.D. Machinable Rogowski coil, design, and calibration. IEEE Trans. Instrum. Meas. 1996, 45, 511–515. [Google Scholar] [CrossRef]
- Ward, D.A. Measurement of Current Using Rogowski Coils. Proc. IEE Colloq. Instrum. Electr. Supply Ind. 1993, 1, 1–3. [Google Scholar]
- Ward, D.A.; Exon, J. Using Rogowski Coils for Transient Current Measurements. Eng. Sci. Educ. J. 1993, 2, 105–113. [Google Scholar] [CrossRef]
- Karrer, N.; Hofer-Noser, P. PCB Rogowski coil for high di/dt current measurement. In Proceedings of the 2000 IEEE 31st Annual Power Electronics Specialists Conference, Galway, Ireland, 23 June 2000; pp. 1296–1301. [Google Scholar]
- Kojovic, L.A. PCB Rogowski coil designs and performances for novel protective relaying. In Proceedings of the 2003 IEEE Power Engineering Society General Meeting (IEEE Cat. No. 03CH37491), Toronto, ON, Canada, 13–17 July 2003; Volume 2. [Google Scholar]
- Yang, N.; Duan, X. A new Rogowski coil-PCB Rogowski coil. High Volt. Electr. Appl. 2005, 41, 209211. [Google Scholar]
- Robles, G.; Argueso, M.; Sanz, J.; Giannetti, R.; Tellini, B. Identification of parameters in a Rogowski coil used for the measurement of partial discharges. In Proceedings of the 2007 IEEE Instrumentation & Measurement Technology Conference IMTC 2007, Warsaw, Poland, 1–3 May 2007. [Google Scholar]
- Tao, T.; Zhao, Z.; Ma, W.; Pan, Q.; Hu, A. Design of PCB Rogowski coil and analysis of anti-interference property. IEEE Trans. Electromagn. Compat. 2016, 58, 344–355. [Google Scholar] [CrossRef]
- Wang, J.; Chen, W.; Chen, P. A Design Method of PCB Rogowski Coil in limited space and modified integral circuit. IEEE Sens. J. 2020, 20, 5801–5808. [Google Scholar] [CrossRef]
- Xu, Z.; Ming, L.; Shi, Y.; Xin, Z.; Lu, B. Switching current measurement of silicon carbide devices based on twisted pair four-layer PCB Rogowski coil. J. Mot. Control 2021, 25, 46–57. [Google Scholar]
- Ming, L.; Xin, Z.; Yin, C.; Loh, P.C.; Liu, Y. Screen-returned PCB Rogowski coil for the switch current measurement of SiC devices. In Proceedings of the 2019 IEEE Applied Power Electronics Conference and Exposition (APEC), Anaheim, CA, USA, 17–21 March 2019. [Google Scholar]
- Fu, S.; Zhang, G.; Zhan, Y.; Peng, C.; Zhao, Z.; Li, X.; Cui, X. Method of segmented turns arrangement of PCB Rogowski coil with anti-interference ability. IEEE Trans. Instrum. Meas. 2021, 70, 1–12. [Google Scholar] [CrossRef]
- Chen, L. Research on Characteristics and Drive Protection of High Power SiC MOSFET Devices; Beijing Jiaotong University: Beijing, China, 2019. [Google Scholar]
- Wei, W.; Cai, L.; Zhang, C. Design of C type multilayer lightning current detector based on PCB Rogowski coil. J. Sichuan Inst. Technol. Nat. Sci. Ed. 2019, 32, 29–34. [Google Scholar]
- Gu, P.-Y.; Chen, Q.; Li, H.-B.; Hu, C.; Gong, H.; Jiao, Y. PCB Rogowski coils for 300 kA current measurement on a multi-split conductor. IEEE Sens. J. 2019, 19, 6786–6794. [Google Scholar] [CrossRef]
- Hasegawa, K.; Sho, S.; Tsukuda, M.; Omura, I.; Ichiki, M.; Kato, T. Output-current measurement of a PWM inverter with a tiny PCB rogowski sensor integrated into an IGBT module. In Proceedings of the 2019 IEEE Energy Conversion Congress and Exposition (ECCE), Baltimore, MD, USA, 29 September–3 October 2019. [Google Scholar]
- C37.235-2007; IEEE Guide for the Application of Rogowski Coils Used for Protective Relaying Purposes. IEEE: New York, NY, USA, 2007.
- Mingotti, A.; Peretto, L.; Tinarelli, R. Smart characterization of rogowski coils by using a synthetized signal. Sensors 2020, 20, 3359. [Google Scholar] [CrossRef]
- Riehl, R.R.; de Castro, B.A.; Fraga, J.R.C.P.; Puccia, V.; Lucas, G.B.; Andreoli, A.L. Assessment of Rogowski Coils for Measurement of Full Discharges in Power Transformers. Eng. Proc. 2021, 10, 16. [Google Scholar]
- Tan, Q.; Zhang, W.; Tan, X.; Yang, L.; Ren, Y.; Hu, Y. Design of Open-Ended Structure Wideband PCB Rogowski Coil Based on New Winding Method. Electronics 2022, 11, 381. [Google Scholar] [CrossRef]
- Mingotti, A.; Costa, F.; Peretto, L.; Tinarelli, R. Accuracy Type Test for Rogowski Coils Subjected to Distorted Signals, Temperature, Humidity, and Position Variations. Sensors 2022, 22, 1397. [Google Scholar] [CrossRef]
- Fritz, J.N.; Neeb, C.; De Doncker, R.W. A PCB integrated differential Rogowski coil for non-intrusive current measurement featuring high bandwidth and dv/dt immunity. In Proceedings of the Power and Energy Student Summit (PESS) 2015, Dortmund, Germany, 13–14 January 2015; pp. 1–6. [Google Scholar]
- Shi, Y.; Xin, Z.; Loh, P.C.; Blaabjerg, F. A review of traditional helical to recent miniaturized printed circuit board rogowski coils for power-electronic applications. IEEE Trans. Power Electron. 2020, 35, 12207–12222. [Google Scholar] [CrossRef]
- Kojovic, L.A.; Skendzic, V.; Williams, S.E. High Precision Rogowski Coil. U.S. Patent 6,313,623, 6 November 2001. [Google Scholar]
- Hain, S.; Bakran, M.-M. New Rogowski coil design with a high DV/DT immunity and high bandwidth. In Proceedings of the 2013 15th European Conference on Power Electronics and Applications (EPE), Lille, France, 2–6 September 2013. [Google Scholar]




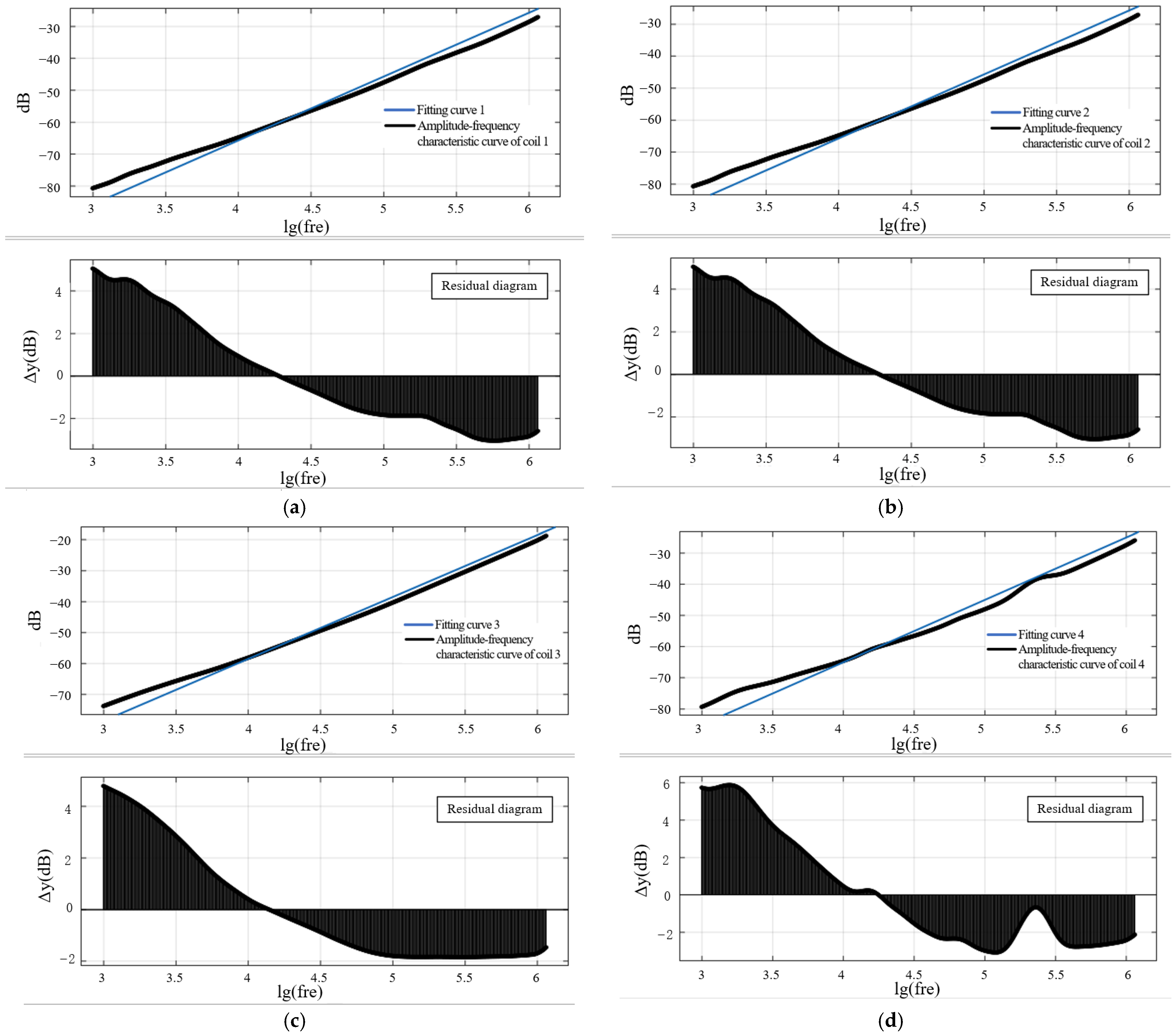
| Serial Number | Inner Radius of Coil a (mm) | Outer Radius of Coil b (mm) | Through Hole Diameter d1 (mm) | Through Hole Pad Diameter d2 (mm) | Trace Width dw (mm) | Copper Coating Thickness dh (mm) | PCB Thickness d (mm) | Number of Turns N |
|---|---|---|---|---|---|---|---|---|
| Coils 1 | 18.6 | 41 | 0.3 | 0.508 | 0.254 | 0.035 | 2 | 60 |
| Coils 2 | 18.6 | 41 | 0.3 | 0.508 | 0.254 | 0.035 | 2 | 60 |
| Coils 3 | 18.6 | 41 | 0.3 | 0.508 | 0.254 | 0.035 | 2 | 60 |
| Coils 4 | 18.6 | 41 | 0.3 | 0.508 | 0.254 | 0.035 | 2 | 60 |
| Serial Number | Mutual Inductance Coefficient M (nH) | Inductance Value Lc (μH) | Resistance Value Rc (Ω) | Capacitance Value Cc (pF) |
|---|---|---|---|---|
| Coils 1 | 18.969 | 1.138 | 2.575 | 24.509 |
| Coils 2 | 18.969 | 1.138 | 2.375 | 24.509 |
| Coils 3 | 18.969 | 1.138 | 2.375 | 24.509 |
| Coils 4 | 18.969 | 1.138 | 2.375 | 24.509 |
| Serial Number | Coil Mutual Inductance Value M (nH) | The Intercept of the Fitted Curve with the Vertical Coordinate | Experimentally Obtained Mutual Inductance Values (nH) | Error (%) |
|---|---|---|---|---|
| Coils 1 | 18.969 | −145.7 | 8.25696 | −56.472 |
| Coils 2 | 18.969 | −145.4 | 8.54713 | −54.942 |
| Coils 3 | 18.969 | −141.5 | 13.39122 | −29.406 |
| Coils 4 | 18.969 | −141.2 | 13.86182 | −26.925 |
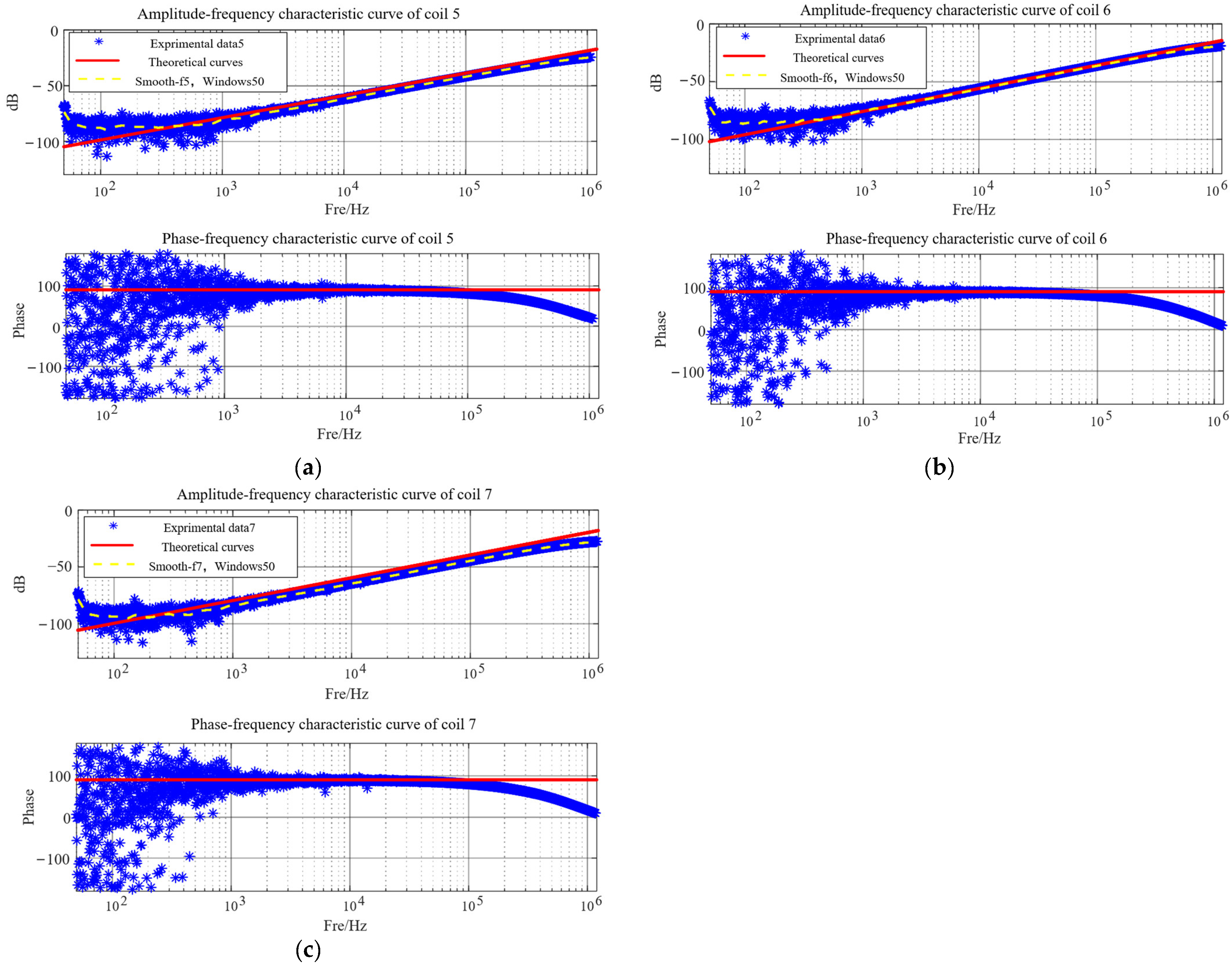
| Serial Number | Coil Inner Diameter a (mm) | Coil Outer Diameter b (mm) | Through Hole Diameter d1 (mm) | Through Hole Pad Diameter d2 (mm) | The radius of the Outer Circle of the Coil r1 (mm) | Trace Width dw (mm) | Copper Coating Thickness dh (mm) | PCB Thickness d (mm) | Number of Turns N |
|---|---|---|---|---|---|---|---|---|---|
| Coils 5 | 18.6 | 41 | 0.3 | 0.508 | 0.8 | 0.254 | 0.035 | 2 | 60 |
| Coils 6 | 18.6 | 52.6 | 0.3 | 0.508 | 0.8 | 0.254 | 0.035 | 2 | 60 |
| Coils 7 | 20.6 | 41 | 0.3 | 0.508 | 0.8 | 0.254 | 0.035 | 2 | 60 |
| Serial Number | Coil Mutual Inductance M (nH) | Coil Inductor Lc (μH) | Coil Resistance Rc (Ω) | Coil Capacitor Cc (pF) |
|---|---|---|---|---|
| Coils 5 | 18.089 | 1.085 | 2.393 | 22.822 |
| Coils 6 | 24.949 | 1.497 | 3.717 | 38.765 |
| Coils 7 | 16.528 | 0.991 | 2.157 | 22.431 |
| Serial Number | Theoretical Value M (nH) | The Intercept of the Fitted Curve with the Vertical Coordinate | Experimental Value (nH) | Error/% |
|---|---|---|---|---|
| Coils 5 | 18.089 | −141.8 | 12.9366 | −28.4833 |
| Coils 6 | 24.949 | −137.6 | 20.98071 | −15.9042 |
| Coils 7 | 16.528 | −152.1 | 12.49741 | −24.3418 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yue, X.; Zhu, G.; Wang, J.V.; Deng, X.; Wang, Q. PCB Rogowski Coils for Capacitors Current Measurement in System Stability Enhancement. Electronics 2023, 12, 1099. https://doi.org/10.3390/electronics12051099
Yue X, Zhu G, Wang JV, Deng X, Wang Q. PCB Rogowski Coils for Capacitors Current Measurement in System Stability Enhancement. Electronics. 2023; 12(5):1099. https://doi.org/10.3390/electronics12051099
Chicago/Turabian StyleYue, Xuxin, Guorong Zhu, Jing V. Wang, Xiangtian Deng, and Qian Wang. 2023. "PCB Rogowski Coils for Capacitors Current Measurement in System Stability Enhancement" Electronics 12, no. 5: 1099. https://doi.org/10.3390/electronics12051099
APA StyleYue, X., Zhu, G., Wang, J. V., Deng, X., & Wang, Q. (2023). PCB Rogowski Coils for Capacitors Current Measurement in System Stability Enhancement. Electronics, 12(5), 1099. https://doi.org/10.3390/electronics12051099





