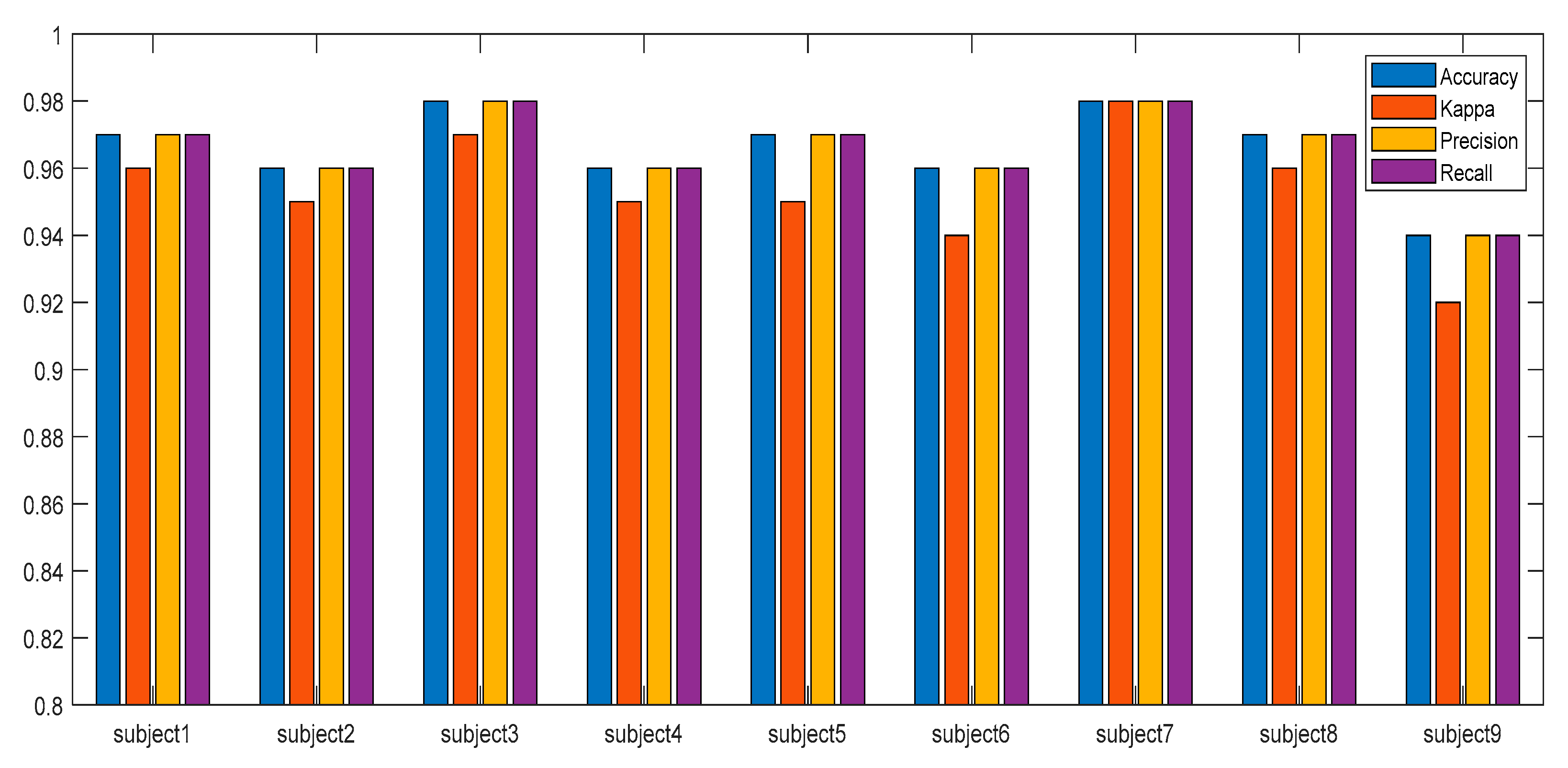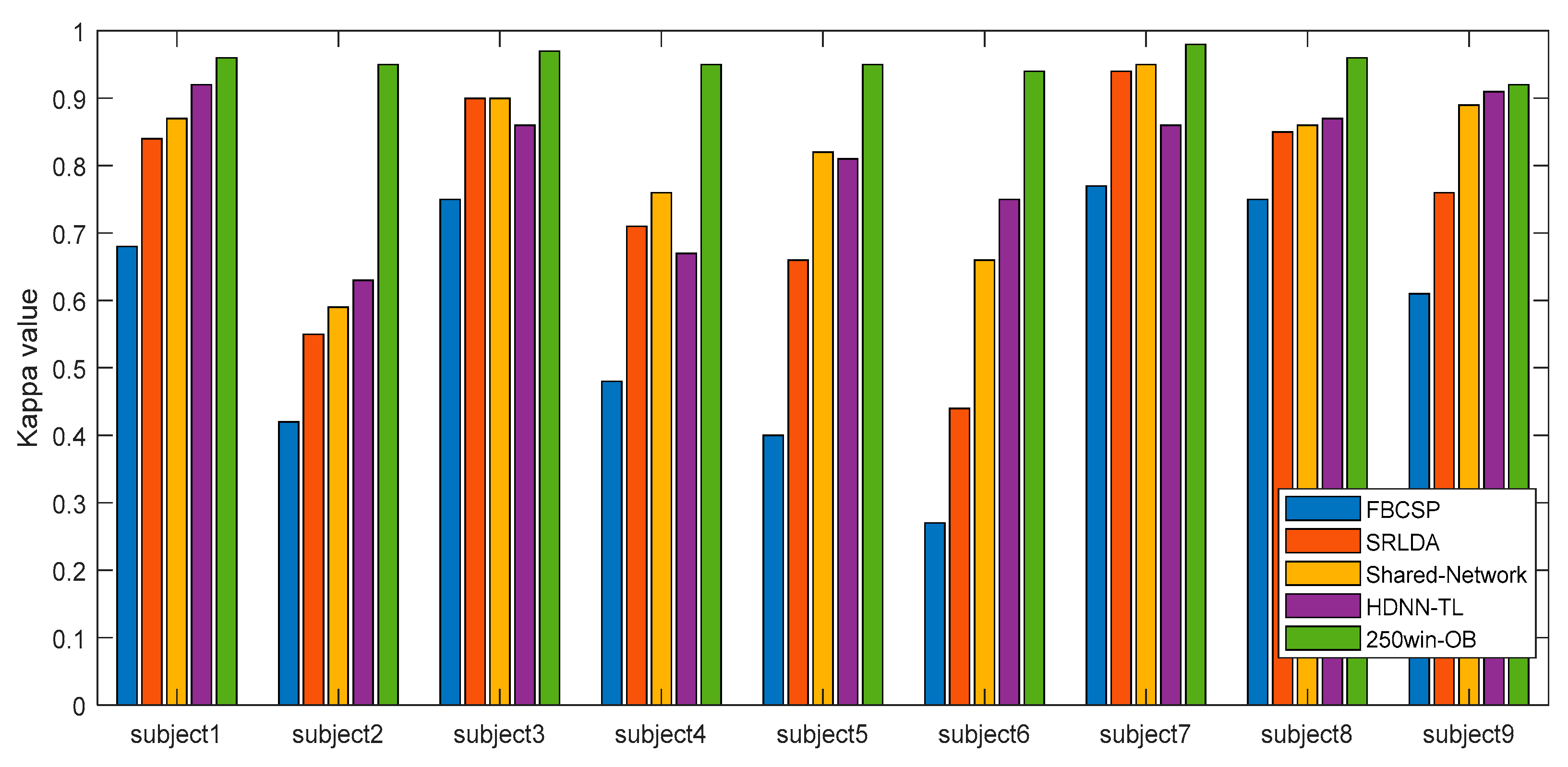Abstract
Motor imagery (MI) electroencephalography (EEG) signals are widely used in BCI systems. MI tasks are performed by imagining doing a specific task and classifying MI through EEG signal processing. However, it is a challenging task to classify EEG signals accurately. In this study, we propose a LSTM-based classification framework to enhance classification accuracy of four-class MI signals. To obtain time-varying data of EEG signals, a sliding window technique is used, and an overlapping-band-based FBCSP is applied to extract the subject-specific spatial features. Experimental results on BCI competition IV dataset 2a showed an average accuracy of 97% and kappa value of 0.95 in all subjects. It is demonstrated that the proposed method outperforms the existing algorithms for classifying the four-class MI EEG, and it also illustrates the robustness on the variability of inter-trial and inter-session of MI data. Furthermore, the extended experimental results for channel selection showed the best performance of classification accuracy when using all twenty-two channels by the proposed method, but an average kappa value of 0.93 was achieved with only seven channels.
1. Introduction
Cognitive information and communication technology (CogInfoCom) is a technology used to facilitate interaction between humans and information and communication devices or robots. This technology employs various tools, including brain-computer interface (BCI), gesture control, and eye tracking [1]. BCI is a technology that measures and analyzes brainwave signals to recognize and control user intentions [2]. Ongoing research explores the use of BCI in areas such as behavioral analysis and improving the quality of life for individuals with cognitive impairments, with BCI being integrated with gesture control or eye tracking technologies for this purpose [3,4,5]. Furthermore, with the development of low-cost BCI devices, researchers are exploring the use of BCI to control robots in real-life situations [6,7] and for virtual reality-based education [8]. Brainwaves, which are now being integrated into various fields, are considered an important biological signal. However, BCI has the characteristic of being greatly influenced by vision, making it a field that requires delicate measurement and precise analysis [9,10,11,12].
The main objective of a BCI system is to detect specific brain activities and use signal patterns to command a computer to perform specific tasks [13,14,15]. The electroencephalogram (EEG) can be used to recognize a person’s intention to control an external device [16]. When people imagine moving their hand or foot, a specific region of their cerebral cortex is activated, resulting in a decrease in amplitude of the EEG rhythm signal within a specific frequency band detected in that region. This is referred to as event-related desynchronization (ERD), while an increase in amplitude of the rhythm signal in other regions is called event-related synchronization (ERS). ERS and ERD are mainly characterized by mu (8–14 Hz) and beta wave (14–30 Hz) spectra, respectively. These imagination-based activities in BCI are referred to as motor-imagery (MI) [17,18,19], and EEG data for MI tasks in a BCI system are collected using electrodes attached to the scalp [17,20].
EEG signals are widely used as a major brain signal in the BCI system due to their non-invasive nature [21]. However, since brain activity can be affected by multiple sources of environmental, physiological, and activity-specific noise [22,23], it is important to consider the following properties of EEG signals. EEG signals are naturally non-stationary. Diverse behavioral and mental states continuously change the statistical properties of brain signals. Thus, it poses a problem that signals other than the information signals we want to obtain are always irregularly present [24]. In addition, EEG signals that are recorded often have a low signal-to-noise ratio (SNR) due to the presence of various types of artifacts, such as electrical power line interference, electromyogram (EMG), and electrooculogram (EOG) interference [25]. To improve the signal-to-noise ratio and eliminate artifacts from the EEG signals, effective preprocessing is necessary before feature extraction [26]. Furthermore, EEG reveals inherent inter-subject variability in brain dynamics, which can be attributed to differences in physiological artifacts among individuals. This phenomenon can significantly impact the performance of learning models [27].
To address these problems, many researchers have implemented various feature extraction techniques for MI classification. The most important thing in the MI-based BCI system is to extract discriminative characteristics of the EEG signals that affect system performance. Common spatial pattern (CSP) is a popular method of extracting different MI features. The CSP spatial filtering method well represents the spatial characteristics of the EEG signal for each motion image. However, the CSP algorithm has limitations in that the frequency band, acquisition time, and the number of source signals must be determined in advance [28,29]. To solve this problem, an FBCSP method [30] that divides the EEG signal into several narrow frequency bands and extracts features by applying different CSP filters to each of the divided signals has been proposed. However, there are limitations in selecting the signal acquisition time or the number of spatial features to be extracted [31].
Recently, many studies have been proposed for automatic feature extraction and classification using deep learning methods such as CNN, LSTM, and restricted Boltzmann machine (RBM). The results of these approaches have shown that it reduces the time-consuming preprocessing and achieves a higher accuracy [32,33]. A RBM with a four-layer neural network was applied to accomplish better performance for motor imagery classification in [32]. Zhang et al. proposed a hybrid deep network model based on CNN and LSTM to extract and learn the spatial and temporal features of the MI task [33]. CNN combined with short-time fourier transformation (STFT) was applied for two-class MI classification in [34]. In another study [35], LSTM using dimension-aggregate approximation (1d-AX) channel weighting technique to extract features from EEG is proposed to enhance classification accuracy. In [36], EEG signals were classified by constructing a convolutional neural network (CNN) using an image-based approach. Meanwhile, some studies [33,37,38,39,40,41] have suggested adding time segments based on FBCSP, but the performance improvement in accuracy was not significant. The authors of [37] showed that multiple time segments by sliding windows from a continuous stream of EEG can extract more discriminable features. In [38], regularized CSP algorithms were proposed to promote the learning of good spatial filters, including extracting features from a fixed time segment of 2s. Moreover, Zhang et al. developed a hybrid deep learning method to extract discriminative features, combining the time domain method and the frequency domain method for a four-class MI task [33]. In [41], to address the issue of nonstationary EEG signals, sliding window-based CSP methods have been proposed to consider session-to-session and trial-to-trial variability. Experimental results showed that the sliding window-based methods outperformed the existing models for both healthy individual and stroke patients. EEG signals are sequential data, and a recurrent neural network (RNN) is one of the architectures to train the sequential processing, demonstrating good performance in time-series signals analysis. The most popular type of RNN is the long short-term memory (LSTM) network [33,42]. Although many EEG classification methods based on neural network have been proposed, there are a few studies that applied LSTM to multi-class MI task.
In this study, a framework is presented to improve the classification accuracy of four-class MI EEG signals using an LSTM-based classification method for extracting temporal features from time-varying EEG signals. We apply an overlapping sliding window approach not only to augment training data sets, but also to acquire time series data of EEG signals. Moreover, considering that the phenomena of ERD and ERS appearing in the sensorimotor cortex during motion imagination occur in different frequency bands for each subject, an overlapping band-based FBCSP is used to extract the subject-specific spatial features. In addition, to explore the effectiveness of channel selection processing, we investigate whether feature extraction from channels filtered by channel correlation affects the classification accuracy of MI task.
The rest of this paper is organized as follows. Section 2 provides a review of related work. Section 3 describes the proposed LSTM-based method with or without channel selection for four-class MI EEG classification. The experimental results and analysis are discussed in Section 4, and Section 5 concludes the paper.
2. Related Work
The extraction of discriminative features from EEG signals is an important factor affecting the performance of BCI systems in classifying MI tasks. Feature extraction is carried out in the spatial, time, and frequency domains [26].
2.1. Feature Extraction and Classification Techniques
CSP is generally used as a spatial domain feature extraction method for MI EEG classification [26]. CSP aims to learn a spatial filter that maximizes the variance of spatially filtered data in one class while minimizing the variance of filtered data in another class [28,43]. This approach has shown a noticeable effect in two-class EEG signals classification. Furthermore, various CSP-based algorithms including FBCSP [29,44,45,46], an improved version of CSP algorithm, have been proposed to extract spatial patterns from EEG signals. In [44], regularization on the CSP filter coefficients was proposed to deal with CSP problems using many electrodes, and this study has shown that the number of electrodes can be reduced with little performance loss. Arvaneh et al. [45] proposed a sparse multi-frequency band CSP (SMFBCSP) algorithm that was optimized using a mutual information-based approach. Their proposed method achieved better performance than other methods based on CSP, sparse CSP, and FBCSP. In a study [46], they suggested a method to select the most discriminative filter banks by using mutual information of features extracted channels. They employed CSP features extracted from multiple overlapping sub-bands, and classification was performed using a support vector machine. Spatial domain approach can be combined with temporal domain approach to enhance the classification performance [27,47]. Ai et al. [43] introduces a new method to combine the features by the CSP and local characteristic-scale decomposition (LCD) algorithms to extract multiscale features of MI EEG signals. To archive high-classification accuracy and low-computational cost, they considered that EEG signals represent brain activity by fusing features extracted from the associated brain regions. Hamedi et al. [48] explored the use of neural network-based algorithms with EEG time-domain features. This work used multilayer perceptron and radial basis function neural networks for feature classification. Lu et al. [32] used the restricted Boltzmann machine (RBM) for EEG classification, where frequency domain representations of EEG signals were pretrained using fast Fourier transform (FFT) and wavelet packet decomposition (WPD) in stacked RBMs. They achieved better performance over other state-of-the-art methods in experimental results. In [49], Park et al. presented a new method to avoid overfitting problems and improve performance of MI BCIs, using wavelet packet decomposition CSP and kernel extreme learning machine. The proposed method outperformed existing methods in terms of classification accuracy. Tabar et al. [50] proposed a deep network, combining CNN and stacked autoencoders (SAE) to classify EEG motor imagery signals. They used the short-time Fourier transform (STFT) to construct 2D images for training their network. The features extracted by the CNN are classified through the deep network SAE. Lee et al. proposed a classification approach utilizing the continuous wavelet transform (CWT) and a CNN [51]. The CWT was utilized to generate an EEG image that incorporates time-frequency and electrode location information, resulting in a highly informative representation.
Recently, many researchers have utilized neural network techniques as an effective architecture for classifying MI tasks. These techniques combine all three phases of extraction, selection, and classification into a single pipeline [27,35]. Several studies have employed deep learning frameworks to classify EEG signals, and these have shown improvements in classification accuracy. Dai et al. used a CNN with hybrid convolution scale and experimented with different kernel sizes to obtain high classification accuracy [29]. They demonstrated that using a single convolution scale limits the classification performance. Sakhavi et al. introduced a temporal representation of the EEG to preserve information about the signal’s dynamics and used a CNN for classification [52]. Moreover, a hybrid deep learning scheme that combines CNN and LSTM has been proposed, where CNN extracts spatial information and LSTM processes temporal information. Zhang et al. developed a deep learning network based on CNN-LSTM for four-class MI, which was trained using all subjects’ training data as a single model [33]. This study showed a better result than an SVM classifier. They also proposed a hybrid deep neural network with transfer learning (HDNN-TL) in [53], which aimed to improve classification accuracy when dealing with the individual differences problem and limited training samples. RNN (recurrent neural network) is a type of ANN whose computing units are connected in a directed graph along a sequence, making it a popular choice for analyzing time-series data in various applications, including speech recognition, natural language processing, and more [35,42,47]. The most popular type of RNN is the LSTM network, which is an excellent way to expose the internal temporal correlation of time series signals [27,53]. Zhou et al. applied wavelet envelope analysis and LSTM to consider the amplitude modulation characteristics and time-series information of MI-EEG [54]. In [55], a RNN-based parallel method was applied to encode spatial and temporal sequential raw data with bidirectional LSTM (bi-LSTM), and its results showed superior performance compared to other methods.
2.2. Channel Selection Approach
EEG signal processing, scalp regions where the signal recordings are collected, are called channels or electrodes [56]. High-density EEG electrodes reveal more information about the underlying neuronal activity, but increase redundancy due to noise, and generate high-dimensional data. Therefore, it is crucial to have efficient channel selection methods that can identify optimal channels and reduce system complexity [56,57,58].
Several studies have used channel selection algorithms to enhance system performance, in which some channels are generally selected, considering channel location, dependency, and redundancy [56,59]. An improved binary gravitation search algorithm (IBGSA) is used for detecting effective channels for MI classification [57]. In this study, the results showed that detecting effective channels can obtain a better performance. In [56], an optimization-based channel selection method was proposed for MI tasks to reduce the computational complexity associated with the large number of channels. The proposed method initializes a reference candidate solution and then iteratively identifies the most relevant EEG channels. Yang et al. utilized a filtering technique in channel selection, where the most correlated channels are selected based on the consideration of mutual information and redundancy between channels [59]. In [60], to obtain high classification accuracy, a filtering method has been proposed to reduce the number of channels by iteratively optimizing the number of relevant channels. In another study [61], an optimization method using channel contribution score was used for channel selection, resulting in an average accuracy of 90% with only seven channels. To represent the brain functional relationships for MI tasks, Ma et al. [62] used the correlation matrix that expresses the functional relevance between channels. The proposed method showed MI decoding performance of above 87.03%. Li et el. [63] proposed an EEG decoding framework to consider spatial dependency and temporal scale information for MI classification. In this study, they extracted both spatial features by channel projection and temporal features, and then applied CNN to classify EEG tasks.
3. Improving Multi-Class MI Classification
The proposed method performs feature extraction based on overlapping band-based FBCSP (Filter Bank Common Spatial Pattern) and performs classification based on LSTM. This section describes the preprocessing for feature extraction and then explain classification using overlapping band-based FBCSP and LSTM.
3.1. Prepocessing
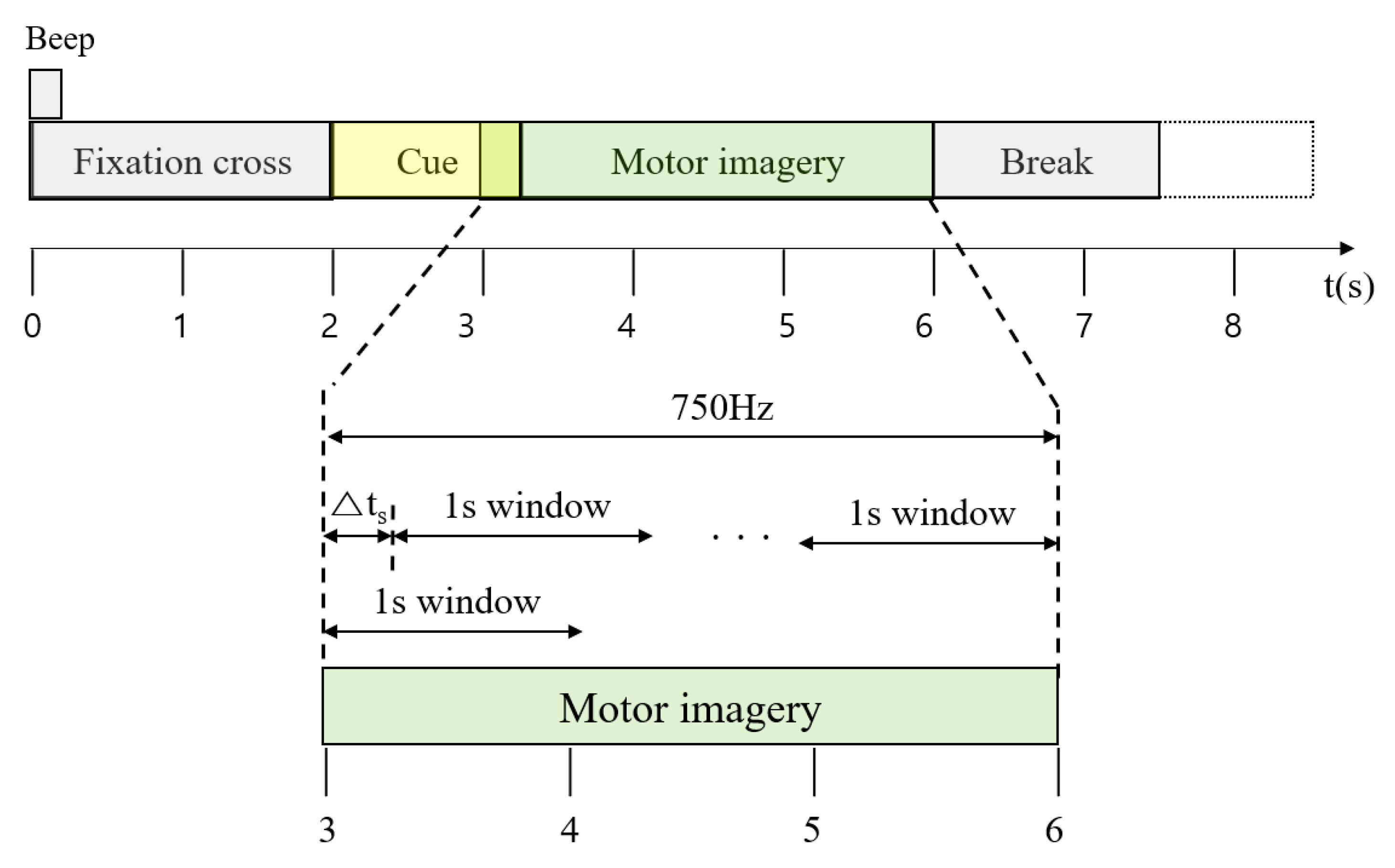
The proposed method utilized the publicly available BCI competition IV dataset 2a [64], which was recorded using twenty-two EEG channels (C = 22) and three EOG channels at a sampling rate of 250 Hz (R = 250). The EEG channels represent brain waves, and the EOG channels represent eye blink signals. Figure 1 shows the window determination process for feature extraction from a single-trial EEG. We used data collected from twenty-two EEG channels for 3 seconds (3s), starting 1 s after the cue sign, after removing three EOG channels from the BCI dataset. That is, the number of samples, , acquired in a single trial of the ith subject is as follows.
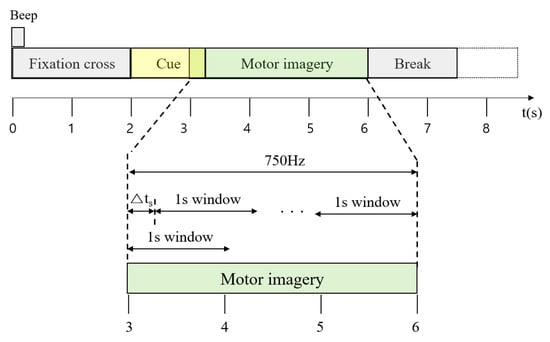
Figure 1.
Feature extraction from a single-trial EEG.
If the number of valid trials after removing rejected trials generated during EEG data measurement is V, the total number of data Ni acquired from the ith subject is as follows.
EEG signals require extraction of many features in a single session. The number of features extracted from overlapping windows is much greater than the number of features extracted from non-overlapping windows, and the shorter the length of the sliding window, the more features that can be extracted. Therefore, in this study, an overlapping window of 1 s from 1 s after the cue sign was applied and an interval of 0.1 s was placed between consecutive sliding windows to extract more distinguishable features from EEG signals and improve classification accuracy. The number of samples included in the 1 s window is R∗C. Furthermore, it is essential to extract more features within a session rather than extract features from three 1 s windows due to the inherent non-stationarity in the EEG data. Therefore, we performed feature extraction while moving the 1 s window by Δts. As a result, the number of samples, , extracted from a single trial from the ith subject is shown in Equation (3).
Therefore, the total samples, Ni, that can be obtained from the ith subject is shown in Equation (4).
3.2. LSTM-Based FBCSP with Overlapped Band
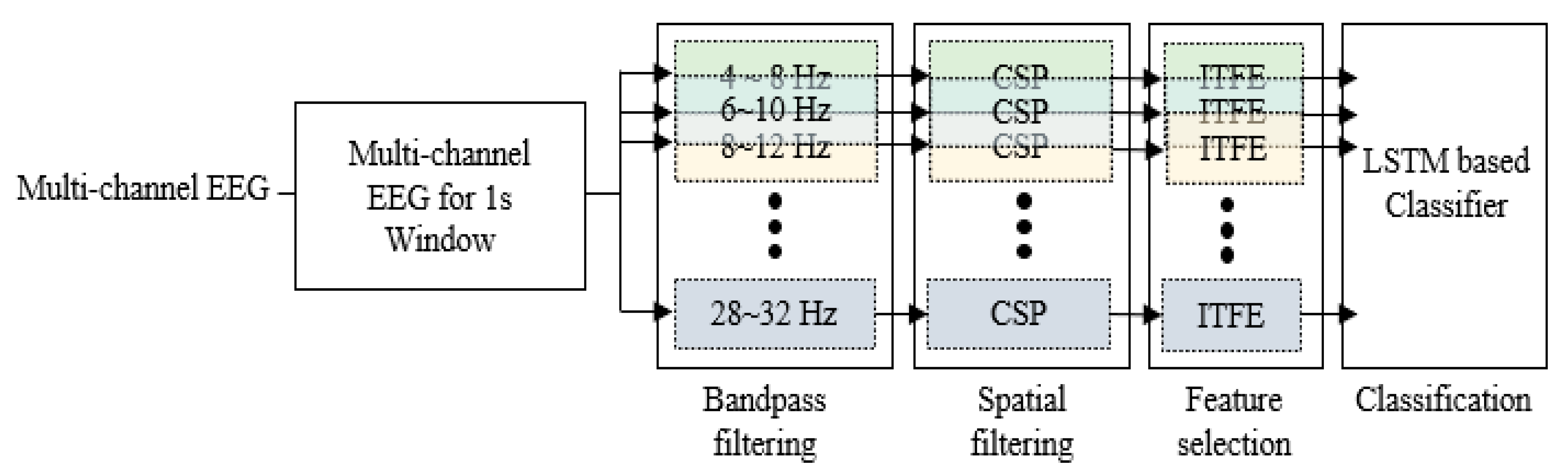
After determining the window for feature extraction, feature extraction was performed. We used the overlapping band-based FBCSP algorithm in this study. This algorithm, like the conventional FBCSP, consisted of four steps: bandpass filtering, spatial filtering using CSP, feature selection, classification. Figure 2 shows the general framework for the proposed approach.
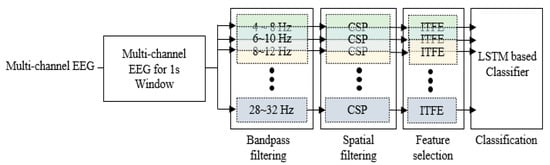
Figure 2.
Processing steps of the filter bank common spatial pattern.
A filter bank that decomposes the EEG into multiple frequency passbands was employed in the first step, starting from 4 to 32 Hz with the bandwidth of 4 Hz and overlap of 2 Hz. A total of 13 bandpass filters were used, namely, 4–8, 6–10, 8–12, 10–14, …, 28–32 Hz due to the overlapping between two frequency bands. The signals were bandpass filtered by Chebyshev type II filter. As suggested by many studies [33,52,53], CSP features extracted from overlapping sub-bands led to an improved performance of motor imagery EEG-based BCI systems. Inspired by these research results, we used multiple overlapping filter bands to achieve higher classification accuracy.
In the second step, filtered signals were transformed to spatial subspace using CSP algorithm for feature extraction, and CSP features in each frequency band were extracted. In the third step, the discriminative features were selected from the filter bank which consisted of overlapping frequency bands, using the ITFE algorithm [65] which optimized the approximation of mutual information between class labels and extracted EEG/MEG components for multiclass CSP. The fourth step employed two-stacked LSTM layers to classify the selected CSP features. Thus, the selected features were then fed into LSTM networks.
LSTM network is an advanced RNN that allows information to persist. It can handle the vanishing gradient problem of RNN [33,42]. The key to LSTM is cell state, which consists of three gates. The forget gate decides to remember or forget the previous time step’s information. The input gate attempts to learn new information, while the output gate transmits the updated information from the current time step to the next. At last, in the output gate, the cell passes the updated information from the current time step to the next time step. In other words, LSTM can control important information to be retained and unrelated information to be released by using three gates. Therefore, LSTM is an excellent way to reveal the internal temporal correlation of time series signals and can learn one time step at a time from EEG channels, so we adopt LSTM to extract discriminative features of time-varying EEG signals.
As mentioned above, we employ an overlapping bandpass filter as well as overlapping window-based feature extraction method to further improve classification accuracy of four-class MI EEG signals. Moreover, LSTM is used for classification that enables better quality learning by storing the correlation information from EEG signals through time. In this scenario, we anticipate that our approach will provide us more discriminative information for feature extraction from EEG signals.
3.3. LSTM Based FBCSP with Overlapped Band Applying Channel Selection
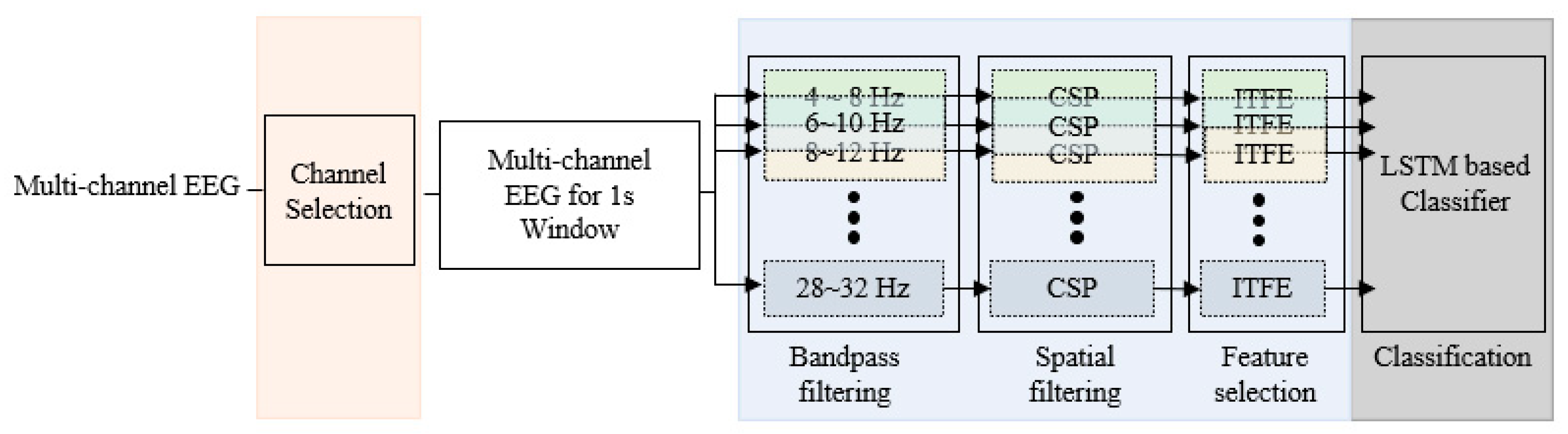
EEG is measured by a BCI device with many channels. To explore the effectiveness of channel selection, we first carried out the channel selection task by correlation between channels and then performed feature extraction and classification with only selected channels among multiple channels. Figure 3 shows the EEG classification processing step including the channel selection step.
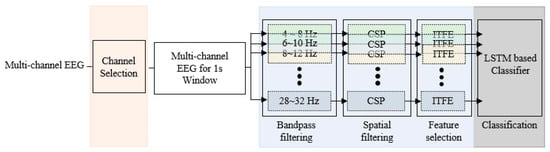
Figure 3.
Processing steps of the FBCSP with channel selection.
Pearson’s correlation coefficient is used to find channel correlation for subject’s MI in channel selection task. We calculated the correlation coefficient between channels for each MI and determined that the correlation between the two channels was high when the absolute value of the correlation coefficient is greater than 0.8. MICoeffj,k,l, which stores high correlation information between channels for each MI, is calculated by Equation (5) and stores 1 if the correlation between channel j and channel k in the lth motion is high or 0 otherwise, where l is the lth MI for each subject and j and k mean the jth and kth channels.
where j and k = 0, …, 21, and l = 1, …, 4.
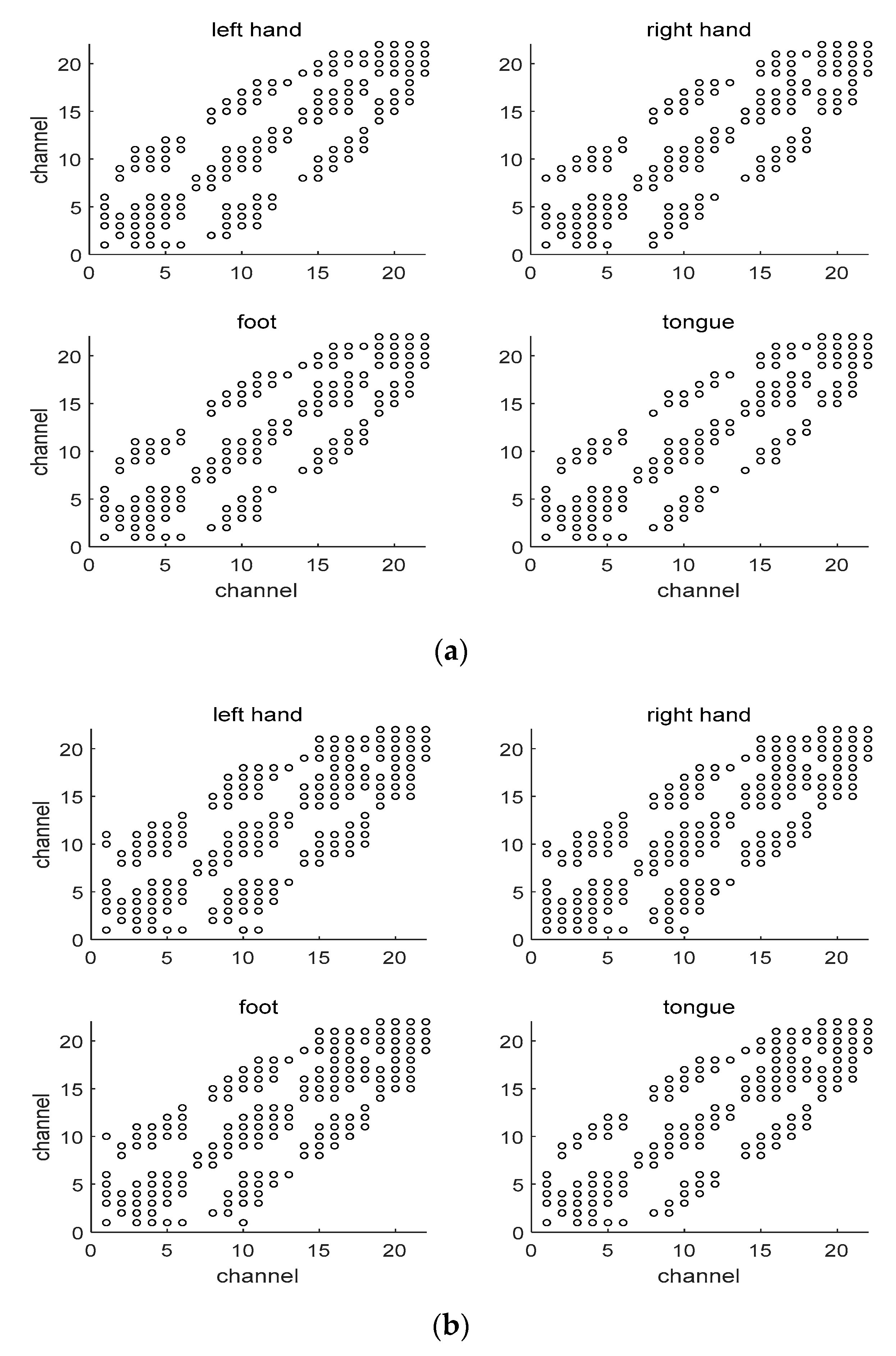
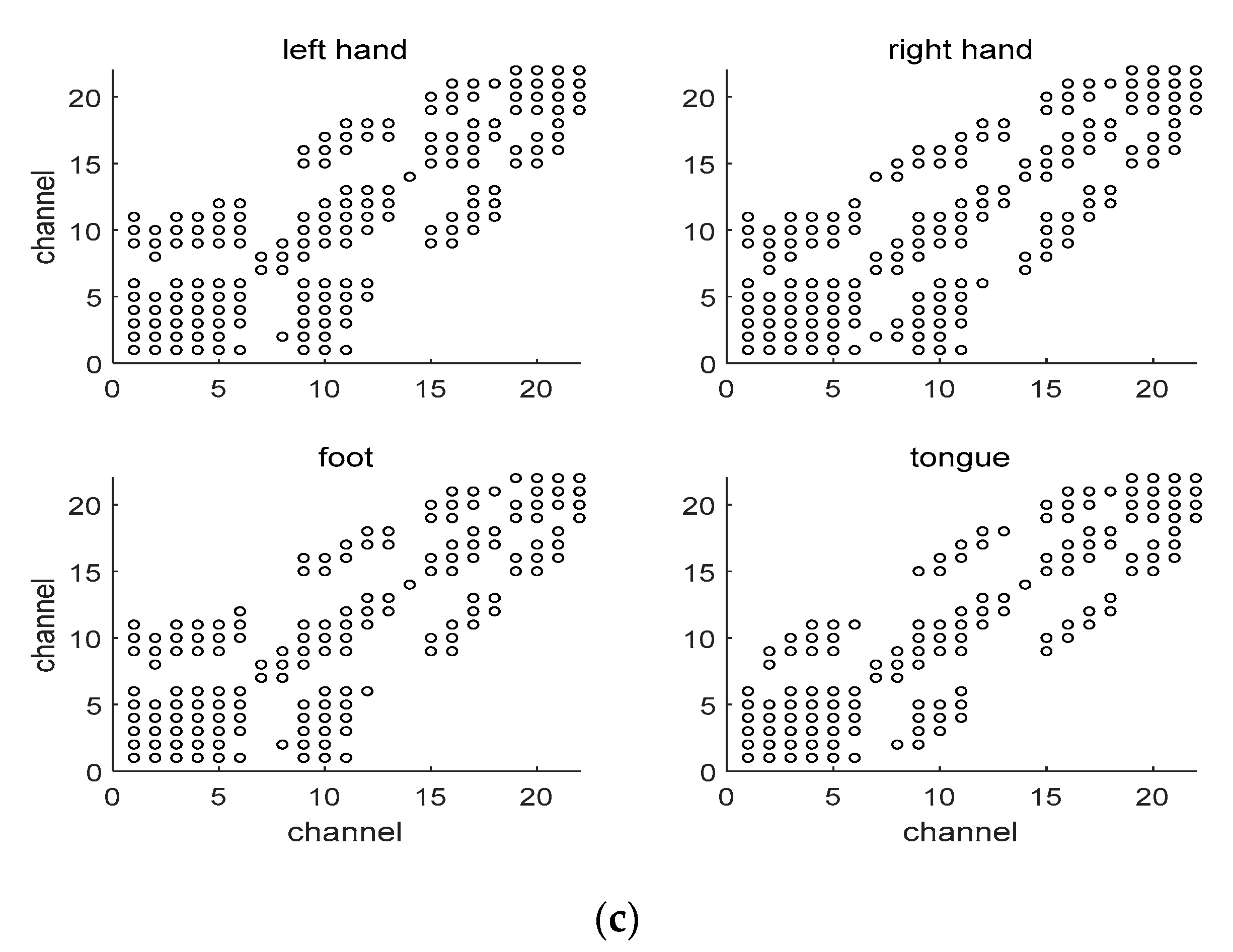
Figure 4 shows an example of MICoeff showing high correlation by channel during one trial for several subjects. That is, channels having a high inter-channel correlation for each MI are shown. For example, for subject1, channel 0 showed high correlation with channels 2, 3, and 4 in all motions but high correlation with channel 7 only in right motions. Channels with high correlation for all MIs can interfere with unambiguously determining the class in MI classification, thus those channels were removed. That is, channels with high correlation between channels for each MI of all subjects are checked, and the high correlation between all channels is ranked, eliminating the channels in order of maximum correlation. Thus, only channels that allow the subject MI to be discriminated are selected.
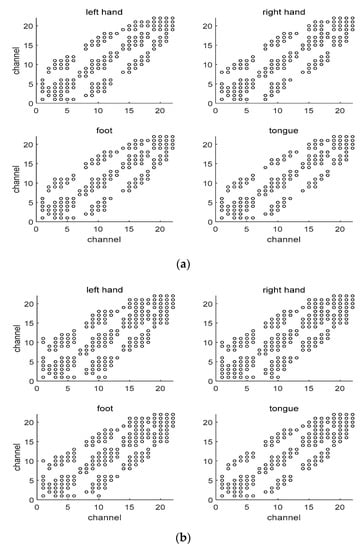
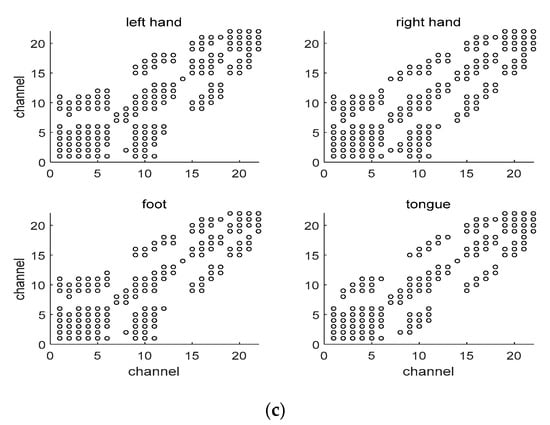
Figure 4.
Correlation between channels for each MI. The circle (o) represents a high correlation between two channels. (a) Subject 1; (b) Subject 3; (c) Subject 8.
4. Experimental Results
4.1. Dataset and Experimental Environment
In this study, we used the BCI competition IV-2a dataset [64]. This dataset was collected while imagining movements of the left hand, right hand, feet, and tongue from twenty-two EEG electrodes and three EOG channels with a sampling frequency of 250 Hz and a bandpass filtered between 0.5 Hz and 100 Hz from nine subjects. All experiments were carried out using Python in an Intel i9-7920X CPU and an Nvidia GTX 1080 Ti GPU environment. The window size for feature extraction was set to 750 (750win) and 250 (250win); 750win is a window without applying window sliding, and the window movement time Δts of 250win with window sliding was set to 0.1 s. Subject-specific features were extracted using FBCSP in each channel except for the EOG channel. 250win-OB is a technique that extracts features by applying an overlapped band in FBCSP to 250win. The overlap size applied to the bandpass filter was set to two. In FBCSP, the classifier used two-layer-stacked LSTM. Of the total trials for each user, 80% was used as a training dataset and 20% as a testing dataset, and the epoch was set to 400. We evaluated the proposed method based on various evaluation metrics such as accuracy, kappa coefficient, precision, recall, and the results of all the evaluation metrics were represented as the average value of 10 repetitions. The kappa value was mainly used as the evaluation metric for comparison evaluation with previously proposed algorithms. The kappa value is a scale that reflects the classification accuracy by correcting the classification results caused by chance, and the BCI competition committee that provides the data used in this experiment also recommends this scale [64,66].
4.2. Experimental Evaluation
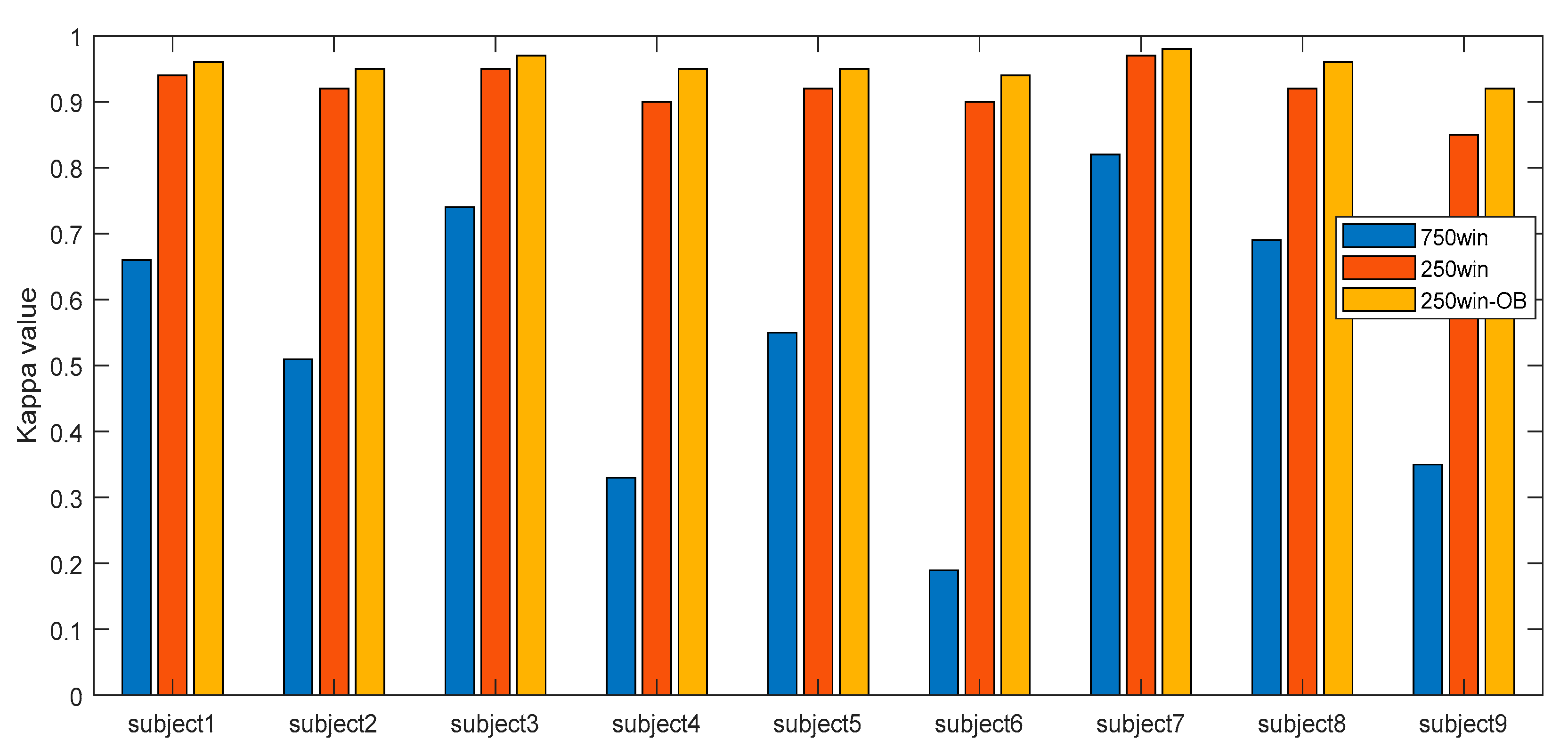
We first compared the kappa values of 750win, 250win, and 250win-OB. As shown in Figure 5, in subject7 with the highest kappa value, 750win was 0.82, whereas 250win was 0.97 and 250win-OB was 0.98. In subject6 with the lowest kappa value, the kappa value was 0.19 for 750win, while it was 0.90 for 250win and 0.94 for 250win-OB. The average kappa value of all subjects in 750win was 0.54, whereas it was 0.92 in 250win and 0.95 in 250win-OB. These results show that the window size, application of a sliding window, and overlap of the bandpass filter greatly affect MI EEG classification results.
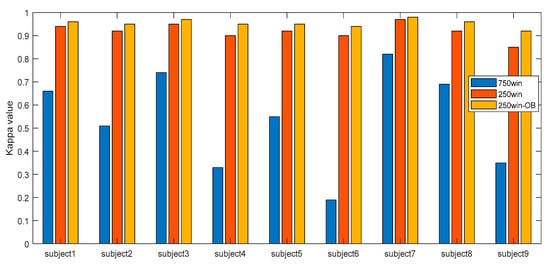
Figure 5.
Kappa value according to window size.
Figure 6 shows the results of an MI EEG classification of 250win-OB. All indicators for subject3 and subject7 appeared higher than other subjects, and subject9 showed lower indicators than other subjects. The average index of all subjects showed 0.97 in accuracy, precision, and recall, and a slightly lower kappa value of 0.95. These results have shown that the algorithm proposed in this study classifies the MI EEG of various subjects quite well.
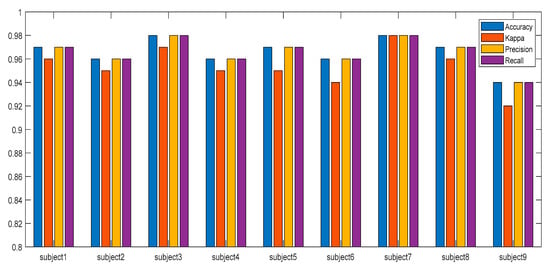
Figure 6.
Index of classification result of 250win-OB.
We compared the performance of the existing methods and the 250win-OB method proposed in this study. Figure 7 shows the results of the comparison by kappa value. Through this result, the 250win-OB method shows better performance than other previously proposed methods. Existing techniques showed a large difference in the kappa value according to the subject, whereas the 250win-OB maintained a significantly high value for all subjects. In more detail, FBCSP [30] had an average kappa value of 0.57 and a standard deviation of 0.18 for each subject, SRLDA [67] showed 0.74 and 0.17, shared network [33] showed 0.81 and 0.12, and HDNN-TL [53] showed 0.81 and 0.10. On the other hand, the method proposed in this work showed an average of 0.95 and a standard deviation of 0.02. Therefore, through this comparison, it was shown that the proposed method is more suitable for the MI EEG classification of various subjects than existing algorithms.
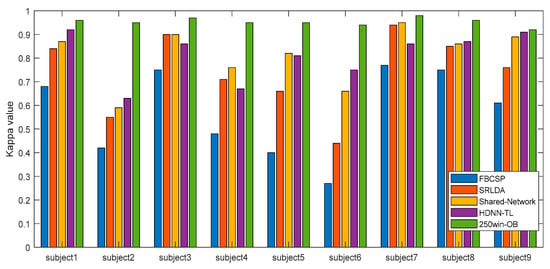
Figure 7.
Performance comparison between existing methods and the proposed method.
In addition, the experimental results showed differences in classification results for each algorithm. In FBCSP, SRLDA, and 250win-OB, subject7 had the highest kappa value, while subject1 had the highest in HDNN-TL. The subject with the lowest kappa value was subject6 in FBCSP and SRLDA, whereas subject2 had the lowest in shared network and HDNN-TL, and the 250win-OB showed the lowest result in subject9. The lowest kappa value of 250win-OB also improved by about 340.7% from 0.27 to 0.92 compared to FBCSP, and by about 68.5% from 0.63 to 0.92 compared to HDNN-TL, which showed the best performance among existing techniques.
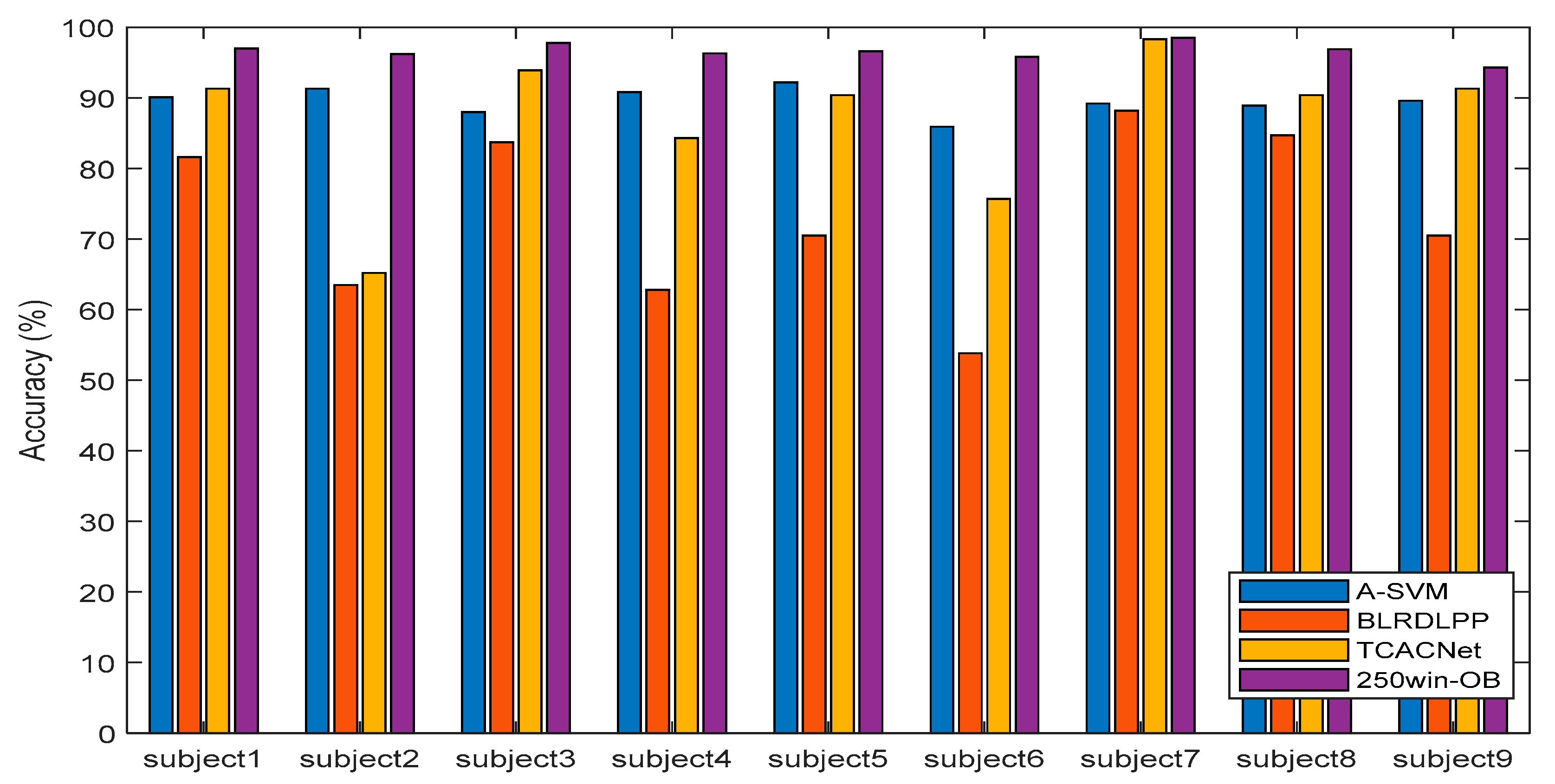
Figure 8 shows the comparison of classification accuracy with existing techniques. A-SVM [68] and BLRDLPP [69] are techniques that extract features and use the machine learning algorithm SVM for classification, while TCANET [70] is a new CNN-based classification technique. The experimental results show that the proposed method in this paper, 250win-OB, which extracts detailed features and learns through deep learning classification, outperforms A-SVM or BLRDLPP techniques that classify with machine learning algorithms after feature extraction, as well as TCANET, which learns with overall deep learning. Through such experiments, our findings showed that the suggested algorithm outperforms other existing algorithms in classifying the four-class MI EEG.
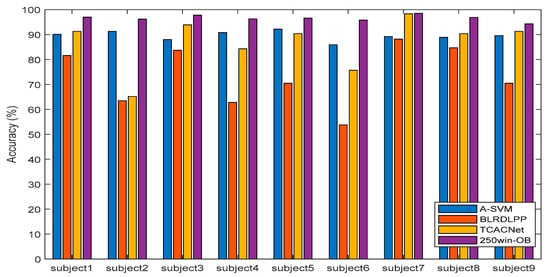
Figure 8.
Comparison of accuracy with existing methods and the proposed method.
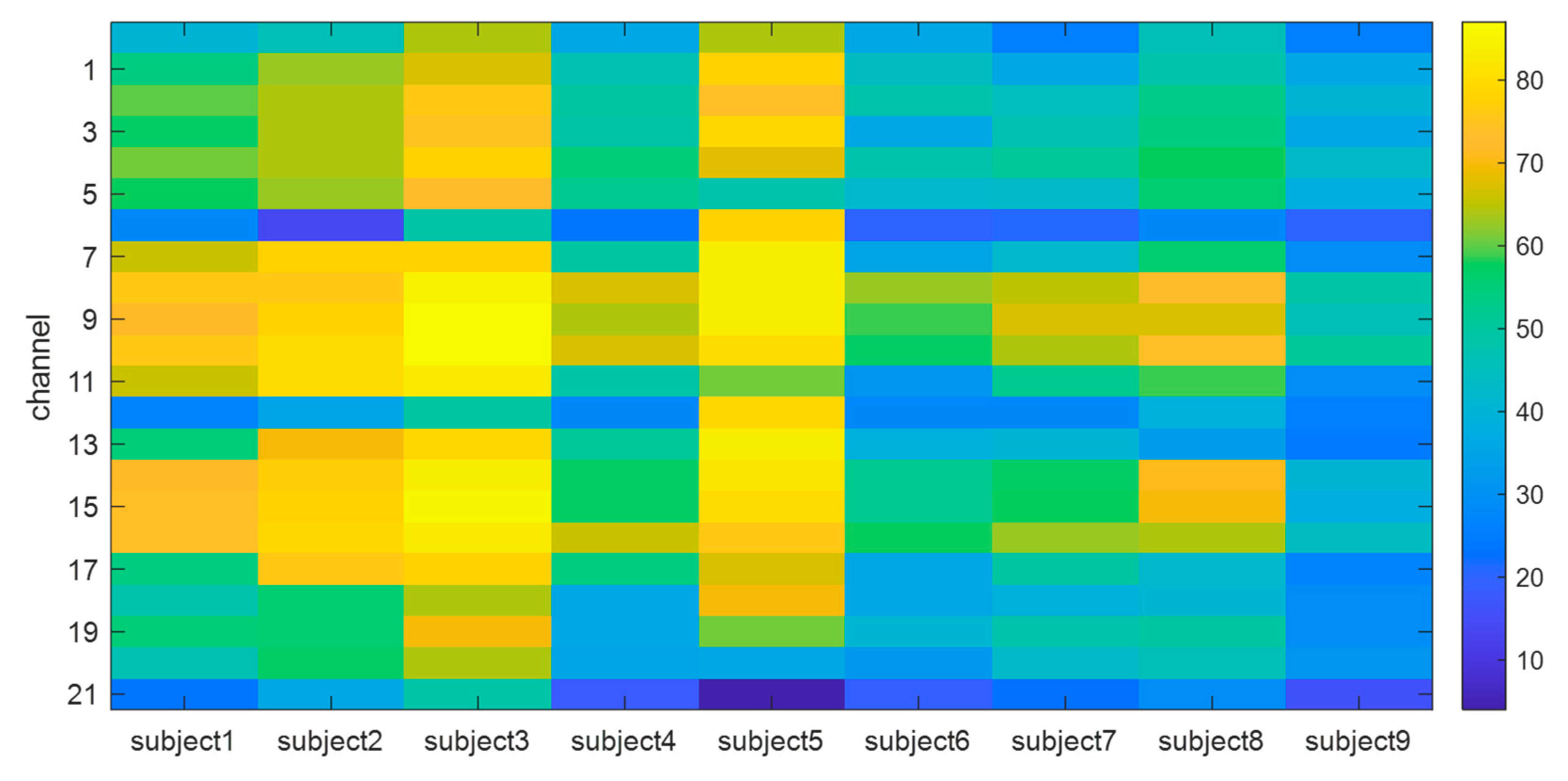
The correlation coefficients between channels are calculated to conduct channel selection for classifying EEG. Figure 9 shows a heat map of the correlation between channels for each user. As shown in the experimental results, the channel correlation coefficient values for each user showed a lot of variation. Subject3 and subject5 show a much higher correlation between channels than other subjects, whereas subject6 and subject9 show a relatively low correlation compared to other subjects. Overall, there are differences in the value of cumulative correlation, but channels with high inter-channel correlation showed high correlation in most subjects.
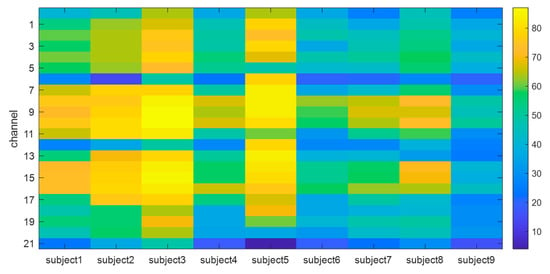
Figure 9.
Cumulative channel correlation heatmap by subject. The heatmap is based on the cumulative value of the number of times the correlation between channels is greater than 0.8.
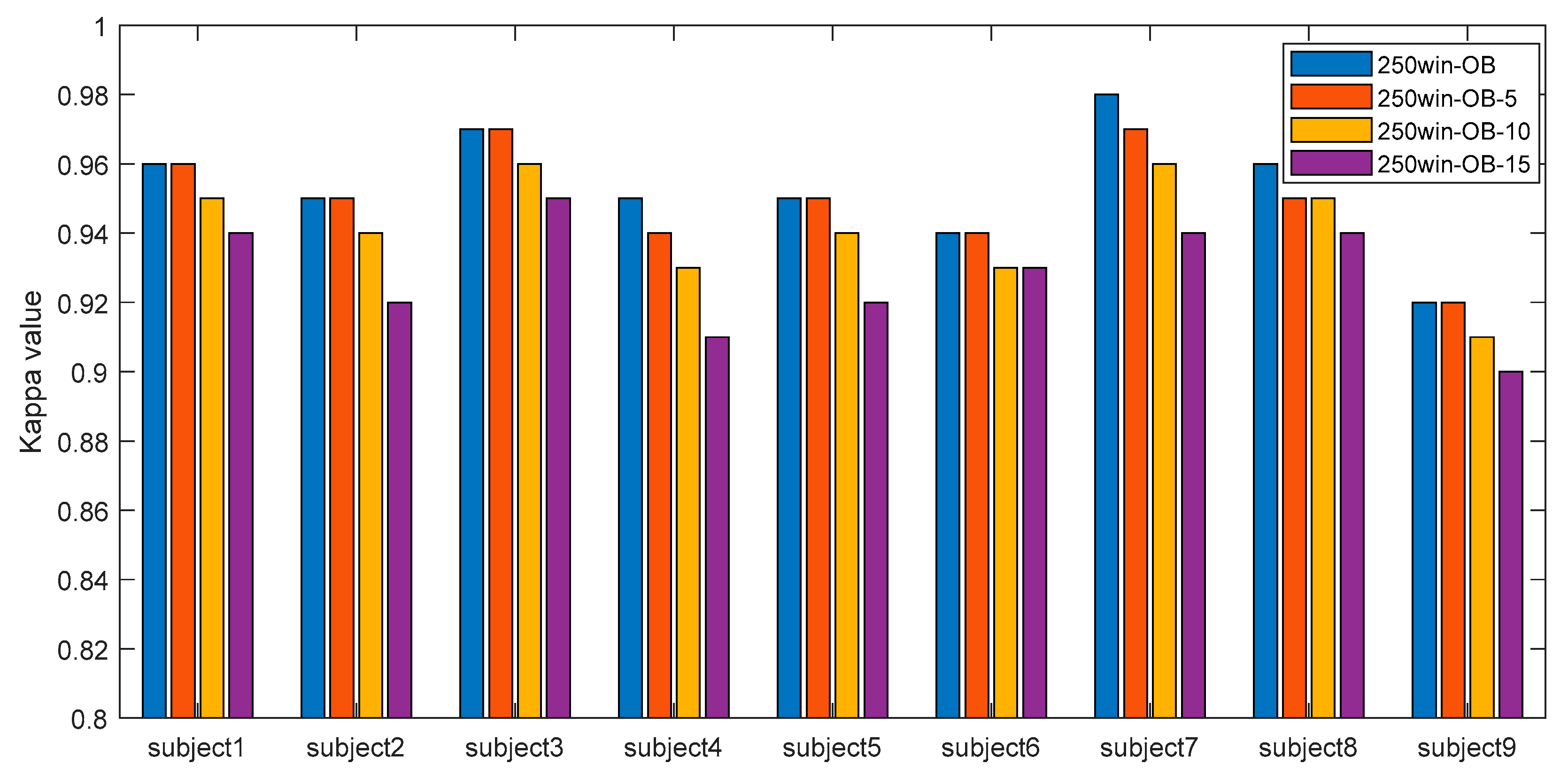
To analyze the effect of the number of channels on the classification accuracy, the results using all 22 channels and the results after removing channels with high correlations were compared. The number of channels to be removed can be specified, and in this experiment, the results after removing 5, 10, and 15 channels were compared with the results using all channels, and the results are shown in Figure 10 with the comparison of kappa values. The proposed 250win-OB method was used in the experiments.
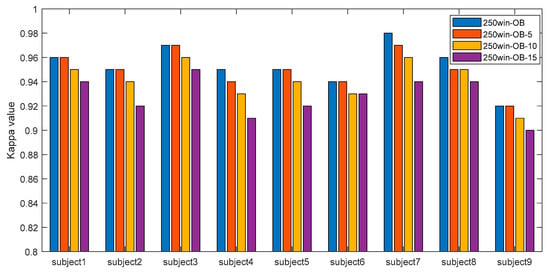
Figure 10.
Change of kappa value according to channel removal.
When five channels with high correlation were removed, subject4, subject7, and subject8 showed slightly lower results than 250win-OB with all channels, but with these exceptions, most subjects showed the same performance as 250win-OB. In the case of 250win-OB-10 with 10 channels deleted, the average performance was lowered by 1.35% compared to 250win-OB. In the case of 250win-OB-15, using only seven channels after deleting fifteen channels, it showed 2.87% lower performance than 250win-OB. Experimental results showed that classification was best performed when all twenty-two channels were used, but an average kappa value of 0.93 was maintained even when only seven channels were used.
5. Conclusions
The EEG used in the BCI system has a problem in that end-to-end learning is difficult because it is greatly affected by noise and has a great effect on performance depending on the frequency range used. To classify the four-class MI EEG for each subject, we proposed an overlapped band-based FBCSP with an LSTM classifier. The proposed algorithm applied a sliding window for each channel, tried to overcome the dependence on frequency band by extracting features for each window using FBCSP-based on overlapped band, and tried to classify features over time using LSTM. Through experiments, we showed that the algorithm proposed in this study can classify the four-class MI EEG of all subjects better than other existing algorithms. In future work, we plan to conduct a study on selecting the minimum required number of channels based on the set accuracy and finding the channel selection threshold for choosing the number of channels. Based on the findings of this paper, we believe that our research can be extended to EEG-based emotion recognition, preference recognition in neuromarketing and game control, and so on.
Author Contributions
Conceptualization, J.H. and J.C.; methodology, J.C.; software, S.P. and J.C.; validation, J.H. and J.C.; formal analysis, J.H. and J.C.; investigation, J.H.; writing—original draft preparation, J.H. and J.C.; writing—review and editing, J.H., S.P. and J.C.; supervision, J.C. All authors have read and agreed to the published version of the manuscript.
Funding
Funding for this paper was provided by Namseoul University.
Data Availability Statement
https://www.bbci.de/competition/iv/ (accessed on 18 February 2023).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Katona, J. A Review of Human–Computer Interaction and Virtual Reality Research Fields in Cognitive InfoCommunications. Appl. Sci. 2021, 11, 2646. [Google Scholar] [CrossRef]
- McFarland, D.J.; Wolpaw, J.R. Brain-computer interfaces for communication and control. Commun. ACM 2011, 54, 60–66. [Google Scholar] [CrossRef] [PubMed]
- Izso, L. The significance of cognitive infocommunications in developing assistive technologies for people with non-standard cognitive characteristics: CogInfoCom for people with non-standard cognitive characteristics. In Proceedings of the 2015 6th IEEE International Conference on Cognitive Infocommunications (CogInfoCom), Gyor, Hungary, 19–21 October 2015; pp. 77–82. [Google Scholar]
- Eisapour, M.; Cao, S.; Domenicucci, L.; Boger, J. Virtual Reality Exergames for People Living with Dementia Based on Exercise Therapy Best Practices. Proc. Hum. Factors Ergon. Soc. Annu. Meet. 2018, 62, 528–532. [Google Scholar] [CrossRef]
- Amprimo, G.; Rechichi, I.; Ferraris, C.; Olmo, G. Measuring Brain Activation Patterns from Raw Single-Channel EEG during Exergaming: A Pilot Study. Electronics 2023, 12, 623. [Google Scholar] [CrossRef]
- Katona, J.; Ujbanyi, T.; Sziladi, G.; Kovari, A. Speed control of Festo Robotino mobile robot using NeuroSky MindWave EEG headset based brain-computer interface. In Proceedings of the 2016 7th IEEE International Conference on Cognitive Infocommunications (CogInfoCom), Wroclaw, Poland, 16–18 October 2016; pp. 000251–000256. [Google Scholar] [CrossRef]
- Stephygraph, L.R.; Arunkumar, N. Brain-Actuated Wireless Mobile Robot Control through an Adaptive Human–Machine Interface. In Proceedings of the International Conference on Soft Computing Systems: ICSCS 2015; Advances in Intelligent Systems and Computing. Springer: New Delhi, India, 2015; Volume 1, pp. 537–549. [Google Scholar] [CrossRef]
- Markopoulos, E.; Lauronen, J.; Luimula, M.; Lehto, P.; Laukkanen, S. Maritime safety education with VR technology (MarSEVR). In Proceedings of the 2019 10th IEEE International Conference on Cognitive Infocommunications (CogInfoCom), Naples, Italy, 23–25 October 2019; pp. 283–288. [Google Scholar]
- Spaak, E.; Fonken, Y.; Jensen, O.; de Lange, F.P. The Neural Mechanisms of Prediction in Visual Search. Cereb. Cortex 2015, 26, 4327–4336. [Google Scholar] [CrossRef]
- de Vries, I.E.; van Driel, J.; Olivers, C.N. Posterior α EEG dynamics dissociate current from future goals in working memory-guided visual search. J. Neurosci. 2017, 37, 1591–1603. [Google Scholar] [CrossRef]
- Qian, L.; Ge, X.; Feng, Z.; Wang, S.; Yuan, J.; Pan, Y.; Shi, H.; Xu, J.; Sun, Y. Brain Network Reorganization During Visual Search Task Revealed by a Network Analysis of Fixation-Related Potential. IEEE Trans. Neural Syst. Rehabil. Eng. 2023, 31, 1219–1229. [Google Scholar] [CrossRef]
- Liu, Y.; Yu, Y.; Ye, Z.; Li, M.; Zhang, Y.; Zhou, Z.; Hu, D.; Zeng, L.-L. Fusion of Spatial, Temporal, and Spectral EEG Signatures Improves Multilevel Cognitive Load Prediction. IEEE Trans. Human-Mach. Syst. 2023, 1–10. [Google Scholar] [CrossRef]
- Yusoff, M.Z.; Kamel, N.; Malik, A.; Meselhy, M. Mental task motor imagery classifications for noninvasive brain computer interface. In Proceedings of the 2014 5th International Conference on Intelligent and Advanced Systems (ICIAS), Kuala Lumpur, Malaysia, 3–5 June 2014; pp. 1–5. [Google Scholar]
- Djemal, R.; Bazyed, A.G.; Belwafi, K.; Gannouni, S.; Kaaniche, W. Three-Class EEG-Based Motor Imagery Classification Using Phase-Space Reconstruction Technique. Brain Sci. 2016, 6, 36. [Google Scholar] [CrossRef]
- Wolpaw, J.; Birbaumer, N.; Heetderks, W.; McFarland, D.; Peckham, P.; Schalk, G.; Donchin, E.; Quatrano, L.; Robinson, C.; Vaughan, T. Brain-computer interface technology: A review of the first international meeting. IEEE Trans. Rehabil. Eng. 2000, 8, 164–173. [Google Scholar] [CrossRef]
- Kaiser, V.; Bauernfeind, G.; Kreilinger, A.; Kaufmann, T.; Kübler, A.; Neuper, C.; Müller-Putz, G.R. Cortical effects of user training in a motor imagery based brain–computer interface measured by fNIRS and EEG. Neuroimage 2014, 85, 432–444. [Google Scholar] [CrossRef]
- Pfurtscheller, G.; Neuper, C. Motor imagery activates primary sensorimotor area in humans. Neurosci. Lett. 1997, 239, 65–68. [Google Scholar] [CrossRef] [PubMed]
- Pfurtscheller, G.; Neuper, C. Motor imagery and direct brain-computer communication. Proc. IEEE 2001, 89, 1123–1134. [Google Scholar] [CrossRef]
- Siuly, S.; Li, Y.; Wen, P. Modified CC-LR algorithm with three diverse feature sets for motor imagery tasks classification in EEG based brain–computer interface. Comput. Methods Programs Biomed. 2014, 113, 767–780. [Google Scholar] [CrossRef]
- Pfurtscheller, G.; Neuper, C.; Flotzinger, D.; Pregenzer, M. EEG-based discrimination between imagination of right and left hand movement. Electroencephalogr. Clin. Neurophysiol. 1997, 103, 642–651. [Google Scholar] [CrossRef]
- He, B.; Baxter, B.; Edelman, B.J.; Cline, C.C.; Ye, W.W. Noninvasive Brain-Computer Interfaces Based on Sensorimotor Rhythms. Proc. IEEE 2015, 103, 907–925. [Google Scholar] [CrossRef] [PubMed]
- Barbati, G.; Porcaro, C.; Zappasodi, F.; Rossini, P.M.; Tecchio, F. Optimization of an independent component analysis approach for artifact identification and removal in magnetoencephalographic signals. Clin. Neurophysiol. 2004, 115, 1220–1232. [Google Scholar] [CrossRef]
- Ferracuti, F.; Casadei, V.; Marcantoni, I.; Iarlori, S.; Burattini, L.; Monteriù, A.; Porcaro, C. A functional source separation algorithm to enhance error-related potentials monitoring in noninvasive brain-computer interface. Comput. Methods Programs Biomed. 2020, 191, 105419. [Google Scholar] [CrossRef]
- Shenoy, P.; Krauledat, M.; Blankertz, B.; Rao, R.P.N.; Müller, K.-R. Towards adaptive classification for BCI. J. Neural Eng. 2006, 3, R13–R23. [Google Scholar] [CrossRef]
- Nicolas-Alonso, L.F.; Gomez-Gil, J. Brain computer interfaces, a review. Sensors 2012, 12, 1211–1279. [Google Scholar] [CrossRef]
- Dai, G.; Zhou, J.; Huang, J.; Wang, N. HS-CNN: A CNN with hybrid convolution scale for EEG motor imagery classification. J. Neural Eng. 2019, 17, 016025. [Google Scholar] [CrossRef]
- Alzahab, N.A.; Apollonio, L.; Di Iorio, A.; Alshalak, M.; Iarlori, S.; Ferracuti, F.; Porcaro, C. Hybrid deep learning (hDL)-based brain-computer interface (BCI) systems: A systematic review. Brain Sci. 2021, 11, 75. [Google Scholar] [CrossRef] [PubMed]
- Müller-Gerking, J.; Pfurtscheller, G.; Flyvbjerg, H. Designing optimal spatial filters for single-trial EEG classification in a movement task. Clin. Neurophysiol. 1999, 110, 787–798. [Google Scholar] [CrossRef]
- Wang, Y.; Gao, S.; Gao, X. Common spatial pattern method for channel selection in motor imagery based brain-computer interface. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology—Proceedings, Shanghai, China, 31 August–3 September 2005; Volume 7, pp. 5392–5395. [Google Scholar] [CrossRef]
- Ang, K.K.; Chin, Z.Y.; Zhang, H.; Guan, C. Filter bank common spatial pattern (FBCSP) in brain-computer interface. In Proceedings of the 2008 IEEE International Joint Conference on Neural Networks (IEEE World Congress on Computational Intelligence), Hong Kong, China, 1–8 June 2008; pp. 2390–2397. [Google Scholar]
- Ma, Y.; Ding, X.; She, Q.; Luo, Z.; Potter, T.; Zhang, Y. Classification of Motor Imagery EEG Signals with Support Vector Machines and Particle Swarm Optimization. Comput. Math. Methods Med. 2016, 2016, 4941235. [Google Scholar] [CrossRef]
- Lu, N.; Li, T.; Ren, X.; Miao, H. A Deep Learning Scheme for Motor Imagery Classification based on Restricted Boltzmann Machines. IEEE Trans. Neural Syst. Rehabil. Eng. 2016, 25, 566–576. [Google Scholar] [CrossRef] [PubMed]
- Zhang, R.; Zong, Q.; Dou, L.; Zhao, X. A novel hybrid deep learning scheme for four-class motor imagery classification. J. Neural Eng. 2019, 16, 066004. [Google Scholar] [CrossRef]
- Shovon, T.H.; Al Nazi, Z.; Dash, S.; Hossain, M.F. Classification of motor imagery EEG signals with multi-input convolutional neural network by augmenting STFT. In Proceedings of the 2019 5th International Conference on Advances in Electrical Engineering (ICAEE), Dhaka, Bangladesh, 26–28 September 2019; pp. 398–403. [Google Scholar] [CrossRef]
- Wang, P.; Jiang, A.; Liu, X.; Shang, J.; Zhang, L. LSTM-based EEG classification in motor imagery tasks. IEEE Trans. Neural Syst. Rehabil. Eng. 2018, 26, 2086–2095. [Google Scholar] [CrossRef] [PubMed]
- Yang, T.; Phua, K.S.; Yu, J.; Selvaratnam, T.; Toh, V.; Ng, W.H.; So, R.Q. Image-based motor imagery EEG classification using convolutional neural network. In Proceedings of the 2019 IEEE EMBS International Conference on Biomedical & Health Informatics (BHI), Chicago, IL, USA, 19–22 May 2019; pp. 1–4. [Google Scholar]
- Blankertz, B.; Tomioka, R.; Lemm, S.; Kawanabe, M.; Muller, K.-R. Optimizing Spatial filters for Robust EEG Single-Trial Analysis. IEEE Signal Process. Mag. 2007, 25, 41–56. [Google Scholar] [CrossRef]
- Lotte, F.; Guan, C. Regularizing Common Spatial Patterns to Improve BCI Designs: Unified Theory and New Algorithms. IEEE Trans. Biomed. Eng. 2010, 58, 355–362. [Google Scholar] [CrossRef]
- Ang, K.K.; Chin, Z.Y.; Zhang, H.; Guan, C. Mutual information-based selection of optimal spatial–temporal patterns for single-trial EEG-based BCIs. Pattern Recognit. 2012, 45, 2137–2144. [Google Scholar] [CrossRef]
- Yahya-Zoubir, B.; Bentlemsan, M.; Zemouri, E.T.; Ferroudji, K. Adaptive time window for EEG-based motor imagery classification. In Proceedings of the International Conference on Intelligent Information Processing, Security and Advanced Communication, Batna, Algeria, 23–25 November 2015; pp. 1–6. [Google Scholar]
- Gaur, P.; Gupta, H.; Chowdhury, A.; McCreadie, K.; Pachori, R.B.; Wang, H. A Sliding Window Common Spatial Pattern for Enhancing Motor Imagery Classification in EEG-BCI. IEEE Trans. Instrum. Meas. 2021, 70, 4002709. [Google Scholar] [CrossRef]
- Liu, Y.; Huang, Y.-X.; Zhang, X.; Qi, W.; Guo, J.; Hu, Y.; Zhang, L.; Su, H. Deep C-LSTM Neural Network for Epileptic Seizure and Tumor Detection Using High-Dimension EEG Signals. IEEE Access 2020, 8, 37495–37504. [Google Scholar] [CrossRef]
- Ai, Q.; Chen, A.; Chen, K.; Liu, Q.; Zhou, T.; Xin, S.; Ji, Z. Feature extraction of four-class motor imagery EEG signals based on functional brain network. J. Neural Eng. 2019, 16, 026032. [Google Scholar] [CrossRef] [PubMed]
- Farquhar, J.; Hill, N.J.; Lal, T.N.; Schölkopf, B. Regularised CSP for Sensor Selection in BCI. In Proceedings of the 3rd International BCI workshop, Graz, Austria, 21–24 September 2006; pp. 1–2. [Google Scholar]
- Arvaneh, M.; Guan, C.; Ang, K.K.; Quek, C. Multi-frequency band common spatial pattern with sparse optimization in Brain-Computer Interface. In Proceedings of the 2012 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Kyoto, Japan, 25–30 March 2012; pp. 2541–2544. [Google Scholar] [CrossRef]
- Kumar, S.; Sharma, A.; Tsunoda, T. An improved discriminative filter bank selection approach for motor imagery EEG signal classification using mutual information. BMC Bioinform. 2017, 18, 125–137. [Google Scholar] [CrossRef]
- Al-Saegh, A.; Dawwd, S.A.; Abdul-Jabbar, J.M. Deep learning for motor imagery EEG-based classification: A review. Biomed. Signal Process. Control. 2020, 63, 102172. [Google Scholar] [CrossRef]
- Hamedi, M.; Salleh, S.-H.; Noor, A.M.; Mohammad-Rezazadeh, I. Neural network-based three-class motor imagery classification using time-domain features for BCI applications. In Proceedings of the 2014 IEEE REGION 10 SYMPOSIUM, Kuala Lumpur, Malaysia, 14–16 April 2014; pp. 204–207. [Google Scholar] [CrossRef]
- Park, H.-J.; Kim, J.; Min, B.; Lee, B. Motor imagery EEG classification with optimal subset of wavelet based common spatial pattern and kernel extreme learning machine. In Proceedings of the 2017 39th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Jeju, Korea, 11–15 July 2017; pp. 2863–2866. [Google Scholar] [CrossRef]
- Tabar, Y.R.; Halici, U. A novel deep learning approach for classification of EEG motor imagery signals. J. Neural Eng. 2016, 14, 016003. [Google Scholar] [CrossRef]
- Lee, H.K.; Choi, Y.-S. Application of Continuous Wavelet Transform and Convolutional Neural Network in Decoding Motor Imagery Brain-Computer Interface. Entropy 2019, 21, 1199. [Google Scholar] [CrossRef]
- Sakhavi, S.; Guan, C.; Yan, S. Learning Temporal Information for Brain-Computer Interface Using Convolutional Neural Networks. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 5619–5629. [Google Scholar] [CrossRef]
- Zhang, R.; Zong, Q.; Dou, L.; Zhao, X.; Tang, Y.; Li, Z. Hybrid deep neural network using transfer learning for EEG motor imagery decoding. Biomed. Signal Process. Control. 2020, 63, 102144. [Google Scholar] [CrossRef]
- Zhou, J.; Meng, M.; Gao, Y.; Ma, Y.; Zhang, Q. Classification of motor imagery eeg using wavelet envelope analysis and LSTM networks. In Proceedings of the 2018 Chinese Control and Decision Conference (CCDC), Shenyang, China, 9–11 June 2018; pp. 5600–5605. [Google Scholar] [CrossRef]
- Ma, X.; Qiu, S.; Du, C.; Xing, J.; He, H. Improving EEG-based motor imagery classification via spatial and temporal recurrent neural networks. In Proceedings of the 2018 40th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Honolulu, HI, USA, 18–21 July 2018; pp. 1903–1906. [Google Scholar]
- Handiru, V.S.; Prasad, V.A. Optimized Bi-Objective EEG Channel Selection and Cross-Subject Generalization with Brain–Computer Interfaces. IEEE Trans. Hum.-Mach. Syst. 2016, 46, 777–786. [Google Scholar] [CrossRef]
- Ghaemi, A.; Rashedi, E.; Pourrahimi, A.M.; Kamandar, M.; Rahdari, F. Automatic channel selection in EEG signals for classification of left or right hand movement in Brain Computer Interfaces using improved binary gravitation search algorithm. Biomed. Signal Process. Control. 2017, 33, 109–118. [Google Scholar] [CrossRef]
- Baig, M.Z.; Aslam, N.; Shum, H.P.H. Filtering techniques for channel selection in motor imagery EEG applications: A survey. Artif. Intell. Rev. 2019, 53, 1207–1232. [Google Scholar] [CrossRef]
- Yang, H.; Guan, C.; Wang, C.C.; Ang, K.K. Maximum dependency and minimum redundancy-based channel selection for motor imagery of walking EEG signal detection. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013; pp. 1187–1191. [Google Scholar] [CrossRef]
- Shenoy, H.V.; Vinod, A.P. An iterative optimization technique for robust channel selection in motor imagery based Brain Computer Interface. In Proceedings of the 2014 IEEE International Conference on Systems, Man, and Cybernetics (SMC), San Diego, CA, USA, 5–8 October 2014; pp. 1858–1863. [Google Scholar] [CrossRef]
- Li, M.; Ma, J.; Jia, S. Optimal combination of channels selection based on common spatial pattern algorithm. In Proceedings of the 2011 IEEE International Conference on Mechatronics and Automation, Beijing, China, 7–10 August 2011; pp. 295–300. [Google Scholar] [CrossRef]
- Ma, X.; Qiu, S.; Wei, W.; Wang, S.; He, H. Deep Channel-Correlation Network for Motor Imagery Decoding from the Same Limb. IEEE Trans. Neural Syst. Rehabil. Eng. 2019, 28, 297–306. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Zhang, X.-R.; Zhang, B.; Lei, M.-Y.; Cui, W.-G.; Guo, Y.-Z. A Channel-Projection Mixed-Scale Convolutional Neural Network for Motor Imagery EEG Decoding. IEEE Trans. Neural Syst. Rehabil. Eng. 2019, 27, 1170–1180. [Google Scholar] [CrossRef]
- Brunner, C.; Leeb, R.; Müller-Putz, G.; Schlögl, A.; Pfurtscheller, G. BCI Competition 2008–Graz Data Set A; Laboratory of Brain-Computer Interfaces, Institute for Knowledge Discovery, Graz University of Technology: Graz, Austria, 2008; Volume 16, pp. 1–6. [Google Scholar]
- Grosse-Wentrup, M.; Buss, M. Multiclass Common Spatial Patterns and Information Theoretic Feature Extraction. IEEE Trans. Biomed. Eng. 2008, 55, 1991–2000. [Google Scholar] [CrossRef] [PubMed]
- Schlögl, A.; Lee, F.; Bischof, H.; Pfurtscheller, G. Characterization of four-class motor imagery EEG data for the BCI-competition 2005. J. Neural Eng. 2005, 2, L14–L22. [Google Scholar] [CrossRef]
- Nicolas-Alonso, L.F.; Corralejo, R.; Gomez-Pilar, J.; Alvarez, D.; Hornero, R. Adaptive Stacked Generalization for Multiclass Motor Imagery-Based Brain Computer Interfaces. IEEE Trans. Neural Syst. Rehabil. Eng. 2015, 23, 702–712. [Google Scholar] [CrossRef]
- Antony, M.J.; Sankaralingam, B.P.; Mahendran, R.K.; Gardezi, A.A.; Shafiq, M.; Choi, J.-G.; Hamam, H. Classification of EEG Using Adaptive SVM Classifier with CSP and Online Recursive Independent Component Analysis. Sensors 2022, 22, 7596. [Google Scholar] [CrossRef]
- Zhu, J.; Zhu, L.; Ding, W.; Ying, N.; Xu, P.; Zhang, J. An improved feature extraction method using low-rank representation for motor imagery classification. Biomed. Signal Process. Control. 2023, 80, 104389. [Google Scholar] [CrossRef]
- Liu, X.; Shi, R.; Hui, Q.; Xu, S.; Wang, S.; Na, R.; Sun, Y.; Ding, W.; Zheng, D.; Chen, X. TCACNet: Temporal and channel attention convolutional network for motor imagery classification of EEG-based BCI. Inf. Process. Manag. 2022, 59, 103001. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).