Consensus-Based Distributed Optimal Dispatch of Integrated Energy Microgrid
Abstract
:1. Introduction
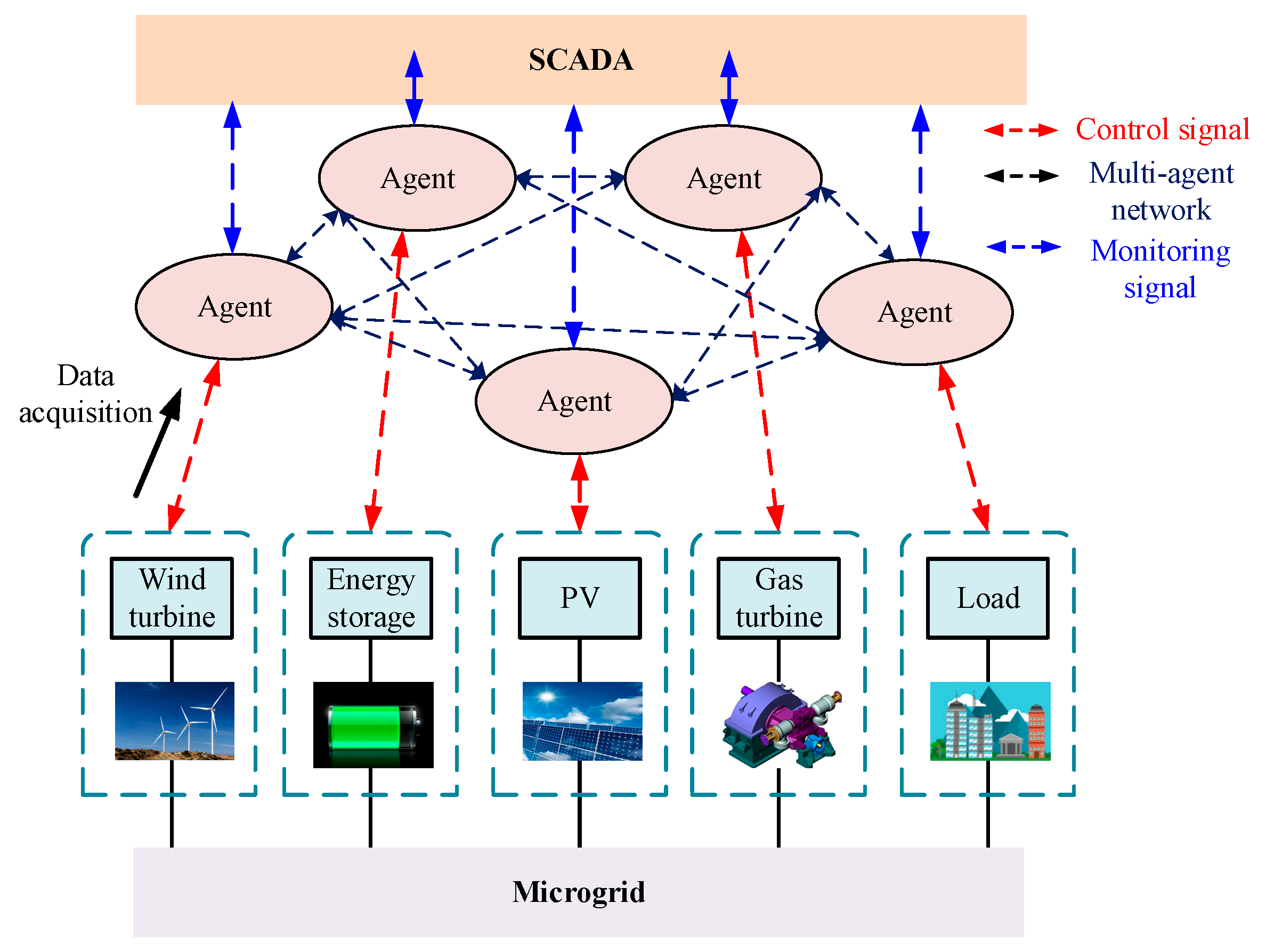
2. Decentralized Architecture for IEM
3. Decentralized Architecture for IEM
3.1. First-Order Consensus Theory
3.2. Economic Optimization Control of IEM
3.3. Equal Incremental Cost Rate Principle of Microgrid
4. Consensus-Based Optimal Power Dispatch of IEM
4.1. Algorithm Description
4.2. Convergence Proof
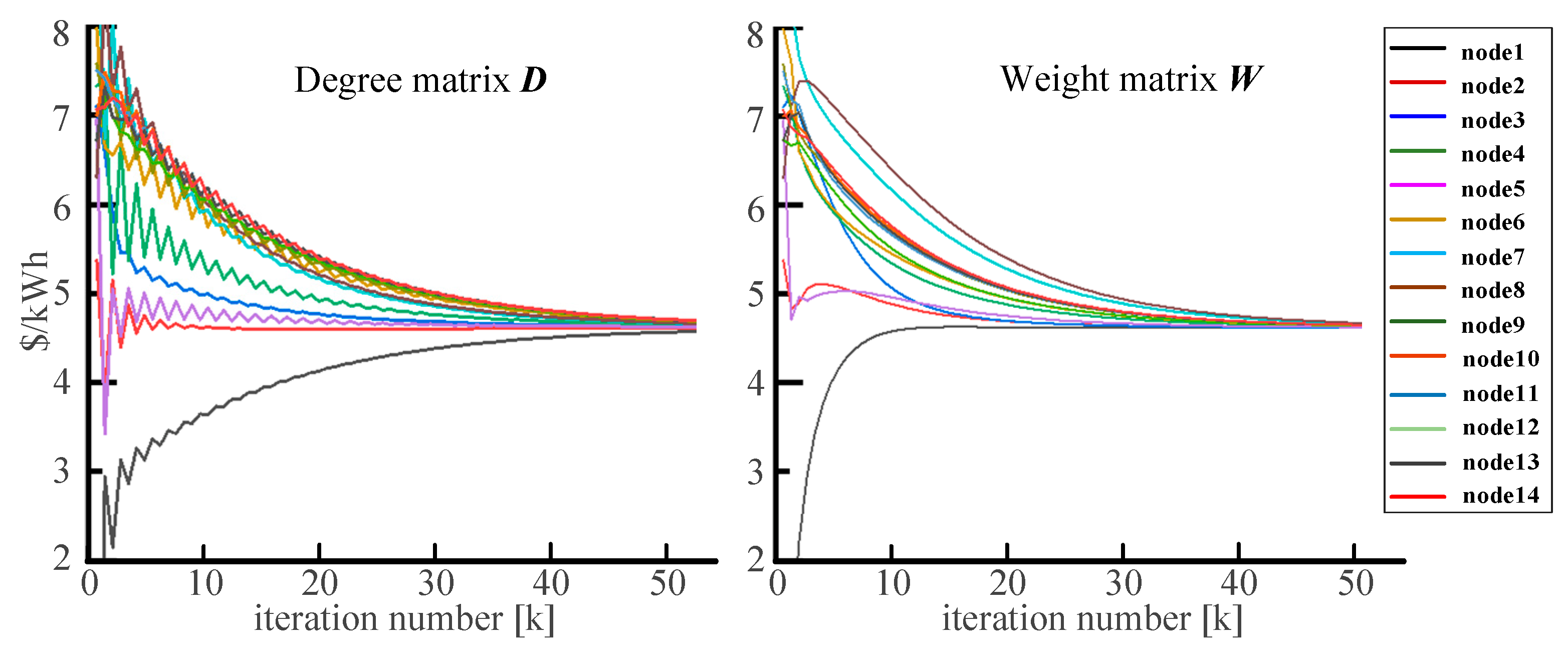
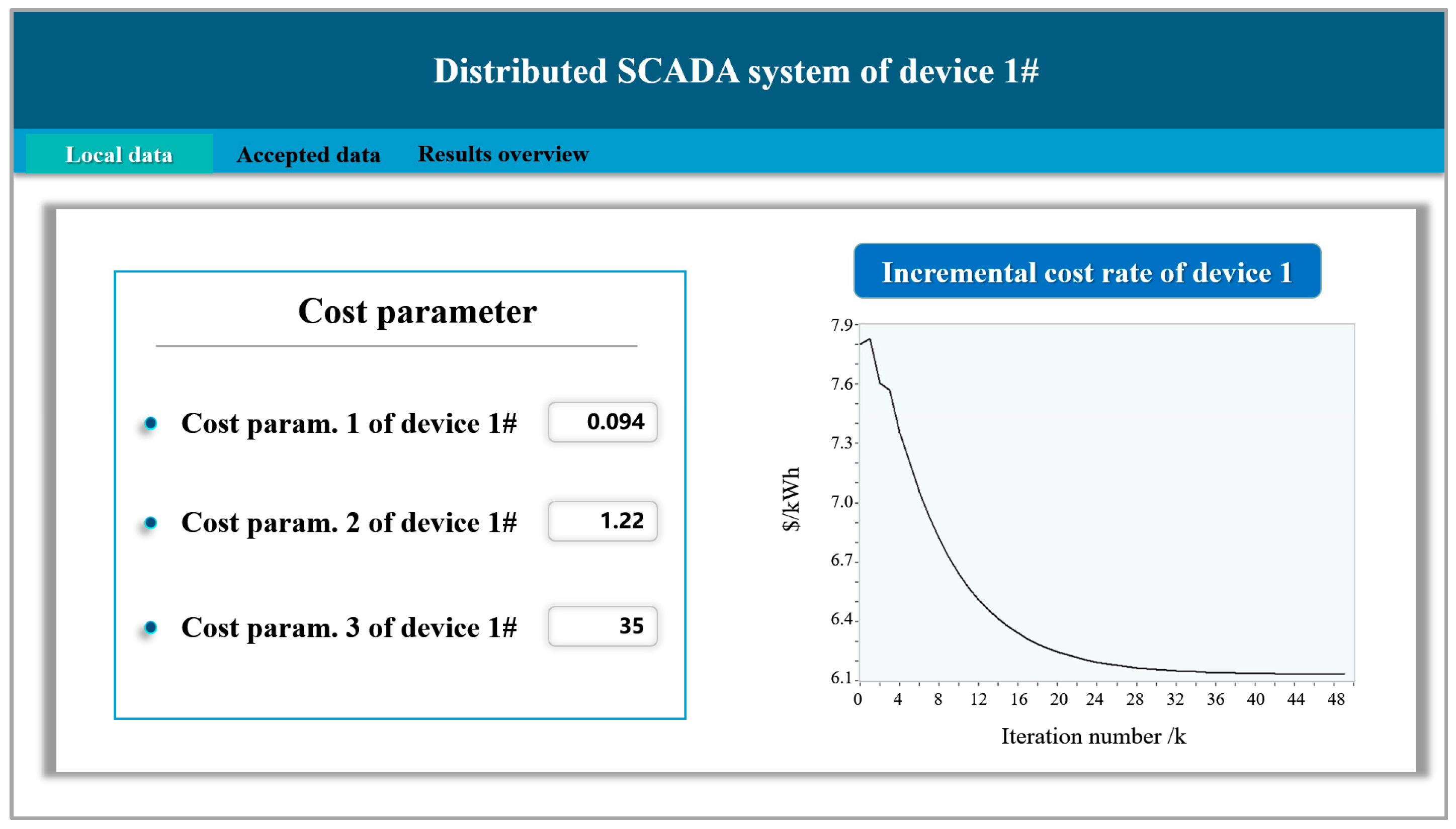
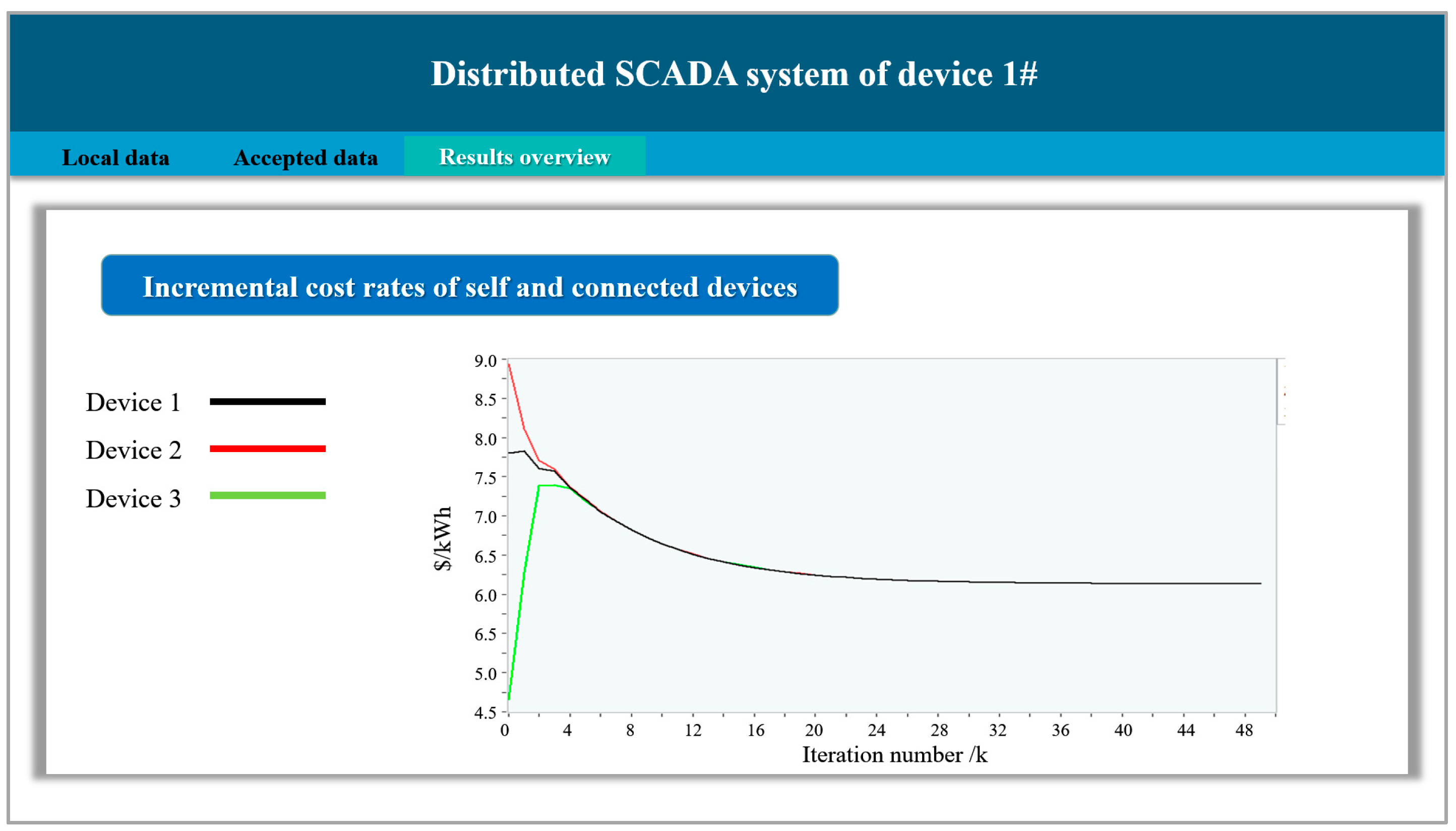
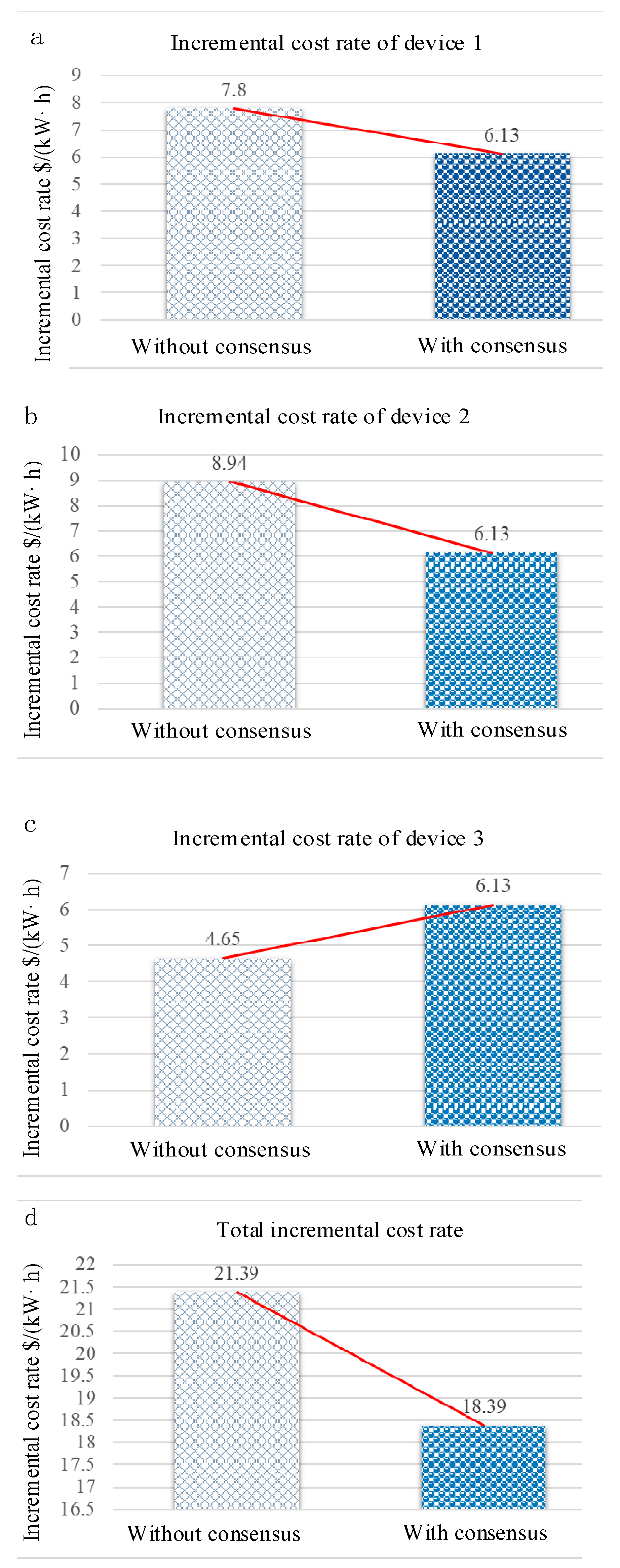
5. Experiment and Simulation Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hao, R.; Ai, Q.; Zhu, Y. Cooperative optimal control of energy internet based on multi-agent consistency. Autom. Electr. Power Syst. 2017, 41, 10–17, 57. [Google Scholar]
- Do, H.; Hong, S.; Kim, J. Robust Loop Closure Method for Multi-Robot Map Fusion by Integration of Consistency and Data Similarity. IEEE Robot. Autom. Lett. 2020, 5, 5701–5708. [Google Scholar] [CrossRef]
- Han, J.; Shi, H.; Tong, J.; Zhang, Q.; Li, J. Time consistency technique of multi-aircrafts simulation system for cooperative mission. In Proceedings of the 2019 14th IEEE Conference on Industrial Electronics and Applications (ICIEA), Xi’an, China, 19–21 June 2019; pp. 1006–1010. [Google Scholar]
- Qian, L.; Xu, X.; Zeng, Y.; Huang, J. Deep, Consistent Behavioral Decision Making with Planning Features for Autonomous Vehicles. Electronics 2019, 8, 1492. [Google Scholar] [CrossRef] [Green Version]
- Mojumdar, M.R.R.; Cano, J.M.; Orcajo, G.A. Estimation of Impedance Ratio Parameters for Consistent Modeling of Tap-Changing Transformers. IEEE Trans. Power Syst. 2021, 36, 3282–3292. [Google Scholar] [CrossRef]
- Yao, M.; Molzahn, D.K.; Mathieu, J.L. An optimal power-flow approach to improve power system voltage stability using demand response. IEEE Trans. Control. Netw. Syst. 2019, 6, 1015–1025. [Google Scholar] [CrossRef]
- Mignoni, N.; Scarabaggio, P.; Carli, R.; Dotoli, M. Control frameworks for transactive energy storage services in energy communities. Control. Eng. Pract. 2023, 130. [Google Scholar] [CrossRef]
- Meiqin, M.; Rui, X. Economic dispatch method for islanding microgrids based on distributed control. J. Electr. Eng. 2018, 13, 8–13. [Google Scholar]
- Yang, G.; Qian, A.; Jing, W. Consensus cooperative control of AC/DC hybrid microgrids based on multi-agent system. High Volt. Eng. 2018, 44, 2372–2377. [Google Scholar]
- Yingfeng, X.; Haining, W. Structure of decision support system based on multi-agent for micro-grid operation. J. Electr. Eng. 2016, 11, 30–36, 49. [Google Scholar]
- Zhang, L.; Li, Y. A game-theoretic approach to optimal scheduling of parking-lot electric vehicle charging. IEEE Trans. Veh. Technol. 2016, 65, 4068–4078. [Google Scholar] [CrossRef]
- Scarabaggio, P.; Carli, R.; Dotoli, M. Noncooperative equilibrium-seeking in distributed energy systems under AC power flow nonlinear constraints. IEEE Trans. Control. Netw. Syst. 2022, 9, 1731–1742. [Google Scholar] [CrossRef]
- Wang, R.; Li, Q.; Zhang, B.; Wang, L. Distributed consensus-based algorithm for economic dispatch in a microgrid. IEEE Trans. Smart Grid 2019, 10, 3630–3640. [Google Scholar] [CrossRef]
- Pu, T.; Liu, W.; Chen, N.; Wang, X.; Dong, L. Distributed optimal dispatching of active distribution network based on consensus algorithm. Proc. CSEE 2017, 37, 1579–1590. [Google Scholar]
- Olfati-Saber, R.; Murray, R.M. Consensus problems in networks of agents with switching topology and time-delays. IEEE Trans. Autom. Control. 2004, 49, 1520–1533. [Google Scholar] [CrossRef] [Green Version]
- Olfati-Saber, R.; Fax, J.A.; Murray, R.M. Consensus and cooperation in networked multi-agent systems. Proc. IEEE 2007, 95, 215–233. [Google Scholar] [CrossRef] [Green Version]
- Rahbari-Asr, N.; Ojha, U.; Zhang, Z.; Chow, M. Incremental welfare consensus algorithm for cooperative distributed generation/demand response in smart grid. IEEE Trans. Smart Grid 2014, 5, 2836–2845. [Google Scholar] [CrossRef]
- Chen, G.; Ren, J.; Feng, E. Distributed Finite-Time Economic Dispatch of a Network of Energy Resources. IEEE Trans. Smart Grid 2016, 8, 822–832. [Google Scholar] [CrossRef]
- Cai, K.; Ishii, H. Average consensus on arbitrary strongly connected digraphs with time-varying topologies. IEEE Trans. Autom. Control. 2014, 59, 1066–1071. [Google Scholar] [CrossRef] [Green Version]
- Chen, W.; Li, X.; Jiao, L. Quantized consensus of second-order continuous-time multi-agent systems with a directed topology via sampled data. Automatica 2013, 49, 2236–2242. [Google Scholar] [CrossRef]
- Dai, Z.; Xie, H. Condition number of semi-simple eigenvalue of quadratic eigenvalue problem. Numer. Math. A J. Chin. Univ. 2017, 39, 153–167. [Google Scholar]
- Li, S. Research on Distributed Cooperative Control of AC-DC Hybrid Microgrid; NCUT: Beijing, China, 2018. [Google Scholar]



| Node | Pi | αi | βi |
|---|---|---|---|
| 1 | 0 | 0.020 | 0.14 |
| 2 | 0 | 0.062 | 4.20 |
| 3 | 0 | 0.075 | 3.25 |
| 4 | 0 | 0.072 | 8.25 |
| 5 | 0 | 0.066 | 7.20 |
| 6 | 0 | 0.070 | 4.05 |
| 7 | 0 | 0.350 | 0 |
| 8 | 0 | 0.075 | 7.80 |
| 9 | 0 | 0.060 | 8.05 |
| 10 | 0 | 0.078 | 8.45 |
| 11 | 0 | 0.080 | 8.75 |
| 12 | 0 | 0.085 | 9.00 |
| 13 | 0 | 0.069 | 7.05 |
| 14 | 0 | 0.077 | 8.15 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, S.; Peng, K.; Hu, C.; Ma, R. Consensus-Based Distributed Optimal Dispatch of Integrated Energy Microgrid. Electronics 2023, 12, 1468. https://doi.org/10.3390/electronics12061468
Luo S, Peng K, Hu C, Ma R. Consensus-Based Distributed Optimal Dispatch of Integrated Energy Microgrid. Electronics. 2023; 12(6):1468. https://doi.org/10.3390/electronics12061468
Chicago/Turabian StyleLuo, Shanna, Kaixiang Peng, Changbin Hu, and Rui Ma. 2023. "Consensus-Based Distributed Optimal Dispatch of Integrated Energy Microgrid" Electronics 12, no. 6: 1468. https://doi.org/10.3390/electronics12061468
APA StyleLuo, S., Peng, K., Hu, C., & Ma, R. (2023). Consensus-Based Distributed Optimal Dispatch of Integrated Energy Microgrid. Electronics, 12(6), 1468. https://doi.org/10.3390/electronics12061468







