1. Introduction
Detection of abnormal events in automated video surveillance systems is one of the most challenging, overriding, and time-sensitive tasks. Recently, deep-learning-based algorithms have been dominating the literature as the deep learning solutions for crowd events detection have outperformed the conventional machine learning solutions. Motion and appearance features are widely used in video anomaly detection algorithms. In deep-learning-based video anomaly detection algorithms, a common technique is to build reconstruction model considering motion and/or appearance features. A common assumption is that the reconstruction error of the frame of normal event is small but that of the frame of abnormal event is large [
1,
2,
3]. To learn normal data patterns of videos, the deep model is trained solely on videos of normal events. Consequently, during testing with videos of normal events, the deep model demonstrates its ability to show normal events with low reconstruction error, but the deep model suffers from exhibiting high reconstruction error needed for abnormal events. As a result, the error gap between the low reconstruction error and the high reconstruction error differentiates the normal and abnormal events in videos. Normally, research in this direction is targeted to increase this error gap [
2,
3]. In brief, a larger error gap plays the vital role to detect anomaly in videos.
A burning question is: can the reconstruction-based model guarantee the expected large reconstruction error (i.e., high error gap) of the anomaly? Liu et al. [
2] claimed that the deep model trained by minimizing the reconstruction error of normal data cannot guarantee a higher reconstruction error of an abnormal event at the testing phase. Further, Gong et al. [
4] stated that abnormal events may not correspond to larger reconstruction errors due to the improved capacity and generalization of deep neural network. Thus, reconstruction errors of normal and abnormal events will be indistinguishable, resulting in a very small error gap [
2]. Both Gong et al. [
4] and Park et al. [
5] suggested the addition of a memory module for solving this pitfall. Nonetheless, the restricted memory cannot fully reveal the distinctiveness of normal events and the effective size of memory is not facile to find out [
3]. To keep away from this problem, Zhong et al. [
3] adopted a cascade reconstruction model to increase the reconstruction error of anomaly in videos. Motivated by the performance of the video prediction model of Mathieu et al. [
6], Liu et al. [
2] presented an appearance-motion model for video frame prediction that applied a U-Net structure [
7] to predict a frame from a number of recent ones and then estimated the corresponding optical flow. Their model was optimized according to the difference between the output and original versions of video frame as well as the optical flow together with an adversarial loss.
In this paper, we design a generalized architecture (rpNet) as shown in
Figure 1, which includes a group of different deep models. Each model integrates an rNet (an image frame reconstruction network or an appearance-only stream) and a pNet (a video frame prediction network or an appearance-motion stream), in which every stream possesses its own contribution for the task of detecting abnormal frames. Both streams can promise substantial anomaly scores. The fusion of outputs from two streams guarantees a certain degree of augmentation of the error gap. Our approach is inspired by the Zhong et al. [
3] model but with distinct modules and designs. Primarily, Zhong et al. [
3] applied a traditional autoencoder (AE) as an rNet and the squeeze-and-excitation network of Hu et al. [
8] as a pNet to handle motion. Differently, we apply a convolutional AE (ConvAE) or a skip connected ConvAE (AEc) as an rNet and we adopt Liu et al.’s [
2] future frame prediction model as a pNet to handle appearance and motion. The performance of a ConvAE in rNet is better than a traditional AE. The ConvAE extends the basic structure of the simple AE by changing the fully connected layers to convolution layers. The ConvAE is more suitable for the images as it uses a convolution layer. The reason of choosing Liu et al. [
2] prediction model is that a fixed and optimized procedure of optical flow estimation (e.g., FlowNet [
9]) is embedded in it. Mainly, Liu et al. [
2] applied a traditional U-Net [
7] as the heart of their model. We also employ a traditional U-Net [
7] as the first option of our pNet. Aside from a traditional U-Net [
7], we propose to use two more of its derivatives, namely a non-local block U-Net and an attention block U-Net (aUnet), for performance improvements.
A U-Net [
7] is an improved CNN (convolutional neural network) model that can train data with fewer samples and segment images more accurately, but its efficiency and effectiveness can be limited by using the local operators (e.g., convolutions and down-sampling operators) only [
10]. However, non-local blocks can strengthen the temporal and spatial characteristics and establish the long-distance dependencies of video frames [
11]. Buades et al. [
12] explained non-local mean operation, and later Wang et al. [
11] wrapped the non-local operation into a non-local block. A new non-local block can be inserted in a U-Net [
7] without breaking its initial behavior [
10]. Because of this, Zhang et al. [
13] adopted three non-local blocks in their U-Net frame prediction model to detect surveillance video anomaly. However, Wang et al. [
11] showed that more non-local blocks lead to better performance. To this end, we adopt four non-local blocks in the U-Net architecture as the second option of our pNet. In addition to non-local blocks, attention mechanism puts down less fitting features and highlights more salient features. Oktay et al. [
14] introduced attention gates in the intermediate layers of a U-Net architecture for pancreas segmentation. Yet, due to better breast-tumor segmentation performance in ultrasound images, Vakanski et al. [
15] applied attention blocks at beginning layers of a U-Net architecture. Following Vakanski et al. [
15], we propose an aUnet as the third option of our pNet. There exist some internal architectural differences at our proposed aUnet from Vakanski et al. [
15]. For example, Vakanski et al. [
15] employed external auxiliary inputs in the form of visual saliency maps, whereas we employ an internal motion saliency map and original video frame as inputs of the aUnet.
We presume that if any frame
contains an appearance anomaly then our rNet can improve its determinability, whereas if
contains an appearance-motion anomaly, then our pNet can improve its determinability. The rNet and pNet enforce both the reconstructed frame and the predicted frame to be close to their ground truth frame, respectively. Therefore, we combine the error scores of both networks to calculate the final anomaly score of each frame for detecting its anomalousness by considering the anomaly scores of consecutive multi-frames (e.g., past, present, and future frames). This also helps to exploit the persistent flow of abnormal events. In essence, we propose six deep models by combining two-alternative of rNets and three-alternative of pNets from our generalized framework in
Figure 1: (1) AE-Unet (convolutional autoencoder and U-Net), (2) AEcUnet (convolutional autoencoder with skip connection and U-Net), (3) AEnUnet (convolutional autoencoder and non-local block U-Net), (4) AEcnUnet (convolutional autoencoder with skip connection and non-local block U-Net), (5) AEaUnet (convolutional autoencoder and attention block U-Net), and (6) AEcaUnet (convolutional autoencoder with skip connection and attention block U-Net). Although these models can provide an improved error gap for abnormal events, they have different degrees of feature extraction capabilities required for crowd video anomaly detection. Consequently, in experimental setups, some of these models showed inferior results, while others presented superior results. For example, AEcaUnet demonstrated the best results and outperformed its alternatives by both confirming better error gap and extracting high quality features from the available videos.
Our key contributions are summarized as follows:
We propose six different deep models for crowd anomaly detection by designing a generalized framework (rpNet).
We propose an aUnet (see
Figure 2) for an option of the pNet of our rpNet architecture.
Experiments on five benchmark datasets and a rigorous statistical analysis demonstrate the potential of our models with competitive performance compared with the state-of-the-art models.
The rest of this paper is organized as follows.
Section 2 addresses the most relevant previous studies.
Section 3 overviews our generalized architecture of rpNet.
Section 4 discusses the rNet of our rpNet.
Section 5 illustrates the pNet of our rpNet.
Section 6 exemplifies mainly the non-local block U-Net and our proposed aUnet.
Section 7 illustrates anomaly detection on testing datasets.
Section 8 hints a simulation to show that a larger error gap is guaranteed by rpNet.
Section 9 explains experimental setup and results on publicly datasets.
Section 10 compares our experimental results with the state-of-the-art methods.
Section 11 makes a rigorous statistical analysis to find superiority among models.
Section 12 concludes the paper.
3. Overview of the Generalized Architecture (rpNet)
Fundamentally, we design a generalized architecture named rpNet as depicted in
Figure 1. It consists of two neural networks connected in parallel namely reconstruction network (rNet) and prediction network (pNet). The rNet depends on appearance only as it works with images, but the pNet relies on both appearance and motion as it works with video frames. The key difference between images and video frames is that the video frames are sequential and correlated, whereas the images are static. Video frames need to be measured in both space and time dimensions, but images need to be measured in space dimension. The rpNet includes information of both images and video frames simultaneously.
Machine learning methods in computer vision and image processing problems [
37] have been applied for a good deal of research applications (e.g., [
38,
39,
40,
41,
42,
43,
44,
45,
46,
47,
48,
49,
50,
51]). Deep learning is a subset of machine learning that utilizes huge volumes of data and sophisticated algorithms for training a model. Nowadays, deep learning models are used to detect anomalies in various kinds of applications (e.g., [
52,
53,
54,
55,
56,
57]). The extraction of appropriate features plays a decisive role for detecting anomalies in deep learning models. Recently, due to powerful capability of deep learning models in reconstruction, it has unquestionably made advancement in abnormal event detection tasks. The video anomaly detection models (e.g., [
1,
52]) indicated that convolution is predominantly applied for extracting features. Thereupon, such structure scarcely encodes temporal dependencies in a long video sequence. Basically, our rNet is a convolutional autoencoder, which is similar to those models [
1,
52].
Figure 3 details the two variants of the presented block diagram of the rNet in
Figure 1. In general, the rNet comprises an encoding path and a decoding path. The block diagram of the pNet in
Figure 1 is typically a prediction network of Liu et al. [
2] to predict future frames. One of its most important components is its generator, which is a traditional U-Net [
7]. However, we propose to use either non-local block U-Net or attention block U-Net as discussed in
Section 6.
In a nutshell, the rpNet both reconstructs the current frame using its rNet for scoring reconstruction error and predicts the future frame using its pNet for scoring prediction error in a parallel manner for anomaly detection by providing better error gaps via information fusion (e.g., see
Section 8). Both rNet and pNet can show some degree of performance, but the performance of rpNet is better than that of either rNet or pNet individually. The straightforward simulation in
Section 8 and later the experimental results support this proposition. Essentially, the rpNet brings about six separate models namely AE-Unet, AEcUnet, AEnUnet, AEcnUnet, AEaUnet, and AEcaUnet by combining the two-variant of rNets and the three-variant of pNets.
Figure 3a demonstrates encoder and decoder networks of our ConvAE without skip connection. The encoder network consists in a stack of four hidden layers with convolutional filters of 64, 128, 256, and 512, kernel sizes of 5, 5, 3, and 3, and strides of (1,2), (2,2), (2,2), and (2,2), respectively. Regarding the decoder network, it has four transposed convolutional layers that mirror the encoder layers. Due to the loss of some features, the reconstructed image of ConvAE may not match exactly with the input image. The difference
between the original input
f and the reconstructed
is called the reconstruction error. The learning process of ConvAE is to minimize the reconstruction error. Loss functions play an important role in achieving the desired reconstructed image.
5. Appearance-Motion Stream
In this section, we discuss details of our prediction network and summarize the loss functions for optimization.
Only appearance constraints cannot guarantee to characterize the motion information well. Further, both spatial and temporal information is an important feature of videos. Inspired by Liu et al. [
2], we used an optical flow constraint into the objective function to guarantee the motion consistency for normal events in training set, which further boosts the performance for anomaly detection. The pipeline of our video frame prediction network is shown in
Figure 1, where we adopt a traditional U-Net [
7] as generator to predict next frame. The traditional U-Net [
7] is a fully convolutional neural network, and it uses convolutional and pooling layers. To reduce the number of parameters, it does not have any fully connected layer. It contains a contraction path and an expansion path. Its contraction path is employed to extract the features through the convolutional layer and downsampling. Its expansion path accurately locates and restores the information as much as possible. There is also a shortcut operation before each upsampling convolutional layer to concatenate the information.
To generate high quality image, we adopt the constraints in terms of appearance (e.g., intensity and gradient) as well as motion (e.g., optical flow) losses. Optical flow is a widely used estimator of motion. The Flownet [
9] is a pre-trained network used to calculate optical flow. We also clenched the adversarial training to discriminate whether the prediction is real or fake. The aim of our appearance-motion stream is not only to predict frames to be close to their ground truth in spatial space but also to match the optical flow between predicted frames and the ground truth. In common, this stream is expected to associate typical motions to common appearance objects while ignoring the static background patterns.
Given a video with consecutive
t frames as
. We predict the future video frame
using previous video frames
. Following the work by Mathieu et al. [
6], to make the predicted
close to its ground truth
, we minimize their distances with reference to intensity and gradient. Following the work of Liu et al. [
2], to preserve the temporal coherence between neighboring frames, we enforce the optical flow between
and
as well as the optical flow between
and
to be close. We assume that normal events can be predicted very well. Therefore, we can include the difference between the predicted frame
and its ground truth
for anomaly detection score. Following the work by Liu et al. [
2], we employ a traditional U-Net [
7], which serves as the main prediction network for a shortcut between a high-level layer and a low-level layer with the output resolution unchanged for each two convolution layers to decrease gradient vanishing and to increase information symmetry. The kernel sizes are configured to all convolution and deconvolution as
, and the max pooling layers as
.
5.1. Appearance Loss
To make the prediction close to its ground truth, following the work of Mathieu et al. [
6], intensity and gradient difference can be employed.
5.1.1. Intensity Loss
Intensity loss is the
-norm or
-norm between the predicted frame
and its ground true
, which is used to maintain similarity between pixels in the RGB space. By definition, the sum of the absolute values is the
-norm, and the sum of squared values is the
-norm. While the
-norm increases at a constant rate, the
-norm increases exponentially. Minimization of the norm encourages the weights to be small. Specifically, we minimize the distance measured by
-norm between
and
as intensity loss
of the prediction network by Equation (
4) [
2]:
5.1.2. Gradient Loss
There exists a flaw in calculating pixel intensity loss by
-norm, which produces blur in the output. Henceforth, it is vital to apply gradient difference loss for sharpening the predicted frame
by using the
-norm. As compared to
-norm,
-norm is more likely to reduce some weights to 0. The gradient loss
of the prediction network can be calculated by Equation (
5) as:
where
denotes the pixel at the
i-th row and
j-th column in
, and
returns the absolute value.
5.1.3. Motion Loss
To detect anomaly the coherence of motion is an important factor for the evaluation of normal events. Only difference between intensity and gradient for future frame generation cannot guarantee to predict a frame with the correct motion. Optical flow is a good estimator of motion [
62]. We adopt a temporal loss defined as the difference between optical flow of predicted frames and ground truth to improve the coherence of motion in the predicted frame. We employ the Flownet [
9] denoted as
F, which is a CNN-based approach for optical flow estimation. We consider that
F is pre-trained on a synthesized dataset [
9] and all the parameters in
F are fixed. The motion loss
in terms of optical flow can be measured by
-norm using Equation (
6) as:
5.1.4. Adversarial Generator Loss
Usually, a generative adversarial network (GAN) contains a generator
G and a discriminator
D. The
G learns to generate frames that are hard to be classified by
D. Similar to Liu et al. [
2], we use a U-Net-based prediction network as
G. As for
D, we follow Isola et al. [
63] and utilize a patch discriminator, which means each output scalar of
D corresponds a patch of an input image. The goal of training
D is to classify
into class 1 (i.e., genuine label) and
into class 0 (i.e., fake label), respectively. The goal of training
G is to generate frames, whereas
D classify them into class 1. The adversarial generator loss
is minimized to confuse
D as much as possible such that it cannot discriminate the generated predictions, and is given by the MSE loss function as:
where
denotes real decision by
D for patch
,
indicates fake decision, and
is the mean squared error function.
5.2. Minimization Objective Function
We combine the losses on appearance, motion, and adversarial training to obtain the following minimization objective function:
where
,
,
,
,
, and
are the corresponding training time weights for the losses. To train the model, the intensity of pixels in all frames can be normalized (e.g., [−1, 1]). An Adam [
64]-based stochastic gradient descent method can be used for parameter optimization.
7. Anomaly Detection on Testing Data
If we assume that normal events can be well predicted, then we can easily apply the difference between the predicted frame
and its ground truth
for anomaly prediction. In anomaly detection methods, two common metrics, namely MSE and PSNR, are widely employed to calculate the anomaly scores. The MSE is used to measure the quality of predicted images by computing a Euclidean distance between the prediction and its ground truth of all pixels, whereas the PSNR represents a measure of the peak error. The MSE is easy to compute, but sensitive to outliers. On the other hand, in the absence of error, if two images
and
(or
) are identical, then the MSE is zero but the PSNR becomes infinite (or division by zero) [
73]. In spite of that, Mathieu et al. [
6] showed that PSNR is a better way for image quality assessment.
We assume that if any frame
holds an appearance anomaly (e.g., someone carrying a gun) then the rNet can improve its determinability, whereas if
contains a motion anomaly (e.g., people fighting on the street) the pNet can improve its determinability. Therefore, we bring the error scores of appearance and prediction into a cascaded score to compute the final error score of each frame for detecting its anomalousness. We evaluate the anomaly of appearance based on reconstruction error of the entire frame. This technique preserves the complete appearance of target objects in frame. We define pixel-wise partial anomaly score individually estimated on the prediction error of
and the reconstruction error of
from prediction and reconstruction networks, respectively, sharing for the same frame as:
where
W,
H,
are the width, height, and spatial index of the frame, respectively. The maximum pixel value of an image is 255. Large
or
of a frame hints that it is more likely to be normal. Roughly, it is possible to use
or
for determining whether an abnormal event has occurred. For example, if
or
is greater than any defined threshold, the frame is normal, otherwise abnormal. Nevertheless, it expects more refinement for better performance.
The partial frame-level score of the
t-th frame
is computed as a weighted combination of the two incomplete scores as follows:
where
and
are the weights, which normalize the two scores to the same scale. They can be calculated on the training data of
n images using Equations (
16) and (
17) as:
The hyper parameters of
and
are used to control the contribution of corresponding score to the summation, which can be adjusted appropriately for the importance of the appearance and motion. We perform a normalization of
using Equation (
18) as:
where
and
belong to shape and scale parameters, respectively [
74]. The occurrence of abnormal events in video has continuity, i.e., abnormal events cannot appear in a single frame, but appear in multiple consecutive frames. Consequently, we utilize not only the current frame but also the past and future frames to compute the final anomaly score using Equation (
19) as:
where the anomaly score of the
t-th frame
consists of the
as current frame and the
with
of
past and future frames. The score of
estimated from a frame of abnormal event is expected to be higher compared with the ones of normal event. Therefore, we can predict whether a frame is normal or abnormal based on
. One can set a threshold to distinguish normal or abnormal frames.
8. Larger Error Gap Guaranteed by rpNet
Ideally, both pNet and rNet can produce their own outputs. We assume that the output of either pNet or rNet can individually provide necessary anomaly scores, but may not provide sufficient anomaly scores used for anomaly detection. The gain of the rpNet individually relies on pNet and rNet. The overall gain of the rpNet equals to the product of the individual gain of pNet and rNet. Mathematically, if
and
indicate the gains of pNet and rNet, respectively, then the overall gain
can be formulated by Equation (
20) as:
When the gain of pNet and rNet applies the decibel (dB) expression, the Equation (
20) yields:
For example,
Figure 10 conveys a simplified schematic diagram of the rpNet along with any instance of video frames if pNet and rNet achieve 41.44 dB and 40.80 dB, respectively, then the overall process has a gain of 82.24 dB.
Using a simple simulation, we wish to explain that the rpNet can provide better anomalous detection results by providing higher anomaly scores for abnormal cases in videos than that of either pNet or rNet individually. Explicitly, the rpNet can provide an improved reconstruction error gap by increasing the output signal strength of pNet and rNet.
Assume that a hypothetical video surveillance system has captured the following four scenarios of people: (i) Normal walk and gather but sudden evacuation after an unwanted event, (ii) normal walk and sudden split after an incident, (iii) someone intentionally passing opposite of the main stream, and (iv) sudden run after an explosion. In addition, assume that both pNet and rNet are trained with a normal video cases and can detect those abnormal video events by providing the anomaly scores as depicted in
Figure 11. The ground truths for four scenarios are given, but the anomaly scores of the rpNet are calculated.
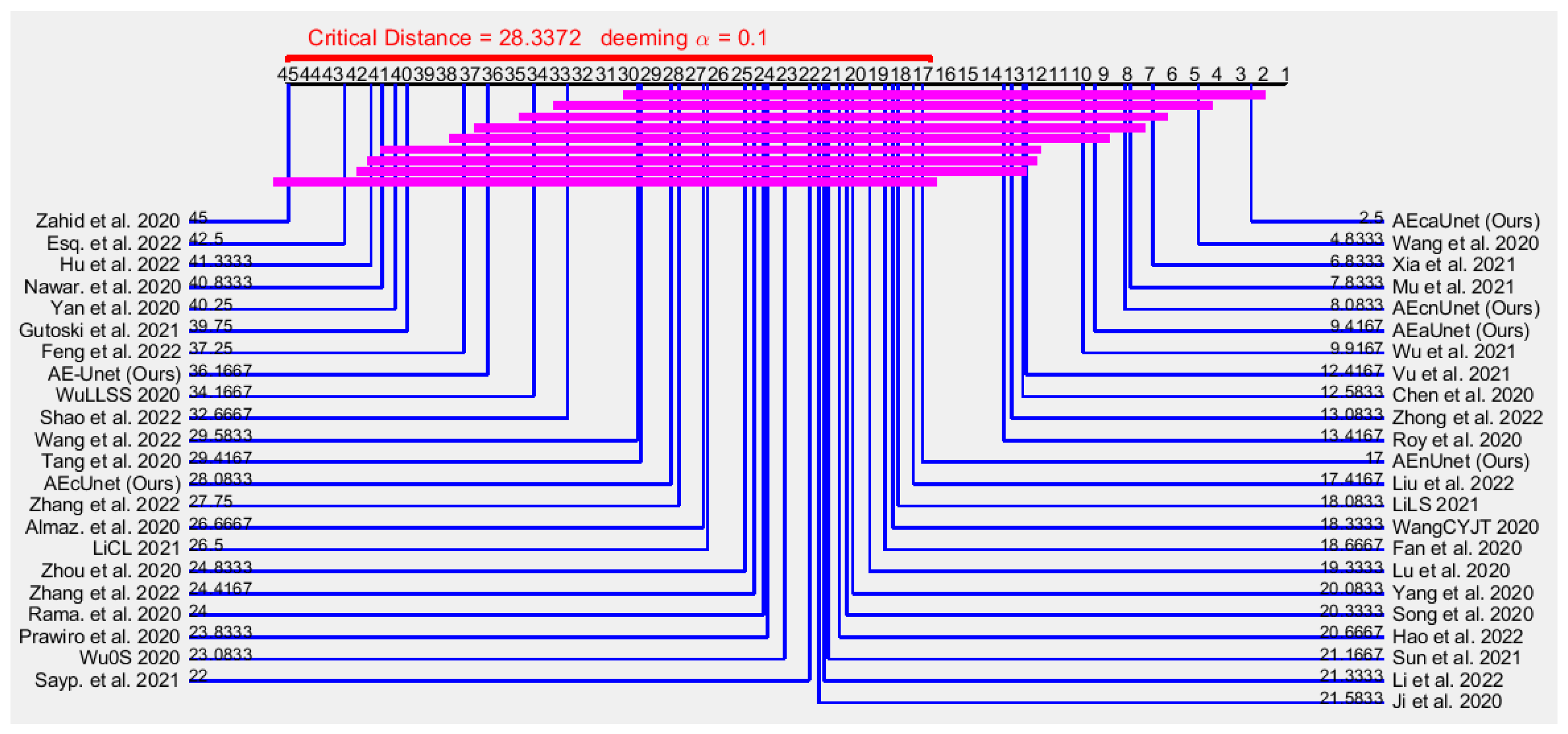
Table 2 shows the analyzing report of
Figure 11 in qualitatively and quantitatively. The mean ACC scores of pNet and rNet are 0.7740 and 0.8762, respectively. The mean ACC of the rpNet is 0.9595, which is definitely higher than those scores. To gain such ACC score, the rpNet has to come up against a mean false alarm rate of 0.0313. Nevertheless, on the average, the rpNet achieves 16.74% better ACC score than the mean ACC score of the pNet and rNet. At the rising edge, the values of root MSE (RMSE) are 15.0416, 6.4226, and 3.2404 for the rNet, pNet, and rpNet, respectively. The RMSE is
times less in the rpNet compared with the mean RMSE of rNet and pNet. Similarly, at the falling edge, the RMSE is
times less in the rpNet. The coefficient of variation of the RMSE, denoted as CV(RMSE), is
and
times less in the rpNet at rising and falling edges, respectively, compared with the mean CV(RMSE) of rNet and pNet.
Taking into account the data in
Table 2, upon ROC curve analysis the scores of 0.674, 0.841, and 0.973 can be obtained from rNet, pNet, and rpNet, respectively. From
Figure 12, it is noticeable that the rpNet became the highest performative model considering data in
Table 2. The rpNet achieves 1.3002 times or 30.02% better AUC scores than the mean AUC score of rNet and pNet. Explicitly, the simulated events in
Figure 11 show evidence that the rpNet can guarantee larger error gap on the identical ground of both rNet and pNet. This proposition is also supported by the practical results from the experimental setup.
In essence, the aforementioned straightforward simulation shows that the rpNet is capable of achieving certain incremental factor of the reconstruction error gap by increasing the signal strength of the anomaly scores.
10. Experimental Result Comparison
In the literature, there are widely used common datasets that are used to test the performance of different deep models, while other datasets were mainly used to test the generalization ability of those models for detecting crowd anomaly in video streams.
Table 5 compares frame-level AUC scores among miscellaneous methods and the most frequently used crowd datasets.
From
Table 5, it is notable that our method could not demonstrate an outright accuracy score. However, from
Table 5, it is hard to notice the best performative method as an individual method could not achieve an absolute better performance. For example, Mu et al. [
109], Cho et al. [
131], Xia et al. [
104], Zahid et al. [
87], and Roy et al. [
91] achieved the best AUC scores of 0.952, 0.992, 0.922, 0.940, and 0.997 from UCSD-Ped1 [
31], UCSD-Ped2 [
31], CUHK-Avenue [
32], ShanghaiTech-Campus [
18], and UMN [
36], respectively. Unambiguously, considering experimental results in
Table 5, it is very hard to find that one algorithm is better than its alternatives. Usually, the nonparametric statistical analysis can be used for superiority measure [
134], but all models were not tested against always the same five datasets in
Table 5. Henceforth, based on the chosen datasets by the authors of various models in
Table 5, mainly for statistical analysis, we can divide the tabular data in
Table 5 into six following groups:
Methods of this group were tested against the datasets of UCSD-Ped1 [
31], UCSD-Ped2 [
31], CUHK-Avenue [
32], ShanghaiTech-Campus [
18], and UMN [
36] or the methods existed before 2020 (i.e.,
Table 6).
Methods of this group were tested against the datasets of UCSD-Ped2 [
31], CUHK-Avenue [
32], and ShanghaiTech-Campus [
18] (i.e.,
Table 7).
Methods of this group were tested against the datasets of UCSD-Ped1 [
31], UCSD-Ped2 [
31], and CUHK-Avenue [
32] (i.e.,
Table 8).
Methods of this group were tested against the datasets of UCSD-Ped1 [
31], UCSD-Ped2 [
31], CUHK-Avenue [
32], and ShanghaiTech-Campus [
18] (i.e.,
Table 9).
Methods of this group were tested against the datasets of UCSD-Ped1 [
31], UCSD-Ped2 [
31], CUHK-Avenue [
32], and UMN [
36] (i.e.,
Table 10).
Methods of this group were tested against the datasets of UCSD-Ped1 [
31], UCSD-Ped2 [
31], and UMN [
36] (i.e.,
Table 11).
The frame-level
failure score of AUC (fAUC) is defined by Equation (
24) as:
Table 6.
The fAUC scores of . Column-wise the best numerical result is shown in bold.
Table 6.
The fAUC scores of . Column-wise the best numerical result is shown in bold.
| Models | Obtained fAUC Scores from Different Datasets | Mean of fAUC Scores |
|---|
| Ped1 [31] | Ped2 [31] | Avenue [32] | Campus [18] | UMN [36] | Arithmetic | Geometric | Harmonic |
|---|
| Zhang et al. [127] | 0.0580 | 0.0710 | 0.1950 | 0.1970 | 0.0120 | 0.1066 | 0.0717 | 0.0400 |
| Roy et al. [91] | 0.1500 | 0.0250 | 0.1300 | 0.1900 | 0.0030 | 0.0996 | 0.0488 | 0.0127 |
| Liu et al. [2] | 0.1690 | 0.0460 | 0.1510 | 0.2720 | - | 0.1595 | 0.1337 | 0.1054 |
| Hasan et al. [1] | 0.2500 | 0.1500 | 0.2000 | 0.3910 | - | 0.2478 | 0.2327 | 0.2195 |
| LuoLG [78] | 0.2450 | 0.1190 | 0.2300 | - | - | 0.1980 | 0.1886 | 0.1782 |
| Luo et al. [18] | - | 0.0780 | 0.1830 | 0.3200 | - | 0.1937 | 0.1659 | 0.1401 |
| Nguyen et al. [27] | - | 0.0380 | 0.1310 | - | - | 0.0845 | 0.0706 | 0.0589 |
| Ionescu et al. [22] | 0.3160 | 0.1780 | 0.1940 | - | - | 0.2293 | 0.2218 | 0.2153 |
| AE-Unet (Ours) | 0.1520 | 0.0980 | 0.1750 | 0.2660 | 0.0700 | 0.1522 | 0.1372 | 0.1233 |
| AEcUnet (Ours) | 0.1380 | 0.0660 | 0.1370 | 0.2390 | 0.0350 | 0.1230 | 0.1009 | 0.0801 |
| AEnUnet (Ours) | 0.1280 | 0.0430 | 0.1290 | 0.2260 | 0.0230 | 0.1098 | 0.0819 | 0.0577 |
| AEcnUnet (Ours) | 0.1120 | 0.0290 | 0.1260 | 0.2180 | 0.0240 | 0.1018 | 0.0735 | 0.0512 |
| AEaUnet (Ours) | 0.1250 | 0.0310 | 0.1130 | 0.2200 | 0.0200 | 0.1018 | 0.0719 | 0.0482 |
| AEcaUnet (Ours) | 0.0820 | 0.0110 | 0.0840 | 0.2020 | 0.0130 | 0.0784 | 0.0457 | 0.0254 |
Table 6 presents the fAUC scores of
group with related evaluation. Although many methods are related to this group, rigorous statistical analysis is very difficult to perform. For example, the method of Nguyen et al. [
27] was only tested on two datasets, whereas the method of Zhang et al. [
127] was tested on five datasets. Thus, instead of using rigorous statistical analysis, for evaluation we use arithmetic, geometric, and harmonic means only. The method of Zhang et al. [
127] presented the best performance from UCSD-Ped1 [
31], whereas AEcaUnet (Ours) demonstrated the best performance from UCSD-Ped2 [
31] and CUHK-Avenue [
32]. The method of Roy et al. [
91] showed slightly better performance from UMN [
36]. However, methods of Zhang et al. [
127], Roy et al. [
91], and AEcaUnet (Ours) showed approximately the same performance from ShanghaiTech-Campus [
18]. Nevertheless, the overall performance of AEcaUnet (Ours) is better than that of either Roy et al. [
91] or Zhang et al. [
127]. Explicitly, by referring to
Table 6, AEcaUnet (Ours) seemingly showed the best performance from
.
For , , , and , on the other hand, it is not show any direct indication of superiority. As they contain necessary and sufficient different data, we perform nonparametric statistical analysis to measure the superiority among models.