A Robust Fault Diagnosis Scheme for Converter in Wind Turbine Systems
Abstract
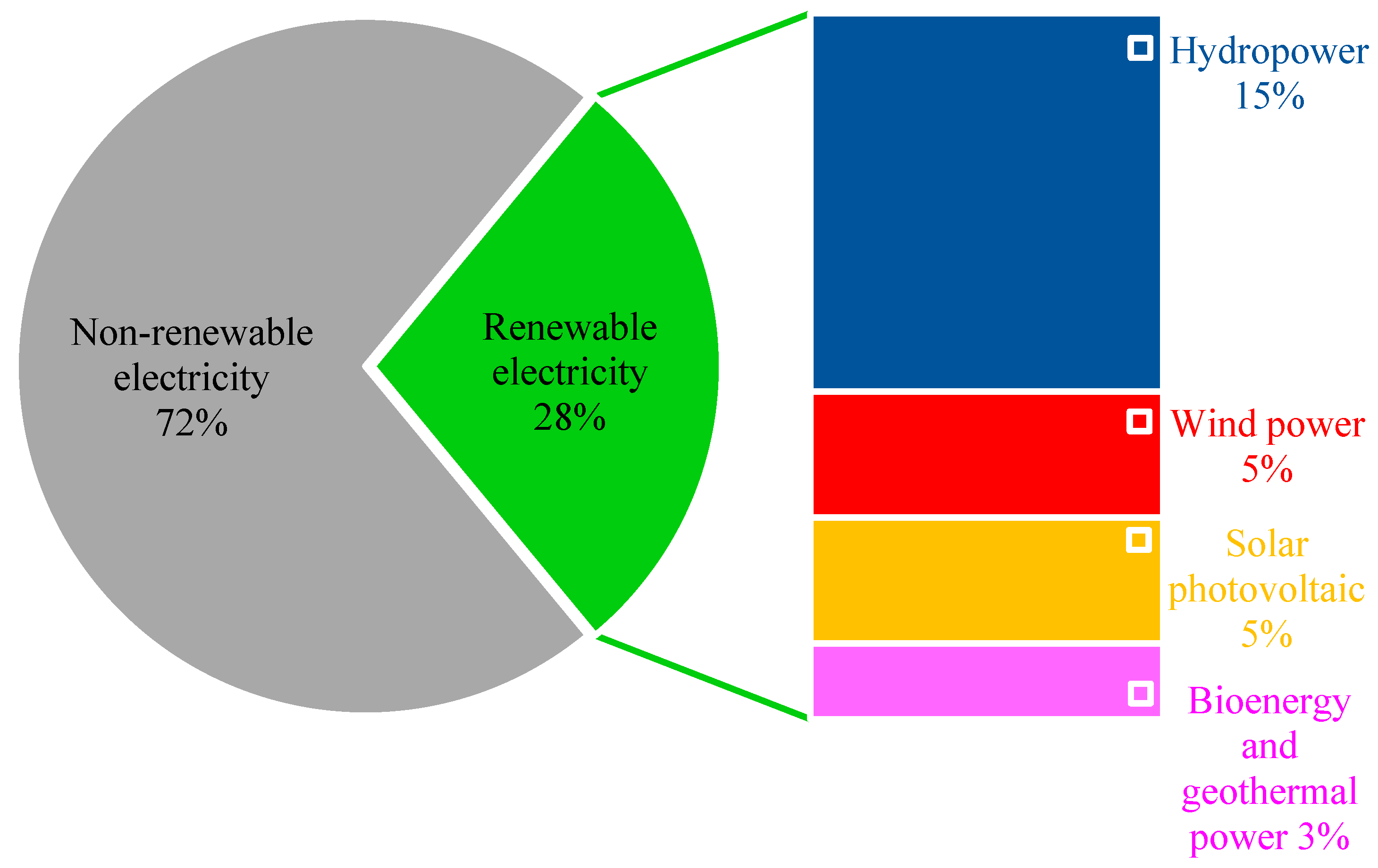
1. Introduction
- EEMD realizes the adaptive processing of nonlinear and non-stationary signals, and its application mitigates mode mixing and the effects of noise interference;
- The complexity measure of PE enhances the robustness against variations in the operating conditions and signal noise;
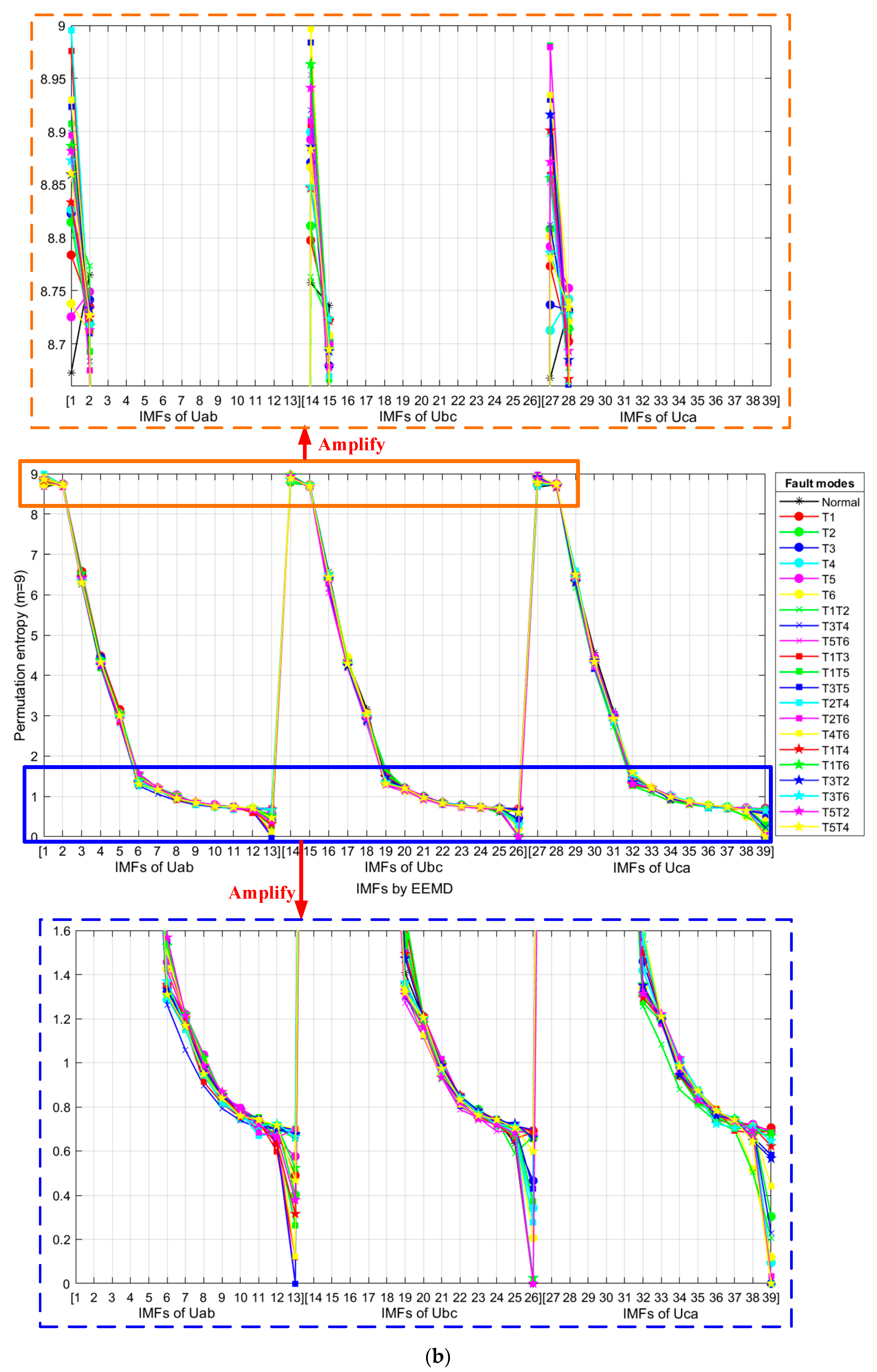
- IMF-PE highlights the signal local characteristics;
- The effects of the embedding dimension on the fault diagnosis results are studied, and the optimal value is selected;
- The scheme has high reliability and robustness and low time consumption. It also has a stable diagnostic performance.
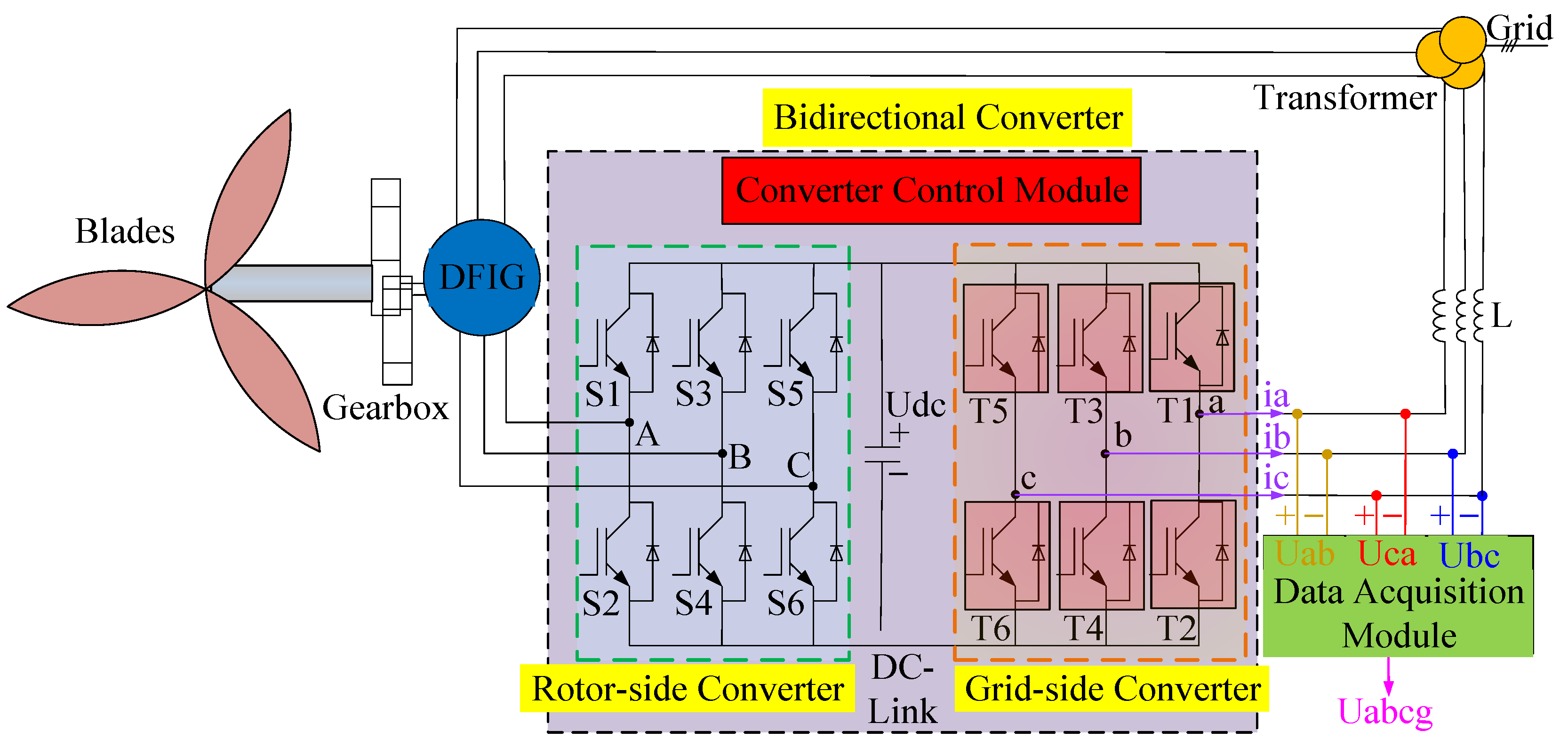
2. Fault Analysis and Diagnostic Requirements for Wind Power Converter
2.1. Fault Analysis
2.2. Diagnostic Requirements
3. Fault Diagnosis Method
3.1. The Proposed Fault Diagnosis Method
- Acquiring three-phase line-to-line voltages Uabcg (Uab, Ubc, Uca) from simulation under both healthy and faulty operating condition, then using them as fault signals to train and test the proposed fault diagnosis method;
- Decomposing each fault signal into a group of IMFs using EEMD;
- Obtain the minimum number of all IMFs of all fault signals and noted as ;
- Calculating the PE of each IMF as a fault feature to reflect the complexity of the signal. The IMF-PE feature is expressed as:
- Diagnosing the faults using SVM. The fault features are marked as fault labels and further randomly divided into training samples and testing samples, and the ratio of training samples to testing samples is set as 3:2.
3.2. Signal Decomposition Using EEMD
3.3. Feature Extraction Using PE
- Step 1.
- Reconstruct the phase space of the signal, and each subsequence is represented as , then the results can be obtained:where, is the embedding dimension, is the time delay.
- Step 2.
- Rearrange each in ascending order:where is the location index of the elements in after reordering. If two values are equal, they are sorted according to the value of . In this way, each is mapped to a symbol sequence:which is one of the permutations, and , .
- Step 3.
- The probability distribution of all the symbol sequences is expressed as , and is defined as:where is the occurrence times of the k-th symbol sequence.
- Step 4.
- PE is defined as:when , there is no repetition in the symbol sequence, the signal complexity is the highest and PE obtains the maximum, which is .
4. Simulation Results and Discussion
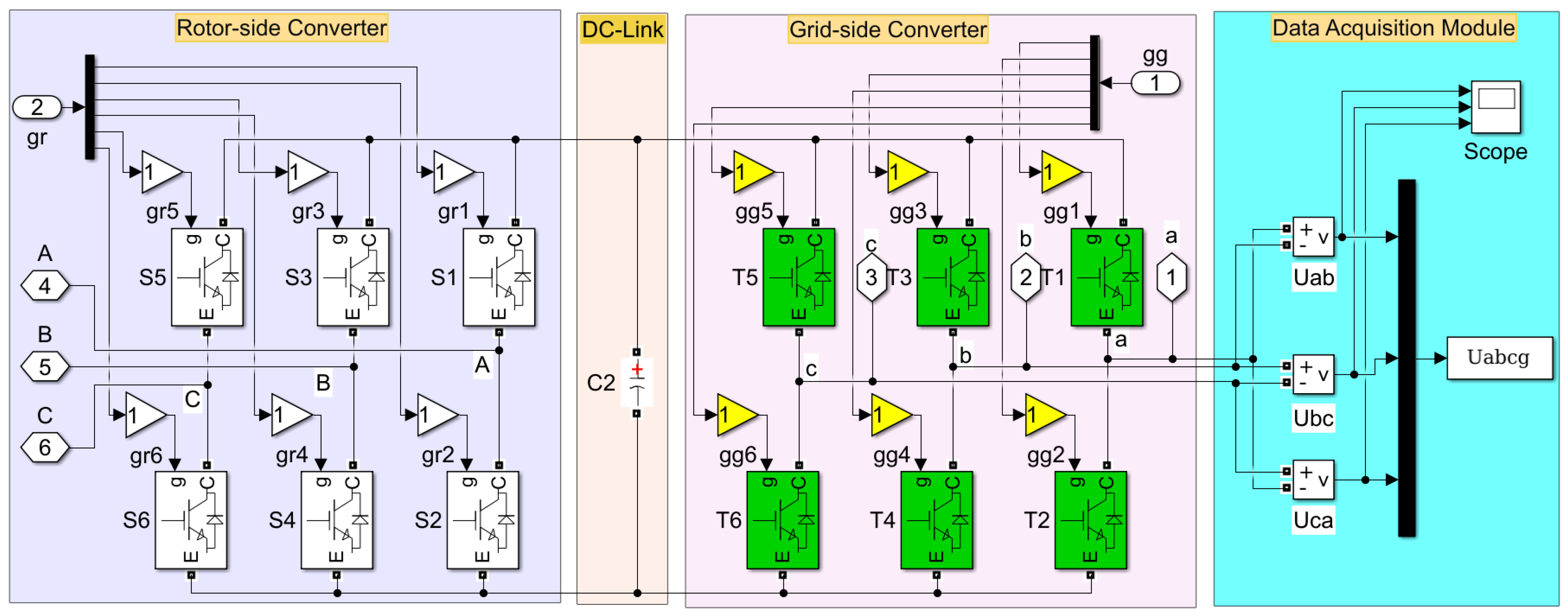
4.1. Simulation Platform
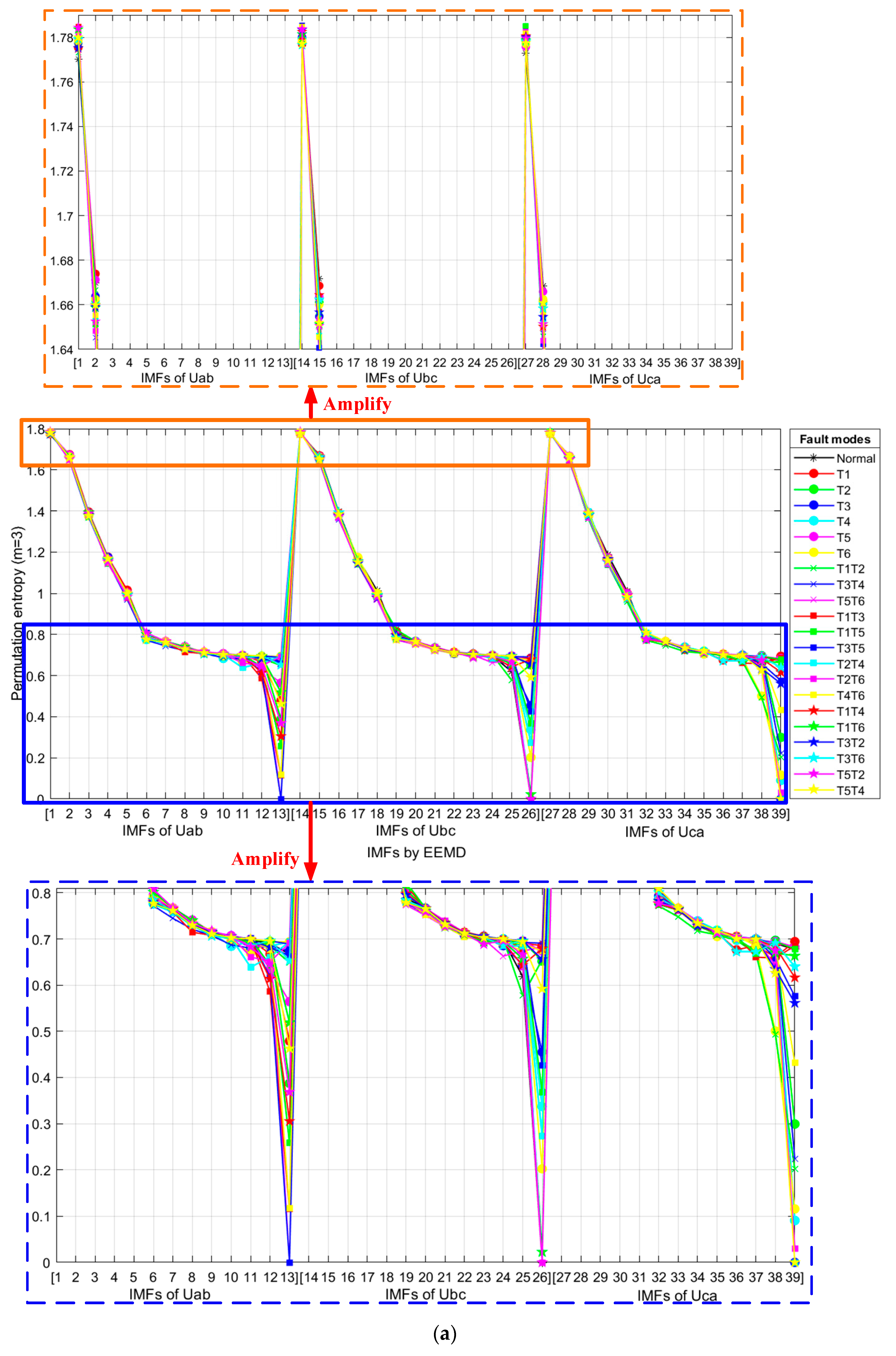
4.2. Results of EEMD-IMF-PE Feature
4.3. Results of Classification
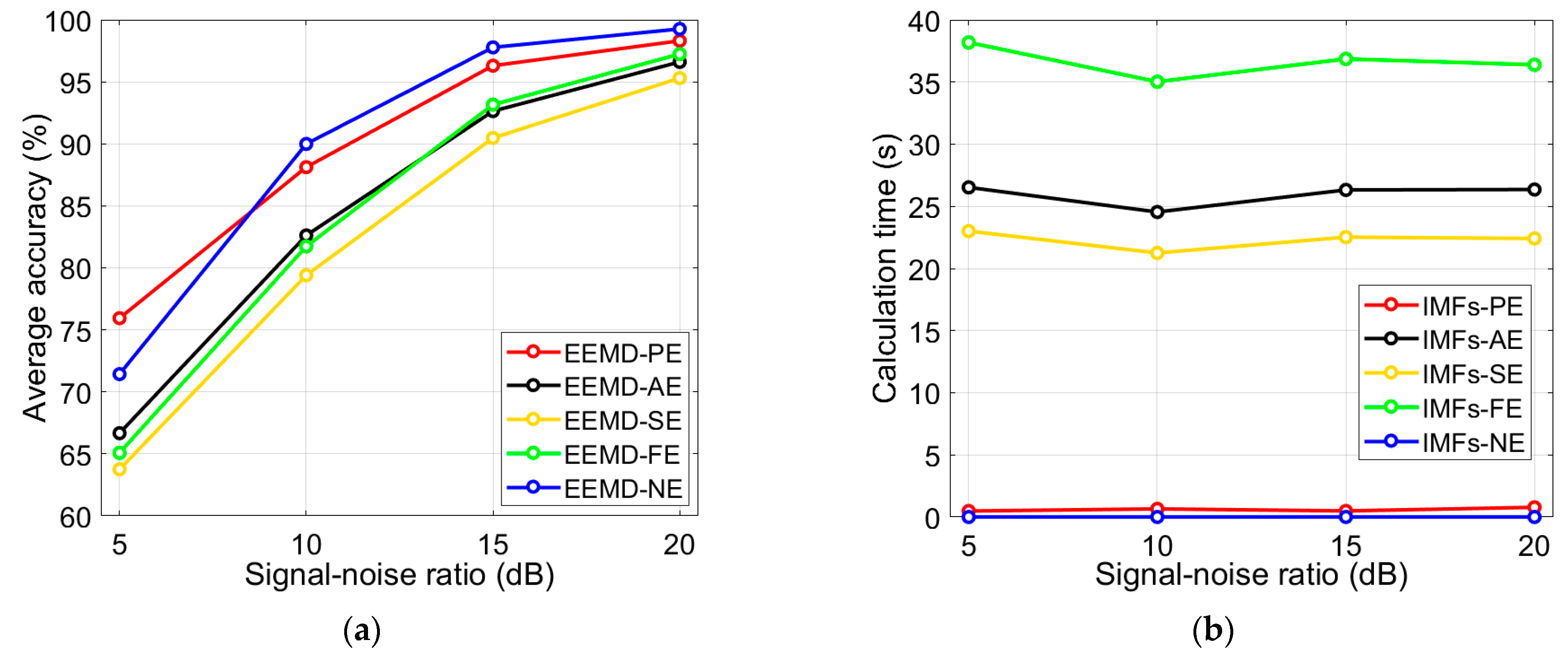
4.4. Analysis of Robustness
4.5. Comparison of Different Methods
4.6. Comparison with Previous Schemes
4.7. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Papadopoulos, P.; Coit, D.W.; Ezzat, A.A. Seizing Opportunity: Maintenance Optimization in Offshore Wind Farms Considering Accessibility, Production, and Crew Dispatch. IEEE Trans. Sustain. Energy 2022, 13, 111–121. [Google Scholar] [CrossRef]
- Javidsharifi, M.; Pourroshanfekr, H.; Kerekes, T.; Sera, D.; Guerrero, J. Stochastic Optimal Strategy for Power Management in Interconnected Multi-Microgrid Systems. Electronics 2022, 11, 1424. [Google Scholar] [CrossRef]
- Yang, L.; Li, G.; Zhang, Z.; Ma, X.; Zhao, Y. Operations & Maintenance Optimization of Wind Turbines Integrating Wind and Aging Information. IEEE Trans. Sustain. Energy 2021, 12, 211–221. [Google Scholar]
- REN21. Renewables 2022 Global Status Report. Available online: https://www.ren21.net/wp-content/uploads/2019/05/GSR2022_Full_Report.pdf (accessed on 23 March 2023).
- Saidi, L.; Benbouzid, M. Prognostics and Health Management of Renewable Energy Systems: State of the Art Review, Challenges, and Trends. Electronics 2021, 10, 2732. [Google Scholar] [CrossRef]
- Guo, Y.; Sheng, S.; Phillips, C.; Keller, J.; Veers, P.; Williams, L. A methodology for reliability assessment and prognosis of bearing axial cracking in wind turbine gearboxes. Renew. Sustain. Energy Rev. 2020, 127, 109888. [Google Scholar] [CrossRef]
- Li, S.; Cao, B.; Cui, Y.; Kang, Y.; Gao, S.; Li, H.; Dong, H. Terahertz-Based Insulation Delamination Defect Inspection of Vehicle Cable Terminals. IEEE Trans. Transp. Electrif. 2023, 9, 1765–1774. [Google Scholar] [CrossRef]
- Li, S.; Cao, B.; Kang, Y.; Cui, Y.; Dong, H. Nonintrusive Inspection of Moisture Damp in Composited Insulation Structure Based on Terahertz Technology. IEEE Trans. Instrum. Meas. 2021, 70, 10. [Google Scholar] [CrossRef]
- Liang, J.; Zhang, K.; Durra, A.A.; Muyeen, S.M.; Zhou, D. A state-of-the-art review on wind power converter fault diagnosis. Energy Rep. 2022, 8, 5341–5369. [Google Scholar] [CrossRef]
- Johnston, B.; Foley, A.; Doran, J.; Littler, T. Levelised cost of energy, A challenge for offshore wind. Renew. Energy 2020, 160, 876–885. [Google Scholar] [CrossRef]
- Liang, J.; Zhang, K.; Durra, A.A.; Zhou, D. A novel fault diagnostic method in power converters for wind power generation system. Appl. Energy 2020, 266, 114851. [Google Scholar] [CrossRef]
- Liang, J.; Zhang, K. A New Hybrid Fault Diagnosis Method for Wind Energy Converters. Electronics 2023, 12, 1263. [Google Scholar] [CrossRef]
- Mahdhi, H.B.; Azza, H.B.; Jemli, M. Experimental investigation of an open-switch fault diagnosis approach in the IGBT-based power converter connected to permanent magnet synchronous generator-DC system. Int. Trans. Electr. Energ. Syst. 2020, 30, 12436. [Google Scholar]
- Li, S.; Cao, B.; Li, J.; Cui, Y.; Kang, Y.; Wu, G. Review of condition monitoring and defect inspection methods for composited cable terminals. High Volt. 2023. early access. [Google Scholar] [CrossRef]
- Mtepele, K.O.; Campos-Delgado, D.U.; Valdez-Fernández, A.A.; Pecina-Sánchez, J.A. Model-based strategy for open-circuit faults diagnosis in n-level CHB multilevel converters. IET Power Electron. 2019, 12, 648–655. [Google Scholar] [CrossRef]
- Liu, H.; Ma, K.; Loh, P.C.; Blaabjerg, F. Online fault identification based on an adaptive observer for modular multilevel converters applied to wind power generation systems. Energies 2015, 8, 7140–7160. [Google Scholar] [CrossRef]
- Naseri, F.; Schaltz, E.; Lu, K.; Farjah, E. Real-time open-switch fault diagnosis in automotive permanent magnet synchronous motor drives based on kalman filter. IET Power Electron. 2020, 13, 2450–2460. [Google Scholar] [CrossRef]
- Al-Gahtani, S.F.; Azazi, H.Z.; Nelms, R.M.; Elbarbary, Z.M. Detection of negative sequence components in diagnosing and tolerating open-gate fault for a voltage-source inverter in an induction motor drive. IET Power Electron. 2020, 13, 4194–4203. [Google Scholar] [CrossRef]
- Qiu, Y.; Jiang, H.; Feng, Y.; Cao, M.; Zhao, Y.; Li, D. A new fault diagnosis algorithm for PMSG wind turbine power converters under variable wind speed conditions. Energies 2016, 9, 548. [Google Scholar] [CrossRef]
- Zhao, H.; Cheng, L. Open-circuit faults diagnosis in back-to-back converters of DF wind turbine. IET Renew. Power Gener. 2017, 11, 417–424. [Google Scholar] [CrossRef]
- Wang, T.; Xu, H.; Han, J.; Elbouchikhi, E.; Benbouzid, M.E. Cascaded H-bridge multilevel inverter system fault diagnosis using a PCA and multiclass relevance vector machine approach. IEEE Trans. Power Electron. 2015, 30, 7006–7018. [Google Scholar] [CrossRef]
- Wang, T.; Qi, J.; Xu, H.; Wang, Y.; Liu, L.; Gao, D. Fault diagnosis method based on FFT-RPCA-SVM for cascaded-multilevel inverter. ISA Trans. 2016, 60, 156–163. [Google Scholar] [CrossRef]
- Cai, B.; Zhao, Y.; Liu, H.; Xie, M. A data-driven fault diagnosis methodology in three-phase inverters for PMSM drive systems. IEEE Trans. Power Electron. 2017, 32, 5590–5600. [Google Scholar] [CrossRef]
- Dhumale, R.B.; Lokhande, S.D. Neural network fault diagnosis of voltage source inverter under variable load conditions at different frequencies. Measurement 2016, 91, 565–575. [Google Scholar] [CrossRef]
- Wu, F.; Hao, Y.; Liu, J.Z.Y. Current similarity based open-circuit fault diagnosis for induction motor drives with discrete wavelet transform. Microelectron. Reliab. 2017, 75, 309–316. [Google Scholar] [CrossRef]
- Gomathy, V.; Selvaperumal, S. Fault detection and classification with optimization techniques for a three-phase single-inverter circuit. J. Power Electron. 2016, 16, 1097–1109. [Google Scholar] [CrossRef]
- Zhang, J.; Sun, H.; Sun, Z.; Dong, W.; Dong, Y. Fault Diagnosis of Wind Turbine Power Converter Considering Wavelet Transform, Feature Analysis, Judgment and BP Neural Network. IEEE Access 2019, 7, 179799–179809. [Google Scholar] [CrossRef]
- Zhang, X. Fault Diagnosis for PWM Inverter Based on LMD. Int. Conf. Mech. Control Comput. Eng. 2020, 27, 167–171. [Google Scholar]
- Yan, H.; Xu, Y.; Cai, F.; Zhang, H.; Zhao, W.; Gerada, C. PWM-VSI fault diagnosis for a PMSM drive based on the fuzzy logic approach. IEEE Trans. Power Electron. 2019, 34, 759–768. [Google Scholar] [CrossRef]
- Kou, L.; Liu, C.; Cai, G.; Zhou, J.; Yuan, Q.; Pang, S. Fault diagnosis for open-circuit faults in NPC inverter based on knowledge-driven and data-driven approaches. IET Power Electron. 2020, 13, 1236–1245. [Google Scholar] [CrossRef]
- Gmati, B.; Jlassi, I.; Khil, S.; Cardoso, A. Open-switch fault diagnosis in voltage source inverters of PMSM drives using predictive current errors and fuzzy logic approach. IET Power Electron. 2021, 14, 1059–1072. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, T.; Tang, T.; Wang, Y. A principal components rearrangement method for feature representation and its application to the fault diagnosis of CHMI. Energies 2017, 10, 1273. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.-C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R Soc. Lond. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Rilling, G.; Flandrin, P.; Goncalves, P. On empirical mode decomposition and its algorithms. IEEE-EURASIP 2003, 3, 8–11. [Google Scholar]
- Wu, Z.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Bandt, C.; Pompe, B. Permutation entropy: A natural complexity measure for time series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef] [PubMed]
- Torres, M.E.; Colominas, M.A.; Schlotthauer, G.; Flandrin, P. A complete ensemble empirical mode decomposition with adaptive noise. In Proceedings of the 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Prague, Czech Republic, 22–27 May 2011; pp. 4144–4147. [Google Scholar] [CrossRef]
- Colominas, M.A.; Schlotthauer, G.; Torres, M.E. Improved complete ensemble EMD: A suitable tool for biomedical signal processing. Biomed. Signal Process. Control 2014, 14, 19–29. [Google Scholar] [CrossRef]




| Steps | EMD Decomposition |
|---|---|
| Step 1 | Initialization: , |
| Step 2 | Calculate the th oscillation mode |
| Step 2 (a) | Set , |
| Step 2 (b) | Calculate the local extremum of |
| Step 2 (c) | Use cubic spline to interpolate the local extremum to obtain the lower envelope and upper envelope |
| Step 2 (d) | Average the lower and upper envelopes: |
| Step 2 (e) | Calculate the detailed component: . If satisfies IMF conditions, then set , that is ; else go to step 2 (b) and |
| Step 3 | Obtain residue: . If has more than one extreme, then go to Step 2 and ; else the procedure is ended and is residue |
| Steps | EEMD Decomposition |
|---|---|
| Step 1 | Add white noise to the original signal to obtain a new signal: , where is the number of ensemble realizations, is the th independent white noise |
| Step 2 | by EMD and obtain a group of IMFs: , where is the number of IMFs, is the th IMF of the th realization |
| Step 3 | Average all realizations to obtain final , where and |
| Quantity | Value | Quantity | Value |
|---|---|---|---|
| Rated voltage | 575 V | Stator leak inductance | 0.18 pu |
| Rated power | 1.5 MW | Rotor leak inductance | 0.16 pu |
| Pole pairs number | 3 | Stator resistance | 0.023 pu |
| Magnetizing inductance | 2.9 pu | Rotor resistance | 0.016 pu |
| Fault Mode | Accuracy (%) | ||||||
|---|---|---|---|---|---|---|---|
| m = 3 | m = 4 | m = 5 | m = 6 | m = 7 | m = 8 | m = 9 | |
| Normal | 96.8750 | 100 | 100 | 100 | 100 | 100 | 100 |
| T1 | 90.6250 | 90.6250 | 93.7500 | 100 | 93.7500 | 96.8750 | 96.8750 |
| T2 | 100 | 100 | 100 | 96.8750 | 100 | 100 | 100 |
| T3 | 90.6250 | 90.6250 | 100 | 93.7500 | 96.8750 | 96.8750 | 100 |
| T4 | 81.2500 | 84.3750 | 90.6250 | 93.7500 | 93.7500 | 96.8750 | 96.8750 |
| T5 | 93.7500 | 93.7500 | 100 | 100 | 100 | 100 | 100 |
| T6 | 100 | 90.6250 | 100 | 100 | 96.8750 | 100 | 100 |
| T1T2 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| T3T4 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| T5T6 | 96.8750 | 96.8750 | 100 | 100 | 100 | 100 | 100 |
| T1T3 | 87.5000 | 90.6250 | 87.5000 | 96.8750 | 100 | 100 | 93.7500 |
| T1T5 | 96.8750 | 84.3750 | 96.8750 | 100 | 100 | 96.8750 | 100 |
| T3T5 | 93.7500 | 100 | 90.6250 | 100 | 96.8750 | 96.8750 | 96.8750 |
| T2T4 | 93.7500 | 96.8750 | 100 | 96.8750 | 100 | 96.8750 | 100 |
| T2T6 | 96.8750 | 96.8750 | 100 | 96.8750 | 96.8750 | 96.8750 | 96.8750 |
| T4T6 | 96.8750 | 100 | 100 | 100 | 100 | 100 | 100 |
| T1T4 | 100 | 100 | 100 | 96.8750 | 100 | 96.8750 | 100 |
| T1T6 | 93.7500 | 100 | 100 | 96.8750 | 96.8750 | 100 | 100 |
| T3T2 | 71.8750 | 90.6250 | 93.7500 | 100 | 96.8750 | 93.7500 | 96.8750 |
| T3T6 | 100 | 100 | 100 | 96.8750 | 100 | 100 | 100 |
| T5T2 | 93.7500 | 100 | 100 | 96.8750 | 96.8750 | 100 | 96.8750 |
| T5T4 | 93.7500 | 96.8750 | 100 | 100 | 100 | 100 | 100 |
| Average | 94.0341 | 95.5966 | 97.8693 | 98.2955 | 98.4375 | 98.5795 | 98.8636 |
| Standard deviation | 6.8131 | 5.2521 | 3.9039 | 2.0968 | 2.1019 | 1.8619 | 1.8159 |
| Noise Conditions | Stability | Evaluation Indicators (%) | ||||||
|---|---|---|---|---|---|---|---|---|
| Accuracy | Precision | Recall | F1-Score | Specificity | FAR | MAR | ||
| 20 dB | Minimum | 96.8750 | 96.9758 | 96.8750 | 96.8654 | 99.8512 | 0.0541 | 1.1364 |
| Maximum | 98.8636 | 98.8965 | 98.8636 | 98.8629 | 99.9459 | 0.1488 | 3.1250 | |
| Average | 97.8220 | 97.9108 | 97.8220 | 97.8186 | 99.8963 | 0.1037 | 2.1780 | |
| Standard deviation | 0.5735 | 0.5387 | 0.5735 | 0.5756 | 0.0273 | 0.0273 | 0.5735 | |
| 15 dB | Minimum | 94.3182 | 94.5155 | 94.3182 | 94.3085 | 99.7294 | 0.0947 | 1.9886 |
| Maximum | 98.0114 | 98.0806 | 98.0114 | 98.0086 | 99.9053 | 0.2706 | 5.6818 | |
| Average | 96.3021 | 96.4387 | 96.3021 | 96.2939 | 99.8239 | 0.1761 | 3.6979 | |
| Standard deviation | 0.8616 | 0.8381 | 0.8616 | 0.8660 | 0.0410 | 0.0410 | 0.8616 | |
| 10 dB | Minimum | 85.7955 | 86.2573 | 85.7955 | 85.8105 | 99.3236 | 0.4532 | 9.5170 |
| Maximum | 90.4830 | 90.7074 | 90.4830 | 90.4658 | 99.5468 | 0.6764 | 14.2045 | |
| Average | 88.1203 | 88.5073 | 88.1203 | 88.0924 | 99.4343 | 0.5657 | 11.8797 | |
| Standard deviation | 1.0354 | 1.0319 | 1.0354 | 1.0320 | 0.0493 | 0.0493 | 1.0354 | |
| 5 dB | Minimum | 72.3011 | 72.6030 | 72.3011 | 72.2741 | 98.6810 | 1.0011 | 21.0227 |
| Maximum | 78.9773 | 79.5929 | 78.9773 | 78.9605 | 98.9989 | 1.3190 | 27.6989 | |
| Average | 75.9375 | 76.4467 | 75.9375 | 75.8553 | 98.8542 | 1.1458 | 24.0625 | |
| Standard deviation | 1.6764 | 1.7411 | 1.6764 | 1.6651 | 0.0798 | 0.0798 | 1.6764 | |
| Scheme | Fault Types | Training to Testing Ratio | Number of Runs | Noise Conditions | Average Accuracy (%) | Standard Deviation of Accuracy (%) |
|---|---|---|---|---|---|---|
| EEMD-PE | 22 OC faults | 3:2 | 30 | 20 dB | 97.8220 | 0.5735 |
| 15 dB | 96.3021 | 0.8616 | ||||
| 10 dB | 88.1203 | 1.0354 | ||||
| 5 dB | 75.9375 | 1.6764 | ||||
| MEMD-FE [12] | 22 OC faults | 3:2 | 30 | 30 dB | 95.5758 | 1.9344 |
| 20 dB | 92.1477 | 1.3312 | ||||
| 10 dB | 84.2338 | 1.7167 | ||||
| EEMD-NE [11] | 22 OC faults | 3:2 | 30 | 20 dB | 99.2756 | - |
| 15 dB | 97.8598 | - | ||||
| 10 dB | 90.0758 | - | ||||
| 5 dB | 71.8040 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, J.; Zhang, K. A Robust Fault Diagnosis Scheme for Converter in Wind Turbine Systems. Electronics 2023, 12, 1597. https://doi.org/10.3390/electronics12071597
Liang J, Zhang K. A Robust Fault Diagnosis Scheme for Converter in Wind Turbine Systems. Electronics. 2023; 12(7):1597. https://doi.org/10.3390/electronics12071597
Chicago/Turabian StyleLiang, Jinping, and Ke Zhang. 2023. "A Robust Fault Diagnosis Scheme for Converter in Wind Turbine Systems" Electronics 12, no. 7: 1597. https://doi.org/10.3390/electronics12071597
APA StyleLiang, J., & Zhang, K. (2023). A Robust Fault Diagnosis Scheme for Converter in Wind Turbine Systems. Electronics, 12(7), 1597. https://doi.org/10.3390/electronics12071597





