Moving Target Defense for Detecting Coordinated Cyber-Physical Attacks on Power Grids via a Modified Sensor Measurement Expression
Abstract
:1. Introduction
- We propose a modified sensor measurement expression that is applied to identify CCPAs after MTD activation. In the expression, a supplement state factor, notated as , is added. We provide an in-depth discussion of the construction characteristics of the supplemental state factor.
2. System Model
2.1. Preliminary System Model
2.2. State Estimation and Bad Data Detection
3. Coordinated Cyber-Physical Attacks
3.1. Undetectable FDI Attacks
3.2. Coordinated Cyber-Physical Attacks
3.3. Knowledge Required to Launch a CCPA
4. Moving-Target Defense for CCPAs
4.1. Preliminary MTD
4.2. MTD Perturbation Frequency and Practical Implementation
4.3. Defending against CCPAs
5. Modified Sensor Measurement Expression
5.1. Production Mechanism of CCPAs after MTD Activation
5.2. The Reason for Modifying Sensor Measurement Expression
5.3. Sensor Measurement Expression Modified
6. Simulation
6.1. The Correctness and Completeness of the Simulation Scenario
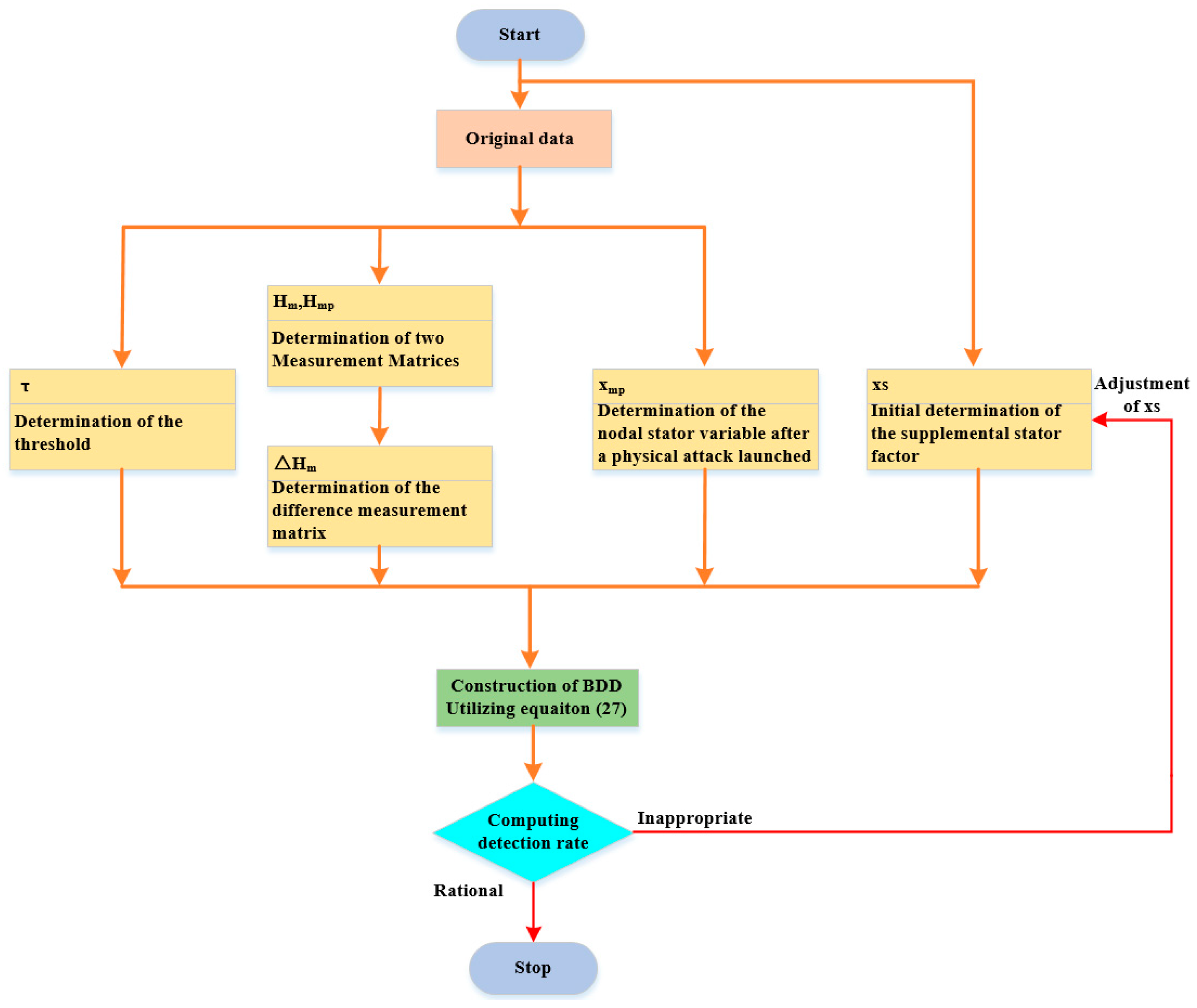
6.2. The Steps of the Proposed Method
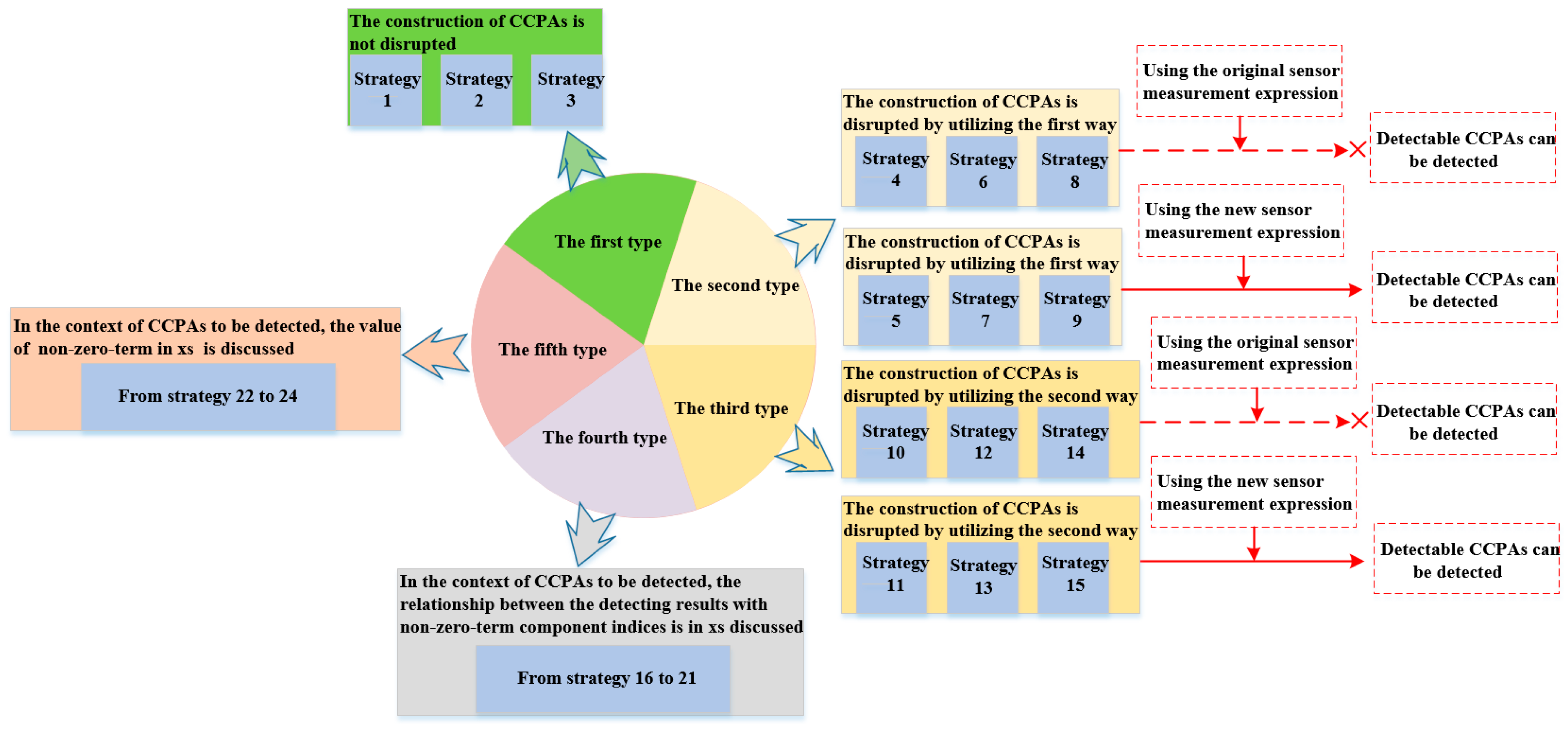
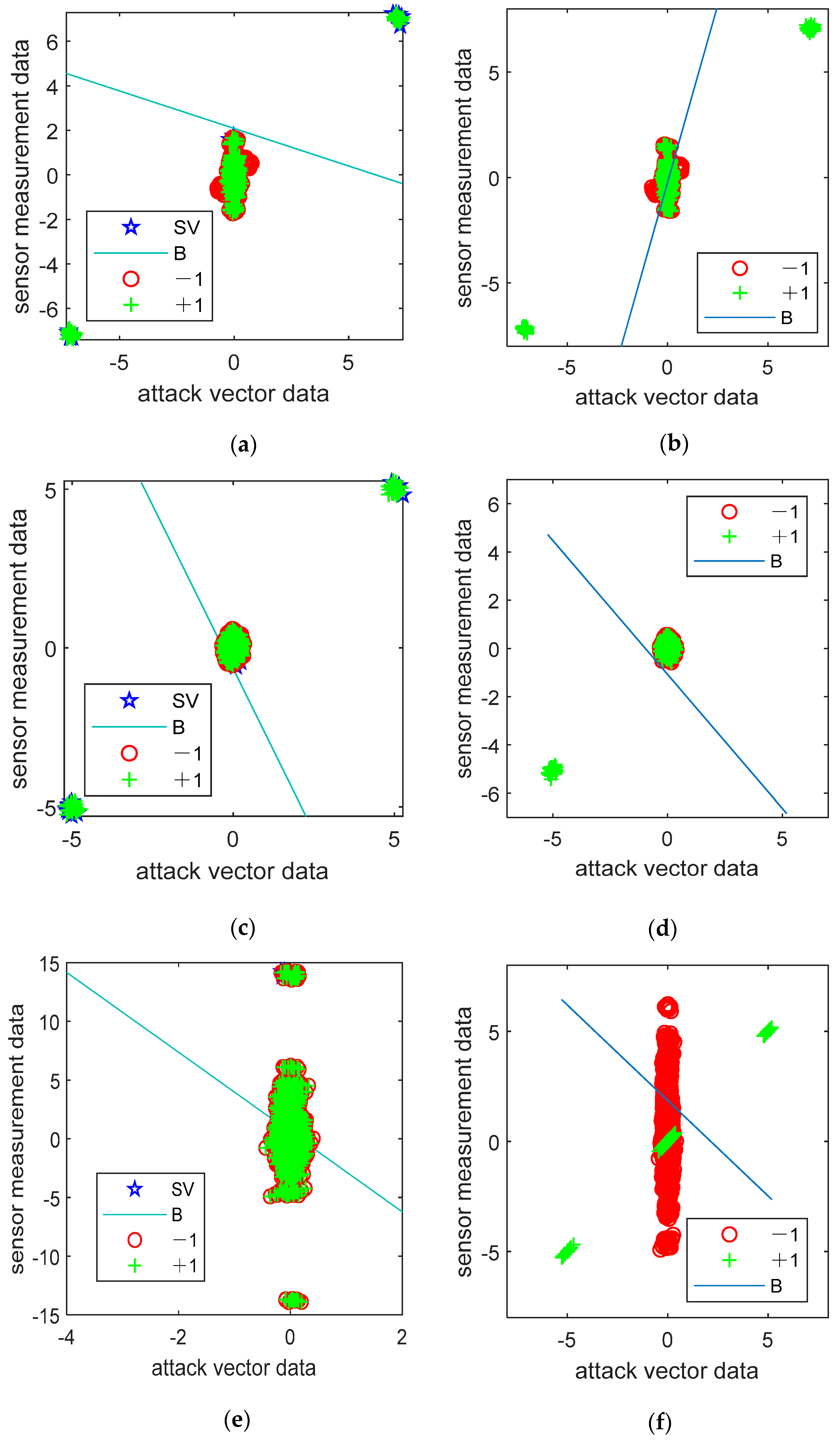
6.3. Undetectable CCPAs
6.4. Detectable CCPAs When the Susceptance of the Disconnected Branch Is Altered
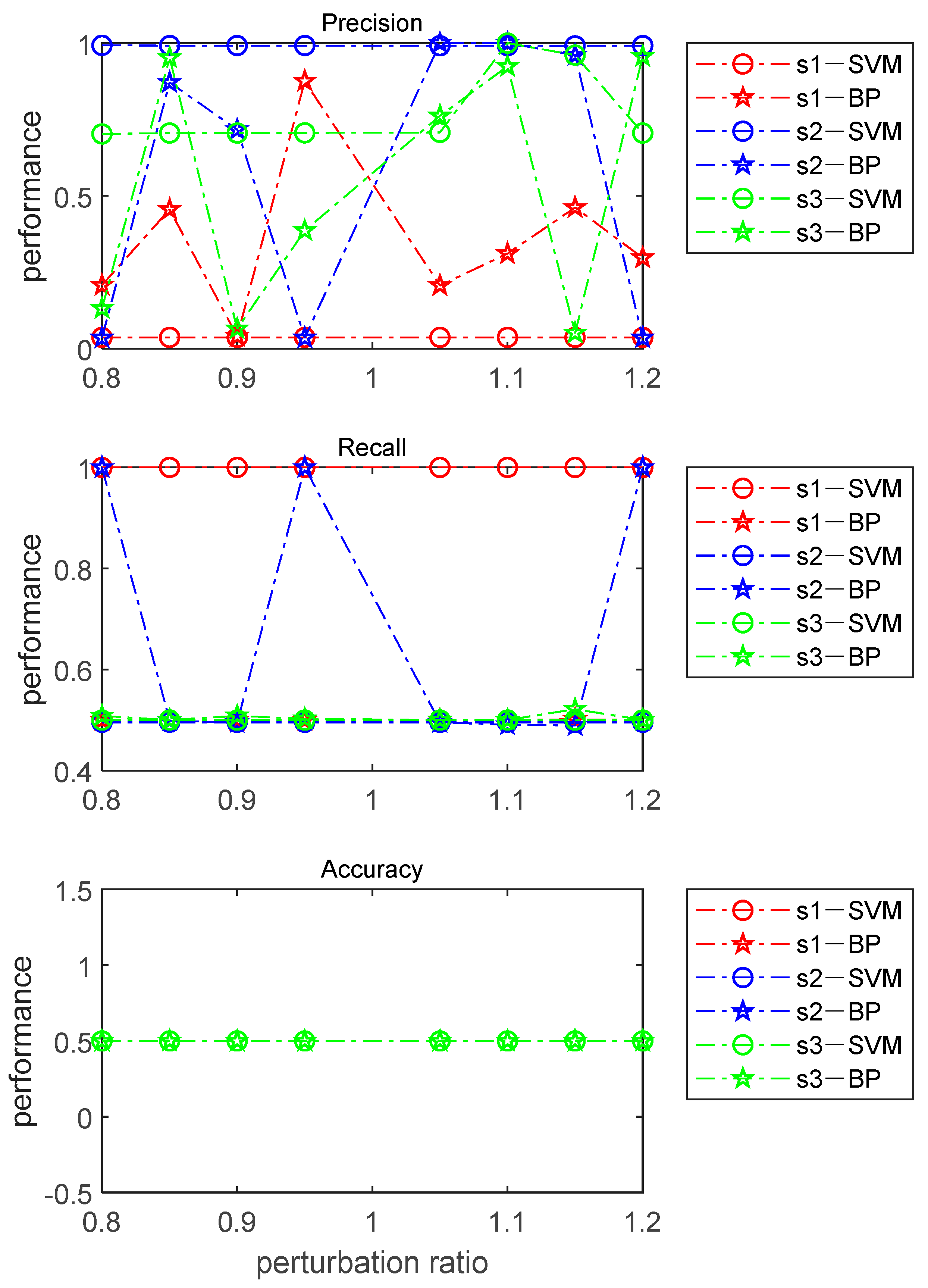
6.4.1. Computing the Detection Rate via the General Mathematical and Statistical Method
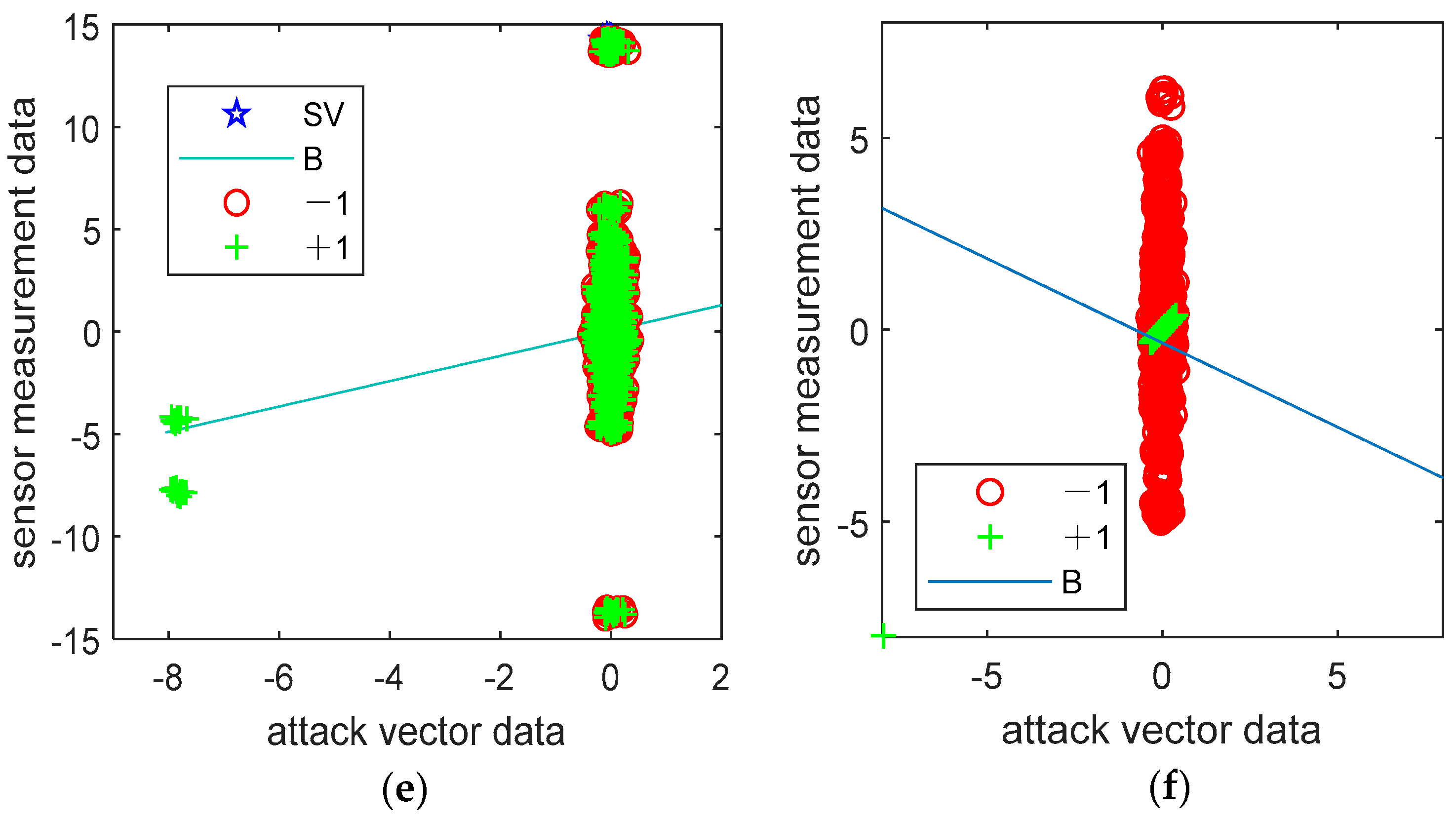
6.4.2. Computing Detection Rate via Machine Learning Methods
6.5. Detectable CCPAs When the Susceptances of at Least One Branch in Any of the Alternate Paths between the Two Endpoints of a Tripped Branch Changes before a Physical Attack
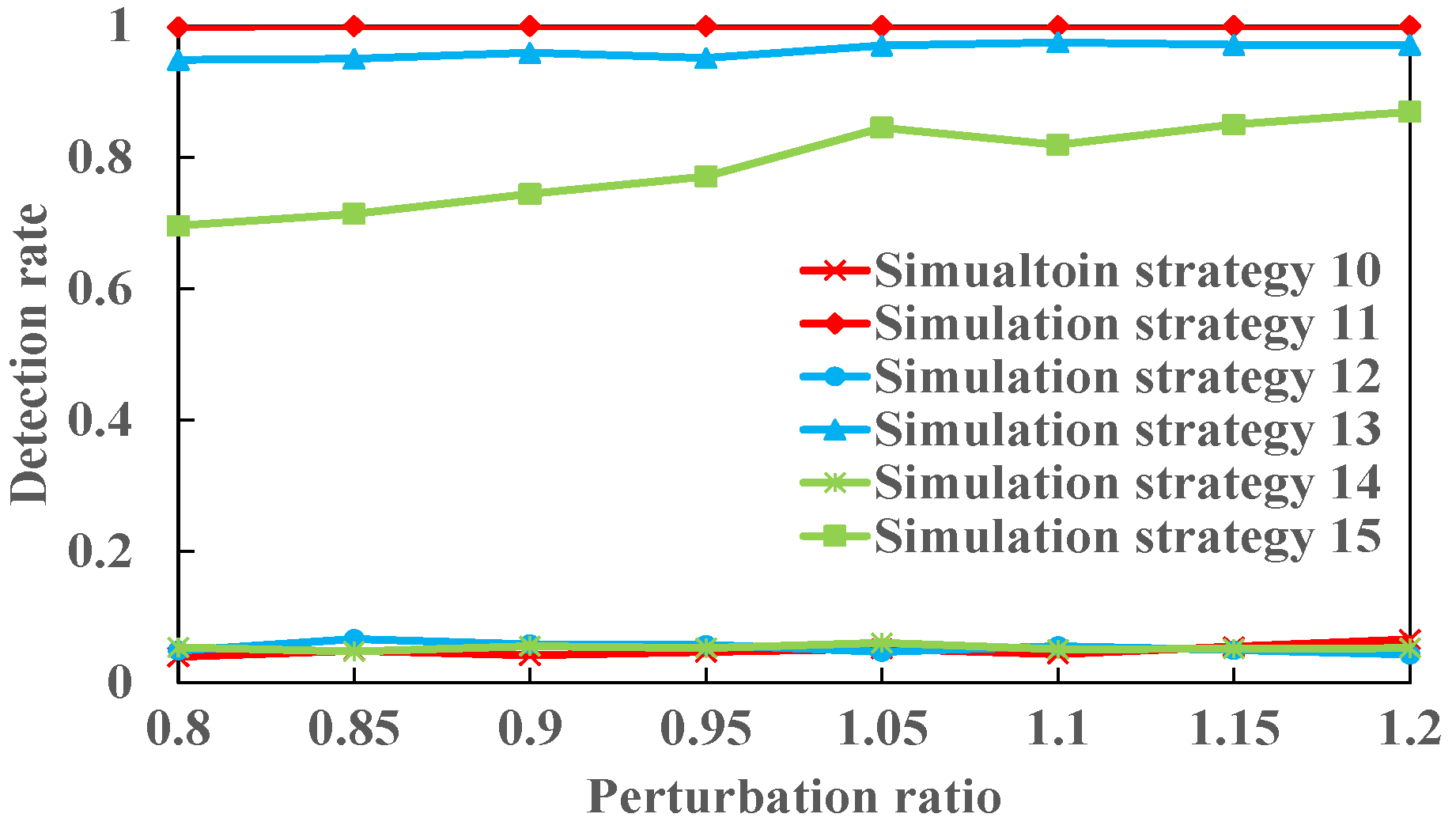
6.5.1. Computing the Detection Rate via the General Mathematical and Statistical Method
6.5.2. Computing the Detection Rate via the General Mathematical and Statistical Method
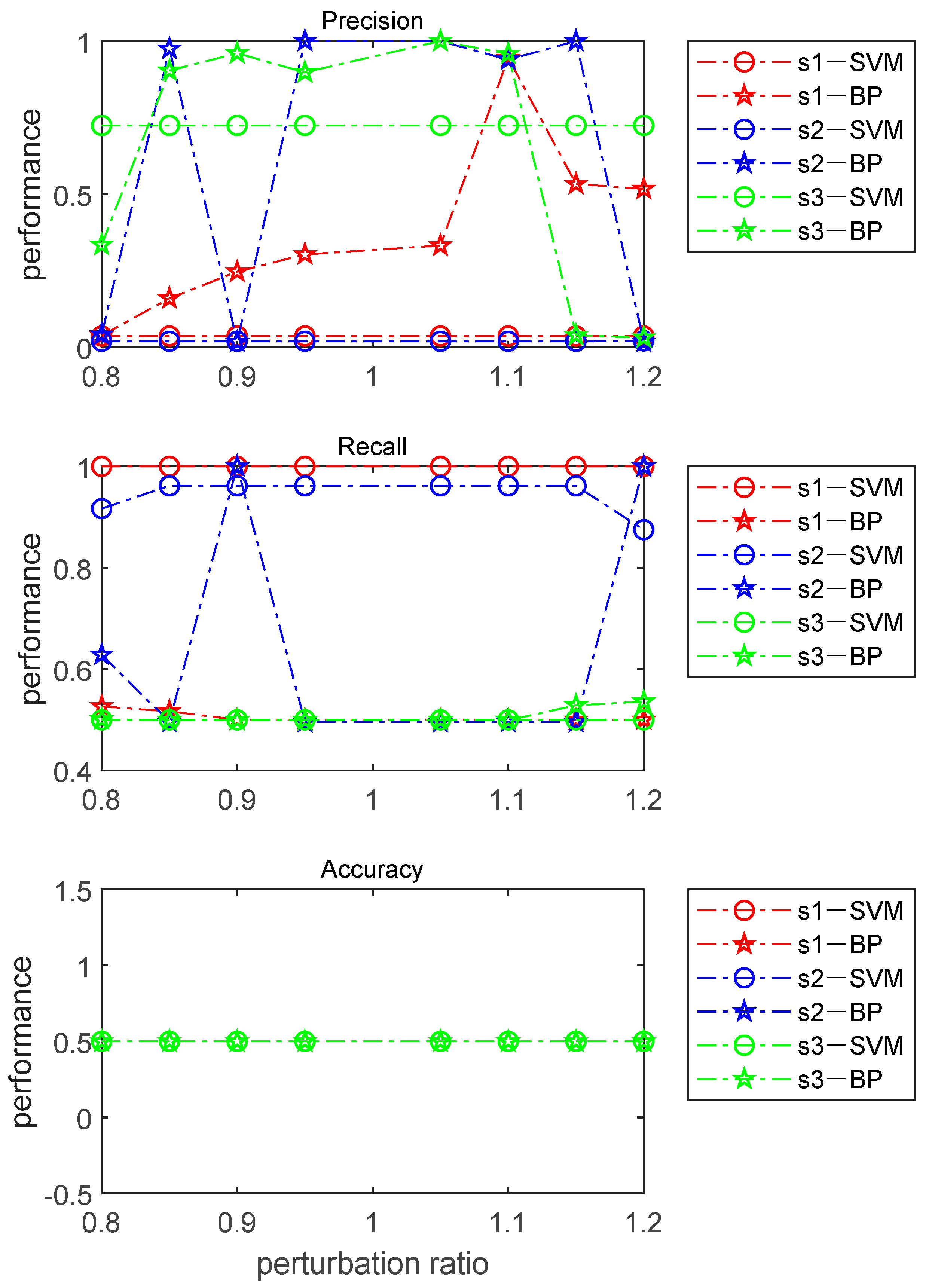
6.6. Component Index of the Unique Non-Zero Entry in the Supplemental Stator Factor
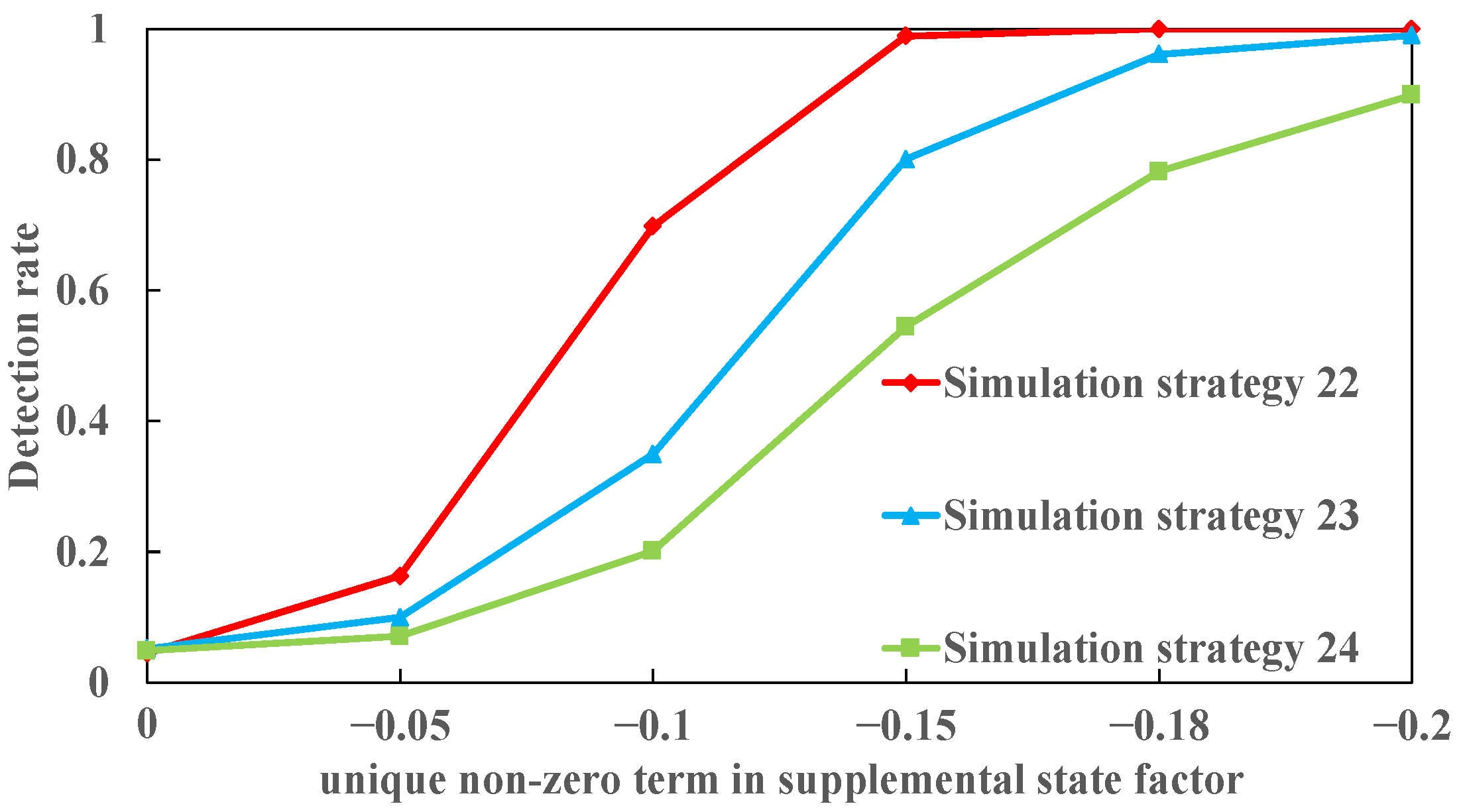
6.7. Value of the Unique Non-Zero Entry in the Supplemental Stator Factor
6.8. Analysis of Results
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Deng, R.; Zhuang, P.; Liang, H. CCPA: Coordinated cyber-physical attacks and countermeasures in smart grid. IEEE Trans. Smart Grid 2017, 8, 2420–2430. [Google Scholar] [CrossRef]
- Lakshminarayana, S.; Belmega, E.V.; Poor, H.V. Moving-target defense against cyber-physical attacks in power grids via game theory. IEEE Trans. Smart Grid 2021, 12, 5244–5257. [Google Scholar] [CrossRef]
- Zhou, M.; Liu, C.; Jahromi, A.A.; Kundur, D.; Wu, J.; Long, C. Revealing vulnerability of N-1 secure power systems to coordinated cyber-physical attacks. IEEE Trans. Power Syst. 2022, 38, 1044–1057. [Google Scholar] [CrossRef]
- Li, Z.; Shahidehpour, M.; Alabdulwahab, A.; Abusorrah, A. Bilevel model for analyzing coordinated cyber-physical attacks on power systems. IEEE Trans. Smart Grid 2015, 7, 2260–2272. [Google Scholar] [CrossRef]
- Shepard, D.P.; Humphreys, T.E.; Fansler, A.A. Evaluation of the vulnerability of phasor measurement units to GPS spoofing attacks. Int. J. Crit. Infrastruct. Prot. 2012, 5, 146–153. [Google Scholar] [CrossRef]
- He, Y.; Mendis, G.J.; Wei, J. Real-time detection of false data injection attacks in smart grid: A deep learning-based intelligent mechanism. IEEE Trans. Smart Grid 2017, 8, 2505–2516. [Google Scholar] [CrossRef]
- Habibi, M.R.; Baghaee, H.R.; Dragičević, T.; Blaabjerg, F. Detection of false data injection cyber-attacks in DC microgrids based on recurrent neural networks. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 5294–5310. [Google Scholar] [CrossRef]
- Habibi, M.R.; Baghaee, H.R.; Dragičević, T.; Blaabjerg, F. False data injection cyber-attacks mitigation in parallel DC/DC converters based on artificial neutral networks. IEEE Trans. Circuits Syst. Ⅱ Exp. Briefs 2021, 68, 717–721. [Google Scholar] [CrossRef]
- Sayghe, A.; Anubi, O.M.; Konstantinou, C. Adversarial examples on power systems state estimation. In Proceedings of the IEEE Power Energy Society Innovative Smart Grid Technologies Conference (ISGT), Washington, DC, USA, 17–20 February 2020; pp. 1–5. [Google Scholar]
- Li, B.; Lu, R.; Xiao, G.; Li, T.; Choo, K.K.R. Detection of false data injection attacks on smart girds: A resilience-enhanced scheme. IEEE Trans. Power Syst. 2022, 37, 2679–2692. [Google Scholar] [CrossRef]
- Xiahou, K.; Liu, Y.; Wu, Q.H. Decentralized detection and mitigation of multiple false data injection attacks in multiarea power systems. IEEE J. Emerg. Select. Top. Ind. Electron. 2022, 3, 101–112. [Google Scholar] [CrossRef]
- Divan, D.; Johal, H. Distributed FACTS—A new concept for realizing grid power flow control. IEEE Trans. Power Electron. 2007, 22, 2253–2260. [Google Scholar] [CrossRef]
- Morrow, K.L.; Heine, E.; Rogers, K.M.; Bobba, R.B.; Overbye, T.J. Topology perturbation for detecting malicious data injection. In Proceedings of the ICSS—2012 45th Hawaii International Conference on System Sciences, Maui, HI, USA, 4–7 February 2012; pp. 2104–2113. [Google Scholar] [CrossRef]
- Davis, K.R.; Morrow, K.L.; Bobba, R.; Heine, E. Power flow cyber attacks and perturbation-based defense. In Proceedings of the IEEE SmartGridComm, Taiwan, China, 5–8 November 2012; pp. 342–347. [Google Scholar] [CrossRef]
- Rahman, M.A.; Al-Shaer, E.; Bobba, R.B. Moving target defense for hardening the security of the power system state estimation. In Proceedings of the First ACM Workshop on Moving Target Defense, Scottsdale, AZ, USA, 3 November 2014; pp. 59–68. [Google Scholar] [CrossRef]
- Lakshminarayana, S.; Yau, D.K.Y. Cost-benefit analysis of moving-target defense in power grids. IEEE Trans. Power Syst. 2020, 36, 1152–1163. [Google Scholar] [CrossRef]
- Liu, C.; Wu, J.; Long, C.; Kundur, D. Reactance perturbation for detecting and identifying FDI attacks in power system state estimation. IEEE J. Sel. Top. Signal Process. 2018, 12, 763–776. [Google Scholar] [CrossRef]
- Tian, J.; Tan, R.; Guan, X.; Liu, T. Enhanced hidden moving target defense in smart grids. IEEE Trans. Smart Grid 2018, 10, 2208–2223. [Google Scholar] [CrossRef]
- Zhang, Z.; Deng, R.; Yau, D.K.Y.; Cheng, P.; Chen, J. Analysis of moving target defense against false data injection attacks on power grid. IEEE Trans. Inf. Forensics Secur. 2019, 15, 2320–2335. [Google Scholar] [CrossRef] [Green Version]
- Liu, B.; Wu, H. Optimal D-FACTS placement in moving target defense against false data injection attacks. IEEE Trans. Smart Grid 2020, 11, 4345–4357. [Google Scholar] [CrossRef]
- Zhang, Z.; Deng, R.; Cheng, P.; Chow, M.-Y. Strategic protection against FDI attacks with moving target defense in power grids. IEEE Trans. Control Netw. Syst. 2021, 9, 245–256. [Google Scholar] [CrossRef]
- Zhang, Z.; Tian, Y.; Deng, R.; Ma, J. A Double-benefit moving target defense against cyber–physical attacks in smart grid. IEEE Internet Things J. 2022, 9, 17912–17925. [Google Scholar] [CrossRef]
- Chen, Y.; Lakshminarayana, S.; Teng, F. Localization of coordinated cyber-physical attacks in power grids using moving target defense and deep learning. In Proceedings of the SmartGridComm, Singapore, 25–28 October 2022; pp. 387–392. [Google Scholar] [CrossRef]
- Liu, Y.; Ning, P.; Reiter, M.K. False data injection attacks against state estimation in electric power grids. In Proceedings of the ACM Conference of Computer and Communications Security (CCS), Chicago, IL, USA, 9–13 November 2009; pp. 21–32. [Google Scholar]
- Deng, R.; Xiao, G.; Lu, R. Defending against false data injection attacks on power system state estimation. IEEE Trans. Ind. Inform. 2015, 13, 198–207. [Google Scholar] [CrossRef]
- Giani, A.; Bitar, E.; Garcia, M.; McQueen, M.; Khargonekar, P.; Poolla, K. Smart grid data integrity attacks. IEEE Trans. Smart Grid 2013, 4, 1244–1253. [Google Scholar] [CrossRef]
- Zhao, J.; Mili, L.; Wang, M. A generalized false data injection attacks against power system nonlinear state estimator and countermeasures. IEEE Trans. Power Syst. 2018, 33, 4868–4877. [Google Scholar] [CrossRef]
- Lin, H.; Kalbarczyk, Z.T.; Iyer, R.K. RAINCOAT: Randomization of network communication in power grid cyber infrastructure to mislead attackers. IEEE Trans. Smart Grid 2018, 10, 4893–4906. [Google Scholar] [CrossRef]
- Yang, Q.; Li, D.; Yu, W.; Liu, Y.; An, D.; Yang, X.; Lin, J. Toward data integrity attacks against optimal power flow in smart grid. IEEE Internet Things J. 2017, 4, 1726–1738. [Google Scholar] [CrossRef]
- Zhou, Y.; Cheng, G.; Zhao, Y.; Chen, Z.; Jiang, S. Toward proactive and efficient DDoS mitigation in IIoT systems: A moving target defense approach. IEEE Trans. Ind. Inform. 2021, 18, 2734–2744. [Google Scholar] [CrossRef]
- Li, B.; Xiao, G.; Lu, R.; Deng, R.; Bao, H. On feasibility and limitations of detecting false data injection attacks on power grid state estimation using D-FACTS devices. IEEE Trans. Ind. Inform. 2019, 16, 854–864. [Google Scholar] [CrossRef]
- Ozay, M.; Esnaola, I.; Vural, F.T.Y.; Kulkarni, S.R.; Poor, H.V. Machine learning methods for attack detection in the smart grid. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 1773–1785. [Google Scholar] [CrossRef] [PubMed] [Green Version]

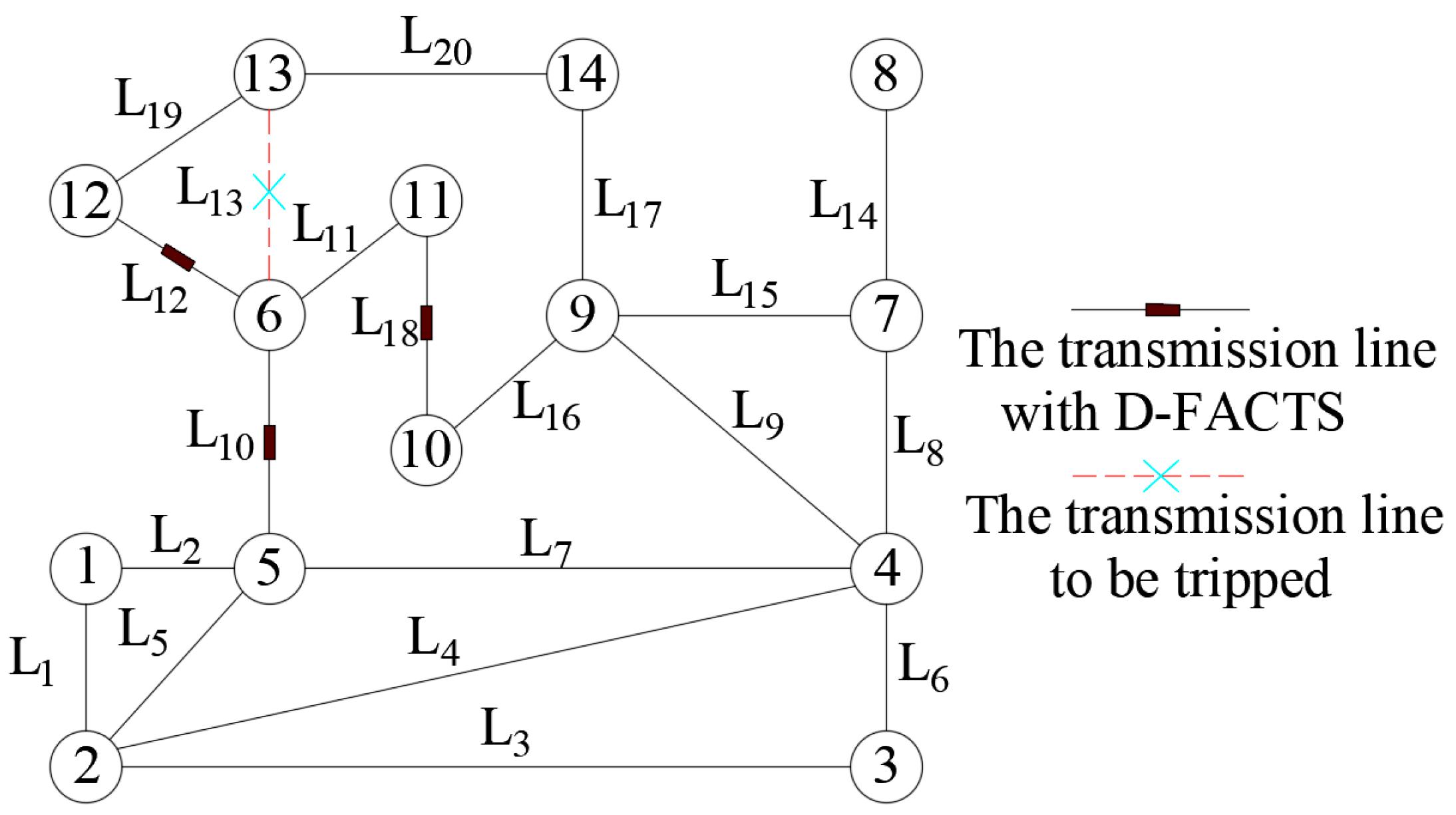






| Alternate Paths | All Transmission Lines of an Alternate Path |
|---|---|
| Simulation Strategy Index | Specific Measures | Systems Being Applied | Simulation Strategy Index | Specific Measures | Systems Being Applied |
|---|---|---|---|---|---|
| 1 | The disconnected line is ; | IEEE 14-bus system | 2 | The disconnected line is ; | IEEE 30-bus system |
| 3 | The disconnected line is ; | IEEE 118-bus system | 4 | The disconnected line is ; the original sensor measurement expression is used. | IEEE 14-bus system |
| 5 | The disconnected line is ; the modified sensor measurement expression is used. | IEEE 14-bus system | 6 | The disconnected line is ; ; the original sensor measurement expression is used. | IEEE 30-bus system |
| 7 | The disconnected line is ; the modified sensor measurement expression is used. | IEEE 30-bus system | 8 | The disconnected line is ; the original sensor measurement expression is used. | IEEE 118-bus system |
| 9 | The disconnected line is ; the modified sensor measurement expression is used. | IEEE 118-bus system | 10 | The disconnected line is ; the original sensor measurement expression is used. | IEEE 14-bus system |
| 11 | The disconnected line is ; the modified sensor measurement expression is used. | IEEE 14-bus system | 12 | The disconnected line is ; the original sensor measurement expression is used. | IEEE 30-bus system |
| 13 | The disconnected line is ; the modified sensor measurement expression is used. | IEEE 30-bus system | 14 | The disconnected line is ; the original sensor measurement expression is used. | IEEE 118-bus system |
| 15 | The disconnected line is ; the modified sensor measurement expression is used. | IEEE 118-bus system | 16 | The disconnected line is , the unique non-zero term’s component index in is 5 or 12. | IEEE 14-bus system |
| 17 | The disconnected line is , the unique non-zero term’s component index in belongs to and . | IEEE 14-bus system | 18 | The disconnected line is , the unique non-zero term’s component index in is 13 or 14. | IEEE 30-bus system |
| 19 | The disconnected line is , the unique non-zero term’s component index in belongs to and . | IEEE 30-bus system | 20 | The disconnected line is , ; the unique non-zero term’s component index in is 24 or 71. | IEEE 118-bus system |
| 21 | The disconnected line is , ; the unique non-zero term’s component index in belongs to and | IEEE 118-bus system | 22 | The disconnected line is , the unique non-zero term’s component index in is 5 or 12 and the value of the unique non-zero term monotonically from 0 to −0.2. | IEEE 14-bus system |
| 23 | The disconnected line is , the unique non-zero term’s component index in is 13 or 14, and the value of the unique non-zero term ranges monotonically from 0 to −0.2. | IEEE 30-bus system | 24 | The disconnected line is , , the unique non-zero term’s component index in is 24 or 71, and the value of the unique non-zero term ranges monotonically from 0 to −0.2. | IEEE 118-bus system |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, J.; Li, Q. Moving Target Defense for Detecting Coordinated Cyber-Physical Attacks on Power Grids via a Modified Sensor Measurement Expression. Electronics 2023, 12, 1679. https://doi.org/10.3390/electronics12071679
Yu J, Li Q. Moving Target Defense for Detecting Coordinated Cyber-Physical Attacks on Power Grids via a Modified Sensor Measurement Expression. Electronics. 2023; 12(7):1679. https://doi.org/10.3390/electronics12071679
Chicago/Turabian StyleYu, Jian, and Qiang Li. 2023. "Moving Target Defense for Detecting Coordinated Cyber-Physical Attacks on Power Grids via a Modified Sensor Measurement Expression" Electronics 12, no. 7: 1679. https://doi.org/10.3390/electronics12071679
APA StyleYu, J., & Li, Q. (2023). Moving Target Defense for Detecting Coordinated Cyber-Physical Attacks on Power Grids via a Modified Sensor Measurement Expression. Electronics, 12(7), 1679. https://doi.org/10.3390/electronics12071679






